1. Introduction
Nested sampling is a computational technique for Bayesian inference developed by [
1]. Whereas previous statistical sampling algorithms were primarily designed to sample the posterior, the nested sampling algorithm focuses on computing the evidence by estimating how the likelihood function relates to the prior. As discussed in [
2], Bayesian inference consists of parameter estimation and model comparison. In Bayesian parameter estimation, the model parameters
for a given model
and data
d are inferred via Bayes’ theorem,
Here,
is the posterior probability for the model parameters
given the data
d. The likelihood
describes the measurement process, which generated the data
d, and the prior
encodes our prior knowledge of the parameters within the given model. The normalization of the posterior,
is called the evidence and is the focus of this study. In Bayesian parameter estimation, it is common to work with not normalized posteriors. Thus, in this scenario, the computation of the evidence is less critical. In contrast, when comparing different Bayesian models, estimating the evidence for different models is very important. In this case, the aim is to find the most probable model
given the data,
Assuming a uniform prior for all arbitrary models
, this turns out to be equivalent to choosing the model with the highest evidence.
In nested sampling, the possibly multidimensional integral of the posterior in Equation (
2) is transformed into a one-dimensional integral by directly using the prior mass
X. In particular, by transforming the problem into a series of nested spaces, nested sampling provides an elegant way to compute the evidence. The algorithm starts by drawing
N samples from the prior, called the live points. For each of these points, the likelihood is calculated and the live point with the lowest likelihood is removed from the set of live points and added to another set, called the dead points. A new live point is then sampled that has a higher likelihood value than the last added dead point. This type of sampling is commonly referred to as likelihood-restricted sampling. However, the specific methods associated with likelihood-restricted sampling are not discussed further in this paper. As a consequence of the procedure, the prior volume shrinks from one to zero, contracting around the peak of the posterior. The prior mass X contained in the parameter space volume with likelihood values larger than
L can be computed by
Thus, Equation (
2) simplifies to a one-dimensional integral,
where
is the inverse of Equation (
4). Accordingly, this integral can be approximated by the weighted sum over all
m dead points
As proposed in [
1], we calculate the weights via
assuming
and
. Adding dead points to their set and adjusting the evidence accordingly continues until the remaining live points occupy a tiny prior volume that would contribute little to the weighted sum in Equation (
6).
For the calculation in Equation (
6) not only the known live and dead contours of the likelihood are needed but also the corresponding prior volumes encoded in
, which are not precisely known. According to [
1] there are two different approaches to approximate the prior volumes
, a stochastic scheme and a deterministic scheme. In the stochastic scheme the change of volume due to each removed shell
i is a stochastic process characterised by a Beta distributed random variable
,
where we assume a constant number of live points
N. Approaches with a varying number of live points were i.a. introduced in dynamic nested sampling by [
3,
4] and extend beyond the boundaries of this research until the present moment. This probabilistic description of the prior volume evolution allows to draw several samples of prior volumes
X, according to the likelihood values
L, and to thereby get uncertainty estimates on the evidence calculation (Equation (
6)). In the deterministic scheme the logarithmic prior volume is estimated via,
at the
ith iteration. This estimate is derived from the fact that the expectation value of the logarithmic volume changes is
. However, this estimate does not take the uncertainties in the evidence calculation [
5] into account and differs from unbiased approaches introduced and analysed in [
6,
7,
8]. In any case, the imprecise knowledge of the prior volume introduces probing noise that can potentially hinder the accurate calculation of the evidence. In order to improve the accuracy of the posterior integration, we aim to reconstruct the likelihood-prior-volume function given certain a priori assumptions on the function itself using Bayesian inference. Here, we introduce a prior and likelihood model for the reconstruction of the likelihood-prior-volume function, which we will call the reconstruction prior and the reconstruction likelihood to avoid confusion with likelihood contour and prior volume information obtained from nested sampling.
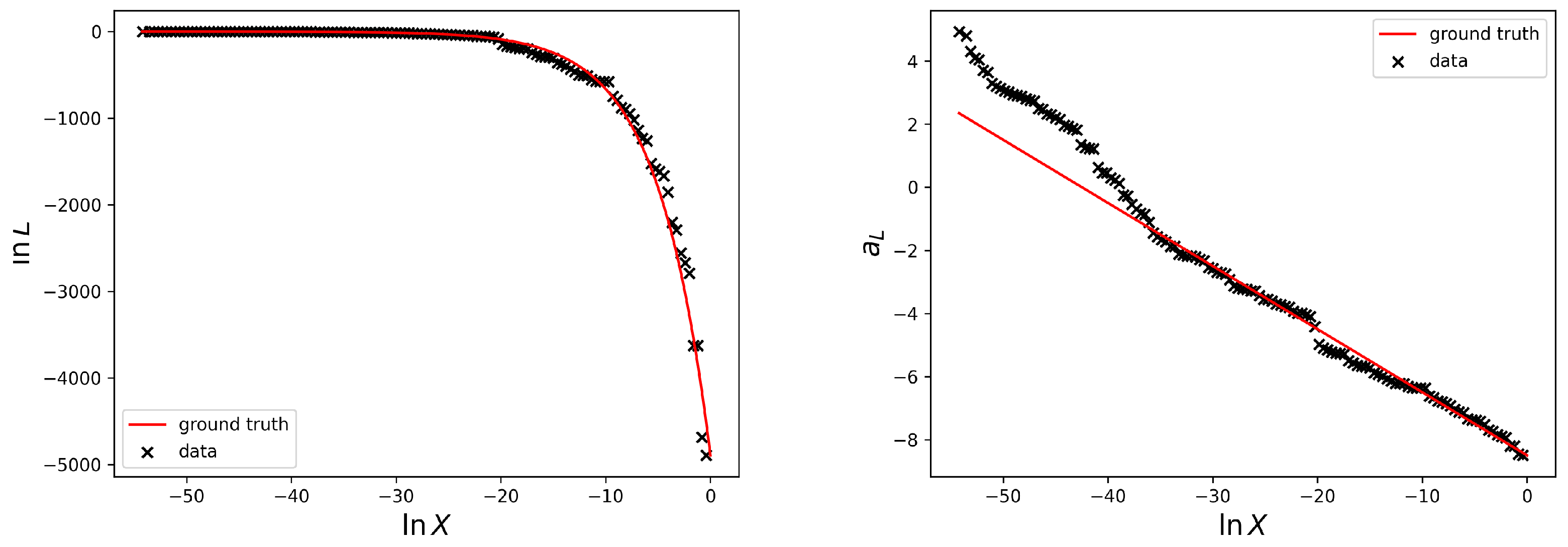
The left side of
Figure 1 illustrates the nested sampling likelihood dead contours generated by the software package anesthetic [
9] for the simple Gaussian example discussed in
Section 2 and two live points (N = 2) as a function of prior volume. In the following, we call the likelihood values of the dead points the likelihood data
and the prior volume, approximated by Equation (
8), the prior volume data
. Additionally, the analytical solution of the likelihood-prior-volume function, which we call the ground truth, is plotted.
In accordance with the here considered example, we assume the likelihood-prior-volume function to be smooth for most real-world applications of nested sampling. In this study, we propose an approach that incorporates this assumption of a-priori-smoothness and enforces monotonicity. In particular, we use Information Field Theory (IFT) [
10] as a versatile mathematical tool to reconstruct a continuous likelihood-prior-volume function from a discrete dataset of likelihood contours and to impose the prior knowledge on the function.
As noted in [
11], the time complexity of the nested sampling algorithm depends on several factors. First, the time complexity depends on the information gain of the posterior over the prior, which is equal to the shrinkage of the prior required to reach the bulk of the posterior. This is described mathematically by the Kullback-Leibler divergence (KL) [
12],
Second, the time complexity increases with the number of live points
N, which defines the shrinkage per iteration. Furthermore, the time for evaluating the likelihood
,
, and the time for sampling a new live point in the likelihood restricted volume,
, contribute to the time complexity. Accordingly, in [
13] the time complexity of the nested sampling algorithm
T and the error
have been characterised via,
Upon examining the error,
, it becomes evident that reducing the error by increasing the number of live points leads to significantly longer execution times. Accordingly, by inferring the likelihood-prior-volume function, we aim to reduce the error in the log-evidence for a given
and a fixed number of live points,
N, avoiding a significant increase in time complexity.
The rest of the paper is structured as follows. In
Section 2, the description of the reconstruction prior of the likelihood-prior-volume curve is discussed. The model for the reconstruction likelihood and the inference of the likelihood-prior-volume function and the prior volumes using IFT is described in
Section 3. The corresponding results for a Gaussian example and the impact on the evidence calculation are shown in
Section 4. And eventually, the conclusion and outlook for future work are given in
Section 5.
2. The Reconstruction Prior Model for the Likelihood-Prior-Volume Function
A priori we assume that the likelihood-prior-volume function is smooth and monotonically decreasing. This is achieved by representing the negative rate of change of the logarithmic prior volume,
, with a monotonic function of the likelihood
as a log-normal process,
In the words of IFT, we model the one-dimensional field
, which assigns to each logarithmic prior volume a value, as a Gaussian process with
. Thereby, we do not assume a fixed power spectrum for the Gaussian process, but reconstruct it simultaneously with
itself. An overview of this Gaussian process model is given in
Appendix A. The details can be found in [
14].
In the most relevant volume for the evidence, the peak region of the posterior is expected to be similar to a Gaussian in a first order approximation. Therefore, the function
is chosen such that
is a constant for the Gaussian case. Deviations from the Gaussian are reflected in deviations of
from the constant. Accordingly, we define,
with
being the maximal likelihood. We consider the simple Gaussian example proposed by [
1],
where
D is the dimension and
is the standard deviation. We find that the function
, defined in Equation (
13), becomes linear in this case,
Figure 1 illustrates the data and the ground truth on log-log-scale on the left and the linear relation
on the right. According to the log-normal process defined in Equation (
12), we define the function
, for arbitrary likelihoods, which is able to account for deviations from the Gaussian case,
By inverting Equation (
13) we then get the desired likelihood-prior-volume function. The logarithmic prior volume values given the likelihood contours are obtained by inversion of Equation (
16). In
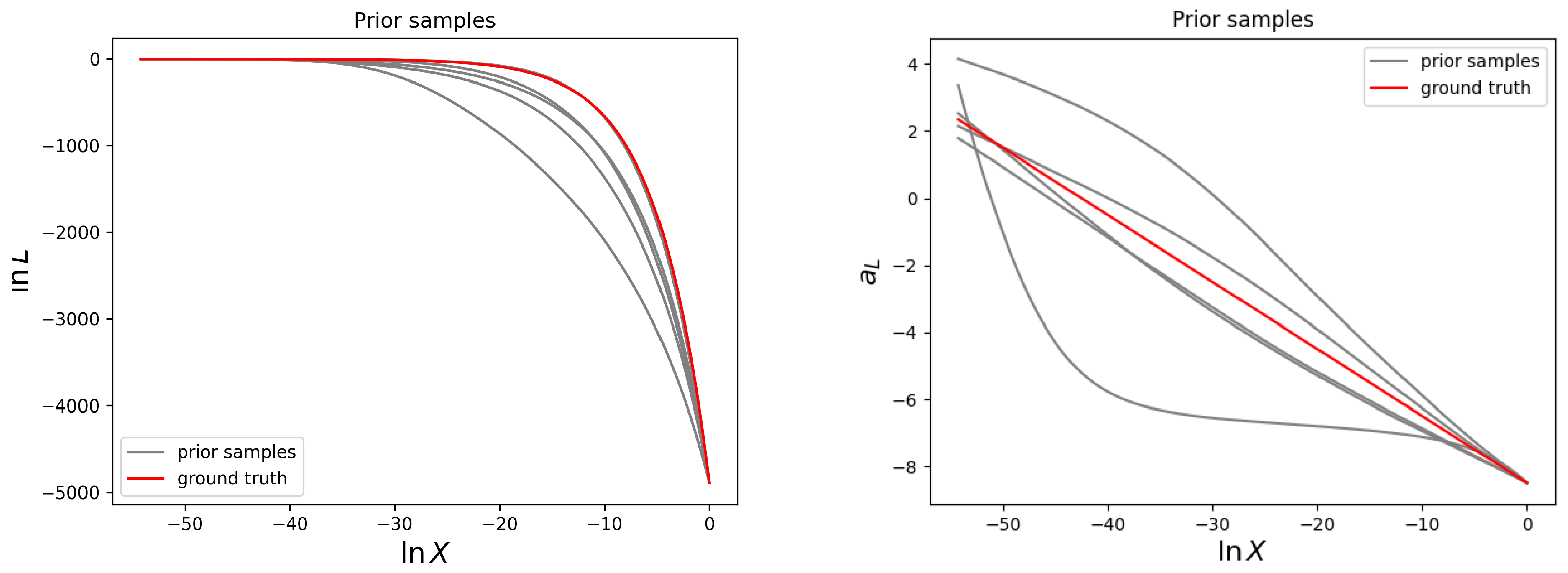
Figure 2 several prior samples given the model for the reconstruction prior according to Equation (
16) are shown.
However, often the maximum log-likelihood,
, is not known. In [
15], the calculation of the maximum Shannon entropy
is given. Using this approach, we can calculate the logarithmic maximum likelihood
and thus calculate
for unknown likelihoods.
Hence, based on the likelihood contours obtained from the nested sampling run, we calculate the data based evidence,
, using the approximated prior volumes according to Equation (
8). This allows us to obtain an estimate of the maximum log-likelihood,
, of the model for reparametrisation,
4. Results
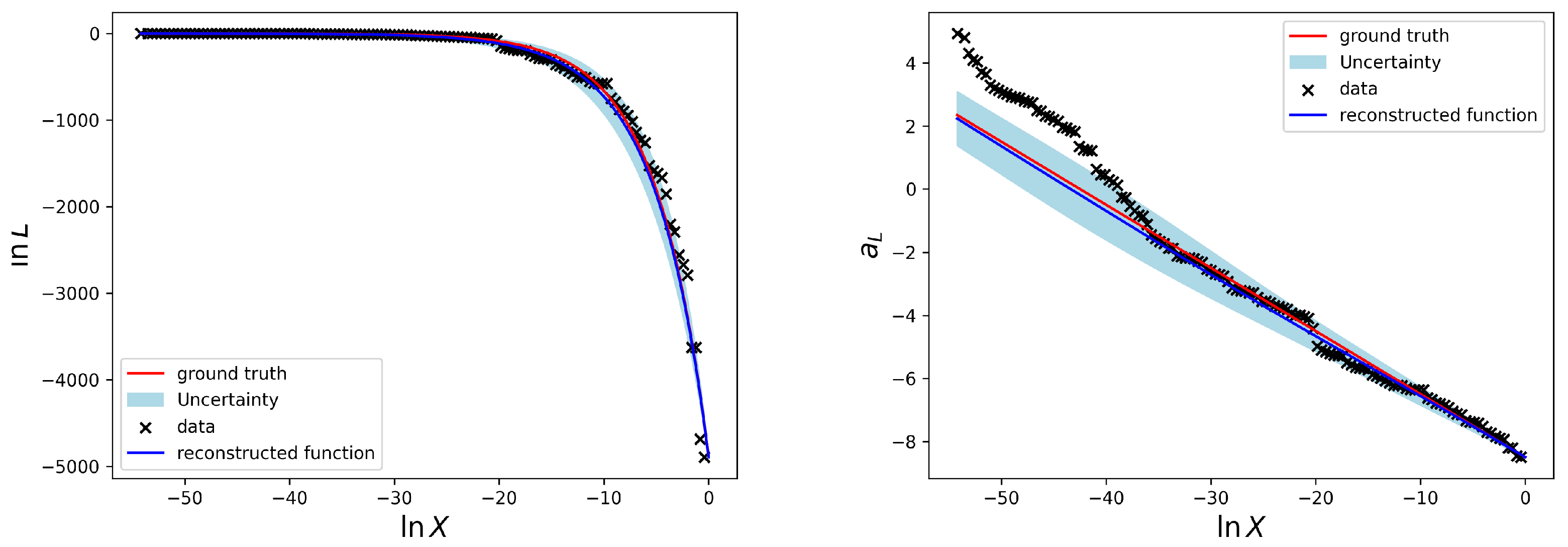
To test the presented method we perform a reconstruction for the simple Gaussian example discussed in
Section 2 and introduced in
Figure 1. The according results for the likelihood-prior-volume function are shown in
Figure 3.
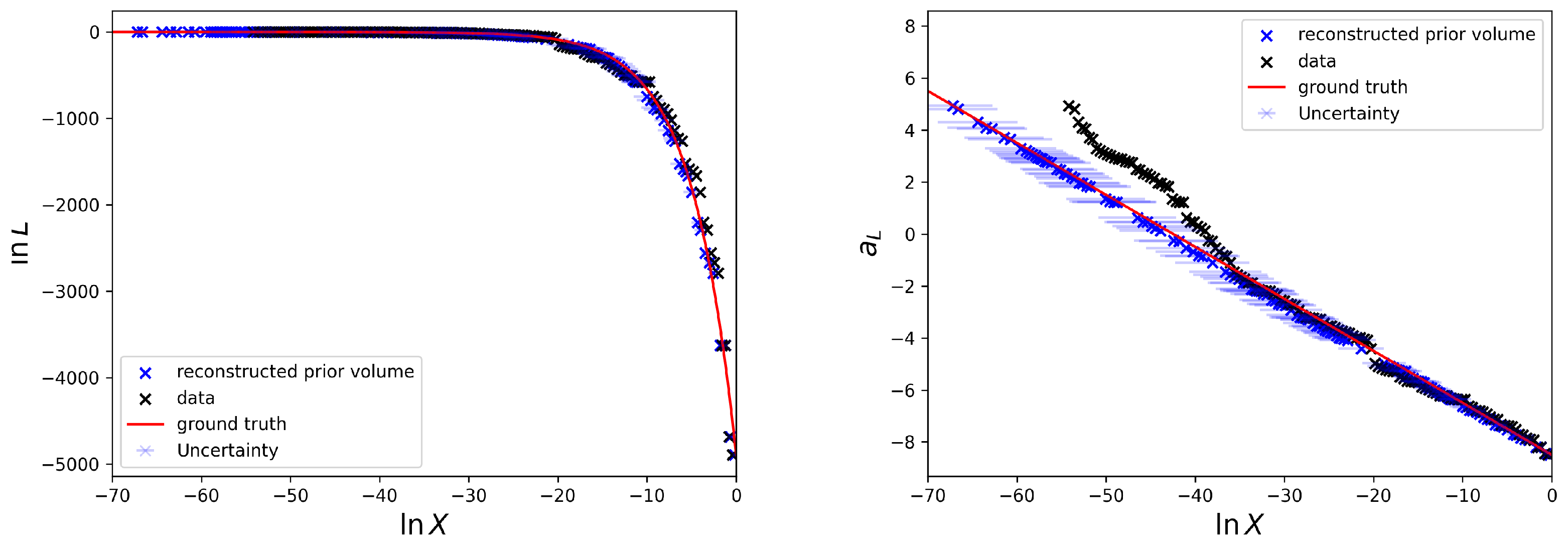
Moreover, the posterior estimates of the logarithmic prior volumes to the according likelihood data
are shown in
Figure 4.
Since the main goal of nested sampling is to compute the evidence, we want to quantify the impact of the proposed method on the evidence calculation. To do this, we use
posterior samples for the prior volumes
and calculate the evidence given the likelihood contours
for each of these samples according to Equation (
6),
Similarly, we generate by means of anesthetic [
9]
samples of the prior volume via the probabilistic nested sampling approach described in Equation (
7). Also for these samples we calculate the evidence according to Equation (
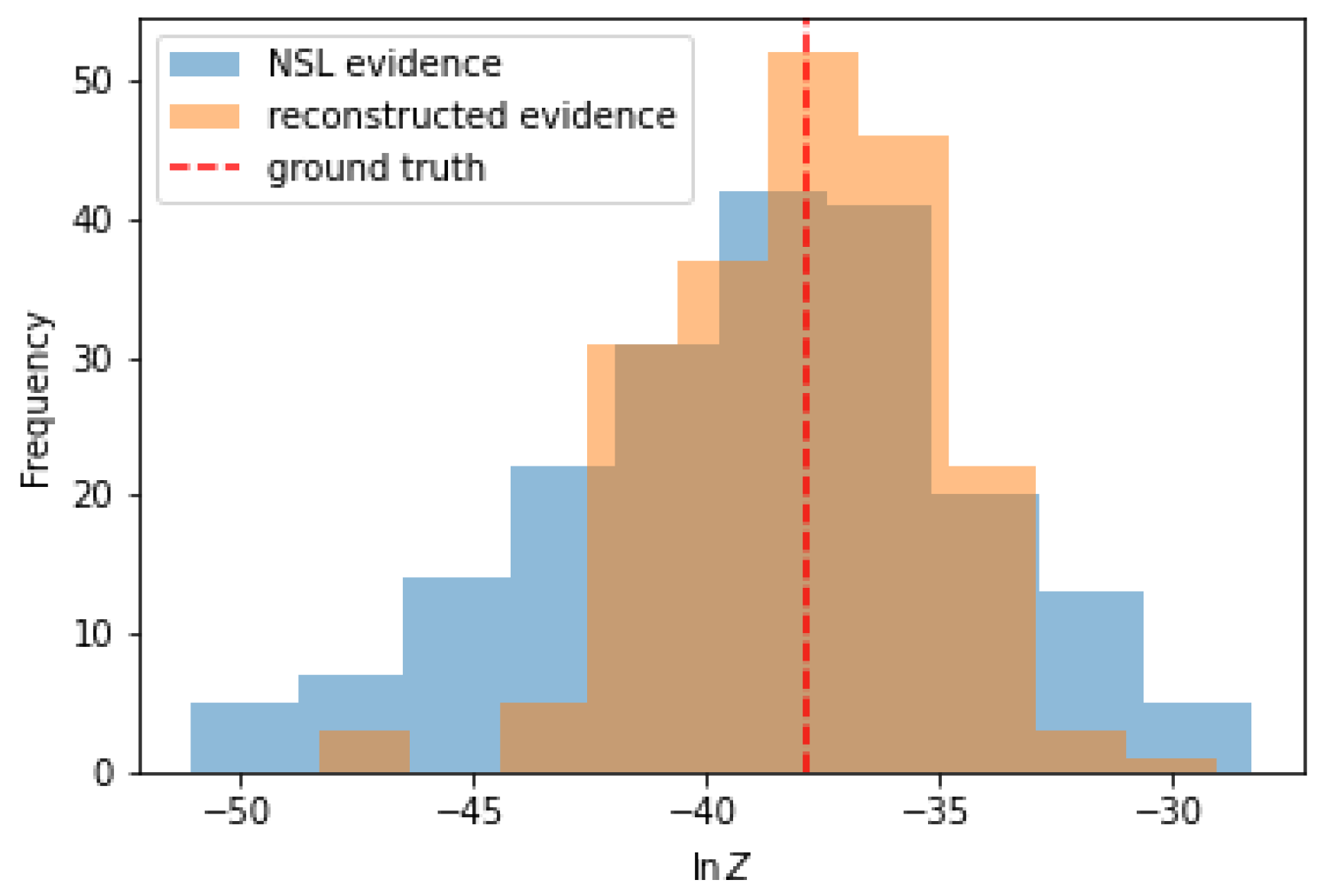
24). A comparison of the histograms of evidences for both sample sets (classical nested sampling and reconstructed prior volumes) is shown in
Figure 5.
From the comparison of the histograms, one can already see that the standard deviation for the posterior sample evidences for the reconstructed prior volumes got smaller. This is also mirrored as soon as we look at numbers: The ground truth logarithmic evidence for this Gaussian case is . The result for the evidence for the classical nested sampling approach given is . And finally, the result for the evidence inferred with the here presented approach from the likelihood contours assuming smoothness and enforcing monotonicity is .