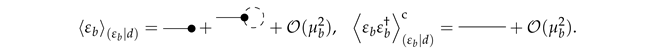2. Information Field Theory
In many areas of science, technology, and economics, the task of interpreting incomplete, noisy, and finite datasets arises [
12,
13]. Especially, if the quantity of interest is a field, there is an infinite number of possible signal field realizations that meet the constraints of a finite number of measurements. For such problems, which are called field inference problems, IFT was developed.
A physical field
is a function that assigns a value to each point in time and
u-dimensional position space. Here, the space and time will be handled in same the manner as in [
14,
15] and are denoted by the space-time location
,
. For definiteness, we let the time axis start at
. As the field
has an infinite number of degrees of freedom, the integration is represented by path integrals over the integration measure
[
16]. In the following, these space-time coordinate-dependent fields are denoted as abstract vectors in Hilbert space, such that the scalar product can be written as
, where
denotes the complex conjugate.
In order to get to know a field
, one has to measure it. Bayes’ theorem states how to update any existing knowledge given a finite number of measurement constraints. In this probabilistic logic, knowledge states are described by probability distributions. Accordingly, the prior knowledge
is updated given a data vector
d to the posterior probability [
17]
To construct the posterior, we need to have the prior
and the likelihood
. However, the evidence,
is the normalization of the posterior and can be calculated from the prior and the likelihood. The prior probability of the signal,
, specifies the knowledge on the signal before any measurement, whereas the likelihood describes the measurement process. Any measurement process can be described by a response of an instrument
R, which converts some discrete dataset to a continuous signal, and some additive noise
n,
. The statistics of the noise then determine the likelihood. Particularly, if we assume Gaussian noise with known covariance
N, we get
Here, we can also define initial conditions via initial data . In this case, the response is defined as and the noise vanishes, . Thus, the initial data likelihood is represented by and can be combined with any data on the later evolution, , via , with .
For the reconstruction, particularly the cumulants of first and second order are of interest, as they describe the mean,
, and the uncertainty dispersion,
. These posterior-connected correlation functions, or cumulants can be obtained via the moment-generating partition function
,
where
is the so-called information Hamiltonian.
3. Dynamical Field Inference
In DFI, a signal, for which we have prior information on the dynamics of the system, is inferred. In particular, we consider a signal which obeys a stochastic differential equation
The first part of the stochastic differential equation,
, describes the deterministic dynamics of the field and the excitation field,
, turns this deterministic evolution into a stochastic one. Here, the signal field,
, is defined for all
, while
and
live on
. Therefore, Equation (
4) makes only statements about fields on
. Equation (
4) can be summarized by an operator
,
, which contains all the time and space derivatives of the stochastic differential equation up to order
n in space
where
and
. In order to define the prior information given by the stochastic differential equation, we assume Gaussian statistics for the excitation field,
, with known covariance
. We define the combined vector of fields
that determines the dynamics with
and extend the operator
by the initial conditions to
with
such that
. Assuming that there is a unique solution to the stochastic differential equation in Equation (
5), the prior probability can be calculated via
as follows:
where
.
From this, we see that the prior contains a signal-dependent term from the excitation statistics as well as a functional determinant, the Jacobian, . For nonlinear dynamics, i.e., , where L is some linear operator, the Jacobian becomes field-dependent and the term becomes highly non-Gaussian. To represent these terms conveniently, we introduce Fadeev–Popov ghost fields in the following.
The Jacobian in DFI can be represented via an integral over independent Grassmann fields,
and
, which are scalar fields that obey the Pauli principle,
For the representation of the term
, we step back to the initial formulation including the excitation field and introduce a Lagrange multiplier
for the substitution of the
-function,
This leads to the prior,
where
is the information on the initial conditions. In the end, if we integrate over the excitation
, we can write the data-free partition function via an integral over the tuple of fields
,
Here,
is the information Hamiltonian for the field tuple
, given some initial position
, defined by Equation (
9),
The dynamic information, , contains the time derivatives of the fermionic and bosonic fields, whereas the meaning of the static information shall be analyzed in the following section.
4. Ghost Fields in Dynamical Field Inference
In the previous section, we introduced auxiliary fields, to substitute the Jacobian and the
-function. In this section, we want to analyze the meaning of those fermionic and bosonic fields and the corresponding terms in the information Hamiltonian. The auxiliary fields are called ghost fields, as they are only part of the formalism, but cannot be measured. It can be shown that the corresponding information Hamiltonian is only well defined, if these ghost fields do not exist at the initial time
[
18].
In case of a white excitation field, the partition function of DFI for a bosonic and fermionic field can be derived via the Markov property, i.e.,
where
is the field at the initial time
, while there is no
. By assigning field operators to the fermionic and bosonic fields,
and
, as well as their momenta,
and
, respectively, this partition function can be rewritten in terms of the generalized Fokker–Planck operator of the states
according to [
16,
19,
20,
21],
. At this stage, these are just formal definitions, with time-localized states
and not time-localized states
. The transfer operator
describes the mapping between states at time
and
. Here,
is not to be confused with the information Hamiltonian
. The precise relation of these will be established in the following. Taking the limit
and
, we can make the definition of the function
and with this in mind and the definition of the field tuple
, the partition function can be rewritten to
In the end, the partition functions in Equations (
10) and (
11) need to be the same to guarantee the consistency of the theory. This permits the identifications,
and
. To sum up, it was shown that the auxiliary fields
and
are simply the momenta of the fields
and
, whereas the time evolution is governed by the static information
. If we introduce the functional
, for some
X, we can bring the static information in a
Q-exact form. This means that
only depends on the introduced functional
, for specific
,
The important finding is that the time evolution is governed by a Q-exact static information, i.e.,
. In [
9], it was shown that the defined functional
is the path-integral version of the exterior derivative
in the exterior algebra. Thus, it is demonstrated that the time-evolution is
-exact and it commutes with the exterior derivative, as it is nilpotent. The exterior derivative as the operator representative of
interchanges fermions and bosons. As a physical system is symmetric with regard to an operator, if it commutes with the time-evolution, the conclusion is made that the field dynamics is supersymmetric. The supersymmetry of a system can be broken spontaneously, which coincides with the appearance of chaos as derived in [
8,
9,
10,
11]. The corresponding separation of infinitesimal close trajectories in a dynamical system is then characterized by the Lyapunov exponents. In the following, we investigate the impact of measurements on the supersymmetry of the field knowledge encoded in the partition function. Furthermore, it is intuitively clear that the occurrence of chaos should reduce the predictability of the system. To show the exact impact of chaos on the predictability of a system, we will analyze two instructive scenarios.
5. SUSY and Measurements
First, we want to make some abstract considerations before we look at linear and nonlinear examples. Taking in account
Section 4, we can rewrite the moment-generating function in Equation (
3),
From Equation (
12), we see that the combined information,
, representing the knowledge from measurement data
d and the dynamics consists of several parts. The first part,
, describes the dynamics of the field
and that of the ghost fields
and
for times after the initial moment. The evolution of the dynamics can be described by a
Q-exact term, meaning that supersymmetry is conserved for non-initial times
. The middle term,
, describes the knowledge on the initial conditions instead. The last term,
, contains the knowledge gain by the measurement. Thus, if the measurement addresses non-initial times, the information gets non-Q-exact by the inclusion of the measurement information. By the measurement, “external forces” need to be introduced into the system, which are not stationary nor necessarily Gaussian, which guide the systems evolution through the constraints set by the measurement. Precisely, the posterior knowledge on the excitation is described by
which has an explicitly time-dependent mean and correlation structure in
.
Let us consider idealized linear dynamics to illustrate the impact of chaos on the predictability of a system. As in the previous sections, we assume
to be initially
at
and to obey Equation (
4) afterwards with
, i.e.,
. We define the classical field,
, which follows excitation-free dynamics
and a deviation,
, between the actual signal,
, and the classical field,
. Here, we assume that only a short period after
is considered and perform for the dynamics a first-order expansion in the deviation field, with the initial deviation
,
where we can assume that a time dependence in
A can be ignored for short periods after
. Further, we assume that
A can be fully expressed in terms of a set of orthonormal eigenmodes,
with
, where the
denotes the adjoint with respect to the spatial coordinates only. In the linear case, the real parts of the eigenvalues of the operator
A are the Lyapunov exponents. We imagine a system measurement at time
that probes perfectly a normalized eigendirection
b of
A, such that we get noiseless data according to
with
. The eigenmode
b then fulfills
, which leads to a stable mode if
and an unstable mode if
. In the linear case, we get a Gaussian prior for the deviation, as
can be represented by a linear operator,
. For some Gaussian measurement noise
n with a vanishing covariance
N, we get an information which contains no field interactions:
where the information source
, the information propagator
, and
or
, were introduced. The latter both contain all the terms of the information that are constant in the deviation
. The information can be expressed in terms of the field
by completing the square in Equation (16), which is also known as the generalized Wiener filter solution [
22]. As all cumulants of an order higher than
vanish, the posterior distribution can be represented by a Gaussian with mean
m and uncertainty covariance
D,
. The prior dispersion in the eigenbasis can be calculated to
where
is the a priori temporal correlation function of a field eigenmode
a. Expressing the mean and the posterior uncertainty in the eigenbasis of A then leads to
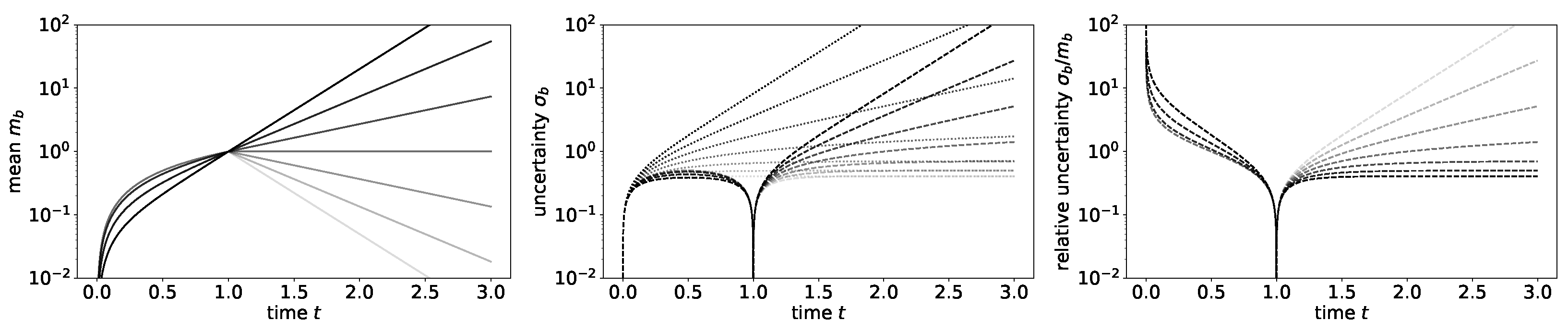
Figure 1 shows the prior and posterior mean and uncertainty for three different Lyapunov exponents
and a perfect measurement at
. As we can see from Equation (20), the correlation between different modes
vanishes, and therefore, any mode
behaves like a prior mode shown in gray in
Figure 1. Moreover, the propagator for the measured mode
b is in general non-zero, but we can show that it vanishes for times, which are separated by the measurement, i.e.,
for
. In other words, the measurement introduces a Markov blanket. This Markov blanket separates the periods before and after the measurement from each other.
The impact of the Lyapunov exponents on the predictability of the system is clearly visible in
Figure 1. The illustration shows that Lyapunov exponents which are greater than one lead to diverging uncertainties. In other words, chaos makes the inference more difficult on an absolute scale.
In
Figure 2, we can see that the uncertainty grows faster for a larger Lyapunov exponent. Moreover, the relative uncertainty grows slower with increasing Lyapunov exponents, which mirrors the memory effect of a chaotic system. Thus, small initial disturbances can be remembered for long times.
In the case of nonlinear dynamics, the posterior knowledge becomes non-Gaussian, or in other words, the theory becomes interactive, i.e., it does not only incorporate the propagator and the source term but also interaction terms between more than two fields. At first, we will consider the case
and extend it to the next higher order in
,
This leads to an information Hamiltonian that contains a free and an interaction part,
,
The free information Hamiltonian
defines the Wiener process field inference problem we addressed before and has the classical field as well as the bosonic and fermionic propagators and interactions between the fields for
. It can be shown that all first-order diagrams with bosonic three-vertex are zero for
[
18]. Thus, the posterior mean and uncertainty dispersion for
only contain corrections due to the fermion loop,
Now, we consider the case
, i.e.,
, such that
The only changed vertex for this information Hamiltonian is the bosonic three-vertex, which does not vanish for
, leading to the following Feynman diagram representation of the posterior mean and uncertainty:
In any case, we can see that the fermionic loop correction appears independently of the eigenvalue of the measured mode
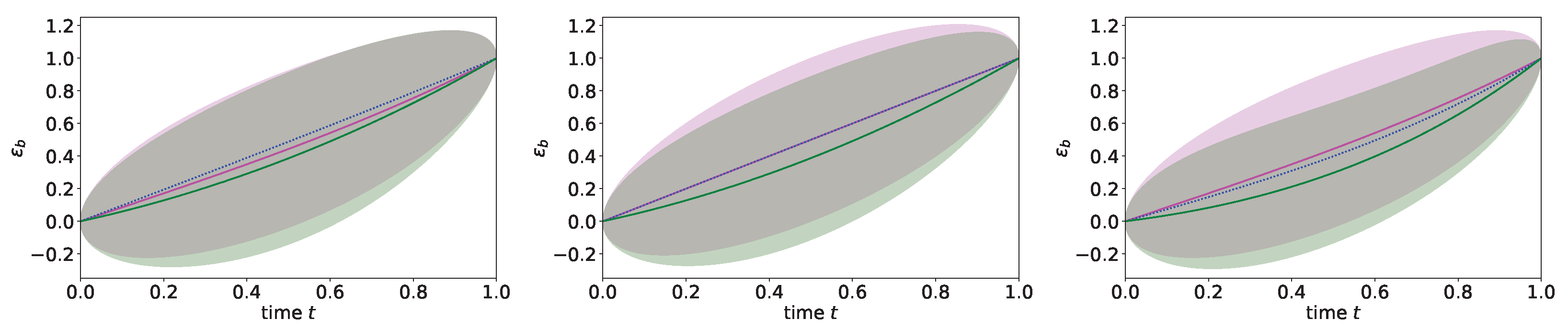
in the nonlinear case. Thus, taking into account the functional determinant, represented by the fermionic fields here, is important to arrive at the correct posterior values. The posterior values are calculated with the computer algebra system
SymPy [
23] and represented in
Figure 3.
Note that the a priori mean and uncertainty dispersion are both infinite for any time , as without the measurement, trajectories reaching positive infinity within finite times are not excluded from the ensemble of permitted possibilities. For times , the posterior mean should stay finite as well as its uncertainty. The reason is that any diverging trajectory in this region is excluded by the measurement, as the dynamics do not allow trajectories to return from infinity as this would require an infinite excitation. The figure shows that in all displayed cases (), the posterior trajectories avoid to get close to easily diverging regimes, and the more the dynamics is unstable, for larger values in , the more they avoid such regimes. Interestingly though, the posterior uncertainty of unstable systems with in the period before the measurement is reduced in comparison with the posterior uncertainty of the stable system. In the end, this is in accordance with the statement that chaotic systems are harder to predict, as for chaotic systems the trajectories diverge, and thus, the variety of trajectories that pass through the initial and the measurement condition is smaller. Thus, for a chaotic system, the measurement provides more information on the period before the measurement but less for the period after the measurement.