Chromatic Dispersion of Chalcogenide Glass-Based Photonic Crystal Fiber with Ultra-High Numerical Aperture ^†

Abstract

We report a graded index chalcogenide glass (As₂Se₃)-based photonic crystal fiber having a solid core. The proposed PCF has ultra-high numerical aperture value reaching up to 1.82 for the explored wavelength range of 1.8–10 μm in the mid-infrared region. The value of numerical aperture increases as the pitch increase from 0.92 to 0.96 to 1 micrometer, at a particular value of wavelength. With this high value of numerical aperture, a PCF is capable of gathering a high amount of light in its core. With negative dispersion reaching up to −2000 ps/km/nm at 4.8 µm, the fiber acts as a dispersion-compensating fiber, with confinement loss being close to zero for higher values of wavelength. The confinement loss of the designed PCF is also significantly less and it decreases as the wavelength increases. Also, the value of dispersion is significantly less due to the regular variation in the size of the holes in the transverse direction, as compared to the design when there is no gradation. The design has been optimized with an appropriate value of the perfectly matched layer to achieve the best results.

1. Introduction

Photonic crystal fibers have been gaining attention since 1995, when the first PCF was introduced. PCFs are holey structures where the air holes run through the entire length of the fiber. The flexibility to alter various properties of a PCF just by varying its geometrical properties like the hole size, pitch or number of rings makes it versatile and more convenient to use as compared to the normal optical fibers. In conventional optical fibers, light is guided by total internal reflection, but in photonic crystal fibers, light is guided either via an index-guided mechanism for a solid-core PCF or by a bandgap-guided feature for a hollow-core PCF. Within the periodic structure of the fiber, a break in periodicity at the center makes a localized core at the center, where the light guidance takes place. The guidance of light in a PCF is unique and the flexibility of designing PCFs is commendable [1,2]. There are generally two ways of light guidance in the PCF. One is through an index-guided mechanism, applicable for solid-core PCFs, and the other one is via a bandgap-guided mechanism for hollow-core PCFs. The periodic arrangement of the holes makes the effective cladding structure, and a break in this periodicity acts as the localized core of the fiber for our solid-core PCF, as shown in Figure 1a. This periodic arrangement can be of any shape—hexagonal, circular, square, and many more [3,4]. PCFs are a promising platform for exploring novel optical phenomena and developing advanced photonic devices with enhanced performance and functionality. Researchers are conducting intensive research on PCFs for making them applicable in all possible fields, and especially the arenas of importance, which are either not explored yet or are less explored. There are so many versatile properties of PCFs which make them widely applicable and beneficial, like chromatic dispersion, effective area, splice loss, birefringence, spot size, etc. The numerical aperture (NA) of a fiber is also one of the very interesting parameters as it concerns the light-gathering capacity of the fiber, and hence, the number of modes propagating through it.

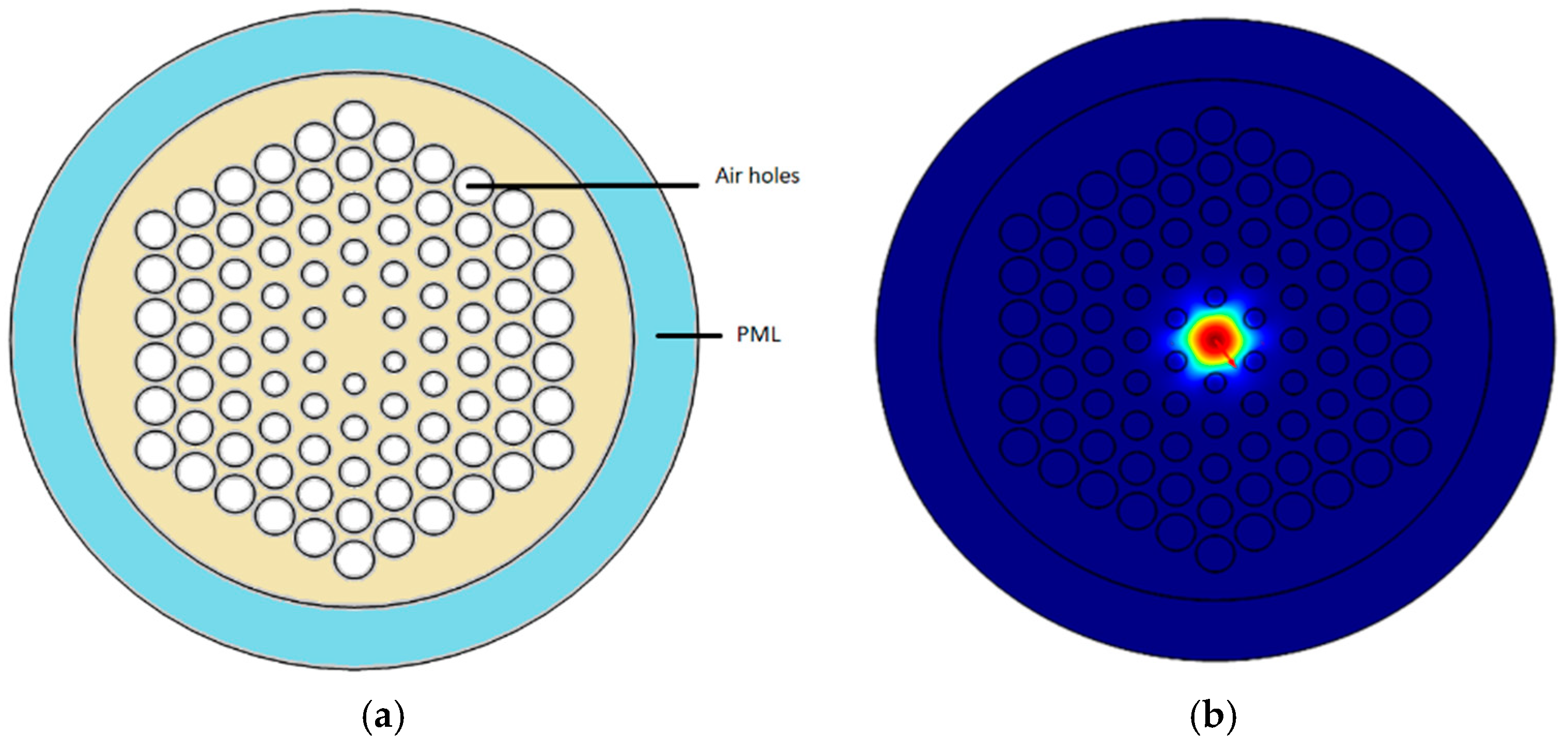
2. Proposed Design and Fabrication Techniques

As shown in Figure 1a, we propose a graded index photonic crystal fiber having a base made of chalcogenide glass, to be explored in the mid-infrared range of wavelength. The region surrounding the localized solid core at the center behaves like an effective cladding for the structure. Ours is a solid-core PCF, so light guidance takes place through an index-guided mechanism leading to the confinement of light in the core of the fiber, as depicted in Figure 1b. The proposed structure has five rings of air holes arranged hexagonally. The diameter of the respective layers of the air holes is ˄*0.35, ˄*0.55, ˄*0.75, ˄*0.95, ˄*1.15. The hole diameter decreases as we move from the outer boundary of the fiber towards its core—this variation makes the fiber appear as if there is a refractive index variation—to the light that propagates through the fiber, and hence, the structure is called the graded index PCF [5]. Pitch is the distance between any two holes from each other, also known as the lattice constant of the material. ˄ is the pitch of our fiber and is kept at 1 micrometer. Perfectly matched layer (PML) was optimized to achieve the best confinement of light alongwith the high numerical aperture value. The material used for PML is the same as the one used (As₂Se₃) for the base material of the PCF.

The base used for designing the PCF is As₂Se₃, a chalcogenide glass material. This material is preferred because of its high transparency and low loss in the infrared region. Glass is generally a very fragile material; hence, its fabrication needs great attention. Maintaining a controlled environment is also very important to avoid any contamination of the fiber. This can be achieved by having an environment with controlled temperature and moisture during the fiber-drawing process. The application of protective coating or cladding can further shield the fiber from various mechanical stress, like applying appropriate PML to the fiber. To avoid any mechanical stress to the fiber, the use of vapor deposition or a gas molding technique of fiber drawing is preferred [5,6].

The refractive index of the base material varies with wavelength and can be calculated using the Sellmeier equation given below [7]:

$$n(\lambda )=\sqrt{1+{\lambda }^2({\displaystyle \frac{{A_1}^2}{{\lambda }^2-{A_1}^2}}+{\displaystyle \frac{{A_2}^2}{{\lambda }^2-{19}^2}}+{\displaystyle \frac{{A_3}^2}{{\lambda }^2-4{A_1}^2}})}$$

(1)

where A₀ = 2.234921, A₁ = 0.24164, A₂ = 0.347441, and A₃ = 1.308575, and λ is the operating wavelength (µm).

3. Results and Discussion

3.1. Chromatic Dispersion

A pulse of light on propagation through the fiber broadens in time; this is called pulse dispersion. Chromatic dispersion in fibers gives an account of the broadening of a pulse and is one of the important characteristics of an optical fiber. For our designed PCF, chromatic dispersion can be calculated using the equation mentioned below [8]:

$$D\left(\lambda \right)=-{\displaystyle \frac{\lambda }{c}}{\displaystyle \frac{d^2{n}_{eff}(\lambda )}{d{\lambda }^2}}$$

(2)

where D is the chromatic dispersion in ps/km/nm and c is the speed of light, 3 × 10⁸ m/s. Figure 2 shows the negative dispersion of our proposed PCF to be as low as approx. −2000 ps/km/nm at 4.8 µm of wavelength. This negative dispersion is useful in compensating the dispersion in fibers, which occurs due to the broadening of pulse as light propagates through the fiber. Negative dispersion in fibers can compensate for the broadening of pulse for long distance, so that light can more effectively traverse the fiber with minimum or no loss. Figure 2 shows that at a wavelength of over 3.2 µm, the dispersion is entirely negative, reaching its maximum value at 4.8 µm. To achieve this value of dispersion, the fabrication of the PCF should be very precise to maintain a balance between achieving high negative dispersion and low loss. Also, the negative value of the dispersion can be further decreased by varying the pitch and the size of the air holes in the mid-infrared regime [9,10].

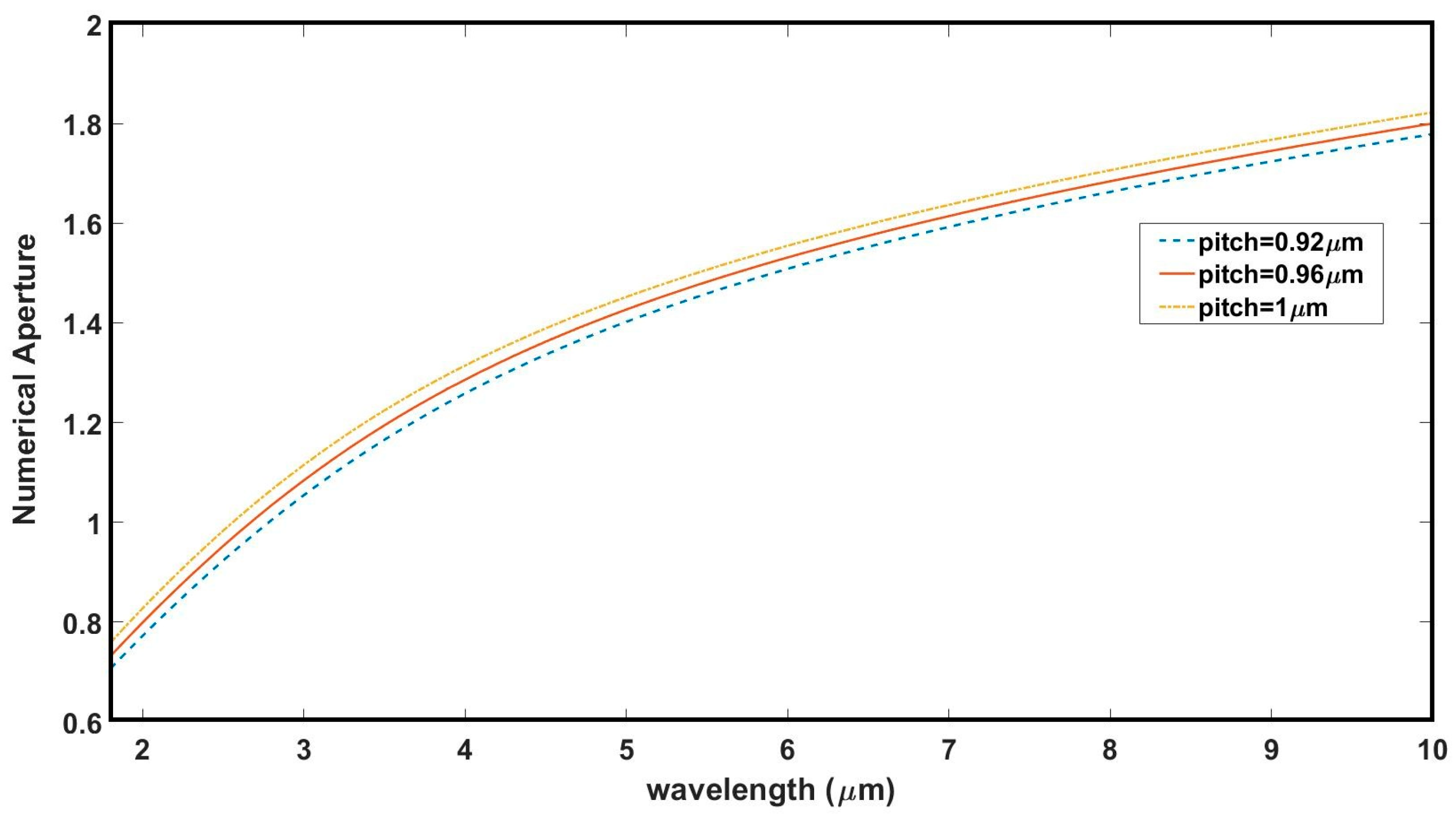
3.2. Numerical Aperture

Numerical aperture of a fiber gives an idea of the light-gathering capacity of the fiber. For the proposed graded index PCF, we obtained ultra-high numerical aperture value greater than 0.75 for a wavelength of 1.8–10 µm in mid-IR range. Numerical aperture was evaluated using the expression given by equation below [11]:

$$NumericalAperture(NA)=\sqrt{{n_c}^2-{n_{eff}}^2}$$

(3)

where n_c and n_eff are the refractive indices of the core (As₂Se₃) and the effective cladding, respectively.

Figure 3 shows that the value of NA can further be varied just by varying the pitch of the fiber. NA is greater for the higher values of the pitch. This ultra-high value of numerical aperture can be of great importance for a higher number of modes to be propagated through the fiber. A high NA allows a multi-mode fiber to support more modes by increasing the range of the incident angles for light that is to be guided. This can improve light coupling efficiency and can also lead to greater intermodal dispersion and intermodal coupling. Having an increased number of modes can lead to energy exchange between the modes, and this may lead to low signal integrity at high-speed communication systems, but this has been taken into account here by employing the gradation in the proposed optical fiber. Also, the mode filtering technique can be further employed to address this challenge.

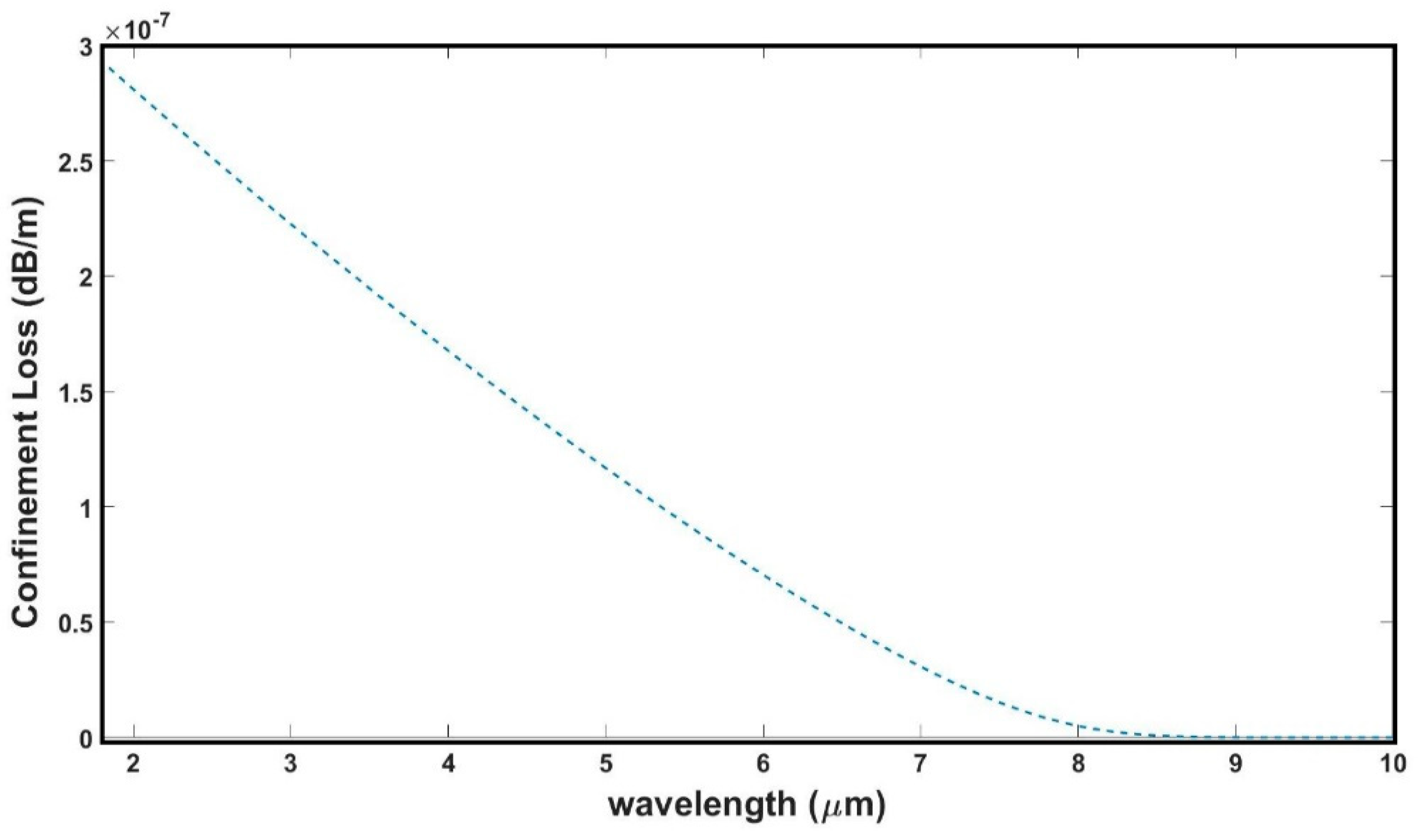
3.3. Confinement Loss

The amount of light confined in the core of the PCF is determined by the confinement loss. Confinement loss can be calculated using the expression written below [5]:

$$ConfinementLoss(CL)=8.686\times {\displaystyle \frac{2\pi }{\lambda }}\times Im(n_{eff})$$

(4)

where Im is the imaginary part of the effective refractive index n_eff of the cladding. Figure 4 shows the confinement loss for the proposed PCF. The confinement loss is significantly less for the entire range of the wavelength as the order is of 10⁻⁷ dB/m, which is an impressively low loss. This loss approaches approx. complete zero value as the wavelength increases further. This is also justified by Figure 1b, as it shows good confinement of light solely in the core region, making our designed fiber a good candidate for various applications for low-loss-mode propagation. Although a better value of CL was already achieved previously, it was not with this ultra-high numerical aperture feature.

4. Conclusions

In this paper, we report the computational modeling and analysis of a graded index, chalcogenide glass-based photonic crystal fiber for the mid-infrared region. Since chalcogenide glass has high transparency in the mid-IR range, it was selected as the base material. Our designed PCF has a ultra-high numerical aperture. The numerical aperture value of the proposed structure can reach up to 1.82, which is a fairly high value. To the best of our knowledge, this high value of NA for a chalcogenide glass in the mid-IR region has not been reported thus far. This makes the proposed fiber a novel design. A high value of numerical aperture implies that the modes are strongly guided in the PCF. The guided modes are confined in the core region of the proposed PCF with significantly less confinement loss, which further decreases as the wavelength increases. The low loss and high numerical aperture value of the proposed PCF makes it a good candidate for various applications with such requirements. The chromatic dispersion of this PCF is entirely negative, reaching up to −2000 ps/km/nm at 4.8 µm, and this value of dispersion can further be improved to make the designed PCF more versatile for areas where dispersion compensation is a priority. Our proposed design can be of great interest to the researchers working on photonic crystal fibers for the mid-infrared region.