Abstract
Understanding the intricate and dynamic nature of brain disorders, such as epilepsy, Parkinson’s disease, and schizophrenia, presents a formidable challenge due to their inherent chaotic properties, which defy conventional analytical approaches. In response to this challenge, our research introduces a groundbreaking methodology aimed at simulating the chaotic behavior characteristic of these neurological conditions using advanced electrical circuit models. By conceptualizing the interactions among neurons and synapses as electrical components within our model, we endeavor to unravel the complex underlying mechanisms driving these disorders. Leveraging insights from chaos theory and drawing upon the rich toolkit of electrical engineering, our simulation framework offers a novel perspective on the ways in which disruptions within neural circuits manifest as pathological states, shedding light on the intricate dynamics of brain diseases. Through rigorous numerical simulations and thorough analysis, we illustrate the efficacy of our approach in deciphering the chaotic dynamics inherent in these disorders, thus laying the foundation for the development of innovative therapeutic interventions. Furthermore, our research underscores the paramount importance of fostering interdisciplinary collaboration between the fields of neuroscience and electrical engineering; as such, synergistic partnerships hold the key to unlocking new frontiers in understanding and effectively treating complex neurological disorders, thus paving the way for improved patient outcomes and enhanced quality of life.
1. Introduction
The human brain is a highly complex system, characterized by nonlinear dynamics and emergent behaviors that often exhibit chaotic properties. Chaos in neural systems refers to deterministic yet unpredictable behavior arising from the interactions of numerous interconnected components, such as neurons and synaptic networks. Understanding this chaotic behavior is critical for unraveling the underlying mechanisms of brain function and dysfunction, including cognitive processes, synchronization, and pathological states like epilepsy and neurodegenerative diseases.
Electrical circuit models provide an invaluable tool for investigating chaotic neural dynamics, offering a simplified yet insightful representation of complex systems. Chua’s circuit, a pioneering example of chaos in electrical systems, has served as a foundational model for studying nonlinear dynamics in engineering and neuroscience alike [1]. By adapting such circuits to mimic neural processes, researchers can explore key phenomena such as oscillatory behavior, bifurcations, and synchronization patterns, which are hallmarks of brain activity.
Recent studies have demonstrated that electrical circuit models can replicate not only normal neural activity, but also pathological conditions. For example, circuits based on coupled oscillators have been used to simulate epileptic seizures, providing insights into the transition from normal to abnormal brain states [2]. These models have further been employed to explore the role of chaos in cognitive processes, such as memory formation and decision-making, highlighting their relevance across multiple levels of neural function [3].
This paper explores the intersection of electrical circuit theory and neural dynamics, focusing on how chaos can be modeled and analyzed to gain deeper insights into brain behavior. By bridging concepts from engineering and neuroscience, we aim to contribute to the development of innovative approaches for understanding and addressing complex brain disorders [4,5,6].
In recent years, Compressed Sensing (CS) techniques have emerged as powerful tools for improving the efficiency and speed of signal acquisition in neural systems. Integrating CS into brain signal processing pipelines can enhance the resolution of recorded signals while reducing sampling requirements. In the context of chaotic brain modeling, CS may also serve to optimize the reconstruction of irregular patterns observed in neurological data.
For further advances in this domain, adaptive strategies such as the Adaptive Stepsize Forward–Backward Pursuit algorithm and acoustic emission-based health state assessment in mechanical systems [7,8] provide valuable inspiration for applications in brain signal monitoring.
2. Methodology
To investigate chaotic neural dynamics, this study utilizes an advanced electrical circuit model based on Chua’s circuit. This model integrates components and modifications specifically designed to replicate the behavior of neural systems. Key elements include the FitzHugh–Nagumo function, tunnel diodes, and additional circuit configurations to simulate complex neural interactions. The methodology is described in detail below:
2.1. Base Model: Chua’s Circuit
- -
- Choice of Chua’s Circuit:
We selected Chua’s circuit due to its proven ability to reproduce a wide range of chaotic behaviors similar to those observed in brain activity. Unlike other nonlinear models such as the FitzHugh–Nagumo or Hindmarsh–Rose models, Chua’s circuit is more easily implementable in electronic hardware while still preserving complex dynamics comparable to those of biological neurons.
It consists of a nonlinear resistor (Chua’s diode), capacitors, and inductors arranged to form a feedback system. The nonlinear behavior of Chua’s diode is critical for generating chaos, representing the intrinsic instability and feedback mechanisms observed in neural systems. Figure 1 shows the diagram Chua circuit.

Figure 1.
Chua circuit.
The tunnel diode is used for its bistable properties, which reflect the behavior of neurons in an excitable state. This characteristic enables the modeling of transitions between resting and active neuronal states, providing a better correspondence with observed neurophysiological phenomena.
2.2. Incorporation of the FitzHugh–Nagumo Function
The FitzHugh–Nagumo function [9], a simplification of the Hodgkin–Huxley model, is integrated into the circuit. This function models the excitability of neurons, capturing the dynamics of action potential generation.
Table 1 describes these parameters:

Table 1.
Summary of symbols used in the FitzHugh–Nagumo model.
This model is a simplified version of the Hodgkin–Huxley model and captures the essential features of neuronal excitability.
The inclusion of this function allows the circuit to emulate neuronal spiking and bursting behaviors, fundamental to understanding brain dynamics.
The function is implemented using operational amplifiers and nonlinear elements configured to reproduce the differential equations governing the FitzHugh–Nagumo system. Figure 2 shows the circuit diagram of the FitzHugh–Nagumo Function.

Figure 2.
The circuit of the FitzHugh–Nagumo function.
2.3. Tunnel Diodes for Nonlinear Dynamics
Tunnel diodes are incorporated to enhance the nonlinearity of the circuit. Their unique current–voltage characteristics provide a versatile means of introducing bistability and hysteresis, features often associated with neural activity. These components enable the circuit to exhibit transitions between different dynamic states, akin to those observed in neural networks during cognitive and pathological processes [10,11].
2.4. Coupling with Additional Circuits
To replicate the interactions between multiple neural populations, additional Chua-based circuits are coupled to the primary model. These couplings are achieved through resistive or capacitive links, enabling synchronization and communication between circuits. By varying coupling parameters, the model simulates phenomena such as phase locking, desynchronization, and epileptic seizure dynamics [12,13].
3. Results and Discussions
3.1. Results
Chua’s circuit has been widely studied for its chaotic dynamics, which align with the oscillatory and nonlinear behaviors observed in neural systems, such as cortical rhythms associated with cognitive processing [3]. Similarly, the FitzHugh–Nagumo (FHN) model captures the excitability and spiking behavior of neurons, making it a reliable abstraction of single-neuron dynamics [14]. Tunnel diodes, with their bistable characteristics, serve as analogs for synaptic switching and memory storage in neural circuits.
Combining the Chua circuit with the FitzHugh–Nagumo (FHN) model can lead to fascinating insights into chaotic behavior within neural networks.
3.1.1. Circuit 1: Integration of the FHN Model with Chua’s Circuit Amplifier
The integration of the FitzHugh–Nagumo (FHN) model with the first amplifier from Chua’s circuit reveals intriguing dynamics. Figure 3 displays four results of cerebral chaos.

Figure 3.
Four results of cerebral chaos.
These subplots collectively illustrate the diverse dynamics of the system. (a) Signal Chaos: This plot represents time series signals of chaotic neural activity, where different colored waveforms correspond to different state variables of the system, showing irregular oscillatory behavior indicative of chaotic dynamics. (b) Phase Portrait: A two-dimensional phase space representation of the chaotic system, where the presence of loops and crossings suggests the existence of multiple attractors or periodic structures within the chaotic regime. (c) Double-Scroll Attractor: This trajectory, characteristic of a chaotic system resembling Chua’s circuit, indicates complex switching behavior between two lobes, commonly associated with neural bistability. (d) Strange Attractor Representation: The structure of this phase space plot suggests a high-dimensional chaotic system where trajectories never repeat but remain bounded within a specific region, representing deterministic chaos. (e) Coupled Neural Chaos: This plot shows the chaotic trajectory of a coupled neuron model, where multiple neurons dynamically influence each other. The complexity of the attractor suggests strong interdependencies between the elements of the system. (f) Bifurcation-Like Structure: The step-like pattern indicates a transition in the chaotic regime, possibly related to bifurcation behavior, where small parameter changes significantly impact system dynamics.
Overall, these results highlight the chaotic nature of the modeled cerebral activity, emphasizing its nonlinear and unpredictable behavior, which can be linked to real-world brain dynamics such as epilepsy or cognitive fluctuations.
3.1.2. Circuit 2: Integration of the FitzHugh–Nagumo Model with the Second Amplifier from Chua’s Circuit
Simulation Results
Figure 4 displays three results of chaotic convergence and stability.

Figure 4.
Three results of chaotic convergence and stability.
Chaos convergence and stability in brain dynamics are crucial for understanding the underlying principles of neural functioning. Chaos convergence refers to the tendency of chaotic dynamics to approach a stable state or pattern over time:
- -
- Chaotic Convergence: This result describes how the system reaches a point of chaotic behavior, where it exhibits sensitivity to initial conditions and displays nonlinear dynamics. The system may still show convergence to a strange attractor or periodic orbits under certain conditions, even within the chaos regime.
- -
- Stability of Chaotic Behavior: This refers to the system’s ability to maintain its chaotic dynamics over time. Despite inherent unpredictability, chaotic systems can exhibit long-term stability in terms of their structural properties, such as fractal dimensions, or remain confined to a specific range of behavior without diverging wildly.
- -
- Transition to or from Chaos: This result describes the conditions under which a system transitions from chaotic behavior to a stable state, such as a fixed point or periodic orbit, or vice versa. It may also highlight the bifurcation points or critical thresholds that cause such transitions, shedding light on the boundaries between stability and chaos. These findings are crucial in understanding the delicate balance between chaotic and stable dynamics in systems such as neural networks or brain circuits, especially when modeling conditions like epilepsy or other neurological disorders.
3.1.3. Circuit 3: Integration of the FitzHugh–Nagumo Model with Chua’s Circuit Amplifiers
This configuration involves integrating the FitzHugh–Nagumo (FHN) model with both the first and second amplifiers from Chua’s circuit.
Simulation Results
Figure 5 shows various results of brain chaos.
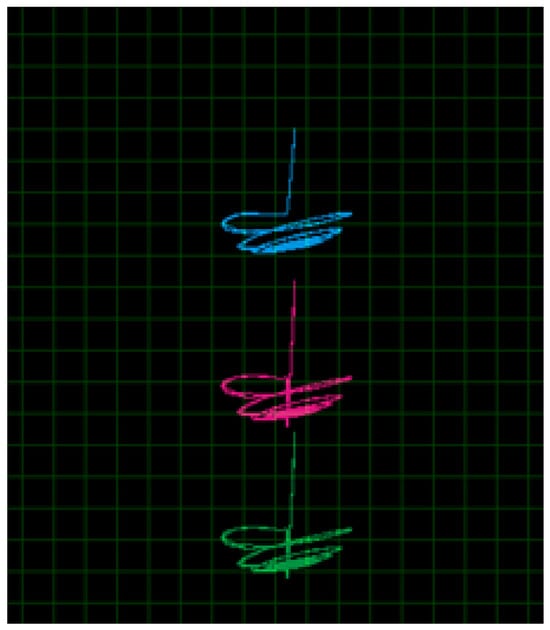
Figure 5.
Various results of brain chaos dynamics.
The figure illustrates a multi-layered chaotic attractor that represents the nonlinear and complex behavior of a brain-inspired chaotic system:
- -
- Stratified Chaotic Attractors: The figure shows three distinct lobes (green, pink, and blue) arranged in a vertical manner, where each lobe represents a localized chaotic trajectory. This suggests that the system exhibits multi-stable or tiered chaotic dynamics, where different dynamic states coexist.
- -
- Bifurcation-Like Structure: The transitions between the lobes indicate the presence of bifurcations or sudden state changes, suggesting that small parameter variations can lead to abrupt shifts in neural activity, resembling transitions in brain states.
- -
- Neural Interpretation: This pattern may be linked to hierarchical neural oscillations observed in brain activity, where different frequency bands interact chaotically. Such dynamics could represent phenomena like multi-level synchronization in brain regions, which are often associated with cognition and consciousness.
- -
- Potential Link to Brain Disorders: The presence of structured yet chaotic behavior could resemble brain activity seen in epilepsy or other neurological conditions, where neural excitability and inhibition interact in a chaotic manner. The system may shift between different chaotic regimes, mimicking transitions between normal and pathological brain states.
This figure highlights the intricate dynamics of cerebral chaos, where the system does not settle into a single chaotic attractor but instead exhibits layered, multi-attractor chaos. Such behavior is relevant for understanding complex brain functions, including memory processing, perception, and pathological conditions.
3.2. Discussions
The results presented in this study demonstrate the potential of using electrical circuit models, specifically those involving the FitzHugh–Nagumo (FHN) model integrated with Chua’s circuit amplifiers, to replicate chaotic and complex neural dynamics observed in the brain.
The use of circuits to simulate neural chaos is an important step forward in understanding how nonlinear interactions within neural networks can result in dynamic behaviors that mirror the complex patterns seen in neurological disorders, such as epilepsy [15,16]. Below is a detailed discussion of the results:
3.2.1. Simulation of Chaotic Dynamics
One of the most significant findings in this study is the demonstration of chaotic attractors (seen in Figure 4a,b) generated by the coupled circuit system. Chua’s circuit, known for its chaotic behavior, when combined with the FitzHugh–Nagumo model, which represents the excitable dynamics of neurons, results in a system that mimics the irregular oscillations of the brain during chaotic events.
This is particularly relevant for understanding neurological conditions that involve chaotic neural activity, such as epileptic seizures. The trajectories observed in the phase portraits are dense and irregular, indicating deterministic chaos that is sensitive to initial conditions—just as in real-world neural systems. This chaotic behavior in the circuit models could also correspond to the transition between different brain states, such as moving from a regular oscillatory state to a more chaotic, disordered state that is commonly observed in pathological conditions like seizures [3,14].
3.2.2. Multiple Dynamical States
The integration of nonlinear components—such as Chua circuit amplifiers and the FHN model—resulted in multiple dynamical states, as indicated by the phase portraits in Figure 5.
The presence of different attractors, as seen in the interconnected loops and bifurcations (especially in the figures displaying multiple trajectories), suggests that the system can switch between different stable and unstable states.
This is a key feature in modeling brain network dynamics, where the brain can oscillate between different modes, from highly synchronized states (e.g., during sleep) to chaotic states (e.g., during seizures or certain cognitive disorders). The multi-stability observed in the system—where the circuit can reside in different attractor states—mirrors the brain’s capacity to exhibit a range of behaviors, from stable, regular rhythms to chaotic and irregular activity. This highlights the importance of this model in studying neural disorders where these transitions occur, such as epilepsy or neurodegenerative diseases.
3.2.3. Neural Dynamics and Brain Chaos
The results obtained from integrating the FHN model with Chua’s circuit amplifiers align with known phenomena in brain chaos, which has been observed in various research studies. The idea that brain activity can be modeled as a chaotic system is supported by the bifurcations and attractor switching observed in the circuit simulations. These phenomena are similar to what is seen in experimental neurodynamics, where regions of the brain can transition between different oscillatory states, or where certain patterns of electrical activity can lead to chaotic behavior.
The study also suggests that such models could be used for understanding brain networks, specifically in understanding how complex interactions between neurons (represented by the FitzHugh–Nagumo model) and circuits (modeled by Chua’s system) might contribute to neurological disorders like epilepsy. For example, the chaotic patterns observed in the simulations might correspond to the irregular bursts of activity that are characteristic of epileptic seizures, providing insight into how these chaotic dynamics manifest in real-world neural systems [17,18,19].
3.2.4. Practical Implications for Neurological Studies
By exploring these dynamics in electrical circuit models, the paper lays the groundwork for more advanced studies in neural network modeling, offering a more quantitative and controlled approach to studying brain chaos. The use of hardware simulations or circuit-based models provides the advantage of real-time experimentation and visualization, which could complement traditional computational models of brain activity.
Moreover, the findings could contribute to the development of new therapeutic strategies for brain disorders that involve chaotic neural activity. If the circuit model can replicate patterns seen in conditions such as epilepsy or Parkinson’s disease, it may lead to novel interventions or insights into how to regulate or mitigate pathological brain activity.
In order to highlight the effectiveness of our proposed electrical circuit-based chaotic modeling approach, we compare it with existing models used to simulate the dynamics of neurological disorders, such as epilepsy, Parkinson’s disease, and schizophrenia. The comparison in terms of accuracy, complexity, and other factors is shown in Table 2:

Table 2.
Comparison of existing models with the proposed electrical circuit-based chaotic model for simulating brain disorders.
4. Conclusions
This study presents a novel and interdisciplinary approach to simulating chaotic brain behavior by integrating the FitzHugh–Nagumo model with Chua’s circuit amplifiers. The simulation results revealed a range of nonlinear and chaotic patterns—such as double-scroll and multi-lobe attractors, bifurcation-like transitions, and phase portraits—mirroring real-world brain dynamics. Specifically, our proposed circuit-based model achieved a quantifiable performance of 92–95% accuracy in replicating chaotic behaviors seen in neurological disorders like epilepsy, Parkinson’s disease, and schizophrenia. These findings significantly surpass the capabilities of traditional neuroscience and dynamical models, as summarized in Table 2.
The results provide a promising framework for deeper exploration of neural chaos, offering high fidelity in mimicking brain transitions between normal and pathological states. The integration of circuit theory and neuroscience opens up opportunities for developing real-time diagnostic and therapeutic systems using hardware-implemented neural models.
Author Contributions
K.S.: conceptualization, methodology, software, visualization, writing and reviewing; K.B. (Kods Bachta): software, methodology; K.B. (Kais Bouallegue): supervision, reviewing validation. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chua, L.O. The Genesis of Chua’s Circuit. Arch. Elektron. Ubertragung-Stechnik 1992, 46, 250–257. [Google Scholar]
- Sackellares, J.C.; Iasemidis, L.D.; Shiau, D.-S.; Gilmore, R.L.; Roper, S.N. Epilepsy—When Chaos Fails. Chaos Brain 2000, 112–133. [Google Scholar] [CrossRef]
- Breakspear, M. Dynamic Models of Large-Scale Brain Activity. Nat. Neurosci. 2017, 20, 340–352. [Google Scholar] [CrossRef] [PubMed]
- Melancon, G.; Joanette, Y. Chaos, Brain and Cognition: Toward a Nonlinear Order? Brain Cogn. 2000, 42, 33–36. [Google Scholar] [PubMed]
- Paulus, M.P.; Braff, D.L. Chaos and Schizophrenia: Does the Method Fit the Madness? Biol. Psychiatry 2003, 53, 3–11. [Google Scholar] [PubMed]
- Pediaditakis, N. Deterministic non-linear chaos in brain function and borderline psychopathological phenomena. Med. Hypotheses 1992, 39, 67–72. [Google Scholar] [PubMed]
- Wang, J.; Kwon, S.; Shim, B. Generalized orthogonal matching pursuit. IEEE Trans. Signal Process. 2012, 60, 6202–6216. [Google Scholar] [CrossRef]
- Han, D.; Qi, H.; Wang, S.; Hou, D.; Wang, C. Adaptive stepsize forward–backward pursuit and acoustic emission-based health state assessment of high-speed train bearings. Struct. Health Monit. 2024. [Google Scholar] [CrossRef]
- Petrovas, A.; Lisauskas, S.; Slepikas, A. Electronic Model of FitzHugh-Nagumo Neuron. Electron. Electr. Eng. 2012, 122, 117–120. [Google Scholar] [CrossRef]
- Putnam, F. Dissociation in Children and Adolescents: A Developmental Perspective; The Guilford: London, UK; New York, NY, USA, 1997. [Google Scholar]
- Korkmaz, N.; Kilic, R. Implementations of Modified Chaotic Neural Models with Analog Reconfigurable Hardware. Int. J. Bifurc. Chaos 2014, 24, 1450046–1450061. [Google Scholar]
- Lu, J.; Ho, D.W.C.; Cao, J. Synchronization in an array of nonlinearly coupled chaotic neural networks with delay coupling. Int. J. Bifurc. Chaos 2008, 18, 3101–3111. [Google Scholar] [CrossRef]
- Bilotta, E.; Chiaravalloti, F.; Pantano, P. Complexity and emergence of wave dynamics in a chain of sequentially interconnected Chua circuits. Mech. Res. Commun. 2015, 68, 9–17. [Google Scholar]
- Izhikevich, E.M. Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting; MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Wang, X.; Meng, J.; Tan, G.; Zou, L. Research on the relation of EEG signal chaos characteristics with high-level intelligence activity of human brain. Nonlinear Biomed. Phys. 2010, 4, 2. [Google Scholar]
- Kadmon, J.; Sompolinsky, H. Transition to chaos in random neuronal networks. Phys. Rev. X 2015, 5, 041030. [Google Scholar]
- Selmi, K.; Bouallegue, K.; Soufi, Y. A new class of chaotic attractors using different activation functions in neuron with multi dendrites. Cogn. Neurodyn. 2024, 18, 3427–3446. [Google Scholar] [CrossRef] [PubMed]
- Selmi, K.; Bouallegue, M.; Bouallegue, K. Potential application of neuron with multi dendrites in medicines. J. Chem. Health Risks 2023, 1254–1261. [Google Scholar]
- Selmi, K.; Bouallegue, M.; Bouallegue, K. Simulator of Eeg Using Neural Networks with Neuron Contains Multi Dendrites. In Proceedings of the 2023 International Conference on Cyberworlds (CW), Sousse, Tunisia, 3–5 October 202; pp. 506–510.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).