Water-Sorption Isotherms and Air-Drying-Kinetics Modelling of Andean Tubers and Tuberous Roots †
Abstract
:1. Introduction
2. Materials and Methods
2.1. Raw Materials and Sample Preparation
2.2. Determination of Drying Kinetics
Drying Kinetics: Mathematical Modelling
2.3. Determination of Water-Sorption Isotherms
Water-Sorption Isotherms: Mathematical Modelling
2.4. Statistical Analysis
3. Results and Discussion
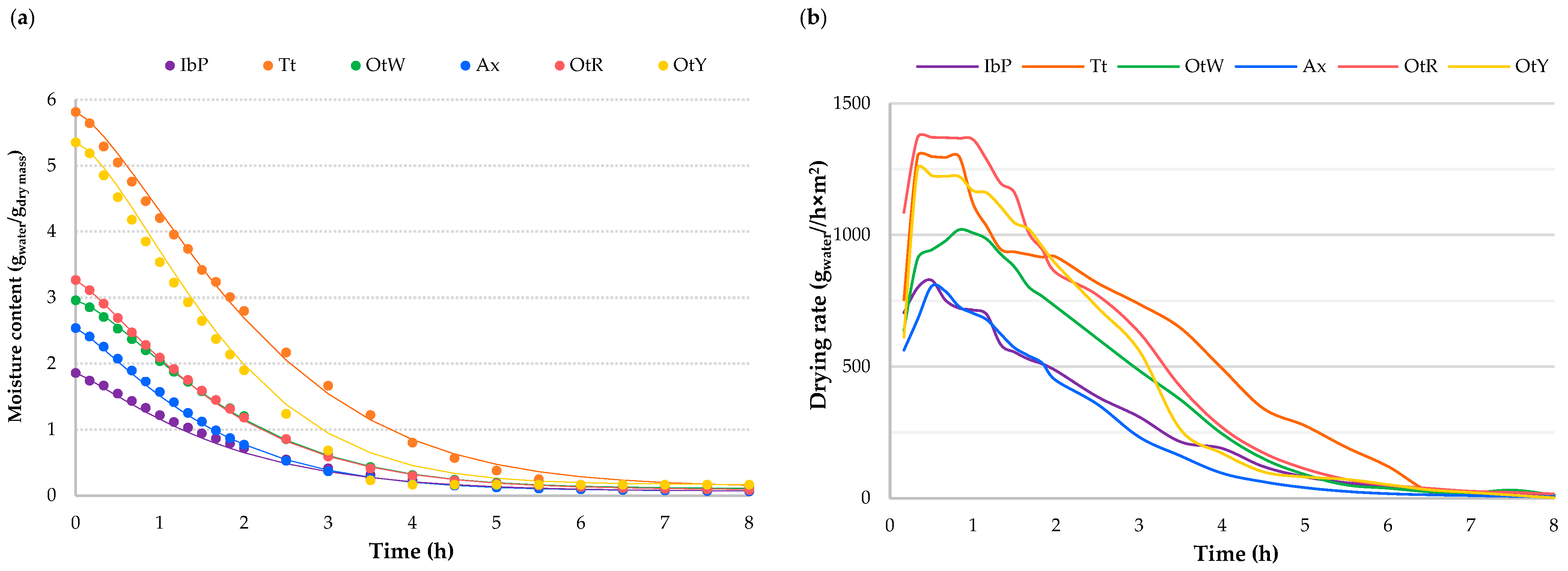
3.1. Drying Kinetics
Drying Kinetics: Mathematical Modelling
3.2. Water-Sorption Isotherms
Water-Sorption Isotherms. Mathematical Modelling
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Flores, H.E.; Walker, T.S.; Guimarães, R.L.; Bais, H.P.; Vivanco, J.M. Andean root and tuber crops: Underground rainbows. HortScience 2003, 38, 161–168. [Google Scholar] [CrossRef]
- Alam, M.K. A comprehensive review of sweet potato (Ipomoea batatas [L.] Lam): Revisiting the associated health benefits. Trends Food Sci. Technol. 2021, 115, 512–529. [Google Scholar] [CrossRef]
- Guevara-Freire, D.A.; Valle-Velástegui, L.; Barros-Rodríguez, M.; Vásquez, C.; Zurita-Vásquez, H.; Dobronski-Arcos, J.; Pomboza-Tamaquiza, P. Nutritional composition and bioactive components of mashua (Tropaeolum tuberosum Ruiz and Pavón). Trop. Subtrop. Agroecosyst. 2018, 21, 53–68. [Google Scholar] [CrossRef]
- Ayala, G. Aporte de los cultivos andinos a la nutrición humana. In Raíces Andinas: Contribuciones al Conocimiento y a la Capacitación. I. Aspectos Generales y Recursos Genéticos de las Raíces Andinas; Seminario, J., Ed.; International Potato Center: Lima, Peru, 2004; pp. 101–112. [Google Scholar]
- Zhu, F.; Cui, R. Comparison of physicochemical properties of oca (Oxalis tuberosa), potato, and maize starches. Int. J. Biol. Macromol. 2020, 148, 601–607. [Google Scholar] [CrossRef] [PubMed]
- Jimenez, M.E.; Rossi, A.; Sammán, N. Health properties of oca (Oxalis tuberosa) and yacon (Smallanthus sonchifolius). Food Funct. 2015, 6, 3266–3274. [Google Scholar] [CrossRef] [PubMed]
- Aniesrani Delfiya, D.; Prashob, K.; Murali, S.; Alfiya, P.; Samuel, M.P.; Pandiselvam, R. Drying kinetics of food materials in infrared radiation drying: A review. J. Food Process Eng. 2022, 45, e13810. [Google Scholar] [CrossRef]
- Troller, J. Water Activity and Food; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Wang, J.; Yang, X.-H.; Mujumdar, A.; Wang, D.; Zhao, J.-H.; Fang, X.-M.; Zhang, Q.; Xie, L.; Gao, Z.-J.; Xiao, H.-W. Effects of various blanching methods on weight loss, enzymes inactivation, phytochemical contents, antioxidant capacity, ultrastructure and drying kinetics of red bell pepper (Capsicum annuum L.). LWT 2017, 77, 337–347. [Google Scholar] [CrossRef]
- Shazman, A.; Mizrahi, S.; Cogan, U.; Shimoni, E. Examining for possible non-thermal effects during heating in a microwave oven. Food Chem. 2007, 103, 444–453. [Google Scholar] [CrossRef]
- Farhat, A.; Fabiano-Tixier, A.-S.; El Maataoui, M.; Maingonnat, J.-F.; Romdhane, M.; Chemat, F. Microwave steam diffusion for extraction of essential oil from orange peel: Kinetic data, extract’s global yield and mechanism. Food Chem. 2011, 125, 255–261. [Google Scholar] [CrossRef]
- Shen, H.; Fan, D.; Huang, L.; Gao, Y.; Lian, H.; Zhao, J.; Zhang, H. Effects of microwaves on molecular arrangements in potato starch. RSC Adv. 2017, 7, 14348–14353. [Google Scholar] [CrossRef]
- Lewandowicz, G.; Fornal, J.; Walkowski, A. Effect of microwave radiation on physico-chemical properties and structure of potato and tapioca starches. Carbohydr. Polym. 1997, 34, 213–220. [Google Scholar] [CrossRef]
- Acurio, L.; Salazar, D.; García-Segovia, P.; Martínez-Monzó, J.; Igual, M. Third-Generation Snacks Manufactured from Andean Tubers and Tuberous Root Flours: Microwave Expansion Kinetics and Characterization. Foods 2023, 12, 2168. [Google Scholar] [CrossRef]
- Salazar, D.; Arancibia, M.; Ocaña, I.; Rodríguez-Maecker, R.; Bedón, M.; López-Caballero, M.E.; Montero, M.P. Characterization and technological potential of underutilized ancestral andean crop flours from Ecuador. Agronomy 2021, 11, 1693. [Google Scholar] [CrossRef]
- O’Callaghan, J.R.; Menzies, D.J.; Bailey, P.H. Digital simulation of agricultural drier performance. J. Agric. Eng. Res. 1971, 16, 223–244. [Google Scholar] [CrossRef]
- Page, G.E. Factors Influencing the Maximum Rates of Air Drying Shelled Corn in Thin Layers; Purdue University: West Lafayette, IN, USA, 1949. [Google Scholar]
- Overhults, D.G.; White, G.; Hamilton, H.; Ross, I. Drying soybeans with heated air. Trans. ASAE 1973, 16, 112. [Google Scholar] [CrossRef]
- Henderson, S.M.; Pabis, S. Grain drying theory, I. Temperature effect on drying coefficient. J. Agric. Eng. Res. 1961, 6, 169–173. [Google Scholar]
- Yagcioglu, A. Drying characteristic of laurel leaves under different conditions. In Proceedings of the 7th International Congress on Agricultural Mechanization and Energy, Adana, Turkey, 26–27 May 1999; pp. 565–569. [Google Scholar]
- Thompson, T.L.; Peart, M.; Foster, G.H. Mathematical Simulation of Corn Drying—A New Model. Trans. ASAE 1968, 11, 582–0586. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion; Oxford University Press: Oxford, UK, 1979. [Google Scholar]
- Greenspan, L. Humidity fixed points of binary saturated aqueous solutions. J. Res. Natl. Bur. Stand. 1977, 81, 89. [Google Scholar] [CrossRef]
- Spiess, W.E.; Wolf, W. Critical evaluation of methods to determine moisture sorption isotherms. In Water Activity: Theory and Applications to Food; Routledge: London, UK, 2017; pp. 215–233. [Google Scholar]
- Honorable Provincial Government of Tungurahua. Tungurahua Hydrometeological Network. Available online: https://rrnn.tungurahua.gob.ec/red/promedios_mensuales (accessed on 14 October 2023).
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of gases in multimolecular layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- Van den Berg, C.; Bruin, S. Water activity and its estimation in food systems. In Proceedings of the International Symposium Properties of Water in Relation to Food Quality and Stability, Osaka, Japan, 10–16 September 1978. [Google Scholar]
- Restrepo Victoria, Á.H.; Burbano Jaramillo, J.C. Disponibilidad térmica solar y su aplicación en el secado de granos. Sci. et Tech. 2005, 1, 127–132. [Google Scholar]
- Ananias, R.A.; Vallejos, S.; Salinas, C. Estudio de la cinética del secado convencional y bajo vacío del pino radiata. Maderas. Cienc. y Tecnol. 2005, 7, 37–47. [Google Scholar] [CrossRef]
- García-Mogollón, C.; Torregroza-Espinosa, A.; Sierra-Bautista, M. Cinética de Secado de Chips de Yuca (Manihot esculenta crantz) en Horno Microondas. Rev. Técnica De la Fac. De Ing. Univ. del Zulia 2016, 39, 098–103. [Google Scholar]
- Salcedo-Mendoza, J.; Contreras-Lozano, K.; García-López, A.; Fernandez-Quintero, A. Modelado de la cinética de secado del afrecho de yuca (Manihot esculenta Crantz). Rev. Mex. De Ing. Química 2016, 15, 883–891. [Google Scholar] [CrossRef]
- Navia, D.; Ayala, A.; Villada, H.S. Isotermas de adsorción de bioplásticos de harina de yuca moldeados por compresión. Biotecnol. En El Sect. Agropecu. Y Agroindustrial 2011, 9, 77–87. [Google Scholar]
- Martins Oyinloye, T.; Byong Yoon, W. Effect of freeze-drying on quality and grinding process of food produce: A review. Processes 2020, 8, 354. [Google Scholar] [CrossRef]
- Saavedra Layza, G.E. Effect of Temperature on the Monolayer Value of Sweet Potato (Ipomoea batata L.) Flour Yellow Variety through the GAB Isotherm. Bachelor’s Thesis, National University of Trujillo, Trujillo, Perú, 2022. [Google Scholar]
- Gutierrez Balarezo, J.; Diaz Viteri, J.E.; Mendieta Taboada, O.W.; Pulla Huilca, P.V.; Chañi Paucar, L.O. Conservación de la harina de plátano (Musa paradisiaca) en Puerto Maldonado, Madre de Dios. Biodivers. Amaz. 2019, 4, 74–86. [Google Scholar]
- Ceballos, A.M.; Giraldo, G.I.; Orrego, C.E. Evaluacion de varios modelos de isotermas de adsorcion de agua de un polvo de fruta deshidratada. Vector 2009, 1, 107–117. [Google Scholar]

| Model | Equation | Equation Number | References |
|---|---|---|---|
| Newton | (1) | [16] | |
| Page | (2) | [17] | |
| Modified Page | (3) | [18] | |
| Henderson and Pabis | (4) | [19] | |
| Logarithmic | (5) | [20] | |
| Thomson | (6) | [21] | |
| Fick | (7) | [22] |
| Name | Nomenclature | aw * | Name | Nomenclature | aw * |
|---|---|---|---|---|---|
| Lithium chloride | LiCl | 0.1178 | Sodium bromide | NaBr | 0.5732 |
| Potassium acetate | CH3CO2K | 0.2982 | Ammonium sulphate | (NH4)2SO4 | 0.8012 |
| Magnesium chloride | MgCl2 | 0.3425 |
| Model | Equation | Equation Number | References |
|---|---|---|---|
| Brunauer, Emmett, and Teller (BET) | (8) | [26] | |
| Guggenheim, Anderson, and de Boer (GAB) | (9) | [27] |
| Sample | Models | |||||||
|---|---|---|---|---|---|---|---|---|
| Newton | Page | Modified Page | Henderson and Pabis | Logarithmic | Thomson | Fick | ||
| IbP (Sweet potato) | Model constants | k: 0.691 | k: 0.4985 n: 1.173 | k: 0.5524 n: 1.173 | k: 0.704 a: 1.4597 | k: 0.518 | a: 0.3497 b: 0.0298 | Def: |
| a: 1.082 | ||||||||
| c: 0.0394 | ||||||||
| Adj. r2 | 0.982 | 0.9923 | 0.9923 | 0.988 | 0.9586 | 0.99 | 0.9611 | |
| RMSE | 0.134 | 0.027 | 4.051 | 5.0432 | 0.9293 | 0.1169 | 2.232 | |
| MRPD | 0.528 | 0.0265 | 11.9376 | 18.6275 | 4.2325 | 3.94 | 10.877 | |
| Tt (Mashua) | Model constants | k: 0.66 | k: 0.308 n: 1.375 | k: 0.4245 n: 1.375 | k: 0.738 a: 2.059 | k: 0.3136 | a: 0.2788 b: 0.0185 | Def: |
| a: 1.192 | ||||||||
| c: 0.1465 | ||||||||
| Adj. r2 | 0.8962 | 0.989 | 0.989 | 0.9244 | 0.9363 | 0.9977 | 0.8627 | |
| RMSE | 1.014 | 0.196 | 5.582 | 23.8585 | 3.5523 | 23.8585 | 4.1564 | |
| MRPD | 1.086 | 0.1234 | 0.1184 | 22.1583 | 4.0482 | 22.1583 | 5.574 | |
| Ax (Zanahoria blanca) | Model constants | k: 0.7684 | k: 0.5399 n: 1.2194 | k: 0.6164 n: 1.2194 | k: 0.75 a: 1.3872 | k: 0.6151 | a: 0.3746 b: 0.0337 | Def: |
| a: 1.08 | ||||||||
| c: 0.0262 | ||||||||
| Adj. r2 | 0.995 | 0.9977 | 0.999 | 0.9864 | 0.9636 | 0.9636 | 0.996 | |
| RMSE | 0.171 | 0.039 | 4.4474 | 6.4694 | 1.1864 | 1.1864 | 2.632 | |
| MRPD | 0.521 | 0.121 | 9.8944 | 18.841 | 4.1582 | 4.1582 | 10.49 | |
| OtW (Oca white variety) | Model constants | k: 0.7261 | k: 0.3893 n: 1.3656 | k: 0.2037 n: 1.3656 | k: 0.745 a: 1.6428 | k: 0.4682 | a: 0.3569 b: 0.0296 | Def: |
| a: 1.14 | ||||||||
| c: 0.0645 | ||||||||
| Adj. r2 | 0.9845 | 0.9986 | 0.999 | 0.9497 | 0.952 | 0.9955 | 0.9887 | |
| RMSE | 1.2457 | 0.023 | 4.755 | 8.122 | 1.3943 | 0.16 | 2.6244 | |
| MRPD | 0.9342 | 0.013 | 7.5582 | 19.32 | 4.11 | 3.95 | 8.8533 | |
| OtY (Oca yellow variety) | Model constants | k: 0.8689 | k: 0.3816 n: 1.46 | k: 1.5997 n: 1.291 | k: 0.922 a: 2.139 | k: 0.444 | a: 0.3523 b: 0.0285 | Def: |
| a: 1.158 | ||||||||
| c: 0.082 | ||||||||
| Adj. r2 | 0.9727 | 0.9921 | 0.976 | 0.888 | 0.9464 | 0.9953 | 0.9727 | |
| RMSE | 3.129 | 20.376 | 5.216 | 23.1519 | 1.286 | 11.6696 | 4.0237 | |
| MRPD | 1.2 | 18.901 | 2.684 | 30.15 | 0.422 | 16.451 | 5.7033 | |
| OtR (Oca red variety) | Model constants | k: 0.7743 | k: 0.4692 n: 1.243 | k: 1.838 n: 1.243 | k: 0.7 a: 1.4396 | k: 0.527 | a: 0.3525 b: 0.03 | Def: |
| a: 1.089 | ||||||||
| c: 0.038 | ||||||||
| Adj. r2 | 0.991 | 0.998 | 0.9997 | 0.9822 | 0.9685 | 0.9893 | 0.9905 | |
| RMSE | 0.127 | 7.4486 | 4.765 | 3.78 | 0.5553 | 3.151 | 1.9936 | |
| MRPD | 0.226 | 17.252 | 11.927 | 12.376 | 0.4327 | 10.973 | 6.5661 | |
| Samples | Models | Samples | Models | Samples | Models | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| BET | GAB | BET | GAB | BET | GAB | ||||||
| Sweet potato | Model constants | X0: 0.04 C: 17.875 | X0: 0.05 C: 17.79 K: 0.9 | Oca white variety | Model constants | X0: 0.05 C: 12.5 | X0: 0.059 C: 13.82 K: 0.9 | Oca yellow variety | Model constants | X0: 0.051 C: 4.443 | X0: 0.053 C: 4.795 K: 0.97 |
| Adj. r2 | 0.98 | 0.999 | Adj. r2 | 0.98 | 0.98 | Adj. r2 | 0.98 | 0.97 | |||
| RMSE | 0.016 | 0.022 | RMSE | 0.0032 | 0.0037 | RMSE | 0.02 | 0.023 | |||
| MRPD | 19.98 | 19.99 | MRPD | 7.052 | 7.154 | MRPD | 12.72 | 13.74 | |||
| Mashua | Model constants | X0: 0.065 C: 16.4 | X0: 0.07 C: 11.47 K: 0.96 | Zanahoria blanca | Model constants | X0: 0.051 C: 15.24 | X0: 0.055 C: 12.13 K: 0.91 | Oca red variety | Model constants | X0: 0.055 C: 21.89 | X0: 0.057 C: 20.26 K: 0.98 |
| Adj. r2 | 0.989 | 0.999 | Adj. r2 | 0.972 | 0.988 | Adj. r2 | 0.989 | 0.998 | |||
| RMSE | 0.004 | 0.005 | RMSE | 0.01 | 0.013 | RMSE | 0.01 | 0.011 | |||
| MRPD | 19.999 | 19.999 | MRPD | 19.07 | 19.87 | MRPD | 12.56 | 13.74 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acurio, L.; Baquerizo, A.; Borja, A.; Vayas, M.; García-Segovia, P.; Martínez-Monzó, J.; Igual, M. Water-Sorption Isotherms and Air-Drying-Kinetics Modelling of Andean Tubers and Tuberous Roots. Biol. Life Sci. Forum 2023, 26, 71. https://doi.org/10.3390/Foods2023-15141
Acurio L, Baquerizo A, Borja A, Vayas M, García-Segovia P, Martínez-Monzó J, Igual M. Water-Sorption Isotherms and Air-Drying-Kinetics Modelling of Andean Tubers and Tuberous Roots. Biology and Life Sciences Forum. 2023; 26(1):71. https://doi.org/10.3390/Foods2023-15141
Chicago/Turabian StyleAcurio, Liliana, Ariel Baquerizo, Alexandra Borja, Marcelo Vayas, Purificación García-Segovia, Javier Martínez-Monzó, and Marta Igual. 2023. "Water-Sorption Isotherms and Air-Drying-Kinetics Modelling of Andean Tubers and Tuberous Roots" Biology and Life Sciences Forum 26, no. 1: 71. https://doi.org/10.3390/Foods2023-15141
APA StyleAcurio, L., Baquerizo, A., Borja, A., Vayas, M., García-Segovia, P., Martínez-Monzó, J., & Igual, M. (2023). Water-Sorption Isotherms and Air-Drying-Kinetics Modelling of Andean Tubers and Tuberous Roots. Biology and Life Sciences Forum, 26(1), 71. https://doi.org/10.3390/Foods2023-15141









