New Approaches in Finite Control Set Model Predictive Control for Grid-Connected Photovoltaic Inverters: State of the Art
Abstract
1. Introduction
2. Modelling of MPC
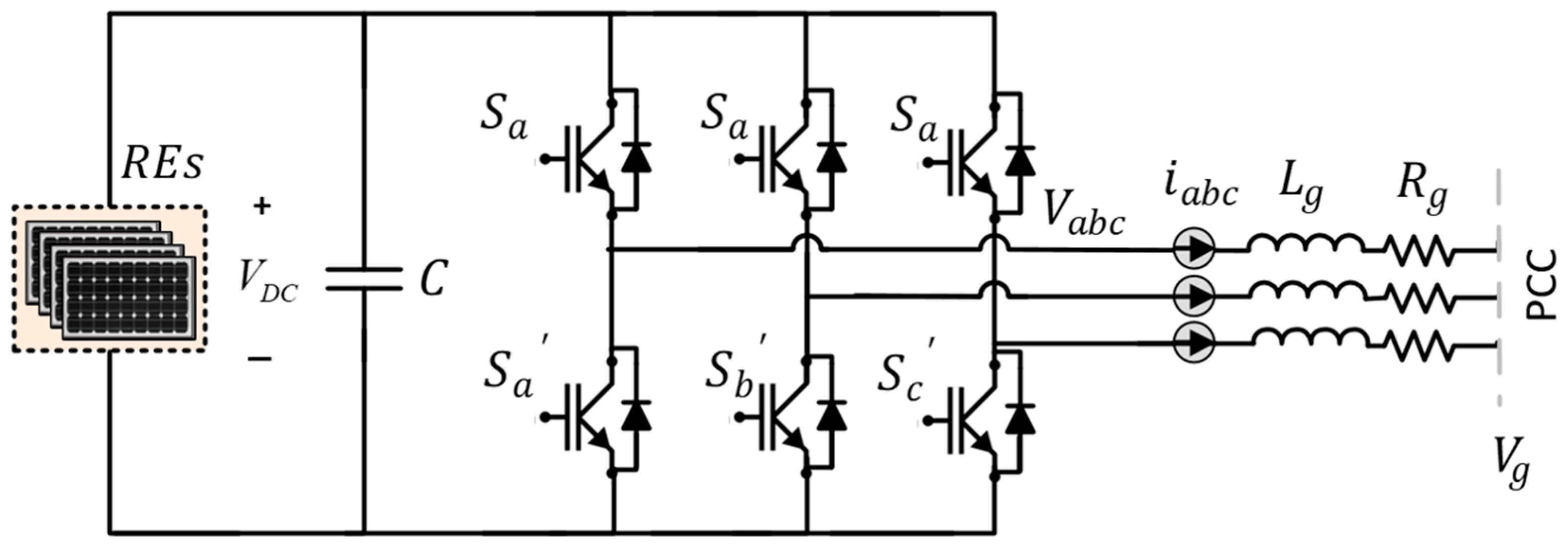
2.1. Grid-Connected Inverter
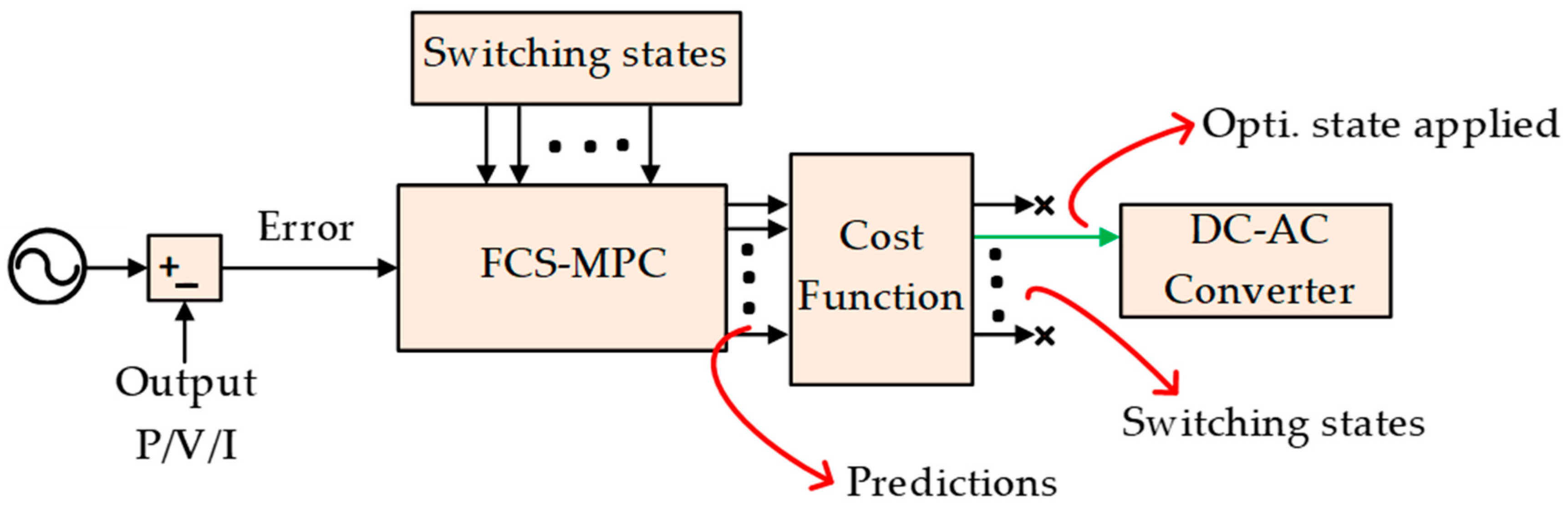
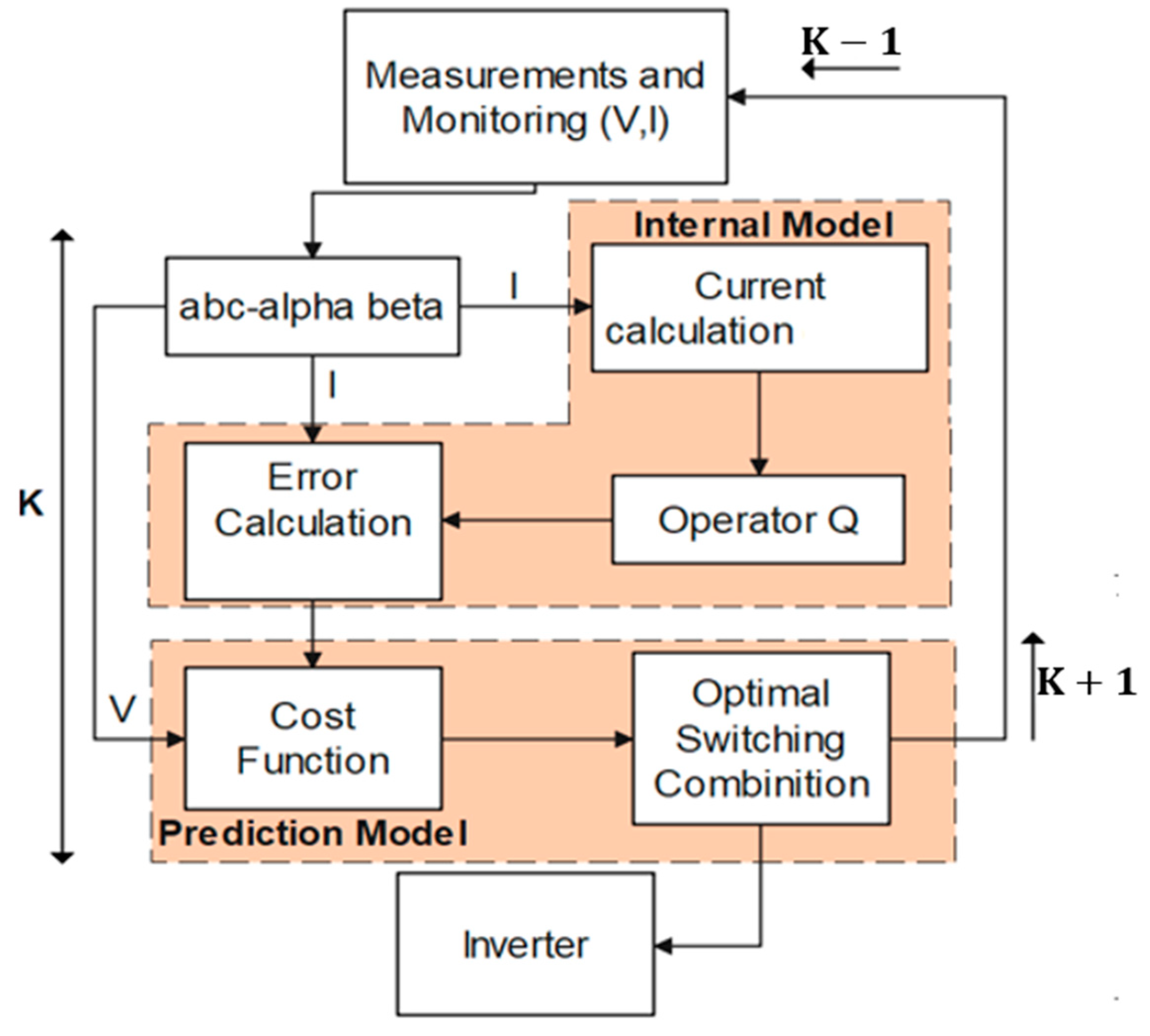
2.2. MPC and the Working Principle
2.3. Cost Function and the Control Law
3. Model Predictive Control Strategies
3.1. Active and Reactive Power Control
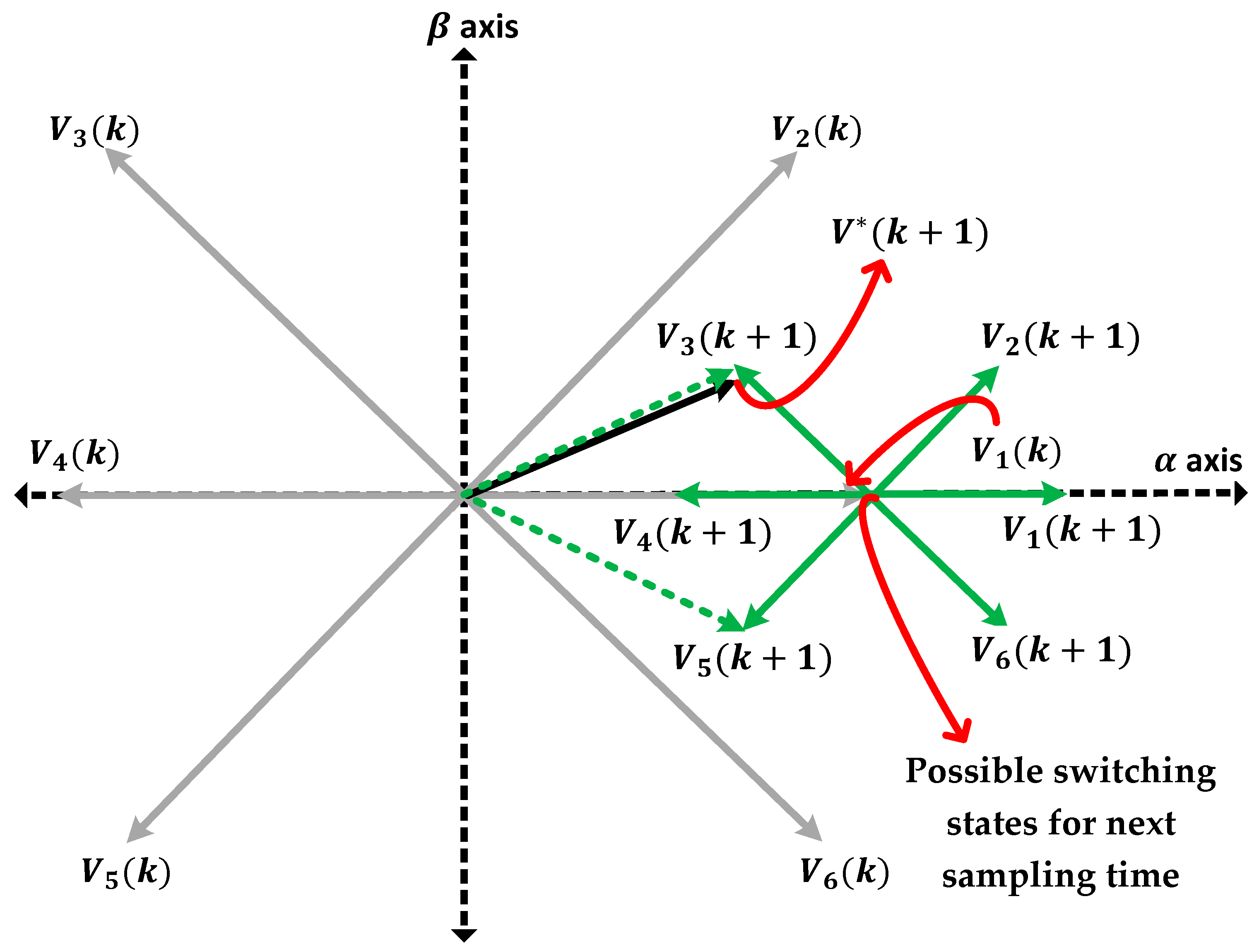
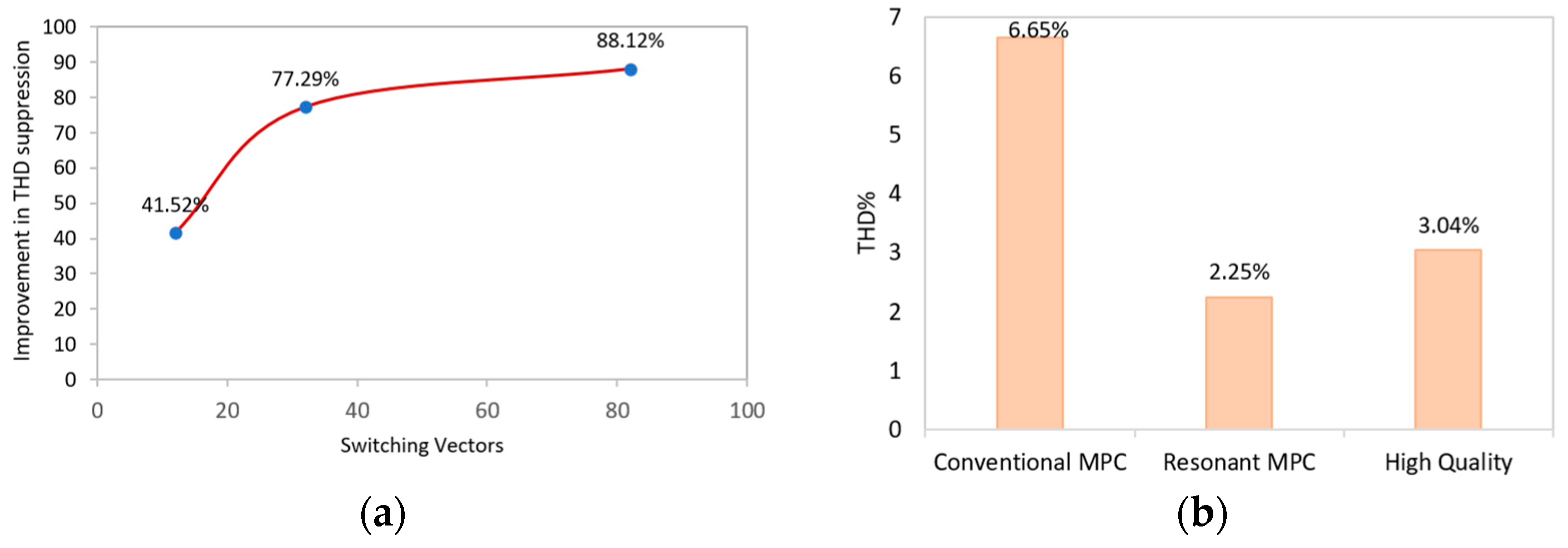
3.2. Increased Switching States
3.3. Robust MPC Approaches
3.4. Resonant MPC
3.5. Lyapunov Function MPC
4. Optimization Techniques
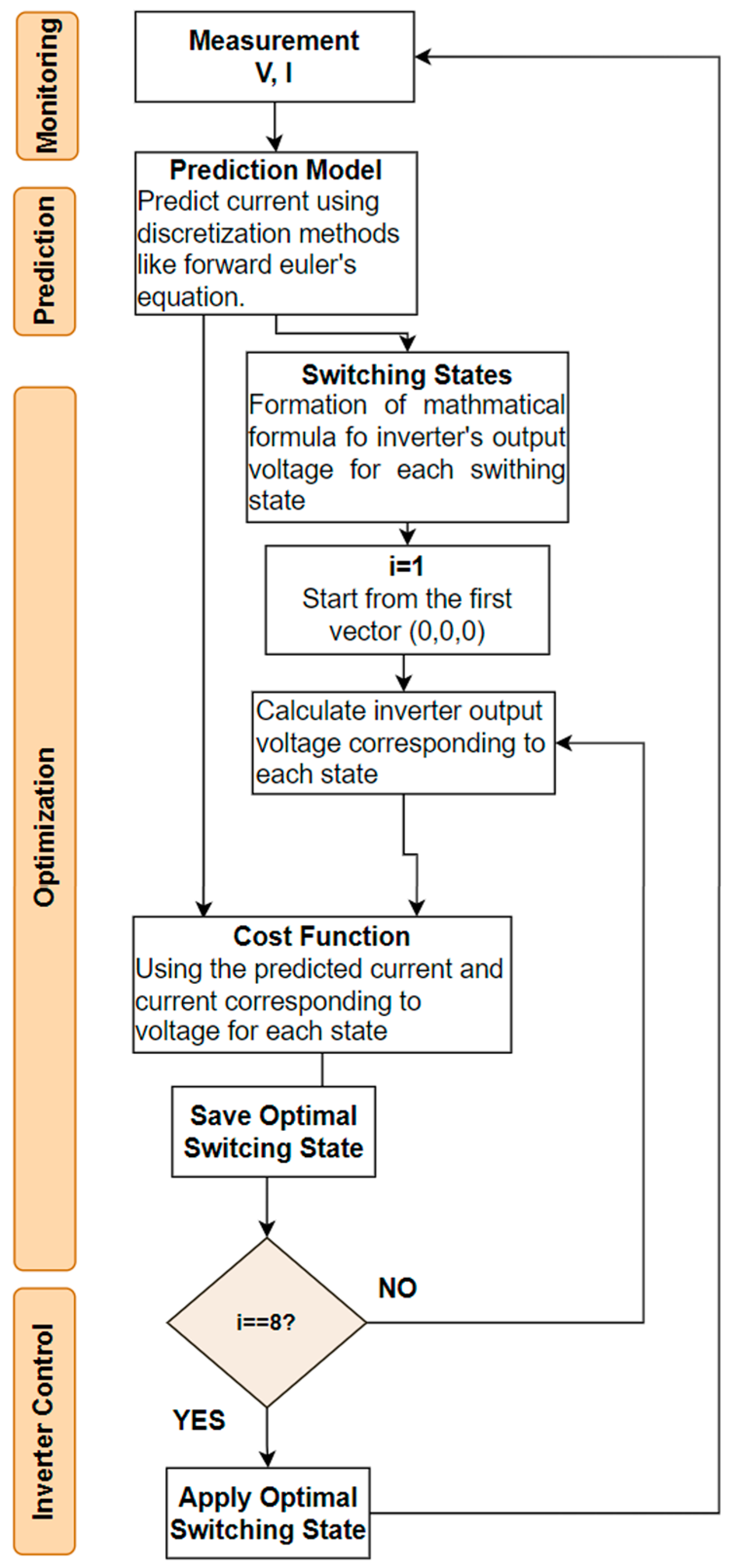
- The optimization technique is implemented on the predicted model obtained in first step and the cost function is designed. For example. if the optimization technique is based on the increased switching state as discussed in [23], the corresponding output voltage for each newly added switching states is calculated and used in the next step to obtain the optimal switching state.
- Each switching combination is applied on the prediction model, and the output behavior of the inverter is predicted for each switching combination.
- The combination with least predicted error is opted and applied for the next sampling time.
5. Discussion and Recommendations for Future Development of MPC for Grid Connected Inverters
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vazquez, S.; Leon, J.I.; Franquelo, L.G.; Rodriguez, J.; Young, H.A.; Marquez, A.; Zanchetta, P. Model predictive control: A review of its applications in power electronics. IEEE Ind. Electron. Mag. 2014, 8, 16–31. [Google Scholar] [CrossRef]
- Valverde, G.; Van Cutsem, T. Model predictive control of voltages in active distribution networks. IEEE Trans. Smart Grid 2013, 4, 2152–2161. [Google Scholar] [CrossRef]
- Rodriguez, J.; Kazmierkowski, M.P.; Espinoza, J.R.; Zanchetta, P.; Abu-Rub, H.; Young, H.A.; Rojas, C.A. State of the art of finite control set model predictive control in power electronics. IEEE Trans. Ind. Inform. 2012, 9, 1003–1016. [Google Scholar] [CrossRef]
- Morari, M.; Lee, J.H. Model predictive control: Past, present and future. Comput. Chem. Eng. 1999, 23, 667–682. [Google Scholar] [CrossRef]
- Camacho, E.F.; Bordons, C. Model Predictive Control; Springer: London, UK, 1999. [Google Scholar]
- Bordons, C.; Montero, C. Basic principles of MPC for power converters: Bridging the gap between theory and practice. IEEE Ind. Electron. Mag. 2015, 9, 31–43. [Google Scholar] [CrossRef]
- Vazquez, S.; Rodriguez, J.; Rivera, M.; Franquelo, L.G.; Norambuena, M. Model predictive control for power converters and drives: Advances and trends. IEEE Trans. Ind. Electron. 2017, 64, 935–947. [Google Scholar] [CrossRef]
- Karamanakos, P.; Geyer, T.; Kennel, R. Reformulation of the long-horizon direct model predictive control problem to reduce the computational effort. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 3512–3519. [Google Scholar]
- Novak, M.; Dragicevic, T. Supervised imitation learning of finite-set model predictive control systems for power electronics. IEEE Trans. Ind. Electron. 2020, 68, 1717–1723. [Google Scholar] [CrossRef]
- Rivera, M.; Wilson, A.; Rojas, C.A.; Rodriguez, J.; Espinoza, J.R.; Wheeler, P.W.; Empringham, L. A comparative assessment of model predictive current control and space vector modulation in a direct matrix converter. IEEE Trans. Ind. Electron. 2012, 60, 578–588. [Google Scholar] [CrossRef]
- Golzari, S.; Rashidi, F.; Farahani, H.F. A Lyapunov function based model predictive control for three phase grid connected photovoltaic converters. Solar Energy 2019, 181, 222–233. [Google Scholar] [CrossRef]
- Pozo, C.G.; Gonzalez, E.E.; Rodriguez, C.; Diaz, M. Comparison of FCS-MPC and PI internal controllers for a Primary Control in a DC Microgrid. In Proceedings of the 2021 IEEE Congreso Estudiantil de Electrónica y Electricidad (INGELECTRA), Valparaíso, Chile, 17–19 November 2021; pp. 1–6. [Google Scholar]
- Babqi, A.J.; Alamri, B. A Comprehensive Comparison between Finite Control Set Model Predictive Control and Classical Proportional-Integral Control for Grid-tied Power Electronics Devices. Acta Polytech. Hung. 2021, 18, 67–87. [Google Scholar] [CrossRef]
- Lu, M.; Al-Durra, A.; Muyeen, S.M.; Leng, S.; Loh, P.C.; Blaabjerg, F. Benchmarking of stability and robustness against grid impedance variation for LCL-filtered grid-interfacing inverters. IEEE Trans. Power Electron. 2017, 33, 9033–9046. [Google Scholar] [CrossRef]
- Xin, Z.; Mattavelli, P.; Yao, W.; Yang, Y.; Blaabjerg, F.; Loh, P.C. Mitigation of grid-current distortion for LCL-filtered voltage-source inverter with inverter-current feedback control. IEEE Trans. Power Electron. 2017, 33, 6248–6261. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A.V. Overview of control and grid synchronization for distributed power generation systems. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef]
- Alepuz, S.; Busquets-Monge, S.; Bordonau, J.; Cortes, P.; Rodriguez, J.; Vargas, R. Predictive current control of grid-connected neutral-point-clamped converters to meet low voltage ride-through requirements. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 2423–2428. [Google Scholar]
- Rodriguez, J.; Pontt, J.; Silva, C.A.; Correa, P.; Lezana, P.; Cortés, P.; Ammann, U. Predictive current control of a voltage source inverter. IEEE Trans. Ind. Electron. 2007, 54, 495–503. [Google Scholar] [CrossRef]
- Vargas, R.; Rodríguez, J.; Ammann, U.; Wheeler, P.W. Predictive current control of an induction machine fed by a matrix converter with reactive power control. IEEE Trans. Ind. Electron. 2008, 55, 4362–4371. [Google Scholar] [CrossRef]
- Kouro, S.; Cortés, P.; Vargas, R.; Ammann, U.; Rodríguez, J. Model predictive control—A simple and powerful method to control power converters. IEEE Trans. Ind. Electron. 2008, 56, 1826–1838. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Z.; Li, K.; Zhang, P.; Gao, F. Predictive current control for voltage source inverters considering dead-time effect. CES Trans. Electr. Mach. Syst. 2020, 4, 35–42. [Google Scholar] [CrossRef]
- Akter, M.P.; Mekhilef, S.; Tan, N.M.L.; Akagi, H. Model predictive control of bidirectional AC-DC converter for energy storage system. J. Electr. Eng. Technol. 2015, 10, 165–175. [Google Scholar] [CrossRef]
- Bighash, E.Z.; Sadeghzadeh, S.M.; Ebrahimzadeh, E.; Blaabjerg, F. High quality model predictive control for single phase grid-connected photovoltaic inverters. Electr. Power Syst. Res. 2018, 158, 115–125. [Google Scholar] [CrossRef]
- Lunardi, A.; Conde, D.E.R.; de Assis, J.; Fernandes, D.A.; Sguarezi Filho, A.J. Model predictive control with modulator applied to grid inverter under voltage distorted. Energies 2021, 14, 4953. [Google Scholar] [CrossRef]
- Shan, Y.; Hu, J.; Guerrero, J.M. A model predictive power control method for PV and energy storage systems with voltage support capability. IEEE Trans. Smart Grid 2019, 11, 1018–1029. [Google Scholar] [CrossRef]
- Li, X.; Shadmand, M.B.; Balog, R.S.; Rub, H.A. Model predictive decoupled power control for single-phase grid-tied inverter. In Proceedings of the 2015 IEEE Power and Energy Conference at Illinois (PECI), Champaign, IL, USA, 20–21 February 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–7. [Google Scholar]
- Hu, J.; Zhu, J.; Dorrell, D.G. Model predictive control of grid-connected inverters for PV systems with flexible power regulation and switching frequency reduction. IEEE Trans. Ind. Appl. 2014, 51, 587–594. [Google Scholar] [CrossRef]
- Hu, J.; Xu, Y.; Cheng, K.W.; Guerrero, J.M. A model predictive control strategy of PV-Battery microgrid under variable power generations and load conditions. Appl. Energy 2018, 221, 195–203. [Google Scholar] [CrossRef]
- Shan, Y.; Hu, J.; Chan, K.W.; Fu, Q.; Guerrero, J.M. Model predictive control of bidirectional DC–DC converters and AC/DC interlinking converters—A new control method for PV-wind-battery microgrids. IEEE Trans. Sustain. Energy 2018, 10, 1823–1833. [Google Scholar] [CrossRef]
- Yoo, D.K.; Wang, L. A model predictive resonant controller for grid-connected voltage source converters. In Proceedings of the IECON 2011-37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, VIC, Australia, 7–10 November 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 3082–3086. [Google Scholar]
- Cordero, R.; Estrabis, T.; Brito, M.A.; Gentil, G. Development of a Resonant Generalized Predictive Controller for Sinusoidal Reference Tracking. IEEE Trans. Circuits Syst. II Express Briefs 2021, 69, 1218–1222. [Google Scholar] [CrossRef]
- Yoo, D.K.; Wang, L.; Rogers, E. Model predictive resonant control of a three-phase voltage source converter with selective harmonic compensation. In Proceedings of the 2015 IEEE 24th International Symposium on Industrial Electronics (ISIE), Buzios, Brazil, 3–5 June 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1480–1485. [Google Scholar]
- Lunardi, A.; Conde, E.; Assis, J.; Meegahapola, L.; Fernandes, D.A.; Sguarezi Filho, A.J. Repetitive Predictive Control for Current Control of Grid-Connected Inverter Under Distorted Voltage Conditions. IEEE Access 2022, 10, 16931–16941. [Google Scholar] [CrossRef]
- Francis, B.A.; Wonham, W.M. The internal model principle of control theory. Automatica 1976, 12, 457–465. [Google Scholar] [CrossRef]
- Fayyaz, M.M.; Syed, I.M.; Meng, Y.; Aman, M.N. Comprehensive Predictive Control Model for a Three-Phase Four-Legged Inverter. Energies 2023, 16, 2650. [Google Scholar] [CrossRef]
- Meng, J.; Zhang, Z.; Zhang, G.; Ye, T.; Zhao, P.; Wang, Y.; Yang, J.; Yu, J. Adaptive model predictive control for grid-forming converters to achieve smooth transition from islanded to grid-connected mode. IET Gener. Transm. Distrib. 2023, 17, 2833–2845. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, Z.; Hu, B. Model predictive power control with Kalman filter for grid-tied inverter with parameter variation. IET Power Electron. 2022, 15, 621–630. [Google Scholar] [CrossRef]
- Hu, B.; Chen, Z.; Zhang, Z.; Deng, W.; Zhao, D. Model predictive DC-component power control for grid-connected inverters under unbalanced network. J. Power Electron. 2021, 21, 235–246. [Google Scholar] [CrossRef]
- Song, W.; Yang, Y.; Qin, W.; Wheeler, P. Switching State Selection for Model Predictive Control Based on Genetic Algorithm Solution in an Indirect Matrix Converter. IEEE Trans. Transp. Electrif. 2022, 8, 4496–4508. [Google Scholar] [CrossRef]
- Scoltock, J.; Geyer, T.; Madawala, U.K. A model predictive direct current control strategy with predictive references for MV grid-connected converters with LCL-filters. IEEE Trans. Power Electron. 2014, 30, 5926–5937. [Google Scholar] [CrossRef]
- Choi, J.-W.; Kim, Y.-K.; Kim, H.-G. Digital PLL control for single-phase photovoltaic system. IEE Proc.-Electr. Power Appl. 2006, 153, 40–46. [Google Scholar] [CrossRef]
- Li, C.; Liu, Z.; Wu, X.; He, F.; Lv, Z.; Li, J.; Tan, G. Analysis and Robustness Improvement of Finite-Control-Set Model Predictive Current Control for IPMSM With Model Parameter Mismatches. IEEE Access 2022, 10, 93381–93394. [Google Scholar] [CrossRef]
- Young, H.A.; Perez, M.A.; Rodriguez, J. Analysis of finite-control-set model predictive current control with model parameter mismatch in a three-phase inverter. IEEE Trans. Ind. Electron. 2016, 63, 3100–3107. [Google Scholar] [CrossRef]
- Umar, M.F.; Khan, A.; Easley, M.; D’Silva, S.; Nun, B.; Shadmand, M.B. Resonance Suppression based on Predictive Control of Grid-following Inverters with LCL Filter in Weak Grid Condition. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 4742–4748. [Google Scholar]
- Muñoz, C.; Rivera, M.; Villalón, A.; Baier, C.R.; Muñoz, J.; Ramirez, R.O.; Wheeler, P. Predictive Control with Current-Based Maximum Power Point-Tracking for On-Grid Photovoltaic Applications. Sustainability 2021, 13, 3037. [Google Scholar] [CrossRef]
- Ali, S.W.; Verma, A.K.; Terriche, Y.; Sadiq, M.; Su, C.-L.; Lee, C.-H.; Elsisi, M. Finite-Control-Set Model Predictive Control for Low-Voltage-Ride-Through Enhancement of PMSG Based Wind Energy Grid Connection Systems. Mathematics 2022, 10, 4266. [Google Scholar] [CrossRef]
- Young, H.A.; Marin, V.A.; Pesce, C.; Rodriguez, J. Simple finite-control-set model predictive control of grid-forming inverters with LCL filters. IEEE Access 2020, 8, 81246–81256. [Google Scholar] [CrossRef]
- Perez, M.A.; Rodriguez, J.; Fuentes, E.J.; Kammerer, F. Predictive control of AC–AC modular multilevel converters. IEEE Trans. Ind. Electron. 2011, 59, 2832–2839. [Google Scholar]
- Riar, B.S.; Geyer, T.; Madawala, U.K. Model predictive direct current control of modular multilevel converters: Modeling, analysis, and experimental evaluation. IEEE Trans. Power Electron. 2014, 30, 431–439. [Google Scholar] [CrossRef]
- Moon, J.-W.; Gwon, J.-S.; Park, J.-W.; Kang, D.-W.; Kim, J.-M. Model predictive control with a reduced number of considered states in a modular multilevel converter for HVDC system. IEEE Trans. Power Deliv. 2014, 30, 608–617. [Google Scholar] [CrossRef]
- Böcker, J.; Freudenberg, B.; The, A.; Dieckerhoff, S. Experimental comparison of model predictive control and cascaded control of the modular multilevel converter. IEEE Trans. Power Electron. 2014, 30, 422–430. [Google Scholar] [CrossRef]
- Yang, Y.; Wen, H.; Fan, M.; Xie, M.; Chen, R. Fast finite-switching-state model predictive control method without weighting factors for T-type three-level three-phase inverters. IEEE Trans. Ind. Inform. 2018, 15, 1298–1310. [Google Scholar] [CrossRef]
- Xue, C.; Ding, L.; Li, Y.; Zargari, N.R. Improved model predictive control for high-power current-source rectifiers under normal and distorted grid conditions. IEEE Trans. Power Electron. 2019, 35, 4588–4601. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Z.; Kazmierkowski, M.P.; Rodríguez, J.; Kennel, R. Robust predictive control of three-level NPC back-to-back power converter PMSG wind turbine systems with revised predictions. IEEE Trans. Power Electron. 2018, 33, 9588–9598. [Google Scholar] [CrossRef]
- Zhang, X.; Xie, Z.; Zhang, X.; Yang, S. Model Predictive Control of a DFIG-Based Wind Turbine Using Three-Level NPC Converter. In Proceedings of the 2021 IEEE International Conference on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), Jinan, China, 20–22 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 18–22. [Google Scholar]
- Zhang, H.; Ma, Z.; Li, Z.; Zhang, X.; Liao, Z.; Lin, G. Multivariable Sequential Model Predictive Control of LCL-type Grid Connected Inverter. In Proceedings of the 2021 IEEE International Conference on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), Jinan, China, 20–22 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 777–781. [Google Scholar]
- Sun, Y.; Zhang, Z.; Wang, Y.; Li, Z.; Rodriguez, J. Robust Predictive Control of Grid-Tied Modular Multilevel Converters for HVDC Systems with Virtual-Flux Based Online Inductance Estimation. IEEE Trans. Power Deliv. 2021, 37, 3189–3199. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, J.; Yang, H.; Fan, S. New insights into model predictive control for three-phase power converters. IEEE Trans. Ind. Appl. 2018, 55, 1973–1982. [Google Scholar] [CrossRef]
- Mora, A.; Cardenas, R.; Aguilera, R.P.; Angulo, A.; Lezana, P.; Lu, D.D.-C. Predictive optimal switching sequence direct power control for grid-tied 3L-NPC converters. IEEE Trans. Ind. Electron. 2020, 68, 8561–8571. [Google Scholar] [CrossRef]
- Komurcugil, H.; Guler, N.; Bayhan, S. Weighting factor free Lyapunov-function-based model predictive control strategy for single-phase T-type rectifiers. In Proceedings of the IECON 2020 The 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 4200–4205. [Google Scholar]
- Alam, K.S.; Akter, M.P.; Shakib, S.S.I.; Xiao, D.; Zhang, D.; Rahman, M.F. Lyapunov-function based predictive approach for load voltage control of four-leg inverter with an output LC filter. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 6880–6885. [Google Scholar]
- Dadu, A.M.; Mekhilef, S.; Soon, T.K. Lyapunov model predictive control to optimise computational burden, reference tracking and THD of three-phase four-leg inverter. IET Power Electron. 2019, 12, 1061–1070. [Google Scholar] [CrossRef]
- Wei, X.; Wang, H.; Wang, K.; Li, K.; Li, M.; Luo, A. Robust Two-Layer Model Predictive Control for Full-Bridge NPC Inverter-Based Class-D Voltage Mode Amplifier. Electronics 2019, 8, 1346. [Google Scholar] [CrossRef]
- Vazquez, S.; Montero, C.; Bordons, C.; Franquelo, L.G. Model predictive control of a VSI with long prediction horizon. In Proceedings of the 2011 IEEE International Symposium on Industrial Electronics, Gdansk, Poland, 27–30 June 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1805–1810. [Google Scholar]
- Mirza, S.; Hussain, A.; Kim, C.-H. Quasi-resonant FCS model predictive control for three phase grid connected highly intermittent PV-inverter with voltage support. Electr. Power Syst. Res. 2023, 221, 109413. [Google Scholar] [CrossRef]
- Kim, Y.; Tran, T.V.; Kim, K.-H. Robust EMPC-Based Frequency-Adaptive Grid Voltage Sensorless Control for an LCL-Filtered Grid-Connected Inverter. Electronics 2024, 13, 998. [Google Scholar] [CrossRef]
- Wang, L.; Chai, S.; Rogers, E.; Freeman, C.T. Multivariable repetitive-predictive controllers using frequency decomposition. IEEE Trans. Control Syst. Technol. 2011, 20, 1597–1604. [Google Scholar] [CrossRef]
- Komurcugil, H.; Altin, N.; Ozdemir, S.; Sefa, I. Lyapunov-function and proportional-resonant-based control strategy for single-phase grid-connected VSI with LCL filter. IEEE Trans. Ind. Electron. 2015, 63, 2838–2849. [Google Scholar] [CrossRef]
- Oyama, H.; Durand, H. Lyapunov-based economic model predictive control for online model discrimination. Comput. Chem. Eng. 2022, 161, 107769. [Google Scholar] [CrossRef]
- Oyama, H.; Messina, D.; Rangan, K.K.; Durand, H. Lyapunov-based economic model predictive control for detecting and handling actuator and simultaneous sensor/actuator cyberattacks on process control systems. Front. Chem. Eng. 2022, 4, 810129. [Google Scholar] [CrossRef]
- Narasingam, A.; Kwon, J.S.-I. Koopman Lyapunov-based model predictive control of nonlinear chemical process systems. AIChE J. 2019, 65, e16743. [Google Scholar] [CrossRef]
- Grandia, R.; Taylor, A.J.; Singletary, A.; Hutter, M.; Ames, A.D. Nonlinear model predictive control of robotic systems with control lyapunov functions. arXiv 2020, arXiv:2006.01229. [Google Scholar]
- Abad, M.G.N.M.; Ghadimi, A.A.; Ebadi, M.; Daeichian, A. Lyapunov-based model predictive control for a single-phase grid-connected cascaded multilevel asymmetrical inverter. Int. J. Electr. Power Energy Syst. 2023, 147, 108789. [Google Scholar] [CrossRef]
- Xia, Z.; Liu, Z.; Guerrero, J.M. Multi-Objective Optimal Model Predictive Control for Three-Level ANPC Grid-Connected Inverter. IEEE Access 2020, 8, 59590–59598. [Google Scholar] [CrossRef]
- Alquennah, A.N.; Trabelsi, M.; Rayane, K.; Vahedi, H.; Abu-Rub, H. Real-Time Implementation of an Optimized Model Predictive Control for a 9-Level CSC Inverter in Grid-Connected Mode. Sustainability 2021, 13, 8119. [Google Scholar] [CrossRef]
- Chen, Q.; Luo, X.; Zhang, L.; Quan, S. Model Predictive Control for Three-Phase Four-Leg Grid-Tied Inverters. IEEE Access 2017, 5, 2834–2841. [Google Scholar] [CrossRef]


| Switching States | Voltage Space Vector | ||
|---|---|---|---|
| V | |||
| 0 | 0 | 0 | |
| 0 | 0 | 1 | |
| 0 | 1 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 0 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 | |
| 1 | 1 | 1 | |
| Optimizing Parameter | Control Objective | Characteristic | Reference Frame | Cost Function | Reference |
|---|---|---|---|---|---|
| Power | To control active/reactive power | Long prediction horizon | SRF | [27] | |
| Harmonic suppression, Kalman filtering | SRF | [25,37,38] | |||
| LCL filter Resonance suppression | Optional current feedback | SRF | [44] | ||
| Current | Minimizing harmonics | Increased switching states, long prediction horizon | SP, SRF | [26,30] | |
| To regulate output current/voltage | Model predictive power control, MPPT-MPC | SRF | [45] | ||
| Regulate reactive power for LVRT | Priority-based weighting for P and Q injection, | RRF | [17,46] | ||
| To track ac reference signal, | Long prediction horizon, multilevel | SRF, SP, RRF | [26,47,48,49,50,51] | ||
| Reduced computational burden, robust control against parameter changes | SRF, RRF | [42,43,52,53,54,55] | |||
| Multivariable | SRF | [56] | |||
| Voltage | To track voltage command signal | Multiple vectors, a hybrid predictive controller, modulated switching | SRF | [57,58,59] | |
| Lyapunov function, robust, multilayer | SRF | [11,60,61,62,63] | |||
| Long prediction horizon | SRF | [64] | |||
| Internal model based | SRF | [30] | |||
| Quasi-resonant MPC | SRF | [65] |
| Prediction Steps | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Switching frequency (kHz) | 35.175 | 30.425 | 26.925 | 26.050 | 25.375 |
| THD (%) | 1.13 | 1.09 | 1.07 | 1.02 | 1.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mirza, S.; Hussain, A. New Approaches in Finite Control Set Model Predictive Control for Grid-Connected Photovoltaic Inverters: State of the Art. Solar 2024, 4, 491-508. https://doi.org/10.3390/solar4030023
Mirza S, Hussain A. New Approaches in Finite Control Set Model Predictive Control for Grid-Connected Photovoltaic Inverters: State of the Art. Solar. 2024; 4(3):491-508. https://doi.org/10.3390/solar4030023
Chicago/Turabian StyleMirza, Shakil, and Arif Hussain. 2024. "New Approaches in Finite Control Set Model Predictive Control for Grid-Connected Photovoltaic Inverters: State of the Art" Solar 4, no. 3: 491-508. https://doi.org/10.3390/solar4030023
APA StyleMirza, S., & Hussain, A. (2024). New Approaches in Finite Control Set Model Predictive Control for Grid-Connected Photovoltaic Inverters: State of the Art. Solar, 4(3), 491-508. https://doi.org/10.3390/solar4030023





