The Impact of Roof Material Profile and Pigmentation on the Performance of Photovoltaic Modules
Abstract
1. Introduction
2. Solution Procedures
2.1. Governing Equations and Heat Transfer
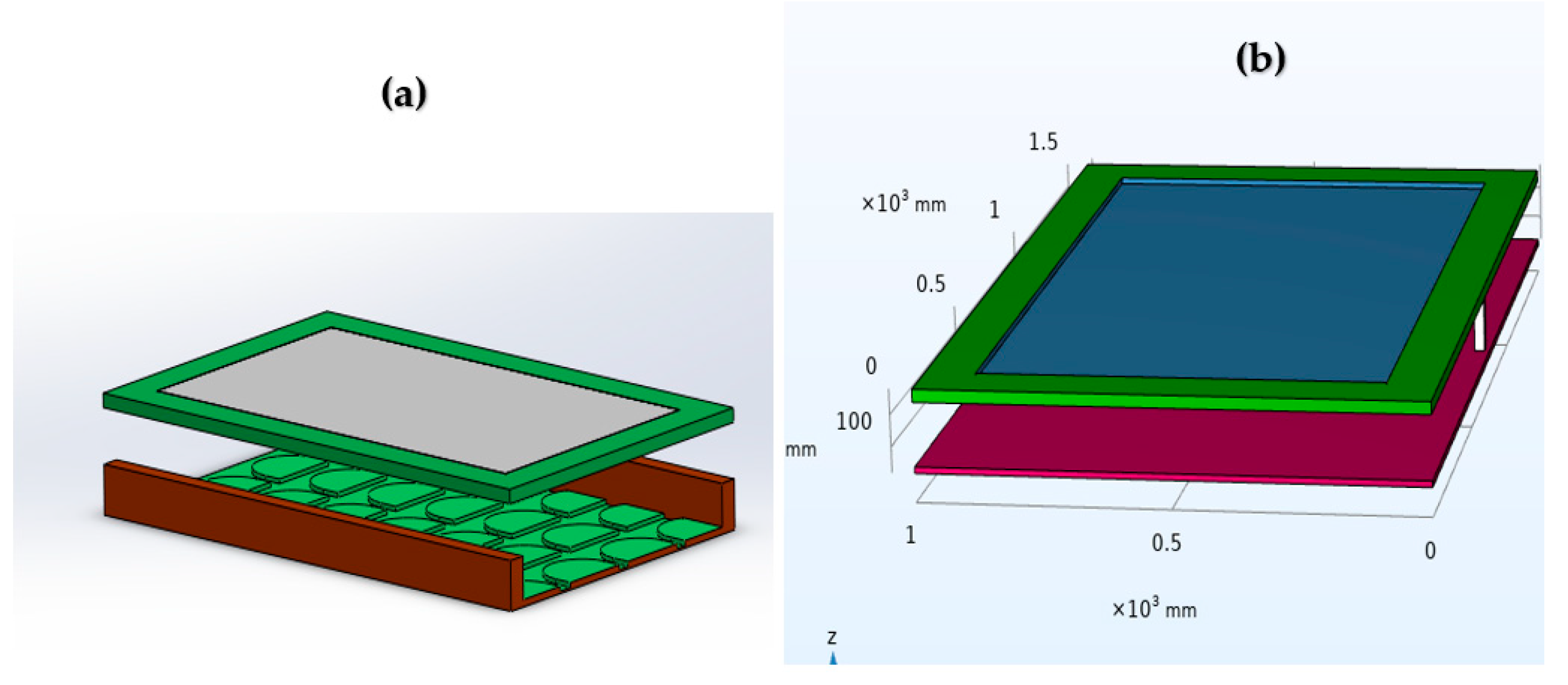
2.2. Model Development
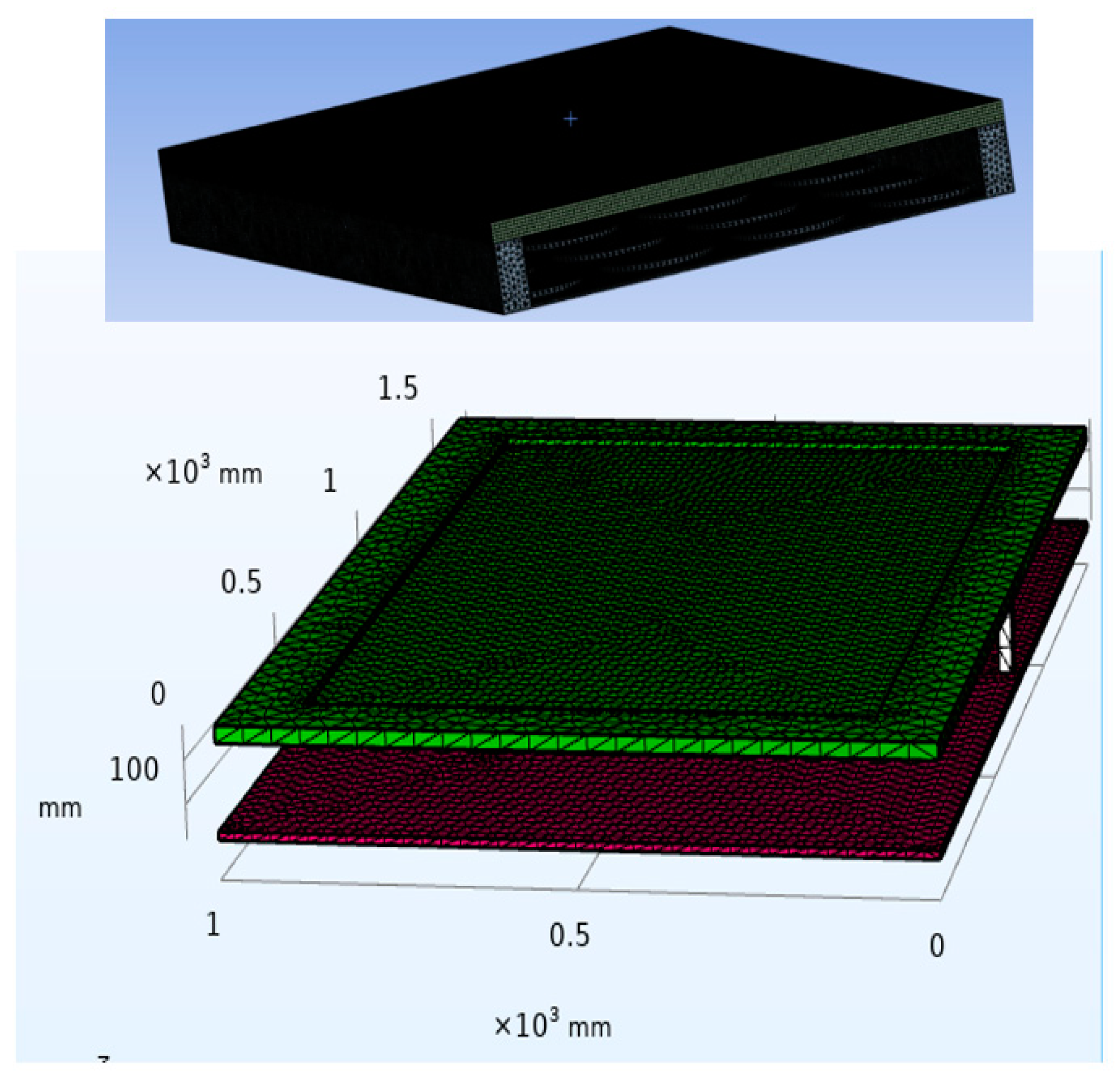
2.3. Simulation Procedures
2.4. Model Assumptions
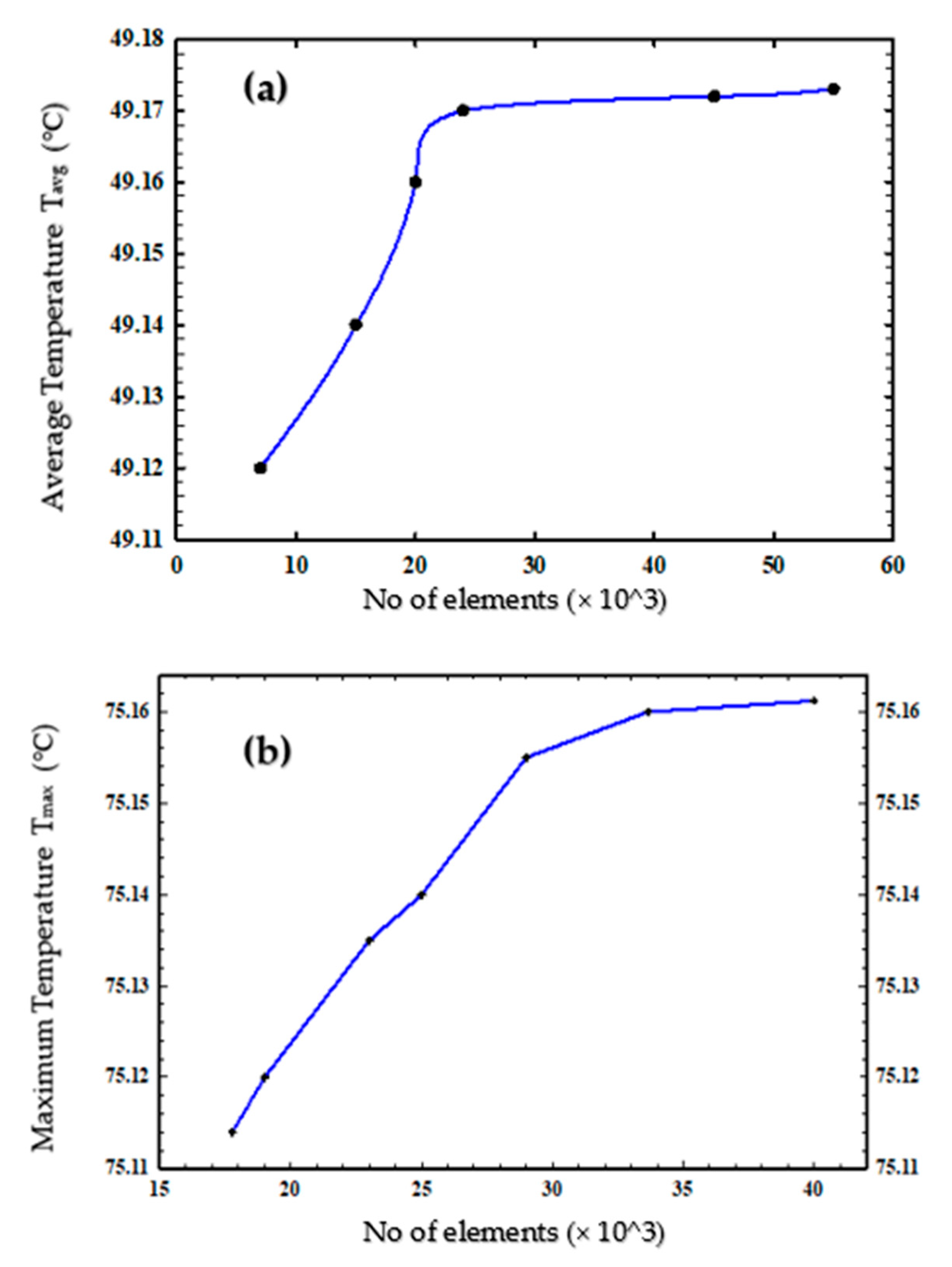
2.5. Model Validation Procedures
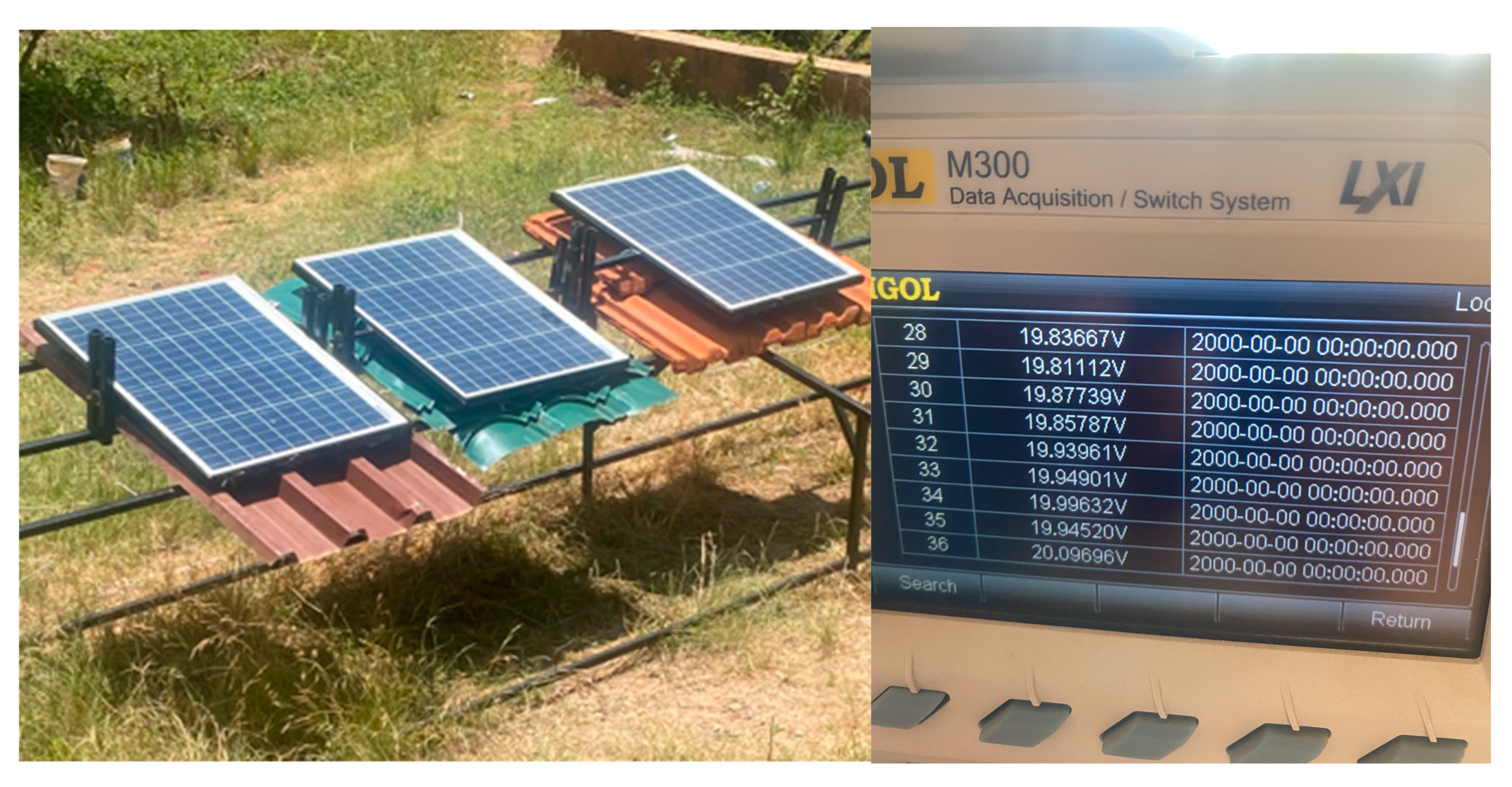
2.6. Experimental Method
3. Results and Discussion
3.1. Model Validation
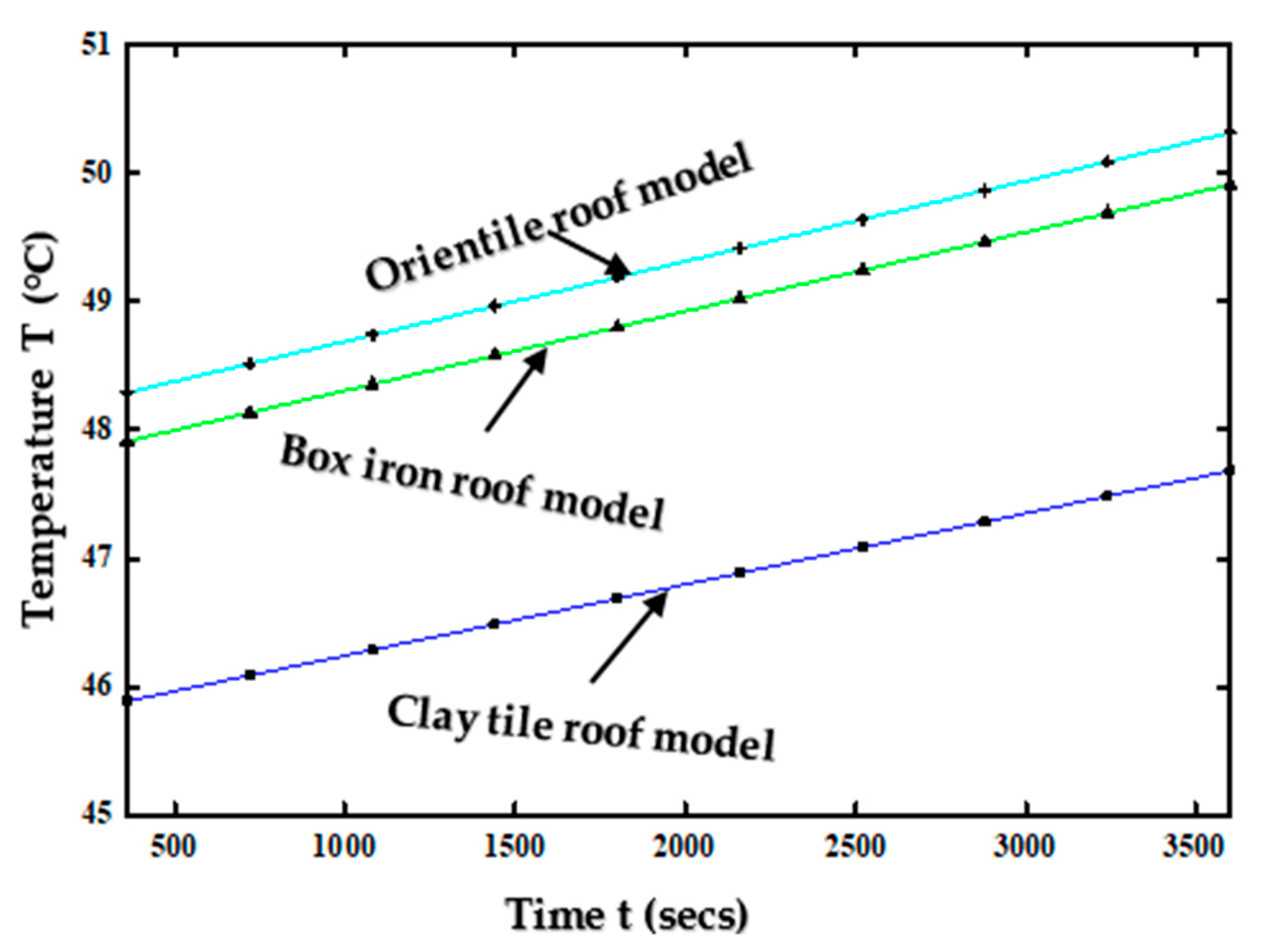
3.2. Effects of Roof Material Geometry
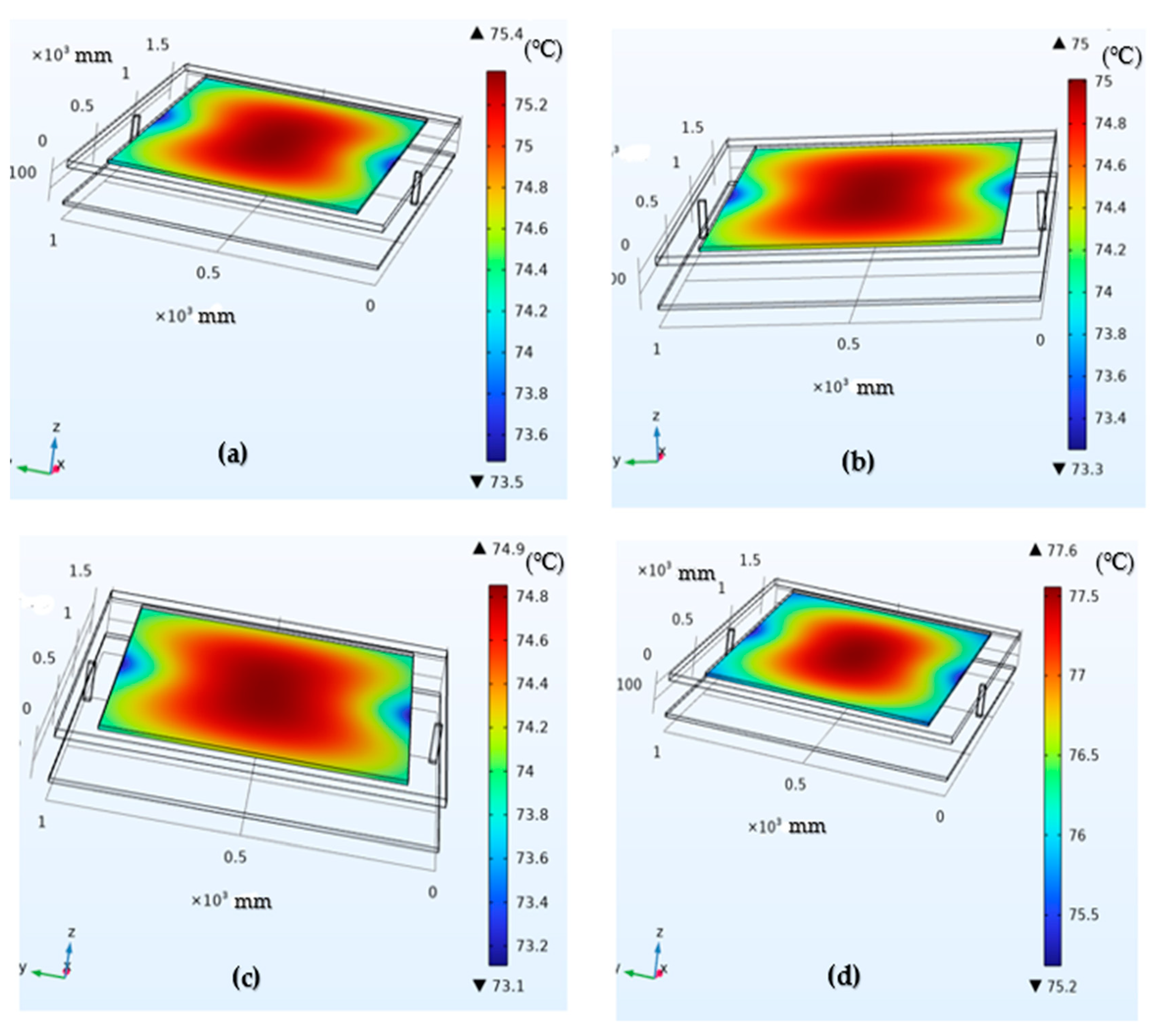
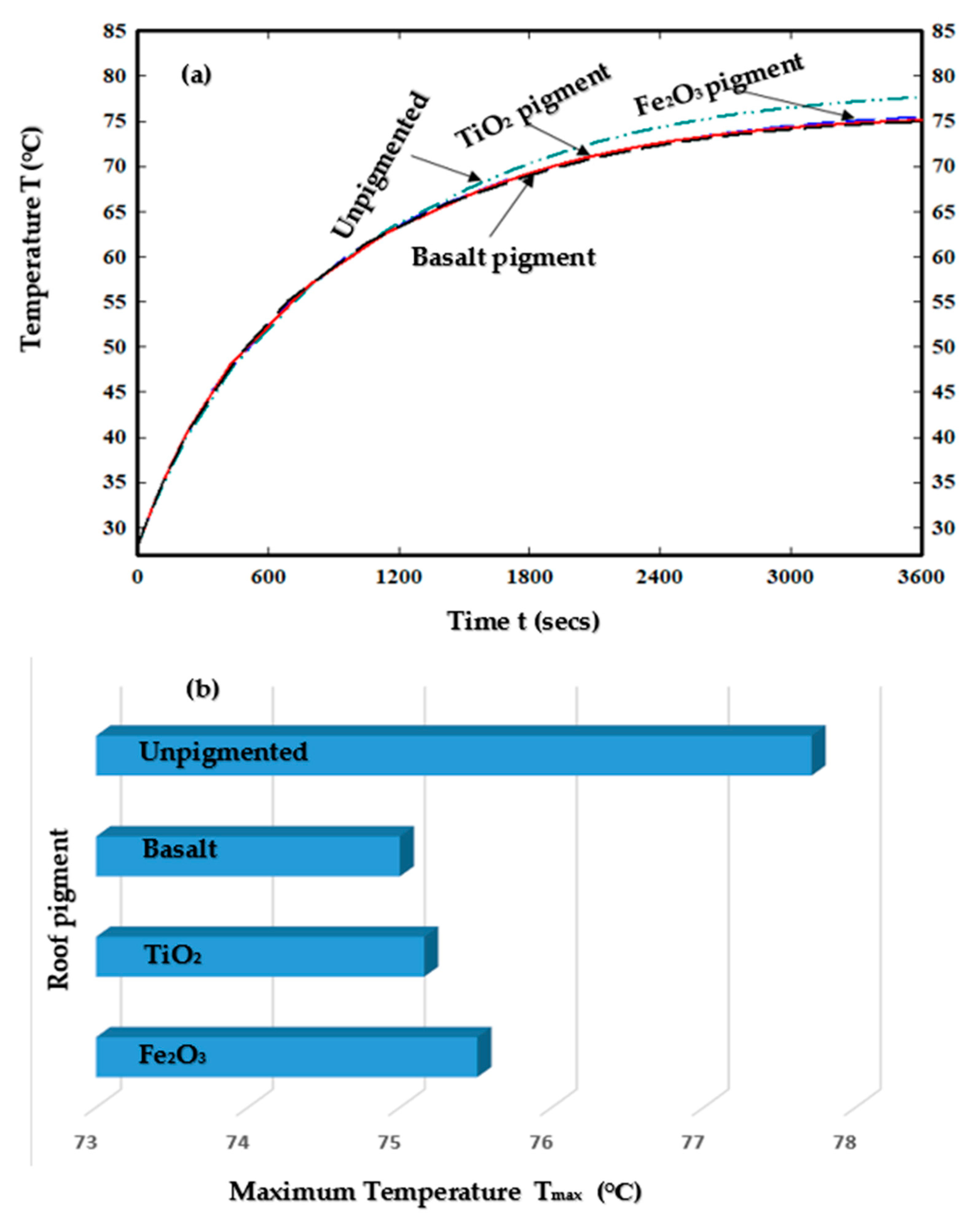
3.3. Effects of Roof Pigmentation
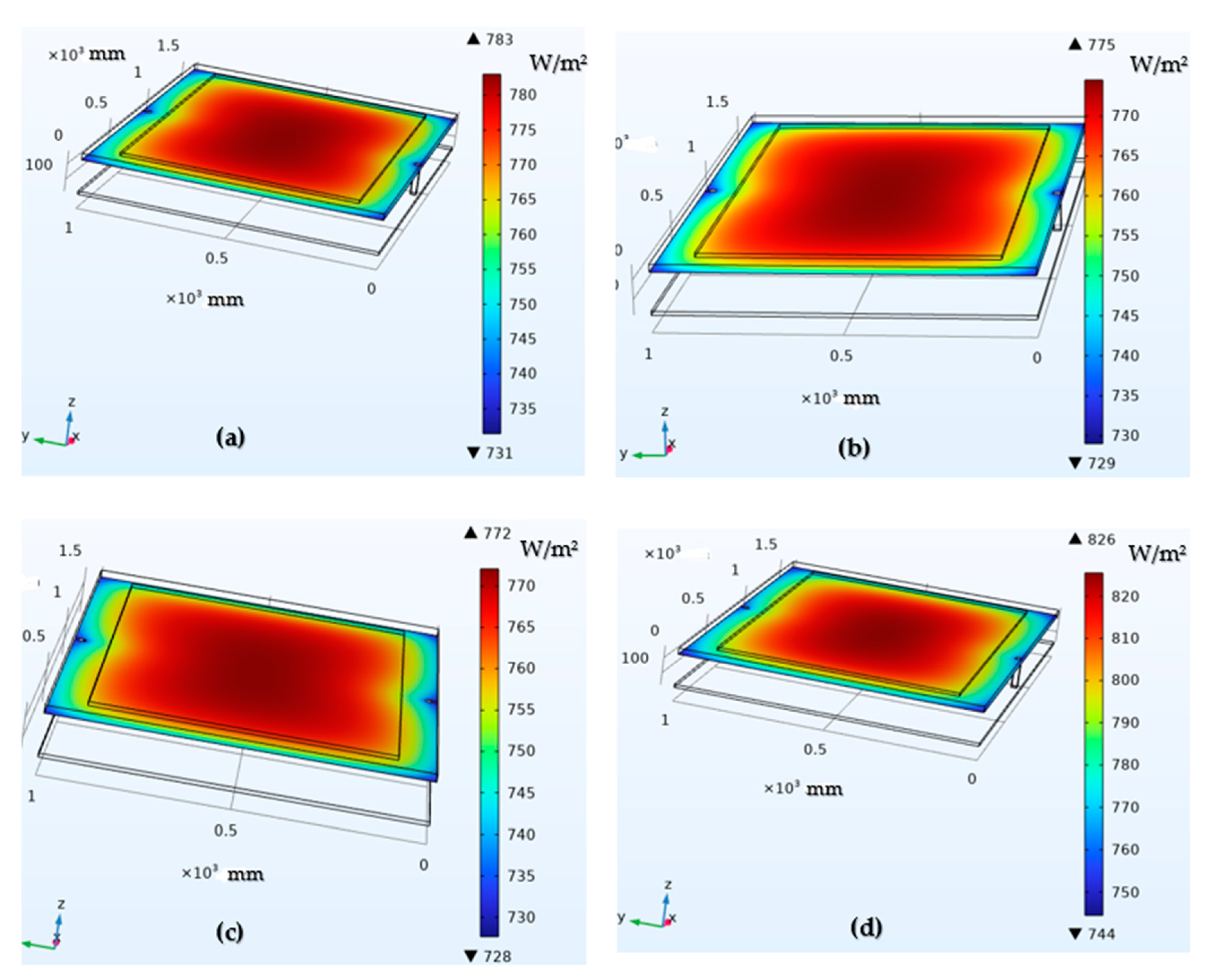
3.4. Surface Radiosity
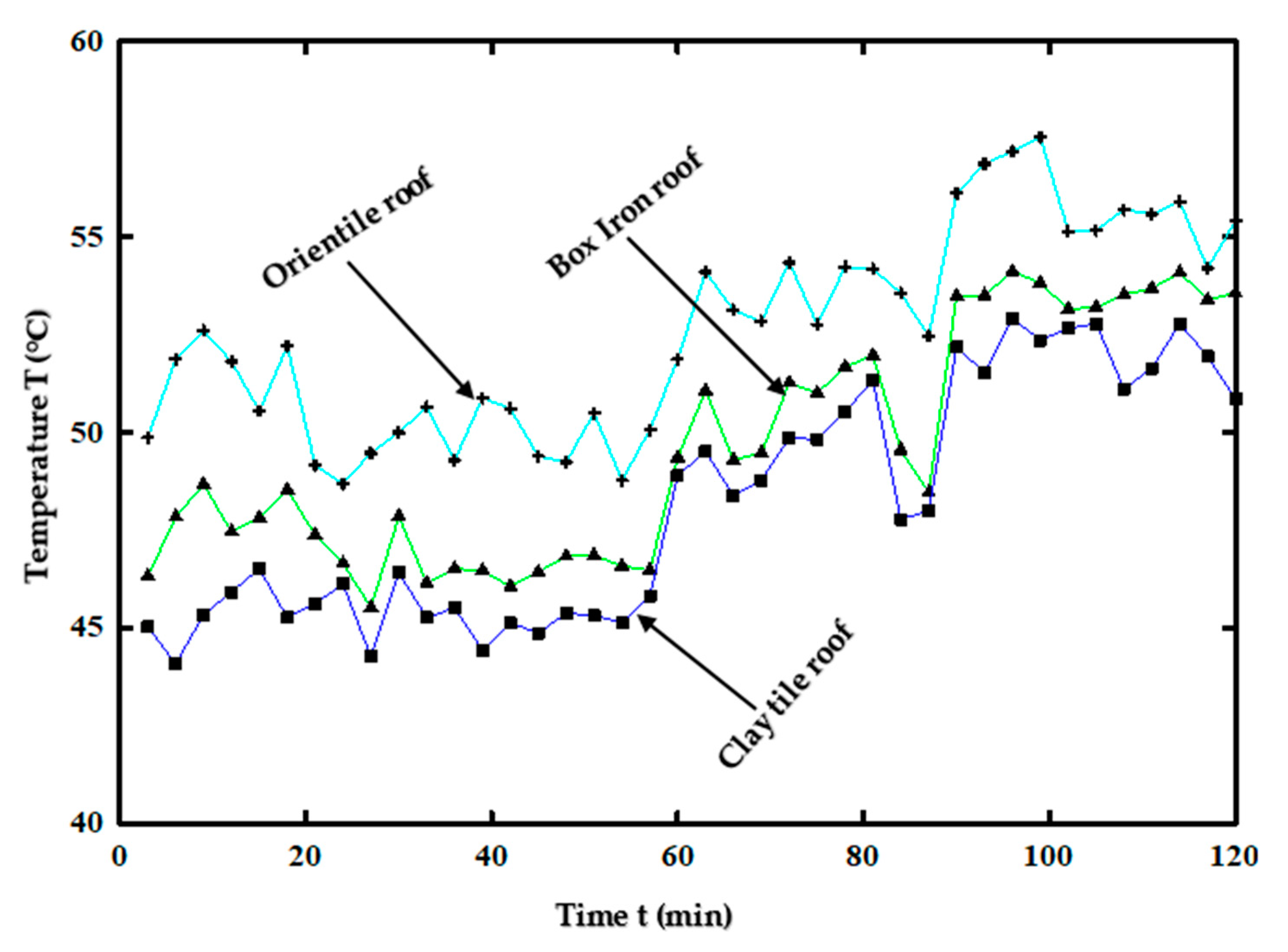
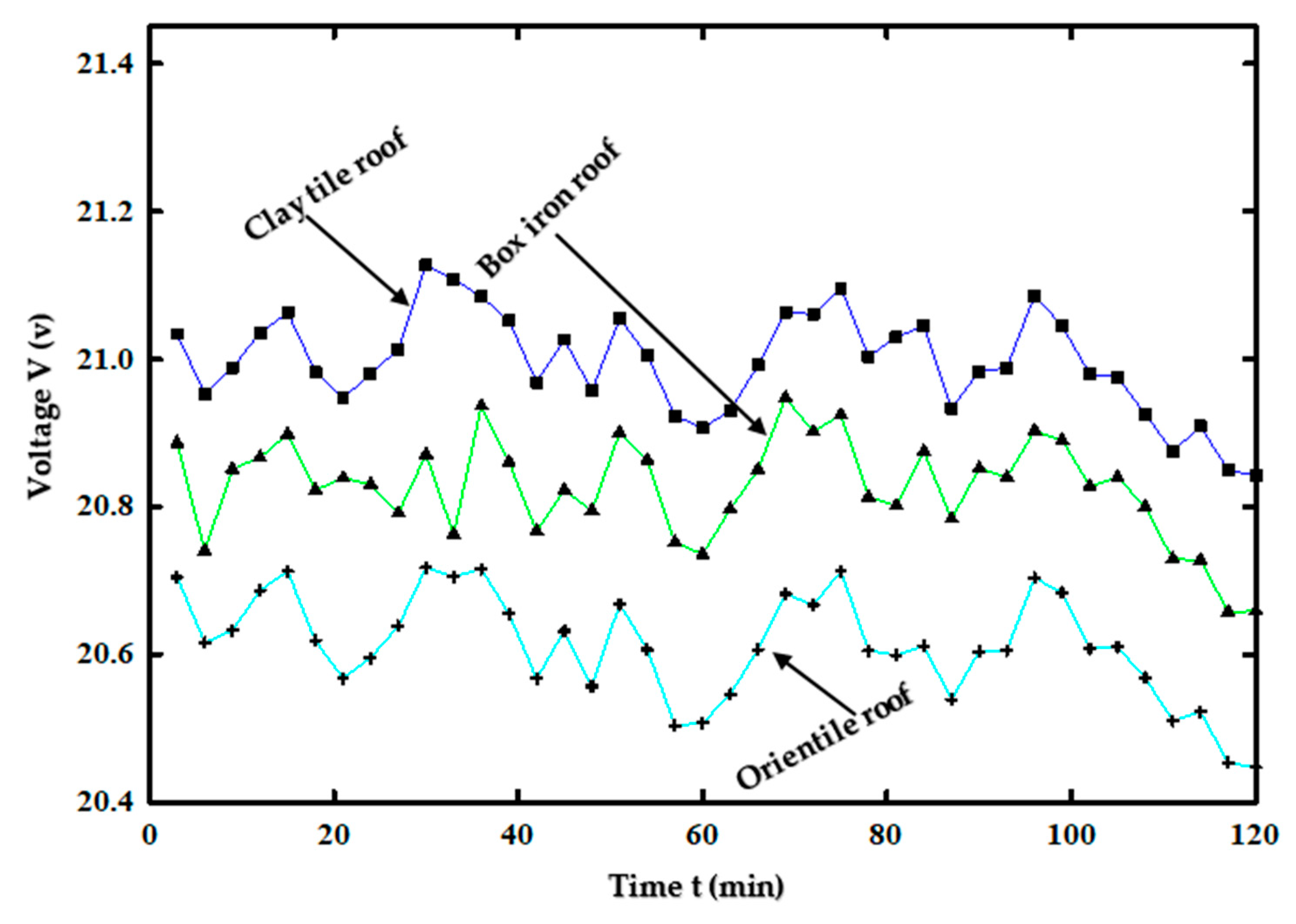
3.5. Experimental Results
3.6. Economic Implication and Sustainability
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Adounkpe, J.G.; Lawin, A.E.; Ahouannou, C.; Akiyo, R.O.L.; Sinsin, B.A. Modeling Solar Energy Transfer through Roof Material in Africa Sub-Saharan Regions. ISRN Renew. Energy 2013, 2013, 480137. [Google Scholar] [CrossRef]
- Roy, K.; Dani, A.A.; Ichhpuni, H.; Fang, Z.; Lim, J.B.P. Improving Sustainability of Steel Roofs: Life Cycle Assessment of a Case Study Roof. Appl. Sci. 2022, 12, 5943. [Google Scholar]
- Koumbem, W.N.D.; Ouédraogo, I.; Ilboudo, W.D.A.; Kieno, P.F. Numerical Study of the Thermal Performance of Three Roof Models in Hot and Dry Climates. Model. Numer. Simul. Mater. Sci. 2021, 11, 35–46. [Google Scholar]
- Zou, Q.; Li, Z.; Zou, F.; Zeng, X.; Wang, C.; Pan, Y. A study on the characteristics of roof wind field by wind tunnel test. J. Build. Eng. 2021, 43, 103155. [Google Scholar]
- Mahdavinejad, M.; Javanroodi, K. Impact of roof shape on air pressure, wind flow and indoor temperature of residential buildings. Int. J. Sustain. Build. Technol. Urban Dev. 2016, 7, 87–103. [Google Scholar] [CrossRef]
- Moustafa, W.; Hegazy, I.; Eldabosy, M. Roof geometry as a factor of thermal behavior: Simulation based study of using vaults and domes in the Middle East zone. Int. J. Low-Carbon Technol. 2018, 13, 204–211. [Google Scholar] [CrossRef]
- Bottarelli, M.; Bortoloni, M.; Zannoni, G.; Allen, R.; Cherry, N. CFD analysis of roof tile coverings. Energy 2017, 137, 391–398. [Google Scholar]
- Cherry, N.; Haig, J.; de With, G. Thermal Benefits of Tiled Roofs with Above-sheathing Ventilation. J. Build. Phys. 2009, 33, 171–194. [Google Scholar]
- Di Giuseppe, E.; Sabbatini, S.; Cozzolino, N.; Stipa, P.; D’Orazio, M. Optical properties of traditional clay tiles for ventilated roofs and implication on roof thermal performance. J. Build. Physic 2018, 42, 484–505. [Google Scholar] [CrossRef]
- Pisello, A.L. Thermal-energy analysis of roof cool clay tiles for application in historic buildings and cities. Sustain. Cities Soc. 2015, 219, 271–280. [Google Scholar]
- D’Orazio, M.; Stazi, A.; Di Perna, C.; Di Giuseppe, E. The physics of vented roofs in hot and temperate climates: Analysis of different strategies for the reduction of energy consumption and the improvement of environmental comfort. In Energy and Buildings: Efficiency, Air Quality and Conservation; Utrick, J.B., Ed.; Nova Science Publishers: Hauppauge, NY, USA, 2011; pp. 349–367. [Google Scholar]
- Di Perna, C.; Stazi, F.; Casalena, A.; D’orazio, M. Influence of the internal inertia of the building envelope on summertime comfort in buildings with high internal heat loads. Energy Build. 2011, 43, 200–206. [Google Scholar]
- Arsenović, M.; Pezo, L.; Radojević, Z. Response surface method as a tool for heavy clay firing process optimization: Roofing tiles. Process. Appl. Ceram. 2012, 6, 209–214. [Google Scholar] [CrossRef]
- Carrascosa, L.A.M.; Facio, D.S.; Mosquera, M.J. Producing superhydrophobic roof tiles. Nanotechnology 2016, 27, 95604. [Google Scholar] [CrossRef] [PubMed]
- Lesado, A.; James, A.J. Clay Roofing Tile: A Cool Roof? Open J. Sci. Technol. 2018, 1, 6–8. [Google Scholar] [CrossRef]
- Hamzah, N.; Firman, F.; Djalal, M.R. Characteristic Analysis of Solar Panels on Clay and Ceramic Roof Tiles. Prz. Elektrotechniczny 2022, 98, 39–45. [Google Scholar] [CrossRef]
- James, R.; Kirby, R. Selecting and Specifying Roof Coatings. Construction Specifier, July 2015. Available online: https://www.constructionspecifier.com/selecting-and-specifying-roof-coatings/#:~:text=The most common types of,asphalt%2C polyurethane%2C and silicone.&text=Acrylic water-based coatings are,white%2C tan%2C and grey (accessed on 25 August 2023).
- Saber, H.H. Energy & Buildings Experimental characterization of reflective coating material for cool roofs in hot, humid and dusty climate. Energy Build. 2021, 242, 110993. [Google Scholar] [CrossRef]
- Fortuno-Morte, M.; Serna-Gallén, P.; Beltrán-Mir, H.; Cordoncillo, E. A new series of environment-friendly reddish inorganic pigments based on AFeO3 (A = Ln, Y) with high NIR solar reflectance. J. Mater. 2021, 7, 1061–1073. [Google Scholar]
- Carrasco-Tenezaca, M.; Jatta, E.; Jawara, M.; Bradley, J.; Pinder, M.; D’Alessandro, U.; Knudsen, J.; Lindsay, S.W. Effect of roof color on indoor temperature and human comfort levels, with implications for malaria control: A pilot study using experimental houses in rural Gambia. Malar. J. 2021, 20, 423. [Google Scholar] [CrossRef]
- Maestri, A.; Luis, D.; Lamberts, R.; Guths, S. Energy & Buildings Measurement of solar reflectance of roofs: Effect of paint aging and a discussion on ASTM E1918 standard. Energy Build. 2021, 245, 111057. [Google Scholar] [CrossRef]
- Badin, G.; Ahmad, N.; Ali, H.M.; Ahmad, T.; Jameel, M.S. Effect of addition of pigments on thermal characteristics and the resulting performance enhancement of asphalt. Constr. Build. Mater. 2021, 302, 124212. [Google Scholar] [CrossRef]
- Pfaff, G. Iron oxide pigments. Phys. Sci. Rev. 2021, 6, 535–548. [Google Scholar] [CrossRef]
- Middlemas, S.; Fang, Z.Z.; Fan, P. A new method for production of titanium dioxide pigment. Hydrometallurgy 2013, 131–132, 107–113. [Google Scholar] [CrossRef]
- Chakartnarodom, P.; Prakaypan, W.; Ineure, P.; Chuankrerkkul, N.; Laitila, E.A.; Kongkajun, N. Properties and performance of the basalt-fiber reinforced texture roof tiles. Case Stud. Constr. Mater. 2020, 13, e00444. [Google Scholar] [CrossRef]
- Zubielewicz, M.; Kamińska-Tarnawska, E.; Ślusarczyk, A.; Langer, E. Prediction of heat build-up of solar reflecting coatings based on physico-chemical properties of complex inorganic colour pigments (CICPs). Prog. Org. Coat. 2011, 72, 65–72. [Google Scholar] [CrossRef]
- Badarnah, L. A biophysical framework of heat regulation strategies for the design of biomimetic building envelopes. Procedia Eng. 2015, 118, 1225–1235. [Google Scholar] [CrossRef]
- Garshasbi, S.; Santamouris, M. Solar Energy Materials and Solar Cells Using advanced thermochromic technologies in the built environment: Recent development and potential to decrease the energy consumption and fight urban overheating. Sol. Energy Mater. Sol. Cells 2019, 191, 21–32. [Google Scholar] [CrossRef]
- Raj, A.K.V.; Rao, P.P.; Divya, S.; Ajuthara, T.R. Terbium doped Sr2MO4 [M = Sn and Zr] yellow pigments with high infrared re fl ectance for energy saving applications. Powder Technol. 2017, 311, 52–58. [Google Scholar] [CrossRef]
- Pisello, A.L.; Rossi, F.; Cotana, F. Summer and winter effect of innovative cool roof tiles on the dynamic thermal behavior of buildings. Energies 2014, 7, 2343–2361. [Google Scholar] [CrossRef]
- Puesan, C.W.; Mestre, J.L. Technical evaluation of an improved paint coating with NIR pigments designed to reduce thermal discomfort caused by incident solar radiation: Application in the Caribbean area. Energy Procedia 2017, 115, 463–479. [Google Scholar] [CrossRef]
- Lv, J.; Tang, M.; Quan, R.; Chai, Z. Synthesis of solar heat-reflective ZnTiO3 pigments with novel roof cooling effect. Ceram. Int. 2019, 45, 15768–15771. [Google Scholar] [CrossRef]
- Alshayeb, M.; Chang, J.D. Photovoltaic Energy Variations Due to Roofing Choice. Procedia Eng. 2016, 145, 1104–1109. [Google Scholar] [CrossRef]
- Klugmann-Radziemska, E. The effect of temperature on the power drop in crystalline solar cells. Renew. Energy 2003, 28, 2675–2699. [Google Scholar]
- Sun, C.; Zou, Y.; Qin, C.; Zhang, B.; Wu, X. Temperature effect of photovoltaic cells: A review. Adv. Compos. Hybrid Mater. 2022, 5, 2675–2699. [Google Scholar] [CrossRef]
- Hossain, R.; Ahmed, A.J.; Islam, S.M.; Saha, N.; Debnath, P.; Kouzani, A.Z.; Mahmud, M.P. New Design of Solar Photovoltaic and Thermal Hybrid System for Performance Improvement of Solar Photovoltaic. Int. J. Photoenergy 2020, 2020, 8825489. [Google Scholar] [CrossRef]
- Karki, I.B. Effect of Temperature on the I-V Characteristics of a Polycrystalline Solar Cell. J. Nepal Phys. Soc. 2016, 3, 35–40. [Google Scholar] [CrossRef]
- Dwivedi, P.; Sudhakar, K.; Soni, A.; Solomin, E.; Kirpichnikova, I. Advanced cooling techniques of P.V. modules: A state of art. Case Stud. Therm. Eng. 2020, 21, 100674. [Google Scholar] [CrossRef]
- Dastbelaraki, A.H.; Yaghoubi, M.; Tavakol, M.M.; Rahmatmand, A. Numerical analysis of convection heat transfer from an array of perforated fins using the Reynolds averaged Navier–Stokes equations and large-eddy simulation method. Appl. Math. Model. 2018, 63, 660–687. [Google Scholar] [CrossRef]
- Motsanos, G. The Law of Conservation of Energy. Fluid Mech. Open Access 2017, 4, 172. [Google Scholar] [CrossRef]
- Bhat, T.; Chevali, V.; Liu, X.; Feih, S.; Mouritz, A.P. Fire structural resistance of basalt fibre composite. Compos. Part A Appl. Sci. Manuf. 2015, 71, 107–115. [Google Scholar] [CrossRef]
- Shilenje, Z.; Ongoma, V.; Ogwang, B. Upper Tropospheric and Stratospheric Ozone Over Equatorial East Africa; Case Study of Nairobi County, Kenya. Ethiop. J. Environ. Stud. Manag. 2015, 8, 290. [Google Scholar] [CrossRef][Green Version]
- Miller, W.A.; Desjarlais, A.O. Cool Color Roofs with Complex Inorganic Color Pigments Surface Properties Affecting Reflectance. Resid. Build. Technol. Des. Perform. Anal. Build. Ind. Trends. 2002, pp. 195–206. Available online: www.aceee.org/files/proceedings/2002/data/papers/SS02_Panel1_Paper16.pdf (accessed on 5 September 2023).
- Leow, W.Z.; Irwan, Y.M.; Safwati, I.; Irwanto, M.; Amelia, A.R.; Syafiqah, Z.; Fahmi, M.I.; Rosle, N. Simulation study on photovoltaic panel temperature under different solar radiation using computational fluid dynamic method. J. Phys. Conf. Ser. 2020, 1432, 012052. [Google Scholar]
- ASTM. AS for T and M. Designation D2244-93: Standard Test Method for calculation of Color Differences from Instrumentally Measured Color; American Society for Testing and Materials: West Conshohocken, PA, USA, 1997. [Google Scholar]
- Witman. Quantification of the Passive Cooling of Photo-Voltaics Using a Green Roof; The Pennsylvania State University: University Park, PA, USA, 2010. [Google Scholar]
- Sun, Q.; Ji, Y.; Sun, J. Improved Radiation Heat Transfer Model in RELAP5 for Compact Fuel Rod Bundles by the Absorption Factor Modification. Front. Energy Res. 2022, 10, 841631. [Google Scholar]
- Guimarães, B.D.S.; Farias, L.; Filho, D.O.; Kazmerski, L.; Sônia, A.; Diniz, A.C. Roof-mounted photovoltaic generator temperatue modeling based on common brazil roofing materials. Renew. Energy Environ. Sustain. 2022, 7, 5. [Google Scholar]






| Material | Thickness (mm) | Thermal Conductivity (W/m-K) | Specific Heat Capacity (J/kg-K) | Density (kg/m3) | Emissivity |
|---|---|---|---|---|---|
| Glass | 3 | 1.8 | 500 | 3000 | -- |
| Eva | 0.5 | 0.35 | 2090 | 960 | -- |
| Solar cell | 0.4 | 148 | 677 | 2330 | -- |
| Tedlar | 0.1 | 0.2 | 1250 | 1200 | 0.71 |
| Aluminum frame | 20 | 204 | 996 | 2707 | -- |
| Clay roof tile | 15.26 | 0.98 | 878 | 1702 | 0.88 |
| Box-profile metal roof | 0.27 | 80 | 460 | 7800 | 0.71 |
| Orientile metal roof | 0.34 | 84 | 502 | 6730 | 0.78 |
| Galvanized iron roof sheet | 0.35 | 80 | 460 | 7800 | 0.3 |
| Iron oxide (Fe2O3) pigmentation | 0.4 | 12 | 650 | 5240 | 0.74 |
| Titanium oxide (TiO2) pigmentation | 0.4 | 8.3 | 690 | 4230 | 0.87 |
| Basalt pigmentation | 0.4 | 0.035 | 850 | 2750 | 0.9 |
| Roofing Material | Cost per Square Meter (KES) | Total Cost for 200 Square Meters (KES) | Cost of Maintenance and Repair | Environmental Impact | Sustainability |
|---|---|---|---|---|---|
| Clay tile roof | 2000 | 400,000 | High | Environmentally friendly | Good |
| Box-Profile metal roof | 1020 | 204,000 | Low | Noisy during rainfall | Poor |
| Orientile metal roof | 1200 | 240,000 | Low | Noisy during rainfall, heat accumulation under intense heat | Poor |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aigbedion, N.; Njoka, F.; Munji, M. The Impact of Roof Material Profile and Pigmentation on the Performance of Photovoltaic Modules. Solar 2023, 3, 618-637. https://doi.org/10.3390/solar3040033
Aigbedion N, Njoka F, Munji M. The Impact of Roof Material Profile and Pigmentation on the Performance of Photovoltaic Modules. Solar. 2023; 3(4):618-637. https://doi.org/10.3390/solar3040033
Chicago/Turabian StyleAigbedion, Nosakhare, Francis Njoka, and Mathew Munji. 2023. "The Impact of Roof Material Profile and Pigmentation on the Performance of Photovoltaic Modules" Solar 3, no. 4: 618-637. https://doi.org/10.3390/solar3040033
APA StyleAigbedion, N., Njoka, F., & Munji, M. (2023). The Impact of Roof Material Profile and Pigmentation on the Performance of Photovoltaic Modules. Solar, 3(4), 618-637. https://doi.org/10.3390/solar3040033






