Picture Hesitant Fuzzy Clustering Based on Generalized Picture Hesitant Fuzzy Distance Measures
Abstract
:1. Introduction
- To develop the GPHDMs as a generalization of GPDMs.
- To initiate the properties of developed distance measures are investigated, and the generalization of developed theory is proved with the help of some remarks and examples.
- To explore the clustering problem by using the GPHDMs and the results obtained are explored.
- Some advantages of the proposed work are discussed, and some concluding remarks based on the summary of the proposed work and some future directions are added.
2. Literature Review
- ;
- .
3. Methodology of Development
- ;
- ;
- ;
- .
- ;
- ;
- ;
- .
4. Applications
Algorithm
| S. No | Comfort | Price | Fuel |
|---|---|---|---|
| Car 1 | |||
| Car 2 | |||
| Car 3 | |||
| Car 4 |
5. Conclusions
- We examined the GPHDM and defined the special cases like GPHHDM and GPHEDM.
- We worked on GPHNDM and defined special cases like GPHNHDM and GPHNEDM.
- We evaluated the application and show whose concepts are assigned the best results in distance measure.
- Finally, we proposed the numerical data table and described their applications with the help of an algorithm.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Klir, G.; Yuan, B. Fuzzy Sets and Fuzzy Logic; Prentice Hall: Upper Saddle River, NJ, USA, 1995; Volume 4, pp. 1–12. [Google Scholar]
- Dubois, D.J. Fuzzy Sets and Systems: Theory and Applications; Academic Press: New York, NY, USA; London, England; Toronto, Canada; Sydney, Australia; San Francisco, CA, USA, 1980; Volume 144, pp. 1–8. [Google Scholar]
- Yager, R.R.; Zadeh, L.A. An Introduction to Fuzzy Logic Applications in Intelligent Systems; Springer Science & Business Media: Wilmersdorf, Berlin, Germany, 2012; Volume 16, pp. 1–9. [Google Scholar]
- Kandel, A.; Lee, S.C.; Wang, C.Y. Fuzzy switching and automata. IEEE Trans. Syst. Man. Cybern. 1980, 10, 690. [Google Scholar] [CrossRef]
- Karwowski, W.; Mital, A. Potential applications of fuzzy sets in industrial safety engineering. Fuzzy Sets Syst. 1986, 19, 105–120. [Google Scholar] [CrossRef]
- Zimmermann, H.J. Applications of fuzzy set theory to mathematical programming. Inf. Sci. 1985, 36, 29–58. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Burillo, P.J.; Bustince, H. Intuitionistic fuzzy relations (Part I). Mathw. Soft Comput. 1995, 2, 5–38. [Google Scholar]
- Cuong, B.C. Picture fuzzy sets-First results. Part 1. Semin. Neuro-Fuzzy Syst. Appl. 2013, 4, 1–16. [Google Scholar]
- Cường, B.C. Picture fuzzy sets. J. Compu. Sci. Cybern. 2014, 30, 409. [Google Scholar] [CrossRef] [Green Version]
- Garg, H. Some picture fuzzy aggregation operators and their applications to multicriteria decision-making. Arab. J. Sci. Eng. 2017, 42, 5275–5290. [Google Scholar] [CrossRef]
- Wang, C.; Zhou, X.; Tu, H.; Tao, S. Some geometric aggregation operators based on picture fuzzy sets and their application in multiple attribute decision making. Ital. J. Pure Appl. Math 2017, 37, 477–492. [Google Scholar]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Torra, V.; Narukawa, Y. On hesitant fuzzy sets and decision. In Proceedings of the 2009 IEEE Inter Conference on Fuzzy Systems, Jeju, Korea, 20–24 August 2009; Volume 1, pp. 1378–1382. [Google Scholar]
- Xia, M.; Xu, Z. Hesitant fuzzy information aggregation in decision making. Int. J. Approx. Reason. 2011, 52, 395–407. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Ju, Y.; Yang, S. Hesitant intuitionistic fuzzy linguistic aggregation operators and their applications to multiple attribute decision making. J. Int. Fuzzy Syst. 2014, 27, 1187–1201. [Google Scholar]
- Zhu, B.; Xu, Z.; Xia, M. Dual hesitant fuzzy sets. J. Appl. Math 2012, 1, 1–19. [Google Scholar] [CrossRef]
- Mahmood, T.; Ullah, K.; Khan, Q. Some Aggregation Operators for Bipolar-Valued Hesitant Fuzzy Information. J. Fund Appl. Sci. 2018, 10, 240–245. [Google Scholar]
- Mahmood, T.; Ullah, K.; Jan, N.; Deli, I.; Khan, Q. Some Aggregation Operators for Bipolar-Valued Hesitant Fuzzy Information based on Einstein Operational Laws. J. Engine Appl. Sci. 2017, 36, 1–27. [Google Scholar]
- Ullah, K.; Mahmood, T.; Jan, N.; Broumi, S.; Khan, Q. On bipolar-valued hesitant fuzzy sets and their applications in multi-attribute decision making. Nucleus 2018, 55, 85–93. [Google Scholar]
- Wang, R.; Li, Y. Picture hesitant fuzzy set and its application to multiple criteria decision-making. Symmetry 2018, 10, 295. [Google Scholar] [CrossRef] [Green Version]
- Son, L.H. Generalized picture distance measure and applications to picture fuzzy clustering. Appl. Soft Comput. 2016, 46, 284–295. [Google Scholar] [CrossRef]
- Pandit, S.; Gupta, S. A comparative study on distance measuring approaches for clustering. Int. J. Res. Comput. Sci. 2011, 2, 29–31. [Google Scholar] [CrossRef] [Green Version]
- Ackermann, M.R.; Blömer, J.; Sohler, C. Clustering for metric and nonmetric distance measures. ACM Trans. Algorithms (TALG) 2010, 6, 59. [Google Scholar] [CrossRef]
- Pelekis, N.; Iakovidis, D.K.; Kotsifakos, E.E.; Kopanakis, I. Fuzzy clustering of intuitionistic fuzzy data. Int. J. Bus. Intell. Data Min. 2008, 3, 45–65. [Google Scholar] [CrossRef]
- Son, L.H.; Cuong, B.C.; Lanzi, P.L.; Thong, N.T. A novel intuitionistic fuzzy clustering method for geo-demographic analysis. Expert Syst. Appl. 2012, 39, 9848–9859. [Google Scholar] [CrossRef]
- Mahmood, T.; Ullah, K.; Khan, Q.; Jan, N. An approach toward decision-making and medical diagnosis problems using the concept of spherical fuzzy sets. Neural Comp. Appl. 2019, 31, 7041–7053. [Google Scholar] [CrossRef]
- Ali, Z.; Mahmood, T.; Yang, M.S. TOPSIS method based on complex spherical fuzzy sets with Bonferroni mean operators. Mathematics 2020, 8, 1739. [Google Scholar] [CrossRef]
- Ali, Z.; Mahmood, T.; Yang, M.S. Complex T-spherical fuzzy aggregation operators with application to multi-attribute decision making. Symmetry 2020, 12, 1311. [Google Scholar] [CrossRef]
- Mahmood, T. A Novel Approach towards Bipolar Soft Sets and Their Applications. J. Math. 2020, 2020, 4690808. [Google Scholar] [CrossRef]
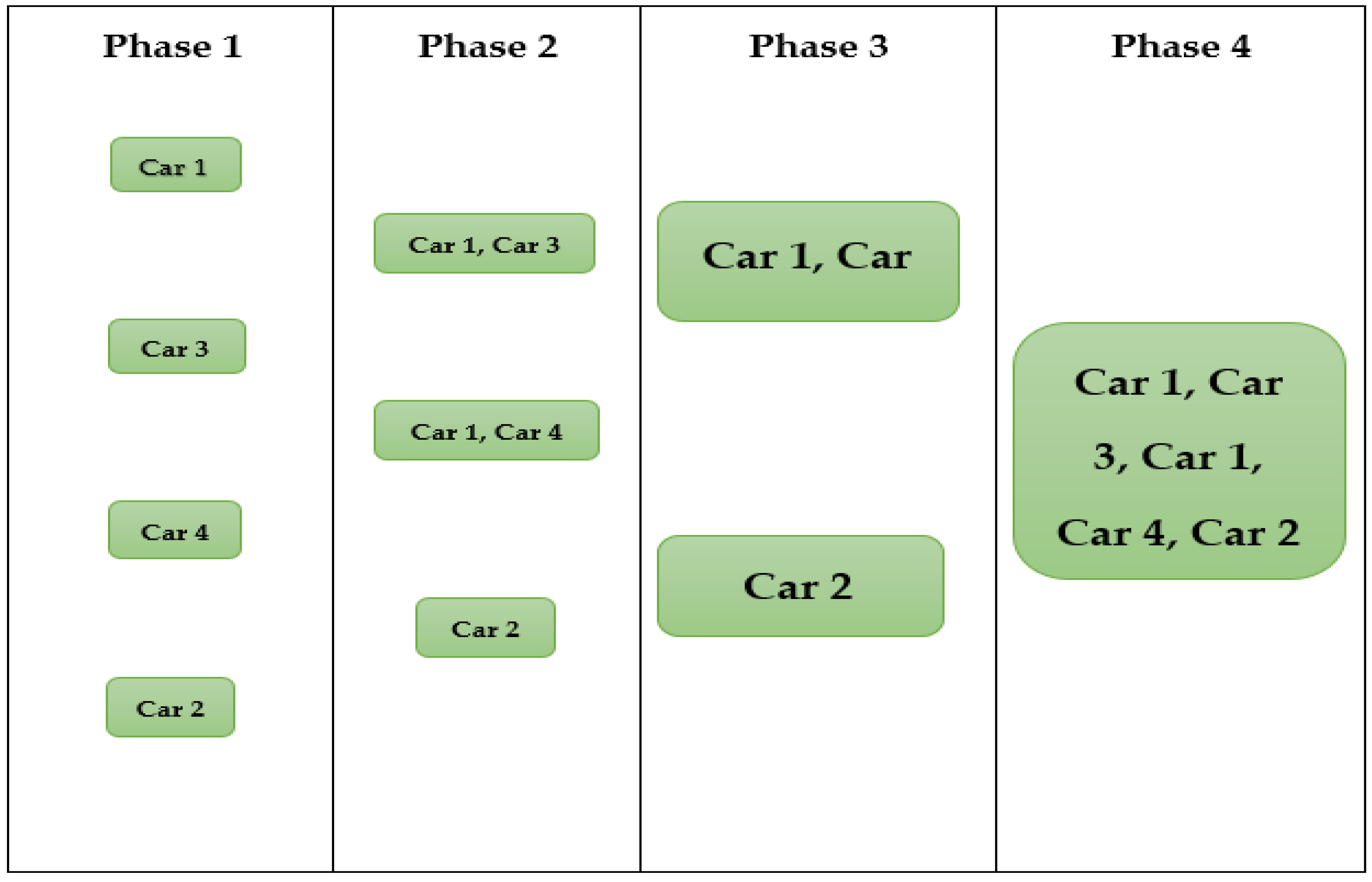
| D. Table | Comfort | Price | Fuel |
|---|---|---|---|
| Phases 1 | |||
| Car 1 | 0.23 | 0.28 | 0.27 |
| Car 2 | 0.27 | 0.32 | 0.25 |
| Car 3 | 0.20 | 0.25 | 0.25 |
| Car 4 | 0.25 | 0.30 | 0.20 |
| Phases 2 | |||
| Car 13 | 0.2 | 0.27 | 0.26 |
| Car 14 | 0.25 | 0.29 | 0.23 |
| Phases 3 | |||
| Car 1314 | 0.24 | 0.25 | 0.25 |
| Car 2 | 0.27 | 0.32 | 0.25 |
| D. T | Comfort | Price | Fuel |
|---|---|---|---|
| Car 13 | |||
| Car 14 |
| D. T | Comfort | Price | Fuel |
|---|---|---|---|
| Car 1314 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, Z.; Mahmood, T.; Ullah, K. Picture Hesitant Fuzzy Clustering Based on Generalized Picture Hesitant Fuzzy Distance Measures. Knowledge 2021, 1, 40-51. https://doi.org/10.3390/knowledge1010005
Ali Z, Mahmood T, Ullah K. Picture Hesitant Fuzzy Clustering Based on Generalized Picture Hesitant Fuzzy Distance Measures. Knowledge. 2021; 1(1):40-51. https://doi.org/10.3390/knowledge1010005
Chicago/Turabian StyleAli, Zeeshan, Tahir Mahmood, and Kifayat Ullah. 2021. "Picture Hesitant Fuzzy Clustering Based on Generalized Picture Hesitant Fuzzy Distance Measures" Knowledge 1, no. 1: 40-51. https://doi.org/10.3390/knowledge1010005
APA StyleAli, Z., Mahmood, T., & Ullah, K. (2021). Picture Hesitant Fuzzy Clustering Based on Generalized Picture Hesitant Fuzzy Distance Measures. Knowledge, 1(1), 40-51. https://doi.org/10.3390/knowledge1010005








