Numerical Evidence for a Bipartite Pure State Entanglement Witness from Approximate Analytical Diagonalization

Abstract

We show numerical evidence for a bipartite $d\times d$ pure state entanglement witness that is readily calculated from the wavefunction coefficients directly, without the need for the numerical computation of eigenvalues. This is accomplished by using an approximate analytic diagonalization of the bipartite state that captures dominant contributions to the negativity of the partially transposed state. We relate this entanglement witness to the Log Negativity, and show that it exactly agrees with it for the class of pure states whose quantum amplitudes form a positive Hermitian matrix. In this case, the Log Negativity is given by the negative logarithm of the purity of the amplitudes considered a density matrix. In other cases, the witness forms a lower bound to the exact, numerically computed Log Negativity. The formula for the approximate Log Negativity achieves equality with the exact Log Negativity for the case of an arbitrary pure state of two qubits, which we show analytically. We compare these results to a witness of entanglement given by the linear entropy. Finally, we explore an attempt to extend these pure state results to mixed states. We show that the Log Negativity for this approximate formula is exact for the class of pure state decompositions, for which the quantum amplitudes of each pure state form a positive Hermitian matrix.

1. Introduction

Entanglement is a key quantum resource for information tasks including timing/sensing [1], communication and networking [2], and computation [3]. It is a fundamental quantum phenomenon, first discussed by Schrödinger [4,5] in response to the criticisms of the incompleteness of quantum mechanics by Einstein, Podolsky, and Rosen [6], manifesting its effects at the atomic scale and possibly even the cosmic scale in theories of formation of spacetime itself [7]. One of the important research areas in modern quantum information science is the difficult issue of the quantification and characterization of entanglement from bipartite to multi-partite quantum systems (see [8,9] and references therein).

For pure states, an important measure of bipartite entanglement is the von Neuman entropy (VNE) $S\left({\rho }_a\right)=-{\sum }_n{\lambda }_n{log}_2{\lambda }_n$ of the reduced subsystem ${\rho }_a={\mathrm{Tr}}_b\left[{\rho }_{ab}\right]$ of the composite state ${\rho }_{ab}$. This, of course, requires the diagonalization of ${\rho }_a$ to obtain its eigenvalues $\left\{{\lambda }_n\right\}$. Another widely used way to compute the measure of pure state bipartite entanglement is the linear entropy $LE=1-\mathrm{Tr}\left[{\rho }_a^2\right]$, whose popularity stems from not having to compute the eigenvalues of ${\rho }_a$.

While the above measures of entanglement are applicable to pure states, entanglement measures for mixed states are harder to come by [8]. Measures of mixed state entanglement exist only for particular systems, such as Wotter’s concurrence [10] for a pair of qubits and for a qubit–qutrit system. A widely used “measure” of entanglement for both pure and mixed states, both discrete and continuous variable, is the Log Negativity ($LN$) [11,12,13] given by $LN\left({\rho }_{ab}\right)={log}_2(1+2\mathcal{N})$ where the negativity $\mathcal{N}$ is given by the sum of the absolute values of the negative eigenvalues of the partial transpose of ${\rho }_{ab}$. This entanglement monotone is based on the fact that a separable state ${\rho }_{ab}^{\left(sep\right)}={\sum }_i{p}_i{\rho }_a^{\left(i\right)}\otimes {\rho }_b^{\left(i\right)}$ remains positive under partial transpose. It is not a true entanglement measure since it does not detect bound entanglement (i.e., states that are entangled, yet have positive partial transposes).

In this work, we present numerical evidence for a pure state entanglement witness that exactly agrees with the $LN$ when the quantum amplitudes $\left\{c_{nm}\right\}\to C$ of ${|\psi \rangle }_{ab}={\sum }_{n=0}^{d-1}{\sum }_{m=0}^{d-1}{c}_{nm}{|n,m\rangle }_{ab}$ (a $d^2\times 1$ column vector) form a $d\times d$ Hermitian matrix, $C^{†}=C$, $C\ge 0$, with normalization $\langle {\psi }_{ab}|{\psi }_{ab}\rangle =\mathrm{Tr}\left[C{C}^{†}\right]=1$. That is,

$$\begin{array}{ccc}\mathrm{if}C& \stackrel{\mathrm{def}}{=}& {\displaystyle \frac{\rho }{\sqrt{\mathrm{Tr}\left[{\rho }^2\right]}}},\mathrm{with}\rho ={\rho }^{†},\Rightarrow L{N}_e\\ \Rightarrow L{N}_e& =& L{N}_a=-{log}_2\left(\mathrm{Tr}\left[{\rho }^2\right]\right)\mathrm{for}\mathrm{Tr}\left[\rho \right]=1,\end{array}$$

(1)

where $\mathrm{Tr}\left[{\rho }^2\right]$ is the purity of $\rho$. Here, we denote our approximate expression for the Log Negativity as $L{N}_a$ (a for approximate), and distinguish it from the exact expression for the Log Negativity $L{N}_e$ (e for exact) obtained by numerical computation of the eigenvalues of the partial transpose of the pure state density matrix ${\rho }_{ab}\stackrel{\mathrm{def}}{=}{|\psi \rangle }_{ab}\langle \psi |$).

Note that we use the term entanglement witness to mean a positive semi-definite approximation $L{N}_a\ge 0$ that acts as a lower bound (not necessarily the greatest lower bound) to the standard, computable, exact Log Negativity $L{N}_e$. To be a proper entanglement witness, the quantifier should not increase under local operations and classical communication (LOCC). We find that for the case of two qubits, $L{N}_a\equiv L{N}_e$ for arbitrary complex C (which we derive analytically) and does not increase under local operations, and hence is a proper entanglement witness. For more than two qubits, it is only when C is Hermitian that again $L{N}_a\equiv L{N}_e$ and does not increase under local operations. When C is an arbitrary complex matrix, $L{N}_a$ does increase under local operations; however, it never exceeds the exact value $L{N}_e$. Thus, $L{N}_a$ acts as a lower bound to the exact Log Negativity, $L{N}_a\left({\rho }_{ab}\right)\le L{N}_e\left({\rho }_{ab}\right)$ and can be said to “witness” the presence of entanglement in the bipartite system. We compare our witness with that of linear entropy $LE$.

While we are not able to provide a bona fide analytic derivation of $L{N}_a$, we do provide a plausibility argument modeled on the analytic diagonalization of correlated pure states of the form ${|\psi \rangle }_{ab}={\sum }_{n=0}^{d-1}{c}_n|n,n\rangle$ by Agarwal [13]. This form encompasses both discrete and continuous variable states (where the latter is truncated in each subspace to a maximum Fock number state $|M\rangle$ with $d=M+1$ such that $|c_{n>M}{|}^2<ϵ\ll 1$ for some arbitrary chosen $ϵ$). Agarwal’s derivation can be interpreted as a generalization of the analytic diagonalization of the Schmidt decomposition of the pure state ${|\psi \rangle }_{ab}$, which yields $L{N}_e$ in terms of the magnitudes of the complex quantum amplitudes $\left\{c_n\right\}$.

In brief, the goal and motivation of this article is to generalize and explore for higher bipartite states the curious exact form of an entanglement witness $L{N}_a$ for two qubits in terms of its quantum amplitudes (vs. eigenvalues of a partially transposed density matrix), and to explore how well it might reveal (“witness”) entanglement present in such higher-dimensional bipartite states. The analytic plausibility argument we provide surprisingly reveals that a simple generalization of the exact two qubit Log Negativity formula $L{N}_a$ non-trivially captures some of the entanglement for higher-dimensional bipartite states, which unexpectedly is exact and a proper entanglement witness when the coefficient matrix is Hermitian, $C=C^{†}$.

We subsequently attempt to extend our witness from pure states to mixed states, with limited success, though with interesting, non-trivial special cases, in the sense that we are able to provided numerical evidence that

$${\mathcal{LN}}_a^{avg}\left(\rho \right)\le L{N}_e\left(\rho \right)\le L{N}_a\left(\rho \right)$$

(2)

when the mixed state is written as a pure state decomposition (PSD) ${\rho }_{ab}={\sum }_i{p}_i|{\psi }_i{\rangle }_{ab}\langle {\psi }_i|$ with the quantum amplitude matrix $C_i$ of each pure state component $|{\psi }_i{\rangle }_{ab}={\sum }_{nm}{C}_{i,nm}{|n,m\rangle }_{ab}$ uniformly generated (over the Haar measure) as a positive Hermitian matrix, $C_i=C_i^{†}\ge 0$. In Equation (2), we have defined the average of our approximate Log Negativity on a PSD as

$${\mathcal{LN}}_a^{avg}\left({\rho }_{ab}\right)\stackrel{\mathrm{def}}{=}\sum _i{p}_{i}L{N}_a{\left(\right|{\psi }_i\rangle }_{ab}),$$

(3)

where the notation $L{N}_a{\left(\right|{\psi }_i\rangle }_{ab})$ is used to denote our witness formula for pure states, defined in Equation (11b). The rightmost term $L{N}_a\left(\rho \right)$ in Equation (2) is computed with our generalized mixed-state formula ansatz given in Equation (17c). Lastly, we find that the second inequality is saturated, $L{N}_e\left(\rho \right)=L{N}_a\left(\rho \right)$ in Equation (2), if the uniformly randomly generated $C_i$ matrices above are real, i.e., $C_i=C_i^T$. (A discussion of the uniform generation of Hermitian matrices over the Haar measure is given in Appendix B).

This paper is outlined as follows. In Section 2, we discuss Agarwal’s derivation [13] of the analytic diagonalization of correlated pure states of the form ${|\psi \rangle }_{ab}={\sum }_n{c}_n|n,n\rangle$ and present an analytic formula for $L{N}_e$ in terms of the the Schmidt coefficients of the pure state. In Section 3, we present our ansatz for an entanglement witness $L{N}_a$ and numerical evidence for it on the pure state ${|\psi \rangle }_{ab}={\sum }_{nm}{c}_{nm}|n,m\rangle$ based solely on its quantum amplitudes $\left\{c_{nm}\right\}$ without the need for numerical diagonalization of ${\rho }_{ab}={|\psi \rangle }_{ab}\langle \psi |$. We present numerical evidence that $L{N}_a\equiv L{N}_e$ when $\left\{c_{nm}\right\}\to C$, considered a complex matrix, is positive and Hermitian and that $L{N}_a=0$ on separable pure states. While not a formal proof, we present a plausibility argument leading to our formula for an approximate Log Negativity $L{N}_a$ inspired by the previous Agarwal’s derivation [13] in Section 2, based on an ansatz for the dominant analytic contributions to the negativity. For C, an arbitrary complex matrix (subject to normalization), we present numerical evidence that $L{N}_a$ acts as a lower bound to $L{N}_e$ (better than $LE$) and hence acts as an entanglement witness. For the case of two arbitrary qubits, we analytically show that our approximate formula for the Log Negativity agrees with the exact formula. In Section 4, we attempt to provide a generalization of $L{N}_a$ to mixed states that reduces to the original formula for pure states, and again does not require the numerical diagonalization of matrices derived from ${\rho }_{ab}$. This generalization is zero on separable states ${\rho }_{ab}={\sum }_i{p}_i{\rho }_a^{\left(i\right)}\otimes {\rho }_b^{\left(i\right)}$ only when either or both ${\rho }_a^{\left(i\right)},{\rho }_b^{\left(i\right)}$ are real. While this witness does detect a wide class of separable states, it does not detect them all (a notoriously difficult problem in its own right [8,9]). By examining Werner states of arbitrary dimension (mixing a generalized Bell state with a maximally mixed state of appropriate dimension), we are led to an ansatz for a mixed-state witness, for which we can numerically show that Equation (2) holds over pure state decompositions (PSDs) for which the quantum amplitudes of the pure state components, when considered $d\times d$ matrices, are positive and Hermitian. In Section 5, we discuss other approaches to bipartite pure-state entanglement quantities without matrix diagonalization, and possible relationship to our proposed approximate Log Negativity. In Section 6, we summarize our results and present our conclusions. This work also include several appendices provided to explore and further clarify certain topics raised in the main text. In Appendix A we explore various forms of our approximate Negativity and Log Negativity formulas for pure bipartite states. In Appendix B we provide a discussion of the methods used for the uniform generation of Hermitian matrices over the Haar measure utilized in the numerical explorations in this work. In Appendix C we provide a list and description of the various Log Negativity formulas, for both pure and mixed states used in this work. 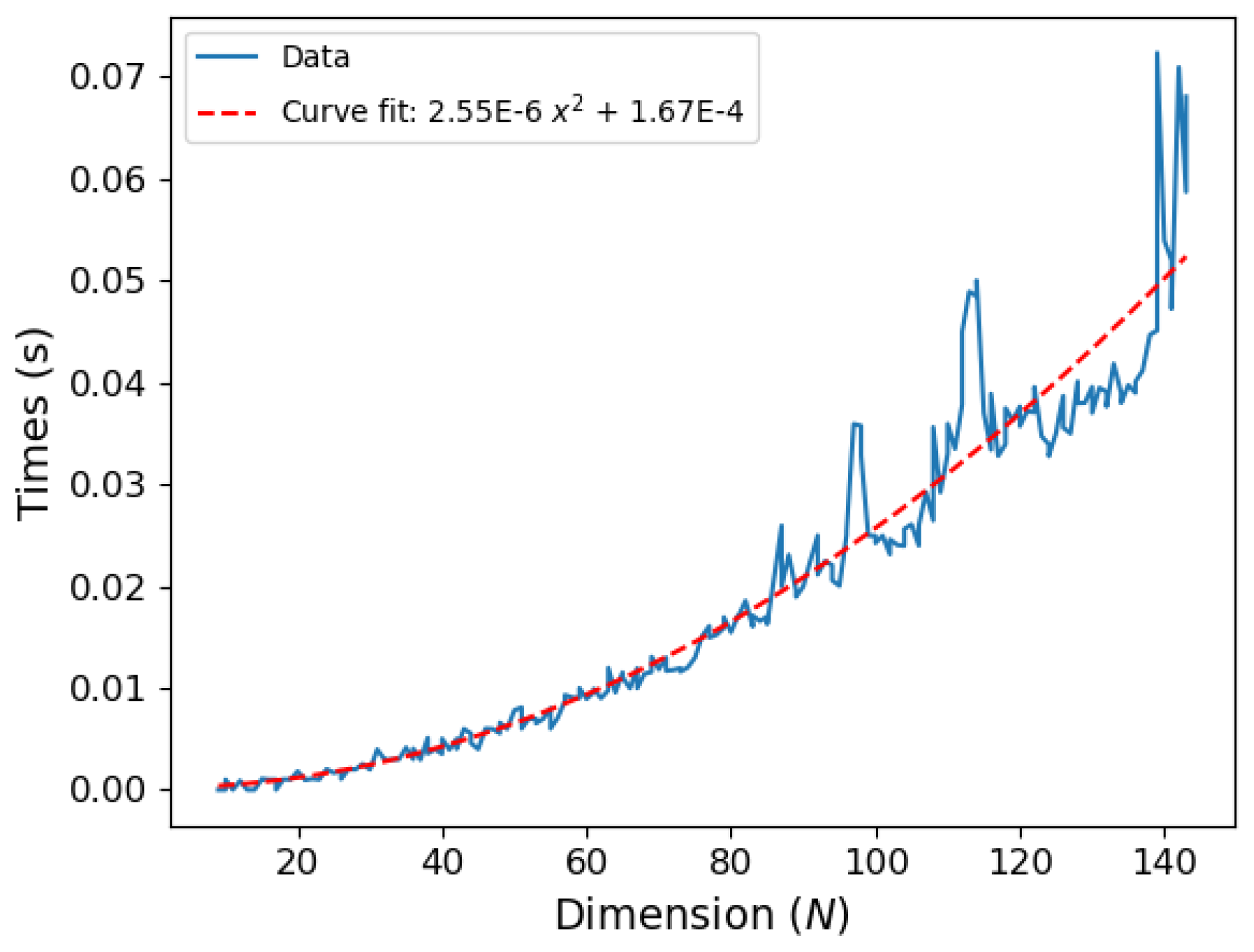Finally, in Appendix D we provide a numerical analysis of the computational scaling for computation of our approximate Log Negativty formula for pure bipartite states, versus the exact Log Negativity involving the computation of the eigenvalues of the partially transposed bipartite density matrix, as well as the computation of the linear entropy involving matrix multiplication.

The intent and focus of this work is on demonstrating that the information contained solely within the pure (mixed) state quantum amplitudes (matrix elements) directly provides inherent entanglement information that is normally associated with the eigenvalues of matrices derived from the quantum state (e.g., partial transpose, and reduced density matrices). While the numerical computation of eigenvalues does not present a practical impediment to the calculation of entanglement measures, it is the surprising relationship (and unexpected equality for certain classes of physically relevant pure and mixed states) of the proposed entanglement witness $L{N}_a$ to the exact (numerically computed) Log Negativity $L{N}_e$, that was the impetus for this current investigation (see Appendix C for a list and usage of the various Log Negativity functions used in this work).

2. The Log Negativity for Arbitrary Pure States

Any bipartite pure state ${|\psi \rangle }_{ab}\equiv {\sum }_{n=0}^M{\sum }_{m=0}^M{c}_{nm}{|nm\rangle }_{ab}$ with complex amplitudes $c_{nm}\in \mathbb{C}$ and computational dual orthonormal basis states ${|nm\rangle }_{ab}$ admits a Schmidt decomposition (SD) ${|\psi \rangle }_{ab}={\sum }_n\sqrt{{\sigma }_n}|u_n{v}_n{\rangle }_{ab}\to {\sum }_n\sqrt{{\sigma }_n}{|nn\rangle }_{ab}$ (written as $|u_n{v}_n{\rangle }_{ab}\to {|nn\rangle }_{ab}$ for notational simplicity) obtained by a singular value decomposition (SVD) [3] of the amplitudes $c_{nm}\to C=U\Sigma V^{†}$, with U and V unitary, and $\Sigma =\mathrm{diagonal}\{\sqrt{{\sigma }_1},\sqrt{{\sigma }_2},\dots \}>0$ and ${\sum }_n{\sigma }_n=1={\sum }_{n,m}{\left|c_{nm}\right|}^2=\mathrm{Tr}\left[C{C}^{†}\right]$. We are interested in computing the Log Negativity (LN) given by $LN={log}_2(1+2\mathcal{N})$, where the negativity $\mathcal{N}$ is the sum of the absolute values of the negative eigenvalues of the partial transpose ${\rho }_{ab}^{\Gamma }$ (on subsystem b) of the pure state density matrix ${\rho }_{ab}={|\psi \rangle }_{ab}\langle \psi |$. Here, M is the largest Fock state employed in each subsystem, set large enough so that $\left\{\right|c_{nm}{|}^2\le ϵ\}$ is negligible for $n,m>M$. This allows us to model both discrete and continuous variable states numerically.

2.1. LN for Diagonal Wavefunctions or SD

As shown in Agarwal ([13], p. 57), we can diagonalize ${\rho }_{ab}^{\Gamma }$ analytically as follows. First, let us consider a more general and pure state with diagonal complex amplitudes $c_{nm}=c_n{\delta }_{m,n}$. We then have

$$\begin{array}{cccc}\hfill {\rho }_{ab}& =& \sum _n\sum _m{c}_n{c}_m^{*}{|nn\rangle }_{ab}\langle mm|,\hfill & (4a)\\ \hfill \Rightarrow {\rho }_{ab}^{\Gamma }& =& \sum _n\sum _m{c}_n{c}_m^{*}{|nm\rangle }_{ab}\langle mn|,\hfill & (4b)\\ & =& \sum _n|c_n{|}^2{|nn\rangle }_{ab}\langle nn|\hfill \\ & +& {\displaystyle \frac{1}{2}}\sum _n\sum _{m\ne n}\left|c_n{c}_m\right|\left(e^{i{\theta }_{nm}}{|nm\rangle }_{ab}\langle mn|+e^{-i{\theta }_{nm}}{|mn\rangle }_{ab}\langle nm|\right),\hfill & (4c)\end{array}$$

where we define $c_n{c}_m^{*}=\left|c_n{c}_m\right|e^{i{\theta }_{nm}}$. Now, the last term in Equation (4c) can be written as

$$\begin{array}{ccc}\hfill e^{i{\theta }_{nm}}{|nm\rangle }_{ab}\langle mn|& +& e^{-i{\theta }_{nm}}{|mn\rangle }_{ab}\langle nm|\hfill \\ & =& |e_{n,m}^{+}\rangle \langle e_{n,m}^{+}|-|e_{n,m}^{-}\rangle \langle e_{n,m}^{-}|,& (5a)\\ \hfill |e_{n,m\ne n}^{\pm }\rangle & \equiv & {\displaystyle \frac{1}{\sqrt{2}}}\left(|nm\rangle \pm e^{-i{\theta }_{nm}}|mn\rangle \right).\hfill & (5b)\end{array}$$

Note that the set of eigenstates $\left\{\right|e_{n,m\ne n}^{\pm }\rangle ,|nn\rangle \}$ forms a complete orthonormal set which diagonalizes ${\rho }_{ab}^{\Gamma }$ and therefore allows us to read off the negative eigenvalue ${\lambda }_{n,m\ne n}^{-}=-\frac{1}{2}\left|c_n{c}_m\right|$ for $m\ne n$ in Equation (5a). We then conclude that

$$\begin{array}{cccc}\hfill {|\psi \rangle }_{ab}& =& \sum _n{c}_n|nn\rangle ,\hfill & (6a)\\ \hfill \Rightarrow {\mathcal{N}}^I& \stackrel{\mathrm{def}}{=}& {\displaystyle \frac{1}{2}}\sum _n\sum _{m\ne n}\left|c_n{c}_m\right|,\hfill & (6b)\\ \hfill \Rightarrow LN& =& {log}_2\left[1+\sum _n\sum _{m\ne n}\left|c_n{c}_m\right|\right],\hfill & (6c)\\ & =& {log}_2\left[{\left(\sum _n\left|c_n\right|\right)}^2\right],\hfill & (6d)\end{array}$$

where in the last line, we use $1={\sum }_n{\left|c_n\right|}^2$.

Note that for the case of an SD, we have $c_n\to \sqrt{{\sigma }_n}$ so that we have for an arbitrary bipartite pure state

$$L{N}^{\left(SD\right)}\equiv {log}_2\left[{\left(\sum _n\sqrt{{\sigma }_n}\right)}^2\right],$$

(7)

in terms of its Schmidt coefficients ${\sigma }_n$. However, as mentioned above, to obtain the Schmidt coefficients, one has to perform a SVD (or diagonalizaiton) on the pure state.

2.2. LN for NmmN States

Another class of relevant states for our discussion is generalizations of the N00N states, which we denote as $NmmN$ states, of the form $|NmmN\rangle \equiv \frac{1}{\sqrt{2}}\left(|nm\rangle +|mn\rangle \right)$. Then it is straightforward to show that the PT of this state is given by

$$\begin{array}{cccc}\hfill {\rho }^{\Gamma }& =& {\displaystyle \frac{1}{2}}\left(|nm\rangle \langle nm|+|mn\rangle \langle nm|+|nn\rangle \langle mm|+|mm\rangle \langle nn|\right),\hfill & (8a)\\ & \equiv & \left(|nm\rangle \langle nm|+|mn\rangle \langle nm|+|f_{nm}^{+}\rangle \langle f_{nm}^{+}|-|f_{nm}^{-}\rangle \langle f_{nm}^{-}|\right),\hfill & (8b)\\ & & |f_{n,m\ne n}^{\pm }\rangle \equiv {\displaystyle \frac{1}{\sqrt{2}}}\left(|nn\rangle \pm |mm\rangle \right),\hfill & (8c)\end{array}$$

where we define the orthonormal set of eigenstates $|f_{n,m\ne n}^{\pm }\rangle$ in Equation (8c). Note that the first two terms in Equation (8a) are diagonal and orthogonal to $|f_{n,m\ne n}^{\pm }\rangle$. From Equation (8b), we read off that ${\lambda }_{\left(NmmN\right)}^{-}=-1/2$ for all $n,m$ and so $\mathcal{N}=1/2\Rightarrow LN={log}_2(1+2\mathcal{N})=1$.

From the above, we note that if we have a pure state of the form $|\psi \rangle ={\sum }_{n,m}{c}_{nm}{\displaystyle \frac{1}{\sqrt{2}}}\left(|n,m\rangle +|m,n\rangle \right)$, for arbitrary complex $c_{nm}$, i.e., a superposition of $NmmN$ states, then each component state $|NmmN\rangle$ contributes a negativity of $1/2$ for each $n,m\ne n$ so that the total negativity is just

$$\begin{array}{cccc}\hfill |\psi \rangle & =& \sum _{n,m}{c}_{nm}{\displaystyle \frac{1}{\sqrt{2}}}\left(|nm\rangle +|mn\rangle \right),\hfill & (9a)\\ \hfill \Rightarrow {\mathcal{N}}^{II}& \stackrel{\mathrm{def}}{=}& {\displaystyle \frac{1}{2}}\sum _n\sum _{m\ne n}\left|c_{nm}{c}_{mn}\right|,\hfill & (9b)\\ \hfill \Rightarrow L{N}^{II}& =& {log}_2\left(1+2{\mathcal{N}}^{II}\right)={log}_2(1+\sum _n\sum _{m\ne n}|c_{nm}{c}_{mn}\left|\right).\hfill & (9c)\end{array}$$

3. Ansatz for an Entanglement Witness

From the previous section, we identify two types of states in the PT ${\rho }_{ab}^{\Gamma }$ and their contributions to the negativity: (without loss of generality and for notational simplicity, we treat $c_{nm}$ as real for now, and re-insert the absolute values at the very end of the discussion)

$$\begin{array}{cccc}\hfill |nm\rangle \langle mn|+|mn\rangle \langle nm|& \leftrightarrow & {\mathcal{N}}^I\equiv {\displaystyle \frac{1}{2}}\sum _{n,m\ne n}{c}_{nn}{c}_{mm}\hfill & (10a)\\ \hfill |nn\rangle \langle mm|+|mm\rangle \langle nn|& \leftrightarrow & {\mathcal{N}}^{II}\equiv {\displaystyle \frac{1}{2}}\sum _{n,m\ne n}{c}_{nm}{c}_{mn},\hfill & (10b)\end{array}$$

where Equation (10a) comes from states eigenstates $\left\{\right|e_{n,m\ne n}^{\pm }\rangle \}$ from Equation (5b) leading to the negativity in Equation (6b) (where $c_n\to c_{nn}$), and Equation (10b) comes from eigenstates $\left\{\right|f_{n,m\ne n}^{\pm }\rangle \}$ from Equation (8c) leading to the negativity in Equation (10b).

The main premise of our proposed entanglement witness (EW) is that these two types of terms constitute the majority contributions to the negativity for the general pure state ${|\psi \rangle }_{ab}={\sum }_{n,m}{c}_{nm}$. Below we argue that the LN can be lower bounded by the following expression built solely from the wavefunction amplitudes $c_{nm}$,

$$\begin{array}{cc}\hfill {\mathcal{N}}_a{(|\psi \rangle }_{ab})\stackrel{\mathrm{def}}{=}{\displaystyle \frac{1}{2}}\sum _n\sum _{m\ne n}\left|\mathrm{Det}\left(\begin{array}{cc}{c}_{nn}& c_{nm}\\ c_{mn}& c_{mm}\end{array}\right)\right|,& (11a)\\ \hfill L{N}_a{\left(\right|\psi \rangle }_{ab})={log}_2\left(1+2{\mathcal{N}}_a\right).& (11b)\end{array}$$

At first glance Equation (11a) looks a bit odd since if one were to take ${\mathcal{N}}_a={\mathcal{N}}^I+{\mathcal{N}}^{II}$ (again, subscript a for approximate) one would expect to sum over the permanent $\mathcal{P}\equiv |c_{nn}{c}_{mm}+c_{nm}{c}_{mn}|$ as opposed to the determinant $\mathcal{D}=|c_{nn}{c}_{mm}-c_{nm}{c}_{mn}|$ (We note that the closest related antisymmetric structure we have found is the norm-squared of the wedge product $D(u,v)={\sum }_{n<m}{|u_n{v}_n-u_m{v}_n|}^2$ used in Meyer and Wallach’s multiparticle global entanglement monotone Q [14] involving the pure states $u={\sum }_n{u}_n{|n\rangle }_a$ and $v={\sum }_m{v}_m{|m\rangle }_b$.) However, using $\mathcal{D}$ enforces ${\mathcal{N}}_a=0$ on separable (product) pure states (i.e., the Det is identically zero if $c_{nm}=a_n{b}_m$). As mentioned previously, the set of eigenstates $\left\{\right|e_{n,m\ne n}^{\pm }\rangle ,|nn\rangle \}$ giving rise to ${\mathcal{N}}^I$ forms an orthonormal subset, while the set of eigenstates $\left\{\right|f_{n,m\ne n}^{\pm }\rangle ,|nn\rangle \}$ giving rise to ${\mathcal{N}}^{II}$ does not. Thus, ${\mathcal{N}}^{II}$ is being “overcounted” in ${\mathcal{N}}_a={\mathcal{N}}^I+{\mathcal{N}}^{II}$ and we find that ${\mathcal{N}}_a\stackrel{\mathrm{def}}{=}{\mathcal{N}}^I-{\mathcal{N}}^{II}$ produces much better results. Additionally, the use of the latter minus sign assures that if $c_{nm}=\frac{1}{\sqrt{d}}{\delta }_{nm}$ then we obtain ${|\psi \rangle }_{ab}=\frac{1}{\sqrt{d}}{\sum }_n{|nn\rangle }_{ab}\equiv {|Bel{l}^{\left(d\right)}\rangle }_{ab}$, the d-dimensional maximally entangled Bell state, for which $L{N}_a=L{N}_e={log}_{2}d$.

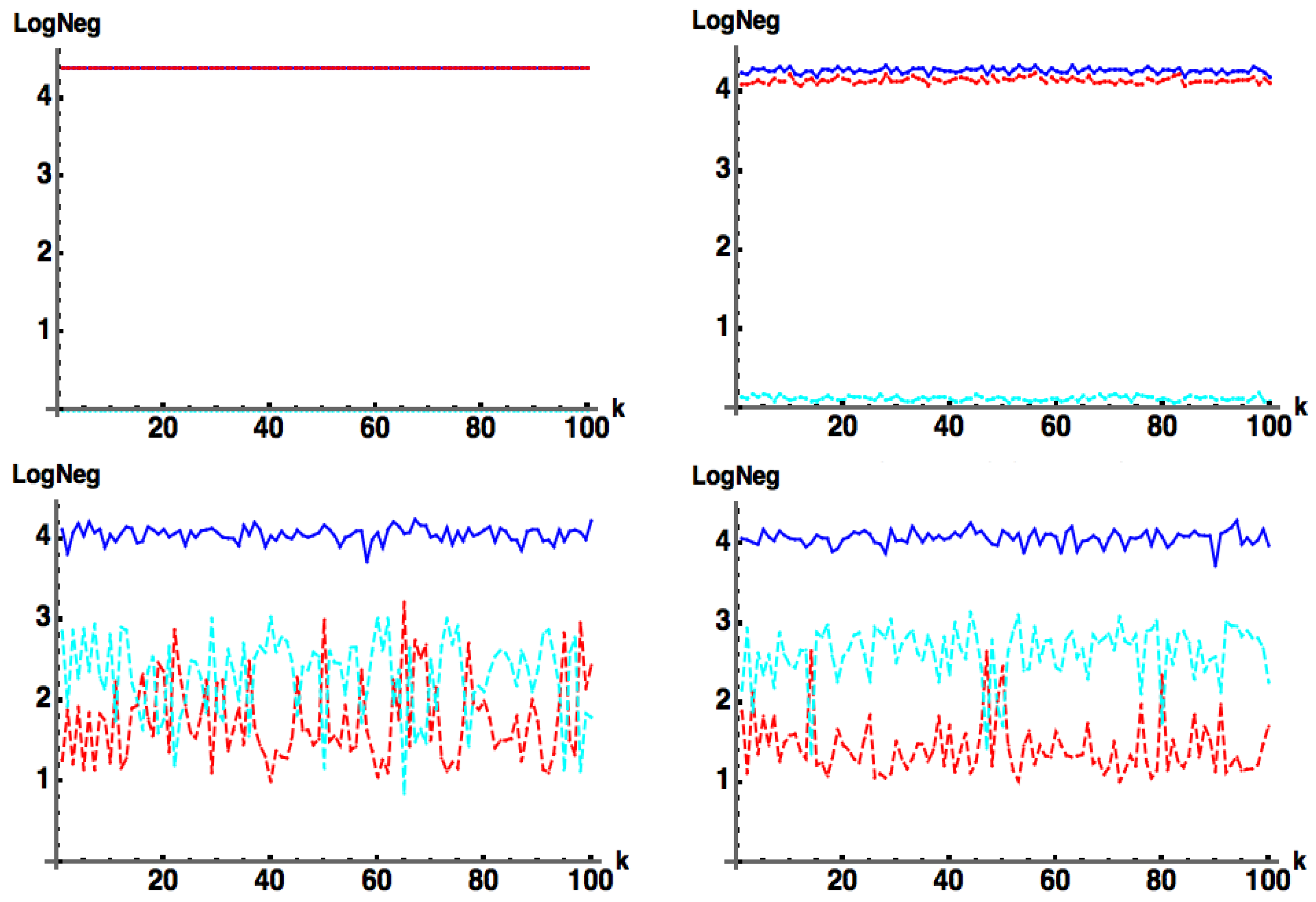
3.1. ${\mathit{LN}}_{\mathit{a}}$: Results

Surprisingly, we have found that Equation (11a,b) produces exactly $L{N}_e$ (obtained from numerically computed eigenvalues) of pure states, for which $c_{nm}$ is a positive Hermitian matrix with both deterministic and random entries as shown in Figure 1. Further, for the case when $c_{nm}$ is a positive Hermitian matrix $C\to \rho >0$, we can derive (see Equation (A7a) and Equation (A7b)) the non-trivial result

$$\begin{array}{cccc}\hfill C\to \rho >0\Rightarrow {\mathcal{N}}_a& =& {\displaystyle \frac{1}{2}}\left({\displaystyle \frac{{\left(\mathrm{Tr}\left[\rho \right]\right)}^2}{\mathrm{Tr}\left[{\rho }^2\right]}}-1\right)={\mathcal{N}}_e,\hfill & (12a)\\ \hfill \Rightarrow L{N}_a& =& {log}_2\left({\displaystyle \frac{{\left(\mathrm{Tr}\left[\rho \right]\right)}^2}{\mathrm{Tr}\left[{\rho }^2\right]}}\right)=L{N}_e,\hfill & (12b)\\ \hfill & \stackrel{\mathrm{Tr}\left[\rho \right]=1}{⟶}& -{log}_2\left(\mathrm{Tr}\left[{\rho }^2\right]\right),\hfill & (12c)\end{array}$$

where the second equalities in the above cannot be derived analytically, but rather are demonstrated numerically from plots such as Figure 1. Here, $C\to \rho =\left(U{\rho }_{diag}{U}^{†}\right)>0$, which is then flattened (stripped by rows) into an ${(M+1)}^2\times 1$ column vector representing ${|\psi \rangle }_{ab}$. ${\rho }_{diag}$ is chosen as a random positive diagonal matrix such that ${\sum }_{n=0}^M{\left({\rho }_{diag}\right)}_n=1$, and U is a uniformly generated (via the Haar measure) $(M+1)\times (M+1)$ random unitary matrix. (Note: ${\rho }_{diag}$ is chosen as the absolute value squared of a random row of another randomly chosen unitary $U^{\prime }$.)

In Figure 2, we relax the positivity condition on C and change ${\rho }_{diag}\to C_{diag}$ to be chosen simply as a random row of separately generated randomly unitary $U^{\prime }$ (vs. the absolute value squared of a random row of $U^{\prime }$ for the previous case of $C\to \rho >0$) so that $C_{diag}$ has random complex entries.

For any number of samples, we always find that $L{N}_a{\left(\right|\psi \rangle }_{ab})\le L{N}_e{\left(\right|\psi \rangle }_{ab})$, i.e., $L{N}_a{\left(\right|\psi \rangle }_{ab})$ acts as a proper lower bound to $L{N}_e{\left(\right|\psi \rangle }_{ab})$. This behavior in Figure 2 is the same if we simply take $C=\left\{c_{nm}\right\}$ as a matrix of random complex entries. This represents one of the main results of this work. In the following subsection we provide a plausibility argument for Equation (11b) indicating the logic of our “derivation”.

As discussed previously, the use of the Det in Equation (11a) enforces ${\mathcal{N}}_a=0$ on separable (product) pure states since the Det is identically zero if $c_{nm}=a_n{b}_m$. This is nicely illustrated for the case of pure states of the form ${|\Psi \rangle }_{ab}=\mathsf{N}\left({|\psi \rangle }_a{|\varphi \rangle }_b+{|\varphi \rangle }_a{|\psi \rangle }_b\right)/\sqrt{2}$, where $\mathsf{N}={\left(1+{\left|\langle \psi |\varphi \rangle \right|}^2\right)}^{-1/2}$. In Figure 3 we show the superposition of two coherent states ${|\Psi \rangle }_{ab}=\mathsf{N}\left(|{\beta }_1{\rangle }_a|{\beta }_2{\rangle }_b+|{\beta }_2{\rangle }_a{|{\beta }_1\rangle }_b\right)/\sqrt{2}$. The state is separable when ${\beta }_2={\beta }_1$ where $LN\to 0$ (both exact and approximate).

Another way to show that Equation (11b) captures a separable pure state is shown in Figure 4 In the left figure ${|\psi \rangle }_a$ and ${|\varphi \rangle }_b$ are taken as two random rows of two different random unitary matrices, while in the right plot, ${|\psi \rangle }_a$ and ${|\varphi \rangle }_b$ are taken as two random rows of the same random unitary matrix. In the latter, when the same row is chosen for both ${|\psi \rangle }_a$ and ${|\varphi \rangle }_b$, the state is separable and $LN\to 0$.

3.2. Plausibility Argument for Equation (11a,b)

In this section we present a plausibility argument that led to the “derivation” of the negativity in Equation (11a) and hence the Log Negativity in Equation (11b).

We begin by considering a general pure state ${|\psi \rangle }_{ab}={\sum }_{n,m}{c}_{nm}{|n,m\rangle }_{ab}$. The pure state density matrix is given by ${\rho }_{ab}={|\psi \rangle }_{ab}\langle \psi |={\sum }_{n,m}{\sum }_{n^{\prime },m^{\prime }}{c}_{nm}{c}_{n^{\prime }{m}^{\prime }}^{*}{|n,m\rangle }_{ab}\langle n^{\prime }{m}^{\prime }|$. Without loss of generality, and for ease of notation, we treat $c_{nm}$ as real in this subsection, and put in appropriate absolute values at the end of the calculation. Also, we drop the $ab$ subscript for now. We now write ${\rho }_{ab}$ as

$$\begin{array}{cccc}\hfill {\rho }_{ab}& =& \sum _{n,n^{\prime }}{c}_{nn}{c}_{n^{\prime }{n}^{\prime }}|nn\rangle \langle n^{\prime }{n}^{\prime }|+{\displaystyle \frac{1}{4}}\sum _{n,m\ne n}\sum _{n^{\prime },m^{\prime }\ne n^{\prime }}{c}_{nm}{c}_{n^{\prime }{m}^{\prime }}\left(|nm\rangle +|mn\rangle \right)\left(\langle n^{\prime }{m}^{\prime }|+\langle m^{\prime }{n}^{\prime }|\right),\hfill & (13a)\\ \hfill & +& {\displaystyle \frac{1}{2}}\sum _n\sum _{n^{\prime },m^{\prime }\ne n^{\prime }}{c}_{nn}{c}_{n^{\prime }{m}^{\prime }}|nn\rangle \left(\langle nm|+\langle mn|\right)+{\displaystyle \frac{1}{2}}\sum _{n,m\ne n}\sum _{n^{\prime }}{c}_{nm}{c}_{n^{\prime }{n}^{\prime }}\left(|nm\rangle +|mn\rangle \right)\langle nn|.\hfill & (13b)\end{array}$$

The PT ${\rho }_{ab}^{\Gamma }$ is then given by

$$\begin{array}{cccc}\hfill {\rho }_{ab}^{\Gamma }& =& \sum _{n,m}{c}_{nn}{c}_{mm}|nm\rangle \langle mn|+{\displaystyle \frac{1}{4}}\sum _{n,m\ne n}\sum _{n^{\prime },m^{\prime }\ne n^{\prime }}{c}_{nm}{c}_{n^{\prime }{m}^{\prime }}\left(|n{m}^{\prime }\rangle \langle n^{\prime }m|+|m{n}^{\prime }\rangle \langle m^{\prime }n|+|n{n}^{\prime }\rangle \langle m^{\prime }m|+|m{m}^{\prime }\rangle \langle n^{\prime }n|\right),\hfill & (14a)\\ \hfill & +& {\displaystyle \frac{1}{2}}\sum _n\sum _{n^{\prime },m^{\prime }\ne n^{\prime }}{c}_{nn}{c}_{n^{\prime }{m}^{\prime }}\left(|n{m}^{\prime }\rangle \langle n^{\prime }n|+|n{n}^{\prime }\rangle \langle m^{\prime }n|\right)+{\displaystyle \frac{1}{2}}\sum _{n,m\ne n}\sum _{n^{\prime }}{c}_{nm}{c}_{n^{\prime }{n}^{\prime }}\left(|n{n}^{\prime }\rangle \langle n^{\prime }m|+|m{n}^{\prime }\rangle \langle n^{\prime }n|\right).\hfill & (14b)\end{array}$$

The first summation in Equation (14a) gives rise to the negativity ${\mathcal{N}}^I=$${\displaystyle \frac{1}{2}}{\sum }_{n,m\ne n}\left|c_{nn}{c}_{mm}\right|$ (putting back in the absolute values) as discussed in Equation (10a) using the eigenstates $|e_{n,m\ne n}^{\pm }\rangle$.

The ansatz we employ is that the negativity is dominated by terms of the form (I), $|nm\rangle \langle mn|+|mn\rangle \langle nm|$, giving rise to eigenstates $|e_{n,m\ne n}^{\pm }\rangle$, and terms (II), $|nn\rangle \langle mm|+|mm\rangle \langle nn|$, giving rise to eigenstates $|f_{n,m\ne n}^{\pm }\rangle$, in the PT ${\rho }_{ab}^{\Gamma }$. We therefore approximate the negativity by only considering “matching terms” of types I and $II$ in ${\rho }_{ab}^{\Gamma }$.

Thus, in the second double summation in Equation (14a), we only consider the terms (i) $n^{\prime }=n,m^{\prime }=m$ which give rise to terms of the form $\frac{1}{4}{\sum }_{n,m\ne n}{c}_{nm}{c}_{nm}\left(\right|nm\rangle \langle nm|+|mn\rangle \langle mn|$ $+|nn\rangle \langle mm|+|mm\rangle \langle nn|)$.

The first two terms of this expression are diagonal, while the last term gives rise to the negativity ${\displaystyle \frac{1}{2}}{\mathcal{N}}^{II}=\frac{1}{4}{\sum }_{n,m\ne n}\left|c_{nm}{c}_{mn}\right|$ as discussed in Equation (10b) using the eigenstates $|f_{n,m\ne n}^{\pm }\rangle$.

However, in the same term in the previous paragraph, we could also consider the case (ii) $n^{\prime }=m,m^{\prime }=n$ leading to terms of the form $\frac{1}{4}{\sum }_{n,m\ne n}{c}_{nm}{c}_{nm}\left(\right|nn\rangle \langle mm|+|mm\rangle \langle nn|$ $+|nm\rangle \langle nm|+|mn\rangle \langle mn|)$. The last two terms of this expression are diagonal, while the first two again contribute a Negativity of ${\displaystyle \frac{1}{2}}{\mathcal{N}}^{II}=\frac{1}{4}{\sum }_{n,m\ne n}\left|c_{nm}{c}_{mn}\right|$ as in the previous paragraph. As part of our ansatz, we conjecture that the terms in Equation (14b) contribute no (significant) terms to the negativity.

Thus, the negativities that we have so far are $\mathcal{N}\approx {\mathcal{N}}^I+{\mathcal{N}}^{II}$, which we can write as

$$\begin{array}{cccc}\hfill \mathcal{N}& \approx & {\mathcal{N}}^I+{\mathcal{N}}^{II},\hfill & (15a)\\ & =& {\displaystyle \frac{1}{2}}\sum _{n,m\ne n}|c_{nn}{c}_{mm}|+{\displaystyle \frac{1}{2}}\sum _{n,m\ne n}|c_{nm}{c}_{mn}|,\hfill & (15b)\\ & \ge & {\displaystyle \frac{1}{2}}\sum _n\sum _m\left|\mathrm{Det}\left(\begin{array}{cc}{c}_{nn}& c_{nm}\\ c_{mn}& c_{mm}\end{array}\right)\right|\stackrel{\mathrm{def}}{=}{\mathcal{N}}_a,\hfill & (15c)\end{array}$$

where in the last line we have simply used the inequality that $\left|a\right|+\left|b\right|\ge |a-b|$ with $a\to c_{nn}{c}_{mm}$ and $b\to c_{nm}{c}_{mn}$. As discussed before, using $\mathcal{N}\approx {\mathcal{N}}^I+{\mathcal{N}}^{II}$ in Equation (15a) overestimates the negativities because the set of eigenstates $\left\{\right|f_{n,m\ne n}^{\pm }\rangle ,|nn\rangle \}$ does not form an orthogonal subset. Thus, we instead use the lower bound $\mathcal{N}\approx {\mathcal{N}}_a$ given by the determinant expression in Equation (15c). ${\mathcal{N}}_a$ is also the same expression as in Equation (11a), giving rise to the $LN$ given in Equation (11b).

While the above does not constitute a formal proof or a proper derivation ${\mathcal{N}}_a$, it is a plausibility argument borne out by numerical evidence. ${\mathcal{N}}_a$ and $L{N}_a$ in Equation (11a,b) also argue that the negativity in a general pure state is dominated by the states ${|nn\rangle }_{ab}\langle mm|+{|mm\rangle }_{ab}\langle nn|$ and ${|nm\rangle }_{ab}\langle mn|+|mn\rangle \langle nm|$ found within ${|\psi \rangle }_{ab}={\sum }_{nm}{c}_{nm}{|nm\rangle }_{ab}$, giving rise in the PT ${\rho }_{ab}^{\Gamma }$ to the eigenstates and negativities ${\left\{\right|e_{n,m\ne n}^{\pm }\rangle }_{ab},|f_{n,m\ne n}^{\pm }{\rangle }_{ab}\}$ and $\{{\mathcal{N}}^I,{\mathcal{N}}^{II}\}$, respectively.

Finally, we return to the case when $c_{nm}=c_n{c}_m^{*}$ is separable so that $L{N}_a=L{N}_e=0$. Let us now consider $C=\left\{c_{nm}\right\}\equiv \rho /\sqrt{Tr\left[{\rho }^2\right]}$, where we define $\rho ={\rho }_0/\sqrt{Tr\left[{\rho }_0^2\right]}+\eta \sigma$, with ${\rho }_0$ and $\sigma$ Hermitian. If we further define $\rho (\eta =0)={\rho }_0\equiv |{\varphi }_0\rangle \langle {\varphi }_0|$ where $|{\varphi }_0\rangle ={\sum }_n{c}_n|n\rangle$ is an arbitrary d-dimensional complex vector (such that $L{N}_a\left({\rho }_0\right)=L{N}_e\left({\rho }_0\right)=0$), then $\rho \left(\eta \right)$ represents an increasing random deviation away from the separable case. In Figure 5 we show plots of $L{N}_e$, $L{N}_a$ and $L{N}_e-L{N}_a$ for $\rho \left(\eta \right)$, such that $L{N}_a\left(\rho \left(0\right)\right)=L{N}_e\left(\rho \left(0\right)\right)=0$, with $M=20$ for increasing values of $\eta$. We see that $L{N}_a$ acts as a lower bound for $L{N}_e$. In Figure 6 we show plots of $L{N}_e$, $L{N}_a$ and $L{N}_e-L{N}_a$ for $\rho \left(\eta \right)=\mathbb{I}/d+\eta \sigma$, such that $L{N}_a\left(\rho \left(0\right)\right)=L{N}_e\left(\rho \left(0\right)\right)=1$, with $M=20$ for increasing values of $\eta$. We again see that $L{N}_a$ acts as a lower bound for $L{N}_e$. Similar behavior occurs for arbitrary values of M.

3.3. $L{N}_a$ and $L{N}_e$ for Perturbed Pure States vs. Purity of a $d\times d$ Hermitian $C=\left\{c_{nm}\right\}$

In the previous sections, we examined $L{N}_a$ vs. $L{N}_e$ for pure bipartite states and found that $L{N}_a\equiv L{N}_e$ when $C=\left\{c_{nm}\right\}=C^{†}$ is considered a uniformly random (with respect to the Haar measure) Hermitian matrix, i.e., C “acts like a $d\times d$ density matrix”. We examined this equivalence (random) shot by shot. In this section, we examine the situation when we treat C as a $d\times d$ density matrix of fixed purity $\mu \stackrel{\mathrm{def}}{=}\mathrm{Tr}\left[C^2\right]{|}_{\eta =0}$, for which $L{N}_a\equiv L{N}_e$, but then perturb it away from this result by adding a uniformly random density matrix $\sigma$ multiplied by a small “noise” coefficient $\eta$. In particular we let $C=\tilde{C}/\sqrt{\mathrm{Tr}[\tilde{C}{\tilde{C}}^{†}}]$ where $\tilde{C}\left(\mu \right)\stackrel{\mathrm{def}}{=}U{\rho }_d\left(\mu \right)U^{†}+\eta \sigma$. Here ${\rho }_d\left(\mu \right)$ is a real, uniformly random, diagonal density matrix of fixed chosen purity value [15] $1/d\le \mu =\mathrm{Tr}\left[{\rho }_d^2\right]\le 1$ (abscissa), U is a uniformly random unitary, $\sigma$ is random Hermitian density matrix, and $\eta <1$ is a small real parameter. For $\eta =0$, C is a Hermitian matrix of fixed purity $\mu$, and for each uniformly selected C, we have $L{N}_a\equiv L{N}_e$. By allowing $\eta >0$, and thus mixing in a uniformly random Hermitian $\sigma$, we perturb C away from its original fixed purity value at $\eta =0$. This allows us to sit at a fixed purity $\mu$ and randomly select samples of $C\left(\mu \right)$, and then calculate and compare the mean and standard deviations of $L{N}_a$ and $L{N}_e$, which are no longer equal for $\eta \ne 0$.

In Figure 7 we consider two values of $\eta =\{0.05,0.015\}$ (left and right columns, respectively), for two different values of $d=\{4,16\}$ (top and bottom rows, respectively). The blue-dashed line is the mean of $L{N}_e$ for 100 sample points for each chosen value of the purity $\mu$. The extreme edges of the shaded blue band about the dashed blue line represent the mean value plus and minus the standard deviation. Similar remarks hold for the solid red line/bands representing $L{N}_a$, and the solid cyan line/bands representing the difference $L{N}_a-L{N}_e$. From the latter difference cyan curve/band, we see that $L{N}_a-L{N}_e<0$, namely that even in these statistically perturbed cases (where again, $L{N}_a=L{N}_e$ for $\eta =0$), our approximate Log Negativity formula for pure bipartite states where $C=C^{†}$ is Hermitian, and $L{N}_a$ acts as a lower bound to $L{N}_e$.

In examining the statistics of Figure 7, note that as in Figure 5 where $C\leftarrow \rho \left(\eta \right)=|{\varphi }_0\rangle \langle {\varphi }_0|+\eta \sigma$ and the pure d-dimensional state $|{\varphi }_0\rangle$ has the highest purity $\mu =1$, the bipartite pure state ${|\psi \rangle }_{ab}={\sum }_{nm}{c}_{nm}{|nm\rangle }_{ab}$ is (counterintuitively) separable, and hence corresponds to $L{N}_a=L{N}_e=0$, i.e., with minimum value (right side of the abscissa). In addition, as in Figure 6, where $C\leftarrow \rho \left(\eta \right)=\mathbb{I}/d+\eta \sigma$, with $\mathbb{I}/d$ having the lowest purity $\mu =1/d$, the bipartite pure state ${|\psi \rangle }_{ab}$ corresponds (again, counterintuitively) to the maximally entangled Bell state, and hence to $L{N}_a=L{N}_e$ with maximum value (left side of the abscissa).

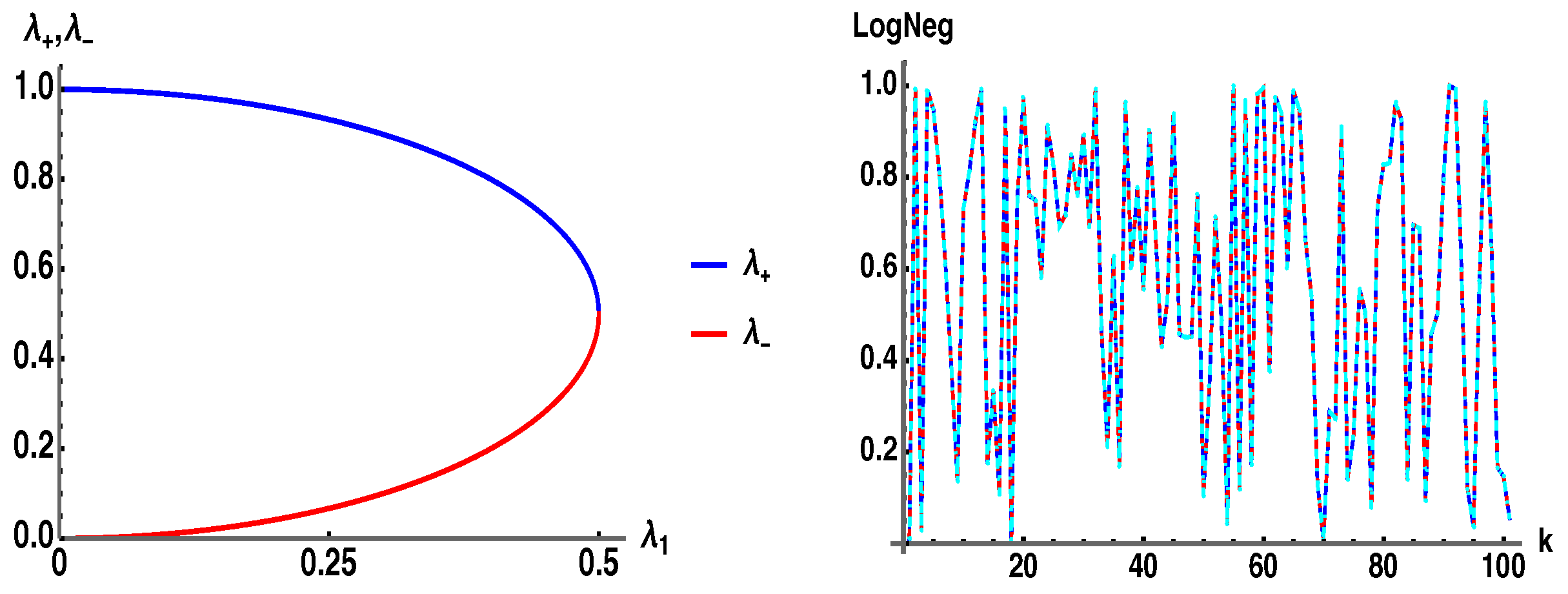
3.4. Analytic Derivation of ${\mathit{LN}}_{\mathit{a}}{\left(\right|\mathit{\psi }\rangle }_{\mathit{ab}})\equiv {\mathit{LN}}_{\mathit{e}}{\left(\right|\mathit{\psi }\rangle }_{\mathit{ab}})$ for the Bipartite Case of Two Qubits, $\mathit{d}=\mathbf{2}$

For the case of two qubits ($M=1,d=2$), take $C=\left\{c_{nm}\right\}$ to be an arbitrary $2\times 2$ complex matrix, for which we can analytically obtain the eigenvalues of the $2^2\times 2^2$ partial transpose ${\rho }_{ab}^{\Gamma }$, Equation (14b), in terms of the $c_{nm}$. After using the normalization of the state $\mathrm{Tr}\left[C{C}^{†}\right]$ $=|c_{00}{|}^2+|c_{01}{|}^2+|c_{10}{|}^2+{\left|c_{11}\right|}^2=1$, the eigenvalues $\{{\lambda }_1,{\lambda }_2,{\lambda }_{+},{\lambda }_{-}\}$ of ${\rho }_{ab}^{\Gamma }$ can be written as

$$\begin{array}{cccc}\hfill {\lambda }_1& =& |c_{00}{c}_{11}-c_{01}{c}_{10}|=-{\lambda }_2,\hfill & (16a)\\ \hfill {\lambda }_{\pm }& =& {\displaystyle \frac{1}{2}}\left(1\pm \sqrt{1-4{\lambda }_1^2}\right).\hfill & (16b)\end{array}$$

Thus, ${\lambda }_2\le 0$ and contributes to the Log Negativity. Since ${\rho }_{ab}^{\Gamma }$ is Hermitian with real eigenvalues, the radical under the square root must be positive $1-4{\lambda }_1\ge 0$, requiring that ${\lambda }_1\le 1/2$.

In Figure 8 (left) we plot ${\lambda }_{\pm }$. In Figure 8 (right) we plot $L{N}_e$ (blue), $L{N}_a$ (red) from Equation (11b), and $LN$ (cyan) using the analytic eigenvalue ${\lambda }_1=\left|{\lambda }_2\right|$ in Equation (16b), for the bipartite state of two qubits, $d=2$. The end result is that for the case of the pure bipartite case of two qubits there is only a single negative eigenvalue of the PT that contributes to the negativity, and it has the precise form of ${\mathcal{N}}_a$ as given in Equation (11a), which has two terms in the sum $(n,m)=\left\{\right(0,1),(1,0\left)\right\}$ summing to $|{\lambda }_2|={\lambda }_1$. For higher dimensions $d>2$, it is then somewhat unexpected and surprising that ${\mathcal{N}}_a$ in Equation (11a) produces the exact negativity ${\mathcal{N}}_e$ when $C=C^{†}$ of dimension d.

3.5. Comparison with Linear Entropy

The archetypal measure of entanglement of bipartite pure states that does not involve the computation of eigenvalues is the linear entropy $LE{\left(\right|\psi \rangle }_{ab})=1-\mathrm{Tr}\left[{\rho }_a^2\right]$ where ${\rho }_a={\mathrm{Tr}}_b{\left[\right|\psi \rangle }_{ab}\langle \psi \left|\right]$ is the reduced density matrix obtained by tracing out over one of the subsystems. $LE=0$ when ${|\psi \rangle }_{ab}$ is separable and $LE=1-\frac{1}{d}$ when ${\rho }_{ab}={|\psi \rangle }_{ab}\langle \psi |$ (a $d^2\times d^2$ matrix) is maximally entangled, and hence ${\rho }_a$ (a $d\times d$ matrix) is maximally mixed.

In Figure 9 we plot $L{N}_e$, $L{N}_a$, and a variation on the approximate negativity formula Equation (11b) given by $L{N}_a^{variation}={log}_2\left(1+|\mathrm{Tr}\left[C\right]\mathrm{Tr}\left[C^{†}\right]-\mathrm{Tr}\left[C{C}^{†}\right]|\right)$ (see Equation (A2)), and the linear entropy $LE$, when $\left\{c_{nm}\right\}=C\to \rho >0$ is a positive Hermitian $d\times d$ matrix (with $d=M+1$) for $M=\{5,10,20,30\}$. In this case, both $L{N}_a$ and $L{N}_a^{variation}$ identically equal $L{N}_e$. The $LE$ is plotted below (in orange) and acts as a lower bound to $L{N}_e$.

Figure 10 is identical to Figure 9, except we now allow $\left\{c_{nm}\right\}=C$ to be a random complex $d\times d$ matrix. We see that $L{N}_a$ acts as a better lower bound than $L{N}_a^{variation}$, which is in turn a better lower bound than the $LE$. As the dimension d increases, the latter three measures are observed to converge to approximately the same lower bound values, with $L{N}_a$ still performing as a slightly better lower bound.

4. An Attempt to Extend ${\mathcal{N}}_{\mathit{a}}$ to General Density Matrices

Extending the negativity and Log Negativity from Equation (11a,b) appropriate for pure states to mixed states is a non-trivial task. In principle the extension of an entanglement measure to mixed states is easy to state but computationally involved to perform [16]. Given a pure state (ensemble) decomposition (PSD) of a mixed state $\rho ={\sum }_i{p}_i|{\psi }_i\rangle \langle {\psi }_i|$ and an entanglement measure E on pure states, one can form the average entanglement $E\left(\rho \right)={\sum }_i{p}_{i}E\left(\right|{\psi }_i\rangle )$. The entanglement measure on mixed states is then taken as the minimum of $E\left(\rho \right)$ over all possible PSDs $\{p_i,|{\psi }_i\rangle \}$ (the so-called convex roof construction). This final result is sometimes referred to as the entanglement of formation, which quantifies the resource required to create a given entangled state. Since $E\left(\rho \right)$ is a convex function, one can apply Legendre transformations [17] to transform the above difficult minimization into the “minmax” problem [18] $E\left(\rho \right)=\underset{X}{\max }\underset{\psi }{\min }\{\mathrm{Tr}\left[X(\rho -|\psi \rangle \langle \psi \left|\right)\right]+E\left(\psi \right)\}$, where the exterior maximum is taken over all Hermitian matrices X. The dimension of the exterior optimization over X can be reduced to a rather small number by the symmetry of the state $\rho$, which greatly simplifies the numerical task as was demonstrated in [19].

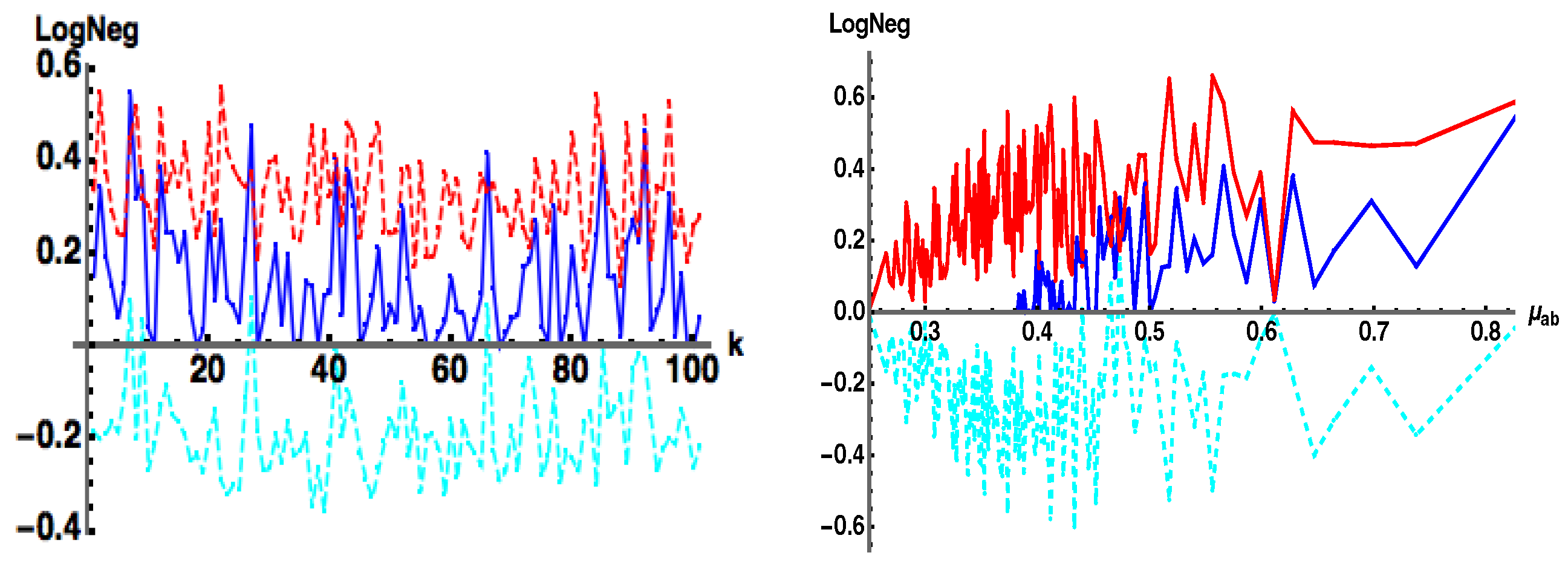
In this work we are not interested in forming a proper entanglement measure, rather a witness, that can lower bound the exact Log Negativity. Therefore, we will forgo the above computationally involved procedure and instead put forth (while somewhat simplistic but computationally tractable) an ansatz for a straightforward generalization of our pure state witness.

$$\begin{array}{cccc}\hfill \rho & =& \sum _{n,m}\sum _{n^{\prime },m^{\prime }}{\rho }_{nm,n^{\prime }{m}^{\prime }}|n,m\rangle \langle n^{\prime },m^{\prime }|,\hfill & (17a)\\ \hfill {\mathcal{N}}_a& \to & {\displaystyle \frac{1}{2}}\sum _{n,m\ne n}\left|{\rho }_{nn,mm}-{\rho }_{nm,mn}\right|,\hfill & (17b)\\ \hfill L{N}_a& =& {log}_2\left(1+2{\mathcal{N}}_a\right).\hfill & (17c)\end{array}$$

The main advantage of Equation (17b) is that upon reduction to a pure state ${\rho }_{nm,n^{\prime }{m}^{\prime }}\to c_{nm}{c}_{n^{\prime }{m}^{\prime }}^{*}$, the above formulas reduce to Equation (11a,b). However, as Figure 11 shows, Equation (17b,c) now acts more as an approximate upper bound as the dimension d increases (left), versus a desired lower bound, but typically at higher purity ${\mu }_{ab}\stackrel{\mathrm{def}}{=}\mathrm{Tr}\left[{\rho }^2\right]$ values (right). Note that $L{N}_a\left({\rho }_{ab}\right)$ does a fairly good job of tracking the up and down random fluctuations of $L{N}_e\left({\rho }_{ab}\right)$ but the former does not do a very good job when the latter is zero. On the negative side, Equation (17b) does not capture separability when ${\rho }_{ab}={\rho }_a\otimes {\rho }_b$. The issue of witnessing separability in general is a difficult, non-trivial problem [12], so it is not surprising that a simple generalization from a pure state witness to a mixed state witness would not be valid. Nonetheless, Figure 11 is intriguing for the relative tracking of $L{N}_a\left({\rho }_{ab}\right)$ with $L{N}_e\left({\rho }_{ab}\right)$. $L{N}_a\left({\rho }_{ab}\right)$ acts “almost” as an upper bound to $L{N}_e\left({\rho }_{ab}\right)$, (i.e., the cyan difference curve $L{N}_e\left({\rho }_{ab}\right)-L{N}_a\left({\rho }_{ab}\right)<0$), but there are places where it also acts as a lower bound, i.e., $L{N}_e\left({\rho }_{ab}\right)-L{N}_a\left({\rho }_{ab}\right)>0$.

4.1. ${\mathit{LN}}_{\mathit{a}}$ on Werner states

Because they are analytically tractable, it is informative to examine the proposed mixed-state witness Equation (17c) for the case of Werner states of dimension $d^2$ (where $d=(M+1)$), i.e.,

$${\rho }_{ab}^{(W,d^2)}=p|{\Psi }_{Bell}{\rangle }_{ab}\langle {\Psi }_{Bell}|+\frac{(1-p)}{d^2}{I}_{d^2\times d^2}\mathrm{with}|{\Psi }_{Bell}{\rangle }_{ab}={\displaystyle \frac{1}{\sqrt{d}}}\sum _{n=0}^{d-1}{|nn\rangle }_{ab}.$$

(18)

(Note: $|{\Psi }_{Bell}\rangle$ is a $d^2\times 1$ vector, so ${\rho }_{ab}^{(W,d^2)}$ is a $d^2\times d^2$ matrix). In Figure 12 we show $L{N}_e$ and $L{N}_a$ for Werner states with (top) $M=1$ (two qubits) and (bottom) $M=50$ using the approximation for the negativity given in Equation (17c).

Here we also introduce the Average Log Negativity (ALN) (for both exact and approximate $LN$) given by $L{N}^{avg}\left({\rho }_{ab}\right)={\sum }_i{p}_{i}LN\left({\rho }_{ab}^{\left(i\right)}\right)$ for mixed states of the form ${\rho }_{ab}={\sum }_i{p}_i{\rho }_{ab}^{\left(i\right)}$. It is straightforward to compute that for the Werner state, the negative eigenvalues of the partial transpose are given by

$${\lambda }_{-}=\frac{1}{d^2}\left(1-(d+1)p\right)\mathrm{for}\frac{1}{d+1}\le p\le 1\mathrm{with}\mathrm{multiplicity}\left({\displaystyle \genfrac{}{}{0pt}{}{d}{2}}\right)=\frac{d(d-1)}{2}.$$

(19)

Therefore, the negativity in this region is given by

$${\mathcal{N}}_e=\frac{1}{2}\frac{d-1}{d}\left((d+1)p-1\right)\mathrm{with}L{N}_e={log}_2(1+2{\mathcal{N}}_e),$$

(20)

yielding

$$L{N}_e(p={\displaystyle \frac{1}{d+1}})=0\mathrm{and}L{N}_e(p=1)={log}_2\left(d\right).$$

(21)

Thus, ${\rho }_{ab}^{(W,d^2)}$ is entangled ($LN>0$) for $\frac{1}{(d+1)}<p\le 1$, and separable ($LN\le 0$) for $0\le p\le \frac{1}{(d+1)}$. Finally, one can also show that the purity $\mu \left(\rho \right)=\mathrm{Tr}\left[{\rho }^2\right]$ for the Werner states is given by ${\mu }_{(W,d^2)}=\frac{1+(d^2-1)p}{d^2}$. This corresponds to a critical value ${\mu }_{(W,d^2)}^{*}=\frac{2}{d(d+1)}$, equivalently $p^{*}={\displaystyle \frac{1}{d+1}}$, where the value of the Log Negativity drops to zero. Some authors [16] refer to phenomena as the “sudden death of entanglement” since in the region $0\le p\le p^{*}$, ${\rho }_{ab}$ is separable, while ${\rho }_{ab}$ is entangled for $p^{*}<p\le 1$.

On the other hand, for a given $d=M+1$, for Werner states, we have

$${\mathcal{N}}_a=p(d-1)/2\Rightarrow L{N}_a={log}_2(1+(d-1)p),$$

(22)

yielding again

$$L{N}_a(p=1)={log}_2\left(d\right),\mathrm{but}\mathrm{this}\mathrm{time}L{N}_a=0\mathrm{at}p=0,$$

(23)

vs. at $p=\frac{1}{d+1}$ as for $L{N}_e$. Therefore, $L{N}_a\left({\rho }_{ab}\right)$ (red curve) never detects separability, and for Werner states, acts as a strict upper bound for $L{N}_e\left({\rho }_{ab}\right)$ (blue curve). Further, for Werner states $L{N}_a\left({\rho }_{ab}\right)\stackrel{d\gg 1}{⟶}L{N}_e\left({\rho }_{ab}\right)$ as demonstrated in the bottom plot in Figure 12 with $M=50$. Note that in the limiting case of $d\to \infty$, the Werner state is always entangled, and never has a region of separability.

The sudden death of entanglement at ${\mu }_{(W,d^2)}^{*}=\frac{2}{d(d+1)}$ introduces a derivative discontinuity in $L{N}_e$ that arises from the definition that the negativity is defined as non-zero only if some eigenvalues of the partial transpose of the density matrix are negative. Equivalently, such a discontinuity could also be introduced for the Werner states by declaring that $L{N}_e\ge 0$ iff ${\mu }_{(W,d^2)}\ge {\mu }_{(W,d^2)}^{*}$. Our definition of the continuous function $L{N}_a$ can never capture this derivative discontinuity. For Werner states one could attempt to capture this feature for any definition of a $L{N}_a$ by simply defining $L{N}_a\to 0$ for ${\mu }_{(W,d^2)}\le {\mu }_{(W,d^2)}^{*}$.

A symmetrization of Equation (17b) is given by

$$\begin{array}{ccc}\hfill {\mathcal{N}}_a^{sym}={\displaystyle \frac{1}{2}}\sum _{n,m\ne n}& & \left|\frac{1}{2}({\rho }_{nn,mm}+{\rho }_{mm,nn})\right.\hfill \\ & -& \left.\frac{1}{2}({\rho }_{nm,mn}+{\rho }_{mn,nm})\right|,\hfill \end{array}$$

(24)

which also reduces to Equation (11a,b) for the case of pure states ${\rho }_{nm,n^{\prime }{m}^{\prime }}\to c_{nm}{c}_{n^{\prime }{m}^{\prime }}^{*}$. (Note that one could also add terms such as ${\displaystyle \frac{1}{2}}{\sum }_n{\sum }_{n\ne m}\left({\rho }_{nn,nn}{\rho }_{mm,mm}-{\rho }_{nn,mm}{\rho }_{mm,nn}\right)$ which reduce to zero on the pure state case ${\rho }_{nm,n^{\prime }{m}^{\prime }}\to$ $c_{nm}{c}_{n^{\prime }{m}^{\prime }}^{*}$. However, we have not found such additional terms useful). Equation (24) also has the additional favorable property that it does detect separability $\rho ={\sum }_i{p}_i{\rho }_a^{\left(i\right)}\otimes {\rho }_b^{\left(i\right)}$ iff, for each i, either $\mathrm{Im}\left[{\rho }_a^{\left(i\right)}\right]$ or $\mathrm{Im}\left[{\rho }_b^{\left(i\right)}\right]$ are zero. This occurs because if ${\rho }_{nm,n^{\prime }{m}^{\prime }}={\sum }_i{p}_i{\left({\rho }_a^{\left(i\right)}\right)}_{n{n}^{\prime }}{\left({\rho }_b^{\left(i\right)}\right)}_{m{m}^{\prime }}$, Equation (24) reduces to

$$\begin{array}{ccc}\hfill {\mathcal{N}}_a^{sym}\to {\displaystyle \frac{1}{2}}\sum _{n,m\ne n}& & \left|\sum _i\frac{1}{2}{p}_i\left({\left({\rho }_a^{\left(i\right)}\right)}_{nm}-{\left({\rho }_a^{*\left(i\right)}\right)}_{nm}\right)\right.\hfill \\ & \times & \left.\left({\left({\rho }_b^{\left(i\right)}\right)}_{nm}-{\left({\rho }_b^{*\left(i\right)}\right)}_{nm}\right)\right|,\hfill \end{array}$$

(25)

where the terms inside the absolute value are proportional to the product of $\mathrm{Im}\left[{\left({\rho }_a^{\left(i\right)}\right)}_{nm}\right]\mathrm{Im}\left[{\left({\rho }_b^{\left(i\right)}\right)}_{nm}\right]$. This implies that either term in the product needs to be zero as a necessary and sufficient condition for the approximate negativity ${\mathcal{N}}_a$ in Equation (19) to yield zero on separable states.

Equation (24) does detect a wide class of separable states, but of course, not all. This is especially apparent since the application of Equation (24) to the ${\rho }_{ab}^{(W,d^2)}$ produces exactly the same plots as shown in Figure 12. We can understand this as follows. For the case of two qubits ($M=1$), we can write

$$\begin{array}{cccc}\hfill {\rho }_{ab}^{(W,d^2)}& =& {\displaystyle \frac{1}{4}}\left(\mathbb{I}+pZ\otimes Z+pX\otimes X-pY\otimes Y\right)\hfill & (26a)\\ & \equiv & {\displaystyle \frac{(1-3p)}{4}}\mathbb{I}+{\displaystyle \frac{p}{4}}\left(\mathbb{I}+Z\otimes Z\right)+{\displaystyle \frac{p}{4}}\left(\mathbb{I}+X\otimes X\right),\hfill \\ & & +{\displaystyle \frac{p}{4}}\left(\mathbb{I}-Y\otimes Y\right),& (26b)\\ & =& {\displaystyle \frac{(1-3p)}{4}}\mathbb{I}+{\displaystyle \frac{p}{2}}\left(|00\rangle \langle 00|+|11\rangle \langle 11|\right),\hfill \\ & +& {\displaystyle \frac{p}{2}}\left(|++\rangle \langle ++|+|--\rangle \langle --|\right)\hfill \\ & +& {\displaystyle \frac{p}{2}}\left(|y_{+}{y}_{-}\rangle \langle y_{+}{y}_{-}|+|y_{-}{y}_{+}\rangle \langle y_{-}{y}_{+}|\right).\hfill & (26c)\end{array}$$

While Equation (26a) is valid for all values of $0\le p\le 1$, Equation (26b,c) is only valid mixed-state representations (since each of the four terms is diagonal in a separable basis, and positive semi-definite) provided that $p\le \frac{1}{3}$. Now the term $|y_{+}\rangle \langle y_{+}|\otimes |y_{-}\rangle \langle y_{-}|=\frac{1}{2}\left(\begin{array}{cc}1& -i\\ i& 1\end{array}\right)\otimes \frac{1}{2}\left(\begin{array}{cc}1& i\\ -i& 1\end{array}\right)\equiv {\rho }_a^{\left(y\right)}\otimes {\rho }_b^{\left(y\right)}$ involves density matrices ${\rho }_a^{\left(y\right)}$ and ${\rho }_b^{\left(y\right)}$ that are both complex, for which our witness in Equation (24) cannot detect separability since at least one of the ${\rho }_a^{\left(y\right)}$ or ${\rho }_b^{\left(y\right)}$ would need to be real $\in \mathbb{R}$.

4.2. Average ${\mathit{LN}}_{\mathit{a}}$ as a Lower Bound for ${\mathit{LN}}_{\mathit{e}}$

We note that for Werner states, the Average Log Negativity (ALN) $L{N}^{avg}\left({\rho }_{ab}\right)={\sum }_i{p}_i{\rho }_{ab}^{\left(i\right)}\equiv {\sum }_i{p}_{i}LN\left({\rho }^{\left(i\right)}\right)$ for both the exact $L{N}_e^{avg}\left({\rho }_{ab}\right)$, and the approximate version $L{N}_a^{avg}\left({\rho }_{ab}\right)$ (using Equation (17c) on the right-hand side), are identically equal throughout all of $0\le p\le 1$, even in the separable region $0\le p\le \frac{1}{(d+1)}$ where $L{N}_e\left({\rho }_{ab}\right)=0$, as shown as the overlapping dashed blue and red lines in Figure 13. This is because $L{N}_e=L{N}_a$ on the ${\rho }^{\left(i\right)}$ components of the pure symmetric Bell state density matrix, and also on the maximally mixed state (yielding value $LN=0$ on the latter). In fact, we see that the $L{N}_e$ is concave $L{N}_e\left(\rho \right)\ge L{N}_a^{avg}\left(\rho \right)$ in the region where entanglement is present, and is convex $L{N}_e\left(\rho \right)\le L{N}_a^{avg}\left(\rho \right)$ in the region where the state is separable. On the other hand, our $L{N}_a\left(\rho \right)$ is concave throughout all of $0\le p\le 1$. Thus, as the dimension $d=M+1$ increases, $L{N}_a^{avg}\left(\rho \right)$ becomes an increasingly better lower bound for $L{N}_e\left(\rho \right)$ for a larger region of p as the region of separability decreases as shown in Figure 13 for $M=\{5,20\}$, and for $M=50$ in (bottom) Figure 12.

The above properties on Werner states prompt us to compare $L{N}_a^{avg}\left({\rho }_{ab}\right)$ to $L{N}_e\left({\rho }_{ab}\right)$ for more general random density matrices written as a pure state ensemble decomposition (PSD), ${\rho }_{ab}={\sum }_i{p}_i|{\psi }_i{\rangle }_{ab}\langle {\psi }_i|$, which we consider (only) for the remainder of this section. We also introduce an additional version of the average approximate Log Negativity given by

$${\mathcal{LN}}_a^{avg}\left({\rho }_{ab}\right)\stackrel{\mathrm{def}}{=}\sum _i{p}_{i}L{N}_a\left(|{\psi }_i{\rangle }_{ab}\right),$$

(27)

which now uses our approximation of the Log Negativity for pure states via Equation (11b) on the ensemble pure state components on the right-hand side, which is denoted as $L{N}_a\left(|{\psi }_i{\rangle }_{ab}\right)$. This is to be distinguished from the notation $L{N}_a\left({\rho }_{ab}\right)$, which we will reserve to denote the Log Negativity using our approximate mixed-state formula Equation (17c), and $L{N}_a^{avg}\left({\rho }_{ab}\right)\stackrel{\mathrm{def}}{=}{\sum }_i{p}_{i}L{N}_a\left({\rho }_{ab}^{\left(i\right)}\right)$ which is the average approximate Log Negativity that also uses Equation (17c) on general mixed states ${\rho }_{ab}={\sum }_i{p}_i{\rho }_{ab}^{\left(i\right)}$.

The trend seen in the above Werner state discussion appears to hold in general for PSDs, namely that as the dimension $d=M+1$ of the pure state components $|{\psi }_i{\rangle }_{ab}$ increases, ${\mathcal{LN}}_a^{avg}\left({\rho }_{ab}\right)>L{N}_a\left({\rho }_{ab}\right)$ becomes an increasingly better proper lower bound of $L{N}_e\left({\rho }_{ab}\right)$ as shown in Figure 14 (top).

Here $M=10$ and $L{N}_e$ is given by the blue curve, $L{N}_a$ by the red curve, and ${\mathcal{LN}}_a^{avg}$ by the magenta curve. We are interested in the comparison of the red and magenta curves to the blue curve, based on how the $C_{i,nm}$ matrices are chosen in each pure state component of the PSD, where ${\rho }_{ab}={\sum }_i{p}_i|{\psi }_i{\rangle }_{ab}\langle {\psi }_i|$, with $|{\psi }_i\rangle ={\sum }_{nm}^M{C}_{i,nm}{|n,m\rangle }_{ab}$. In Figure 14 (top), the $C_i\in \mathbb{C}$ are chosen as a random complex matrices. For this case we have $L{N}_a\left({\rho }_{ab}\right)<{\mathcal{LN}}_a^{avg}\left({\rho }_{ab}\right)<L{N}_e\left({\rho }_{ab}\right)$ (red, magenta, blue curves) as the dimension $d=M+1$ increases. For Figure 14 (middle), the $C_i=C_i^{†}$ are chosen as random Hermitian matrices. Here there is a dramatic change in structure. For this case we have ${\mathcal{LN}}_a^{avg}<L{N}_e\left({\rho }_{ab}\right)<L{N}_a\left({\rho }_{ab}\right)$ (magenta, blue, red curves), for which $L{N}_a\left({\rho }_{ab}\right)$ has switched to a proper upper bound of $L{N}_e\left({\rho }_{ab}\right)$, and these inequalities hold all the way down to $M=1$, the case of two qubits. Further, both $L{N}_a\left({\rho }_{ab}\right)$ and ${\mathcal{LN}}_a^{avg}\left({\rho }_{ab}\right)$ track the fluctuations of $L{N}_e\left({\rho }_{ab}\right)$ surprisingly, extremely well. Finally, in Figure 14 (bottom) the $C_i=C^{\mathrm{T}}$ are chosen as random orthogonal matrices, and now, very surprisingly, we find that we have ${\mathcal{LN}}_a^{avg}\left({\rho }_{ab}\right)<L{N}_e\left({\rho }_{ab}\right)=L{N}_a\left({\rho }_{ab}\right)$ (magenta, blue overlapping red curves), namely that $L{N}_a\left({\rho }_{ab}\right)$ becomes exactly equal to $L{N}_e\left({\rho }_{ab}\right)$, while ${\mathcal{LN}}_a^{avg}\left({\rho }_{ab}\right)$ remains a lower bound (which appears somewhat tighter than in the previous Hermitian case). Again, these inequalities hold all the way down to $M=1$, the case of two qubits.

In general we have found that for $\rho$ written as a PSD, ${\mathcal{LN}}_a^{avg}\left({\rho }_{ab}\right)$ based on our pure state negativity approximation given in Equation (11b) does a better job of acting as a lower bound to $L{N}_e\left({\rho }_{ab}\right)$ than $L{N}_a\left({\rho }_{ab}\right)$ based on the mixed-state negativity approximation given in Equation (17c). As discussed in the Introduction, Equation (2), and shown in Figure 14, we have numerically found that

$${\mathcal{LN}}_a^{avg}\left({\rho }_{ab}\right)\le L{N}_e\left({\rho }_{ab}\right)\le L{N}_a\left({\rho }_{ab}\right)$$

(28)

when the mixed state is written as a pure state decomposition (PSD) ${\rho }_{ab}={\sum }_i{p}_i|{\psi }_i{\rangle }_{ab}\langle {\psi }_i|$, and in addition, the quantum amplitude matrix $C_i$ of each pure state component $|{\psi }_i{\rangle }_{ab}={\sum }_{nm}{C}_{i,nm}{|n,m\rangle }_{ab}$ is uniformly generated (over the Haar measure) as a positive Hermitian matrix, $C_i=C_i^{†}\ge 0$. Further, we find that the second inequality is surprisingly saturated, i.e., $L{N}_e\left({\rho }_{ab}\right)=L{N}_a\left({\rho }_{ab}\right)$ in Equation (28), if the uniformly randomly generated $C_i$ matrices above are real, i.e., $C_i=C_i^T$. A discussion of the uniform generation of Hermitian matrices over the Haar measure used in these numerical studies is given in Appendix B.

5. Other Approaches to Bipartite Pure-State Entanglement Quantities Without Matrix Diagonalization

A proper measure of entanglement for bipartite pure states is the von Neumann entropy (VNE) given by $S\left({\rho }_a\right)=-{\sum }_i{\lambda }_i{log}_2{\lambda }_i$, where $\left\{{\lambda }_i\right\}$ are the eigenvalues of the reduced density matrix ${\rho }_a=\mathrm{Tr}\left[{\rho }_{ab}\right]$, necessitating the need for the diagonalization of ${\rho }_a$. There has been much theoretical and experimental interest in methods for direct detection of the VNE or other quantifiers of entanglement that do not require diagonalization [20,21,22,23,24,25,26]. In the paper by Meurice [26], concerning configurable arrays of Rydberg atoms, they were able to obtain robust and reliable estimates of the VNE using bitstring mutual information from measurements. In the computational basis $|n_{ab}\rangle =|n_a\rangle |n_b\rangle$, the estimated VNE is $S_{ab}^X\stackrel{\mathrm{def}}{=}{\sum }_{n_a{n}_b}{p}_{n_a{n}_b}{log}_2{p}_{n_a{n}_b}$, where the superscript X is short for eXperimental. In this basis, the diagonal elements are the probabilities for bitstring (projective) measurements. Forming the marginal distribution $p_{n_a}={\sum }_{n_b}{p}_{n_a{n}_b}$, the reduced experimental entropy $S_a^X={\sum }_{n_a}{p}_{n_a}{log}_2{p}_{n_a}$, and the experimental mutual information $I_{ab}^X=S_a^X+S_b^X-S_{ab}^X$, they found the upper and lower bound for the exact VNE $S_a^{VNE}=-\mathrm{Tr}\left[{\rho }_a{log}_2{\rho }_a\right]$ given by $I_{ab}^X\le S_a^{VNE}=S_b^{VNE}\le S_a^X$.

5.1. Rényi, Tsallis and Linear Entropy

The necessity of the diagonalization of ${\rho }_a$ obviously stems from the use of the non-linear function $-{log}_{2}x$ in the VNE. For Taylor expanding about $x=1$, we have $-logx={\sum }_{n=1}^{\infty }{\displaystyle \frac{1}{n}}{(1-x)}^n$, from which we can write the VNE as

$$\begin{array}{cccc}\hfill S_a^{VNE}=-\sum _i{\lambda }_i{log}_2{\lambda }_i& =& \sum _{n=1}^{\infty }{\displaystyle \frac{1}{n}}\sum _i{\lambda }_i{(1-{\lambda }_i)}^n,\hfill & (29)\\ & =& \sum _{n=1}^{\infty }\sum _{k=0}^n{\displaystyle \frac{{(-1)}^k}{n}}\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right)\mathrm{Tr}\left[{\rho }_a^{k+1}\right],\hfill & (30)\end{array}$$

where we have used the binomial expansion for ${(1-{\lambda }_i)}^n$, and written ${\sum }_i{\lambda }_i^{k+1}=\mathrm{Tr}\left[{\rho }_a^{k+1}\right]$. Equation (30) reveals that formally one could dispense with the necessity of diagonalizing the reduced density matrix ${\rho }_a$ in place of knowing all its moments $\mathrm{Tr}\left[{\rho }_a^{k+1}\right]$ for $k=\{0,1,\dots ,\infty \}$. The most widely used approximation of the VNE used in the literature is the $n=1$ term in Equation (29), namely, the linear entropy $S_L\equiv LE$,

$$\sum _i{\lambda }_i(1-{\lambda }_i)=1-\mathrm{Tr}\left[{\rho }_a^2\right]\stackrel{\mathrm{def}}{=}{S}_L,0\le S_L\le 1-{\displaystyle \frac{1}{d}},d=\dim {\mathcal{H}}_a,$$

(31)

which is why it is often claimed that the LE is “qualitatively equivalent” to the VNE, although recent work has shown that the former can dramatically disagree with the latter, for example, in low-density regimes of fermionic systems [27]. Note that if we tried to obtain a “better approximation” by retaining just the $k=0$ and $k=1$ terms in Equation (30), we would obtain ${\sum }_{n=1}^{\infty }\left({\displaystyle \frac{1}{n}}-\mathrm{Tr}\left[{\rho }_a^2\right]\right)$, which diverges (i.e., we cannot switch the order of the summations). Thus, the $n=1$ term $S_L$ is the linear approximation to the VNE, and has been widely used in the literature, characterizing entanglement in a variety of systems, without the need to diagonalize ${\rho }_a$ (see references [22–43] of [27]).

The LE is the $q=2$ case of the Quantum Tsallis q-entropy defined as

$$S_q\left(\rho \right)\stackrel{\mathrm{def}}{=}{\displaystyle \frac{1}{q-1}}\left(1-\mathrm{Tr}\left[{\rho }^q\right]\right),q\in \mathbb{R}>0,$$

(32)

which is related to the Rényi entropy $S^{\alpha }$

$$S^{\alpha }\left(\rho \right)\stackrel{\mathrm{def}}{=}{\displaystyle \frac{1}{1-\alpha }}{log}_2\mathrm{Tr}\left[{\rho }^{\alpha }\right]$$

(33)

by

$$S^q\left(\rho \right)={\displaystyle \frac{1}{1-q}}{log}_2\left(1-(q-1)\right)S_q\left(\rho \right).$$

(34)

Both the Rényi and the Tsallis entropies converge to the VNE in the limit $q\to 1$.

The LE has many positive analytic properties such as subadditivity, pseudo-additive for product states, and a lower bound (Araki–Lieb inequality from subadditivity) [28]

$$\begin{array}{c}{S}_L\left({\rho }_{ab}\right)\le S_L\left({\rho }_a\right)+S_L\left({\rho }_a\right),\\ S_L({\rho }_a\otimes {\rho }_b)=S_L\left({\rho }_a\right)+S_L\left({\rho }_a\right)-S_L\left({\rho }_a\right)S_L\left({\rho }_b\right),\\ S_L\left({\rho }_{ab}\right)\ge |S_L\left({\rho }_a\right)-S_L\left({\rho }_b\right)|.\end{array}$$

(35)

In Section 3.5, we compared our approximate Log Negativity for pure bipartite states $L{N}_a$ to the LE and found that in our numerical experiments, $L{N}_a$ was typically greater than the $S_L$ (while both being less than the exact Log Negativity $L{N}_e$), and thus $L{N}_a$ formed a better lower bound to $L{N}_e$.

5.2. The Special Case of 2-Qubits, Concurrence and Linear Entropy

In Section 3.4 we examined the case of 2-qubits ($d=2$) ${|\psi \rangle }_{ab}=c_{00}|00\rangle +c_{01}|01\rangle +c_{10}|10\rangle +c_{11}|11\rangle$ and found that our approximate Log Negativity $L{N}_a$ was analytically equal to the exact Log Negativity $L{N}_e$ since the negativity was given by (the absolute value of the negative eigenvalue of the partial transpose ${\rho }_{ab}^{{\Gamma }_b}$, namely) ${\lambda }_1=|c_{00}{c}_{11}-c_{01}{c}_{10}|$, Equation (16a). For the special case of a 2-qubit pure state, ${\lambda }_1$ is in fact the Wootter’s concurrence [10,21,29,30]

$$\begin{array}{ccc}\hfill C\left({\psi }_{ab}\right)& =& {|}_{ab}\langle \psi |{\sigma }_y\otimes {\sigma }_y|{\psi }^{*}{\rangle }_{ab}|,\hfill \\ & =& |c_{00}{c}_{11}-c_{01}{c}_{10}|,& (36)\\ & =& 2\sqrt{det{\rho }_a},\hfill & (37)\end{array}$$

where ${\Theta }_2{|\psi \rangle }_{ab}\stackrel{\mathrm{def}}{=}{\sigma }_y\otimes {\sigma }_y{|{\psi }^{*}\rangle }_{ab}$ is the local spin-flip operator acting on both qubits individually, taking each qubit to the orthogonal state diametrically opposite on the Bloch sphere, along with a conjugation operation. In addition, ${\lambda }_1^2$ is also the exact value of the LE when normalized (as is often found in the literature) as $S_L^{\prime }={\displaystyle \frac{1}{2}}\left(1-\mathrm{Tr}\left[{\rho }_a^2\right]\right)=det{\rho }_a={\lambda }_1^2$.

Attempts have been made to generalize concurrence to arbitrary dimensions by generalizing ${\Theta }_2$ to a general $\Theta$ for an arbitrary $d_1\times d_2$ system [30,31], and by superoperator methods [32]. For any conjugation $\Theta$, one can define the $\Theta$-concurrence of a pure bipartite state $\Phi$ as $C_{\Theta }(\Phi )=|\langle \Phi |\Theta |\Phi \rangle |$ (and for a mixed state $\rho$ as $C_{\Theta }\left(\rho \right)=\inf {\sum }_j{p}_j{C}_{\Theta }\left({\Phi }_j\right)$ for an ensemble decomposition $D=\{p_j,|{\Phi }_j\rangle \}$).

For a pure state bipartite system with $(i,i^{\prime })$ with $i<i^{\prime }$ labeling two specific basis states for subsystem a, and $(j,j^{\prime })$ with $j<j^{\prime }$ labeling two specific basis states for subsystem b, let $\alpha =\{i,j,i^{\prime },j^{\prime }\}$ be an ordered set of two pairs of labels. Following [31], Wootters [30] considers the higher-dimensional antilinear conjugation operation ${\Theta }_{\alpha }$ for a given ordered set $\alpha$ defined by

$$\begin{array}{ccc}\hfill {\Theta |ij\rangle }_{ab}& =& -|i^{\prime }{j}^{\prime }{\rangle }_{ab},\Theta |i^{\prime }{j}^{\prime }{\rangle }_{ab}=-{|ij\rangle }_{ab},\\ \Theta {|i{j}^{\prime }\rangle }_{ab}& =& |i^{\prime }{j\rangle }_{ab},\Theta |i^{\prime }{j\rangle }_{ab}={|i{j}^{\prime }\rangle }_{ab}.\end{array}$$

(38)

As Wootters states [30], ${\Theta }_{\alpha }$ projects an arbitrary state of the system onto a “two-qubit subspace” and then performs what amounts to a spin-flip on that subspace. For each $\alpha$, collect the $C_{\alpha }$ into a concurrence vector. Wootters shows that the length of the concurrence vector $C^2(\Phi )\stackrel{\mathrm{def}}{=}{\sum }_{\alpha }{C}_{\alpha }^2(\Phi )$ is invariant under local unitary transformations of the two separate subsystems and is given by

$$C^2(\Phi )=2\sqrt{1-\mathrm{Tr}\left[{\rho }_a\right]}=2\sqrt{S_L},$$

(39)

where the latter result agrees with that of [32] using the superoperator formulation $C(\Phi )=\sqrt{\langle \Phi |(S_{d_1}\otimes S_{d_2})(\langle \Phi ||\Phi \rangle )|\Phi \rangle }$ where $S_d=\mathbb{I}-\rho$. Wootters’ method of projection onto two-qubit subspaces is very much in the spirit (but different in implementation since Equation (39) reproduces the LE) of what our approximate Log Negativity formula $L{N}_a$ is doing in Equation (11a,b) i.e., treating $c_{nm}$ in ${|\psi \rangle }_{ab}={\sum }_{nm}{c}_{nm}{|n,m\rangle }_{ab}$ as a collection of two-qubit “subspace”, labeled by indices $(n,m)$, but where n and m are taken only on the diagonal of $c_{nm}$. The relationship between our work and Wootters’ concurrence vector will be explored in future work.

6. Summary and Conclusions

In this work we presented numerical evidence for a witness for bipartite entanglement based solely on the coefficients $\left\{c_{nm}\right\}\to C$ of the pure state wavefunction ${|\psi \rangle }_{ab}={\sum }_{nm}{c}_{nm}{|nm\rangle }_{ab}$ as opposed to the eigenvalues of the partial transpose of ${\rho }_{ab}={|\psi \rangle }_{ab}\langle \psi |$, as appropriate for the Log Negativity. This is achieved by approximating the negativity by diagonally dominant determinants of the coefficients as given in Equation (11a). This ${\mathcal{N}}_a$ agrees exactly with the exact negativity ${\mathcal{N}}_e$ (given by the standard definition obtained by the sum of the absolute values of the negative eigenvalues of the partial transpose ${\rho }_{ab}^{\Gamma }$) when $C=\left\{c_{nm}\right\}$ is a positive Hermitian matrix (i.e., C is itself a non-unit trace density matrix). Interestingly, these include the cases when (i) C is considered a maximally mixed density matrix, then ${|\psi \rangle }_{ab}$ is the maximally entangled d-dimensional Bell state, while (ii) if C is a pure state density matrix, then ${|\psi \rangle }_{ab}$ is separable, and (iii) symmetric superpositions of pure states with real coefficients. In these cases, ${\mathcal{N}}_a{\left(\right|\psi \rangle }_{ab})={\mathcal{N}}_e{\left(\right|\psi \rangle }_{ab})$. Of particular relevance is that for C being a general complex matrix, we find that ${\mathcal{N}}_a{\left(\right|\psi \rangle }_{ab})$ acts as proper (but not tight) lower bound for ${\mathcal{N}}_e{\left(\right|\psi \rangle }_{ab})$, i.e., ${\mathcal{N}}_a{\left(\right|\psi \rangle }_{ab})\le {\mathcal{N}}_e{\left(\right|\psi \rangle }_{ab})$.

In the second half of this work, we attempted to generalize our approximation of the negativity from pure states to mixed states via Equation (17b), which reduces to the diagonally dominant determinants formula Equation (11a) for pure states. We met with partial, yet still interesting, success. One of the key features of a negativity based on Equation (24), a symmetrized version of Equation (11a), is that it yields $L{N}_a\left({\rho }_{ab}\right)=0$ on separable states ${\rho }^{\left(sep\right)}={\sum }_i{p}_i{\rho }_a^{\left(i\right)}\otimes {\rho }_b^{\left(i\right)}$ when either one of the component separable states ${\rho }_a^{\left(i\right)}$ or ${\rho }_b^{\left(i\right)}$ is $\in \mathbb{R}$, real. While this of course does not capture all separable states (a non-trivial task), it does capture a wide range of physically relevant density matrices.

In general, we found that a $L{N}_a\left({\rho }_{ab}\right)$ based on Equation (24) acts more as an (undesired) upper bound to $L{N}_e\left({\rho }_{ab}\right)$ as demonstrated vividly on the analytically tractable d-dimensional Werner states. However, for Werner states we saw that $L{N}_a\left({\rho }_{ab}\right)\stackrel{d\gg 1}{⟶}L{N}_e\left({\rho }_{ab}\right)$ as the dimension d grew large, and the corresponding region of separability grew smaller as $p_{*}=1/(d+1)$.

This led us to consider ${\mathcal{LN}}_a^{avg}\left({\rho }_{ab}\right)\equiv {\sum }_i{p}_{i}L{N}_a{\left(\right|{\psi }_i\rangle }_{ab}\langle {\psi }_i\left|\right)$ for pure state ensemble decomposition (PSD) of the density matrices ${\rho }_{ab}={\sum }_i{p}_i|{\psi }_i{\rangle }_{ab}\langle {\psi }_i|$, now using our approximation of the pure state negativity via Equation (11a). Again, we saw that as the dimension d of the pure state components $|{\psi }_i{\rangle }_{ab}$ increased, ${\mathcal{LN}}_a^{avg}\left({\rho }_{ab}\right)$ acted as a proper lower bound to $L{N}_e\left({\rho }_{ab}\right)$, i.e., ${\mathcal{LN}}_a^{avg}\left({\rho }_{ab}\right)\stackrel{d\gg 1}{\le }L{N}_e\left({\rho }_{ab}\right)$. We speculate that this occurs for similar reasons to for the Werner states, namely that as the dimension d increases, the region of separable states becomes vanishingly small [9,33], and simultaneously our negativity formula Equation (11a) is more accurate on pure states than Equation (17b) on mixed states, and hence the former does a better job of acting as a lower bound.

In summary, the main features of our proposed entanglement witness are (i) a simple formula for an approximate negativity Equation (11a) on bipartite pure states directly in terms of the quantum amplitudes of the quantum states that is also exact for a certain class of physical relevant states (with the Log Negativity related to the negative log of the purity of the quantum amplitude (matrix) when they have the properties of a normalized density matrix, Equation (12c)), and (ii) this negativity formula does not require the need to numerically compute eigenvalues of the partial transpose of the density matrix. An attempted generalization of this pure state negativity formula for pure states to mixed states yields that (iii) in simulations on pure state decompositions (PSDs) of density matrices where the quantum amplitudes $C_i=\left\{c_{i,nm}\right\}$ of each of the pure state components $|{\psi }_i{\rangle }_{ab}$ act as positive Hermitian matrices, ${\mathcal{LN}}_a\left({\rho }_{ab}\right)$ Equation (27), based on the Log Negativity approximation for pure states Equation (11b), yields a proper lower bound to $L{N}_e\left({\rho }_{ab}\right)$, and (iv) on the PSD of density matrices in (iii), $L{N}_a\left({\rho }_{ab}\right)$ provides a proper upper bound to $L{N}_e\left({\rho }_{ab}\right)$ (with equality when $C_i$ are orthogonal matrices), and most interestingly, both ${\mathcal{LN}}_a\left({\rho }_{ab}\right)$ and $L{N}_a\left({\rho }_{ab}\right)$ track, extremely well, the fluctuations in $L{N}_e\left({\rho }_{ab}\right)$ for uniformly randomly generated states.

As stated in the introduction, the numerical computation of eigenvalues does not present a practical impediment to the calculation of entanglement measures. Rather, it is the surprising and unexpected relationship (and equality for certain physically relevant states, both pure and mixed) between the entanglement witness we propose and the exact Log Negativity that was the impetus for this current investigation. In essence, the main contribution of this work is an extension of the class of states that are amenable to Agarwal’s [13] method of exact analytical diagonalization. Our conjecture is that these two types of exactly analytical diagonalizable states form the dominant contribution to the entangle of the state as measured by our approximate Log Negativity formula. What is unexpected and surprising is that (i) it yields exact results on a limited class of pure state, (ii) acts as a lower bound (what we refer to as an entanglement witness) on arbitrary pure states, and, even more surprisingly, (iii) yields exact results on a limited class of mixed states. It is our hope that this work might inspire further investigations into a more complete foundational (and proper) derivation underpinning the results presented in these numerical investigations.