Abstract
We develop the local convergence of the six order Contraharmonic-mean Newton’s method (CHN) to solve Banach space valued equations. Our analysis approach is two fold: The first way uses Taylor’s series and derivatives of higher orders. The second one uses only the first derivatives. We examine the theoretical results by solving a boundary value problem also using the examples relating the proposed method with other’s methods such as Newton’s, Kou’s and Jarratt’s to show that the proposed method performs better. The conjugate maps for second-degree polynomial are verified. We also calculate the fixed points (extraneous). The article is completed with the study of basins of attraction, which support and further validate the theoretical and numerical results.
1. Introduction
Let F be the differentiable mapping of a convex subset D of a Banach space X to itself. We deal with the convergence of the sixth-order Contraharmonic-mean method (CHN) [1]
for , where is the derivative of the operator F. We are seeking to find the solution or by solving the equation
using method (1). Newton’s method has been used to solve Equation (2). However, the convergence order is two [2,3,4,5]. It is given as follows:
Papers have appeared on the variant or modification of Newton’s method in real [5] as well as in Banach space [2,3,4].
Two convergence categories of analysis are usually recognized. The first is local convergence analysis, in which, firstly, we assume that a particular solution exists; around this solution there will be a neighborhood, and starting with any vector in this neighborhood, will lead to a sequence that converges to the solution under some suitable conditions. The second is semilocal convergence analysis; it does not require the existence of a solution but demands the same conditions around the initial vector [6,7]. Kantorovich [8] has provided the semilocal convergence of (3) in Banach space. He used the technique of majorizing sequences. Majorizing sequences have been used by many researchers for the variants of Newton’s method [2].
Earlier work on the six order method CHN for the solution of (2) in many dimensions relies on derivatives of higher order, but the methods depend only on the . Thus, the earlier results are limited. Here, first we have performed the local convergence analysis of the CHN method (1) regarding the root , which depends on the sixth-order derivative of F. Next, we deal with using only . The second local convergence analysis is also important, especially if F has no third or higher order Fréchet derivative. Indeed, set . Consider H on D as
We obtain So, the conclusion of Theorem 1 (see Section 2) may not hold since is not continuous. But the conclusion of Theorem 2 holds (see Section 3) with and
The convergence order in the second case is found using the following formula:
or
These do not require the or (in the Formula (5)).
The numerical results compare the CHN method along with the method of Jarratt [9] and Kou et al. (see [10]) by using some test functions. One important characteristic of this work is the comparability of the CHN method with that of Jarratt [9] and Kou et al. (see [10]) with respect to their dynamics.
2. Analysis 1
Theorem 1.
Let stand for a convex set and . Assume
- (i)
- solves Equation (2) so that is well defined.
- (ii)
- F is sixth-order Fréchet differential in I at some neighborhood S of solution .
Then, the method (1) reaches convergence order six.
Proof.
Set with . By Taylor series of F about , we obtain
So, we can write
Then, by (1) we obtain
Hence, we have
Next, we obtain
Now, by the second sub-step of the CHN method we obtain
We obtain from the third sub-step of the CHN method (1)
Thus, the CHN method (1) has local convergence of the sixth-order to the root of F. □
3. Analysis 2
The analysis uses some real functions and parameters. Set . Suppose:
- (i)
- Equation
- (ii)
- Equation
- (iii)
- Equation
- (iv)
- Equation
- (v)
- Equation
Suppose that equation has the smallest root .
Next,
is shown to be convergence radius for CHN. Consequently,
and
hold for all . Consider conditions (A) in our analysis with the scalars parameter and functions as previously defined:
- (a1)
- has a simple solution satisfying
- (a2)
- For allDefine
- (a3)
- For alland
- (a4)
- and
- (a5)
- There exists satisfying
Set
Based on the conditions (A) and the developed notation, we prove the second result for method (1).
Theorem 2.
Under the conditions (A), pick . Then, the sequence produced by the method CHN starting at is defined well, remains in , and is convergent to , which is an isolated solver of the region .
Proof.
Choose . Then, by and (16) one obtains
By the standard Banach perturbation lemma [8] and the preceding inequality, we have
In particular, if , exists. Since , then exists, and
We set = . So, in view of condition and (16), (20), (21), and (23)
Hence,
We must show that the linear operator is invertible, which will well define . So, by and (16), (25), we have
so
Then, by the second substep of the method CHN, we have
We obtain by , (16), (25), and (28)
so,
Notice that is well defined and (25) holds for . Then, by the third sub-step of CHN:
Now, from (23) (for i = 3), (25), (29), and (32); we obtain inturn that
so, .
Switching by , respectively, in the previous estimations, we obtain
where leading to , and
To show uniqueness, we consider for with By and , we obtain
Finally, the invertability of Q together with the identity
gives
□
4. Numerical Conclusions
In this section, a comparative study of the CHN (1) with fourth-order Jarratt’s (35) [9] and sixth-order Kou’s (36) [10] is undertaken. Iterative expressions for the last two methods are as:
MATLAB 2007 is used for the calculations with the stopping criterion We have taken Example 1, from the paper of Kou et al. [10] with the same starting point.
Example 1.

Let consider be given as
We obtain
The initial approximation is 3.5, and the approximate solution is 3.0. The numerical solution of Example 1 by second-order Newton’s (3), fourth-order Jarratt’s (35) [9], sixth-order Kou’s (36) [10], and sixth-order CHN method (1) is presented in Table 1. We can check from the Table 1 that starting with point 3.5, the CHN method is accelerating the convergence to solution 3.0 at every iteration.

Table 1.
Display of competing methods for Example 1.
Example 2.

Let consider be given as
Then, we obtain
The initial point is 3.5. The approximate solution is 1.0. The numerical solution of Example 2 by different methods is presented in Table 2. These results confirm the proposed method CHN (1) is converging to solution 1.0 in a better way in comparison to the others.

Table 2.
Display of competing methods for Example 2.
Example 3.

Let . Consider an operator as
The initial point is (0.1, 0.1), whereas the approximate solution is (0.57735, 0.57735). The numerical solution of Example 3 by methods is given in Table 3. It is clear that the proposed method (1) along with Kou’s method (36) is converging to the solution in fewer iterations among the methods.

Table 3.
Display of competing methods for Example 3.
Example 4.

Let the following boundary problem
We take Here, and
We discretize the above problem by using the central difference schemes for the first- and second-order derivatives, i.e.,
Thus, we obtain an nonlinear system:
Next, we deal with the above problem for by the developed method using the initial approximations . The solution of the problem is shown in Table 4 with and . Nine iterations are performed to obtain the solution [0.7321436673451523, 0.9820632482087217].

Table 4.
Solution of Example 4 (B V P) by proposed method.
5. Consistent Conjugate Maps for Second-Degree Polynomials
This section deals with the mapping appearing in numerous methods related to a usual polynomial having simple roots.
Theorem 3
(Newton’s method). Rational mapping by Newton’s method (3) related to , is conjugate to through the Mobius transformation presented by , i.e.,
Theorem 4
(Jarratt’s method [9]). Rational mapping by Jarratt’s method (35) related to is conjugate to through the Mobius transformation presented by , i.e.,
where
Theorem 5
(Proposed method CHN). The rational mapping by the Contraharmonic-mean Newton method (CHN) (1) related to is conjugate to through the Mobius transformation presented by , i.e.,
where
Theorem 6
(Newton-like method). The rational mapping by the Newton-like method related to is conjugate to through the Mobius transformation presented by , i.e.,
where is either a unity or a rational function and p is the order of the Newton-like method.
6. Fixed Points (Extraneous)
The Newton type described previously may be viewed as a fixed-point iteration:
Thus, the root of is a fixed point of the method. If the right side of (38) also vanishes at some points for , then is also fixed points of the method. These fixed points are known as fixed points (extraneous) (see [11] ). Now, we describe the fixed points (extraneous) of some Newton-like methods for .
Remark 1.
Newton’s method does not have any fixed points (extraneous) because for Newton’s method,
Theorem 7.
Jarratt’s method [9] given by Equation (35) has six extraneous fixed points.
Proof.
For Jarratt’s method (35), is . Here, the numerator is of degree 6; hence, Jarratt’s method has six extraneous fixed points.
Since the magnitude of the derivative at these points is , these fixed points are repulsive. □
Theorem 8.
The contraharmonic-mean Newton method (CHN) given by Equation (1) has 36 extraneous fixed points.
Proof.
For the Contraharmonic-mean Newton method (1), is given by the following equation. . Clearly, numerator is of degree 36; hence, Contraharmonic-mean Newton method (1) has 36 fixed points (extraneous).
Since the magnitude of the derivative at these points is , these fixed points are repulsive. □
Remark 2.
For the other Newton-like method, we may calculate the fixed points (extraneous) in a similar way since the magnitude of the derivative at these points is . Therefore, these fixed points are repulsive. These fixed points can be located in the basins graph for Example 3 (), Figure 1 (also notice the dynamics in Section 2 for these methods).

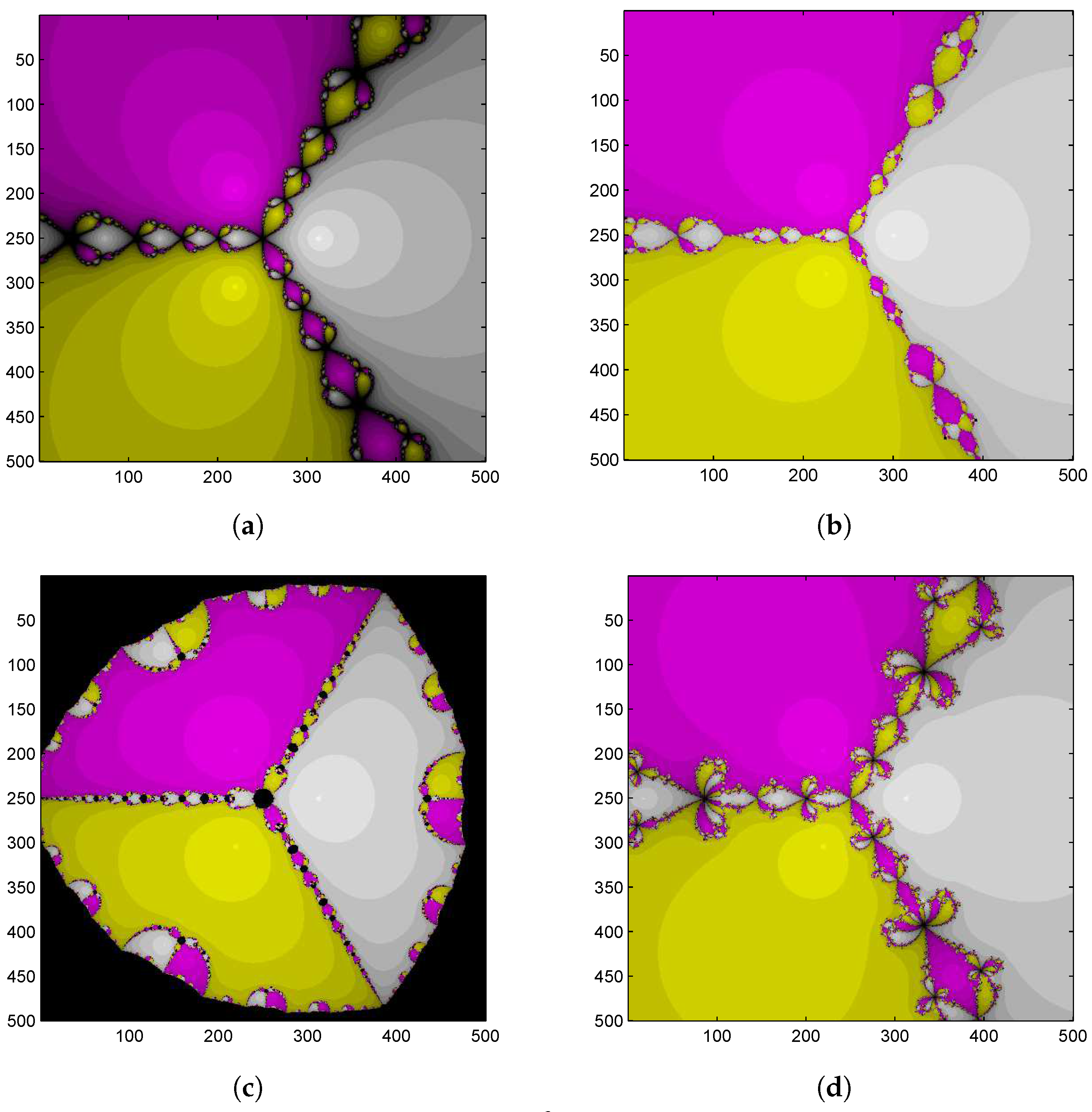
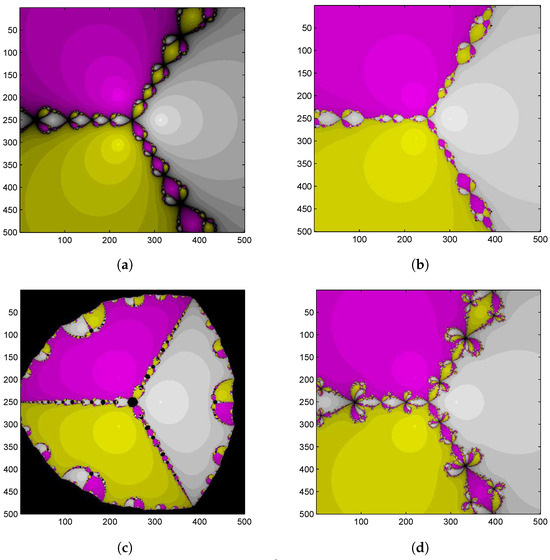
Figure 1.
Basin of attraction for by different methods. (a) Second-order Newton’s method; (b) fourth-order Jarratt’s method; (c) sixth-order Kou et al. method; and (d) sixth-order CHN method.
7. Dynamical Study
Now, we will define the following definitions but in the extended complex plane.
Definition 1
(see [12,13,14]). Let us consider that is a rational map on the Riemann sphere, where I is a subset of the complex numbers . Then, a point is said to be a fixed point of g if
Again for any point , the orbit of the point z can be defined as the set
Definition 2
(see [12,14]). A periodic point is said to be of period k if there a smallest positive integer k exists, i.e. .
Remark 3.
If is a periodic point of period k, then clearly it is a fixed point for .
Definition 3
(see [12,13,14]). Let be a zero of the function F. Then, the basin of attraction of the zero is defined as the set of all initial approximations such that any numerical iterative method starting with converges to . It can be written as
Here, is any fixed-point iterative method.
Remark 4.
For example in case of Newton’s method
We can write the basin of attraction of the zero for the Newton’s method as follows:
Definition 4
(see [12,13,14]). The Julia set of a nonlinear map is denoted as and is defined as a set consisting of the closure of its repulsive periodic points [15]. The complement of the Julia set is called the Fatou set .
Remark 5.
- (i)
- Some times the Fatou set of a nonlinear map may also be defined as the solution space, and the Julia set of a nonlinear map may also be defined as the error space.
- (ii)
- Fractals are a very complicated phenomenon that may be defined as a self-similar surprising geometric object, which repeats at every small scale [16].
The dynamics of the rational map on the Riemann sphere split into two parts [13].
- 1.
- The dynamics of the Fatou set.
- 2.
- The dynamics of the Julia set.
The dynamics of the Fatou set of the rational map may be defined as the solution space that contains the basin of attraction. The dynamics of Julia set of the rational map may be defined as the error space having the chaotic part of the dynamics.
We studied the fractal patterns and dynamics for Example 2 ( ) and a new Example 5 by using different iterative methods. The dynamical analysis helps us in understanding the convergence, divergence, and stability of the methods (see [12,13]).
7.1. For Example 2
Let us choose the square of points with tolerance , taking a maximum of 21 iterations and a different color for each complex root, to study the dynamics of Example 2 ( ) (Figure 1).
- 1.
- Clearly, the proposed sixth-order CHN method has a Fatou set with bigger orbits in comparison to the other methods.
- 2.
- Newton’s method has no fixed points (extraneous). Further, there are 6 fixed points (extraneous) for Jarratt’s method and 36 fixed points (extraneous) for the proposed CHN method.
- 3.
- As we know that the magnitude of the derivative at these points is , these fixed points are repelling and are not the part of solution space. Thus, larger the number of fixed points poor the method will be.
7.2. For Example 5
The dynamics for Example 5 are plotted by the methods with the earlier conditions having different color for each complex root. We described the basins of attraction for second-order Newton’s (3), fourth-order Jarratt’s (35), sixth-order Kou et al. (36), and present sixth-order CHN method (1) (Figure 2).
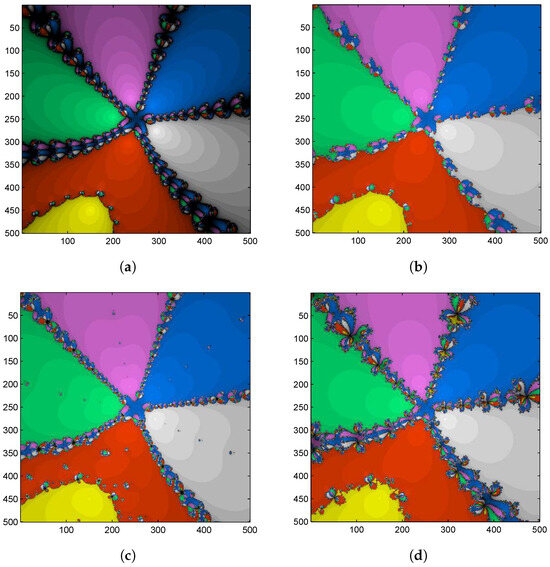
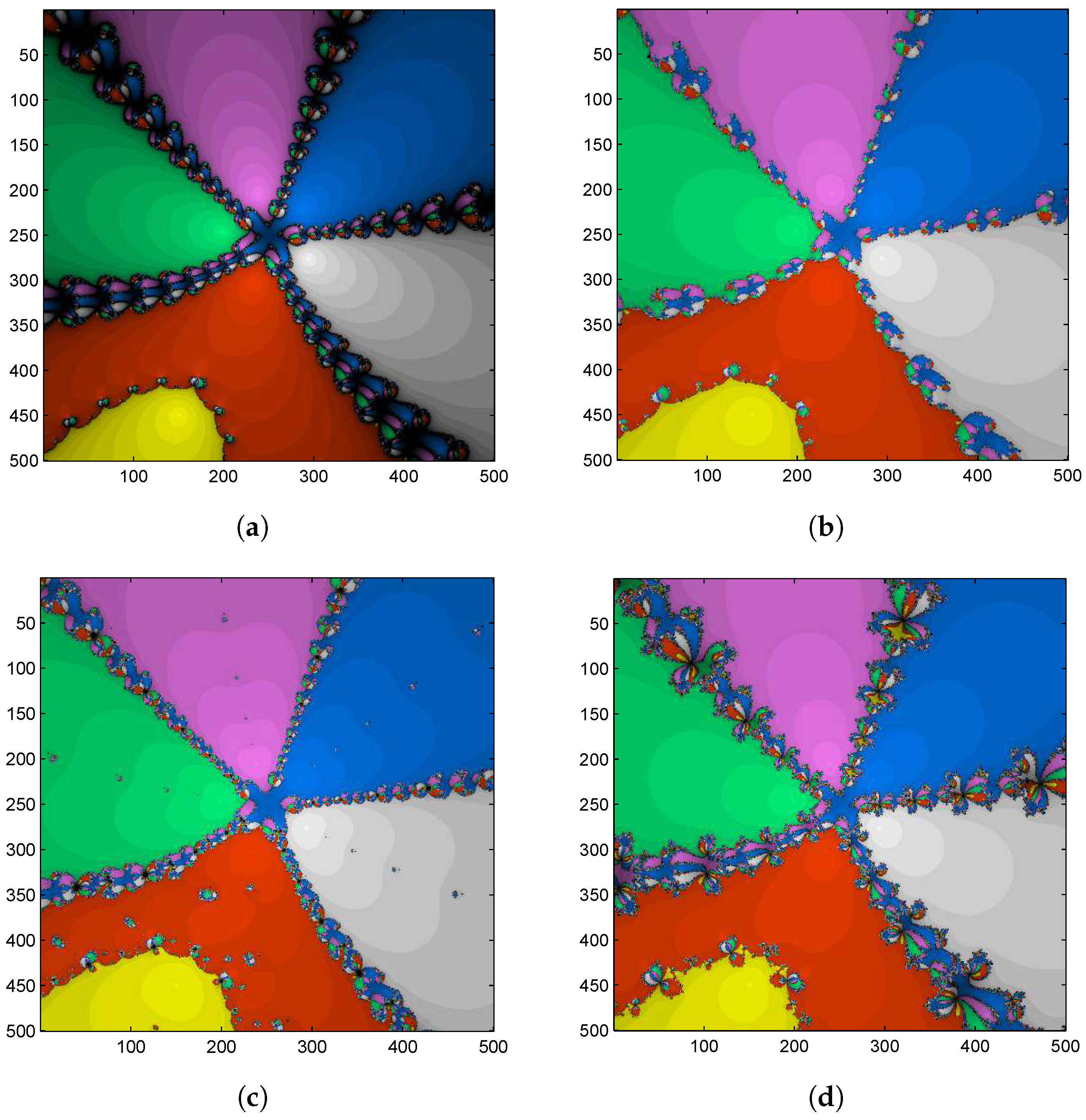
Figure 2.
Basin of attraction for by different methods. (a) Second-order Newton’s method; (b) fourth-order Jarratt’s method; (c) sixth-order Kou et al. method; and (d) sixth-order CHN method.
- 1.
- The dynamics for all the methods contain a Fatou set with similar basins and a fractal Julia set with some chaotic behavior.
- 2.
- The black part is the Julia set, which exhibits chaotic behavior, which means the method fails or diverges. Clearly, Newton’s method obtained the biggest Julia set (Figure 2a).
- 3.
- The colored part with six different colors to each root is the Fatou set, which contains the basins of the methods. From Figure 2, we see that the proposed method (CHN) has a Fatou set with bigger orbits and thus basins, but it also has a Julia set with chaotic behavior at the border of the basins.
8. Conclusions
We studied a sixth-order Newton-like method (CHN) based on a contraharmonic-mean. Two local convergence analyses were performed for the method. Local convergence analysis I demands the sixth-order derivative, but the second version needs only the first-order derivative. We checked the theoretical results by the numerical experiments, and the numerical results were examined with the basins of attraction for some selected examples. The supremacy of the CHN method is shown over the compared methods through the numerical and dynamical results, except for the numerical example 3, where there is a tie with Kou’s method. We obtained consistent conjugate maps for second-degree polynomial , which is useful in the further study of dynamics. We calculated the extraneous fixed points for . These fixed points are repulsive; hence, they are not the part of solution space [11]. The integrated approach of study (dynamical, numerical, and theoretical) is generative for the further study of Newton-like methods. Future work shall deal with furthering the applicability of other methods in a similar fashion [9,17,18,19].
Author Contributions
Conceptualization, M.K.S., I.K.A. and S.R.; methodology, M.K.S., I.K.A. and S.R.; software, M.K.S., I.K.A. and S.R.; validation, M.K.S., I.K.A. and S.R.; formal analysis, M.K.S., I.K.A. and S.R.; investigation, M.K.S., I.K.A. and S.R.; resources, M.K.S., I.K.A. and S.R.; data curation, M.K.S., I.K.A. and S.R.; writing—original draft preparation, M.K.S., I.K.A. and S.R.; writing—review and editing, M.K.S., I.K.A. and S.R.; visualization, M.K.S., I.K.A. and S.R.; supervision, M.K.S., I.K.A. and S.R.; project administration, M.K.S., I.K.A. and S.R.; and funding acquisition, M.K.S., I.K.A. and S.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ostrowski, A.M. Solutions of Equations and Systems of Equations; Academic Press: New York, NY, USA; London, UK, 1966. [Google Scholar]
- Argyros, I.K. Computational Theory of Iterative Methods; Series—Studies in Computational Mathematics; Elsevier: New York, NY, USA, 2007. [Google Scholar]
- Argyros, I.K.; Singh, M.K. On the Contraharmonic-mean Newton’s method (CHN). J. Interdiscip. Math. 2023, 26, 231–243. [Google Scholar] [CrossRef]
- Argyros, I.K.; Singh, M.K. On the semilocal convergence of the Contraharmonic-mean Newton’s method (CHMN). Commun. Korean Math. Soc. 2022, 37, 1009–1023. [Google Scholar] [CrossRef]
- Singh, M.K.; Argyros, I.K. The Dynamics of a Continuous Newton-like Method. Mathematics 2022, 10, 3602. [Google Scholar] [CrossRef]
- Rall, L.B. Computational Solution of Nonlinear Operator Equations; Robert E. Krieger: New York, NY, USA, 1979. [Google Scholar]
- Wang, K.; Kou, J.; Gu, C. Semilocal convergence of a sixth-order jarrat method in Banach spaces. Numer. Algorithms 2011, 57, 441–456. [Google Scholar] [CrossRef]
- Kantorovich, L.V.; Akilov, G.P. Functional Analysis; Pergamon Press: Oxford, UK, 1982. [Google Scholar]
- Jarratt, P. Some fourth order multipoint iterative methods for solving equations. Math. Comp. 1966, 20, 434–437. [Google Scholar] [CrossRef]
- Kou, J.; Li, Y. An improvement of Jarratt method. Appl. Math. Comput. 2007, 189, 1816–1821. [Google Scholar] [CrossRef]
- Vrscay, E.R.; Gilbert, W.J. Extraneous fixed points, basin boundaries and chaotic dynamics for Schroder and Konig rational iteration functions. Numer. Math. 1987, 52, 1–16. [Google Scholar] [CrossRef]
- Amat, S.; Busquier, S.; Plaza, S. Review of some iterative root-finding methods from a dynamical point of view. Scientia 2004, 10, 35. [Google Scholar]
- Argyros, I.K.; Magrenan, A.A. Iterative Methods and Their Dynamics with Applications: A Contemporary Study; CRC Press Taylor and Francis: Boca Raton, FL, USA, 2017. [Google Scholar]
- Scott, M.; Neta, B.; Chun, C. Basin attractors for various methods. Appl. Math. Comput. 2011, 218, 2584–2599. [Google Scholar] [CrossRef]
- Julia, G. Memoire sure l’iteration des fonction rationelles. J. Math. Pures Appl. 1918, 81, 47–235. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; Macmillan: New York, NY, USA, 1983; ISBN 978-0-7167-1186-5. [Google Scholar]
- Parida, P.K.; Gupta, D.K. Recurrence relations for a newton-like method in banach spaces. J. Comput. Appl. Math. 2007, 206, 873–887. [Google Scholar] [CrossRef]
- Veron, M.A.H.; Martinez, E. On the semilocal convergence of a three steps newton-type iterative process under mild convergence conditions. Numer. Algorithms 2015, 70, 377–392. [Google Scholar] [CrossRef]
- Wu, Q.; Zhao, Y. Third-order convergence theorem by using majorizing functions for a modified Newton’s method in Banach spaces. Appl. Math. Comput. 2006, 175, 1515–1524. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).