Abstract
This work communicates line-strength data and associated scripts for the computation and spectroscopic fitting of selected transitions of diatomic molecules. The scripts for data analysis are designed for inclusion in various software packages or program languages. Selected results demonstrate the applicability of the program for data analysis in laser-induced optical breakdown spectroscopy primarily at the University of Tennessee Space Institute, Center for Laser Applications. Representative spectra are calculated and referenced to measured data records. Comparisons of experiment data with predictions from other tabulated diatomic molecular databases confirm the accuracy of the communicated line-strength data.
1. Introduction
Atomic, molecular, optical (AMO) spectroscopy furnishes fundamental insight by decoding light emanating from targets of interest [1,2,3,4,5,6,7,8]. Analytical studies of elements may be straightforward, especially for elements that appear in the first three rows of the period table. Balmer-series hydrogen lines or sodium D-lines usually are well separated from spectral interference for low (∼1 eV)-temperature plasma containing sodium as long as reasonable resolving power is available. For example, for the sodium D-lines, a resolving power, R, of R≃1000 is needed to distinguish the two components D1 and D2, separated by ∼0.06 nm. Resolving individual lines of molecular spectra may require 10,000, or at least of the order of one magnitude better resolution than needed for atoms, of course depending on temperature. In molecular spectroscopy, one tends to focus on molecular bands describing electronic transitions. The study of individual atomic or molecular resonances with continuous-wave radiation typically requires GHz scans with nominal MHz or better laser bandwidths. In this work, the focus is on optical spectrometers that measure near-UV to near-IR molecular bands with a spectral resolution, , of the order of .
A collection of molecular diatomic spectroscopy data and expansive literature review and guidance [9] reveals a volley of recent and updated records in the UV to IR wavelength range. However, this work’s focus is the visible and near-IR, specific sets of electronic transition data that have been tested in the analysis of experimental records. The mentioned databases [9] predict OH spectra among many others for diatomic molecules, e.g., ExoMol [10] and HITEMP [11] that can be visualized using for example PGOPHER [12]—PGOPHER also allows one to model transitions for prediction and comparative analysis. Selected diatomic molecular spectra of AlO, C, CN, OH, N, NO, and TiO, transitions are of interest as these can be observed in laser-induced breakdown spectroscopy (LIBS) [13,14,15] at standard ambient temperature and pressure (SATP). Diatomic AlO and TiO spectra usually occur following the creation of micro-plasma near or at aluminum and titanium surfaces, respectively. In several cases, molecular spectra may not be of primary interest in elemental analysis with LIBS using nanosecond laser pulses, but molecular spectra are readily observed with femtosecond laser-plasma excitation, or after some time delay (of the order of larger than 100 ns for occurrence of CN in CO:N gas mixtures) from optical breakdown when using nanosecond laser pulses. Just as for atomic spectra, reasonably accurate molecular spectra are required for analysis [16,17,18,19,20]. The construction of a molecular spectrum relies on: (i) accurate line positions, and (ii) reasonably accurate transition strengths [21,22,23,24]. For the former, numerical singular value decomposition is employed for upper and lower states of a particular transition. For the latter, Frank–Condon factors and r-centroids are computed, and then combined with the rotational factors that usually decouple from the overall molecular line strength due to the symmetry of diatomic molecules.
This work communicates data files and associated scripts for the computation of diatomic molecular spectra, and equally, for the fitting of measured data using a nonlinear fitting algorithm. Calculated spectra are presented and references to recorded datasets are provided. Applications comprise fields of chemistry, materials science, astronomy, and finally physics including astrophysics, e.g., decoding of light from white dwarf stars such as Procyon B. The data are provided as a set of wave numbers, upper-level term value, and line strength. Originally, FORTRAN/Windows 7 programs computed diatomic molecular spectra [21], but the scripts for the generation of molecular spectra are redesigned for use with MATLAB [25]. Moreover, this work communicates MATLAB-optimized line-strength files (LSFs) containing three columns, namely wave numbers, upper term values, and line strengths. The codes are operating system-independent as long as MATLAB or similar programs are available that allow scripts similar to the ones available in MATLAB. Supplementary data contain programs and nine selected diatomic molecular transitions of AlO, C Swan, CN red, CN violet, OH ultraviolet, N, NO gamma, TiO , and TiO .
2. Materials and Methods
The computation of diatomic molecular spectra uses established line-strength data. Programs in FORTRAN accomplish the generation of spectra, coupled with a separate plotting program for visualization, including convenient implementation using a Microsoft-Windows 7 operating system. This work communicates equivalent MATLAB scripts that appear popular with various research groups. First, the Boltzmann equilibrium spectral program (BESP) generates a theoretical spectrum, and second, the Nelder–Mead temperature (NMT) program accomplishes fitting of experimental and theoretical spectra. In principle, BESP can be used to generate maps as a function of temperature and linewidth with subsequent determination of the optimum solution with minimal errors in the least-square sense. In turn, NMT uses nonlinear optimization using geometric constructs, viz. simplicia. The accumulation of experimental spectra in this work is in accord with laser-induced breakdown spectroscopy, or in general, laser spectroscopy [26].
2.1. MATLAB Scripts
The parameter list includes wavelength minimum, maximum, temperature, number of points, normalization factor, and file name. For the BESP.m and NMT.m scripts, the outputs are generated in graphical form. Table 1 lists constants that could be used (comment line in the scripts) for the determination of the variation of the refractive index, n, of air with wavelength [27],
where is the wavelength in normal air at 15 C and 101,325 Pa (760 mm Hg), expressed in terms of micrometer (range 0.2218–0.9000 m).

Table 1.
Constants for variation of refractive index, n; see Equation (1).
Table 2 lists constants that are used to account for the variation of the refractive index, , of air at 15 C, 101,325 Pa, and 0% humidity, with wavenumber [28],
where is the wavenumber in units of m.

Table 2.
Constants for variation of refractive index; see Equation (2).
Table 3 and Table 4 summarize script constants and input variables that are important for spectra computations, respectively. However, redesign of BESP.m and NMT.m from the FORTRAN/Windows 7 version [21] was accomplished with extensive discussions [24]. Edited versions of BESP.m and NMT.m are communicated in this work along with nine separate data files.

Table 3.
Constants in BESP.m and NMT.m.

Table 4.
Parameters and variables in BESP.m and NMT.m.
2.1.1. BESP.m
The script BESP.m is designed following the FORTRAN/Windows 7 version [21]. The individual diatomic molecular data files for selected transitions are concatenated to only show wavenumbers, upper-term values, and line strengths; see Table 5. Adjustments of input parameters for MATLAB [25] are rather straightforward, equally, for generalizing the script for automatic input by converting the script to a function. Individual lines are computed using Gaussian profiles [21], and for the generation of a spectrum, only one temperature is needed for equilibrium computation. Conversely, as one infers temperature from a measured spectrum, a modified Boltzmann plot [22] is constructed for the determination of the equilibrium temperature. A Gaussian line shape is selected to model the spectrometer/intensifier transfer function profile. However, one usually considers a natural linewidth for electronic state-to-state transitions, and a Gaussian line shape for Doppler broadening [29], viz.
leading to Voigt line shapes. Here, is the full-width half-maximum, the wavelength, T the temperature, and M the molecular weight. For example, with , , and (OH), . The spectral resolution, , for the OH emission spectra-fitting, discussed in the Appendix, amounts to . Consequently, a Gaussian line shape is considered instead of a Voigt line shape for fitting of the OH data in the appendix, but the communicated MATLAB scripts can be adjusted for Voigt profiles, important for cases when individual electronic state-to-state molecular transitions/resonances are investigated. Equally, when investigating individual transitions/resonances, asymmetric molecular line shapes can be implemented in the scripts. There is usually a volley of lines for electronic transitions of a diatomic molecules, e.g., OH [30] in excess of 3 kK, within a wavelength bin and for an experimental spectral resolution of the order of 0.33 nm.

Table 5.
Line-strength data contents: Vacuum wave numbers and upper term values, line strengths.
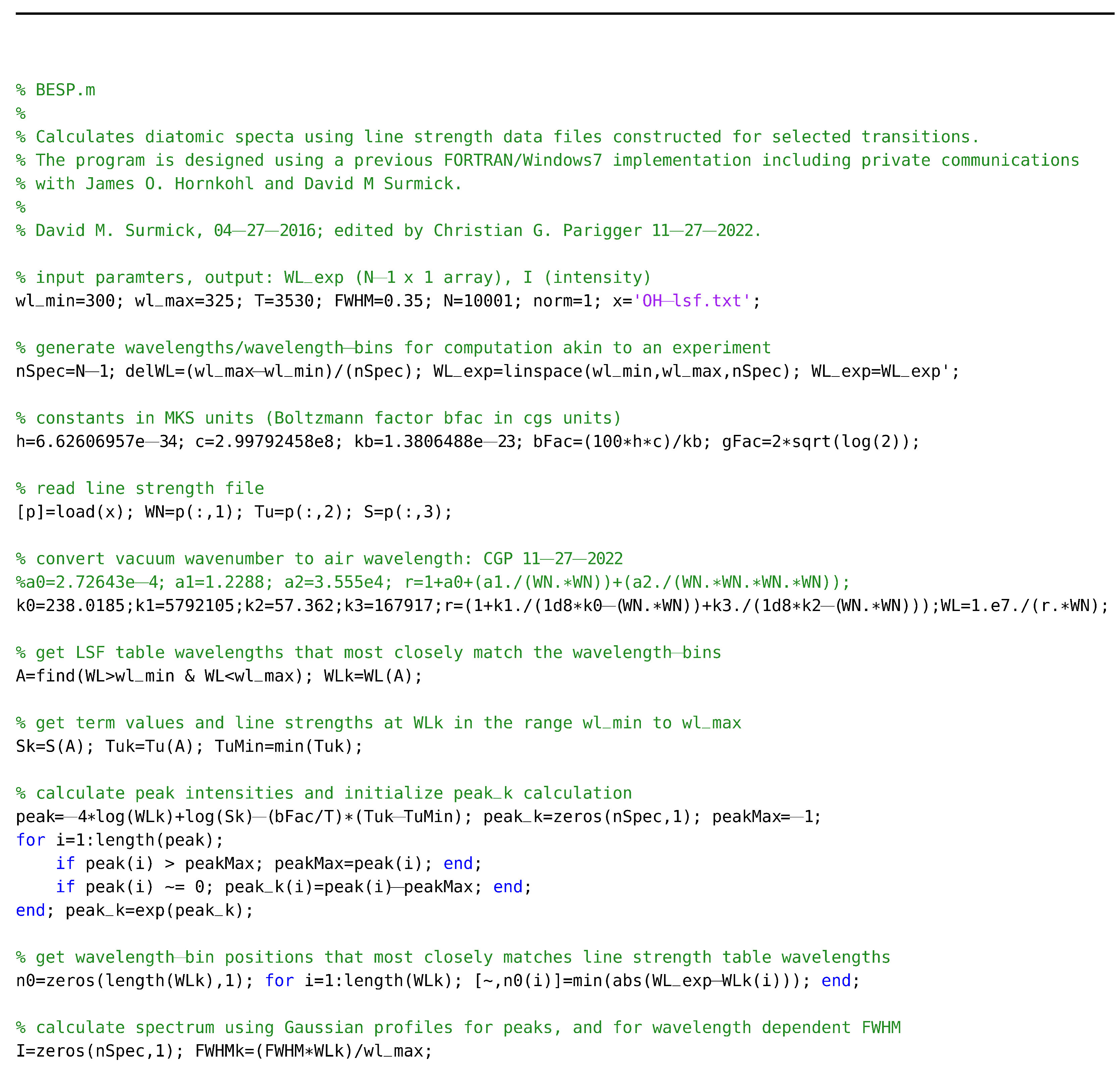
The program BESP.m receives input from the LSFs that contain relative line strengths. The output is generated in graphical format, and the program is slightly adjusted for the generation of the spectra illustrated in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9. However, Figure 6 is generated with the BESP.m script given below.

2.1.2. NMT.m
The NMT script details are deferred to Appendix A. The adaptation of a previous FORTRAN code with Windows 7 libraries for a Microsoft platform is no longer viable due to support discontinuation of the Windows 7 operating system. However, the NMT.m script delivers spectra-fitting results identical to those obtained with the FORTRAN/Windows 7 implementation.
2.1.3. Data Files
This section explains the line-strength data communicated in this work. The line-strength files (LSFs) contain wave numbers, upper term values, and the line strengths. Table 5 summarizes contents of line-strength data. The air wavelength in the program, WL, is in units of nm. The two programs BESP and NMT convert the vacuum wave numbers to air wavelengths for the analysis of measured data; see Equation (1). Table 6 associates the diatomic molecules and their line-strength data, including the wavelength range.

Table 6.
Diatomic molecules, line-strength data files, wavelength range, and number of spectral lines.
The LSFs contain significantly more data than illustrated in this communication. Applications of the LSFs include data analysis of laser-induced fluorescence and computation of absorption spectra. Some of these applications are elaborated on in the discussion of C Swan spectra [23].
3. Results
This section summarizes the communicated line-strength data. Table 7 associates the diatomic molecules and their line-strength files (LSF). The LSFs contain wave numbers, upper term values and the line strength. The two programs BESP and NMT convert the vacuum wave numbers to air wavelengths for the analysis of measured data. Table 7 displays spectral resolution, temperature, and Table 7 also communicates but one reference each for measurement and fitting selected molecular transitions of AlO, C, CN, OH, N, NO, and TiO. Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 illustrate computed spectra that refer to measured ones in the references.

Table 7.
Diatomic molecules, spectral resolution, temperature, and one typical reference each that uses the data.
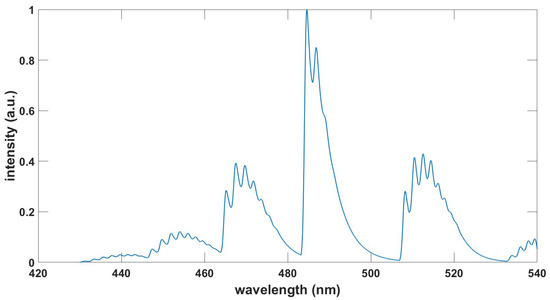
Figure 1.
Computed AlO spectrum, , , T = 3.33 kK.
Figure 1.
Computed AlO spectrum, , , T = 3.33 kK.
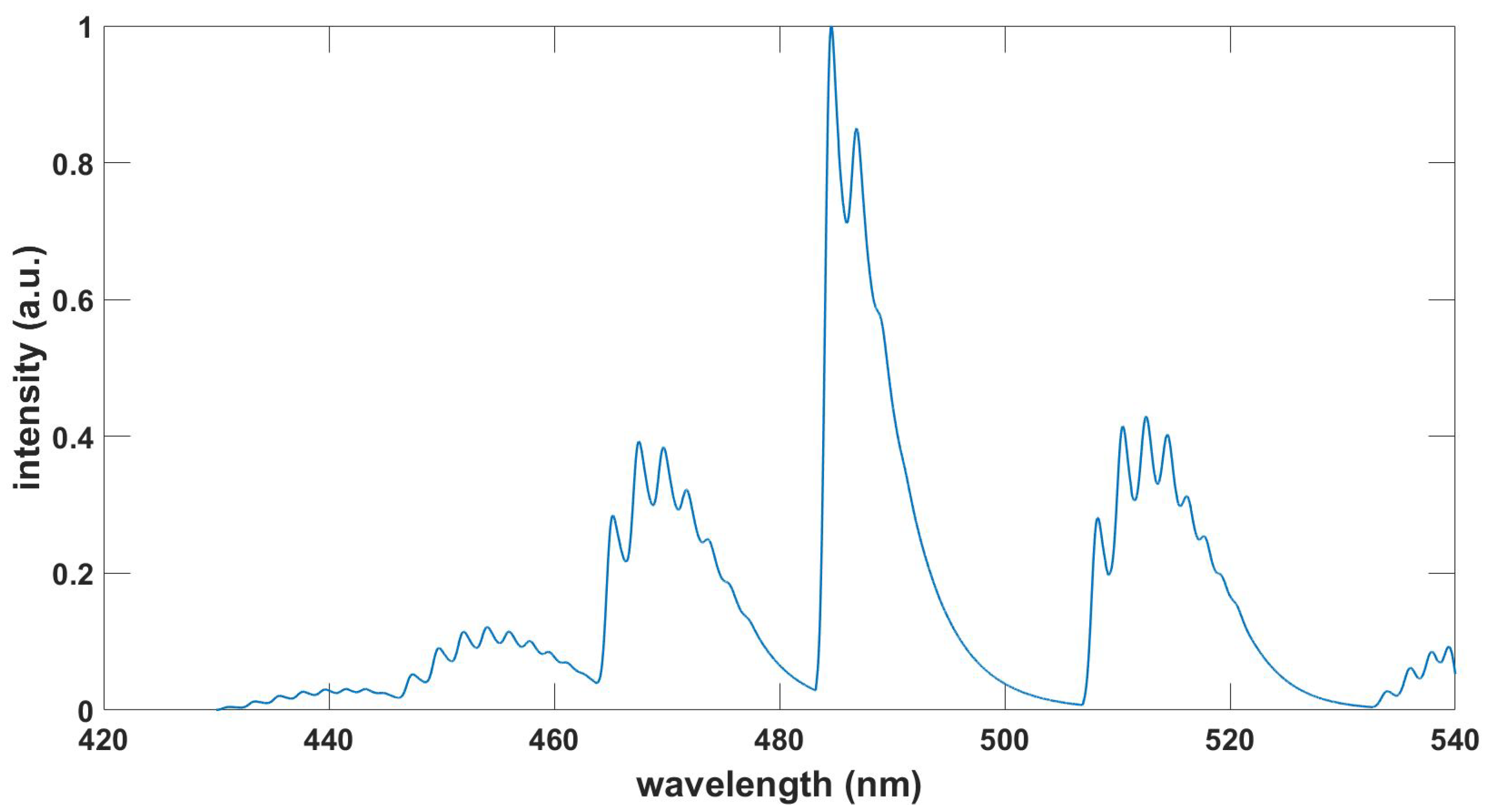
Figure 2.
Computed C Swan spectrum, , , T = 6.75 kK.
Figure 2.
Computed C Swan spectrum, , , T = 6.75 kK.
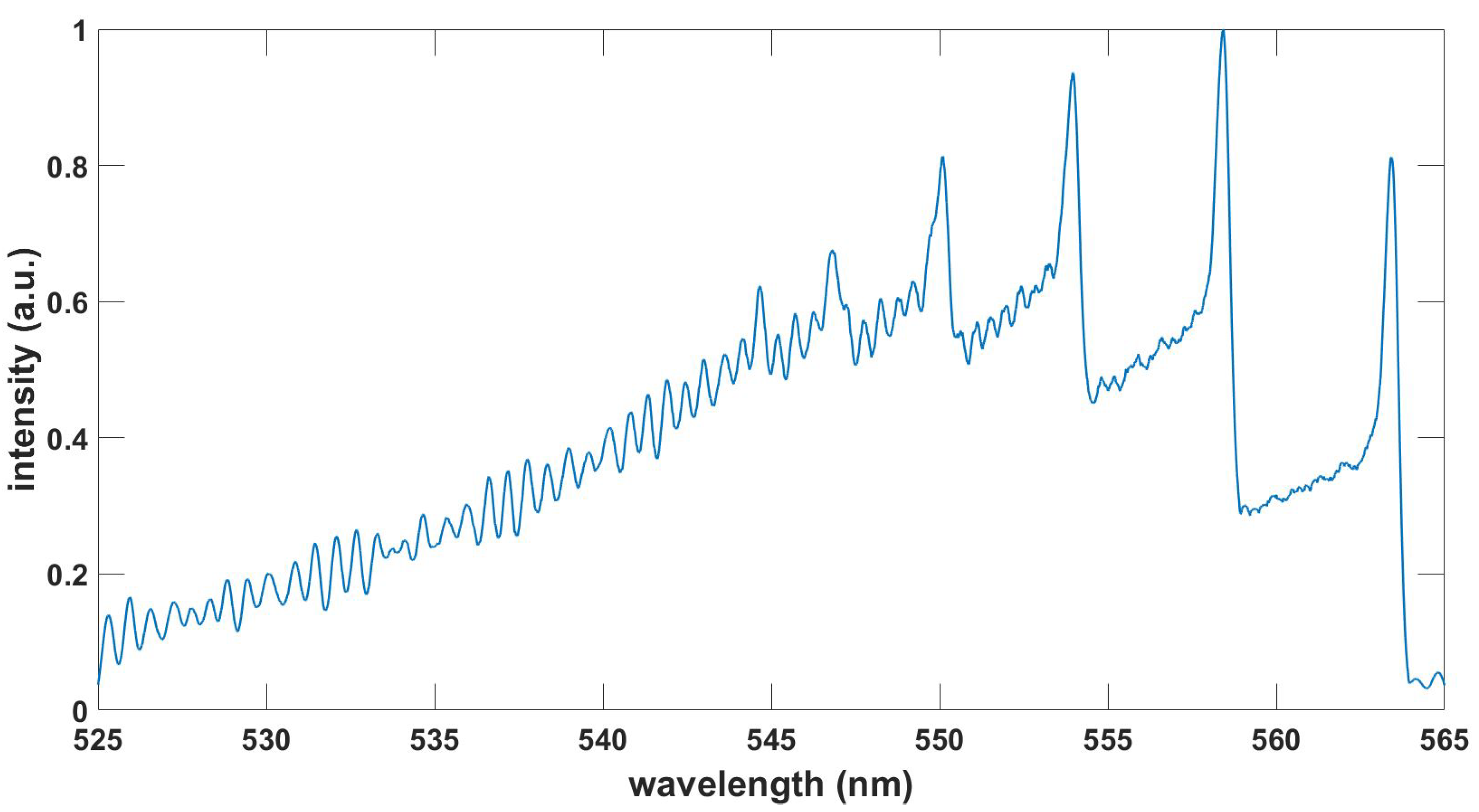
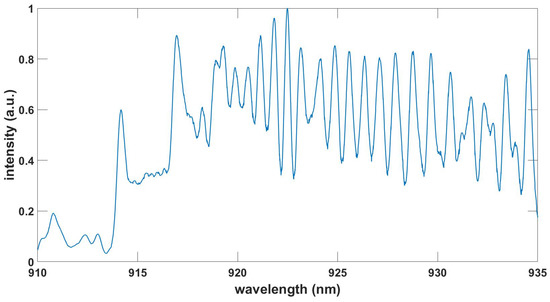
Figure 3.
Computed CN red spectrum, , , T = 7.5 kK.
Figure 3.
Computed CN red spectrum, , , T = 7.5 kK.
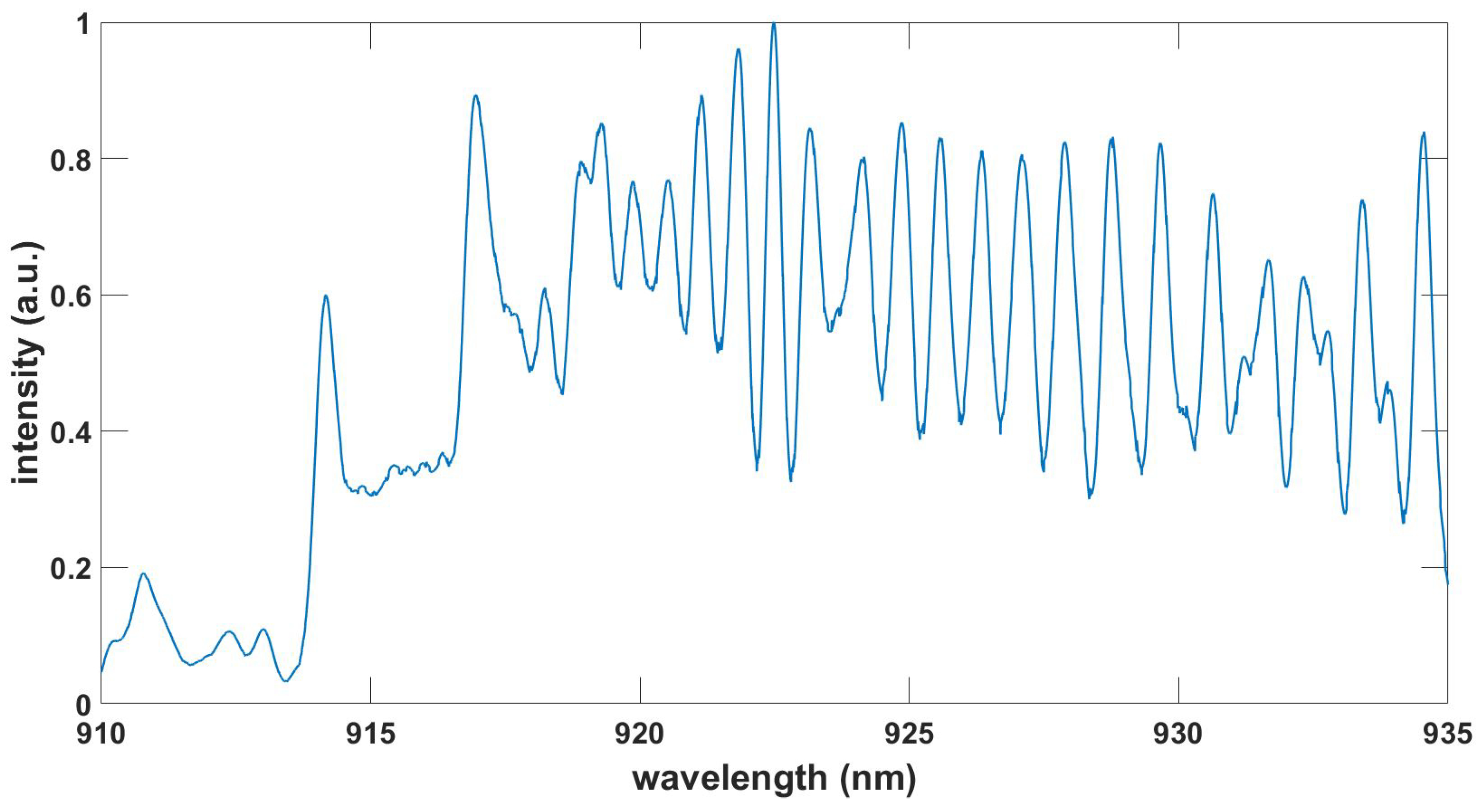
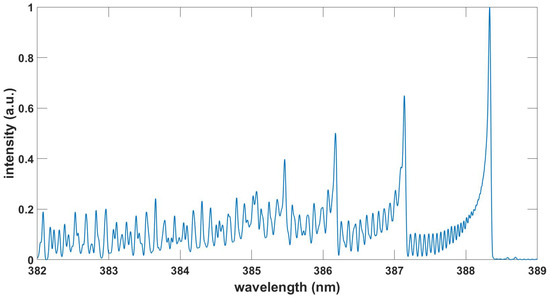
Figure 4.
Computed CN violet spectrum, , , T = 7.94 kK.
Figure 4.
Computed CN violet spectrum, , , T = 7.94 kK.
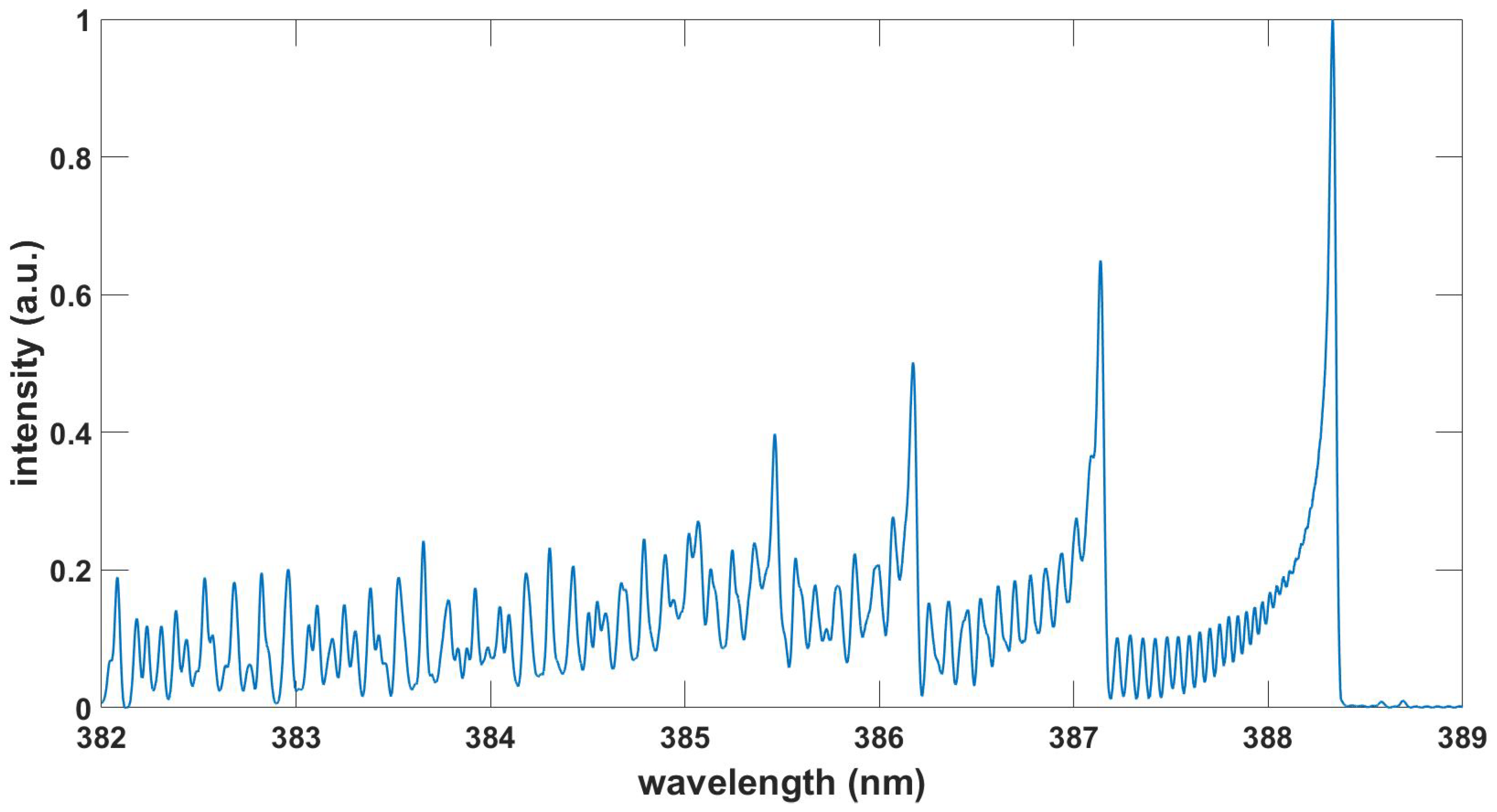
Figure 5.
Computed N spectrum, , , T = 5.1 kK.
Figure 5.
Computed N spectrum, , , T = 5.1 kK.
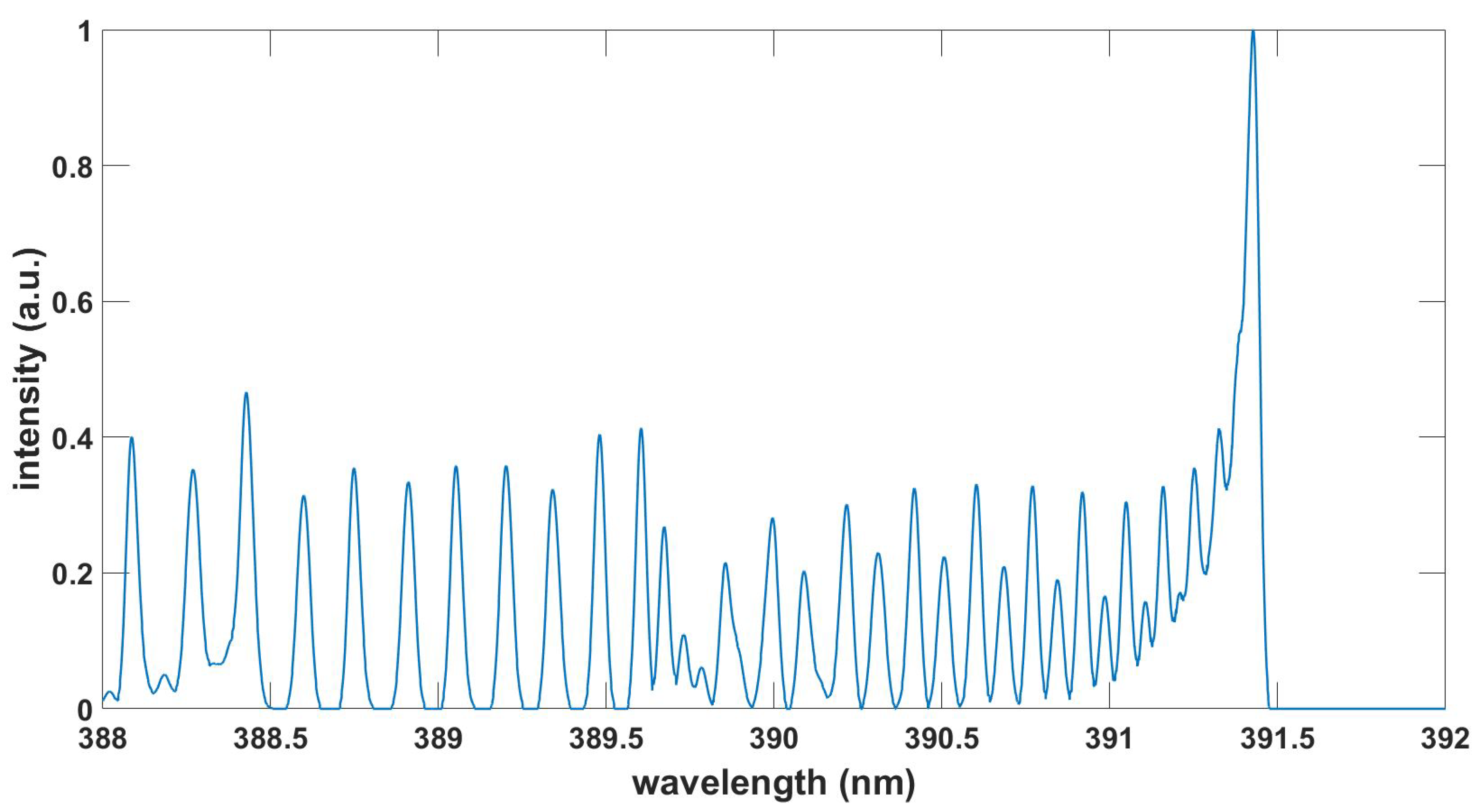
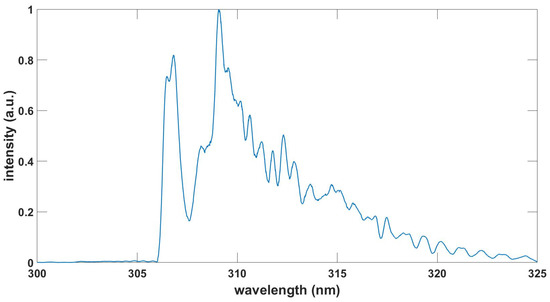
Figure 6.
Computed OH spectrum, , , T = 3.39 kK, see BESP.m script and Ref. [30].
Figure 6.
Computed OH spectrum, , , T = 3.39 kK, see BESP.m script and Ref. [30].
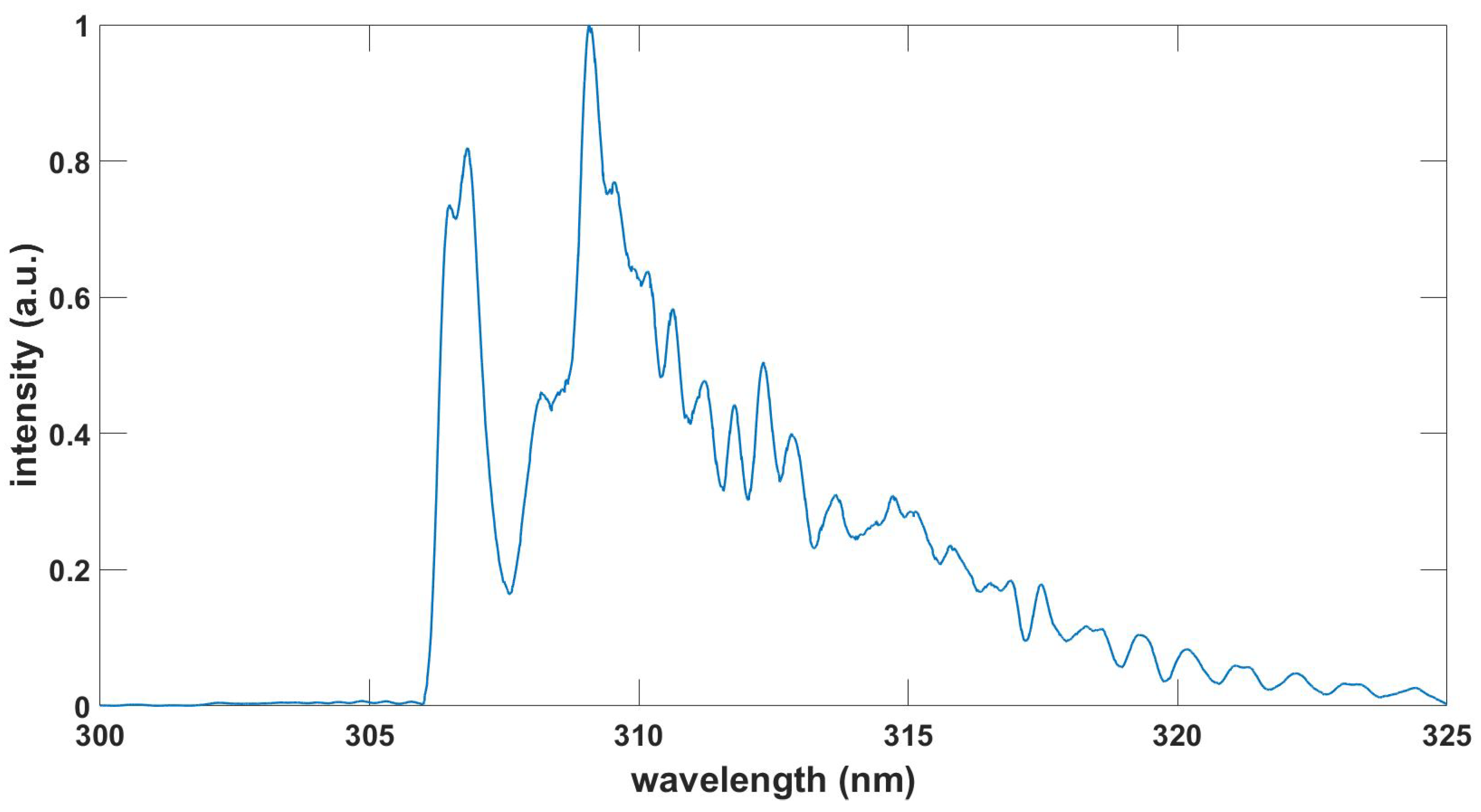
Figure 7.
Computed NO gamma spectrum, , , T = 6.80 kK.
Figure 7.
Computed NO gamma spectrum, , , T = 6.80 kK.
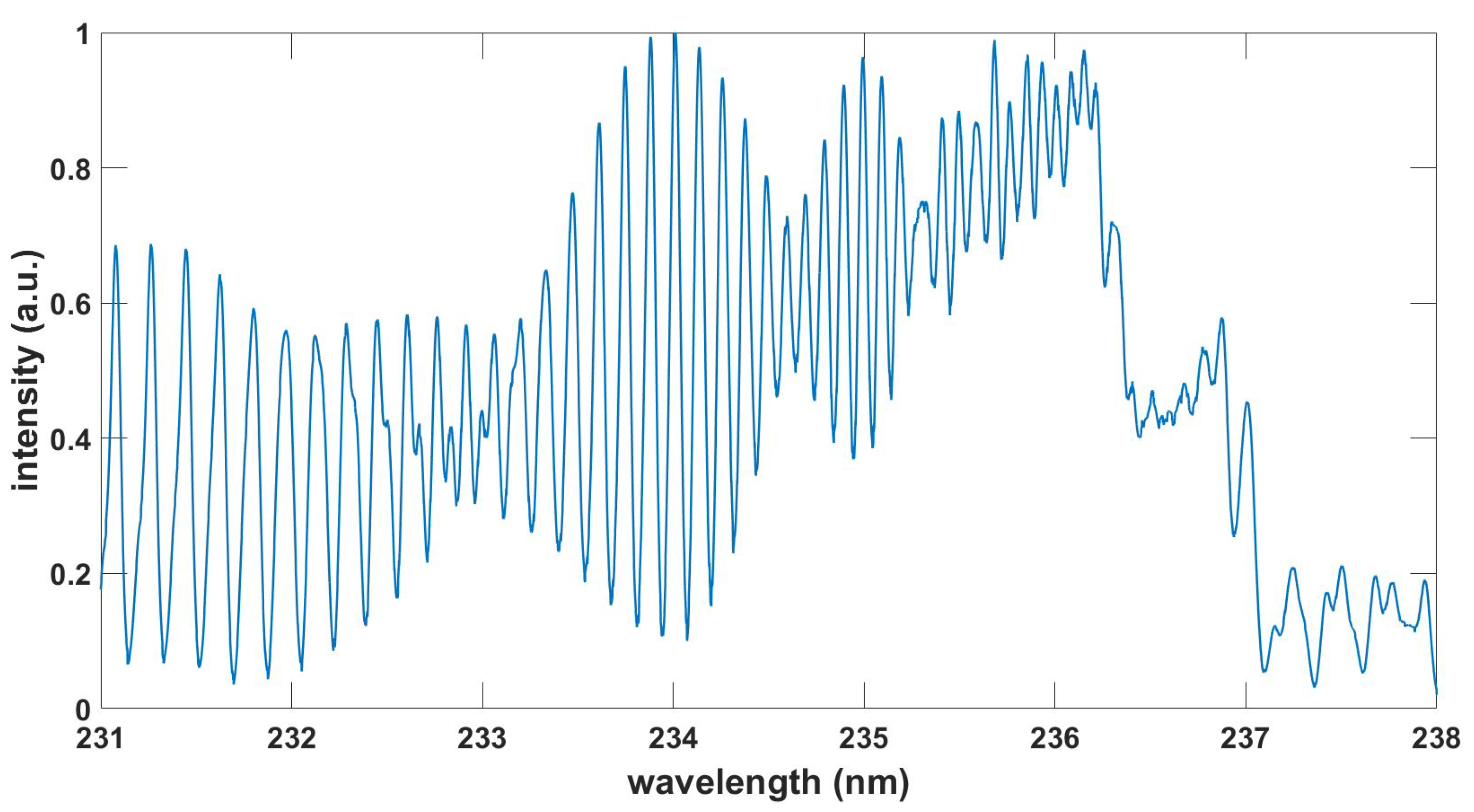
Figure 8.
Computed TiO spectrum, , , T = 3.03 kK.
Figure 8.
Computed TiO spectrum, , , T = 3.03 kK.
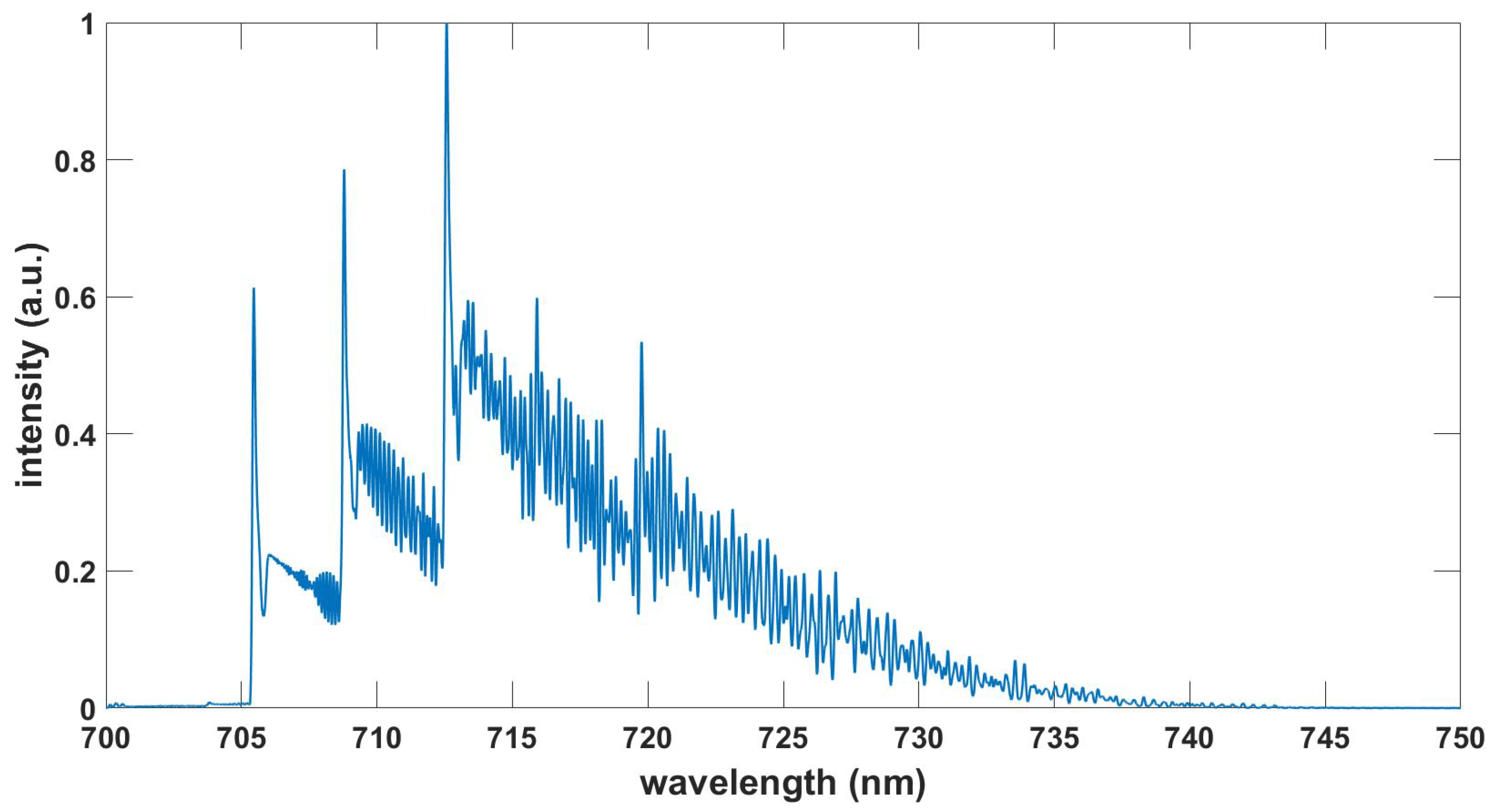
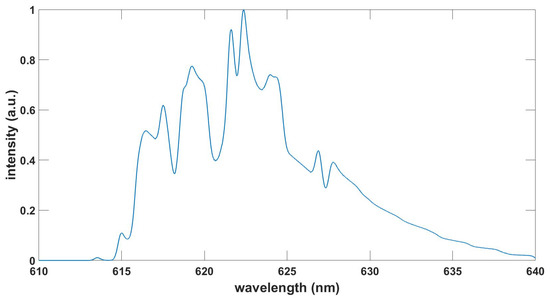
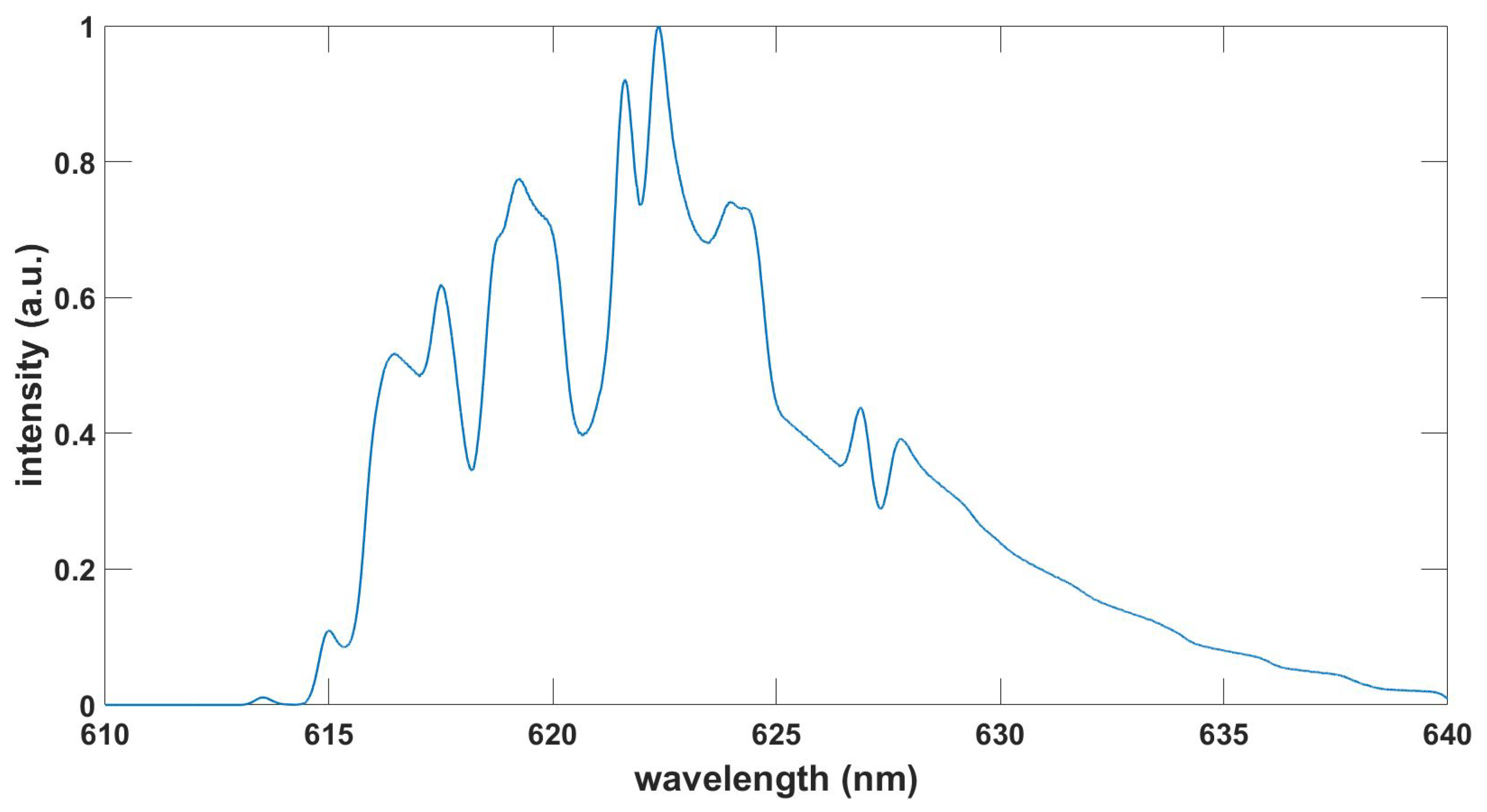
Figure 9.
Computed TiO spectrum, , , T = 3.6 kK.
Figure 9.
Computed TiO spectrum, , , T = 3.6 kK.
4. Discussion
The accurate prediction of line positions of diatomic molecules is important for the identification and of course for the fitting of measured data. The line positions are usually more accurate than the intensity values. The selected transitions for most of the communicated diatomic molecules, especially AlO, C Swan, CN, and OH, have been extensively tested in the study of laser-induced optical breakdown. Comparisons of analysis of an experimental OH ultraviolet data record using the communicated OH table and the recent and updated ExoMol diatomic molecular databases reveal agreements of most wavelength positions, of the order of 10% variations of the line strengths, but better than 3% agreement in fitted temperature, spectral resolution and background. This bodes well for applications of expansive databases such as ExoMol in analytical laser-plasma research for the other diatomic molecules communicated in this work.
Supplementary Materials
The following supporting information can be down-loaded at: https://www.mdpi.com/article/10.3390/foundations3010001/s1. This supplement contains 9 diatomic line strength files plus 1 ExoMol-OH line strength file (see Appendix A), 1 example OH-experiment file, 2 MATLAB programs, and 2 graphical file2 that shows fitting of the OH-experiment with NMT_foundations_2.m - the program BESP_foundations_2.m computes theoretical spectra from the diatomic line strength files, and it also shows 1 graphical file.
Funding
This research received no specific external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors acknowledges the support in part by the Center for Laser Applications at the University of Tennessee Space Institute.
Conflicts of Interest
The author declares no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| BESP | Boltzmann Equilibrium Spectral Program |
| AMO | Atomic, Molecular, Optical |
| AlO | Aluminum Monoxide |
| C | Diatomic Carbon |
| CNr | Cyanide red system |
| CNv | Cyanide violet system |
| ExoMol | Molecular line lists for exoplanet and other hot atmospheres |
| FWHM | Full-Width at Half Maximum |
| HITEMP | High temperature molecular spectroscopic database |
| LIBS | Laser-Induced Breakdown Spectroscopy |
| LSF | Line-Strength file |
| NMT | Nelder–Mead Temperature |
| OH | Hydroxyl |
| N | singly ionized nitrogen |
| NO | Nitrogen Monoxide |
| PGOPHER | Program for simulating rotational, vibrational and electronic spectra |
| SATP | Standard Ambient Temperature and Pressure |
| TiO-AX | Titanium Monoxide band |
| TiO-BX | Titanium Monoxide band |
| wIRE | Wiley interdisciplinary reviews |
Appendix A
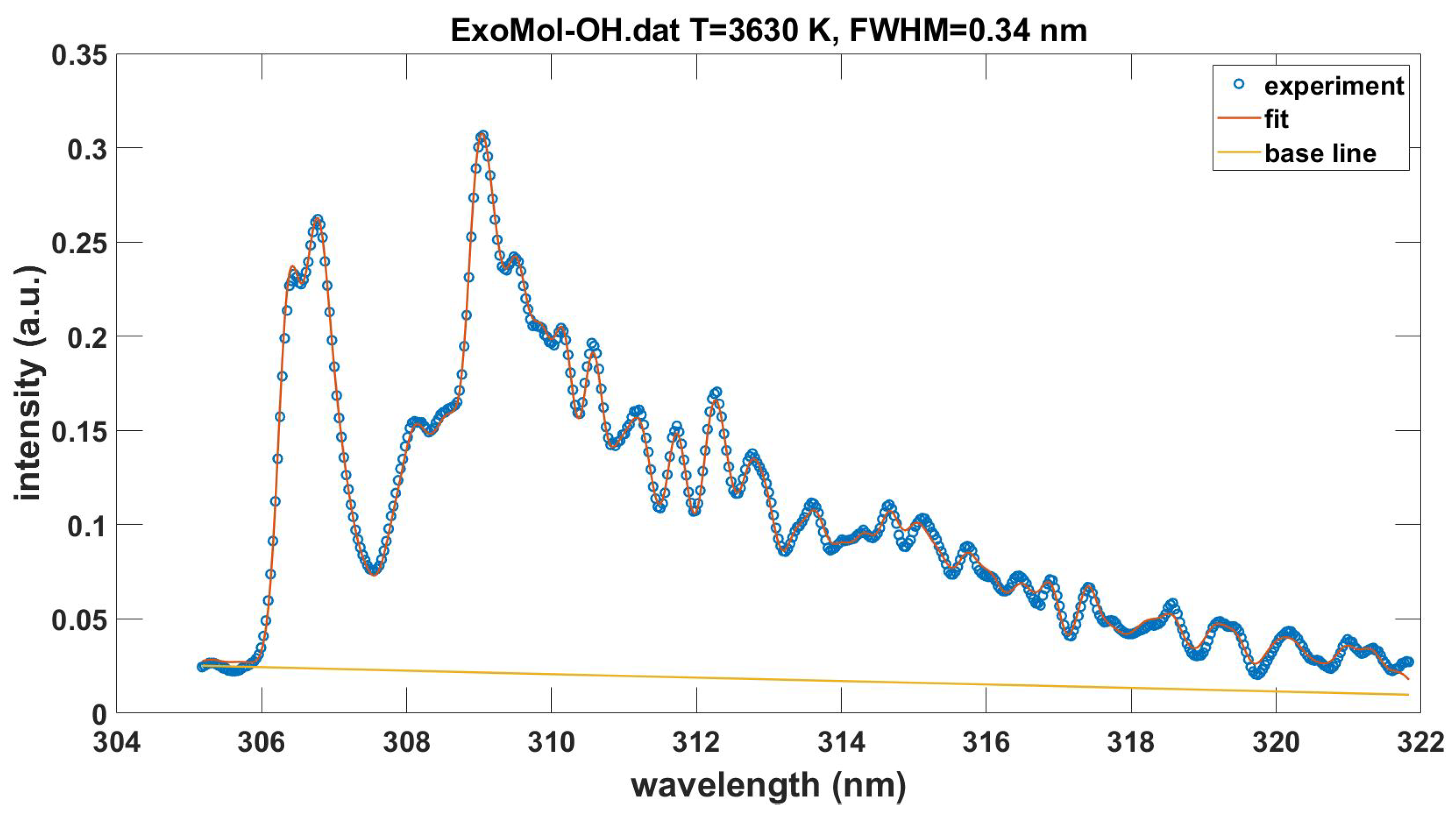
This Appendix communicates the NMT.m script for the fitting of recorded experimental data. Figure A1 shows the output in graphical form when using the data in the file OH-LSF.txt. The data file OH100micros.dat is included in the supplement. The fitting program also incorporates a slight, overall wavelength offset of for the data file OH100micros.dat. Measurement of laser-plasma emissions shows a background from other species as discussed in Ref. [39]. Fitting with the ExoMol [10] OH database [40,41,42] requires preparation of provided transition and state files to be consistent with the NMT.m input portion of the program. Figure A2 displays the results. The temperatures differ by 0.1 kK, spectral resolution by 0.01 nm and there is a slightly different linear background.
The HITEMP [11] database file 13_HITEMP2020.par for OH (57,019 lines) predicts a spectrum that is practically identical to the one from ExoMol (54,276 transitions, 1878 states) in the wavelength range of 305.17 nm to 321.83 nm for the experimental data OH100micros.dat. There are other OH databases that can be applied in the analysis of the OH emission spectra; for example, see LIFBASE [43] with associated OH transition probabilities [44]. LIFBASE shows data for molecules of interest in this work, namely OH (A-X), NO(A-X,B-X,C-X,D-X), CN(B-X) and N(B-X).
Table A1 shows comparisons for the wavelength range of the communicated OH UV (A-X) date file OH100micros.dat. There are 328 extra lines in the ExoMol.dat file, with most lines showing Einstein A coefficients that are larger than and higher vibrational levels than those for OH-LSF.txt. Subsequent to correction of an overall term-value offset in the ExoMol OH data, , of , the 512 transitions are labelled “equal” for transition wave numbers that differ by less than 0.5 cm. It is noteworthy that 497 out of the 512 lines agree within 0.1 cm.

Table A1.
Comparison of ExoMol-OH.dat and OH-LSF.txt line strengths in the wavelength range from 305.17 nm to 321.83 nm in the experimental data OH100micros.dat.
Table A1.
Comparison of ExoMol-OH.dat and OH-LSF.txt line strengths in the wavelength range from 305.17 nm to 321.83 nm in the experimental data OH100micros.dat.
| Data File | Transition Lines | Equal Lines | Vibrational Levels |
|---|---|---|---|
| ExoMol.dat | 856 | 512 | 0,1,2,3,4 |
| OH-LSF.txt | 528 | 512 | 0,1 |
The ExoMol database shows Einstein A coefficients that are converted to line strengths, , for electric dipole transitions [45], using (MKS units)
where denotes the Einstein A coefficient for a transition from an upper, u, to a lower, l, state, and h and are Planck’s constant and vacuum permittivity, respectively. The elementary charge is e, the Bohr radius is , and is the transition strength. The line strength, S, that is used in the MATLAB scripts is expressed in traditional cgs units (stC cm, see Table 5). The wavelength of the transition is , is the upper state degeneracy and the total angular momentum of the upper state.
For the 512 lines with practically equal transition wave numbers, the ratios of ExoMol-OH.dat and OH-LSF.txt strengths show the mean value 1.093 with a standard deviation of 0.071. This line-strength variation may have several causes including differences in Hönl-London terms, Frank–Condon factors, and/or r-centroids. The fitted temperature indicates a 2.8% increase from 3.53 kK to 3.63 kK despite a mean 9.3% difference in line strengths. The NMT.m fitting script requires only relative intensities in the inference of temperature from measured spectra.
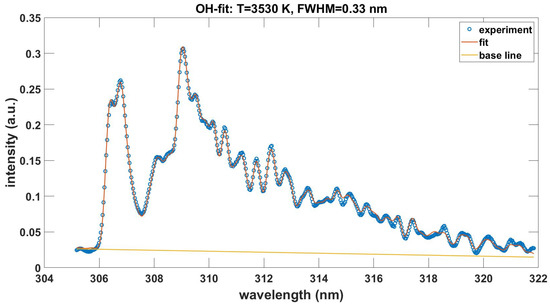
Figure A1.
Measured and with OH-LSF.txt fitted OH emission spectra, , , .
Figure A1.
Measured and with OH-LSF.txt fitted OH emission spectra, , , .
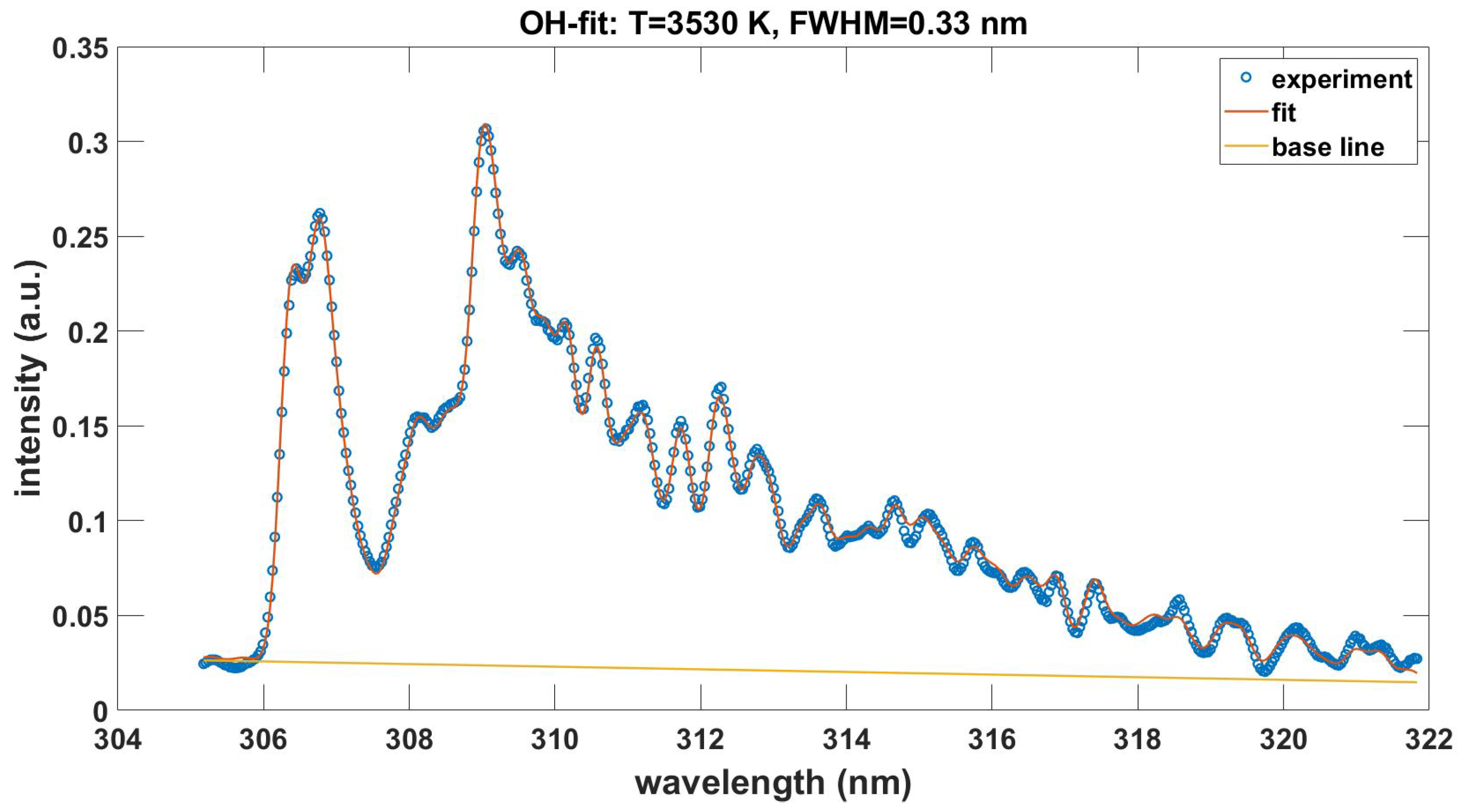
Figure A2.
Measured and with ExoMol-OH.dat fitted OH emission spectra, , , .
Figure A2.
Measured and with ExoMol-OH.dat fitted OH emission spectra, , , .


References
- Kunze, H.-J. Introduction to Plasma Spectroscopy; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Fujimoto, T. Plasma Spectroscopy; Clarendon Press: Oxford, UK, 2004. [Google Scholar]
- Ochkin, V.N. Spectroscopy of Low Temperature Plasma; Wiley-VCH: Weinheim, Germany, 2009. [Google Scholar]
- Omenetto, N. (Ed.) Analytical Laser Spectroscopy; John Wiley & Sons: New York, NY, USA, 1979. [Google Scholar]
- Demtröder, W. Laser Spectroscopy 1: Basic Principles, 5th ed.; Springer: Heidelberg, Germany, 2014. [Google Scholar]
- Demtröder, W. Laser Spectroscopy 2: Experimental Techniques, 5th ed.; Springer: Heidelberg, Germany, 2015. [Google Scholar]
- Hertel, I.V.; Schulz, C.-P. Atoms, Molecules and Optical Physics 1, Atoms and Spectroscopy; Springer: Heidelberg, Germany, 2015. [Google Scholar]
- Hertel, I.V.; Schulz, C.-P. Atoms, Molecules and Optical Physics 2, Molecules and Photons—Spectroscopy and Collisions; Springer: Heidelberg, Germany, 2015. [Google Scholar]
- McKemmish, L.K. Molecular diatomic spectroscopy data. WIREs Comput. Mol. Sci. 2021, 11, e1520. [Google Scholar] [CrossRef]
- Tennyson, J.; Yurchenko, S.N.; Al-Refaie, A.F.; Clark, V.H.J.; Chubb, K.L.; Conway, E.K.; Dewan, A.; Gorman, M.N.; Hill, C.; Lynas-Gray, A.E.; et al. The 2020 release of the ExoMol database: Molecular line lists for exoplanet and other hot atmospheres. J. Quant. Spectrosc. Radiat. Transf. 2020, 255, 107228. [Google Scholar] [CrossRef]
- Rothman, L.S.; Gordon, I.E.; Barber, R.J.; Dothe, H.; Gamache, R.R.; Goldman, A.; Perevalov, V.I.; Tashkun, S.A.; Tennyson, J. HITEMP, the high-temperature molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 2139–2150. [Google Scholar] [CrossRef]
- Western, C.M. PGOPHER, A Program for Simulating Rotational, Vibrational and Electronic Spectra. J. Quant. Spectrosc. Radiat. Transf. 2017, 186, 221–242. [Google Scholar] [CrossRef]
- Miziolek, A.W.; Palleschi, V.; Schechter, I. (Eds.) Laser Induced Breakdown Spectroscopy (LIBS): Fundamentals and Applications; Cambridge Univ. Press: New York, NY, USA, 2006. [Google Scholar]
- Singh, J.P.; Thakur, S.N. (Eds.) Laser-Induced Breakdown Spectroscopy, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- De Giacomo, A.; Hermann, J. Laser-induced plasma emission: From atomic to molecular spectra. J. Phys. D Appl. Phys. 2017, 50, 183002. [Google Scholar] [CrossRef]
- Parigger, C.G. Laser-induced breakdown in gases: Experiments and simulation. In Laser Induced Breakdown Spectroscopy (LIBS): Fundamentals and Applications; Miziolek, A.W., Palleschi, V., Schechter, I., Eds.; Cambridge Univ. Press: New York, NY, USA, 2006; Chapter 4; pp. 171–193. [Google Scholar]
- Parigger, C.G.; Surmick, D.M.; Helstern, C.M.; Gautam, G.; Bol’shakov, A.A.; Russo, R. Molecular Laser-Induced Breakdown Spectroscopy. In Laser Induced Breakdown Spectroscopy, 2nd ed.; Singh, J.P., Thakur, S.N., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; Chapter 7; pp. 167–212. [Google Scholar]
- Parigger, C.G.; Helstern, C.M.; Jordan, B.S.; Surmick, D.M.; Splinter, R. Laser-Plasma Spatiotemporal Cyanide Spectroscopy and Applications. Molecules 2020, 25, 615. [Google Scholar] [CrossRef] [PubMed]
- Parigger, C.G.; Helstern, C.M.; Jordan, B.S.; Surmick, D.M.; Splinter, R. Laser-Plasma Spectroscopy of Hydroxyl with Applications. Molecules 2020, 25, 988. [Google Scholar] [CrossRef]
- Parigger, C.G. Review of spatiotemporal analysis of laser-induced plasma in gases. Spectrochim. Acta Part B At. Spectrosc. 2021, 179, 106122. [Google Scholar] [CrossRef]
- Parigger, C.G.; Woods, A.C.; Surmick, D.M.; Gautam, G.; Witte, M.J.; Hornkohl, J.O. Computation of diatomic molecular spectra for selected transitions of aluminum monoxide, cyanide, diatomic carbon, and titanium monoxide. Spectrochim. Acta Part B At. Spectrosc. 2015, 107, 132–138. [Google Scholar] [CrossRef]
- Parigger, C.G.; Hornkohl, J.O. Quantum Mechanics of the Diatomic Molecule with Applications; IOP Publishing: Bristol, UK, 2020. [Google Scholar]
- Hornkohl, J.O.; Nemes, L.; Parigger, C.G. Spectroscopy of Carbon Containing Diatomic Molecules. In Spectroscopy, Dynamics and Molecular Theory of Carbon Plasmas and Vapors: Advances in the Understanding of the Most Complex High-Temperature Elemental System; Chapter 4; Nemes, L., Irle, S., Eds.; World Scientific: Singapore, 2011; Chapter 4; pp. 113–165. [Google Scholar]
- Surmick, D.M.; Hornkohl, J.O. (The University of Tennessee, University of Tennessee Space Institute, Tullahoma, TN, USA). Personal communication, 2016.
- MATLAB Release R2022a Update 5; The MathWorks, Inc.: Natick, MA, USA, 2022.
- Parigger, C.G.; Woods, A.C.; Witte, M.J.; Swafford, L.D.; Surmick, D.M. Measurement and analysis of atomic hydrogen and diatomic molecular AlO, C2, CN, and TiO spectra following laser-induced optical breakdown. J. Vis. Exp. 2014, 84, e51250. [Google Scholar]
- Barrell, H.; Sears, J.E. The Refraction and Dispersion of Air for the Visible Spectrum. Philos. Trans. R. Soc. Lond. 1939, 238, 1–64. [Google Scholar]
- Ciddor, P.E. Refractive index of air: New equations for the visible and near infrared. Appl. Opt. 1996, 35, 1567–1573. [Google Scholar] [CrossRef] [PubMed]
- Corney, A. Atomic and Laser Spectroscopy; Clarendon Press: Oxford, UK, 1977. [Google Scholar]
- Parigger, C.G. Hydroxyl Spectroscopy of Laboratory Air Laser-Ignition. Foundations 2022, 2, 934–948. [Google Scholar] [CrossRef]
- Dors, I.G.; Parigger, C.; Lewis, J.W.L. Spectroscopic temperature determination of aluminum monoxide in laser ablation with 266-nm radiation. Opt. Lett. 1998, 23, 1778–1780. [Google Scholar] [CrossRef]
- Parigger, C.; Plemmons, D.H.; Hornkohl, J.O.; Lewis, J.W.L. Spectroscopic Temperature Measurements in a Decaying Laser-Induced Plasma Using the C2 Swan System. J. Quant. Spectrosc. Radiat. Transf. 1994, 52, 707–711. [Google Scholar] [CrossRef]
- Trautner, S.; Jasik, J.; Parigger, C.G.; Pedarnig, J.D.; Spendelhofer, W.; Lackner, J.; Veis, P.; Heitz, J. Laser-induced breakdown spectroscopy of polymer materials based on evaluation of molecular emission bands. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2017, 174, 331–338. [Google Scholar] [CrossRef]
- Hornkohl, J.O.; Parigger, C.; Lewis, J.W.L. Temperature Measurements from CN Spectra in a Laser-Induced Plasma. J. Quant. Spectrosc. Radiat. Transf. 1991, 46, 405–411. [Google Scholar] [CrossRef]
- Parigger, C.; Plemmons, D.H.; Hornkohl, J.O.; Lewsi, J.W.L. Temperature measurements from first-negative spectra produced by laser-induced multiphoton ionization and optical breakdown of nitrogen. Appl. Opt. 1995, 34, 3331–3335. [Google Scholar] [CrossRef] [PubMed]
- Hornkohl, J.O.; Fleischmann, J.P.; Surmick, D.M.; Witte, M.J.; Swaffor, L.D.; Woods, A.C.; Parigger, C.G. Emission spectroscopy of nitric oxide in laser-induced plasma. J. Phys. Conf. Ser. 2014, 548, 12040. [Google Scholar] [CrossRef]
- Parigger, C.G.; Woods, A.C.; Keszler, A.; Nemes, L.; Hornkohl, J.O. Titanium monoxide spectroscopy following laser-induced optical breakdown. AIP Conf. Proc. 2012, 1464, 628–639. [Google Scholar]
- Woods, A.C.; Parigger, C.G.; Hornkohl, J.O. Measurement and analysis of titanium monoxide spectra in laser-induced plasma. Opt. Lett. 2012, 37, 5139–5141. [Google Scholar] [CrossRef] [PubMed]
- Parigger, C.G.; Guan, G.; Hornkohl, J.O. Measurement and analysis of OH emission spectra following laser-induced optical breakdown in air. Appl. Opt. 2003, 42, 5986–5991. [Google Scholar] [CrossRef] [PubMed]
- Brooke, J.S.A.; Bernath, P.F.; Western, C.M.; Sneden, C.; Afşar, M.; Li, G.; Gordon, I.E. Line strengths of rovibrational and rotational transitions in the X2Π ground state of OH. J. Quant. Spectrosc. Radiat. Transf. 2016, 138, 142–157. [Google Scholar] [CrossRef]
- Yousefi, M.; Bernath, P.F.; Hodges, J.; Masseron, T. A new line list for the A2Σ − X2Π electronic transition of OH. J. Quant. Spectrosc. Radiat. Transf. 2018, 217, 416–424. [Google Scholar] [CrossRef]
- Bernath, P.F. MoLLIST: Molecular Line Lists, Intensities and Spectra. J. Quant. Spectrosc. Radiat. Transf. 2020, 240, 106687. [Google Scholar] [CrossRef]
- Luque, J.; Crosley, D.R. LIFBASE: Database and Spectral Simulation for Diatomic Molecules. 2021. Available online: https://www.sri.com/platform/lifbase-spectroscopy-tool (accessed on 25 November 2019).
- Luque, J.; Crosley, D.R. Transition probabilities in the A2Σ+ − X2Πi electronic system of OH. J. Chem. Phys. 1998, 109, 439–448. [Google Scholar] [CrossRef]
- Tatum, J. Stellar Atmospheres; Open Education Resource LibreTexts Project: LibreTexts Physics, Shared under CC BY-NC 4.0 Licence; Last Updated March 5; University of Victoria: Victoria, BC, Canada, 2022. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
