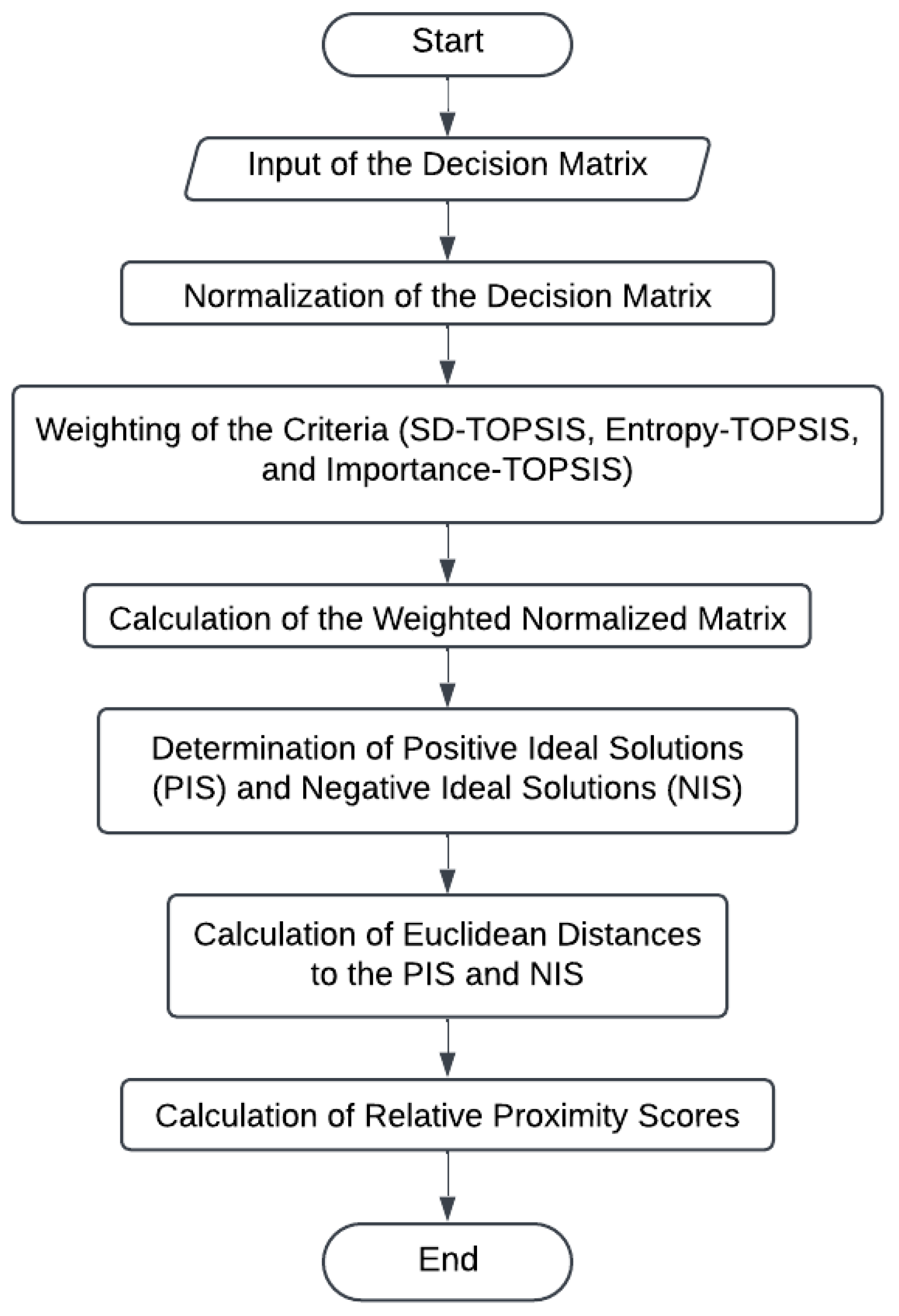
Figure 1.
Flowchart of the TOPSIS algorithm.
Figure 1.
Flowchart of the TOPSIS algorithm.
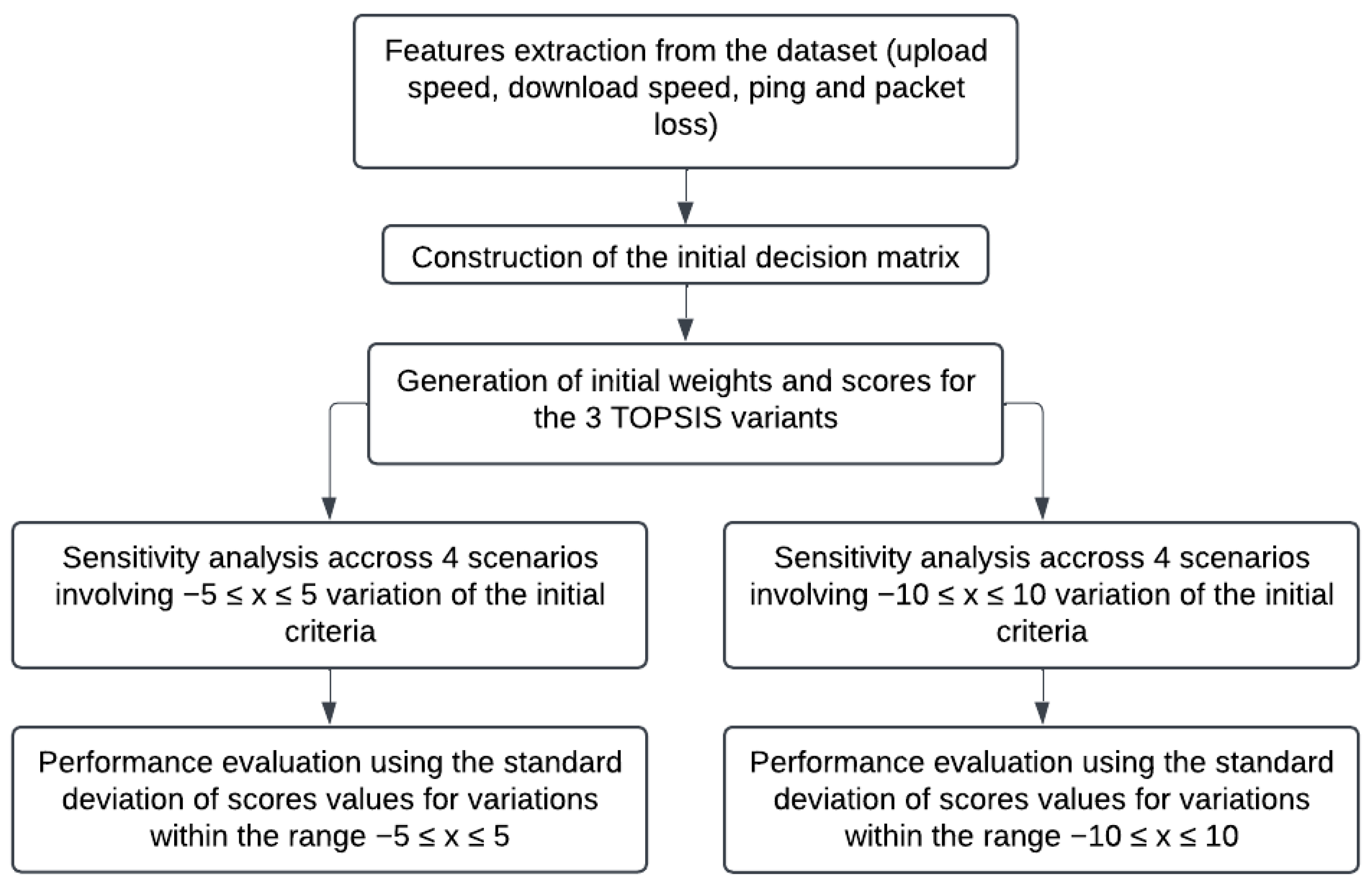
Figure 2.
Block diagram of the methodology.
Figure 2.
Block diagram of the methodology.
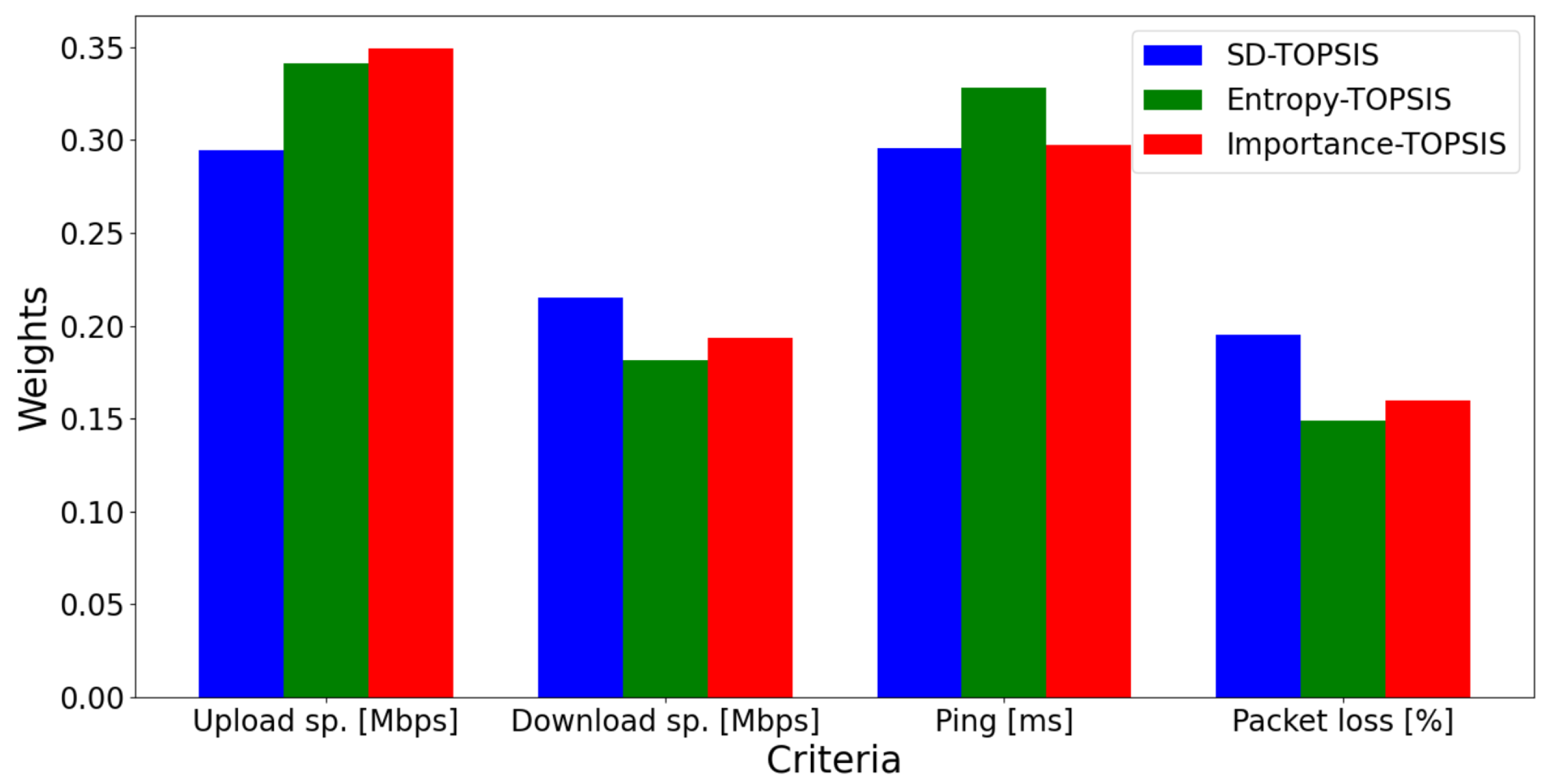
Figure 3.
Criteria weights for the initial decision matrix.
Figure 3.
Criteria weights for the initial decision matrix.
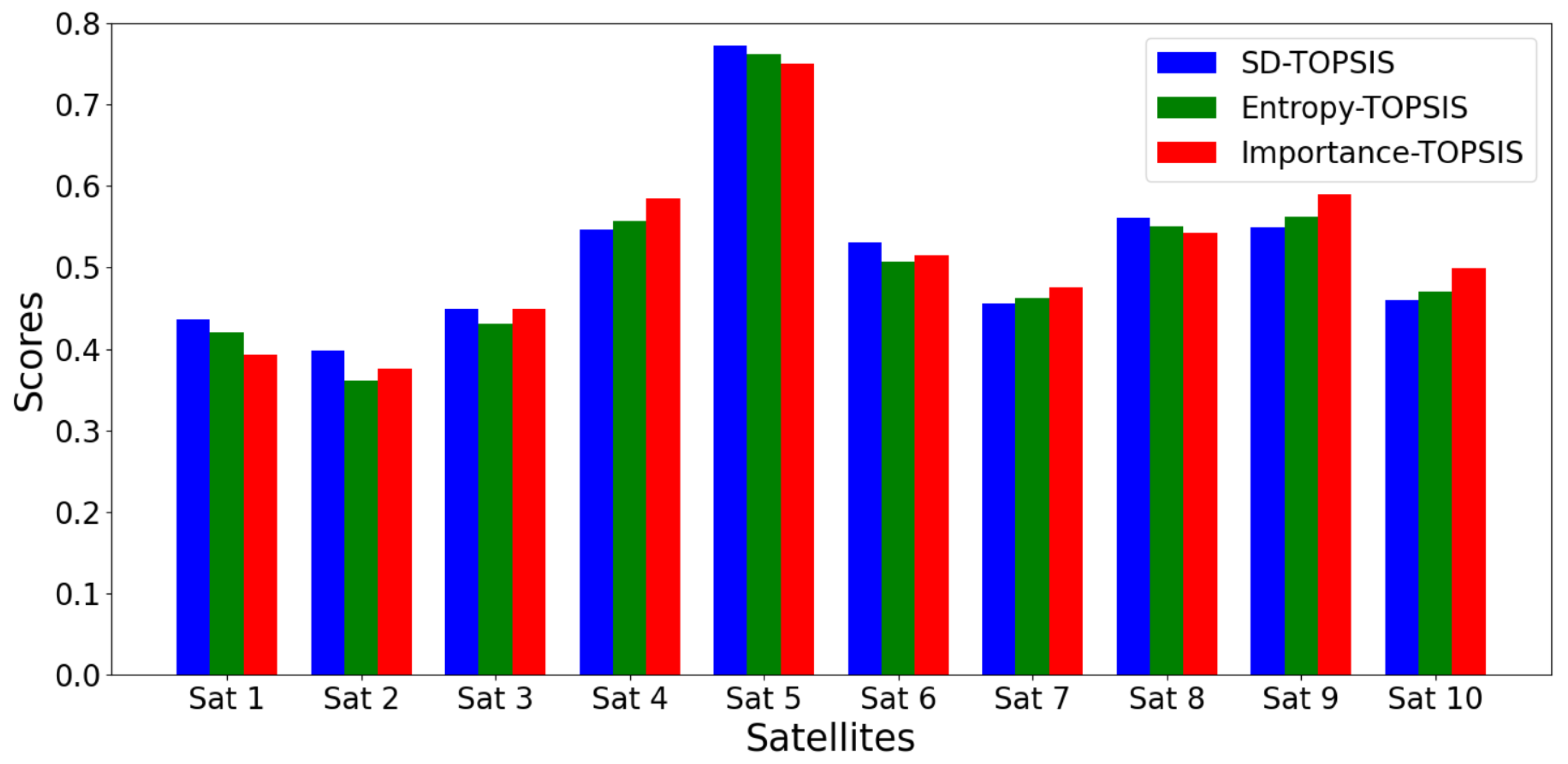
Figure 4.
Satellites scores for the initial decision matrix.
Figure 4.
Satellites scores for the initial decision matrix.
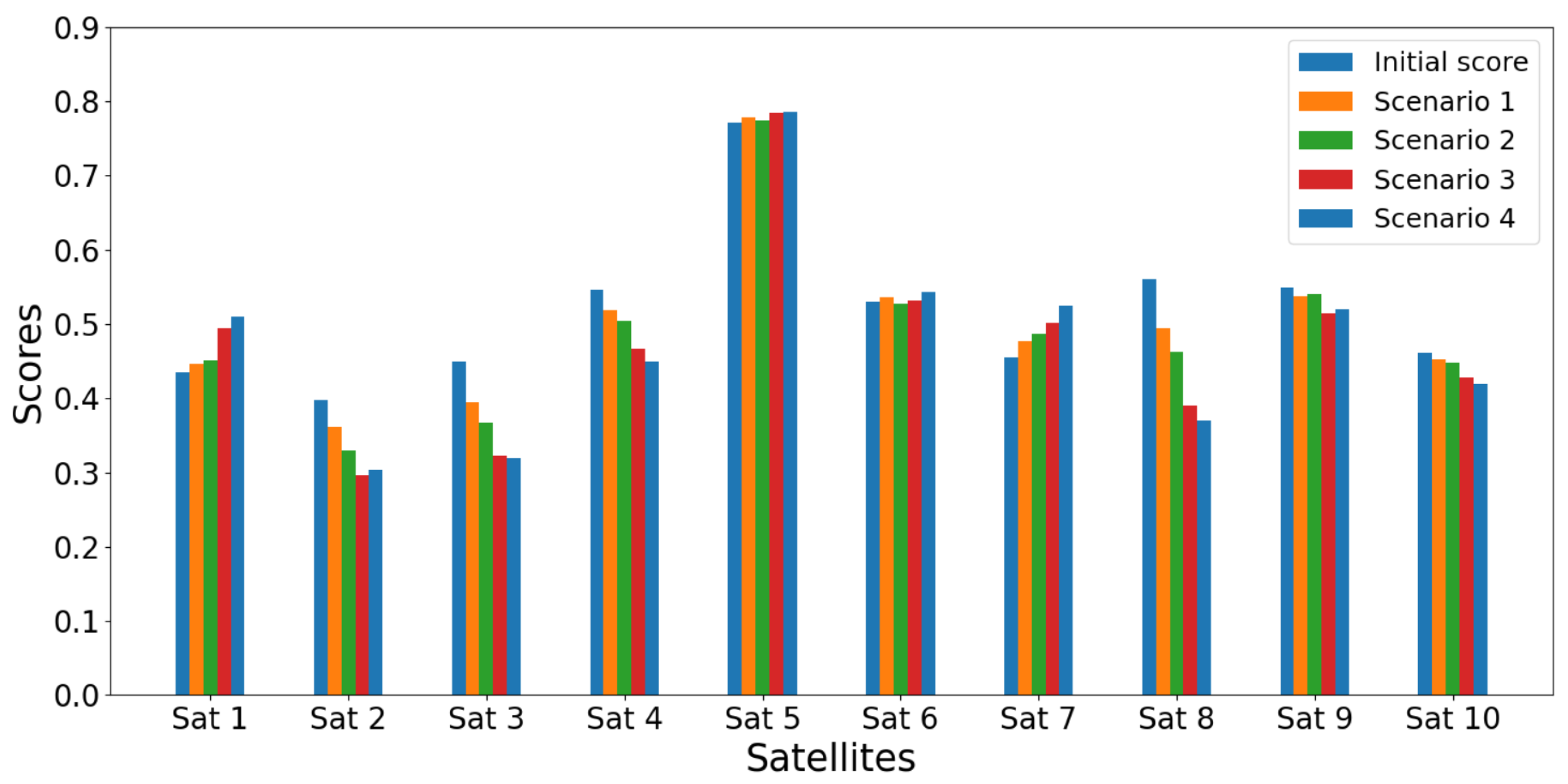
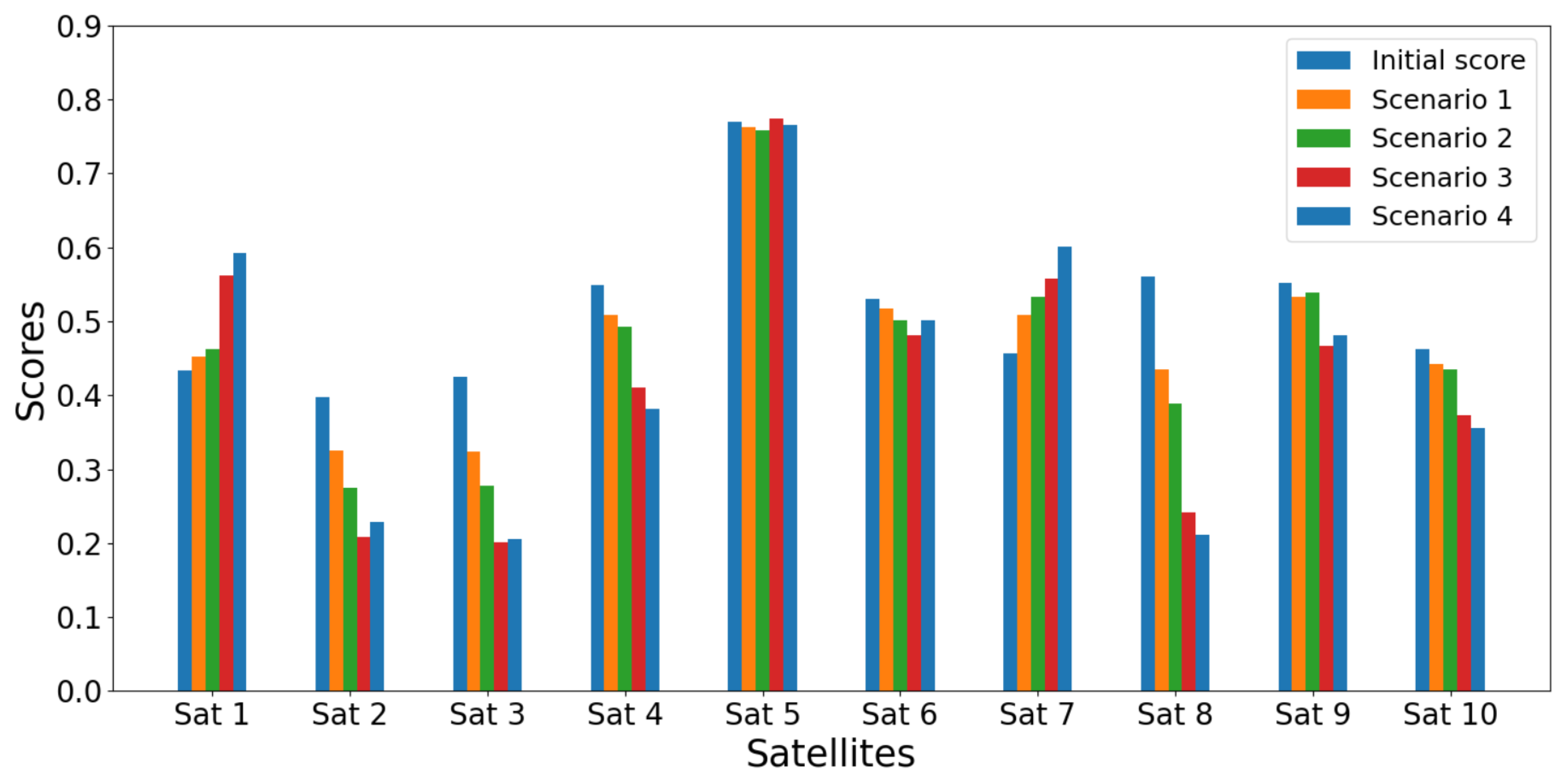
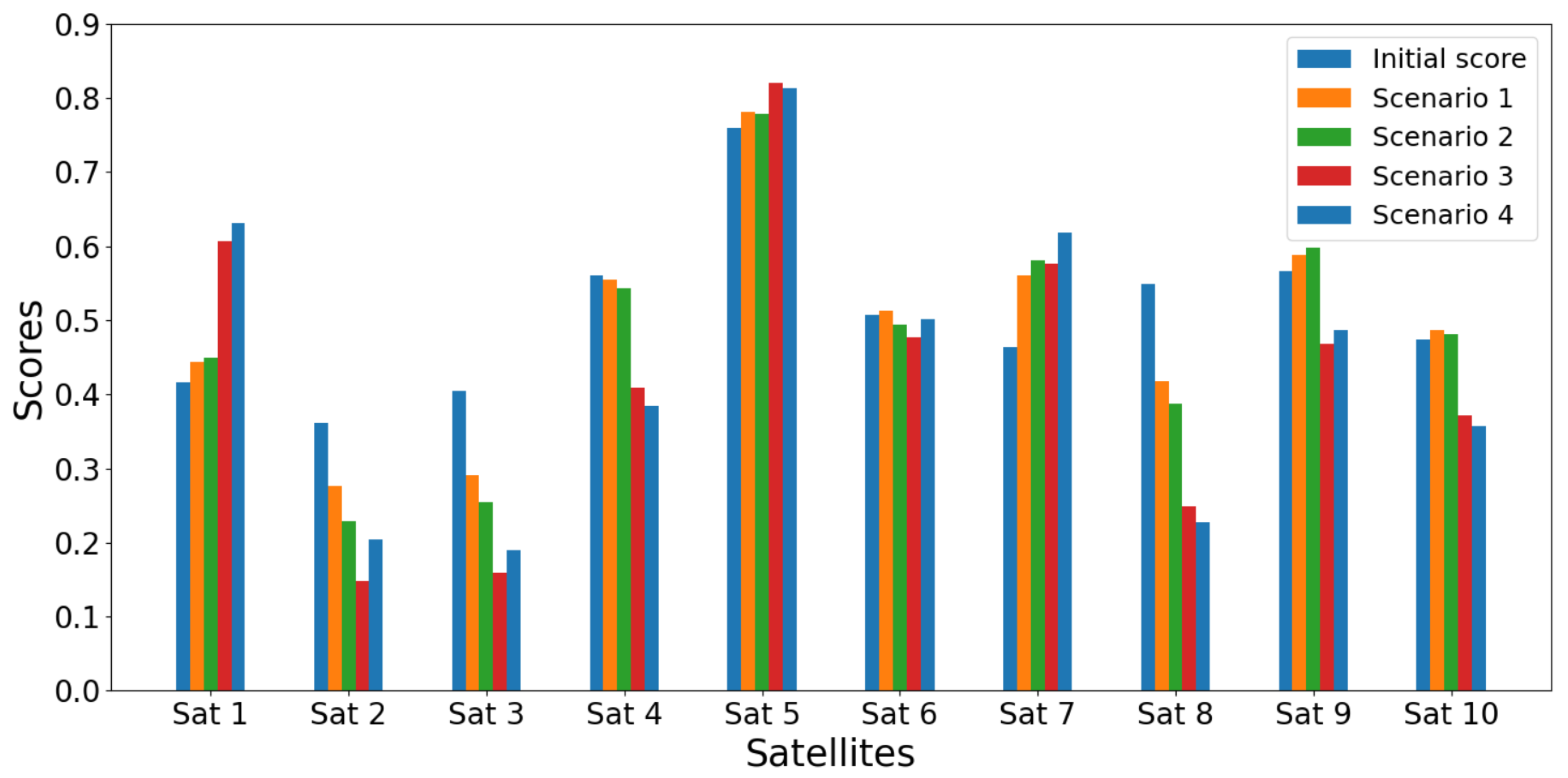
Figure 5.
Satellites scores for the initial case and the four scenarios using SD-TOPSIS, for criterion variation within .
Figure 5.
Satellites scores for the initial case and the four scenarios using SD-TOPSIS, for criterion variation within .
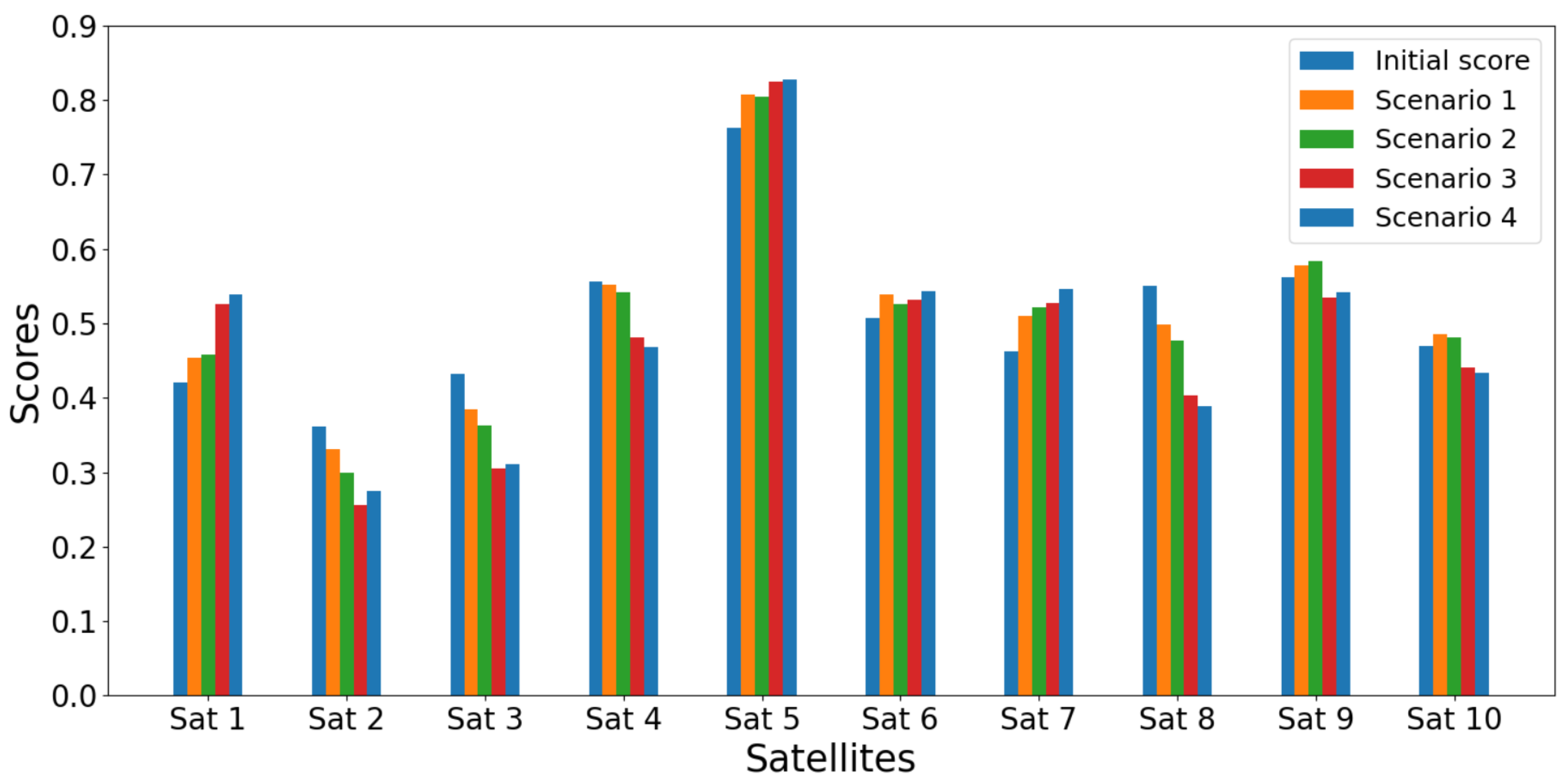
Figure 6.
Satellites scores for the initial case and the four scenarios using Entropy-TOPSIS, for criterion variation within .
Figure 6.
Satellites scores for the initial case and the four scenarios using Entropy-TOPSIS, for criterion variation within .
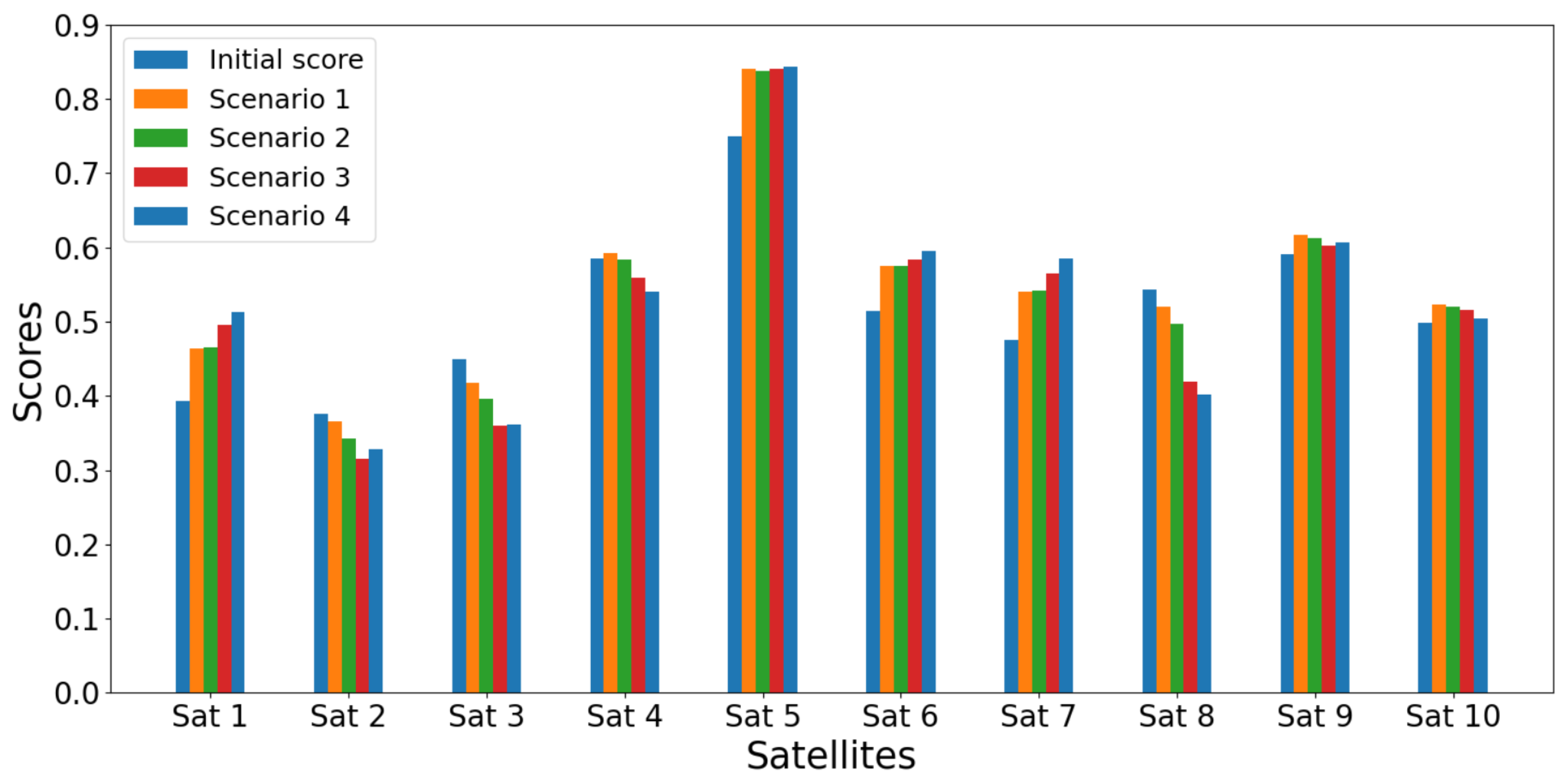
Figure 7.
Satellites scores for the initial case and the four scenarios using Importance-TOPSIS, for criterion variation within .
Figure 7.
Satellites scores for the initial case and the four scenarios using Importance-TOPSIS, for criterion variation within .
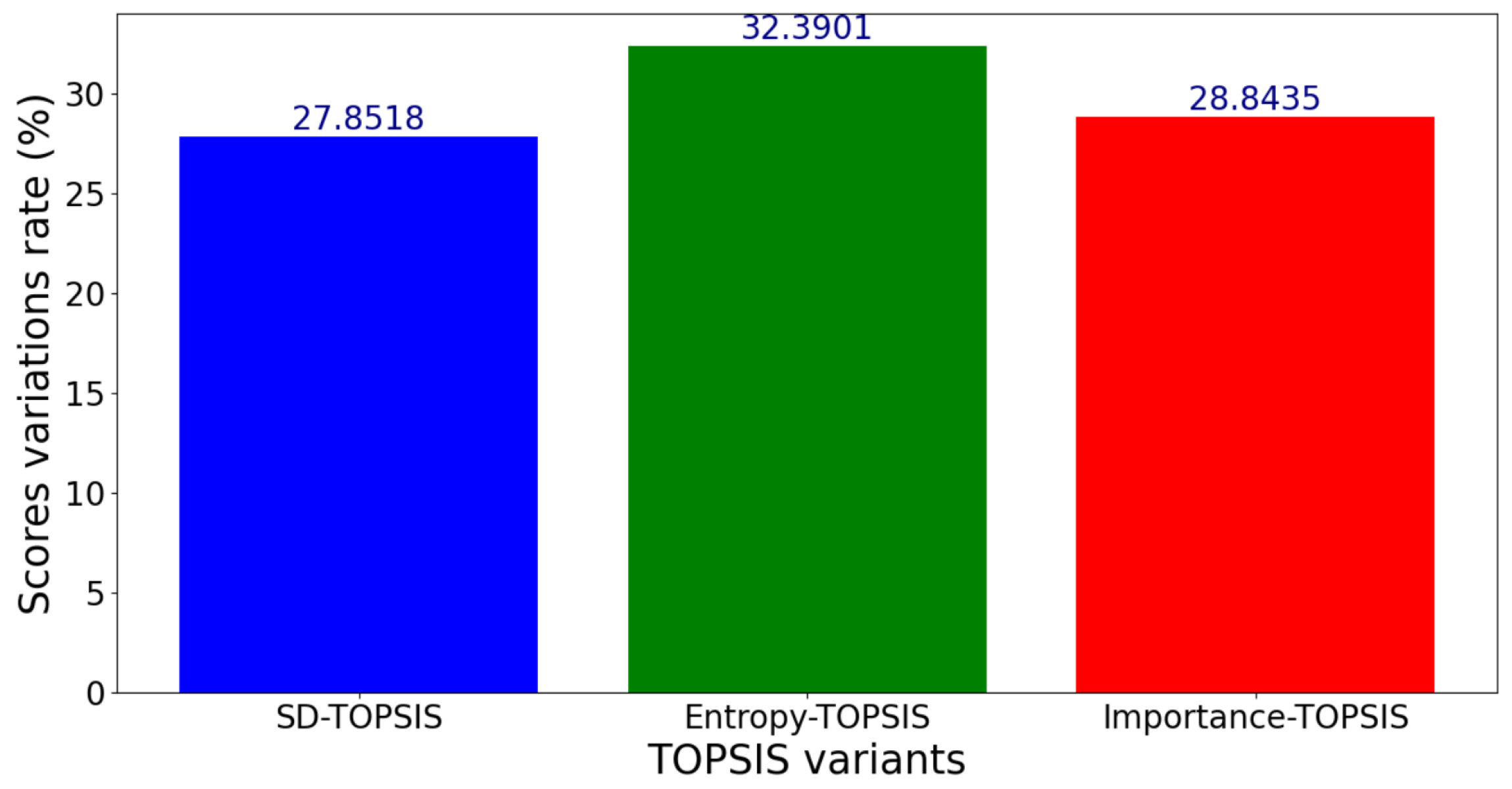
Figure 8.
Variation rates of the scores for the Scenario 1, for criterion variation within .
Figure 8.
Variation rates of the scores for the Scenario 1, for criterion variation within .
Figure 9.
Variation rates of the scores for the Scenario 2, for criterion variation within .
Figure 9.
Variation rates of the scores for the Scenario 2, for criterion variation within .
Figure 10.
Variation rates of the scores for the Scenario 3, for criterion variation within .
Figure 10.
Variation rates of the scores for the Scenario 3, for criterion variation within .
Figure 11.
Variation rates of the scores for the Scenario 4, for criterion variation within .
Figure 11.
Variation rates of the scores for the Scenario 4, for criterion variation within .
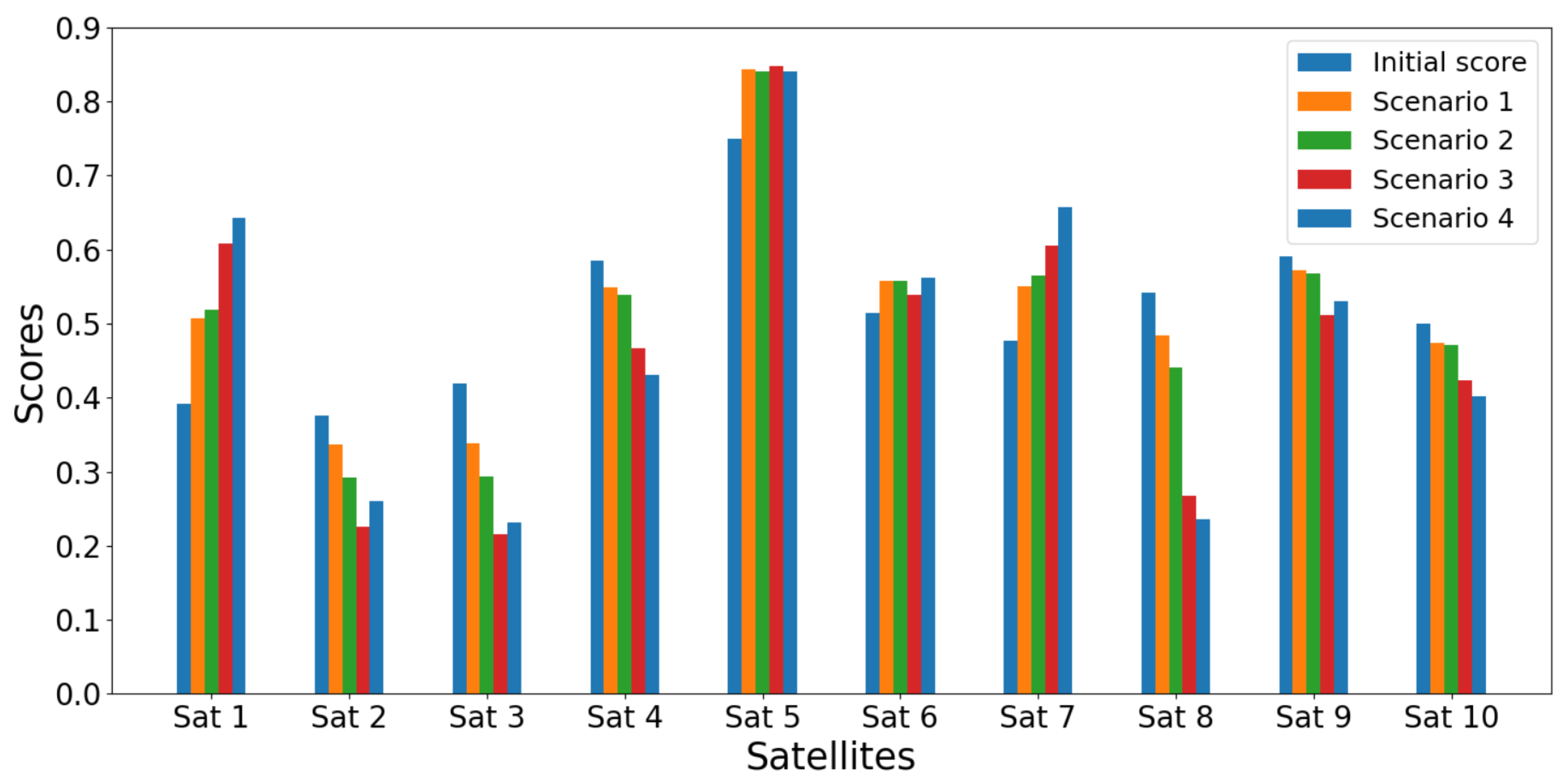
Figure 12.
Satellites scores for the initial case and the four scenarios using SD-TOPSIS, for criterion variation within .
Figure 12.
Satellites scores for the initial case and the four scenarios using SD-TOPSIS, for criterion variation within .
Figure 13.
Satellites scores for the initial case and the four scenarios using Entropy-TOPSIS, for criterion variation within .
Figure 13.
Satellites scores for the initial case and the four scenarios using Entropy-TOPSIS, for criterion variation within .
Figure 14.
Satellites scores for the initial case and the four scenarios using Importance-TOPSIS, for criterion variation within .
Figure 14.
Satellites scores for the initial case and the four scenarios using Importance-TOPSIS, for criterion variation within .
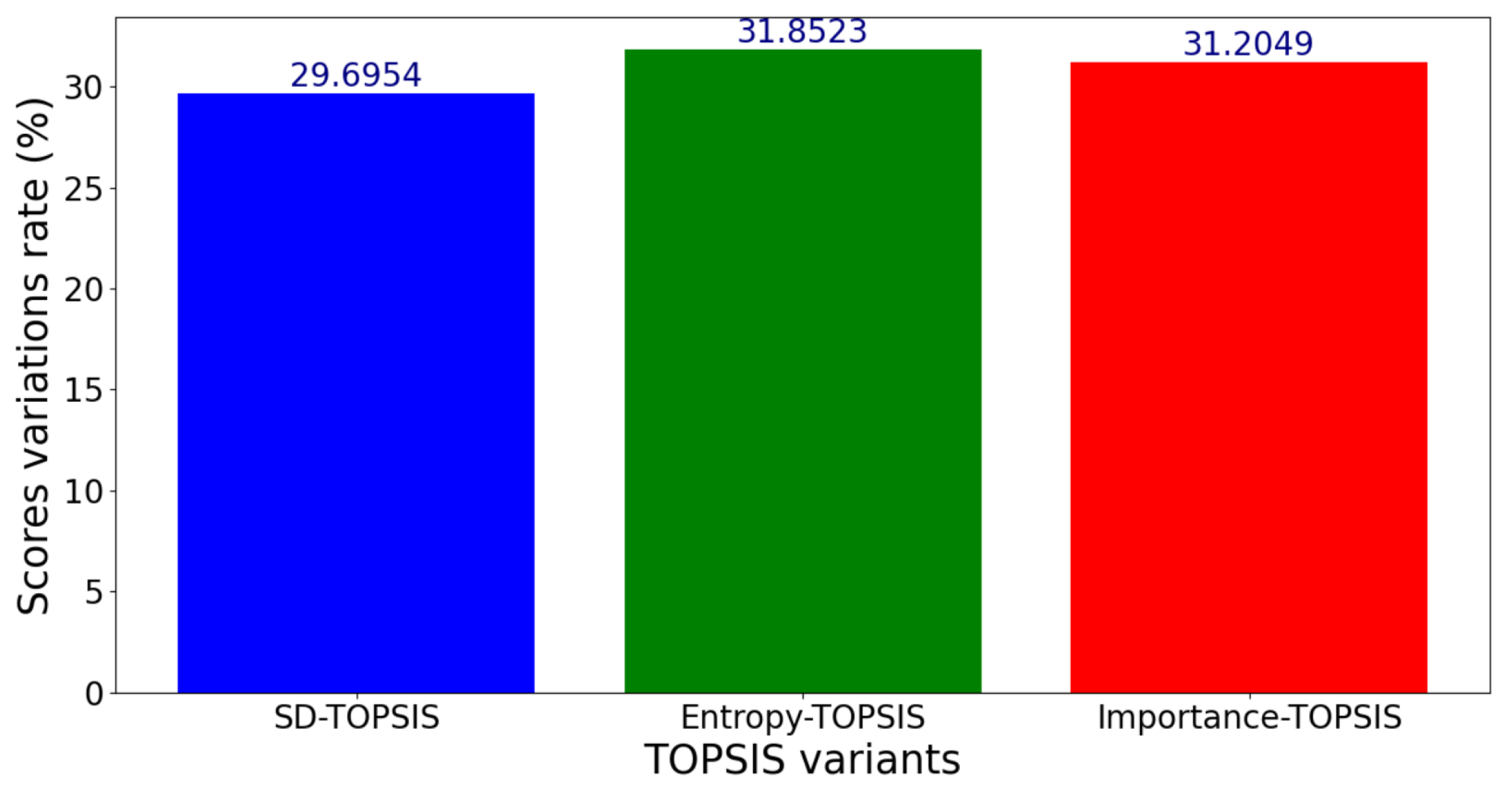
Figure 15.
Variation rates of the scores for the Scenario 1, for criterion variation within .
Figure 15.
Variation rates of the scores for the Scenario 1, for criterion variation within .
Figure 16.
Variation rates of the scores for the Scenario 2, for criterion variation within .
Figure 16.
Variation rates of the scores for the Scenario 2, for criterion variation within .
Figure 17.
Variation rates of the scores for the Scenario 3, for criterion variation within .
Figure 17.
Variation rates of the scores for the Scenario 3, for criterion variation within .
Figure 18.
Variation rates of the scores for the Scenario 4, for criterion variation within .
Figure 18.
Variation rates of the scores for the Scenario 4, for criterion variation within .
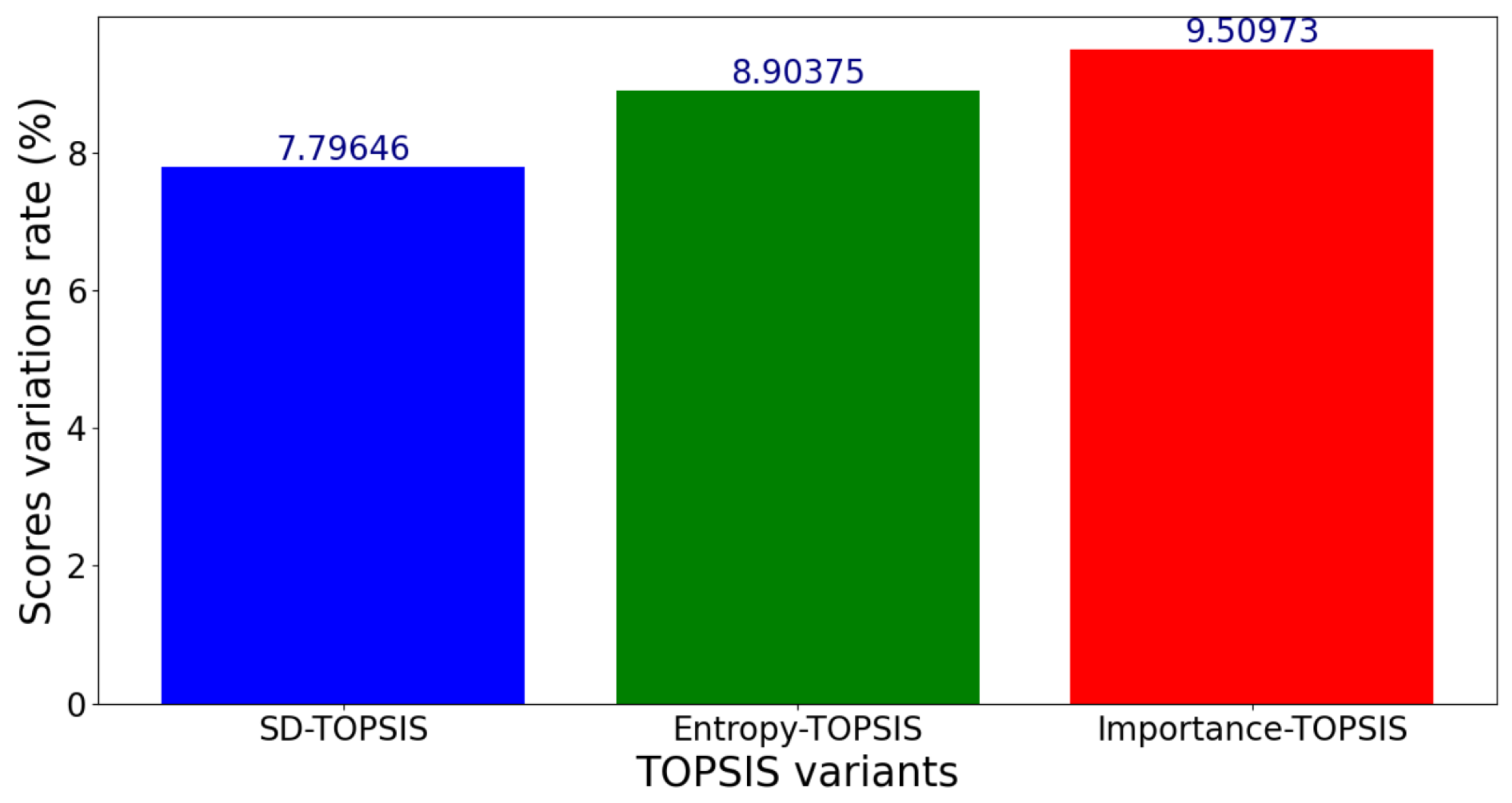
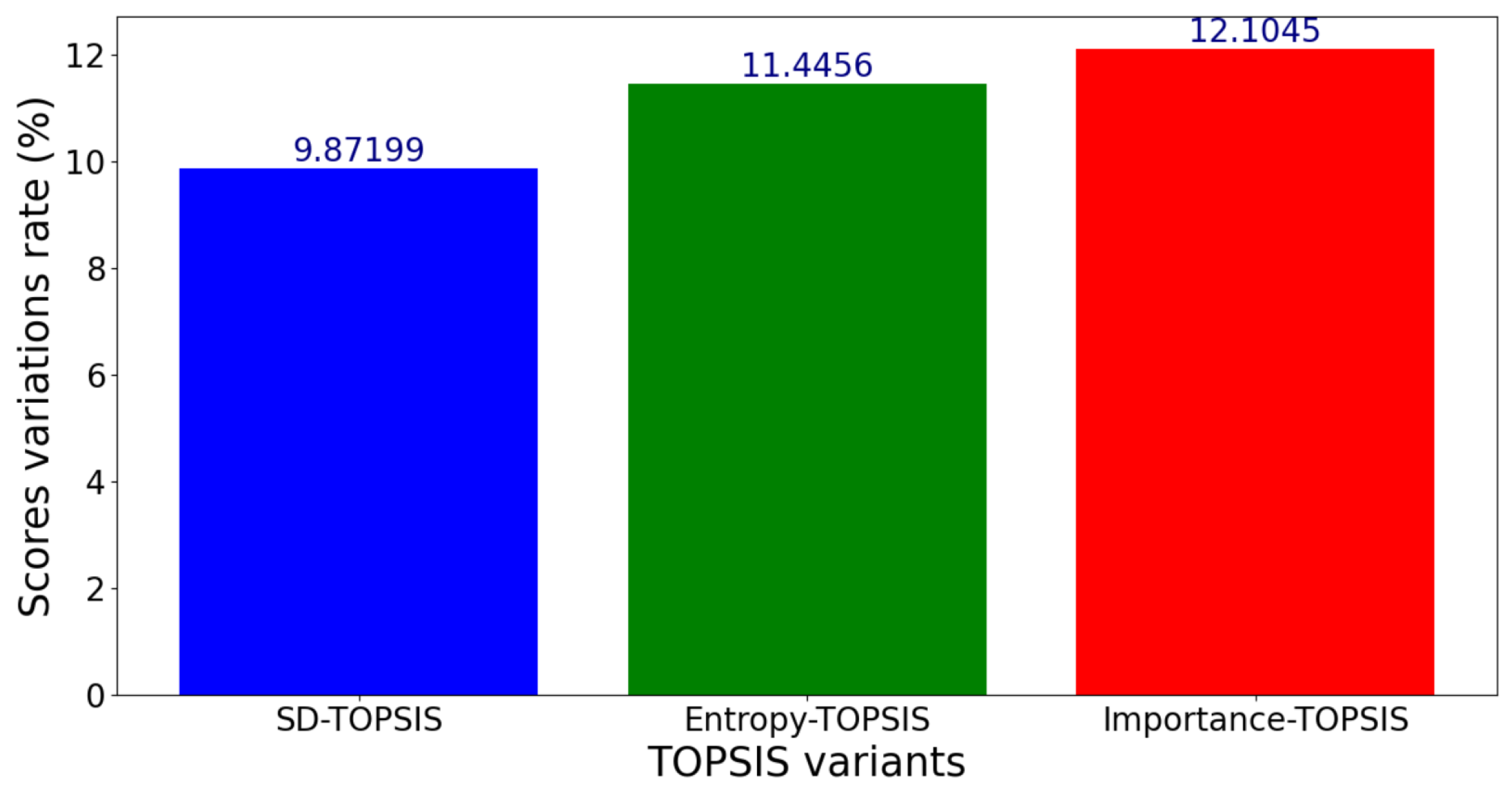
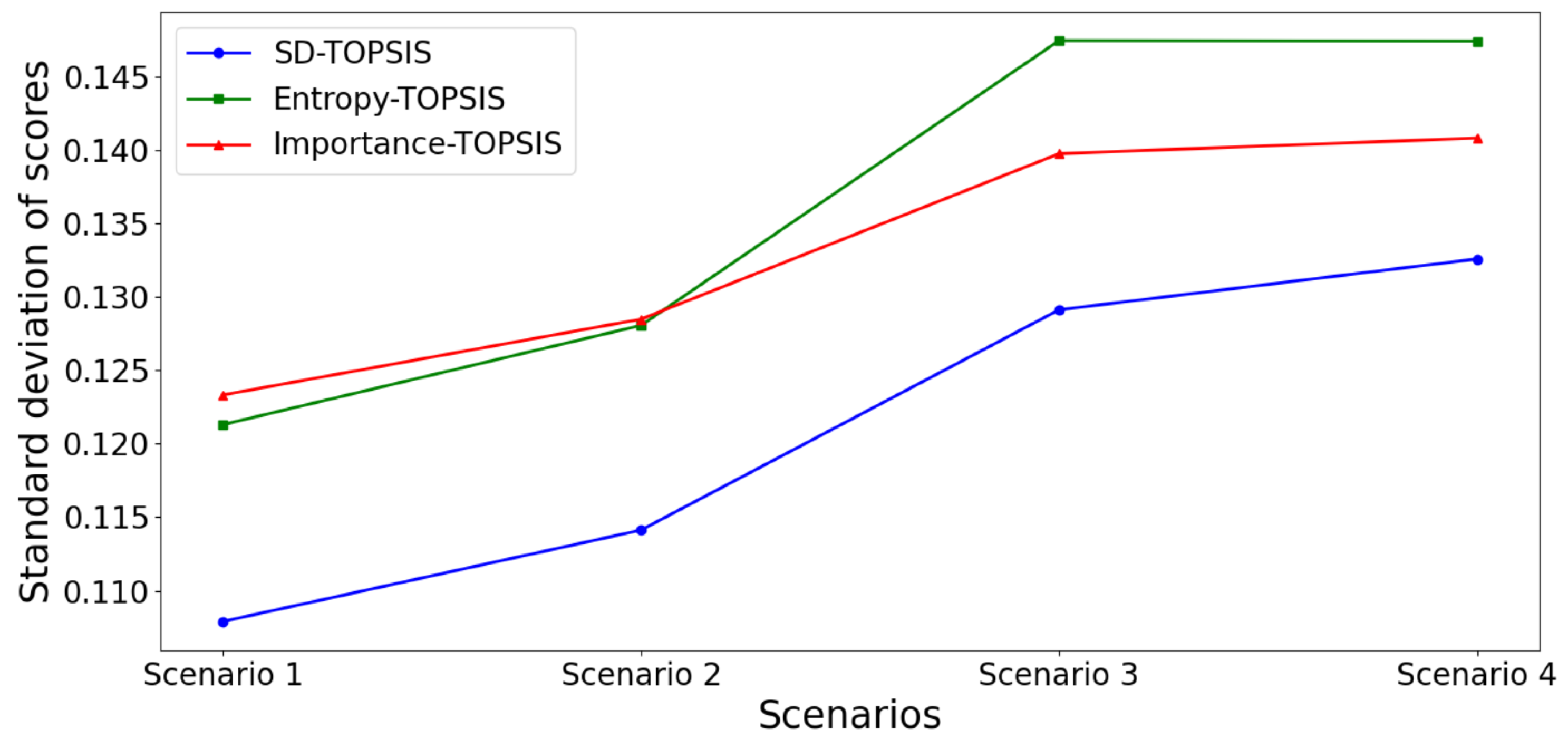
Figure 19.
Standard deviation of scores for a variation range of percent.
Figure 19.
Standard deviation of scores for a variation range of percent.
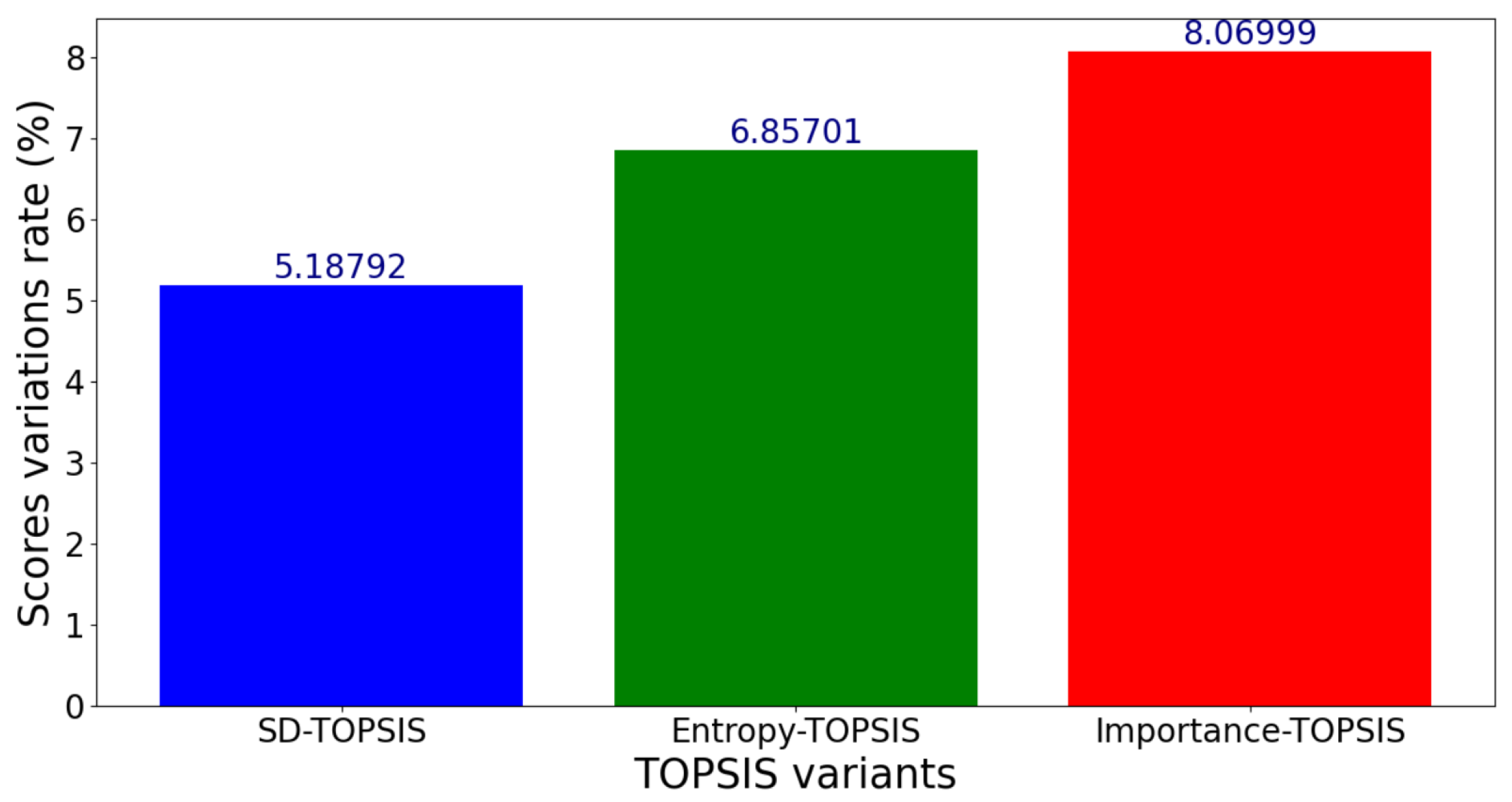
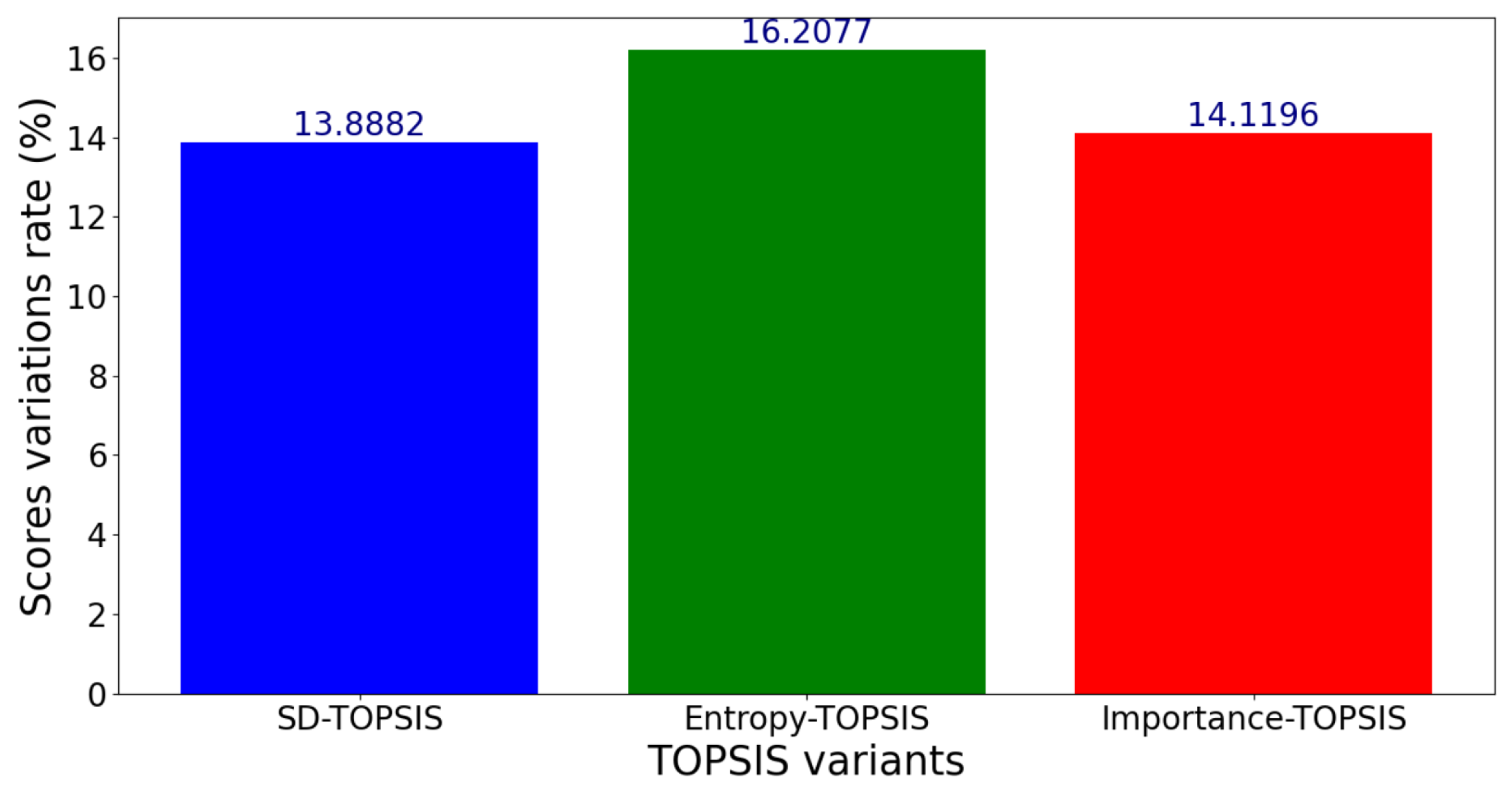
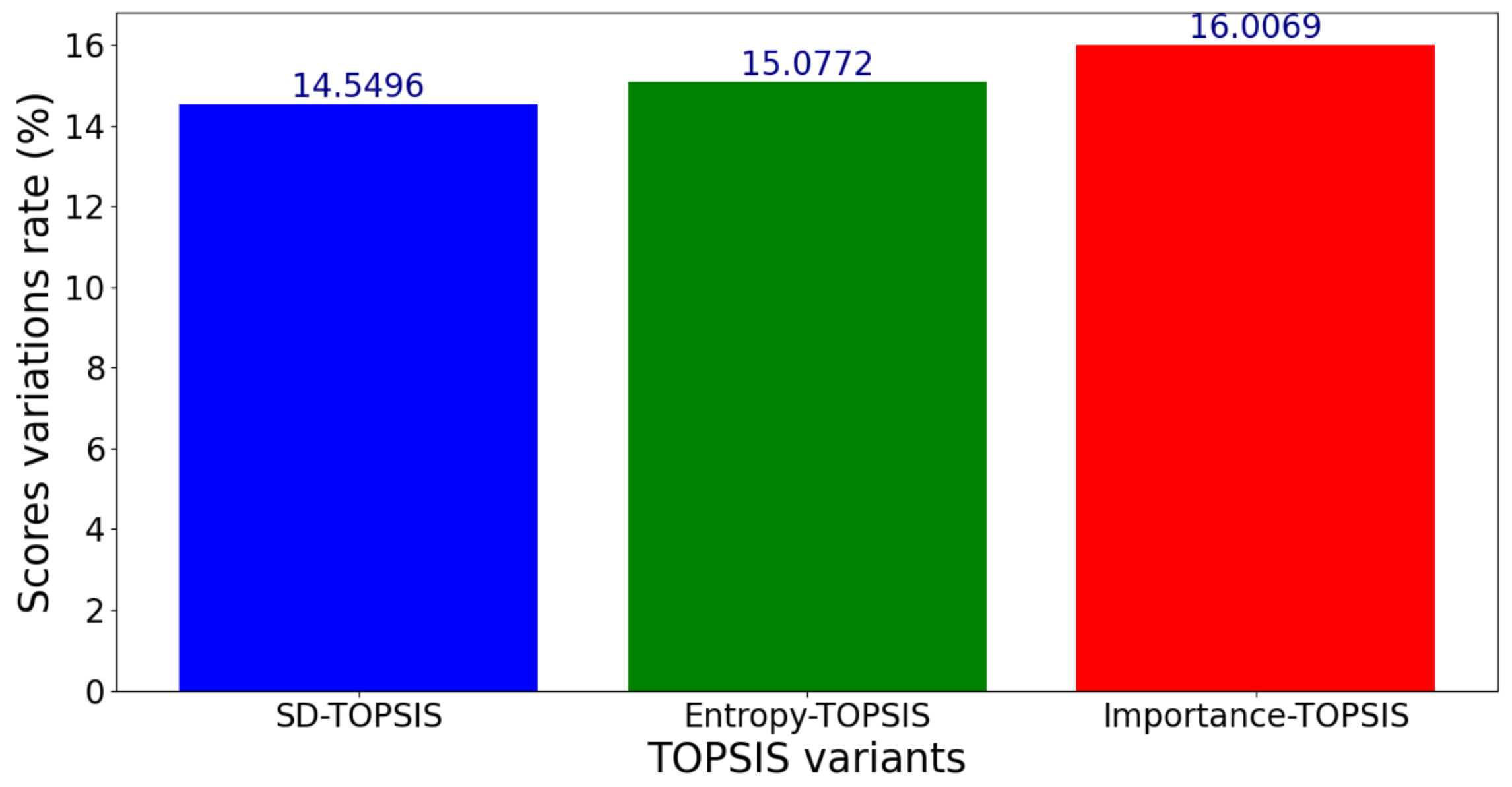
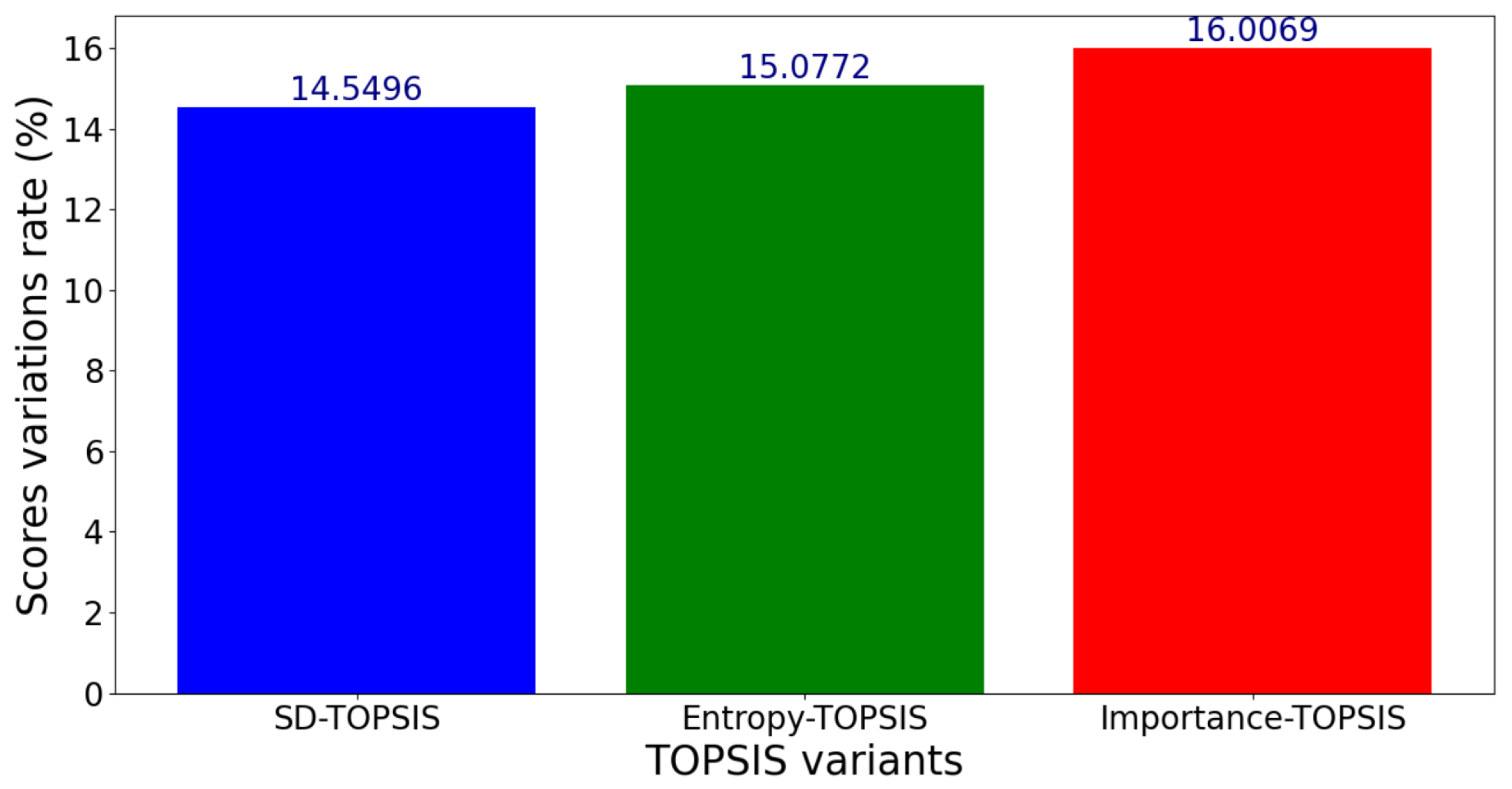
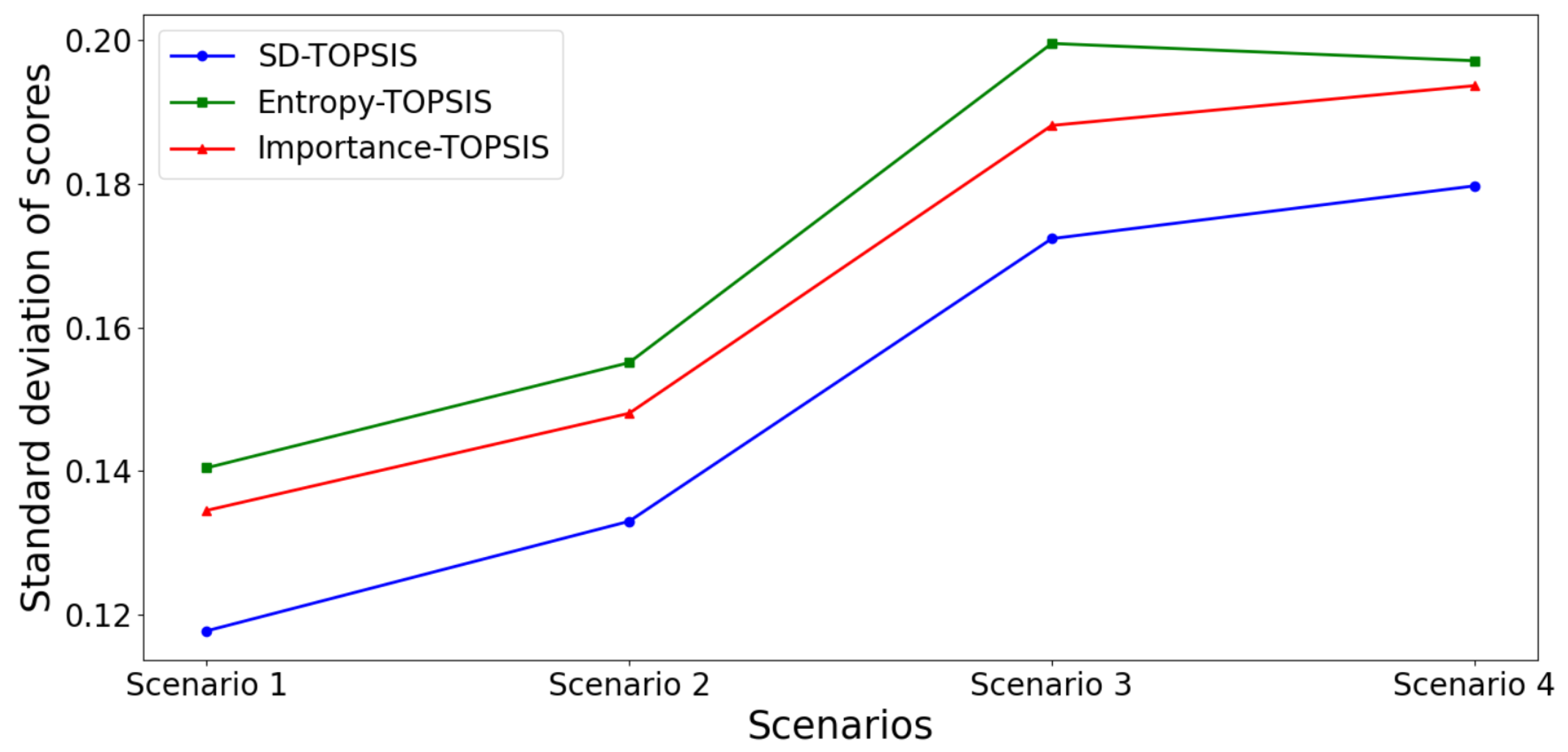
Figure 20.
Standard deviation of scores for a variation range of percent.
Figure 20.
Standard deviation of scores for a variation range of percent.
Table 1.
Summary of related work.
Table 1.
Summary of related work.
| Reference | Methodology Used | Advantages | Limitations | Application Domain |
|---|
| 10 | Entropy-TOPSIS, SD-TOPSIS | Reduces handovers, improves user throughput | Limited to stable cellular networks | Heterogeneous cellular networks |
| 6 | MADM algorithms with utility functions | Reduces ping-pong effect and handoff failures | Lacks sensitivity analysis | Heterogeneous 4G cellular networks |
| 12 | M-ANP for weighting, TOPSIS for ranking | Reduces reversal and ping-pong effects | Lacks sensitivity analysis | Heterogeneous wireless networks |
| 13 | TS-REPLICA (Entropy-TOPSIS) | Improves load balancing and system performance | Not tested in dynamic LEO environments | Distributed computing (Hadoop) |
| 7 | Importance-TOPSIS for ranking LEO Satellites | Reduces handovers, decreases forced connection terminations | Needs adaptation to dynamic satellite environments | GEO/LEO heterogeneous satellite networks |
| 14 | Multi-attribute decision handover scheme | Reduces handover frequency, improves data stream stability | Does not address rapid performance fluctuations in LEO networks | LEO mobile satellite networks |
| 4 | PASMAD (SINR-based MADM) for access/handover | Enhances QoS, balances network loads, outperforms RSS-based methods | Lacks sensitivity analysis for SINR and bandwidth fluctuations | GEO/LEO heterogeneous satellite networks |
| 5 | User-centric handover scheme with data buffering | Improves throughput, delay, and latency | Does not adress bandwidth and latency fluctuations, lacks sensitivity analysis. | Ultra-dense LEO satellite networks |
Table 2.
Initial decision matrix.
Table 2.
Initial decision matrix.
| Satellite ID | Upload Speed [Mbps] | Download Speed [Mbps] | Ping [ms] | Packet Loss [%] |
|---|
| 1 | 10.45 | 188.94 | 49.50 | 0.01 |
| 2 | 12.72 | 220.21 | 62.67 | 0.16 |
| 3 | 13.37 | 213.23 | 62.34 | 2.88 |
| 4 | 16.04 | 221.39 | 64.16 | 19.46 |
| 5 | 14.65 | 218.55 | 47.31 | 0.01 |
| 6 | 13.57 | 226.767 | 57.13 | 3.52 |
| 7 | 14.24 | 174.59 | 60.84 | 1.28 |
| 8 | 13.39 | 226.22 | 53.19 | 13.28 |
| 9 | 16.85 | 179.44 | 65.85 | 0.48 |
| 10 | 15.36 | 208.83 | 68.96 | 19.04 |
Table 3.
Criteria weights values for the initial decision matrix.
Table 3.
Criteria weights values for the initial decision matrix.
| Criteria | SD-TOPSIS | Entropy-TOPSIS | Importance-TOPSIS |
|---|
| Upload speed | 0.2943 | 0.3412 | 0.3493 |
| Download speed | 0.2151 | 0.1812 | 0.1935 |
| Ping | 0.2954 | 0.3282 | 0.2974 |
| Packet loss | 0.195 | 0.1492 | 0.1597 |
Table 4.
Satellites scores values for the initial decision matrix.
Table 4.
Satellites scores values for the initial decision matrix.
| Criteria | Sat 1 | Sat 2 | Sat 3 | Sat 4 | Sat 5 | Sat 6 | Sat 7 | Sat 8 | Sat 9 | Sat 10 |
|---|
| SD-TOPSIS | 0.43 | 0.39 | 0.42 | 0.54 | 0.77 | 0.53 | 0.45 | 0.56 | 0.55 | 0.46 |
| Entropy-TOPSIS | 0.41 | 0.36 | 0.40 | 0.56 | 0.76 | 0.50 | 0.46 | 0.54 | 0.56 | 0.47 |
| Importance-TOPSIS | 0.39 | 0.37 | 0.41 | 0.58 | 0.74 | 0.51 | 0.47 | 0.54 | 0.59 | 0.49 |
Table 5.
Random variation rates applied to upload speed, for criterion variation within .
Table 5.
Random variation rates applied to upload speed, for criterion variation within .
| Satellite ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Variation rate (%) | 5 | −2 | −3 | −1 | 2 | 3 | 5 | −5 | 1 | 2 |
Table 6.
Decision matrix of Scenario 1, for criterion variation within .
Table 6.
Decision matrix of Scenario 1, for criterion variation within .
| Satellite ID | Upload Speed [Mbps] | Download Speed [Mbps] | Ping [ms] | Packet Loss [%] |
|---|
| 1 | 10.97 | 188.94 | 49.50 | 0.01 |
| 2 | 12.46 | 220.21 | 62.67 | 0.16 |
| 3 | 13.31 | 213.23 | 62.34 | 2.88 |
| 4 | 15.88 | 221.39 | 64.16 | 19.46 |
| 5 | 14.95 | 218.55 | 47.31 | 0.01 |
| 6 | 13.98 | 226.767 | 57.13 | 3.52 |
| 7 | 14.95 | 174.59 | 60.84 | 1.28 |
| 8 | 12.72 | 226.22 | 53.19 | 13.28 |
| 9 | 17.01 | 179.44 | 65.85 | 0.48 |
| 10 | 15.67 | 208.83 | 68.96 | 19.04 |
Table 7.
Random variation rates applied to download speed, for criterion variation within .
Table 7.
Random variation rates applied to download speed, for criterion variation within .
| Satellite ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Variation rate (%) | 4 | −3 | −3 | −1 | 2 | 3 | 5 | −4 | 1 | 2 |
Table 8.
Decision matrix of Scenario 2, for criterion variation within .
Table 8.
Decision matrix of Scenario 2, for criterion variation within .
| Satellite ID | Upload Speed [Mbps] | Download Speed [Mbps] | Ping [ms] | Packet Loss [%] |
|---|
| 1 | 10.97 | 198.39 | 49.50 | 0.01 |
| 2 | 12.46 | 215.81 | 62.67 | 0.16 |
| 3 | 13.31 | 206.83 | 62.34 | 2.88 |
| 4 | 15.88 | 219.18 | 64.16 | 19.46 |
| 5 | 14.95 | 222.93 | 47.31 | 0.01 |
| 6 | 13.98 | 233.57 | 57.13 | 3.52 |
| 7 | 14.95 | 183.32 | 60.84 | 1.28 |
| 8 | 12.72 | 214.9 | 53.19 | 13.28 |
| 9 | 17.01 | 181.23 | 65.85 | 0.48 |
| 10 | 15.67 | 213.01 | 68.96 | 19.04 |
Table 9.
Random variation rates applied to ping, for criterion variation within .
Table 9.
Random variation rates applied to ping, for criterion variation within .
| Satellite ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Variation rate (%) | −4 | 2 | 3 | 1 | −2 | −3 | −5 | 4 | −1 | −2 |
Table 10.
Decision matrix of Scenario 3, for criterion variation within .
Table 10.
Decision matrix of Scenario 3, for criterion variation within .
| Satellite ID | Upload Speed [Mbps] | Download Speed [Mbps] | Ping [ms] | Packet Loss [%] |
|---|
| 1 | 10.97 | 198.39 | 47.52 | 0.01 |
| 2 | 12.46 | 215.81 | 63.92 | 0.16 |
| 3 | 13.31 | 206.83 | 64.21 | 2.88 |
| 4 | 15.88 | 219.18 | 64.80 | 19.46 |
| 5 | 14.95 | 222.93 | 46.36 | 0.01 |
| 6 | 13.98 | 233.57 | 55.41 | 3.52 |
| 7 | 14.95 | 183.32 | 57.79 | 1.28 |
| 8 | 12.72 | 214.9 | 55.31 | 13.28 |
| 9 | 17.01 | 181.23 | 65.19 | 0.48 |
| 10 | 15.67 | 213.01 | 67.58 | 19.04 |
Table 11.
Random variation rates applied to packet loss, for criterion variation within .
Table 11.
Random variation rates applied to packet loss, for criterion variation within .
| Satellite ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Variation rate (%) | −4 | 2 | 3 | 1 | −2 | −3 | −5 | 4 | −1 | −2 |
Table 12.
Decision matrix of Scenario 4, for criterion variation within .
Table 12.
Decision matrix of Scenario 4, for criterion variation within .
| Satellite ID | Upload Speed [Mbps] | Download Speed [Mbps] | Ping [ms] | Packet Loss [%] |
|---|
| 1 | 10.97 | 198.39 | 47.52 | 0.0096 |
| 2 | 12.46 | 215.81 | 63.92 | 0.1632 |
| 3 | 13.31 | 206.83 | 64.21 | 2.97 |
| 4 | 15.88 | 219.18 | 64.80 | 19.65 |
| 5 | 14.95 | 222.93 | 46.36 | 0.0098 |
| 6 | 13.98 | 233.57 | 55.41 | 3.4144 |
| 7 | 14.95 | 183.32 | 57.79 | 1.216 |
| 8 | 12.72 | 214.9 | 55.31 | 13.81 |
| 9 | 17.01 | 181.23 | 65.19 | 0.4752 |
| 10 | 15.67 | 213.01 | 67.58 | 18.66 |
Table 13.
Summary of the scores of the ten satellites in all four scenarios, for criterion variation within .
Table 13.
Summary of the scores of the ten satellites in all four scenarios, for criterion variation within .
| Scenarios | TOPSIS Variants | Satellites |
|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|
| Scenario 1 | SD-TOPSIS | 0.44 | 0.36 | 0.39 | 0.51 | 0.77 | 0.53 | 0.47 | 0.49 | 0.53 | 0.45 |
| Entropy-TOPSIS | 0.43 | 0.31 | 0.36 | 0.52 | 0.76 | 0.51 | 0.48 | 0.47 | 0.55 | 0.46 |
| Importance-TOPSIS | 0.42 | 0.33 | 0.37 | 0.53 | 0.76 | 0.52 | 0.49 | 0.47 | 0.56 | 0.47 |
| Scenario 2 | SD-TOPSIS | 0.45 | 0.32 | 0.36 | 0.50 | 0.77 | 0.52 | 0.48 | 0.46 | 0.54 | 0.44 |
| Entropy-TOPSIS | 0.43 | 0.28 | 0.34 | 0.51 | 0.76 | 0.50 | 0.49 | 0.45 | 0.55 | 0.45 |
| Importance-TOPSIS | 0.42 | 0.31 | 0.35 | 0.53 | 0.76 | 0.52 | 0.49 | 0.45 | 0.55 | 0.47 |
| Scenario 3 | SD-TOPSIS | 0.49 | 0.29 | 0.32 | 0.46 | 0.78 | 0.53 | 0.50 | 0.39 | 0.51 | 0.42 |
| Entropy-TOPSIS | 0.50 | 0.24 | 0.29 | 0.45 | 0.78 | 0.50 | 0.50 | 0.38 | 0.50 | 0.41 |
| Importance-TOPSIS | 0.42 | 0.31 | 0.35 | 0.53 | 0.76 | 0.52 | 0.49 | 0.45 | 0.55 | 0.47 |
| Scenario 4 | SD-TOPSIS | 0.51 | 0.30 | 0.31 | 0.45 | 0.78 | 0.54 | 0.52 | 0.36 | 0.52 | 0.42 |
| Entropy-TOPSIS | 0.51 | 0.26 | 0.29 | 0.44 | 0.78 | 0.52 | 0.52 | 0.37 | 0.51 | 0.41 |
| Importance-TOPSIS | 0.46 | 0.29 | 0.32 | 0.49 | 0.76 | 0.54 | 0.53 | 0.36 | 0.55 | 0.45 |
Table 14.
Random variation rates applied to upload speed, for criterion variation within .
Table 14.
Random variation rates applied to upload speed, for criterion variation within .
| Satellite ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Variation rate (%) | 10 | −5 | −6 | −1 | 2 | 3 | 10 | −10 | 1 | 2 |
Table 15.
Decision matrix of Scenario 1, for criterion variation within .
Table 15.
Decision matrix of Scenario 1, for criterion variation within .
| Satellite ID | Upload Speed [Mbps] | Download Speed [Mbps] | Ping [ms] | Packet Loss [%] |
|---|
| 1 | 11.49 | 188.94 | 49.50 | 0.01 |
| 2 | 12.08 | 220.21 | 62.67 | 0.16 |
| 3 | 12.56 | 213.23 | 62.34 | 2.88 |
| 4 | 15.88 | 221.39 | 64.16 | 19.46 |
| 5 | 14.94 | 218.55 | 47.31 | 0.01 |
| 6 | 13.97 | 226.767 | 57.13 | 3.52 |
| 7 | 15.66 | 174.59 | 60.84 | 1.28 |
| 8 | 12.05 | 226.22 | 53.19 | 13.28 |
| 9 | 17.02 | 179.44 | 65.85 | 0.48 |
| 10 | 15.66 | 208.83 | 68.96 | 19.04 |
Table 16.
Random variation rates applied to download speed, for criterion variation within .
Table 16.
Random variation rates applied to download speed, for criterion variation within .
| Satellite ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Variation rate (%) | 10 | | −6 | −1 | 2 | 3 | 10 | −10 | 1 | 2 |
Table 17.
Decision matrix of Scenario 2, for criterion variation within .
Table 17.
Decision matrix of Scenario 2, for criterion variation within .
| Satellite ID | Upload Speed [Mbps] | Download Speed [Mbps] | Ping [ms] | Packet Loss [%] |
|---|
| 1 | 11.49 | 207.84 | 49.50 | 0.01 |
| 2 | 12.08 | 209.2 | 62.67 | 0.16 |
| 3 | 12.56 | 200.44 | 62.34 | 2.88 |
| 4 | 15.88 | 219.18 | 64.16 | 19.46 |
| 5 | 14.94 | 222.93 | 47.31 | 0.01 |
| 6 | 13.97 | 233.57 | 57.13 | 3.52 |
| 7 | 15.66 | 192.05 | 60.84 | 1.28 |
| 8 | 12.05 | 203.59 | 53.19 | 13.28 |
| 9 | 17.02 | 181.23 | 65.85 | 0.48 |
| 10 | 15.66 | 213.01 | 68.96 | 19.04 |
Table 18.
Random variation rates applied to ping, for criterion variation within .
Table 18.
Random variation rates applied to ping, for criterion variation within .
| Satellite ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Variation rate (%) | −10 | 5 | 6 | 1 | −2 | −3 | −10 | 10 | −1 | −2 |
Table 19.
Decision matrix of Scenario 3, for criterion variation within .
Table 19.
Decision matrix of Scenario 3, for criterion variation within .
| Satellite ID | Upload Speed [Mbps] | Download Speed [Mbps] | Ping [ms] | Packet Loss [%] |
|---|
| 1 | 11.49 | 207.84 | 44.55 | 0.01 |
| 2 | 12.08 | 209.2 | 65.80 | 0.16 |
| 3 | 12.56 | 200.44 | 66.08 | 2.88 |
| 4 | 15.88 | 219.18 | 64.80 | 19.46 |
| 5 | 14.94 | 222.93 | 46.36 | 0.01 |
| 6 | 13.97 | 233.57 | 55.41 | 3.52 |
| 7 | 15.66 | 192.05 | 54.75 | 1.28 |
| 8 | 12.05 | 203.59 | 58.51 | 13.28 |
| 9 | 17.02 | 181.23 | 65.19 | 0.48 |
| 10 | 15.66 | 213.01 | 67.58 | 19.04 |
Table 20.
Random variation rates applied to packet loss, for criterion variation within .
Table 20.
Random variation rates applied to packet loss, for criterion variation within .
| Satellite ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Variation rate (%) | −10 | 5 | 6 | 1 | −2 | −3 | −10 | 10 | −1 | −2 |
Table 21.
Decision matrix of Scenario 4, for criterion variation within .
Table 21.
Decision matrix of Scenario 4, for criterion variation within .
| Satellite ID | Upload Speed [Mbps] | Download Speed [Mbps] | Ping [ms] | Packet Loss [%] |
|---|
| 1 | 11.49 | 207.84 | 44.55 | 0.009 |
| 2 | 12.08 | 209.2 | 65.80 | 0.168 |
| 3 | 12.56 | 200.44 | 66.08 | 3.0528 |
| 4 | 15.88 | 219.18 | 64.80 | 19.65 |
| 5 | 14.94 | 222.93 | 46.36 | 0.0098 |
| 6 | 13.97 | 233.57 | 55.41 | 3.4744 |
| 7 | 15.66 | 192.05 | 54.75 | 1.152 |
| 8 | 12.05 | 203.59 | 58.51 | 14.61 |
| 9 | 17.02 | 181.23 | 65.19 | 0.4752 |
| 10 | 15.66 | 213.01 | 67.58 | 18.66 |
Table 22.
Summary of the scores of the ten satellites in all four scenarios, for criterion variation within .
Table 22.
Summary of the scores of the ten satellites in all four scenarios, for criterion variation within .
| Scenarios | TOPSIS Variants | Satellites |
|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|
| Scenario 1 | SD-TOPSIS | 0.45 | 0.32 | 0.32 | 0.50 | 0.76 | 0.51 | 0.51 | 0.43 | 0.53 | 0.44 |
| Entropy-TOPSIS | 0.42 | 0.26 | 0.27 | 0.52 | 0.74 | 0.48 | 0.53 | 0.39 | 0.56 | 0.46 |
| Importance-TOPSIS | 0.46 | 0.30 | 0.30 | 0.49 | 0.76 | 0.50 | 0.50 | 0.44 | 0.52 | 0.43 |
| Scenario 2 | SD-TOPSIS | 0.46 | 0.27 | 0.28 | 0.49 | 0.75 | 0.50 | 0.53 | 0.38 | 0.53 | 0.43 |
| Entropy-TOPSIS | 0.42 | 0.21 | 0.24 | 0.51 | 0.74 | 0.47 | 0.55 | 0.36 | 0.56 | 0.46 |
| Importance-TOPSIS | 0.47 | 0.26 | 0.26 | 0.48 | 0.76 | 0.50 | 0.51 | 0.40 | 0.51 | 0.42 |
| Scenario 3 | SD-TOPSIS | 0.56 | 0.20 | 0.20 | 0.41 | 0.77 | 0.48 | 0.55 | 0.24 | 0.46 | 0.37 |
| Entropy-TOPSIS | 0.57 | 0.14 | 0.15 | 0.38 | 0.78 | 0.45 | 0.54 | 0.23 | 0.44 | 0.35 |
| Importance-TOPSIS | 0.55 | 0.20 | 0.19 | 0.42 | 0.77 | 0.49 | 0.55 | 0.24 | 0.46 | 0.38 |
| Scenario 4 | SD-TOPSIS | 0.59 | 0.22 | 0.20 | 0.38 | 0.76 | 0.50 | 0.60 | 0.21 | 0.48 | 0.35 |
| Entropy-TOPSIS | 0.60 | 0.19 | 0.18 | 0.36 | 0.77 | 0.47 | 0.58 | 0.21 | 0.46 | 0.33 |
| Importance-TOPSIS | 0.58 | 0.23 | 0.21 | 0.39 | 0.76 | 0.51 | 0.59 | 0.21 | 0.48 | 0.36 |