1. Introduction
In wireless communications, relaying expands communication coverage and offers spatial and temporal diversity to mitigate the effects of fading [
1,
2]. This capability makes relaying critical in enhancing signal reliability, particularly in challenging environments with obstructed direct paths between transmitters and receivers. As networks evolve towards 5G and beyond, the role of relays is becoming increasingly significant, not only for improving coverage but also for supporting the high data rates and low latency required by advanced applications such as the internet of things (IoT) and autonomous systems. Recent studies highlight the growing importance of relaying in heterogeneous networks, where devices with varying capabilities and security levels must interact seamlessly [
3].
Traditionally, network security has been addressed at higher layers using cryptographic techniques. However, these methods often fall short of fully addressing the security demands of emerging applications like smart transportation, the Vehicle to X, and industrial automation networks [
4] due to challenges such as reliance on infrastructure, inefficient spectrum usage, significant resource demands, and the complexity of signal processing. In contrast, physical layer security (PLS), grounded in information theory, leverages the inherent physical characteristics of the communication medium, including shadowing, fading, and interference [
5]. This approach offers a low-complexity security solution that remains effective regardless of the computational power of the devices involved. The critical advantage of PLS is that its security remains unaffected by the computational capabilities of eavesdroppers. Furthermore, PLS provides greater flexibility in deployment compared to bit-level cryptographic methods [
6], making it a promising alternative for securing these advanced applications. Interest in physical layer security for untrusted relay mechanisms has been increasing. While many studies have focused on protocols like amplify-and-forward and compress-and-forward, the decode-and-forward (DF) protocol presents unique challenges for untrusted relaying due to the conflicting needs for reliability and security [
7].
In next-generation networks, 5G and beyond 5G and future mobile IoT networks with densely distributed mobile nodes, including sensor networks for traffic data collection and smart drone systems, will face heightened security concerns. This is particularly true in heterogeneous networks where nodes possess varying levels of security clearance. In such environments, a node that behaves unexpectedly could act as a potential eavesdropper and might pose significant security risks, rendering the relay untrusted [
8]. Specifically, relays with lower trust levels or insufficient security clearance could act as potential unauthorized eavesdroppers [
9]. These untrusted relays are not inherently malicious; rather, their lack of trust or inadequate security clearance makes them less reliable [
9]. A non-zero achievable secrecy rate was indicated in [
10] in a two-way untrusted relay system where the two sources only communicated through an untrusted intermediate relay. The ergodic secrecy capacity in an untrusted relay two-hop network was analyzed, and the compact expressions for the ergodic secrecy capacity were present in [
11] under the assumption that a direct connection between the source and destination is absent.
In the foundational work on untrusted relay networks, [
12] established conditions to achieve a positive secrecy capacity, where the information is securely sent such that the confidentiality of the information surpasses a certain threshold. The security of this confidential information was measured through conditional entropy, focusing on coding/decoding challenges within relay channels. Subsequently, in a different study [
13], Oohama assessed the secrecy-keeping level for confidential information from the relay by analyzing the private information’s entropy rate, given by the relay’s channel outputs.
Later research [
14,
15] demonstrated that bringing in cooperative jamming achieves a positive secrecy rate in scenarios involving single untrusted relaying in the absence of a direct connection between the source and destination. Another study [
16] showed that increasing the number of relays in a bidirectional untrusted relay system could enhance the ergodic secrecy sum rate, even without the aid of jamming signals. Additionally, this study proposed a relay selection method to optimize the instantaneous total secrecy rate with multiple bidirectional untrusted relaying. However, the method focused on selecting the relay with the highest gain from channels to the destination, disregarding the security levels of untrusted relaying.
A recent advancement introduces a cooperative communication strategy based on the traditional DF protocol that accommodates intra-link errors, termed lossy-forward (LF) relaying [
17]. LF relaying ensures the relay forwards decoded information to the destination despite decoding errors during the RF transmission stage. This study presents an LF relaying approach for an air-to-ground network with two untrusted relays, considering factors like atmospheric absorption, scattering, and other terrestrial propagation challenges. By allowing for errors, LF relaying reduces the risk of unauthorized access to confidential data, making it a promising candidate for enhancing PLS in air-to-ground communications. The relay nodes, essential for the relay process, are also potential security threats. LF relaying is utilized to maintain data transmission integrity and confidentiality against these untrusted nodes.
In this context, we propose incorporating cooperative jamming [
18] in a diamond-shaped network featuring two untrusted relays. The jamming signals are deliberately sent from the mobile terminal to safeguard confidential information from being compromised by untrusted relays. To evaluate the effectiveness of our approach, we introduce the reliable and secure probability, which is referred to as RSP in this work, which measures the likelihood that the mobile terminal can correctly retrieve the original information while keeping it confidential from the untrusted relays. Analytical results indicate that optimal outcomes are achieved with balanced power distribution between the source and untrusted relays. This paper focuses on the optimal power allocation problem to maximize the RSP. Given a fixed transmission power, we investigate how to distribute power among the source, untrusted relays, and destination (which sends jamming signals) to achieve the highest RSP. Our findings reveal strategies for optimal power distribution that maximize the RSP, providing a theoretical foundation for enhancing network reliability and security. This optimization framework contributes significantly to understanding secure and reliable communication in networks involving untrusted relays.
The rest of this article is organized as follows:
Section 2 describes a number of related studies and the discussed outcomes. An overview of the system model for analyzing the PLS in an air-to-ground diamond network is presented in
Section 3.
Section 4 introduces the definition of the acceptable rate region and derivation of reliable and secure probability with a formulation of the CEO (chief executive officer) problem for transmissions from untrusted relays to the destination. An optimal power allocation solution in terms of the RSP of diamond untrusted relay networks is presented in
Section 5.
Section 6 concludes this article with some recommendations.
2. Related Works
In recent years, the focus on PLS has intensified, particularly concerning untrusted relay networks. Traditional approaches have primarily employed higher-layer encryption techniques to secure communications, but these methods are increasingly being complemented or replaced by PLS strategies. PLS leverages the inherent properties of wireless channels, such as noise and fading, to ensure that data remains secure irrespective of an eavesdropper’s computational power. This section reviews recent advancements in related areas, highlighting key contributions and identifying gaps our study aims to address.
2.1. Physical Layer Security
Recent studies have explored various PLS techniques to secure data transmissions in wireless networks. Shen et al. developed a hierarchical theoretical framework for energy and secure-efficient design for precoding in a two-way MIMO system with an untrusted relay, demonstrating significant improvements in secrecy energy efficiency through extensive numerical results [
19]. Zhang et al. introduced a novel layered physical layer security model with hierarchical information security and proposed optimal and robust beam-forming schemes to minimize transmitted power while meeting secrecy rate requirements, demonstrating effectiveness through simulations [
20]. Si et al. proposed a zero-forcing beam-forming scheme to optimize the secrecy rate in the presence of both active and passive eavesdroppers, considering perfect and imperfect channel state information, and highlighted that imperfect CSI between the jammer and the legitimate receiver significantly impacts the achievable secrecy rate [
21]. Xu et al. introduced a game-theoretic power allocation strategy for a friendly interferer to enhance wireless network secrecy against strategic eavesdroppers, demonstrating that this approach outperforms conservative power allocation strategies [
22]. A novel physical-layer secure transmission scheme, decomposed and distributed modulation, was introduced that leverages decomposed and distributed modulation to prevent eavesdropping using two cooperative transmitters, effectively enhancing data transmission security through theoretical analysis and simulation [
23].
2.2. Cooperative Jamming for Enhanced Security
Cooperative jamming is another critical strategy to bolster PLS. Tang et al. formulated a social tie-based cooperative jamming game among multiple jammers for physical layer security, proving the existence of a pure Nash equilibrium, developing an algorithm to achieve the minimum secrecy outage probability, and validating the theoretical findings with numerical results [
24]. Hui et al. proposed a secure downlink transmission scheme for IoT networks using cooperative jamming and artificial noise-aided secrecy beam-forming to minimize secrecy outage probability and enhance both security and power efficiency against multiple passive eavesdroppers [
18]. Atapattu et al. addressed secure wireless communications over an untrusted full-duplex relay, deriving optimal power allocation between confidential and jamming signals to maximize the secrecy rate and providing a detailed analysis of secrecy outage probability and average secrecy rate, highlighting the negative impact of transmit-power-dependent self-interference on secrecy performance [
25]. Sadming et al. introduced a joint security approach combining physical layer security and noisy ciphertext, demonstrating that this method can achieve secrecy rates beyond the traditional PhySec capacity and providing optimal power allocation solutions for relay networks with cooperative jamming [
26]. Gui et al. proposed a cooperative jamming-aided secure communication scheme for wireless-powered sensor networks that addressed issues of disguised eavesdroppers, imperfect channel estimation, and distance-related power limitations, significantly improving secrecy rates through a two-level optimization algorithm [
27].
2.3. Optimal Power Allocation
Power allocation plays a crucial role in enhancing both the reliability and security of communications in relay networks. Jia et al. proposed and analyzed two power allocation schemes, optimal adaptive power allocation (OAPA) and suboptimal fixed power allocation (SFPA), to enhance physical layer security in MISO systems with unknown eavesdroppers, demonstrating that SFPA achieves comparable secrecy outage performance to OAPA with lower complexity [
28]. Li et al. proposed a secure communication model for satellite communications using interference relay collaboration at the physical layer, deriving theoretical relay selection standards and optimizing power allocation to minimize secrecy outage probability and presenting performance analyses for various relay selection criteria and power allocation schemes [
29]. In [
30], a joint power allocation and aerial jamming scheme for a UAV-enabled NOMA system were proposed for enhancing reliability and security against eavesdropping, and analytical expressions and numerical results were derived to demonstrate the scheme’s superiority and identify the optimal UAV height for maximizing effective secrecy throughput. Ref. [
31] proposed a joint power and sub-channel allocation algorithm to maximize secrecy capacity in non-orthogonal multiple access (NOMA)-based uplink massive machine type communication (mMTC) networks, demonstrating its superiority over other algorithms and orthogonal multiple access schemes in enhancing secrecy capacity.
This paper builds upon these foundational studies by integrating LF relaying and cooperative jamming in a diamond network with untrusted relays. Our contribution lies in optimizing power allocation to maximize the RSP, thus ensuring both secure and reliable communications. By comparing our results with existing methods, we highlight the novelty and effectiveness of our proposed scheme in enhancing physical layer security.
We need to highlight that this work stands out from prior research in the following ways:
This work addresses the optimization of security and reliability in a diamond network configuration involving two untrusted relays, specifically focusing on the physical layer. The study introduces a cooperative jamming technique to enhance the secure transmission of data while ensuring that the source message remains confidential from untrusted relays. The integration of lossy DF relaying at the untrusted relays helps maintain data confidentiality by allowing for controlled decoding errors, thus minimizing the risk of eavesdropping by the relays.
A novel analytical framework is proposed that explores the optimal power allocation between the source, the relays, and the destination to maximize the RSP. This framework incorporates the impact of cooperative jamming on the overall network performance and provides a comprehensive analysis of the power distribution needed to achieve the highest possible RSP, ensuring both reliability and security in the communication system.
The paper also introduces an RSP metric to evaluate the performance of the proposed system. This metric quantifies the likelihood that the destination successfully decodes the original information while the untrusted relays fail to do so. Numerical results demonstrate that optimizing the power allocation between the source and the relays is critical for achieving the best possible balance between reliability and security in the network.
In modern communication systems, secure and reliable data transmission is critical, particularly in scenarios where sensitive information is transmitted over potentially compromised channels. One specific application scenario for the proposed framework is in military and government communication networks, where the confidentiality and integrity of data are paramount. These networks often operate in environments with a high risk of eavesdropping or unauthorized access, making robust physical layer security essential. Another practical application is in critical infrastructure systems, such as smart grids and industrial control systems, where secure communication is necessary to prevent disruptions or malicious attacks. Wireless sensor networks, commonly used in environmental monitoring and healthcare, also benefit from enhanced security and reliability, particularly in scenarios involving untrusted relays or nodes with varying security clearances.
Existing wireless communication standards and security protocols can be adapted to implement the proposed framework in real-world systems. For example, integrating lossy DF relaying and cooperative jamming techniques into current 5G or next-generation wireless networks could significantly improve their resilience against security threats. Software-defined radio (SDR) platforms provide a practical means to prototype and test the proposed methods, allowing for fine-tuning and optimization before deployment in live environments.
3. System Model
3.1. Diamond Transmission via Untrusted Relays
Consider an air-to-ground transmission system, as illustrated in
Figure 1. An airborne source, labeled S, intends to communicate with a ground destination, D. Due to geographical and environmental challenges, there is no direct link between S and D. The binary sequences from S, which follow a Bernoulli(
) distribution, are first encoded, modulated, and transmitted via RF to two intermediate nodes (untrusted relays),
and
. These relays decode the received message and re-encode it for transmission to D. In air-to-ground communications, the limited availability of relay nodes means that
and
may be considered untrusted, potentially acting as covert eavesdroppers.
Despite imperfections in decoding due to signal degradation, the untrusted relays using LF relaying will always forward the decoded sequences to D. The purpose of utilizing lossy relaying at the untrusted relays is to enhance transmission dependability while ensuring the confidentiality of the message. The sequences received by
and
may include errors due to inaccuracies in decoding, which are influenced by the received SNR. Despite these decoding errors,
and
proceed to interleave, re-encode, and forward the received information sequences to D as part of the lossy DF relaying process. Upon receiving signals from
and
, D performs joint decoding to reconstruct the original information transmitted by S. To decode the messages from
and
, decoding with an iterated process is applied among the decoders, as outlined in [
32].
The transmission process from S to D is split into two distinct stages. In the first stage, S encodes, modulates, and broadcasts the original binary information sequences, which are i.i.d. (independent and identically distributed) following a Bernoulli
distribution, where
is the distribution parameter. In the second stage, untrusted relays
and
decipher the received information and repeat the information, which is encoded again to D via separate channels, utilizing dedicated time slots for orthogonal transmission. Note that transmitting in different time slots may reduce spectral efficiency, a challenge that could be mitigated through non-orthogonal multiple access (NOMA) [
33,
34]. The optimization of the two time phases in the second stage is an area for the next step of research. During this second stage, S remains inactive.
3.2. Channel Model
The transmit power and geometric gain of the respective nodes and links are denoted as
and
. The RF signals received by
and
are given as follows:
and
The signals received at D from the relays are described as follows:
and
where
represents the complex channel gain, influenced by various factors such as multipath effects, weather conditions, and obstructions in air-to-ground communication. Noise is denoted by
, assumed to be additive white Gaussian noise with zero mean. The assumption
holds, assuming block-fading over one block duration.
The geometric gain
for link
i-
j is characterized by a two-ray transmission model [
35], Section 2.4.1. The receive power
is expressed as
where
and
denote the pattern of radiation and the corresponding link distance, respectively. The terms
and
refer to the heights of the source and destination.
The average and instantaneous receive signal-to-noise power ratio (SNR) at
,
, and D are expressed as
and
, where
represents the symbol-level transmit power and
being noise variance.
represents the complex channel gain. We assume that all the wireless channels experience Nakagami-m fading with the probability density function (PDF) of instantaneous SNR
of link
, where
, is given by
where
is the amplitude of the received signal;
m is the shape factor of the Nakagami-m distribution, typically ;
is the average SNR of the link ;
is the Gamma function, defined as .
The cumulative distribution function (CDF) of the Nakagami-m distribution is as follows:
where
is the lower incomplete gamma function, defined as .
All links are assumed to be mutually independent and identically distributed.
4. Reliable and Secure Probability Analyses
In relay-based systems where the trustworthiness of relays may be questionable, ensuring the secure transmission of sensitive data from the source to the intended recipient without compromising confidentiality is crucial. A common approach in this scenario involves transmitting under a pre-established secrecy rate, as outlined by [
36].
In our study, we consider an imperfect link between the source and relays, implying that the relayed information may contain errors. The recipient, aiming to retrieve the original data, must deal with these corrupted versions. This extraction process at the destination mirrors the characteristics of the CEO problem. However, a definitive rate-distortion boundary for this CEO problem has not been established. Therefore, the secrecy transmission rate discussed by [
37] is not utilized in our methodology. Instead, we adopt the "reliable and secure probability" (RSP) metric. This metric, based on the principle of outage probability, is recommended as a relevant physical layer (PHY) security parameter by [
38]. The mathematical representation is as follows:
where
encapsulates the probability of disruptions at the untrusted relay nodes, specifically
and
, and
represents a similar metric for the destination node. RSP measures the likelihood of successful message recovery at the destination while ensuring the message remains unintelligible to untrusted relays. In untrusted relay networks, the basic consideration is to utilize relays to enhance transmission reliability while minimizing the security threats posed by untrusted relays. Therefore, we introduced the RSP metric to assess the balance between security and reliability.
A higher RSP value indicates that the probability of the untrusted relay experiencing an outage is high, while the probability of the destination experiencing an outage is low, signifying the high-security performance of the system. Conversely, a lower RSP value suggests that the probability of the untrusted relay experiencing an outage is low, and the probability of the destination experiencing an outage is high, indicating low reliability and security performance. Additionally, a lower RSP value can also imply that the probability of both the destination and the untrusted relay experiencing an outage simultaneously is high, meaning the system’s reliability is low, or that the probability of both the destination and the untrusted relay experiencing an outage simultaneously is low, indicating the system’s security performance is low.
4.1. Analysis of Error Probability in Source-Relay Links
Given that transmission errors are permissible within the links from the source to untrusted relays, the distortion errors (defined as
and
) in the links between S and
and the link between S and
, respectively, are acknowledged based on the theory of lossy source-channel separation, as in [
39]. These distortions can be expressed as follows:
Here,
and
for
stand for the function of rate-distortion at
(associated with the least distortion level considering the Hamming measure), and the cumulative rate for source-channel joint coding for the associated link, in order. The specific of
is introduced in
Appendix A.
The capacity, which is equivalent to the maximal transmission rate, based on Shannon’s Gaussian codebook, is given by
With the Hamming measure, the minimum distortion for a provided value is tantamount to the error probability within the respective links.
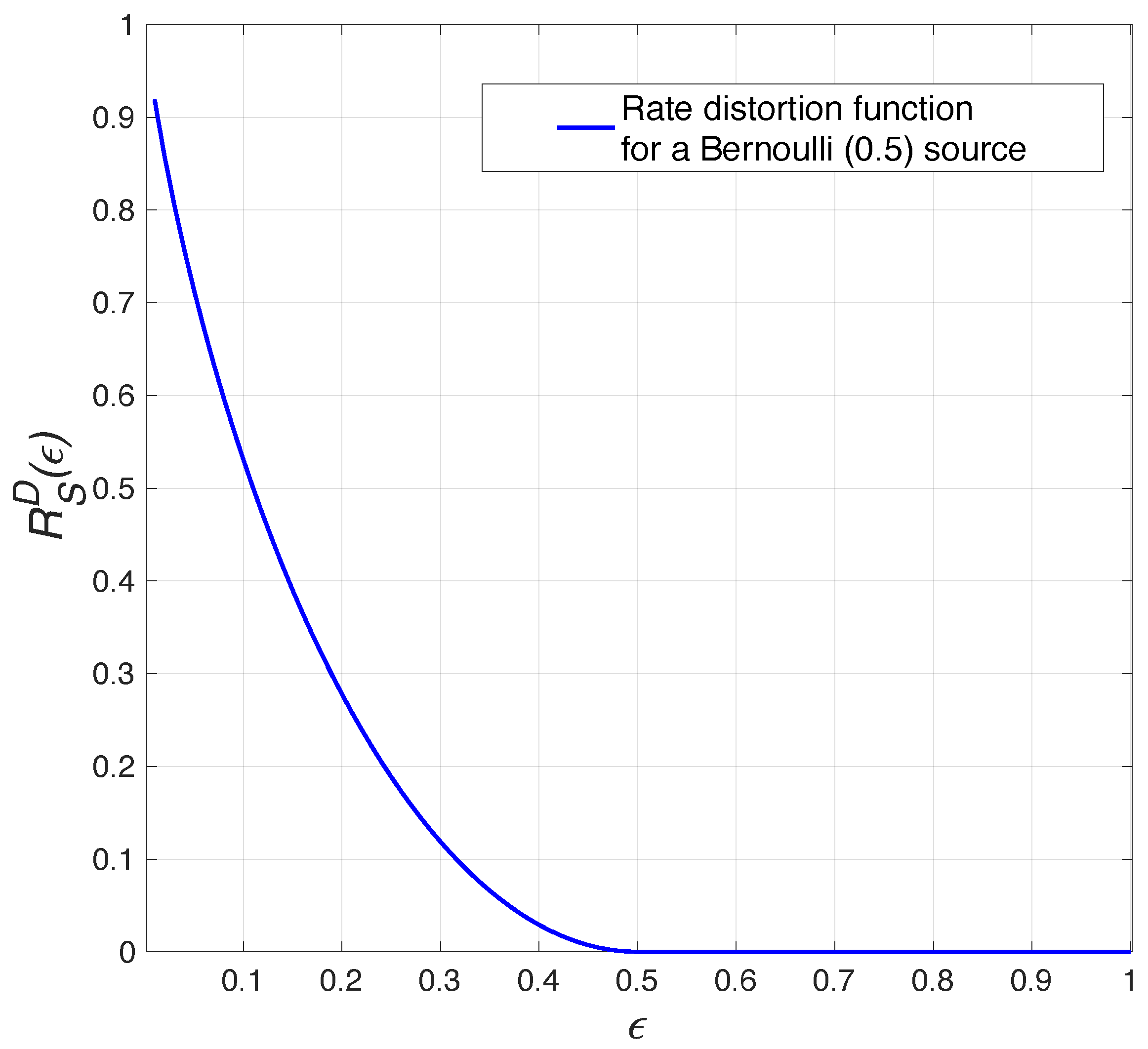
For a binary source following a Bernoulli(
p) distribution, the rate-distortion function
is given by the following:
where
represents the function of binary entropy. The relationship between the distortion
and the rate
with respect to distortion
is depicted in
Figure 2.
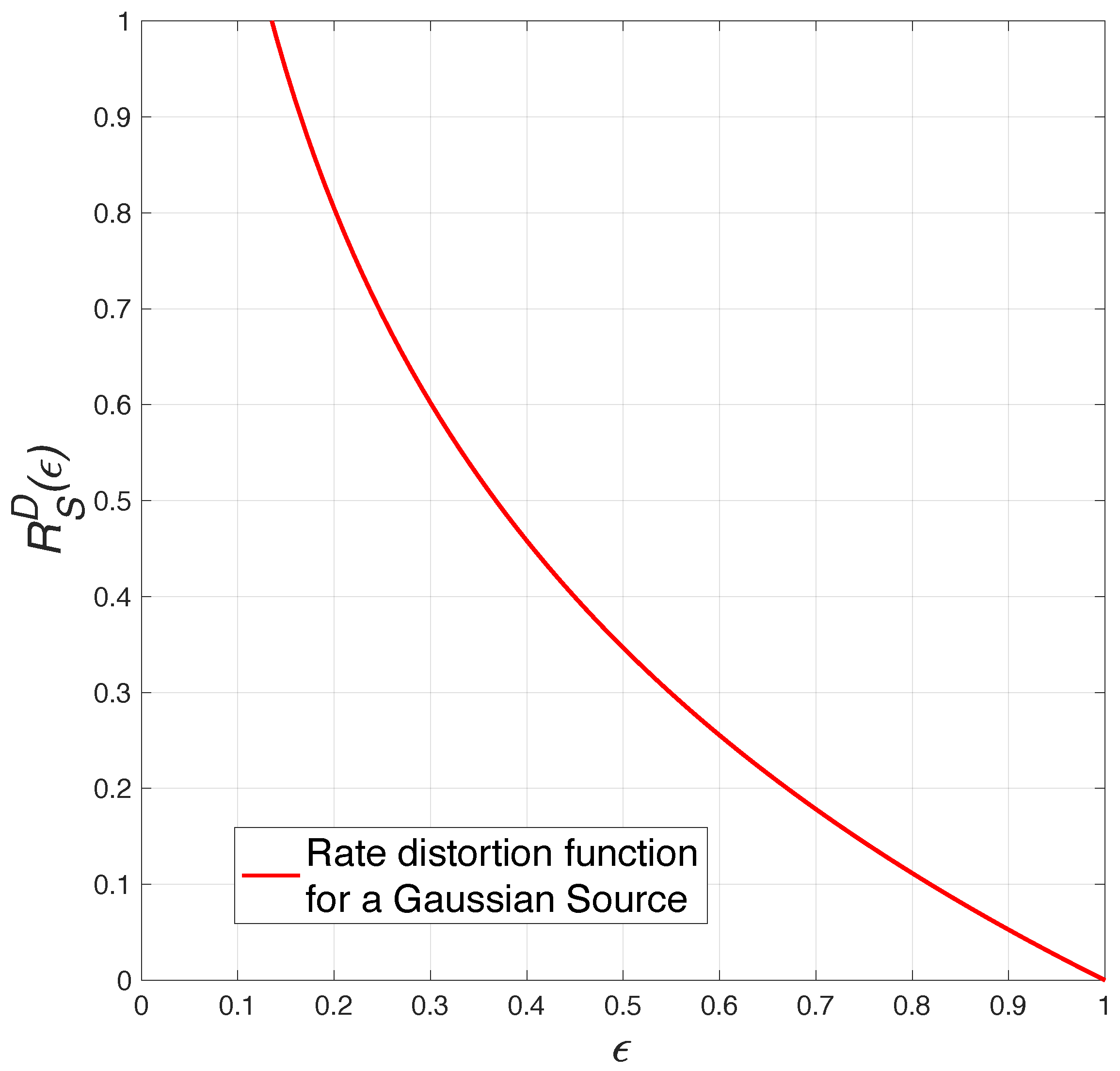
For a Gaussian source with a
distribution, the rate-distortion function
is expressed as follows:
The connection between
and the rate
with squared-error distortion is illustrated in
Figure 3.
With the measure of hamming distortion, the minimum level of the distortion and correspond to the error probabilities in the transmission from the source to and from the source to , respectively, given a specific instantaneous SNR .
Based on (
11)–(
13), the instantaneous SNR
of channel
and
can be related as follows:
for a Bernoulli(
) source. In the case of a Gaussian source, the relationship is given by the following:
Let
and
be the signal strength of the source and
and
be the jamming signal strength of the destination, respectively. The received SNRs at
and
are
where
and
are considered as cooperative jamming (interference) [
40].
4.2. Outage Probability Analysis for Untrusted Relays
Utilizing the description from (
8), we can deduce the outage probability
as follows:
For the sake of clarity, symbol indexes are disregarded. The justification for (
20) comes from the Shannon separation theorem combined with the assumption of independent fading; (
21) is derived from the presumption of Shannon’s Gaussian codebook, while the rationale for (
22) and (
23) is due to the nonergodic Nakagami-m fading channels under consideration. Given the block fading assumption, quasi-static fading channels are perceived as AWGN channels with consistent channel gains as per the fading distribution in every fading realization. As a result, outage probability
can be interpreted as a series of dual integrations spanning the rate region regarding the PDF of the current SNRs for the involved channels.
4.3. Acceptable Rate Region for the CEO Problem in the Slepian–Wolf Framework
Let
represent the original message transmitted by the source, while
and
denote the sequences output by
and
, respectively, characterized by
and
. Because of the lossy DF scheme, even if the sequences that are taken over by
and
have faults (i.e.,
and
with a certain probability),
and
still forward these erroneous sequences to the destination. As a result, the analysis of the transmissions from
to D and
to D falls under the CEO problem category in network information theory [
41]. The conceptual framework of the CEO problem is illustrated in
Figure 4. Note that
and
are not utilized in this paper to maintain consistency in notation. Under the block fading assumption, the errors occurring in the S-
and S-
links have fixed probabilities within a single transmission block.
Since and originate from the same source, they are correlated. This correlation is described using a bit-flipping model: , where is a stochastic variable with . Here, represents the probability of bit-flipping between and .
Since
and
are correlated, the Slepian–Wolf theorem states that successful retrieval of
and
through joint decoding at the destination can be achieved if the source rate pair
for
and
satisfies the following conditions:
where
and
are the estimates of
and
from the destination’s final output. Here,
and
represent conditional entropies. The relationships between
and
and between
and
are modeled using bit-flipping probabilities
and
, respectively. With the consideration of block fading, the possibility of errors occurring in the
-D and
-D links remain steady within a single communication block, making
and
fixed parameters for each stage. Given that the source is i.i.d. in this study, we have
and
, where
.
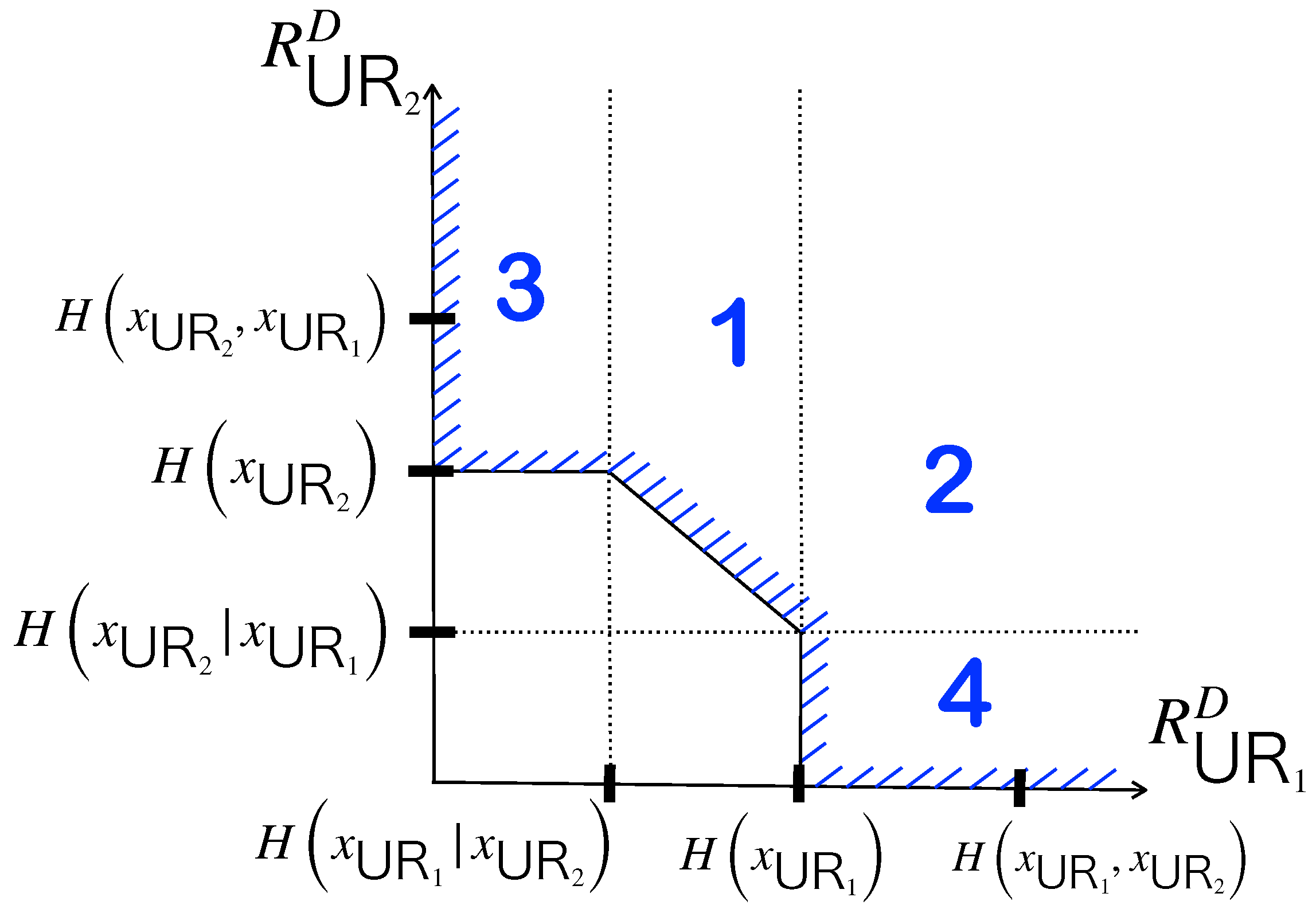
Consider two boundary scenarios. In the first scenario, where both
and
are fully recovered at the destination simultaneously, we have
and
, with
and
. This relates to the scenario where
falls within regions 1 and 2 in
Figure 5. In the second scenario, if
(or
) can be recovered with an arbitrarily small error probability while
(or
) is completely incorrect, then
(or
) provides no useful information about
(or
). In this scenario, the conditions change to
(or
), corresponding to regions 4 (or 3), respectively, in
Figure 5.
4.4. Formulation of the CEO Problem
Both and are derived from the common source. Their mutual correlation can be represented using a bit-flipping model as , where e indicates the probability of bit-flip between and . The equalities and hold, leading to . Here, the function defines the binary entropy.
Relying on the Slepian–Wolf theorem, the correct reconstruction of
via joint decoding at D is possible when the source rate pair
for
and
lies within the regions indicated as 1 and 2 in
Figure 5. Yet, given the permission for errors in the primary stage due to the assumption of imperfect source-relay links, the second stage’s analysis aligns with the CEO problem’s dynamics.
In situations where sequences received by
and
contain discrepancies, both
and
relay these imperfect sequences to D as per the LF configuration. Define
and
as the distortion measures of
and
correspondingly, where
and
symbolize the estimations of
and
. The anticipated Hamming distortion across
symbols is articulated as follows:
with the error propagation likelihood characterized by
Here,
is a minute positive constant, and the function
is the expectation mechanism. Finally, the destination retrieves an estimate of the information sent from the source using majority rule decoding [
42] Section 4.1, or an best decision approach [
43].
4.5. Destination’s Outage Probability
Given in (
8), the definition of outage probability, denoted as
, can be expressed as follows:
In the above expression, for
,
illustrates the rate-distortion function at a distortion level of
, while
stands for the aggregate combined coding rate for source-channel of the pertinent channel. The sequential decoding function, represented as
, is associated with the particular decoding technique employed. The sequential decoding first reconstructs
and
, then makes a decision on
. Comprehensive details on the function
can be found in the literature [
42,
43].
4.6. Overall Reliable-and-Security of Probability
Given that the second-phrase transmission can be modeled as the CEO problem, let
(where
) denote the probability of
residing in region
n, as depicted in
Figure 5. The probability
can be determined by due to the block fading assumption leading to varying
and
values from one block to another (the Berger–Tung bound is not employed as it necessitates a specified distortion level).
It should be highlighted that an outage occurs only if the resulting distortion
surpasses
. Regions 3 and 4 in
Figure 5 can be regarded as permissible regions, following the definition of outage probability given by (
27), especially when
and
.
Factoring in the link between rate
and the associated real-time channel SNR
, as well as the impact from the fluctuations of each link, the outage probability
(with
) is determined by averaging across all second-stage transmissions. This gives us the following:
and
It is evident that if
(
) is completely recovered at D, then
(
), making
(
). Hence, the criteria morphs into
corresponding to Equations (
31) and (
32) and regions 3 and 4 in
Figure 5. When both
and
can be simultaneously retrieved with an insignificantly small error probability, it implies
and
. This establishes the conditions, as highlighted in (
29) and (
30), correlating with regions 1 and 2 in
Figure 5. Notably, the outage probability
is influenced by
and
, which undergo variations with shifts in
and
on a block-by-block basis.
5. Optimal Power Allocation
In this section, we show how to enhance the RSP by properly allocating transmit power between S, , , and D, giving the total power constraint . With the noise variance of each channel being normalized to the unity, the transmit power, which is equivalent to their corresponding average SNR, allocated to S, , , and D are denoted as , , and , respectively. a () and b () are the power allocation ratios. Note that due to the symmetry of the two untrusted relays, we consider ( and ) as a whole in the power allocation investigation.
Since
,
, and
,
(
23) can be written as follows:
and
can be obtained by replacing
and
with
in (
28), as
and
The primary challenge lies in selecting an optimal value for a and b that maximizes the RSP of the system. This entails enhancing the destination’s ability to accurately recover the message sent by the source while concurrently minimizing the untrusted relay’s potential to intercept and decipher the original message. The objective is to optimize the system’s security posture by balancing these two aspects effectively, as formally expressed in the maximization of the RSP metric.
The optimization problem can be formulated as follows:
Theoretically, by taking the partial derivatives of with respect to a and b, the extreme point can be determined by evaluating the determinant and eigenvalues of the Hessian matrix formed from these partial derivatives. Since the explicit expression of is complicated to derive, we use a numerical approach to search for optimal power allocations.
6. Numerical Result of PLS
In
Figure 6, the trends in RSP are illustrated with respect to the source’s transmission power and the untrusted relays, with the shape factor
m being a parameter. The signal strength of the source,
and
, and the signal strength of the relays,
and
, are assumed to be the same, with the jamming signal strength remianing constant. Therefore, the S-
, S-
,
-D, and
-D links have the same average SNR, with the noise normalized to unity. The graph reveals an initial rise in the RSP, followed by a decline as the average power escalates, regardless of the fading severity (different values of
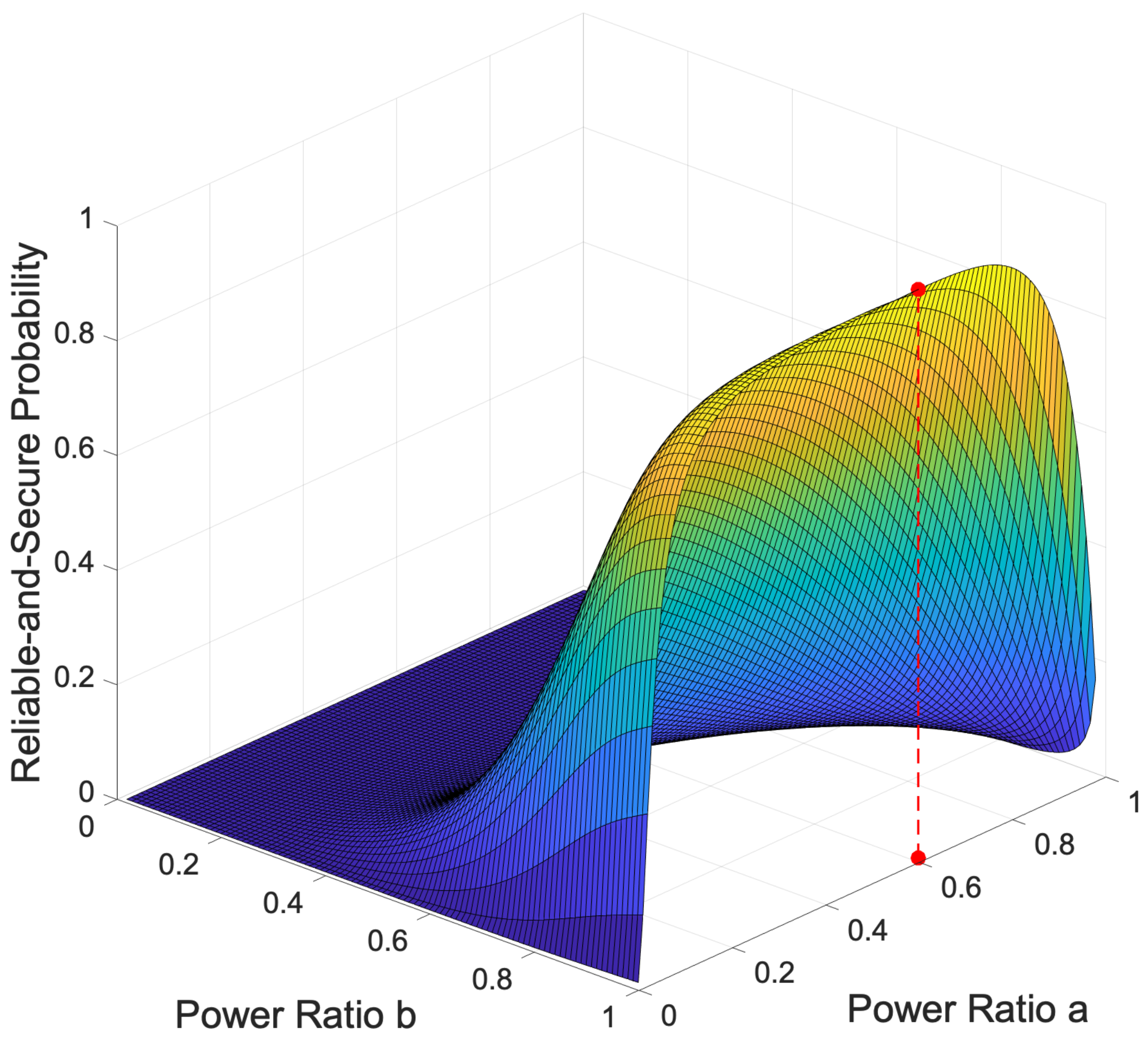
m). This suggests that a mere increment in transmit power doesn’t continually bolster the RSP. As the source’s transmit power augments, the chances of the relays decoding the transmission accurately amplify, leading to a drop in the overall RSP. Peak RSP is observed when the source’s and relays’ transmit power contributions are in equilibrium.
Furthermore,
Figure 6 illustrates how varying the shape factor
m affects the RSP in different Nakagami-m fading scenarios. With higher values of
m, representing less severe fading conditions, the RSP remains higher across a broader range of transmit power levels compared to lower values of
m. This indicates that in more favorable channel conditions, the network maintains a higher level of reliability and security on average. In contrast, under more severe fading conditions (larger values of
m), the RSP decreases sharply, although it increases rapidly with increasing transmit power. Interestingly, regardless of the value of
m, the peak RSP occurs at the same transmit power level, indicating that the optimal point for maximizing reliability and security is unaffected by the severity of fading. This highlights the importance of optimizing power allocation and considering the channel conditions to maximize the reliable and secure performances of the network.
Figure 7 demonstrates that to achieve the optimal RSP in a diamond network under Nakagami-m fading conditions, the majority of the transmit power, approximately 61%, should be allocated to the source, as indicated by the power allocation ratio
a. The remaining transmit power should predominantly be allocated to the untrusted relays, as indicated by the power allocation ratio
b, with only a very small portion allocated to the destination for jamming signals. This optimal power distribution ensures a balanced power allocation that maximizes RSP, highlighting the importance of strategic power allocation in designing efficient and secure communication systems resilient to jamming and fading effects.
7. Conclusions
In this paper, we presented an optimized transmission scheme for enhancing security and reliability in a diamond untrusted relay network using cooperative jamming and LF relaying. Our approach addresses the challenge of secure data transmission in scenarios involving untrusted relays by balancing power allocation between the source, relays, and destination. The introduced RSP metric provides a robust evaluation of the system’s performance. Our results demonstrate that optimal power distribution significantly improves RSP, ensuring that the destination can accurately retrieve the original message while maintaining its confidentiality from untrusted relays. Future research could extend this framework to networks with multiple sources and multiple untrusted relays, further strengthening secure communication strategies in complex relay environments. This analysis underscores the importance of balanced power allocation in achieving maximum RSP, providing valuable insights for designing efficient and secure communication systems under jamming conditions.
To extend the proposed framework to multi-source networks, several key considerations must be addressed. The primary challenge involves managing inter-source interference, which could degrade both the reliability and security of communications. Advanced strategies such as interference alignment and cooperative beamforming could mitigate these effects. Additionally, cooperative strategies among sources, such as coordinated jamming and shared CSI, could enhance overall network performance. The RSP metric could also be generalized to account for the interactions between multiple sources, requiring new analytical approaches. As the complexity of the network increases, scalable algorithms like decentralized optimization or machine learning-based techniques may be necessary to manage the problem’s dimensionality. By addressing these challenges, the framework could be effectively adapted to multi-source networks, enabling its application to more complex and dynamic communication environments, such as IoT systems and vehicular networks. Future research will explore these extensions, aiming to validate the framework’s robustness and scalability in multi-source scenarios.
While the primary focus of this paper is on the theoretical foundations and simulation-based validation of the proposed optimization framework, it is essential to consider the practical challenges associated with implementing these strategies in real-world communication systems. The hardware requirements for cooperative jamming, for instance, would necessitate advanced transceivers capable of generating and managing jamming signals without introducing excessive interference to legitimate communications. Furthermore, the feasibility of the proposed power allocation strategies in dynamic environments, such as mobile networks, must account for the rapidly changing channel conditions and the need for real-time adaptability. This could involve the development of adaptive algorithms that can quickly adjust power levels based on instantaneous channel state information. Additionally, potential latency issues, particularly in time-sensitive applications, must be carefully managed to ensure that the security and reliability enhancements do not come at the cost of increased delay. Addressing these practical considerations is critical for the successful deployment of the proposed framework in real-world scenarios, and these aspects will be explored in greater detail in our future work.
Author Contributions
Conceptualization, S.Q. and M.C.; methodology, S.Q.; software, S.Q.; validation, S.Q. and M.C.; formal analysis, S.Q.; investigation, S.Q.; resources, S.Q.; data curation, S.Q.; writing—original draft preparation, S.Q. and M.C.; writing—review and editing, S.Q. and M.C.; visualization, S.Q.; supervision, M.C.; project administration, M.C.; funding acquisition, M.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
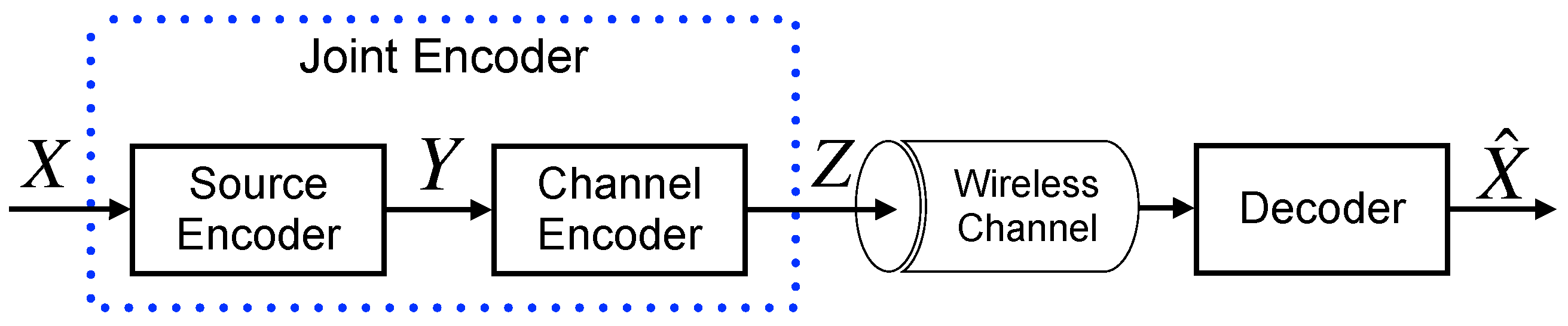
A source-to-destination direct signaling chain is illustrated in
Figure A1, where
X denotes binary i.i.d information sequences of length
,
Y represents the information sequences with
-bit produced by the encoder of the source.
Z corresponds to the symbol sequences with
-bit transmitted to the decoder across a wireless channel. A joint encoder
, functioning as an association of source and channel encoders, maps each sequence
X to a codeword of length
, expressed as
. For simplicity, modulation is omitted in
Figure A1. The transmission from the source S to
and
and that from
and
to the destination are orthogonal due to spatial/temporal separation.
As per the source-channel separation theorem [
41] Theorem 3.7, the overall joint source-channel coding rate is given by the following:
where
denotes the source coding rate, and
represents the spectrum efficiency, which encompasses both the channel coding rate and the modulation order.
Figure A1.
Abstract framework for joint source-channel coding incorporating source-channel separation.
Figure A1.
Abstract framework for joint source-channel coding incorporating source-channel separation.
References
- Gupta, A.; Jha, R.K. A Survey of 5G Network: Architecture and Emerging Technologies. IEEE Access 2015, 3, 1206–1232. [Google Scholar] [CrossRef]
- Van, N.B.; Hyoyoung, J.; Kiseon, K. Physical Layer Security Schemes for Full-Duplex Cooperative Systems: State of the Art and Beyond. IEEE Commun. Mag. 2018, 56, 131–137. [Google Scholar]
- Banafaa, M.; Pepeoğlu, Ö.; Shayea, I.; Alhammadi, A.; Shamsan, Z.; Razaz, M.A.; Alsagabi, M.; Al-Sowayan, S.A. Comprehensive Survey on 5G-and-Beyond Networks with UAVs: Applications, Emerging Technologies, Regulatory Aspects, Research Trends and Challenges. IEEE Access 2024, 12, 7786–7826. [Google Scholar] [CrossRef]
- Feng, C.; Wang, H.-M. Secure short-packet communications at the physical layer for 5G and beyond. IEEE Commun. Stand. Mag. 2021, 5, 96–102. [Google Scholar] [CrossRef]
- Poor, H.V.; Goldenbaum, M.; Yang, W. Fundamentals for IoT networks: Secure and low-latency communications. In Proceedings of the 20th International Conference on Distributed Computing and Networking, New York, NY, USA, 4–7 January 2019; pp. 362–364. [Google Scholar]
- Wu, Y.; Khisti, A.; Xiao, C.; Caire, G.; Wong, K.-K.; Gao, X. A survey of physical layer security techniques for 5G wireless networks and challenges ahead. IEEE J. Sel. Areas Commun. 2018, 36, 679–695. [Google Scholar] [CrossRef]
- He, X.; Yener, A. Cooperation with an Untrusted Relay: A Secrecy Perspective. IEEE Trans. Intell. Transport. Syst. 2021, 56, 3807–3827. [Google Scholar] [CrossRef]
- Zhao, S.; Liu, J.; Shen, Y.; Jiang, X.; Shiratori, N. Secure and energy-efficient precoding for MIMO two-way untrusted relay systems. IEEE Trans. Inf. Forensics Secur. 2021, 16, 3371–3386. [Google Scholar] [CrossRef]
- Xiong, J.; Cheng, L.; Ma, D.; Wei, J. Destination-aided cooperative jamming for dual-hop amplify-and-forward MIMO untrusted relay systems. IEEE Trans. Veh. Technol. 2016, 65, 7274–7284. [Google Scholar] [CrossRef]
- Zhang, R.; Song, L.; Han, Z.; Jiao, B. Physical Layer Security for Two-Way Untrusted Relaying with Friendly Jammers. IEEE Trans. Veh. Technol. 2011, 61, 3693–3704. [Google Scholar] [CrossRef]
- Wang, L.; Elkashlan, M.; Huang, J.; Tran, N.H.; Duong, T.Q. Secure Transmission with Optimal Power Allocation in Untrusted Relay Networks. IEEE Wirel. Commun. Lett. 2014, 3, 289–292. [Google Scholar] [CrossRef]
- Oohama, Y. Coding for relay channels with confidential messages. In Proceedings of the 2001 IEEE Information Theory Workshop, Cairns, QLD, Australia, 2–7 September 2001; pp. 87–89. [Google Scholar]
- Oohama, Y. Capacity Theorems for Relay Channels with Confidential Messages. In Proceedings of the IEEE International Symposium on Information Theory, Nice, France, 24–29 June 2007; pp. 926–930. [Google Scholar]
- He, X.; Yener, A. Two-Hop Secure Communication Using an Untrusted Relay: A Case for Cooperative Jamming. In Proceedings of the IEEE Global Telecommunications Conference, New Orleans, LA, USA, 30 November–4 December 2008; pp. 1–5. [Google Scholar]
- He, X.; Yener, A. A Two-Hop Secure Communication Using an Untrusted Relay. J. Wirel. Commun. Netw. 2009, 2009, 1–13. [Google Scholar] [CrossRef]
- Kuhestani, A.; Mohammadi, A.; Yeoh, P.L. Optimal Power Allocation and Secrecy Sum Rate in Two-Way Untrusted Relaying Networks with an External Jammer. IEEE Trans. Commun. 2018, 66, 2671–2684. [Google Scholar] [CrossRef]
- He, J.; Tervo, V.; Zhou, X.; He, X.; Qian, S.; Cheng, M.; Juntti, M.; Matsumoto, T. A Tutorial on Lossy Forwarding Cooperative Relaying. IEEE Commun. Surv. Tutor. 2019, 21, 66–87. [Google Scholar] [CrossRef]
- Hu, L.; Wen, H.; Wu, B.; Pan, F.; Liao, R.-F.; Song, H.; Tang, J.; Wang, X. Cooperative Jamming for Physical Layer Security Enhancement in Internet of Things. IEEE Internet Things J. 2018, 5, 219–228. [Google Scholar] [CrossRef]
- Shen, H.; Xu, W.; Gong, S.; He, Z.; Zhao, C. Secrecy Rate Maximization for Intelligent Reflecting Surface Assisted Multi-Antenna Communications. IEEE Commun. Lett. 2019, 23, 1488–1492. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, J.; Kuo, Y.; Zhou, Y. Transmit Beamforming for Layered Physical Layer Security. IEEE Trans. Veh. Technol. 2019, 68, 9747–9760. [Google Scholar] [CrossRef]
- Si, J.; Cheng, Z.; Li, Z.; Cheng, J.; Wang, H.-M.; Al-Dhahir, N. Cooperative Jamming for Secure Transmission with Both Active and Passive Eavesdroppers. IEEE Trans. Commun. 2020, 68, 5764–5777. [Google Scholar] [CrossRef]
- Xu, Z.; Baykal-Gürsoy, M. Power Allocation for Cooperative Jamming against a Strategic Eavesdropper over Parallel Channels. IEEE Trans. Inform. Forensics Secur. 2023, 18, 846–858. [Google Scholar] [CrossRef]
- Li, Z.; Le, S.; Chen, J.; Shin, K.G.; Liu, J.; Yan, Z.; Jantti, R. Decomposed and Distributed Modulation to Achieve Secure Transmission. IEEE Trans. Mob. Comput. 2024, 1–18. [Google Scholar] [CrossRef]
- Tang, L.; Chen, H.; Li, Q. Social Tie Based Cooperative Jamming for Physical Layer Security. IEEE Commun. Lett. 2015, 19, 1790–1793. [Google Scholar] [CrossRef]
- Atapattu, S.; Ross, N.; Jing, Y.; Premaratne, M. Source-Based Jamming for Physical-Layer Security on Untrusted Full-Duplex Relay. IEEE Commun. Lett. 2019, 23, 842–846. [Google Scholar] [CrossRef]
- Sadig, T.; Maleki, M.; Tran, N.H.; Bahrami, H.R. Encryption-Aided Physical Layer Security via Cooperative Jamming: Beyond Secrecy Capacity with Noisy Ciphertext. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), Glasgow, UK, 26–29 March 2023; pp. 1–6. [Google Scholar]
- Gui, L.; Zhou, W.; Zhang, P.; Xiao, F. Cooperative Jamming-Aided Secure Communication in Wireless Powered Sensor Networks. IEEE Trans. Dependable Secur. Comput. 2024, 21, 764–774. [Google Scholar] [CrossRef]
- Jia, S.; Zhang, J.; Chen, S.; Hao, W.; Xu, W. JSecure Multiantenna Transmission with an Unknown Eavesdropper: Power Allocation and Secrecy Outage Analysis. IEEE Trans. Inform. Forensics Secur. 2022, 17, 2906–2919. [Google Scholar] [CrossRef]
- Li, J.; Han, S.; Tai, X.; Gao, C.; Zhang, Q. Physical Layer Security Enhancement for Satellite Communication among Similar Channels: Relay Selection and Power Allocation. IEEE Syst. J. 2020, 14, 433–444. [Google Scholar] [CrossRef]
- Diao, D.; Wang, B.; Cao, K.; Dong, R.; Cheng, T. Enhancing Reliability and Security of UAV-Enabled NOMA Communications with Power Allocation and Aerial Jamming. IEEE Trans. Veh. Technol. 2022, 71, 8662–8674. [Google Scholar] [CrossRef]
- Han, S.; Xu, X.; Tao, X.; Zhang, P. Joint Power and Sub-Channel Allocation for Secure Transmission in NOMA-Based mMTC Networks. IEEE Syst. J. 2019, 13, 2476–2487. [Google Scholar] [CrossRef]
- Qian, S.; Zhou, X.; He, X.; He, J.; Juntti, M.; Matsumoto, T. Performance Analysis for Lossy-Forward Relaying over Nakagami-m Fading Channels. IEEE Trans. Veh. Technol. 2017, 66, 10035–10043. [Google Scholar] [CrossRef]
- Wan, D.; Wen, M.; Ji, F.; Yu, H.; Chen, F. On the Achievable Sum-Rate of NOMA-Based Diamond Relay Networks. IEEE Trans. Veh. Technol. 2019, 68, 1472–1486. [Google Scholar] [CrossRef]
- Kara, F.; Kaya, H. Error Probability Analysis of NOMA-Based Diamond Relaying Network. IEEE Trans. Veh. Technol. 2020, 69, 2280–2285. [Google Scholar] [CrossRef]
- Goldsmith, A. Wireless Communications, 1st ed.; Cambridge University Press: Cambridge, UK; Stanford University: Stanford, CA, USA, 2008; pp. 30–36. [Google Scholar]
- Dong, L.; Han, Z.; Petropulu, A.P.; Poor, H. Vincent. Improving Wireless Physical Layer Security via Cooperating Relays. IEEE Trans. Signal Process. 2010, 58, 1875–1888. [Google Scholar] [CrossRef]
- Yang, W.; Schaefer, R.F.; Poor, H. Vincent. Wiretap Channels: Nonasymptotic Fundamental Limits. IEEE Trans. Inform. Theory 2019, 65, 4069–4093. [Google Scholar] [CrossRef]
- Feng, C.; Wang, H.-M.; Poor, H. Vincent.Reliable and Secure Short-Packet Communications. IEEE Trans. Wirel. Commun. 2022, 21, 1913–1926. [Google Scholar] [CrossRef]
- Shen, Q. Reliable and Secure Short-Packet Communications in Untrusted Diamond Relay Networks. IEEE Access 2023, 11, 24686–24695. [Google Scholar]
- Tse, D.; Viswanath, P. Fundamentals of Wireless Communication; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Gamal, A.E.; Kim, Y.-H. Network Information Theory, 1st ed.; Cambridge University Press: Cambridge, UK; Stanford University: Stanford, CA, USA, 2011; p. 336. [Google Scholar]
- Zhou, X.; Yi, N.; He, X.; Hou, J.; Matsumoto, T.; Szott, S.; Gonzales, D.; Wolf, A.; Matthe, M.; Kuhlmorgen, S.; et al. ICT-619555 RESCUE Deliverable D1.2.1-Assessmenton Feasibility, Achievability, and Limits; Technical Report; Oulu University Library Press: Oulu, Finland, 2015. [Google Scholar]
- He, X.; Zhou, X.; Komulainen, P.; Juntti, M.; Matsumoto, T. A Lower Bound Analysis of Hamming Distortion for a Binary CEO Problem with Joint Source-Channel Coding. IEEE Trans. Commun. 2016, 64, 343–353. [Google Scholar] [CrossRef]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).