Classification of Trajectory Types Exhibiting Dynamical Matching in Caldera-Type Hamiltonian Systems

Abstract

In this paper, we study the different types of trajectories that correspond to a particular orbital behavior of caldera-type Hamiltonian systems. This particular orbital behavior is dynamical matching. Dynamical matching is an important chemical phenomenon that is encountered in many caldera-type organic chemical reactions. In this paper we will distinguish the different types of trajectories that correspond to this phenomenon using periodic orbit dividing surfaces.

1. Introduction

Dynamical matching is a fascinating phenomenon in chemical dynamics observed in a range of organic reactions that involve potential energy surfaces (PESs) shaped like a caldera. This concept was first introduced and analyzed in [1,2]. In general, dynamical matching refers to the observation that reaction trajectories passing through a caldera-like PES tend to preserve certain dynamical properties, such as momentum direction, that they possessed upon entering the caldera region.

A caldera potential energy surface is defined by a broad, relatively flat central region or shallow minimum, enclosed by potential barriers, with four symmetry-related index-1 saddles (two upper index-1 saddles and two lower index-1 saddles) that facilitate ingress to and egress from this intermediate zone (see Figure 1). The term “caldera” was first applied in this context by [3], inspired by the similarity to the collapsed crater on the summit of a volcano following an eruption. This model has been the subject of extensive recent studies (see [4,5], among others).

In caldera-type Hamiltonian models, a chemical reaction is considered to occur (see [4,6]) when trajectories originating from initial conditions on the periodic orbit dividing surfaces associated with the upper index-1 saddles subsequently cross the dividing surfaces of the lower index-1 saddles. The reaction products are defined as the trajectories that successfully cross these lower dividing surfaces. Consequently, trajectories that move forward into the central region of the caldera are classified as reactants, since they have a finite probability of crossing the lower dividing surfaces. Conversely, trajectories that move directly toward infinity are classified as non-reactants.

According to previous studies, the phenomenon of dynamical matching refers to a specific type of trajectory behavior in which all trajectories, whose initial conditions lie on the periodic orbit dividing surfaces (PODSs) associated with upper index-1 saddles, pass directly through the caldera and emerge through the region associated with the opposite lower index-1 saddle, or they escape the system (see [4]). This behavior results from the lack of heteroclinic intersections connecting the unstable manifolds of the upper index-1 saddle periodic orbits with the stable manifolds of those in the central caldera (see [4,6]). Dynamical matching can break down only if the caldera potential is elongated in the x-direction (see [5,6]). A stochastic analysis of this phenomenon is an interesting topic for future work (see [7] for a related analysis).

This mechanism plays a role in various organic chemical transformations, including the vinylcyclopropane–cyclopentene rearrangement [8,9], cyclopropane stereomutation [10], and degenerate rearrangements of molecules such as bicyclo[3.1.0]hex-2-ene [11,12] and 5-methylenebicyclo[2.1.0]pentane [13].

Several studies have explored dynamical matching using a variety of potential energy surface (PES) models. For example, Ref. [14] examined the classic caldera system originally proposed by B. Carpenter in his foundational work on caldera potentials [1,2,15,16]. More recently, Ref. [17] introduced a modified caldera-like PES—termed the mesa caldera—that incorporates tunable parameters to control the flatness and tilt of the potential surface. Their analysis focused on how these geometric modifications affect trajectory behavior, including phenomena such as dynamical matching, recrossing, and trapping.

The phenomenon of dynamical matching was also found recently in a 3D extension of the caldera potential in [18,19]. This was conducted through the use of the generalization of the periodic orbit dividing surfaces in Hamiltonian systems with three degrees of freedom [20,21].

In the works [18,19], we not only investigated dynamical matching but also classified the types of trajectories that arise in this context. Additionally, they linked the phase space transport mechanisms to these trajectory types in the case of dynamical matching. However, such a study has never been conducted for the two-dimensional caldera potential. The motivation for this paper is to address this gap in the scientific literature.

In Section 1 and Section 2 we give an introduction to the subject and describe the Hamiltonian model, respectively. We describe our results in Section 3. In the last section we discuss our results.

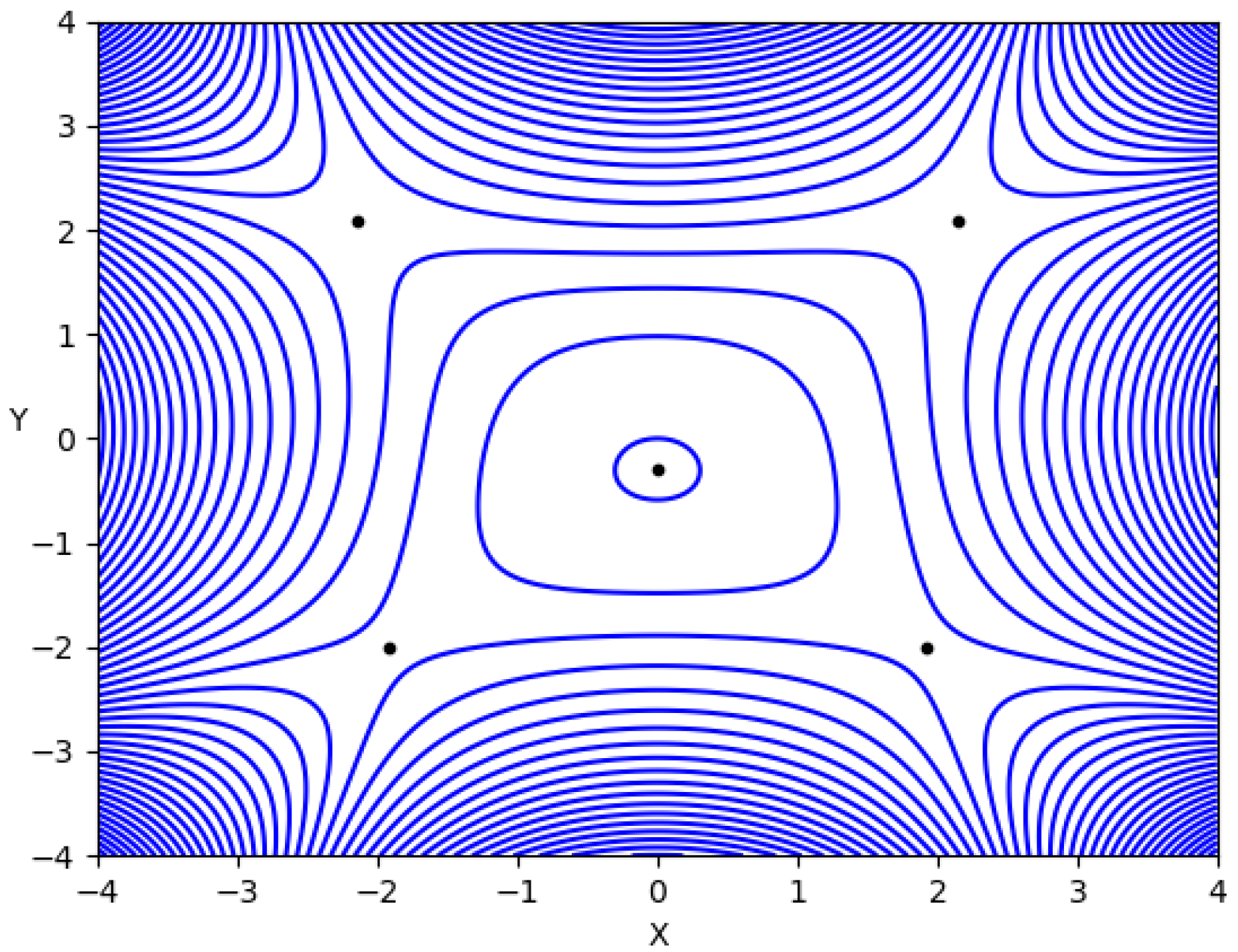
2. Caldera Potential

We begin with a concise overview of the caldera potential energy surface and its associated Hamiltonian, following the general framework outlined in [4]. The caldera potential features a stable equilibrium point at its center, commonly known as the central minimum. This potential exhibits symmetry with respect to the y-axis and is enclosed by potential barriers (see Figure 1). Along these barriers lie four index-1 saddle points: two positioned at lower energy levels (the lower saddles) and two at higher energy levels (the upper saddles). The mathematical expression of the potential is:

$$\begin{array}{c}\hfill V(x,y)=c_1(y^2+x^2)+c_{2}y-c_3(x^4+y^4-6x^2{y}^2)\end{array}$$

(1)

We used the same parameters for this potential as in our previous papers [4], $c_1=5$, $c_2=3$, $c_3=-3/10$. The reader can find the positions of the equilibrium points in [4].

The Hamiltonian of the system is given by the following equation:

$$\begin{array}{c}\hfill H(x,y,p_x,p_y)={\displaystyle \frac{p_x^2}{2m}}+{\displaystyle \frac{p_y^2}{2m}}+V(x,y)\end{array}$$

(2)

We consider the potential $V(x,y)$ as given in (1), with mass m = 1. The numerical value of the Hamiltonian will be referred to as the energy E. The corresponding equations of motion can be found in [4].

3. Results

We begin this section by computing the dividing surfaces defined by the periodic orbits corresponding to the upper right index-1 saddle. Due to the symmetry of the potential, the same results apply to the other upper index-1 saddle. Using these PODS, we compute trajectories—both forward and backward in time—starting from initial conditions on the dividing surfaces and integrate them for a period of 7 time units. This integration time is sufficient for the trajectories to explore the central region of the caldera and its exits (see [4,5]). We repeat this procedure for three energy values above the energy of the upper-right index-1 saddle. Finally, we analyze the forward and backward fates of these trajectories and classify them into one of the four trajectory types described in [18,19].

• First Type (type I): The trajectories, integrated forward and backward in time, pass directly through the central region of the caldera and exit via the region of the opposite lower index-1 saddle.
• Second Type (type II): The trajectories, both forward and backward in time, escape directly to infinity.
• Third type (type III): In this case, integrated forward-time trajectories traverse the central region of the caldera and exit through the region of the opposite lower index-1 saddle. When integrated backward in time, these trajectories escape directly to infinity.
• Fourth type (type IV): This type exhibits the opposite behavior of the third type. The trajectories integrated backward in time pass through the central region of the caldera and exit via the opposite lower index-1 saddle, whereas those integrated forward in time escape directly to infinity.

We computed the periodic orbit dividing surfaces for three values of energy: E = 28, 30, and 32. We used the classical algorithm of Pechukas and Pollak [22,23,24,25,26]:

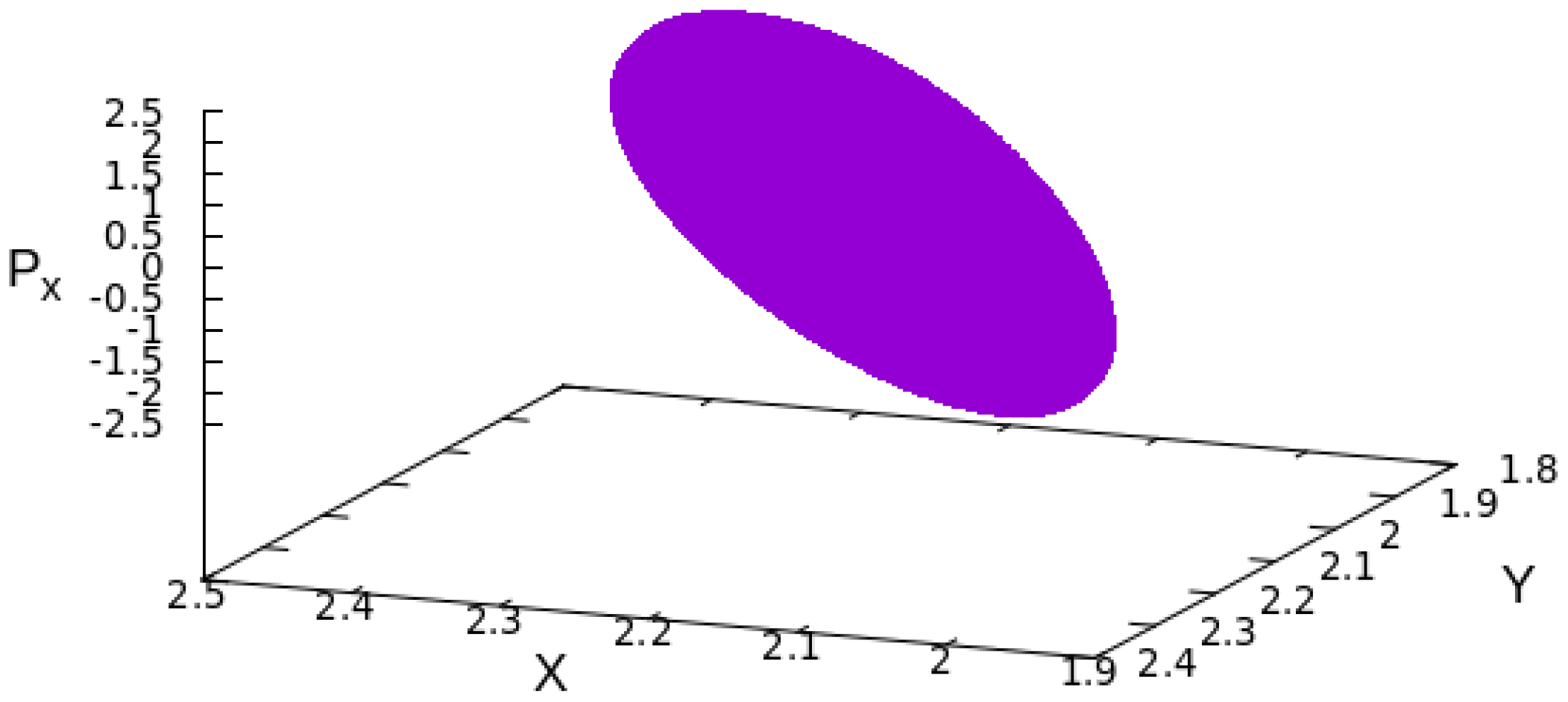
• Identify a periodic orbit.
• Represent the periodic orbit within the configuration space.
• We sample $N_p$ points $(x_i,y_i)$ from the periodic orbit’s projection, with uniform spacing along the orbit.
• For every $(x_i,y_i)$ we find the corresponding $p_{xmax,i}$, using the Hamiltonian and for $p_y=0$:

  $$\begin{array}{c}\hfill H(x_i,y_i,p_x,0)={\displaystyle \frac{p_x^2}{2m}}+V(x_i,y_i)\end{array}$$

  (3)

  where m represents the mass ($m=1$ in our case). Observe that a solution exists only when $E-V(x_i,y_i)\ge 0$, yielding two possible solutions: $\pm p_{xmax,i}$.
• For every point $(x_i,y_i)$, K evenly spaced $p_x$ are chosen from $-p_{xmax,i}$ to $p_{xmax,i}$. Solving $H(x_i,y_i,p_x,p_y)=E$ for each $p_x$ produces two corresponding $p_y$ values: one positive and one negative.

We applied this algorithm to the periodic orbits of the upper-right index-1 saddle for energy values 28, 30, and 32. The corresponding numbers of points were $N_p=965$, $N_p=961$, and $N_p=956$, respectively. In all cases, we used $K=21$. The resulting periodic orbit dividing surfaces (PODSs) have a disk-like structure on the three-dimensional energy surface, as shown in Figure 2, Figure 3 and Figure 4. These figures also reveal that the size of this disk structure increases with energy, particularly along the $p_x$ direction.

We then integrated a total of 38,600, 38,440, and 38,240 trajectories forward and backward in time, respectively, each initialized on the dividing surface defined by the periodic orbit of the upper-right index-1 saddle for energies E = 28, 30, and 32. For E = 28, all trajectories belong to either the third or fourth type, as shown in Figure 5. The distribution is exactly balanced: $50\%$ (19,300 trajectories) exhibit the third type, and $50\%$ (19300 trajectories) exhibit the fourth type. The same result holds for E = 30 and E = 32 (see Figure 6 and Figure 7). In both cases, only the third and fourth trajectory types are present, with the same 1:1 ratio. Specifically, for E = 30, we have 19,220 trajectories of each type, and for E = 32, we have 19,120 trajectories of each type. The only notable difference is that, as the energy increases, the bottleneck opens progressively wider, causing the trajectory bundles to spread out more (compare Figure 5, Figure 6 and Figure 7).

These results show that only the simplest types of trajectories occur: they either originate from infinity (third type) or start in the region of the lower index-1 saddle on the opposite side (fourth type). Third-type trajectories follow the unstable invariant manifold of the unstable periodic orbits associated with the upper-right index-1 saddle and ultimately reach the opposite lower index-1 saddle. Conversely, fourth-type trajectories escape to infinity. For more details, see [4]. In the 2D case, the first and second types of trajectory behavior observed in the 3D caldera system [18] are absent. Specifically, no trajectories correspond to homoclinic intersections between the unstable and stable invariant manifolds of the unstable periodic orbits (Normally Hyperbolic Invariant Manifolds, NHIMs) associated with the opposite lower index-1 saddles, which define the first type of behavior (see [18]). Similarly, there are no trajectories that originate from infinity and then follow the unstable invariant manifolds of the unstable periodic orbits (NHIMs) of the upper index-1 saddles back to infinity, corresponding to the second type of behavior. (This clarifies the second type of trajectories in the 3D caldera [18]: these trajectories originate from infinity and then follow the unstable invariant manifolds of the NHIMs (Normally Hyperbolic Invariant Manifolds) associated with upper index-1 saddles, eventually returning to infinity. In [18], this second type was incorrectly described as corresponding to homoclinic intersections of the invariant manifolds of the NHIMs associated with the upper index-1 saddles.)

The fundamental reason for this, as well as the geometrical and physical significance of the absence of the first and second types of trajectory behavior, is as follows. In two dimensions, homoclinic intersections of the invariant manifolds associated with the NHIMs (Normally Hyperbolic Invariant Manifolds) related to the index-1 saddles, or the guidance of trajectories from infinity along the unstable invariant manifolds back to infinity, do not occur. This is because, in the 2D case, the NHIMs correspond to one-dimensional unstable periodic orbits and their invariant manifolds to two-dimensional objects.

In contrast, in the 3D case, the NHIMs are three-dimensional objects (rather than one-dimensional as in 2D), and their invariant manifolds are four-dimensional structures (rather than two-dimensional as in 2D) embedded in a six-dimensional phase space. In this setting, homoclinic intersections, or the guidance of trajectories from infinity along the unstable manifolds back to infinity, occur beyond the plane of symmetry, which corresponds to the 2D caldera system.

This behavior is clearly illustrated in Figures 11 and 13 of our paper [18], where the variables z and $p_z$ are involved in the homoclinic intersections and the guidance of trajectories from infinity along the unstable manifolds back to infinity.

4. Discussion

In this study, we examine the types of trajectories that emerge in a two-dimensional caldera potential exhibiting dynamical matching. As mentioned in the Introduction, our interest was initially inspired by a previous investigation of a three-dimensional caldera, where we unexpectedly observed four distinct types of trajectories. This observation led us to question whether similar trajectory behaviors could also appear in the two-dimensional scenario, forming the main motivation for the present work. To address this, we start with a caldera-type potential known to exhibit dynamical matching (see Section 2), which corresponds to the potential employed in [4].

We computed the periodic orbit dividing surfaces associated with the upper index-1 saddles for several energy values above these saddles. Using initial conditions on these dividing surfaces, we then integrated thousands of trajectories forward and backward in time and analyzed their outcomes. Our results show that all trajectories exhibit either third- or fourth-type behavior, with no instances of first- or second-type trajectories. This implies the following:

• In the 2D caldera, there are no trajectories with initial conditions on the periodic orbit dividing surfaces of the unstable periodic orbits of the upper index-1 saddles that correspond to homoclinic intersections of the stable and unstable invariant manifolds of the unstable periodic orbits (NHIMs) of lower index-1 saddles.
• In the 2D caldera, likewise, no trajectories initialized on the periodic orbit dividing surfaces of the upper index-1 saddles begin at infinity and return to infinity by evolving along the unstable invariant manifolds of the corresponding unstable periodic orbits (NHIMs).
• These observations indicate that certain dynamical phenomena, such as those corresponding to the first and second types of trajectory behavior, occur only in Hamiltonian systems with three degrees of freedom and not in two-degrees-of-freedom systems. These phenomena warrant further investigation in future studies.