Analysis and Simulation of Dynamic Heat Transfer and Thermal Distribution in Burns with Multilayer Models Using Finite Volumes
Abstract
1. Introduction
2. Mathematical Model and Analysis of Thermal Behavior in Biological Tissues
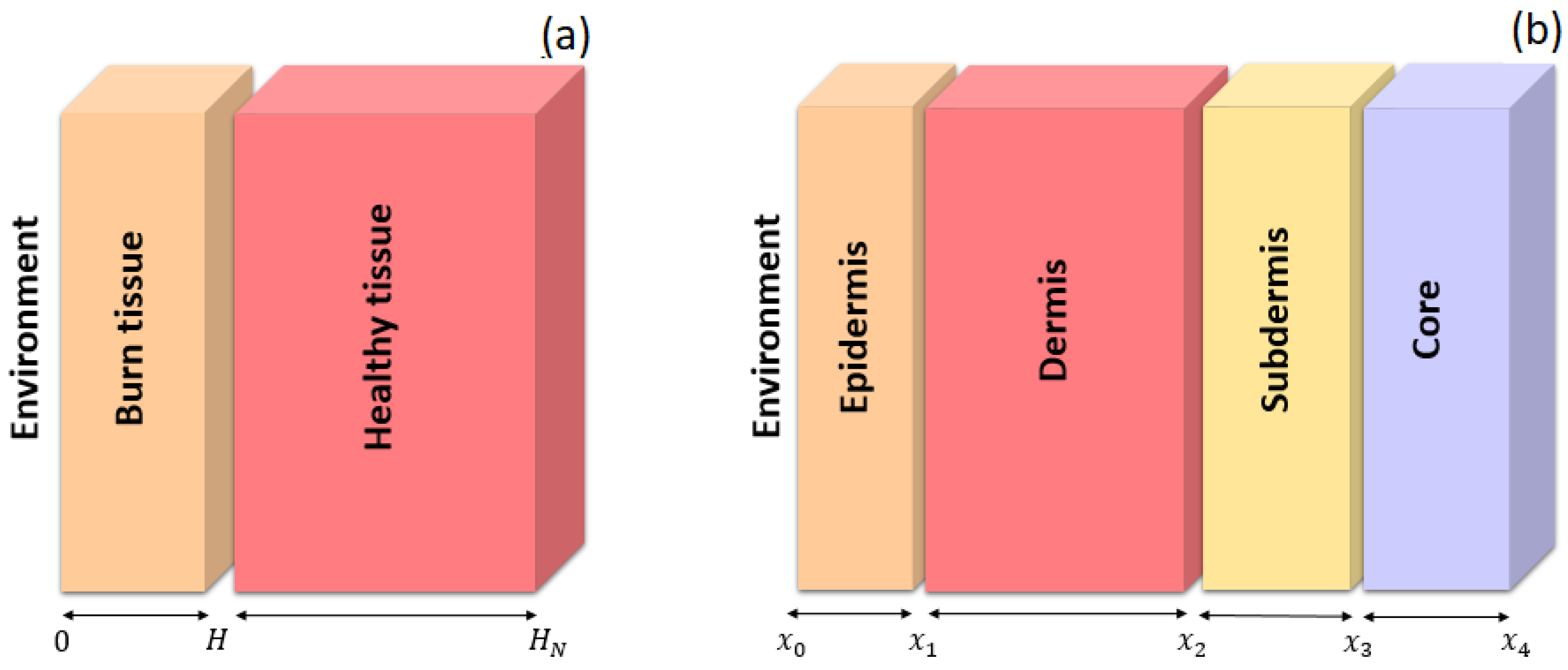
2.1. Burn Classification
2.2. The Pennes Bioheat Transfer Equation
2.3. Numerical Solution of Bioheat Transfer Equation
- A one-dimensional (1D) bilayer model;
- A one-dimensional (1D) multilayer model;
- A three-dimensional (3D) model.
- The boundary conditions for the two regions arewhere Equation (5) represents convective heat flux between the skin surface and the environment. The term corresponds to an external heat source, while a zero heat flux condition is applied at the remaining boundaries, as specified in Equation (8). Equation (6) defines the equality of flows at the interface between the burned tissue and the healthy tissue in order to comply with the conservation of energy at the border between both layers since physically there should not be an accumulation or loss of energy at the interface; likewise, Equation (7) defines that the temperature at the point of the border between tissues is unique and continuous. The initial condition corresponds to the steady-state solution associated with the problem, .
3. Results
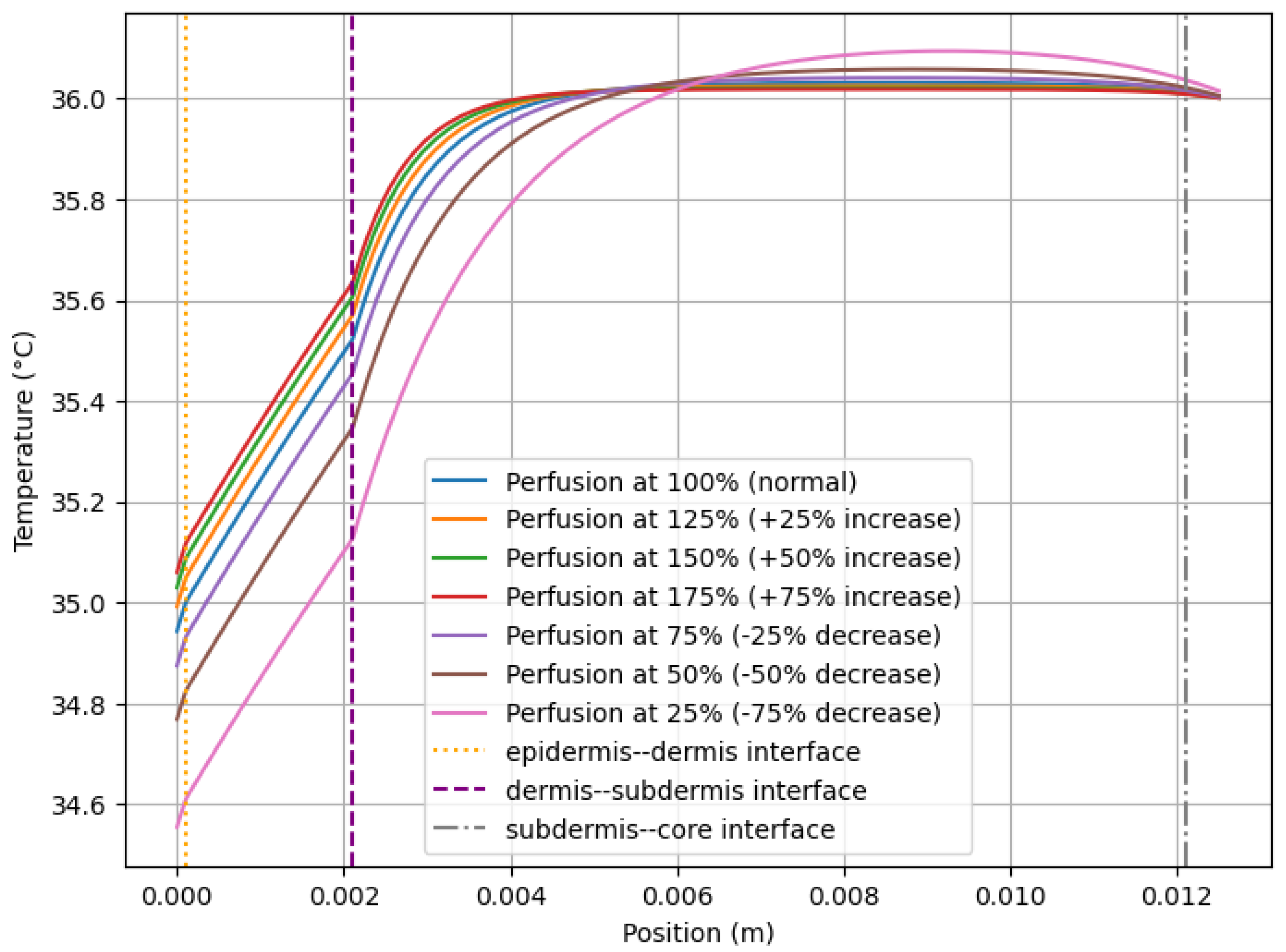
3.1. Effects of Perfusion on Skin Temperature
3.2. Numerical Solution in a 1D with and Without Immune Response (Steady-State)
3.3. Temperature Distribution in Multilayer Models for Different Types of Burns and Comparison with Thermographic Images
3.4. Numerical Transient Solution in a 1D Bilayer for a First-Degree Burn
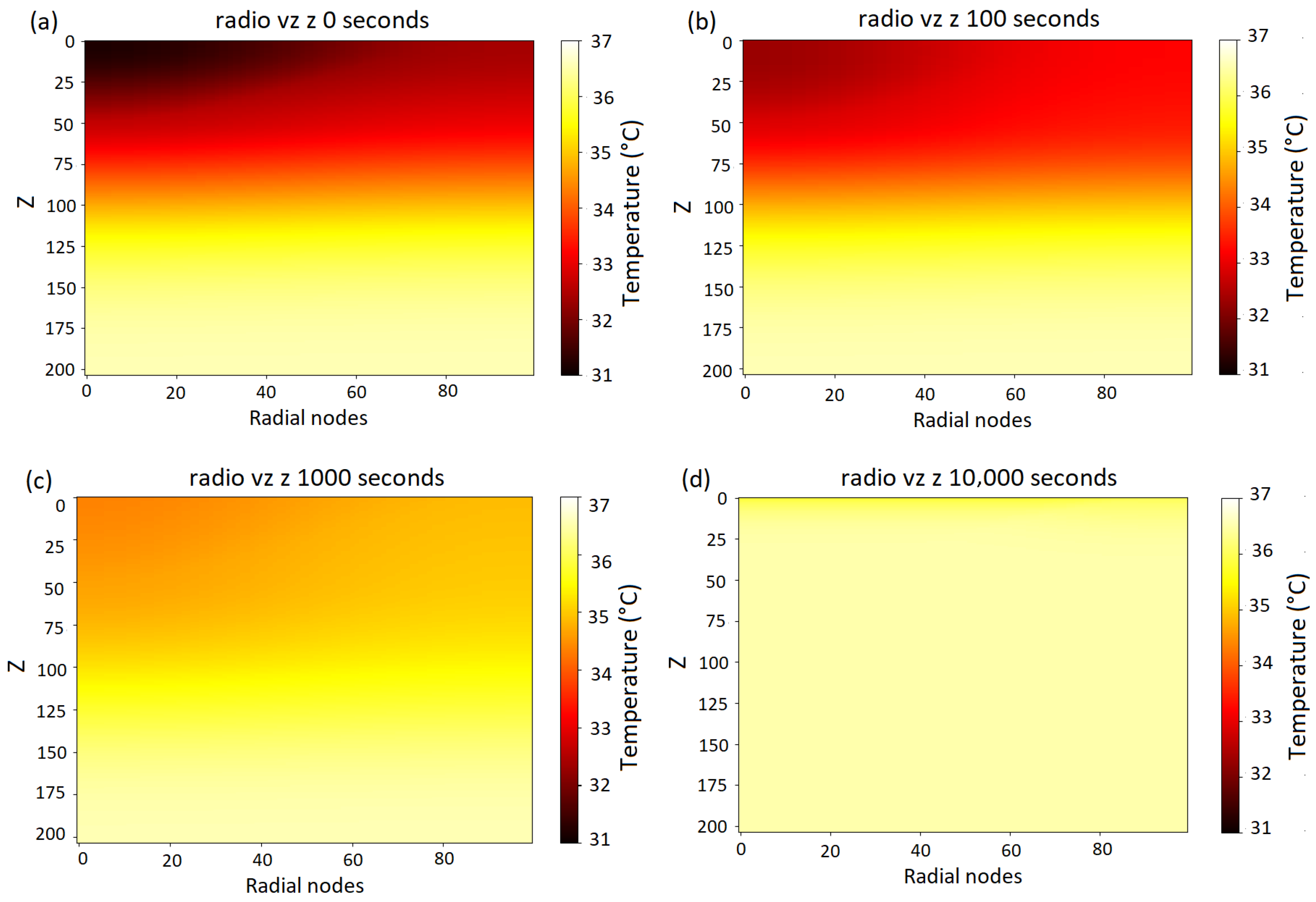
3.5. Numerical Solution in Three Dimensions for a First-Degree Burn
- 1.
- Initial Distribution: Temperature at s: In Figure 8a, the initial temperature distribution shows the presence of a colder region associated with the initial absence of metabolic heat and normal blood perfusion. Inside the uninjured tissue, the temperature values remain within the expected physiological range, approximately between 36.5 °C and 35 °C, on the skin surface; however, the temperature oscillates between 31 °C and 32.5 °C, as observed in the blue curve in Figure 9.
- 2.
- 3.
- Progressive Temperature Increase: Temperature at s: In Figure 8c, the temperature gradually homogenized throughout the bilayer. This process reduced the thermal gradient between the more superficial and deeper layers, raising the temperature. At this time step, a surface temperature between 34 °C and 35 °C is observed, represented by the green curve in Figure 9. Likewise, the internal temperature of the tissue oscillates between 34.2 °C and 37 °C, with the inner tissues having the highest temperature.
- 4.
- Thermal Homogenization in Advanced Stages: Temperature at s: Figure 8d shows a homogeneous temperature distribution within the tissue, along with an overall increase in temperature compared to previous time steps. Likewise, the surface temperature (represented by the pink curve in Figure 9) is close to 36 °C.
| Reference | Affection | Reported Temperature Behavior | Simulation Results |
|---|---|---|---|
| Figure 2A1 from [6] | First and second-degree superficial burns | A surface temperature range between 30 °C and 36.1 °C | Values were obtained from 35.4 °C for first-degree burns (yellow curve, Figure 6), 35.2 °C for superficial second-degree burns (green curve, Figure 6). Additionally, in Figure 9, an increase in surface temperature is observed from 31.0 to 32.4 °C up to 35.8 to 36.0 °C. |
| Figure 2B1,C1 from the reference [6] | Deep second-degree burn | Surface temperature reported between 25.3 °C and 32.8 °C | A value for the surface temperature of 32.1 °C shown in Figure 6 by the red curve. |
| Figure 2B1,C1 from the reference [6] | Third-degree burn | Surface temperature range of 18 °C–24 °C | A surface temperature of 23.6 was obtained °C (purple curve, Figure 6). |
| Table 2 in [50] | Inflammation/infection in the wound | An increase in temperature of 1.5 °C–2.3 °C was reported in cases of inflammation and of +4.5 °C in cases of infection | Figure 3, Figure 4 and Figure 5 show the temperature variations resulting from changes in blood perfusion and metabolic heat generation, which are associated with inflammation and infection processes. Figure 7 and Figure 8 show the increase in temperature of the burn over time. |
| Figure 1 in [10] | Healthy tissue | The thermographic image of a face is shown, where temperature differences can be observed due to variations in physiology and perfusion | Figure 3 shows the different temperature distributions resulting from the variability of blood perfusion. |
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Moore, K.L.; Dalley, A.F.; Agur, A.M.R. Anatomía con Orientación Clínica, 7th ed.; Wolters Kluwer: Barcelona, España, 2013. [Google Scholar]
- Żwierełło, W.; Piorun, K.; Skórka-Majewicz, M.; Maruszewska, A.; Antoniewski, J.; Gutowska, I. Burns: Classification, pathophysiology, and treatment: A review. Int. J. Mol. Sci. 2023, 24, 3749. [Google Scholar] [CrossRef]
- Smolle, C.; Cambiaso-Daniel, J.; Forbes, A.A.; Wurzer, P.; Hundeshagen, G.; Branski, L.K.; Huss, F.; Kamolz, L.P. Recent trends in burn epidemiology worldwide: A systematic review. Burns 2017, 43, 249–257. [Google Scholar] [CrossRef]
- Heimbach, D.; Engrav, L.; Grube, B.; Marvin, J. Burn depth: A review. World J. Surg. 1992, 16, 10–15. [Google Scholar] [CrossRef]
- Atiyeh, B.S.; Gunn, S.W.; Hayek, S.N. State of the art in burn treatment. World J. Surg. 2005, 29, 131–148. [Google Scholar] [CrossRef]
- Martínez-Jiménez, M.A.; Ramirez-GarciaLuna, J.L.; Kolosovas-Machuca, E.S.; Drager, J.; González, F.J. Development and validation of an algorithm to predict the treatment modality of burn wounds using thermographic scans: Prospective cohort study. PLoS ONE 2018, 13, e0206477. [Google Scholar] [CrossRef] [PubMed]
- Carrière, M.E.; de Haas, L.E.; Pijpe, A.; Meij-de Vries, A.; Gardien, K.L.; van Zuijlen, P.P.; Jaspers, M.E. Validity of thermography for measuring burn wound healing potential. Wound Repair Regen. 2020, 28, 347–354. [Google Scholar] [CrossRef] [PubMed]
- Dang, J.; Lin, M.; Tan, C.; Pham, C.H.; Huang, S.; Hulsebos, I.F.; Yenikomshian, H.; Gillenwater, J. Use of infrared thermography for assessment of burn depth and healing potential: A systematic review. J. Burn. Care Res. 2021, 42, 1120–1127. [Google Scholar] [CrossRef]
- Simmons, J.D.; Kahn, S.A.; Vickers, A.L.; Crockett, E.S.; Whitehead, J.D.; Krecker, A.K.; Lee, Y.L.; Miller, A.N.; Patterson, S.B.; Richards, W.O.; et al. Early assessment of burn depth with far infrared time-lapse thermography. J. Am. Coll. Surg. 2018, 226, 687–693. [Google Scholar] [CrossRef]
- Salazar-López, E.; Domínguez, E.; Ramos, V.J.; De la Fuente, J.; Meins, A.; Iborra, O.; Gálvez, G.; Rodríguez-Artacho, M.; Gómez-Milán, E. The mental and subjective skin: Emotion, empathy, feelings and thermography. Conscious. Cogn. 2015, 34, 149–162. [Google Scholar] [CrossRef] [PubMed]
- Avilés-García, Á.; López-Casanova, P.; Segura-Jordá, G.; Verdú-Soriano, J.; Berenguer-Pérez, M. Termografía infrarroja como método de diagnóstico en quemaduras: Una revisión exploratoria de la literatura. Gerokomos 2024, 35, 62–66. Available online: https://www.researchgate.net/publication/378766590_Termografia_infrarroja_como_metodo_de_diagnostico_en_quemaduras_una_revision_exploratoria_de_la_literatura#fullTextFileContent (accessed on 1 July 2024).
- Mason, B.; Graff, A.; Pegg, S. Colour thermography in the diagnosis of the depth of burn injury. Burns 1981, 7, 197–202. [Google Scholar] [CrossRef]
- Ng, E.; Tan, H.; Ooi, E. Boundary element method with bioheat equation for skin burn injury. Burns 2009, 35, 987–997. [Google Scholar] [CrossRef]
- Pennes, H.H. Analysis of tissue and arterial blood temperatures in the resting human forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef]
- Velázquez-Pérez, S.E. Solución analíTica de la Respuesta téRmica de Piel Quemada Expuesta a Una Energía de Radiación. Master’s Thesis, Universidad Autónoma de San Luis Potosí, Facultad de Ingeniería, Instituto de Metalurgia, San Luis Potosí, Mexico, 2011. [Google Scholar]
- Wang, Y.; Lu, X.; Zheng, W.; Wang, Z. Bio-thermal response and thermal damage in biological tissues with non-equilibrium effect and temperature-dependent properties induced by pulse-laser irradiation. J. Therm. Biol. 2023, 113, 103541. [Google Scholar] [CrossRef]
- Gupta, P.K.; Singh, J.; Rai, K. Numerical simulation for heat transfer in tissues during thermal therapy. J. Therm. Biol. 2010, 35, 295–301. [Google Scholar] [CrossRef]
- Durkee, J., Jr.; Antich, P.; Lee, C. Exact solutions to the multiregion time-dependent bioheat equation. II: Numerical evaluation of the solutions. Phys. Med. Biol. 1990, 35, 869. [Google Scholar] [CrossRef]
- Marin, M.; Hobiny, A.; Abbas, I. Finite element analysis of nonlinear bioheat model in skin tissue due to external thermal sources. Mathematics 2021, 9, 1459. [Google Scholar] [CrossRef]
- Trefilov, A.M.I.; Oane, M.; Duta, L. The Key Role of Thermal Relaxation Time on the Improved Generalized Bioheat Equation: Analytical Versus Simulated Numerical Approach. Materials 2025, 18, 3524. [Google Scholar] [CrossRef] [PubMed]
- Ali, L.; Apsari, R.; Abbas, A.; Tak, P. Entropy generation on the dynamics of volume fraction of nano-particles and coriolis force impacts on mixed convective nanofluid flow with significant magnetic effect. Numer. Heat Transf. Part A Appl. 2024, 1–16. [Google Scholar] [CrossRef]
- Weinbaum, S.; Jiji, L.; Lemons, D. Theory and experiment for the effect of vascular microstructure on surface tissue heat transfer—Part I: Anatomical foundation and model conceptualization. J. Biomech. Eng. 1984, 106, 321–330. [Google Scholar] [CrossRef]
- Khaled, A.R.; Vafai, K. The role of porous media in modeling flow and heat transfer in biological tissues. Int. J. Heat Mass Transf. 2003, 46, 4989–5003. [Google Scholar] [CrossRef]
- Becker, S.M.; Kuznetsov, A.V. Heat Transfer and Fluid Flow in Biological Processes; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar] [CrossRef]
- Singh, M. Modified Pennes bioheat equation with heterogeneous blood perfusion: A newer perspective. Int. J. Heat Mass Transf. 2024, 218, 124698. [Google Scholar] [CrossRef]
- Ferrás, L.L.; Ford, N.J.; Morgado, M.L.; Nóbrega, J.M.; Rebelo, M.S. Fractional Pennes’ bioheat equation: Theoretical and numerical studies. Fract. Calc. Appl. Anal. 2015, 18, 1080–1106. [Google Scholar] [CrossRef]
- Romeo, L.M.; Pastor, M.Á. Simulación del Comportamiento Térmico del Ser Humano. 2004. Available online: https://www.researchgate.net/publication/228838164_Simulacion_del_comportamiento_termico_del_ser_humano (accessed on 1 July 2024).
- Kolarsick, P.A.; Kolarsick, M.A.; Goodwin, C. Anatomy and physiology of the skin. J. Dermatol. Nurses Assoc. 2011, 3, 203–213. [Google Scholar] [CrossRef]
- Fu, M.; Weng, W.; Yuan, H. Numerical simulation of the effects of blood perfusion, water diffusion, and vaporization on the skin temperature and burn injuries. Numer. Heat Transf. Part A Appl. 2014, 65, 1187–1203. [Google Scholar] [CrossRef]
- Jiang, S.; Ma, N.; Li, H.; Zhang, X. Effects of thermal properties and geometrical dimensions on skin burn injuries. Burns 2002, 28, 713–717. [Google Scholar] [CrossRef]
- Lee, K.C.; Joory, K.; Moiemen, N.S. History of burns: The past, present and the future. Burn. Trauma 2014, 2, 2321–3868. [Google Scholar] [CrossRef] [PubMed]
- Papini, R. Management of burn injuries of various depths. BMJ 2004, 329, 158–160. [Google Scholar] [CrossRef]
- Acha, B.; Serrano, C.; Fondón, I.; Gómez-Cía, T. Burn depth analysis using multidimensional scaling applied to psychophysical experiment data. IEEE Trans. Med. Imaging 2013, 32, 1111–1120. [Google Scholar] [CrossRef] [PubMed]
- Lipkin, M.; Hardy, J.D. Measurement of some thermal properties of human tissues. J. Appl. Physiol. 1954, 7, 212–217. [Google Scholar] [CrossRef] [PubMed]
- Madhvapathy, S.R.; Arafa, H.M.; Patel, M.; Winograd, J.; Kong, J.; Zhu, J.; Xu, S.; Rogers, J.A. Advanced thermal sensing techniques for characterizing the physical properties of skin. Appl. Phys. Rev. 2022, 9, 041307. [Google Scholar] [CrossRef]
- Ezzat, M.A.; AlSowayan, N.S.; Al-Muhiameed, Z.I.; Ezzat, S.M. Fractional modelling of Pennes’ bioheat transfer equation. Heat Mass Transf. 2014, 50, 907–914. [Google Scholar] [CrossRef]
- Charny, C.K. Mathematical models of bioheat transfer. Adv. Heat Transf. 1992, 22, 19–155. [Google Scholar] [CrossRef]
- Yue, K.; Zhang, X.; Yu, F. An analytic solution of one-dimensional steady-state Pennes’ bioheat transfer equation in cylindrical coordinates. J. Therm. Sci. 2004, 13, 255–258. [Google Scholar] [CrossRef]
- Zhao, J.J.; Zhang, J.; Kang, N.; Yang, F. A two level finite difference scheme for one dimensional Pennes’ bioheat equation. Appl. Math. Comput. 2005, 171, 320–331. [Google Scholar] [CrossRef]
- Romero-Méndez, R.; Jiménez-Lozano, J.N.; Sen, M.; González, F.J. Analytical solution of the Pennes equation for burn-depth determination from infrared thermographs. Math. Med. Biol. A J. IMA 2010, 27, 21–38. [Google Scholar] [CrossRef][Green Version]
- Eymard, R.; Gallouët, T.; Herbin, R. Finite volume methods. Handb. Numer. Anal. 2000, 7, 713–1018. [Google Scholar] [CrossRef]
- Diller, K.R.; Hayes, L. A finite element model of burn injury in blood-perfused skin. J. Biomech Eng. 1983, 105, 300–307. [Google Scholar] [CrossRef]
- Moukalled, F.; Mangani, L.; Darwish, M. The finite volume method. In The Finite Volume Method in Computational Fluid Dynamics: An Advanced Introduction with OpenFOAM® and Matlab; Springer International Publishing: Gewerbestrasse, Cham, Switzerland, 2016; pp. 103–135. [Google Scholar] [CrossRef]
- Saptaningtyas, F.; Setyarsi, A. Finite Volume Method with Explicit Scheme Technique for Solving Heat Equation. J. Phys. Conf. Ser. 2018, 1097, 012089. [Google Scholar] [CrossRef]
- Dokos, S. Modelling Organs, Tissues, Cells and Devices: Using Matlab and Comsol Multiphysics; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Diller, K.R. Modeling thermal skin burns on a personal computer. J. Burn. Care Rehabil. 1998, 19, 420–429. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method, 2nd ed.; Pearson: London, UK, 2007. [Google Scholar]
- Liu, J.; Chen, X.; Xu, L.X. New thermal wave aspects on burn evaluation of skin subjected to instantaneous heating. IEEE Trans. Biomed. Eng. 1999, 46, 420–428. [Google Scholar] [CrossRef] [PubMed]
- Rabin, Y.; Stahovich, T.F. Cryoheater as a means of cryosurgery control. Phys. Med. Biol. 2003, 48, 619. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Fridberg, M.; Bafor, A.; Iobst, C.A.; Laugesen, B.; Jepsen, J.F.; Rahbek, O.; Kold, S. The role of thermography in assessment of wounds. A scoping review. Injury 2024, 55, 111833. [Google Scholar] [CrossRef] [PubMed]






| Parameter | Epidermis | Dermis | Subdermis |
|---|---|---|---|
| Layer thicknesses (m) | 0.0001 | 0.002 | 0.004 |
| Thermal conductivity () (W/m·K) | 0.3 | 0.4 | 0.19 |
| Blood perfusion (W) (kg/m3s) | 0 | 0.00125 | 0.0025 |
| Specific heat (C) (J/kg·K) | 3590 | 3300 | 2500 |
| Density () (kg/m3) | 1000 | 1000 | 1000 |
| Metabolic heat (Q) (W/m3) | 0 | 200 | 200 |
| Parameter | Layer 1 (Burned Region) | Layer 2 (Healthy Region) |
|---|---|---|
| Blood perfusion (W) | 0.5 kg/m3s | 0.5 kg/m3s |
| Specific heat (C) | 4200 J/kg·K | 4200 J/kg·K |
| Thermal conductivity () | 0.1 W/m·K | 0.2 W/m·K |
| Density () | 1000 kg/m3 | 1000 kg/m3 |
| Metabolic heat (Q) | 200 W/m3 | 200 W/m3 |
| Parameter | Epidermis | Dermis | Subdermis |
|---|---|---|---|
| Layer thicknesses (m) | 0.0001 | 0.002 | 0.004 |
| Thermal conductivity () (W/m·K) | 0.3 | 0.4 | 0.19 |
| Blood perfusion (W) (kg/m3s) | 0 | 0.001375 | 0.00275 |
| Specific heat (C) (J/kg·K) | 3590 | 3300 | 2500 |
| Density () (kg/m3) | 1000 | 1000 | 1000 |
| Metabolic heat (Q) (W/m3) | 0 | 200 | 500 |
| Parameter | Epidermis | Dermis | Subdermis |
|---|---|---|---|
| Layer thicknesses (m) | 0.0001 | 0.002 | 0.004 |
| Thermal conductivity () (W/m·K) | 0.3 | 0.4 | 0.19 |
| Blood perfusion (W) (kg/m3s) | 0 | 0.0015125 | 0.003025 |
| Specific heat (C) (J/kg·K) | 3590 | 3300 | 2500 |
| Density () (kg/m3) | 1000 | 1000 | 1000 |
| Metabolic heat (Q) (W/m3) | 0 | 200 | 600 |
| Type of Burn | () (% Change) | (W) (% Change) | (C) (% Change) | (Q) (% Change) |
|---|---|---|---|---|
| First-degree | +10% to +20% | +50% to 100% | +10% | + 30% to 60% |
| Second-degree (superficial) | 0% | +30% to 70% | +10% to +20% | +10% to 30% |
| Second-degree (deep) | −10% to −50% | −30% to −90% | −40% to −80% | −70% |
| Third-degree | −50% to −80% | −100% (0% flow) | −80% to −100% | −100% (null metabolic heat) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez-Pérez, A.S.; Gilardi-Velázquez, H.E.; Velázquez-Pérez, S.E. Analysis and Simulation of Dynamic Heat Transfer and Thermal Distribution in Burns with Multilayer Models Using Finite Volumes. Dynamics 2025, 5, 41. https://doi.org/10.3390/dynamics5040041
Rodríguez-Pérez AS, Gilardi-Velázquez HE, Velázquez-Pérez SE. Analysis and Simulation of Dynamic Heat Transfer and Thermal Distribution in Burns with Multilayer Models Using Finite Volumes. Dynamics. 2025; 5(4):41. https://doi.org/10.3390/dynamics5040041
Chicago/Turabian StyleRodríguez-Pérez, Adriana Sofia, Héctor Eduardo Gilardi-Velázquez, and Stephanie Esmeralda Velázquez-Pérez. 2025. "Analysis and Simulation of Dynamic Heat Transfer and Thermal Distribution in Burns with Multilayer Models Using Finite Volumes" Dynamics 5, no. 4: 41. https://doi.org/10.3390/dynamics5040041
APA StyleRodríguez-Pérez, A. S., Gilardi-Velázquez, H. E., & Velázquez-Pérez, S. E. (2025). Analysis and Simulation of Dynamic Heat Transfer and Thermal Distribution in Burns with Multilayer Models Using Finite Volumes. Dynamics, 5(4), 41. https://doi.org/10.3390/dynamics5040041






