Comparison of Alternative Port-Hamiltonian Dynamics Extensions to the Thermodynamic Domain Toward IDA-PBC-Like Control: Application to a Heat Transfer Model

Abstract

The dynamics of port-Hamiltonian systems is based on energy balance principles (the first law of thermodynamics) embedded in the structure of the model. However, when dealing with thermodynamic subsystems, the second law (entropy production) should also be explicitly taken into account. Several frameworks were developed as extensions to the thermodynamic domain of port-Hamiltonian systems. In our work, we study three of them, namely irreversible port-Hamiltonian systems, entropy-based generalized Hamiltonian systems, and entropy-production-metric-based port-Hamiltonian systems, which represent alternative approaches of selecting the state variables, the storage function, simplicity of physical interpretation, etc. On the example of a simplified lumped-parameter model of a heat exchanger, we study the frameworks in terms of their implementability for an IDA-PBC-like control and the simplicity of using these frameworks for practitioners already familiar with the port-Hamiltonian systems. The comparative study demonstrated the possibility of using each of these approaches to derive IDA-PBC-like thermodynamically consistent control and provided insight into the applicability of each framework for the modeling and control of multiphysics systems with thermodynamic subsystems.

1. Introduction

The port-Hamiltonian (PH) framework is a powerful tool for the modeling, analysis, and control of physical systems grounded on energy exchange and formulated in terms of energy-based gradient dynamics. It is based on the principles of Hamiltonian mechanics but was naturally generalized to other energy domains, thus covering a wide class of physical systems across different domains [1]. Port-Hamiltonian systems (PHS) cover multiphysical systems as well, using the concept of energy as a link between different energy domains. The PHS form a powerful mathematical foundation for developing energy-based control paradigms; among them, the most influential ones are control by interconnection and passivity-based interconnection and damping assignment passivity-based control (IDA-PBC) [2]. The latter approach is mathematically simpler to understand and has been successfully applied to the control of various systems with differing levels of complexity. PH-based control can be extended using traditional PID control [3], optimal control [4], adaptive control [5], etc.

PH systems guarantee consistency with the first law of thermodynamics by explicitly preserving energy balance. For dissipative effects, the port-Hamiltonian systems (PHS) framework is typically well-suited for mechanical or electrical systems, but it is less effective for classes of systems that exhibit nonlinear dynamics in terms of dissipation, entropy production, etc. Such systems require compliance with entropy production constraints required by the second law. These systems are often coupled to other energy domains, such as electrical, mechanical, hydraulic, etc., where PH framework has already shown considerable success, in particular, with IDA-PBC. Consequently, these systems could benefit from the generalization of modeling and control approaches developed within the PHS framework.

Examples of such systems include battery systems [6,7], fuel cell systems [8,9], hybrid energy storages [10], thermal management systems for electric motors [11], recuperators in hybrid vehicles [12], waste heat recovery systems [13], trigeneration and polygeneration systems [14,15], concentrated solar power plants [15], hybrid PV-thermal systems [16], heat pumps [17], etc.

Dealing with such kinds of systems requires a reformulation of the PHS framework to explicitly account for both the first and the second laws. In particular, PHS are based on the Hamiltonian (total energy) function as a storage function, and the gradient dynamics is formulated in terms of the total-energy gradient; for thermodynamic systems, a different storage function can be chosen, namely Gibbs free energy [18,19], entropy [20,21,22,23], enthalpy [24], internal entropy production [25,26,27], internal energy [28,29,30,31], and second-order deviation of the entropy production metric [32,33,34].

Such formulations lead to modified formulations of control for this class of systems; however, in many cases, they can be routed to the control paradigms already developed for the traditional PHS. Thus, Makkar and Dieulot [19] develop IDA-PBC-like control for the continuous chemical reactor in the PH formulation, taking Gibbs free energy as the storage function. Hoang et al. [21] use Hamiltonian formulation and IDA-PBC control of non-isothermal continuous stirred tank reactors with its dynamics formulated in terms of entropy gradient dynamics, while, for the target system, an availability function gradient is used, which allows the system to be driven to the desired equilibrium [20]. Ramírez and co-authors thoroughly develop the theory of irreversible port-Hamiltonian systems (IPHS) based on internal energy as a storage function; they generalize their approach to cover different applications and implement different control strategies, including IDA-PBC-like control [35] with the target system formulated in terms of the energy-based availability function. Dong, Li, and co-authors develop the extended-state passivity-based control by using the second-order deviation of entropy production metric as a storage function with applications to high-temperature gas-cooled reactors [32] and methane steam reforming [33].

In addition to these extensions, there exist more general theoretical frameworks that seek to integrate irreversible processes and thermodynamics into Hamiltonian mechanics. Yoshimura and Gay-Balmaz [36,37] in their works return to the original variational roots of Lagrangian and Hamiltonian mechanics to represent non-equilibrium thermodynamics. De León and Bajo [38] obtain similar evolution equations by using the geometric description. Parallel to these, the GENERIC formalism of Grmela and Öttinger [39,40] and the metriplectic dynamics pioneered by Morrison [41,42] provide alternative structure-preserving formulations of non-equilibrium thermodynamics.

Therefore, the problem of handling irreversible dynamics within the PH-like framework is nontrivial and leads to different control formulations. To the best of our knowledge, no systematic review of these frameworks has been performed. In the current study, we address this gap, but, given the complexity of the problem, we limit ourselves to developing IDA-PBC-like control for a thermodynamic system based on the simplified lumped parameter model of a heat exchanger (HEX) as a representative case of irreversible thermodynamic systems that was first analyzed in [43]. The use of this model narrows the scope of the work to a heat-transfer system, while neglecting spatial temperature gradients, mass transfer, chemical reactions, and other phenomena that can be covered by the frameworks.

Among the different approaches to generalize PHS, we select three, namely:

• The IPHS framework [43] as the one most theoretically developed among the others, with a huge number of publications devoted to the development of control strategies, including IDA-PBC-like control [29];
• The entropy-based generalized Hamiltonian (EBGH) framework [26], which provides a framework for modeling and not proposing control. Here, entropy is taken as a storage function, as several earlier approaches proposed [20,21,22];
• The entropy-production-metric-based PHS ($\epsilon$-PHS) framework [32], a recently emerged prospective one, with only a couple of applications [32,33]; however, in these works, control is not formulated in the form of IDA-PBC-like control.

Here, we should make a small remark about the naming. Although IPHS is a term that the authors use for their framework in their original work, the authors of the other two provide no terms to outline the features of their frameworks. The terms EBGH and $\epsilon$-PHS are proposed by the authors of the current study.

Our objective is to formulate practically implementable and theoretically sound approaches to structure-preserving control of HEX and to gain insight into those approaches, their implementability, and the possibility of achieving the objectives of control (to stabilize the system exactly at the desired equilibrium) and to analyze the impact of the free parameters of the derived control law. We also assume that the success of the framework is also measured by how simple it can be for practitioners to develop control strategies; keeping this in mind, we limit ourselves to the classic IDA-PBC form [44]; in particular, the algebraic form of obtaining the IDA-PBC solution, i.e., the desired storage function is fixed.

The rest of the paper is organized as follows. In Section 2, a mathematical and computer model of the object of the study is depicted. Section 4, Section 5 and Section 6 are devoted to the three frameworks with the same structure of subsections: first, the framework theory is depicted in general; then, it is applied to the HEX to obtain the model of the object; next, the control law is derived based on the obtained model; the section ends with simulations and discussions. Section 7 contains a comparative analysis of the three frameworks, and Section 8 concludes.

2. Object of the Study

2.1. Mathematical Model

We consider a simplified two-compartment HEX lumped-parameter model, neglecting the spatial temperature gradient (Figure 1). The compartments are thermally isolated, except that compartment 2 exchanges heat with an ideally controlled external heat source at temperature $T_{\mathrm{e}}$. Heat transfer is governed by Fourier’s law with the constant heat conductance and constant heat capacities. The model assumes purely conductive heat transfer with no phase change, chemical reactions, or mass or volume changes.

Due to its simplicity, the model is often utilized as a suitable case study for modeling and control purposes [28,43,45,46].

The dynamics of the system is governed by the Equations [43]:

$$\begin{array}{l}{\dot{s}}_1={\displaystyle \frac{\lambda }{T_1}}\left(T_2-T_1\right),\\ {\dot{s}}_2={\displaystyle \frac{\lambda }{T_2}}\left(T_1-T_2\right)+{\displaystyle \frac{{\lambda }_{\mathrm{e}}}{T_2}}\left(T_{\mathrm{e}}-T_2\right)\end{array}$$

(1)

where $s_1$ and $s_2$ are the entropies and $T_1$ and $T_2$ are the temperatures of the compartments 1 and 2, respectively, $T_{\mathrm{e}}$ is the temperature of the external heat source, and $\lambda$ and ${\lambda }_{\mathrm{e}}$ are heat conductance between the compartments and between compartment 2 and the external heat source.

Model (1) is used as an initial form for the three frameworks. However, the three frameworks use slight reformulations of Equation (1), though those are related to the selection of state variables and co-variables and the transformation to matrix form. Thus, the IPHS framework uses entropies as state variables and temperatures as co-variables; the EBGH framework uses internal energies as state variables and reverse temperatures as co-variables; and the $\epsilon$-PHS framework uses temperature deviations from the equilibrium as state variables and more complex expression for co-variables. The transitions from one set of state variables to another are based on the known thermodynamic relations connecting entropy $s$, temperature $T$, gas mass $m$, gas heat capacity $c_v$, internal energy $U$, and heat flow $\dot{Q}$. The transformations of the model (1) are explained in the corresponding sections; here, we only emphasize that the three frameworks are based on the same initial mathematical formulations of the heat exchange process.

2.2. Computer Model for Simulation Studies

Control strategies are verified using the computer model developed in the Matlab R2021b Simscape environment (Figure 2) as a thermal network containing two Thermal Mass blocks representing the two compartments, two Conductive Heat Transfer blocks responsible for modeling inner and external conductive walls described by the Fourier law, a Controlled Temperature Source block representing the external temperature source, and two Temperature Sensor blocks. For further calculations, Conductive Heat Transfer blocks provide information about the heat flow rate using the Simscape Results Explorer. The control law is implemented using a MATLAB Function block. In Figure 2, the two Thermal Mass blocks Compartment 1 and Compartment 2 are set to represent a constant thermal mass during simulation, and the Conductive Heat Transfer blocks Conductive Wall (inner) and Conductive Wall (external) are set to constant thermal conductivity.

The actual value of the entropy production rate within the HEX is calculated using the general thermodynamic relations as ${\sigma }_{12}={\dot{Q}}_{12}\left({\displaystyle \frac{1}{T_1}}-{\displaystyle \frac{1}{T_2}}\right)$, where the values of temperatures and the heat flow rate between the compartments are obtained from the corresponding Simscape blocks using Simscape Results Explorer.

In our simulations, we assume 1 kg of air in each compartment, separated by an aluminum wall. An identical wall separates compartment 2 from the external heat source. The particular parameters are provided in

Table 1. System parameters used for simulation studies.

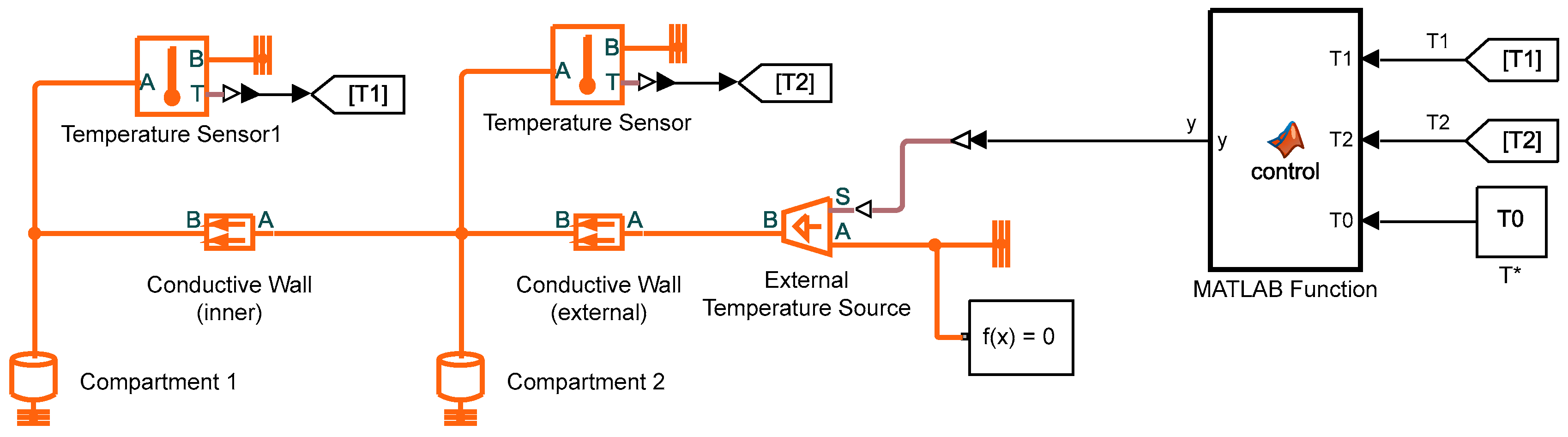
Parameter	Value
Compartments
$\mathrm{Gas} \mathrm{mass} \mathrm{in} \mathrm{the} \mathrm{two} \mathrm{compartments}, m_1=m_2$	1 kg
$\mathrm{Gas} \mathrm{heat} \mathrm{capacity}, c_{v1}=c_{v2}$	500 J/(K·kg)
Conductive walls
$\mathrm{Contact} \mathrm{area}, A$	10 cm2
$\mathrm{Wall} \mathrm{thickness}, d$	1 cm
$\mathrm{Wall} \mathrm{thermal} \mathrm{conductivity}, k$	50 W/(m·K)
$\mathrm{Internal} \mathrm{wall} \mathrm{heat} \mathrm{conductance}, \lambda =kA/d$	50 W/K
$\mathrm{External} \mathrm{wall} \mathrm{heat} \mathrm{conductance}, {\lambda }_{\mathrm{e}}$	50 W/K
Initial temperature
$\mathrm{Initial} \mathrm{temperature} \mathrm{in} \mathrm{compartment} 1, T_{10}$	343 K
$\mathrm{Initial} \mathrm{temperature} \mathrm{in} \mathrm{compartment} 2, T_{20}$	323 K
$\mathrm{Desired} \mathrm{equilibrium} \mathrm{temperature}, T^{\ast }$	293 K

. Such parameters of the conductive walls as contact area $A$, wall thickness $d$, and wall thermal conductivity $k$ (here, its value is taken as for aluminum) are defined to assess realistic wall heat conductance, as demonstrated in the table.

The free parameters of the control expressions are used as variables in the Simulink model, which enables their manipulation from the external Matlab script developed to run the simulations with several free parameter values. The obtained results are transferred to the Matlab Workspace using the Simscape Results Explorer with further visualization in one plot to study their influence on the system’s behavior.

3. Port-Hamiltonian Systems and IDA-PBC

The basic structural element of PHS is the Hamiltonian (total energy) that serves as a storage function that drives the gradient dynamics. The structure matrices depict energy flow between the different energy domains; in the theory of Hamiltonian mechanics, they represent the Poisson bracket operator and depict conservation laws for the open system. Thus, in PH form, the system dynamics is governed by the following equations:

$$\begin{array}{l}\dot{\mathbf{x}}=\left(\mathbf{J}\left(\mathbf{x}\right)-\mathbf{R}\left(\mathbf{x}\right)\right)\nabla H\left(\mathbf{x}\right)+\mathbf{G}\left(\mathbf{x}\right)\mathbf{u},\\ \mathbf{y}=\mathbf{G}{\left(\mathbf{x}\right)}^{\top }\nabla H\left(\mathbf{x}\right),\end{array}$$

(2)

where $\mathbf{x}\left(t\right)\in {\mathbb{R}}^n$ is the state vector of state variables, $H\left(\mathbf{x}\right):{\mathbb{R}}^n\to \mathbb{R}$ is the Hamiltonian (total energy) function, $\nabla H\left(\mathbf{x}\right)={\displaystyle \frac{\partial H\left(\mathbf{x}\right)}{\partial \mathbf{x}}}$ is the vector of partial derivatives of $H$ (energy-conjugated variables of $\mathbf{x}$), $\mathbf{J}\left(\mathbf{x}\right)\in {\mathbb{R}}^{n\times n}$ and $\mathbf{R}\left(\mathbf{x}\right)\in {\mathbb{R}}^{n\times n}$ are square interconnection and damping matrices, respectively, with their structure dictated by physical principles and mathematical requirements to ensure different kinds of dynamics; thus, the interconnection matrix represents conservative dynamics and is skew-symmetric ${\mathbf{J}}^{\top }=-\mathbf{J}$, and the dissipation matrix represents dissipation dynamics and is symmetric positive ${\mathbf{R}}^{\top }=\mathbf{R}\ge 0$; $\mathbf{u}\left(t\right)\in {\mathbb{R}}^m$ is the control vector (in general, $m\ne n$), $\mathbf{G}\left(\mathbf{x}\right)\in {\mathbb{R}}^{m\times n}$ is the input matrix, and $\mathbf{y}\left(t\right)\in {\mathbb{R}}^m$ is the output vector. Here and in the following, arguments are omitted where possible for simplicity.

The structure of matrices $\mathbf{R}$ and $\mathbf{J}$ ensures compliance with the energy balance law (first law of thermodynamics) by ensuring the physical consistency of equality:

$$\dot{H}\left(\mathbf{x}\right)=-\nabla H^{\mathrm{\top }}\mathbf{R}\nabla H+{\mathbf{y}}^{\mathrm{\top }}\mathbf{u},$$

(3)

with the first term in (3) corresponding to energy dissipation and the second to external input power. This implies the inequality

$$\nabla H^{\top }\mathbf{R}\nabla H\ge 0.$$

(4)

The interconnection and damping assignment passivity-based control (IDA-PBC) method aims to assign a new interconnection and damping structure along with a desired energy function to achieve desired closed-loop behavior; i.e., the target (closed-loop) dynamics takes the form

$$\dot{\mathbf{x}}=\left({\mathbf{J}}_{\mathrm{d}}\left(\mathbf{x}\right)-{\mathbf{R}}_{\mathrm{d}}\left(\mathbf{x}\right)\right)\nabla H_{\mathrm{d}}\left(\mathbf{x}\right),$$

(5)

where ${\mathbf{J}}_{\mathrm{d}}$ and ${\mathbf{R}}_{\mathrm{d}}$ are the desired interconnection and damping matrices, respectively, with the same requirements for their structure as it is for $\mathbf{J}$ and $\mathbf{R}$; $H_{\mathrm{d}}$ is the desired storage function, which should satisfy:

$$\begin{array}{l}\nabla H_{\mathrm{d}}\left({\mathbf{x}}^{\ast }\right)=0,\\ {\nabla }^2{H}_{\mathrm{d}}\left({\mathbf{x}}^{\ast }\right)\ge 0.\end{array}$$

(6)

These ensure that the desired Hamiltonian function has a minimum at the desired equilibrium ${\mathbf{x}}^{\ast }$.

$H_{\mathrm{d}}\left(\mathbf{x}\right)$ is non-increasing over time, i.e.,

$${\dot{H}}_{\mathrm{d}}\left(\mathbf{x}\right)=-\nabla H_{\mathrm{d}}^{\top }{\mathbf{R}}_{\mathrm{d}}\nabla H_{\mathrm{d}}\le 0$$

(7)

and ${\dot{H}}_{\mathrm{d}}\left(\mathbf{x}\right)=0$ only for $\mathbf{x}={\mathbf{x}}^{\ast }$ to ensure asymptotic stability.

Control $\mathbf{u}=\mathsf{\beta }\left(\mathbf{x}\right)$ ensuring the closed-loop dynamics (5) can be obtained by equating the corresponding right-hand sides of Equations (2) and (5):

$$\left(\mathbf{J}-\mathbf{R}\right)\nabla H+\mathbf{G}\mathsf{\beta }=\left({\mathbf{J}}_{\mathrm{d}}-{\mathbf{R}}_{\mathrm{d}}\right)\nabla H_{\mathrm{d}}.$$

(8)

Solving (7), by $\mathsf{\beta }$, the solution can be obtained in the form [44]

$$\mathsf{\beta }\left(\mathbf{x}\right)={\left({\mathbf{G}}^{\mathit{\top }}\mathbf{G}\right)}^{-1}{\mathbf{G}}^{\mathit{\top }}\left(\left({\mathbf{J}}_{\mathrm{d}}-{\mathbf{R}}_{\mathrm{d}}\right)\nabla H_{\mathrm{d}}-\left(\mathbf{J}-\mathbf{R}\right)\nabla H\right);$$

(9)

the latter is correct if the following condition is satisfied:

$${\mathbf{G}}^{\perp }\left({\mathbf{J}}_{\mathrm{d}}-{\mathbf{R}}_{\mathrm{d}}\right)\nabla H_{\mathrm{d}}-{\mathbf{G}}^{\perp }\left(\mathbf{J}-\mathbf{R}\right)\nabla H=0,$$

(10)

where ${\mathbf{G}}^{\perp }$ is a left full rank annihilator of $\mathbf{G}$, i.e., ${\mathbf{G}}^{\perp }\mathbf{G}=0$. This is known as the matching equation, which is used to check the correctness of the selection of matrices for the control derivation. The details of the control design can be found in [44].

Interconnection and damping matrices can be written in the following form:

$${\mathbf{J}}_{\mathrm{d}}=\mathbf{J}+{\mathbf{J}}_{\mathrm{a}}\mathrm{and} {\mathbf{R}}_{\mathrm{d}}=\mathbf{R}+{\mathbf{R}}_{\mathrm{a}}$$

implying that in the target system, added interconnection ${\mathbf{J}}_{\mathrm{a}}$ and damping ${\mathbf{R}}_{\mathrm{a}}$ are assigned.

The Port-Hamiltonian framework has been implemented to a wide range of complex multiphysics systems; however, the thermodynamic systems cannot be depicted by these equations, as far as they should ensure physical consistency not only for the first law (i.e., energy balance) but also for the second law (nonnegative entropy production). Several generalizations of the port-Hamiltonian framework have been proposed to ensure the appropriate representation of the irreversible phenomena.

4. Irreversible Port-Hamiltonian Systems Framework

4.1. Theory

One of the approaches to extend a port-Hamiltonian system framework to thermodynamic systems is the irreversible port-Hamiltonian systems (IPHS) framework [43]. According to this approach, the dynamics of the system is represented in a slightly modified form of (2) as

$$\begin{array}{l}\dot{\mathbf{x}}=R\left(\mathbf{x},\nabla U,\nabla S\right)\mathbf{J}\left(\mathbf{x}\right)\nabla U\left(\mathbf{x}\right)+\mathbf{G}\left(\mathbf{x},\nabla U\right)\mathbf{u},\\ \mathbf{y}=\mathbf{G}{\left(\mathbf{x}\right)}^{\top }\nabla U\left(\mathbf{x}\right),\end{array}$$

(11)

and the extended form of the first Equation in (11)

$$\dot{\mathbf{x}}=\gamma \left(\mathbf{x},\nabla U\right){\left\{S,U\right\}}_{\mathbf{J}}\mathbf{J}\left(\mathbf{x}\right)\nabla U\left(\mathbf{x}\right)+\mathbf{G}\left(\mathbf{x},\nabla U\right)\mathbf{u},$$

(12)

with $\mathbf{x}\in {\mathbb{R}}^n$, the state vector, and two functions, $U\left(\mathbf{x}\right):{\mathbb{R}}^n\to \mathbb{R}$, the internal energy (the Hamiltonian) function and $S\left(\mathbf{x}\right):{\mathbb{R}}^n\to \mathbb{R}$, the entropy function, and the corresponding vectors of energy-conjugated $\nabla U\left(\mathbf{x}\right)$ and entropy-conjugated $\nabla S\left(\mathbf{x}\right)$ co-variables; $\mathbf{J}\left(\mathbf{x}\right)$ represents the skew-symmetric interconnection matrix, like in conventional port-Hamiltonian systems, although here it is modulated by the nonlinear modulating function $R\left(\mathbf{x},\nabla U,\nabla S\right)=\gamma \left(\mathbf{x},\nabla U\right){\left\{S,U\right\}}_{\mathbf{J}}$, a product of a positive function $\gamma \left(\mathbf{x},\nabla U\right):{\mathbb{R}}^n\to \mathbb{R}$ (with $\gamma \ge 0$) and the Poisson brackets between the energy and the entropy functions ${\left\{S,U\right\}}_{\mathbf{J}}=\nabla S^{\top }\left(\mathbf{x}\right)\mathbf{J}\left(\mathbf{x}\right)\nabla U\left(\mathbf{x}\right)$, defining the thermodynamic driving force of the irreversible phenomena in the system. The modulating function $R\left(\mathbf{x},\nabla U,\nabla S\right)$ is nonlinear because the Poisson brackets ${\left\{S,U\right\}}_{\mathbf{J}}$ appear explicitly in its definition, making the function dependent on the states and co-states.

To formulate an analog of IDA-PBC for IPHS, Ref. [28] defines an energy-based availability function:

$$A\left(\mathbf{x},{\mathbf{x}}^{\ast }\right)=U\left(\mathbf{x}\right)-U\left({\mathbf{x}}^{\ast }\right)-\nabla U{\left({\mathbf{x}}^{\ast }\right)}^{\top }\left(\mathbf{x}-{\mathbf{x}}^{\ast }\right)\ge 0$$

(13)

as a Lyapunov function candidate that has a global minimum in the desired equilibrium state ${\mathbf{x}}^{\ast }$. This is ensured for monophasic thermodynamic systems if one of the extensive variables is fixed [28].

The desired closed-loop IPHS dynamics (the target system) is formulated as follows [28,29]:

$$\dot{\mathbf{x}}=(-{\sigma }_{\mathrm{d}}\mathbf{M}+R_{\mathrm{d}}{\mathbf{J}}_{\mathrm{d}})\nabla A,$$

(14)

where $R_{\mathrm{d}}={\gamma }_{\mathrm{d}}{\left\{S,A\right\}}_{{\mathbf{J}}_{\mathrm{d}}}$ and ${\mathbf{J}}_{\mathrm{d}}$ are the desired modulating function and interconnection matrix, respectively, with the modulating function being dependent on the Poisson brackets ${\left\{S,A\right\}}_{{\mathbf{J}}_{\mathrm{d}}}$ which defines a thermodynamic driving force of the target system, and ${\gamma }_{\mathrm{d}}\ge 0$ is the desired positive function; the symmetric positive semi-definite matrix $\mathbf{M}\left(\mathbf{x}\right)\ge 0$ is responsible for the irreversible dynamics, and ${\sigma }_{\mathrm{d}}={\gamma }_{\mathrm{d}}{\left\{S,A\right\}}_{{\mathbf{J}}_{\mathrm{d}}}^2\ge 0$ is the desired entropy production rate.

The dissipation function is given as

$$s={\sigma }_{\mathrm{d}}{\left[A,A\right]}_{\mathbf{M}}\ge 0,$$

(15)

where ${\left[A,A\right]}_{\mathbf{M}}=\nabla A^{\top }\mathbf{M}\nabla A$ is the Ginzburg–Landau bracket used in the GENERIC framework to define the dissipative dynamics [39].

For IPHS, the control formulation in terms of an analogue of IDA-PBC is obtained in the same way as (8) is derived [29]:

$$\mathsf{\beta }\left(\mathbf{x},{\mathbf{x}}^{\ast }\right)={\left({\mathbf{G}}^{\mathrm{\top }}\mathbf{G}\right)}^{-1}{\mathbf{G}}^{\mathrm{\top }}\left(R_{\mathrm{d}}{\mathbf{J}}_{\mathrm{d}}-{\sigma }_{\mathrm{d}}\mathbf{M}\right)\left(\nabla U\left(\mathbf{x}\right)-\nabla U\left({\mathbf{x}}^{\ast }\right)\right)-{\left({\mathbf{G}}^{\mathrm{\top }}\mathbf{G}\right)}^{-1}{\mathbf{G}}^{\mathrm{\top }}R\mathbf{J}\nabla U\left(\mathbf{x}\right).$$

(16)

The matching Equation becomes

$${\mathbf{G}}^{\perp }\left(R_{\mathrm{d}}{\mathbf{J}}_{\mathrm{d}}-{\sigma }_{\mathrm{d}}\mathbf{M}\right)\left(\nabla U\left(\mathbf{x}\right)-\nabla U\left({\mathbf{x}}^{\ast }\right)\right)-{\mathbf{G}}^{\perp }R\mathbf{J}\nabla U\left(\mathbf{x}\right)=0,$$

(17)

which is often (with a slight loss of generality) converted to a set of conditions such as [29]

$${\mathbf{G}}^{\perp }\mathbf{M}=0 \mathrm{and} {\mathbf{G}}^{\perp }\mathbf{J}=0 \mathrm{and} {\mathbf{G}}^{\perp }{\mathbf{J}}_{\mathrm{d}}=0,$$

or [35]

$${\mathbf{G}}^{\perp }\mathbf{M}=0 \mathrm{and} {\mathbf{G}}^{\perp }\mathbf{J}\nabla U\left({\mathbf{x}}^{\ast }\right)=0.$$

4.2. Application to HEX

The HEX model using the IPHS approach has already been formulated in [43]. Thus, Equation (1) is rewritten in the IPHS form as:

$$\left[\begin{array}{c}{\dot{s}}_1\\ {\dot{s}}_2\end{array}\right]={\displaystyle \frac{\lambda }{T_1{T}_2}}\left(T_1-T_2\right)\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]\left[\begin{array}{c}{T}_1\\ T_2\end{array}\right]+\left[\begin{array}{c}0\\ {\lambda }_{\mathrm{e}}{\displaystyle \frac{T_{\mathrm{e}}-T_2}{T_{\mathrm{e}}{T}_2}}\end{array}\right]T_{\mathrm{e}},$$

(18)

where the state vector is $\mathbf{x}={\left[\begin{array}{cc}{s}_1& s_2\end{array}\right]}^{\top }$; the Hamiltonian function is the sum of the internal energies of the two compartments $U\left(\mathbf{x}\right)=U_1\left(s_1\right)+U_2\left(s_2\right)$; the co-energy variables $\nabla U\left(\mathbf{x}\right)={\left[\begin{array}{cc}{T}_1& T_2\end{array}\right]}^{\top }$ represent the temperatures of the compartments; the input of the system corresponds to the temperature of the external heat source $T_{\mathrm{e}}$; the interconnection matrix is $\mathbf{J}=\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]$; the total entropy function is given as $S\left(\mathbf{x}\right)=s_1+s_2$; the Poisson bracket

$${\left\{S,U\right\}}_{\mathbf{J}}=\nabla S^{\top }\mathbf{J}\nabla U=T_1-T_2,$$

i.e., the temperature difference is the driving force of heat conduction; the modulating function

$$R=\gamma {\left\{S,U\right\}}_{\mathbf{J}}={\displaystyle \frac{\lambda }{T_1{T}_2}}\left(T_1-T_2\right),$$

(19)

therefore, the relations of irreversible phenomena are described by the function $\gamma ={\displaystyle \frac{\lambda }{T_1{T}_2}}$. In (18), input $u=T_{\mathrm{e}}$, and input matrix $\mathbf{G}=\left[\begin{array}{c}0\\ {\lambda }_{\mathrm{e}}{\displaystyle \frac{T_{\mathrm{e}}-T_2}{T_{\mathrm{e}}{T}_2}}\end{array}\right]$.

4.3. Control Law Derivation

To derive the control law, we use the target dynamics formulation given in (14) and the gradient of the availability function is:

$$\nabla A\left(\mathbf{x},{\mathbf{x}}^{\ast }\right)=\nabla U\left(\mathbf{x}\right)-\nabla U\left({\mathbf{x}}^{\ast }\right)=\left[\begin{array}{c}{T}_1-T^{\ast }\\ T_2-T^{\ast }\end{array}\right].$$

(20)

This implies that equilibrium is achieved when both temperatures equal $T^{\ast }$; therefore, the Poisson brackets

$${\left\{S,A\right\}}_{{\mathbf{J}}_{\mathrm{d}}}=T_1-T^{\ast }-\left(T_2-T^{\ast }\right)=T_1-T_2$$

imply that temperature difference is still the driving force of heat conduction; the nonlinear function ${\gamma }_{\mathrm{d}}={\displaystyle \frac{{\lambda }_{\mathrm{d}}}{T_1{T}_2}}$ repeats the one for an open-loop system; the modulation function and a desired entropy production rate are, therefore,

$$R_{\mathrm{d}}={\gamma }_{\mathrm{d}}{\left\{S,A\right\}}_{{\mathbf{J}}_{\mathrm{d}}}={\displaystyle \frac{{\lambda }_{\mathrm{d}}}{T_1{T}_2}}\left(T_1-T_2\right),$$

(21)

$${\sigma }_{\mathrm{d}}={\gamma }_{\mathrm{d}}{\left\{S,A\right\}}_{{\mathbf{J}}_{\mathrm{d}}}^2={\displaystyle \frac{{\lambda }_{\mathrm{d}}}{T_1{T}_2}}{\left(T_1-T_2\right)}^2.$$

(22)

The first of them is of the same form as the modulating function of the uncontrolled HEX but with $\lambda$ changed to ${\lambda }_{\mathrm{d}}$. The second equation, entropy production rate, can be interpreted in the same way.

The target dynamics is

$$\dot{\mathbf{x}}=\left(-{\displaystyle \frac{{\lambda }_{\mathrm{d}}}{T_1{T}_2}}{\left(T_1-T_2\right)}^2\mathbf{M}+{\displaystyle \frac{{\lambda }_{\mathrm{d}}}{T_1{T}_2}}\left(T_1-T_2\right){\mathbf{J}}_{\mathrm{d}}\right)\left[\begin{array}{c}{T}_1-T^{\ast }\\ T_2-T^{\ast }\end{array}\right],$$

(23)

with free parameters ${\lambda }_{\mathrm{d}}$, $\mathbf{M}$, and ${\mathbf{J}}_{\mathrm{d}}$. The fourth free parameter is the annihilator matrix ${\mathbf{G}}^{\perp }$, that can also be utilized to satisfy the conditions (17) [29]. For the matrix $\mathbf{G}$ as in (18), let ${\mathbf{G}}^{\perp }=\left[\begin{array}{cc}1& 0\end{array}\right]$. For our case, it is convenient to formulate the matching conditions (17) as

$$\begin{array}{r}{\mathbf{G}}^{\perp }\mathbf{M}=0,\\ {\mathbf{G}}^{\perp }{R}_{\mathrm{d}}{\mathbf{J}}_{\mathrm{d}}\left(\nabla U\left(\mathbf{x}\right)-\nabla U\left({\mathit{x}}^{\ast }\right)\right)-{\mathbf{G}}^{\perp }R\mathbf{J}\nabla U\left(\mathbf{x}\right)=0.\end{array}$$

(24)

The matching condition in the IDA-PBC design can help in selecting the appropriate form of free parameters, as well as it can be used to assess the limitations of the design. In our case, the formulated matching conditions (24) have a twofold purpose. Thus, to satisfy the first condition in (24), and the positive and definite conditions for the matrix $\mathbf{M}$, its structure should be $\mathbf{M}=\left[\begin{array}{cc}0& 0\\ 0& m_{22}\end{array}\right]$. From the second condition in (24), selecting ${\mathbf{J}}_{\mathrm{d}}=\mathbf{J}$, we obtain

$${\displaystyle \frac{\lambda \left(T_1-T_2\right)}{T_1}}-{\displaystyle \frac{{\lambda }_{\mathrm{d}}\left(T^{\ast }-T_2\right)\left(T_1-T_2\right)}{T_1{T}_2}}=0$$

(25)

which can be rewritten as ${\lambda }_{\mathrm{d}}=-{\displaystyle \frac{\lambda T_2}{T^{\ast }-T_2}}$. This equation can be misleading if we try to use it to obtain the ${\lambda }_{\mathrm{d}}$ value; thus, when moving to thermodynamic equilibrium $T_1=T_2=T^{\ast }$, ${\lambda }_{\mathrm{d}}$ should increase to infinity. However, we can use this equation to assess the limitations of the control design: assess the admissible relationship between the temperatures with the given ${\lambda }_{\mathrm{d}}$. Thus, since for thermodynamic consistency, ${\lambda }_{\mathrm{d}}>0$, then $T_2>T^{\ast }$, which is the limitation for the control.

The dissipation function of the target dynamics is

$$s={\sigma }_{\mathrm{d}}{\left[A,A\right]}_{\mathbf{M}}={\displaystyle \frac{{\lambda }_{\mathrm{d}}{m}_{22}}{T_1{T}_2}}{\left(T_1-T_2\right)}^2{\left(T^{\ast }-T_2\right)}^2.$$

(26)

From (26), $s\ge 0$ and $s=0$ if $T_1=T_2=T^{\ast }$, which is thermodynamically consistent.

The solution, the expression of the particular form of the external input temperature, is obtained by solving Equation (16):

$$T_{\mathrm{e}}=T_2-{\displaystyle \frac{\lambda }{{\lambda }_{\mathrm{e}}}}\left(T_1-T_2\right)-{\lambda }_{\mathrm{d}}{\displaystyle \frac{\left(T^{\ast }-T_1\right)\left(T_1-T_2\right)}{{\lambda }_{\mathrm{e}}{T}_1}}+m_{22}{\lambda }_{\mathrm{d}}{\displaystyle \frac{\left(T^{\ast }-T_2\right){\left(T_1-T_2\right)}^2}{{\lambda }_{\mathrm{e}}{T}_1}}.$$

(27)

4.4. Simulations and Discussions

The expression for the IPHS-based control (27) contains two free parameters, ${\lambda }_{\mathrm{d}}$ and $m_{22}$. Our analysis of the expression stats with those parameters set to zero. It can be easily demonstrated that in this case, (27) is reduced to the stabilization of $T_2$ while the external heat flow compensates for the one from the compartment 1 as is confirmed by the simulations (Figure 3) which are maintained using the computer model (Figure 2).

The terms with free parameters in (27) correspond to the nonlinear state-dependent feedback with the nonlinear gains depending on the temperature difference between the two compartments. The next simulations were held fixing $m_{22}=10$ while impact of ${\lambda }_{\mathrm{d}}$ is studied (Figure 4), and fixing ${\lambda }_{\mathrm{d}}=10$ while impact of $m_{22}$ is studied (Figure 5). According to (26), these two free parameters appear in the form in which they act similarly on the target dynamic, which is confirmed by Figure 4 and Figure 5. Since the dissipation function (26) depends on the squares of the temperature difference between the two compartments and the deviation of $T_2$ from the equilibrium, the greater the differences, the greater the dissipation. Dissipation vanishes when one of those differences decreases to zero; in an ideal case, for ${T_1=T}_2=T^{\ast }$, but that can be also be for ${T_1=T}_2\ne T^{\ast }$, i.e., the system can be driven to some thermodynamic equilibrium, not necessarily to the desired one. An increase in $m_{22}$ (similarly, for ${\lambda }_{\mathrm{d}}$) leads to the decrease of steady-state error and the transient time, but, at the same time, it requires the drop of $T_{\mathrm{e}}$ at the initial phase of the transient (Figure 4 and Figure 5).

An important point regarding the IPHS-based control law is the physical meaning of the desired entropy production rate (22). We performed simulations with ${\lambda }_{\mathrm{d}}=10$ and $m_{22}=15$ and compared the values of the entropy production rate calculated using the simulated temperatures and heat flow as explained in Section 3 and the normalized desired entropy production rate ${\sigma }_{\mathrm{d}}\lambda / {\lambda }_{\mathrm{d}}$ (Figure 6). These are the same values. Therefore, in the IPHS framework, the desired entropy production rate corresponds to some desired virtual HEX model with the desired thermal conductance ${\lambda }_{\mathrm{d}}$ between the compartments.

5. Entropy-Based Generalized Hamiltonian Framework

5.1. Theory

The second framework used to connect the port-Hamiltonian formalism and thermodynamic phenomena is the entropy-based generalized Hamiltonian (EBGH) framework [26]. The following summary is based on derivations from this reference starting with the equation representing some dynamical system including the thermal phenomena:

$$\dot{\mathsf{\eta }}=\mathbf{M}f\left(\mathsf{\eta }\right)+\mathbf{G}\left(\mathsf{\eta },{\mathsf{\eta }}_{\mathrm{s}}\right)\mathbf{F},$$

(28)

where $\mathsf{\eta }\in {\mathbb{R}}^n$ is the state variable vector (which here contains $n$ extensive quantities), ${\mathsf{\eta }}_{\mathrm{s}}\in {\mathbb{R}}^s$ represents the surrounding, and $f\left(\mathsf{\eta }\right)$ is the vector field of internal forces ${\mathbb{R}}^n\to {\mathbb{R}}^p$, where $p$ is the number of phenomena characterizing the dynamics of the system. $\mathbf{M}\in {\mathbb{R}}^{n\times p}$ is the internal phenomenon interconnection matrix, $\mathbf{F}\in {\mathbb{R}}^m$ is the external flow vector (accounting for exchange with the surrounding), and $\mathbf{G}\left(\mathsf{\eta },{\mathsf{\eta }}_{\mathrm{s}}\right)$ is the vector field of interconnections with surrounding via the flows $\mathbf{F}$.

Introducing the entropy function $S\left(\mathsf{\eta }\right)$ as a storage function, and the entropy gradient vector, i.e., the vector of entropy-conjugated variables, $\mathsf{\zeta }=\nabla S\left(\mathsf{\eta }\right)\in {\mathbb{R}}^n$ containing intensive variables, (28) is transformed into the form reproducing the port-Hamiltonian-like structure:

$$\begin{array}{l}\dot{\mathsf{\eta }}=\left(\mathbf{R}+\mathbf{J}\right)\mathsf{\Psi }\left(\mathsf{\zeta }\right){\mathbf{L}}^{\top }\mathsf{\zeta }+\mathbf{G}\left(\mathsf{\eta },{\mathsf{\eta }}_{\mathrm{s}}\right)\mathbf{F},\\ \mathbf{y}={\mathbf{G}}^{\mathbf{\top }}\left(\mathsf{\eta },{\mathsf{\eta }}_{\mathrm{s}}\right)\mathsf{\zeta },\end{array}$$

(29)

which can be obtained simply from (28) by introducing matrices $\mathbf{R}$, $\mathbf{J}$, $\mathsf{\Psi }\left(\mathsf{\zeta }\right)$, and $\mathbf{L}$ so that

$$\begin{array}{l}f\left(\mathsf{\eta }\right)=\mathsf{\Psi }\left(\mathsf{\zeta }\right){\mathbf{L}}^{\top }\mathsf{\zeta },\\ \mathbf{M}=\mathbf{R}+\mathbf{J}.\end{array}$$

These matrices have a clear interpretation in terms of thermodynamics; thus, ${\mathbf{L}}^{\top }\mathsf{\zeta }$ are driving forces of the system, with $\mathbf{L}\in {\mathbb{R}}^{p\times n}$, the constant driving force matrix that maps the entropy gradients to flows; $\mathsf{\Psi }\left(\mathsf{\zeta }\right)\in {\mathbb{R}}^{p\times p}$ is symmetric positive definite matrix that maps generalized forces into flows and defines the dissipation rate and generalizes the Onsager conductivity matrix for nonlinear driving forces. Within the EBGH framework, constant matrices $\mathbf{R}$ and $\mathbf{J}$ are utilized to depict irreversible and reversible phenomena, as will be demonstrated below.

While (29) is the entropy-based version of Equation (2) depicting the PHS, the entropy-based analog of the energy rate Equation (3) is

$$\dot{S}={\left(\nabla S\left(\mathsf{\eta }\right)\right)}^{\top }\mathbf{R}\mathsf{\Psi }\left(\mathsf{\zeta }\right){\mathbf{L}}^{\mathrm{\top }}\nabla S\left(\mathsf{\eta }\right)+{\mathbf{F}}^{\top }\mathbf{y},$$

(30)

with the first term being related to internal entropy production and the second to the one related to inputs.

Matrix $\mathbf{R}$ is associated with phenomena that produce entropy and matrix $\mathbf{J}$, with reversible phenomena. The thermodynamic consistency is ensured by the structure conditions derived in [26]:

$$\begin{array}{l}\mathbf{R}\mathsf{\Psi }\left(\mathsf{\zeta }\right){\mathbf{L}}^{\top }=\mathbf{L}{\mathsf{\Psi }}^{\mathbf{\top }}\left(\mathsf{\zeta }\right){\mathbf{R}}^{\mathbf{\top }}\ge 0,\\ \mathbf{J}\mathsf{\Psi }\left(\mathsf{\zeta }\right){\mathbf{L}}^{\top }=-\mathbf{L}{\mathsf{\Psi }}^{\mathbf{\top }}\left(\mathsf{\zeta }\right){\mathbf{J}}^{\mathbf{\top }},\end{array}$$

(31)

where $\mathbf{R}\mathsf{\Psi }\left(\mathsf{\zeta }\right){\mathbf{L}}^{\top }$ corresponds to the irreversible structure and $\mathbf{J}\mathsf{\Psi }\left(\mathsf{\zeta }\right){\mathbf{L}}^{\top }$ to reversible structure and the number of non-zero eigenvalues of the matrices is equal to the number of irreversible and reversible phenomena, respectively. These conditions are similar to those for matrices $\mathbf{R}$ and $\mathbf{J}$ in classic PH theory (see Section 3).

Note that the framework uses an approach for representing the system dynamic in a different form as compared to the classic port-Hamiltonian approach summed up in Section 3. However, it is based on Hamiltonian function and can be used not only for modeling purposes but also for control.

In the original work [26], the scope is modeling technique as well as the stability analysis [25], while the control topic is not covered; however, the analog of IDA-PBC control can be formulated as follows. Assume the target system within the EBGH framework as

$$\dot{\mathsf{\eta }}=\left({\mathbf{R}}_{\mathrm{d}}+{\mathbf{J}}_{\mathrm{d}}\right){\mathsf{\Psi }}_{\mathrm{d}}\left(\mathsf{\zeta }\right){\mathbf{L}}^{\top }{\mathsf{\zeta }}_{\mathrm{d}},$$

(32)

and the control as

$$\mathsf{\beta }\left(\mathsf{\eta }\right)={\left({\mathbf{G}}^{\mathit{\top }}\mathbf{G}\right)}^{-1}{\mathbf{G}}^{\mathit{\top }}\left(\left({\mathbf{R}}_{\mathrm{d}}+{\mathbf{J}}_{\mathrm{d}}\right){\mathsf{\Psi }}_{\mathrm{d}}\left(\mathsf{\zeta }\right){\mathbf{L}}^{\mathbf{\top }}{\mathsf{\zeta }}_{\mathrm{d}}-\left(\mathbf{R}+\mathbf{J}\right)\mathsf{\Psi }\left(\mathsf{\zeta }\right){\mathbf{L}}^{\mathit{\top }}\mathsf{\zeta }\right),$$

(33)

where the index “d” corresponds to the matrices and vectors of the desired system.

5.2. Application to HEX

To derive the HEX model using the EBGH formalism, we will start with (28); the first step is to select the state vector, a set of extensive variables. In this case, these are internal energies $\mathsf{\eta }={\left[\begin{array}{cc}{U}_1& U_2\end{array}\right]}^{\top }$ as recommended in [26]. Thus, (1) is rewritten as

$$\begin{array}{l}{\dot{U}}_1=\lambda \left(T_2-T_1\right),\\ {\dot{U}}_2=\lambda \left(T_1-T_2\right)+{\dot{Q}}_{\mathrm{e}},\end{array}$$

(34)

where ${\dot{Q}}_{\mathrm{e}}={\lambda }_{\mathrm{e}}\left(T_{\mathrm{e}}-T_2\right)$ is external heat flow. Equation (34) fits the representation (28):

$$\left[\begin{array}{c}{\dot{U}}_1\\ {\dot{U}}_2\end{array}\right]=\left[\begin{array}{c}1\\ -1\end{array}\right]\lambda \left(T_2-T_1\right)+\left[\begin{array}{c}0\\ 1\end{array}\right]{\dot{Q}}_{\mathrm{e}},$$

(35)

with $\mathbf{M}=\left[\begin{array}{c}1\\ -1\end{array}\right]$, $f\left(\mathsf{\eta }\right)=\lambda \left(T_2-T_1\right)$, $\mathbf{G}=\left[\begin{array}{c}0\\ 1\end{array}\right]$, and $\mathbf{F}={\dot{Q}}_{\mathrm{e}}$. Therefore, the number of extensive variables $n=2$, and number of irreversible processes $p=1$, the heat conduction between the two compartments.

The entropy function for system (35) is the sum of entropies of the compartments:

$$S\left(\mathsf{\eta }\right)=s_1+s_2,$$

therefore, the gradient vector, $\mathsf{\zeta }=\nabla S\left(\mathsf{\eta }\right)={\left[\begin{array}{cc}{\nabla }_{U_1}S\left(\mathsf{\eta }\right)& {\nabla }_{U_2}S\left(\mathsf{\eta }\right)\end{array}\right]}^{\mathrm{\top }}={\left[\begin{array}{cc}{\displaystyle \frac{1}{T_1}}& {\displaystyle \frac{1}{T_2}}\end{array}\right]}^{\mathrm{\top }}$.

The matrix $\mathbf{L}$ can be identified by searching for conditions when $f\left(\mathsf{\eta }\right)=0$; in most physical cases, these conditions are ${\mathbf{L}}^{\mathrm{\top }}\mathsf{\zeta }=0$ [26]. Thus, if $f\left(\mathsf{\eta }\right)=\lambda \left(T_2-T_1\right)=0$, that means $T_2=T_1$, and the driving force matrix is identified as $\mathbf{L}=\left[\begin{array}{c}1\\ -1\end{array}\right]$, and the driving force is

$${\mathbf{L}}^{\top }\mathsf{\zeta }={\displaystyle \frac{1}{T_1}}-{\displaystyle \frac{1}{T_2}}.$$

Therefore, the Onsager conductivity matrix is identified as $\mathsf{\Psi }=\lambda T_1{T}_2$ to match the physical flow $f\left(\mathsf{\eta }\right)$:

$$\mathsf{\Psi }{\mathbf{L}}^{\top }\mathsf{\zeta }=\lambda \left(T_2-T_1\right)=f\left(\mathsf{\eta }\right).$$

Given that $\mathbf{M}=\mathbf{R}+\mathbf{J}$, the constant matrices are selected as $\mathbf{R}=\left[\begin{array}{c}1\\ -1\end{array}\right]$ and $\mathbf{J}=\left[\begin{array}{c}0\\ 0\end{array}\right]$ so that conditions (31) are fulfilled:

$$\begin{gathered} \mathbf{R}\mathsf{\Psi }\left(\mathsf{\zeta }\right){\mathbf{L}}^{\mathrm{\top }}=\left[\begin{array}{cc}\lambda T_1{T}_2& -\lambda T_1{T}_2\\ -\lambda T_1{T}_2& \lambda T_1{T}_2\end{array}\right]=\mathbf{L}{\mathsf{\Psi }}^{\mathbf{\top }}\left(\mathsf{\zeta }\right){\mathbf{R}}^{\mathbf{\top }}\ge 0, \\ \mathbf{J}\mathsf{\Psi }\left(\mathsf{\zeta }\right){\mathbf{L}}^{\top }=0_{2\times 2}=-\mathbf{L}{\mathsf{\Psi }}^{\mathbf{\top }}\left(\mathsf{\zeta }\right){\mathbf{J}}^{\mathbf{\top }}. \end{gathered}$$

(36)

Matrix $\mathbf{R}\mathsf{\Psi }\left(\mathsf{\zeta }\right){\mathbf{L}}^{\mathrm{\top }}$ has two eigenvalues, $\left\{\mathrm{0,2}\lambda T_1{T}_2\right\}$, and one non-zero among them indicating one irreversible phenomenon, heat conduction, while $\mathbf{J}\mathsf{\Psi }\left(\mathsf{\zeta }\right){\mathbf{L}}^{\mathrm{\top }}$ has zero eigenvalues indicating no reversible phenomena, which matches the physical interpretation; and the internal entropy production is

$${\dot{S}}_{\mathrm{i}\mathrm{n}\mathrm{t}}={\mathsf{\zeta }}^{\top }\mathbf{R}\mathsf{\Psi }\left(\mathsf{\zeta }\right){\mathbf{L}}^{\mathrm{\top }}\mathsf{\zeta }=\lambda T_1{T}_2{\left({\displaystyle \frac{1}{T_2}}-{\displaystyle \frac{1}{T_1}}\right)}^2.$$

(37)

It is worth noting that in the EBGH framework, the mathematical description of more complex systems containing not only thermodynamic but also the other subsystems, leads to complex co-variables definitions, as demonstrated in the examples provided in the original publication [26]. This is the limitation of the framework, and it can be the limitation for its applications to complex multiphysics systems.

5.3. Control Law Based on a Thermodynamic Availability Function

Above, in (32) and (33) related to IDA-PBC-like control within the EBGH framework, the gradient vector ${\mathsf{\zeta }}_{\mathrm{d}}$ was not explained in terms of the storage function used to represent the target system. Here, assume that the gradient of the target dynamics is driven by the availability function defined as [20]:

$$A\left(\mathsf{\eta },{\mathsf{\eta }}^{\ast }\right)=S\left(\mathsf{\eta }\right)-S\left({\mathsf{\eta }}^{\ast }\right)-\nabla S{\left({\mathsf{\eta }}^{\ast }\right)}^{\top }\left(\mathsf{\eta }-{\mathsf{\eta }}^{\ast }\right)\ge 0.$$

(38)

Therefore, it can be simply demonstrated that

$${\mathsf{\zeta }}_{\mathrm{d}}=\nabla A\left(\mathsf{\eta },{\mathsf{\eta }}^{\ast }\right)=\nabla S\left(\mathsf{\eta }\right)-\nabla S\left({\mathsf{\eta }}^{\ast }\right)=\left[\begin{array}{c}{\displaystyle \frac{1}{T_1}}-{\displaystyle \frac{1}{T^{\ast }}}\\ {\displaystyle \frac{1}{T_2}}-{\displaystyle \frac{1}{T^{\ast }}}\end{array}\right],$$

(39)

and the added elements of (29) representing the target system are selected as

$${\mathbf{R}}_{\mathrm{a}}=\left[\begin{array}{c}r\\ -r\end{array}\right], {\mathbf{J}}_{\mathrm{a}}=\left[\begin{array}{c}0\\ 0\end{array}\right], \mathrm{and} {\mathsf{\Psi }}_{\mathrm{a}}\left({\mathsf{\zeta }}_{\mathrm{d}}\right)=\psi T_1{T}_2.$$

Therefore, the driving force of the system is

$${\mathbf{L}}^{\top }{\mathsf{\zeta }}_{\mathrm{d}}={\displaystyle \frac{1}{T_1}}-{\displaystyle \frac{1}{T_2}};$$

(40)

it is again the difference of inverse temperatures, and conditions (31)

$$\begin{gathered} {\mathbf{R}}_{\mathrm{d}}{\mathsf{\Psi }}_{\mathrm{d}}\left({\mathsf{\zeta }}_{\mathrm{d}}\right){\mathbf{L}}^{\mathrm{\top }}=\left[\begin{array}{cc}\left(r+1\right)T_1{T}_2\left(\psi +\lambda \right)& -\left(r+1\right)T_1{T}_2\left(\psi +\lambda \right)\\ -\left(r+1\right)T_1{T}_2\left(\psi +\lambda \right)& \left(r+1\right)T_1{T}_2\left(\psi +\lambda \right)\end{array}\right]=\mathbf{L}{{\mathsf{\Psi }}_{\mathrm{d}}}^{\mathbf{\top }}\left({\mathsf{\zeta }}_{\mathrm{d}}\right){{\mathbf{R}}_{\mathrm{d}}}^{\mathbf{\top }}\ge 0, \\ {\mathbf{J}}_{\mathrm{d}}{\mathsf{\Psi }}_{\mathrm{d}}\left({\mathsf{\zeta }}_{\mathrm{d}}\right){\mathbf{L}}^{\mathrm{\top }}=0_{2\times 2}=\mathbf{L}{{\mathsf{\Psi }}_{\mathrm{d}}}^{\mathbf{\top }}\left({\mathsf{\zeta }}_{\mathrm{d}}\right){{\mathbf{J}}_{\mathrm{d}}}^{\mathbf{\top }} \end{gathered}$$

(41)

are also satisfied. Eigenvalues of ${\mathbf{R}}_{\mathrm{d}}{\mathsf{\Psi }}_{\mathrm{d}}\left({\mathsf{\zeta }}_{\mathrm{d}}\right){\mathbf{L}}^{\mathrm{\top }}$ are $\left\{0,2T_1{T}_2\left(r+1\right)\left(\psi +\lambda \right)\right\}$, and ${\mathbf{J}}_{\mathrm{d}}{\mathsf{\Psi }}_{\mathrm{d}}\left({\mathsf{\zeta }}_{\mathrm{d}}\right){\mathbf{L}}^{\mathrm{\top }}$ has zero eigenvalues, implying no changes in reversible–irreversible phenomena; the internal entropy production of the target system is

$${\dot{S}}_{\mathrm{i}\mathrm{n}\mathrm{t}}={{\mathsf{\zeta }}_{\mathrm{d}}}^{\top }{\mathbf{R}}_{\mathrm{d}}{\mathsf{\Psi }}_{\mathrm{d}}\left({\mathsf{\zeta }}_{\mathrm{d}}\right){\mathbf{L}}^{\mathrm{\top }}{\mathsf{\zeta }}_{\mathrm{d}}=\left(\psi +\lambda \right)\left(r+1\right)T_1{T}_2{\left({\displaystyle \frac{1}{T_2}}-{\displaystyle \frac{1}{T_1}}\right)}^2.$$

(42)

The law of change of the input variable is obtained by solving (33), and with

$${\dot{Q}}_{\mathrm{e}}=\mathsf{\beta }\left(\mathsf{\eta }\right)={\lambda }_{\mathrm{e}}\left(T_{\mathrm{e}}-T_2\right),$$

the expression of the control law is obtained in the following form:

$$T_{\mathrm{e}}=T_2-{\displaystyle \frac{\lambda }{{\lambda }_{\mathrm{e}}}}\left(T_1-T_2\right)+{\displaystyle \frac{\left(r+1\right)\left(\psi +\lambda \right)}{{\lambda }_{\mathrm{e}}}}{T}_1{T}_2\left({\displaystyle \frac{1}{T_2}}-{\displaystyle \frac{1}{T_1}}\right).$$

(43)

5.4. Modified Control Law

Observe that the derived control law (43) contains no explicit expression for the desired equilibrium, $T^{\ast }$ (neither is the internal entropy production rate (42)). In fact, by comparing the internal entropy production rate (37) and (42), it can be seen that the derived control changes the thermal conduction from $\lambda$ to $\left(\psi +\lambda \right)\left(r+1\right)$.

One possible approach is to break the symmetry in the gradient variables for the target system. Thus, the weighted entropy function can be selected as a weighted sum of the entropies of the two compartments

$$S_{\mathrm{w}}\left(\mathsf{\eta }\right)={\alpha }_1{s}_1+{\alpha }_2{s}_2,$$

(44)

where ${\alpha }_i$ are the weights and the weighted availability function, correspondingly,

$$A_{\mathrm{w}}\left(\mathsf{\eta },{\mathsf{\eta }}^{\ast }\right)=S_{\mathrm{w}}\left(\mathsf{\eta }\right)-S_{\mathrm{w}}\left({\mathsf{\eta }}^{\ast }\right)-\nabla S_{\mathrm{w}}{\left({\mathsf{\eta }}^{\ast }\right)}^{\top }\left(\mathsf{\eta }-{\mathsf{\eta }}^{\ast }\right)\ge 0,$$

(45)

and the gradient vector,

$${\mathsf{\zeta }}_{\mathrm{d}}=\nabla A_{\mathrm{w}}\left(\mathsf{\eta },{\mathsf{\eta }}^{\ast }\right)=\nabla S_{\mathrm{w}}\left(\mathsf{\eta }\right)-\nabla S_{\mathrm{w}}\left({\mathsf{\eta }}^{\ast }\right)=\left[\begin{array}{c}{\alpha }_1\left({\displaystyle \frac{1}{T_1}}-{\displaystyle \frac{1}{T^{\ast }}}\right)\\ {\alpha }_2\left({\displaystyle \frac{1}{T_2}}-{\displaystyle \frac{1}{T^{\ast }}}\right)\end{array}\right].$$

(46)

The matrices ${\mathbf{R}}_{\mathrm{a}}$, ${\mathbf{J}}_{\mathrm{a}}$, and ${\mathsf{\Psi }}_{\mathrm{a}}\left({\mathsf{\zeta }}_{\mathrm{d}}\right)$ remain unchanged as compared to those in the previous section. Therefore, condition (41) is also the case for the modified control law. However, the driving force is changed to

$${\mathit{L}}^{\top }{\mathsf{\zeta }}_{\mathrm{d}}={\alpha }_1\left({\displaystyle \frac{1}{T_1}}-{\displaystyle \frac{1}{T^{\ast }}}\right)-{\alpha }_2\left({\displaystyle \frac{1}{T_2}}-{\displaystyle \frac{1}{T^{\ast }}}\right),$$

(47)

the weighted difference of the deviations from equilibrium of the first and the second compartment, and the internal entropy production,

$${\dot{S}}_{\mathrm{i}\mathrm{n}\mathrm{t}}={{\mathsf{\zeta }}_{\mathrm{d}}}^{\mathrm{\top }}{\mathbf{R}}_{\mathrm{d}}{\mathsf{\Psi }}_{\mathrm{d}}\left({\mathsf{\zeta }}_{\mathrm{d}}\right){\mathbf{L}}^{\mathrm{\top }}{\mathsf{\zeta }}_{\mathrm{d}}=\left(\psi +\lambda \right)\left(r+1\right)T_1{T}_2{\left({\alpha }_1\left({\displaystyle \frac{1}{T_1}}-{\displaystyle \frac{1}{T^{\ast }}}\right)-{\alpha }_2\left({\displaystyle \frac{1}{T_2}}-{\displaystyle \frac{1}{T^{\ast }}}\right)\right)}^2.$$

(48)

The final expression for the control law:

$$T_{\mathrm{e}}=T_2-{\displaystyle \frac{\lambda }{{\lambda }_{\mathrm{e}}}}\left(T_1-T_2\right)+{\displaystyle \frac{\left(r+1\right)\left(\psi +\lambda \right)}{{\lambda }_{\mathrm{e}}}}{T}_1{T}_2\left({\alpha }_2\left({\displaystyle \frac{1}{T_2}}-{\displaystyle \frac{1}{T^{\ast }}}\right)-{\alpha }_1\left({\displaystyle \frac{1}{T_1}}-{\displaystyle \frac{1}{T^{\ast }}}\right)\right).$$

(49)

Therefore, Equation (43) corresponds to a symmetric controller based on entropy gradients, while Equation (49) introduces weighted asymmetry through parameters ${\alpha }_1$ and ${\alpha }_2$, enabling bias toward one compartment’s deviation.

5.5. Simulations and Discussions

The driving force (40) for the initial control is the same as for the open-loop system, just the difference of reverse temperatures of the compartments, while for the modified control law, the driving force (47) represents the weighted difference between the deviations of the inverse temperatures from the equilibrium ones, i.e., the modified controller sensitivity to deviations in one compartment relative to the other. The same applies for internal entropy production (42) and (48) and the control law (43) and (49). It can be easily seen that for ${\alpha }_1={\alpha }_2$, the term ${1/T}^{\ast }$ in (49) vanishes.

The control law (49) has four free parameters, ${\alpha }_1$ and ${\alpha }_2$, $\psi$ and $r$. From the expression of the particular form of the control law (49) it can be concluded that its influence can be analyzed in pairs. First, we study the influence of the weights ${\alpha }_1$ and ${\alpha }_2$ on the transient behavior with $\psi =r=0$. (Figure 7 and Figure 8). As the value of ${\alpha }_1$ decreases with fixed ${\alpha }_2$, the transient duration decreases (Figure 7), the same is for the increase of ${\alpha }_2$ with fixed ${\alpha }_1$ (Figure 8); i.e., it is desired to keep the difference between the weights larger.

Comparing the open-loop internal entropy production (37) and the closed loop one (48), we can say that $\psi$ and $r$ similarly influence it by modifying the thermal conductance $\lambda$. By comparing Figure 9 and Figure 10 where the influence of those parameters is demonstrated, it can be said that increasing these parameters leads to a reduction in the duration of the transient. It seems appropriate to simplify the expression of the control law by limiting the degrees of freedom of the control law by excluding one of those free parameters. Neither parameter exhibits a clear advantage over the other.

In the EBGH framework, there is a definition of internal entropy production; these are (42) for the control law (43) and (48), for the modified control law (49). Like in the above case for the IPHS framework, we performed simulation to assess the physical meaning of the function. However, for the EBGH framework, two cases should be considered, the first with the desired entropy function corresponding to the sum of real thermodynamic entropies of the two compartments (this is obtained in the control Equation (49) by selecting ${\alpha }_1={\alpha }_2=1$), and the second that uses weighted entropy function (44) (in the same model, this is obtained with ${\alpha }_1\ne {\alpha }_2$). In the first case, the same approach can be used as in Section 4.4, and the entropy production function corresponds to the entropy production of the virtual HEX with thermal conductance $\left(\psi +\lambda \right)\left(r+1\right)$ (Figure 11). In the case of using the weighted function, the desired entropy production rate cannot be obtained so easily (Figure 12), but it can be still treated as the entropy production rate of a virtual HEX with modified compartment heat capacities.

6. Entropy-Production-Metric-Based PHS

6.1. Theory

The final framework considered here is the entropy-production-metric-based PHS ($\epsilon$-PHS) framework [32] based on the definition of entropy production metrics $\epsilon$, which, based on the local equilibrium assumption, yields an expression for the first-order deviations [32]:

$$\delta \epsilon =s\delta T-v\delta p+\sum _i{n}_i\delta {\mu }_i,$$

(50)

where $\delta$ is the first-order deviation operator. Equation (50) expresses the first-order deviation of the entropy production metric in terms of specific entropy $s$ and temperature $T$, specific volume $v$ and pressure $p$, mole number $n_i$ and chemical potential ${\mu }_i$ of the $i$-th substance. Equation (50) is written in first-order deviations of intensive quantities. It is demonstrated in [32] that the second-order deviation ${\delta }^2\epsilon$ is strictly positive definite around equilibrium if certain thermodynamic conditions hold. Therefore, the framework uses a storage function of the form

$$H\left(\mathbf{x}\right)={\displaystyle \frac{1}{2}}{\delta }^2\epsilon \left(\mathbf{x}\right),$$

(51)

where a thermodynamic state vector $\mathbf{x}$ consists of the deviations of the intensive quantities $\delta T$, $\delta p$ and extensive quantity $\delta n_i$ enabling a simpler control-oriented model while preserving thermodynamic behavior. Reference [32] derives an expression of ${\delta }^2\epsilon$ based on (50) as

$${\delta }^2\epsilon ={\displaystyle \frac{c_v}{T}}{\left(\delta T\right)}^2+{\displaystyle \frac{1}{\chi v}}{\left(\delta v\right)}_{\left\{n_i\right\}}^2+\sum _{i,k}{\mu }_{ik}\delta n_i\delta n_k,$$

(52)

in a weighted quadratic form involving thermal, mechanical, and chemical deviations, with weights given by the inverse temperature-scaled heat capacity ${\displaystyle \frac{c_v}{T}}$, where $c_v$ is the constant-volume heat capacity, the inverse compressibility ${\displaystyle \frac{1}{\chi v}}$, where $\chi$ is the isothermal compressibility, and the chemical potential Hessian ${\mu }_{ik}$. From (52), it can be noted that with the storage function defined as in (51), the co-variables can be simply obtained for the thermal variable as ${\displaystyle \frac{c_v}{T}}\delta T$, while, for mechanical and chemical variables, it has implicit structure and thus depends on the specific model formulation and its underlying physics.

Given the state variables and co-variables, the original model can be written in a form

$$\dot{\mathbf{x}}=\mathbf{A}\nabla H\left(\mathbf{x}\right)+\mathbf{G}\mathbf{u}.$$

(53)

Since the structure matrix can be written as $\mathbf{A}=\mathbf{J}-\mathbf{R}$, the corresponding interconnection and damping matrices of the correct form can be obtained using the known relations:

$$\mathbf{J}={\displaystyle \frac{1}{2}}\left(\mathbf{A}-{\mathbf{A}}^{\mathrm{\top }}\right)=-{\mathbf{J}}^{\mathrm{\top }}, \mathrm{and} \mathbf{R}={\displaystyle \frac{1}{2}}\left(\mathbf{A}+{\mathbf{A}}^{\mathrm{\top }}\right)={\mathbf{R}}^{\mathrm{\top }}.$$

(54)

Since the state vector contains deviations from the equilibrium state, the equilibrium point of the drift dynamics $\mathbf{A}\nabla H\left(\mathbf{x}\right)$ is at the origin. Given the above, (53) represents a PHS.

It should also be noted that in [32], a control paradigm termed extended-state passivity-based control is introduced. By following this paradigm, extended state variables are introduced, and the control is formulated in terms of interconnecting the physical system with a system of extended state variables (analogically to control by interconnection for PHS). As long as we are interested in applying the IDA-PBC framework to this formulation of thermodynamic systems and since (53) is analogous to (2), we can directly use (5)–(10) to derive the control.

6.2. Application to HEX and Control Law Derivation

To match the state variables required by the $\epsilon$-PHS framework, we first rewrite (1) in the form:

$$\begin{array}{l}{m}_1{c}_{v1}{\dot{T}}_1=\lambda \left(T_2-T_1\right),\\ m_2{c}_{v2}{\dot{T}}_2=\lambda \left(T_1-T_2\right)+{\lambda }_{\mathrm{e}}\left(T_{\mathrm{e}}-T_2\right),\end{array}$$

(55)

Rearranged to isolate the temperature derivatives on the left-hand side, we have

$$\begin{array}{l}{\dot{T}}_1={\displaystyle \frac{\lambda }{m_1{c}_{v1}}}\left(T_2-T_1\right),\\ {\dot{T}}_2={\displaystyle \frac{\lambda }{m_2{c}_{v2}}}\left(T_1-T_2\right)+{\displaystyle \frac{{\lambda }_{\mathrm{e}}}{m_2{c}_{v2}}}\left(T_{\mathrm{e}}-T_2\right).\end{array}$$

(56)

The latter can be written in the form of deviations from the equilibrium:

$$\begin{array}{l}\delta {\dot{T}}_1={\displaystyle \frac{\lambda }{m_1{c}_{v1}}}\left(\delta T_2-\delta T_1\right),\\ \delta {\dot{T}}_2={\displaystyle \frac{\lambda }{m_2{c}_{v2}}}\left(\delta T_1-\delta T_2\right)+{\displaystyle \frac{{\lambda }_{\mathrm{e}}}{m_2{c}_{v2}}}\left(\delta T_{\mathrm{e}}-\delta T_2\right),\end{array}$$

(57)

where $\delta T_1=T_1-T^{\ast }$, $\delta T_2=T_2-T^{\ast }$, and $\delta T_{\mathrm{e}}=T_{\mathrm{e}}-T^{\ast }$.

By selecting the state vector $\mathbf{x}={\left[\delta \begin{array}{cc}{T}_1& \delta T_2\end{array}\right]}^{\mathrm{\top }}$, Equation (50) for the deviation in entropy production rate is given by

$$\delta \epsilon =s_1\delta T_1+s_2\delta T_2$$

(58)

and the storage function is defined as

$$H\left(\mathbf{x}\right)={\displaystyle \frac{1}{2}}{\delta }^2\epsilon \left(\mathbf{x}\right)={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{c_{v1}}{T^{\ast }}}{\left(\delta T_1\right)}^2+{\displaystyle \frac{c_{v2}}{T^{\ast }}}{\left(\delta T_2\right)}^2\right).$$

(59)

Therefore, the co-variables vector:

$$\nabla H\left(\mathbf{x}\right)={\left[\begin{array}{cc}{\displaystyle \frac{c_{v1}}{T^{\ast }}}\delta T_1& {\displaystyle \frac{c_{v2}}{T^{\ast }}}\delta T_2\end{array}\right]}^{\top }.$$

(60)

Therefore, to express the system in the port-Hamiltonian form (53) using the state vector $\mathbf{x}$, the temperature deviations and the covariables vector as in (60), (56) is transformed into

$$\begin{array}{l}\delta {\dot{T}}_1={\displaystyle \frac{\lambda }{m_1{c}_{v1}}}\left({\displaystyle \frac{T^{\ast }}{c_{v2}}}\left({\displaystyle \frac{c_{v2}}{T^{\ast }}}\delta T_2\right)-{\displaystyle \frac{T^{\ast }}{c_{v1}}}\left({\displaystyle \frac{c_{v1}}{T^{\ast }}}\delta T_1\right)\right),\\ \delta {\dot{T}}_2={\displaystyle \frac{\lambda }{m_2{c}_{v2}}}\left({\displaystyle \frac{T^{\ast }}{c_{v1}}}\left({\displaystyle \frac{c_{v1}}{T^{\ast }}}\delta T_1\right)-{\displaystyle \frac{T^{\ast }}{c_{v2}}}\left({\displaystyle \frac{c_{v2}}{T^{\ast }}}\delta T_2\right)\right)+{\displaystyle \frac{{\lambda }_{\mathrm{e}}}{m_2{c}_{v2}}}\left(\delta T_{\mathrm{e}}-\delta T_2\right).\end{array}$$

(61)

When comparing (50) and (58), the structure matrix $\mathbf{A}$ corresponding to this model is

$$\mathbf{A}=\left[\begin{array}{cc}-{\displaystyle \frac{\lambda T^{\ast }}{m_1{c}_{v1}^2}}& {\displaystyle \frac{\lambda T^{\ast }}{m_2{c}_{v2}^2}}\\ {\displaystyle \frac{\lambda T^{\ast }}{m_1{c}_{v1}^2}}& -{\displaystyle \frac{\lambda T^{\ast }}{m_2{c}_{v2}^2}}\end{array}\right],$$

(62)

and, by using (54), the interconnection and damping matrices are

$$\mathbf{J}={\displaystyle \frac{1}{2}}{\displaystyle \frac{\lambda T^{\ast }}{c_{v1}{c}_{v2}}}\left[\begin{array}{cc}0& {\displaystyle \frac{1}{m_1}}-{\displaystyle \frac{1}{m_2}}\\ {\displaystyle \frac{1}{m_2}}-{\displaystyle \frac{1}{m_1}}& 0\end{array}\right]\mathrm{and} \mathbf{R}={\displaystyle \frac{1}{2}}{\displaystyle \frac{\lambda T^{\ast }}{c_{v1}{c}_{v2}}}\left[\begin{array}{cc}{\displaystyle \frac{c_{v2}}{m_1{c}_{v1}}}& -{\displaystyle \frac{1}{m_1}}-{\displaystyle \frac{1}{m_2}}\\ -{\displaystyle \frac{1}{m_1}}-{\displaystyle \frac{1}{m_2}}& {\displaystyle \frac{c_{v1}}{m_2{c}_{v2}}}\end{array}\right].$$

(63)

From (61), the input matrix and vector are $\mathbf{G}={\left[\begin{array}{cc}0& {\displaystyle \frac{{\lambda }_{\mathrm{e}}}{m_2{c}_{v2}}}\end{array}\right]}^{\mathrm{\top }}$ and $\mathbf{u}=\delta T_{\mathrm{e}}-\delta T_2$.

With the derived port-Hamiltonian form above, the IDA-PBC problem can be formulated. As far as the equations are already written in the deviations, the storage function (59) and the co-variables vector (60) are also valid for the target system. Therefore, the IDA-PBC problem reduces to assigning additional interconnection and damping as:

$${\mathbf{J}}_{\mathrm{a}}=\left[\begin{array}{cc}0& j_{12}\\ -j_{12}& 0\end{array}\right]\mathrm{and} {\mathbf{R}}_{\mathrm{a}}=\left[\begin{array}{cc}{r}_{11}& r_{12}\\ r_{12}& r_{22}\end{array}\right].$$

(64)

By solving Equation (9), the control is obtained in the form

$$\delta T_{\mathrm{e}}=\delta T_2-\left(r_{12}+j_{12}\right){\displaystyle \frac{c_{v1}{c}_{v2}{m}_2\delta T_1}{T^{\ast }{\lambda }_{\mathrm{e}}}}-r_{22}{\displaystyle \frac{c_{v2}^2{m}_2\delta T_2}{T^{\ast }{\lambda }_{\mathrm{e}}}} .$$

(65)

Since in (65), the terms $r_{12}$ and $j_{12}$ appear as a sum, for the sake of simplicity and without loss of generality, reselect ${\mathbf{R}}_{\mathrm{a}}$ in (64) as ${\mathbf{R}}_{\mathrm{a}}=\left[\begin{array}{cc}{r}_{11}& 0\\ 0& r_{22}\end{array}\right]$. Therefore, (65) is simplified to have two free parameters:

$$\delta T_{\mathrm{e}}=\delta T_2-j_{12}{\displaystyle \frac{c_{v1}{c}_{v2}{m}_2\delta T_1}{T^{\ast }{\lambda }_e}}-r_{22}{\displaystyle \frac{c_{v2}^2{m}_2\delta T_2}{T^{\ast }{\lambda }_e}} .$$

(66)

Rewiring (66) as

$$T_{\mathrm{e}}-T^{\ast }=T_2-T^{\ast }-j_{12}{\displaystyle \frac{c_{v1}{c}_{v2}{m}_2\left(T_1-T^{\ast }\right)}{T^{\ast }{\lambda }_{\mathrm{e}}}}-r_{22}{\displaystyle \frac{c_{v2}^2{m}_2\left(T_2-T^{\ast }\right)}{T^{\ast }{\lambda }_{\mathrm{e}}}},$$

(67)

the final form of the control law is

$$T_{\mathrm{e}}=T_2-j_{12}{\displaystyle \frac{c_{v1}{c}_{v2}{m}_2\left(T_1-T^{\ast }\right)}{T^{\ast }{\lambda }_{\mathrm{e}}}}-r_{22}{\displaystyle \frac{c_{v2}^2{m}_2\left(T_2-T^{\ast }\right)}{T^{\ast }{\lambda }_{\mathrm{e}}}}.$$

(68)

6.3. Simulations and Discussions

The control law (68) contains two free parameters, $j_{12}$ and $r_{22}$. When both parameters are set to zero, the external source temperature simply repeats the temperature $T_2$, as confirmed by the simulation results shown in Figure 13.

The influence of free parameters $j_{12}$ and $r_{22}$ on the behavior of the system is similar (Figure 14 and Figure 15). Their increase shortens the transient response. $j_{12}$ is the gain acting to stabilize $T_1$ at the equilibrium $T^{\ast }$, while $r_{22}$ stabilizes $T_2$. Due to the thermal coupling between $T_1$ and $T_2$, it may be sufficient to tune only one of these parameters.

On the other hand, if $c_{v1}$, $c_{v2}$, and $m_2$ are constant, (68) can be reduced to the use of two feedbacks (or even one) that would require no complicated derivations and can be derived using basic control theory principles.

7. Comparative Analysis of the Three Frameworks

7.1. General Discussion on the Three Frameworks

Based on the derivations of IDA-PBC-like control laws and the simulations performed, the results are summarized in

Table 2. Comparison of the three frameworks by means of developing an IDA-PBC-like control law.

Criterion	IPHS	EBGH	$\mathsf{\epsilon }$-PHS
Selection of state variables, in particular, for thermodynamic domain	aligned with the PH approach; entropy for thermodynamic domain	extensive quantities; internal energies for thermal domain	$\mathrm{deviations} \mathrm{of} \mathrm{the} \mathrm{physical} \mathrm{quantities} \mathrm{from} \mathrm{equilibrium}; \delta T$ for the thermodynamic domain
Storage function (Hamiltonian-like) of an open-loop system	internal energy function	entropy function	second-order deviation of the entropy production metric function
Co-variables definition	gradient of internal energy; temperature for thermodynamic domain	gradient of the entropy function; reverse temperature for thermal domain	gradient of the entropy-production-metric-based storage function, dependent on the model structure
Thermodynamic compliance via the first law (energy conservation)	explicit by design, using the storage function time derivative	enforced by deriving thermodynamic relations based on the Gibbs equation	enforced by deriving the storage function based on the Gibbs equation
Thermodynamic compliance via the second law (entropy production conservation)	intrinsic, using the entropy production	explicit by design, using entropy as a storage function	explicit by design, using the entropy production metric
Development of passivity-based control in general	thoroughly developed theory	undeveloped in literature	extended-state passivity-based control
Development of IDA-PBC-like control in literature	yes	no	no
Possibility of developing the IDA-PBC-like control	yes	yes	yes
Storage function for the target system	energy-based availability function	thermodynamic availability function	second-order deviation of the entropy production metric function
Stability analysis tools	convexity of the availability function with a strict minimum at the equilibrium	concavity of the availability function with the maximum at the equilibrium	convexity of the storage function with a strict minimum at the origin
Possibility of using free parameters of the control to adjust the transient behavior	yes	yes	yes

.

First, note that the three frameworks provide thermodynamic consistency via the first and second laws; however, the particular form of consideration of these differs among them. The three frameworks analyzed use different approaches to develop the model of a thermodynamic system in a PH-like form. A conventional PH framework is a well-developed theory with successful applications of IDA-PBC for electrical, mechanical, hydraulic, pneumatic domains, etc., as well as the combination of those. The energy-based storage function of IPHS makes the latter advantageous, since coupling with the more conventional PH systems is straightforward in this case. For the two other frameworks, the coupling is also possible, but it requires additional analytic effort to develop a model.

The IPHS framework is the most developed in terms of control theory; the number of studies related to the development of control based on it is considerable. The literature on EBGH is limited only to modeling problems [26]. The authors of the $\epsilon$-PHS framework are actively developing extended-state passivity-based control, with several successful applications reported in [32,33].

7.2. Comparative Analysis of the Three Derived Control Laws

The three frameworks provide the possibility of developing the IDA-PBC-like control, as demonstrated in our study. $\epsilon$-PHS uses the conventional form of the PHS equations, though based on unconventional physical modeling; therefore, the formulation of the IDA-PBC is almost “classic”, while for the other two frameworks using the unconventional form of the original system’s equations requires a nonstandard formulation of the target dynamics. However, those formulations have strict interpretation in IDA-PBC-like control, as we have demonstrated. Furthermore, in the case of the latter two frameworks, obtaining the entropy production rate is simpler; it can be used, e.g., for optimal control design, as shown in [47].

In terms of degrees of freedom of the designed control laws, in each case, the free parameters can be used to adjust the transient behavior for all three frameworks, though the structure of the control law differs: for our example, IPHS and EBGH yield nonlinear laws, while $\epsilon$-PHS results in a linear one. In addition, the parameters of the IPHS and EBGH-based laws can be more easily physically interpreted (however, depending on the system, their interpretability may vary).

Our next comment corresponds to the entropy production rates, for which equations were derived for IPHS and EBGH frameworks. These are not related to real physical thermodynamic entropies, but they rather correspond to the desired system whose behavior is mimicked in the real system by using the external control.

In our work, a simple example is considered; this can lead to insufficient information on the implementation of the frameworks to more complex systems, in particular multiphysics, which is completely not captured in our simple model. Thus, in the EBGH framework, the co-entropy variables are obtained in ad hoc formulation (see examples in [26] where the thermal subsystem is coupled with a mechanical one). The same can be the case for $\epsilon$-PHS, where the co-variables can depend on the structure of the particular system. This can lead to complicated derivations of control laws for multiphysics systems, and this is a limitation of our analysis and a possible direction of further research.

8. Conclusions

Extending the PH framework to the thermodynamic domain requires reformulating the PH dynamics to ensure compliance not only with the first law (as in classical PHS), but also with the second law. We studied three frameworks that we found promising for the modeling and control of thermodynamic systems in a PH-like formulation for the example of a simplified heat exchanger neglecting the spatial temperature distribution. We selected IDA-PBC as the basis for the development of the control law and explored the extent to which each framework supports the design of IDA-PBC-like control laws, including the tuning of free parameters.

Thus, the three frameworks independent on their particular formulation provide thermodynamic consistency via the first and the second laws, and the control laws formulated on their basis also provide free parameters for adjusting the transient behavior. Therefore, all of them are suitable for developing IDA-PBC-like control for a multiphysics system with a thermal domain.

However, the IPHS framework is deeper studied and well established and already has successful applications of IDA-PBC-like control. For the framework, the energy-based storage function makes it simpler to couple the irreversible subsystem with other domains, as it allows for direct integration with conventional PH systems, while for the two other frameworks it can be more complicated.

In the case where entropy production rate is required for control purposes, it can be more easily obtained in IPHS and EBGH frameworks, the latter also providing formulations that are more physically interpretable.

This study could not address all aspects of developing IDA-PBC-like control for systems with irreversible behavior. However, it demonstrated the implementability of the three analyzed frameworks and provided some insight into the control derivation. The system under study, a simplified model of a heat exchanger, is a quite simple system. There is also no coupling with other subsystems, electrical, mechanical, pneumatical, etc., which is more interesting for practical applications. These limitations suggest several directions for future research.

Our results may guide future work on extending IDA-PBC to coupled multiphysics systems where energy-based and entropy-based formulations must coexist.