Waveguide Arrays: Interaction to Many Neighbors

Abstract

We present an analytical framework for describing light propagation in infinite waveguide arrays, incorporating a generalized long-range coupling to achieve a more realistic model. We demonstrate that the resulting solution can be expressed in terms of generalized Bessel-like functions. Additionally, by applying the concept of eigenstates, we borrow from quantum mechanics a basis given in terms of phase states that allows the analysis of the transition from the discrete to the continuum limit, obtaining a relationship between the field amplitudes and the Fourier series coefficients of a given function. We apply our findings to different coupling functions, providing new insights into the propagation dynamics of these systems.

1. Introduction

The interaction between particles mediated by a field cannot be entirely captured by a distance action, which offers only an approximate description. A more refined approach considers two-body, three-body, and higher-order m-body interactions as successive corrections to this approximation. The relative magnitudes of these interaction terms can be systematically analyzed for different types of classical and quantum fields, such as the electromagnetic [1]. Quantum long-range systems have recently attracted significant interest, driven not only by the need to explore the fundamental physics of nonlocal interactions and their influence on the balance between local and long-distance properties but also by their potential in quantum technology applications. Their collective nature improves the distribution of entanglement and gives rise to unique dynamical scaling effects, as they facilitate the generation of highly entangled or correlated dynamical states [2,3,4]. Nevertheless, the exponential growth of the Hilbert space with system size makes it inherently difficult to efficiently simulate the quantum physics of an interacting many-body system using classical computers. Recognizing this limitation, Feynman proposed a controllable quantum device as an alternative, allowing for an efficient study of the dynamics of another quantum system, and since then, quantum simulation has emerged as an independent and rapidly evolving field of research [5]. Significant progress in experimental techniques and theoretical frameworks has driven intensive research in quantum simulation across diverse physical platforms. Among them, atomic, molecular, and optical systems, ranging from trapped ions and cold atoms to arrays of evanescently coupled waveguides, have garnered significant attention [6,7,8,9,10,11,12,13].

Coupled optical waveguide arrays and periodic photonic lattices have been the focus of intense research because of the diverse physical phenomena that emerge from the interplay of discreteness, periodicity, nonlinearity, and boundary effects. Beyond their fundamental interest, these structures enable the control and manipulation of light propagation, allowing their use in the fabrication of photonic integrated devices [14,15,16,17] and facilitating the observation of phenomena such as Bloch oscillations, Anderson localization, and quantum walks, among others [18,19,20,21,22,23,24]. However, in these structures, coupling is generally assumed to occur only between nearest-neighbor waveguides, while interactions with more distant waveguides are typically neglected under the assumption that the coupling strength decays exponentially with distance. However, second-order couplings can play a significant role in the structure of the waveguide array, as seen in the two-dimensional zigzag waveguide lattice, where an exact solution can be found [25,26,27]. Moreover, higher-order couplings have been observed in circular and helical waveguide arrays [28,29,30], and their advantages have been extensively documented in the literature, particularly in applications such as quantum state modeling, photon-number correlations, and harmonic and Bloch oscillations [31,32,33,34,35,36,37].

The structure of this article is as follows. Section 2 begins by analyzing an infinite waveguide array where interactions extend beyond nearest neighbors. By employing phase states, we derive an exact solution, which closely relates to the case of first-neighbor interactions in an infinite array. In Section 3, we introduce an alternative approach based on operational methods to solve the same system. In Section 4, we extend the waveguide-array interactions to an infinite number of neighbors, which allows the approximation of the discrete solutions as continuous functions and computes the evolution of the amplitude for different coupling functions. Finally, in Section 5, we summarize our findings and present concluding remarks.

2. Interaction with N Neighbors

In coupled mode theory [38,39], the propagation of an optical field through a waveguide array with long-range evanescent coupling without frontiers is governed by the following set of coupled first-order ordinary differential equations:

$$\begin{array}{c}i{\displaystyle \frac{d{E}_j\left(z\right)}{dz}}={\displaystyle \sum _{k=0}^N}{g}_k\left(E_{j+k}+E_{j-k}\right)\hfill \\ =2g_0{E}_j+g_1\left(E_{j+1}+E_{j-1}\right)+g_2\left(E_{j+2}+E_{j-2}\right)+\cdots +g_N\left(E_{j+N}+E_{j-N}\right), j\in \mathbb{Z}.\hfill \end{array}$$

(1)

In this context, z represents the propagation distance, while $g_k;k=0,1,2,\dots ,N$ denotes a set of $N+1$ real and non-negative coupling constants. The index j ranges across all integers from $-\infty$ to ∞.

This framework can also be viewed as the problem of solving the Schrödinger-like equation $i{\displaystyle \frac{d|\psi \left(z\right)⟩}{dz}}=\widehat{H}|\psi \left(z\right)⟩$ with the Hamiltonian

$$\widehat{H}=\sum _{k=0}^N{g}_k({\widehat{V}}^k+{\widehat{V}}^{†k}),$$

(2)

where the operators $\widehat{V}$ and ${\widehat{V}}^{†}$ are the generalized London operators defined as [40,41]

$$\widehat{V}=\sum _{n=-\infty }^{\infty }|n⟩⟨n+1|, {\widehat{V}}^{†}=\sum _{n=-\infty }^{\infty }|n+1⟩⟨n|,$$

(3)

which is in the infinite Hilbert space commute. The sum in the Hamiltonian (2) may define either a polynomial for finite N or a function in the limit $N\to \infty$.

If we denote the solution of the Schrödinger-type equation associated with the Hamiltonian (2) as $|\psi \left(z\right)⟩$, it is easy to demonstrate that the solutions of system (1) are given by $E_j\left(z\right)=⟨j\left|\psi \right(z)⟩, j\in \mathbb{Z}$. Using operational methods [42], we solve the Schrödinger-like equation derived from the Hamiltonian (2) and subsequently obtain the solution for the infinite system in (1). Taking into account an arbitrary initial condition $|\psi \left(0\right)⟩$, the formal solution of the Schrödinger-like equation is expressed as $|\psi \left(z\right)⟩=exp\left(-iz{\sum }_{k=0}^N{g}_k({\widehat{V}}^k+{\widehat{V}}^{†k})\right)|\psi \left(0\right)⟩$; to solve this equation, we introduce the phase states [43,44,45] defined as

$$|\Phi ⟩={\displaystyle \frac{1}{\sqrt{2\pi }}}\sum _{n=-\infty }^{\infty }{e}^{in\Phi }|n⟩,$$

(4)

in such a way that it is easy to prove that ${\widehat{V}}^k|\Phi ⟩=e^{ik\Phi }|\Phi ⟩$, and that ${\widehat{V}}^{†k}|\Phi ⟩=e^{-ik\Phi }|\Phi ⟩$. The phase states defined above form a complete basis, so the unity operator may be written as $\widehat{I}={\int }_0^{2\pi }|\Phi ⟩⟨\Phi |d\Phi$, and the initial condition may be given in terms of phase states as

$$|\psi \left(0\right)⟩={\int }_0^{2\pi }{C}_{\psi \left(0\right)}(\Phi )|\Phi ⟩d\Phi ,$$

(5)

with $C_{\psi \left(0\right)}(\Phi )=⟨\Phi |\psi \left(0\right)⟩$.

Given that $\widehat{V}$ and ${\widehat{V}}^{†}$ commute, the propagation of an arbitrary field can be formulated applying the operators and carrying out some algebraic steps, and we get the following:

$$|\psi \left(z\right)⟩={\int }_0^{2\pi }{C}_{\psi \left(0\right)}(\Phi )exp\left(-2iz\sum _{k=0}^N{g}_{k}cos(k\Phi )\right)|\Phi ⟩d\Phi ,$$

(6)

and in order to find the amplitudes $E_j$ that are the solutions of the system (1), we project the above expression over the state $|j⟩$ and use the fact that $⟨j|\Phi ⟩={\displaystyle \frac{1}{\sqrt{2\pi }}}exp\left(ij\Phi \right)$ to obtain

$$⟨j\left|\psi \right(z)⟩={\displaystyle \frac{1}{\sqrt{2\pi }}}{\int }_0^{2\pi }{C}_{\psi \left(0\right)}(\Phi )exp\left(-2iz\sum _{k=0}^N{g}_{k}cos\left(k\Phi \right)\right)exp\left(ij\Phi \right)d\Phi .$$

(7)

We now take as initial condition $|\psi \left(0\right)⟩=|m⟩$, where m is an integer and thus $C_{\psi \left(0\right)}(\Phi )=⟨\Phi |m⟩={\displaystyle \frac{1}{\sqrt{2\pi }}}exp\left(-im\Phi \right)$, which substituted in Equation (7) gives

$$E_j\left(z\right)=⟨j\left|\psi \right(z)⟩={\displaystyle \frac{1}{2\pi }}{\int }_0^{2\pi }exp\left(-2iz\sum _{k=0}^N{g}_{k}cos\left(k\Phi \right)\right)exp\left(i(j-m)\Phi \right)d\Phi .$$

(8)

Although the above integral can be efficiently solved using numerical methods to determine the evolution of the amplitude in each waveguide along the propagation direction, an exact solution can also be obtained following Dattoli’s studies [46,47,48], so that we proceed to introduce generalized Bessel functions with N variables $\left\{x_1,x_2,x_3,\dots ,x_N\right\}$ and $N-1$ parameters $\left\{s_1,s_2,s_3,\dots ,s_{N-1}\right\}$ (GBF-N) by means of integral representation:

$$\begin{array}{c}{J}_n\left(x_1,\dots ,x_N;s_1,\dots ,s_{N-1}\right)={\displaystyle \frac{i}{2\pi }}\oint {\displaystyle \frac{1}{t^{n+1}}}exp[{\displaystyle \frac{x_1}{2}}\left(t-{\displaystyle \frac{1}{t}}\right)+{\displaystyle \frac{x_2}{2}}\left(s_1{t}^2-{\displaystyle \frac{1}{s_1{t}^2}}\right)\hfill \\ +{\displaystyle \frac{x_3}{2}}\left(s_2{t}^3-{\displaystyle \frac{1}{s_2{t}^3}}\right)+\dots +{\displaystyle \frac{x_N}{2}}\left(s_{N-1}{t}^N-{\displaystyle \frac{1}{s_{N-1}{t}^N}}\right)]dt\hfill \end{array}$$

(9)

where the contour of integration encircles the origin once counterclockwise [47].

Changing the variable in the integral from t to $iexp\left(-i\Phi \right)$, making $s_k={\left(-i\right)}^k,$$k=1,2,3,\dots ,N-1$, and identifying $x_k\to -2g_{k}z, k=1,2,3,\dots ,N$, we arrive at

$$\begin{array}{c}{J}_n\left(-2g_{k}z, k=1,2,\dots ,N;s_k={(-i)}^k, k=1,2,\dots ,N-1\right)=\hfill \\ {\displaystyle \frac{1}{2\pi i^n}}{\int }_0^{2\pi }exp\left(-2iz{\displaystyle \sum _{k=1}^N}{g}_{k}cos\left(k\Phi \right)\right)exp\left(in\Phi \right)d\Phi .\hfill \end{array}$$

(10)

Thus, from Equation (8), we can write

$$E_j\left(z\right)=exp\left(-2i{g}_{0}z\right)i^{j-m}{J}_{j-m}\left(-2g_{k}z, k=1,2,3,\dots ,N;s_k={(-i)}^k, k=1,2,3,\dots ,N-1\right).$$

(11)

Structurally, this result is analogous to the infinite case of an optical field propagating in a waveguide array with nearest-neighbor evanescent coupling, differing only in the substitution of Bessel functions with GBF-N. Moreover, it is easy to show that for $N=1$, solution (11) reduces to that case, and for $N=2$, we obtain the solution for the next-nearest-neighbor evanescent coupling, following the recursion of the N-variables and $N-1$-parameters generalized Bessel functions of integer order n (GBF-N) $J_n(x_1,x_2,x_3,\dots ,x_N;s_1,s_2,\dots ,s_{N-1})$ as

$$J_n(x_1,x_2,\dots ,x_N;s_1,s_2,\dots ,s_{N-1})=\sum _{l=-\infty }^{\infty }{s}_{N-1}^l{J}_{n-Nl}(x_1,x_2,\dots ,x_{N-1};s_1,s_2,\dots ,s_{N-2})J_l\left(x_N\right),$$

(12)

with $J_n(x_1,x_2;s_1)$ the 2-variables and 1-parameter generalized Bessel functions of integer order (GBF2-1) defined by the series representation

$$J_n(x_1,x_2;s_1)=\sum _{l=-\infty }^{\infty }{s}_1^l{J}_{n-2l}\left(x_1\right)J_l\left(x_2\right), n\in \mathbb{Z},$$

(13)

with $J_l\left(z\right)$ being the ordinary Bessel functions of the first kind [47,48] and $\{s_1,s_2,\dots ,s_{N-1}\}$ a set of complex number parameters.

3. Interaction with N Neighbors Using the Generating Function of the Generalized Bessel Functions of N Variables and N − 1 Parameters

The previous result may also be obtained using the generating function of (GBF-N). Consider the interaction up to N neighbors, with N being a finite non-negative integer. The Hamiltonian in that case is the one exposed in Equation (2), which we reproduce here for ease of reading, $\widehat{H}={\sum }_{k=0}^N{g}_k({\widehat{V}}^k+{\widehat{V}}^{†k})$. The propagator corresponding to this Hamiltonian is

$$\widehat{U}\left(z\right)=exp\left[-iz\sum _{k=0}^N{g}_k\left({\widehat{V}}^k+{\widehat{V}}^{†k}\right)\right];$$

(14)

as $\widehat{V}{\widehat{V}}^{†}=\widehat{I}$, we can cast (14) as

$$\widehat{U}\left(z\right)=exp\left[-z\sum _{k=0}^N{g}_k\left(i{\widehat{V}}^{†k}-{\displaystyle \frac{1}{i{\widehat{V}}^{†k}}}\right)\right].$$

(15)

We now introduce the generalized Bessel functions with N variables $\left\{x_1,x_2,x_3,\dots ,x_N\right\}$ and $N-1$ parameters $\left\{s_1,s_2,s_3,\dots ,s_{N-1}\right\}$ (GBF-N) by means of the generating function

$$\begin{array}{cc}\hfill & \sum _{n=-\infty }^{\infty }{t}^n{J}_n\left(x_1,x_2,x_3,\cdots ,x_N;s_1,s_2,\dots ,s_{N-1}\right)=\hfill \\ & exp\left[{\displaystyle \frac{x_1}{2}}\left(t-{\displaystyle \frac{1}{t}}\right)+{\displaystyle \frac{x_2}{2}}\left(s_1{t}^2-{\displaystyle \frac{1}{s_1{t}^2}}\right)+\dots +{\displaystyle \frac{x_N}{2}}\left(s_{N-1}{t}^N-{\displaystyle \frac{1}{s_{N-1}{t}^N}}\right)\right].\hfill \end{array}$$

(16)

If we identify $t\to i{\widehat{V}}^{†}$, $x_k\to -2g_{k}z, k=1,2,3,\dots ,N$ and $s_k\to {(-i)}^k,$$k=1,2,3,\dots ,N-1$ in Equation (15), we obtain

$$\widehat{U}\left(z\right)=exp\left(-2i{g}_{0}z\right)\sum _{n=-\infty }^{\infty }{i}^n{J}_n(-2g_{k}z, k=1,2,3,\dots ,N;{(-i)}^k, k=1,2,3,\dots ,N-1){\widehat{V}}^{†n},$$

(17)

and we have the solution to our problem for an initial condition $|\psi \left(0\right)⟩$ as

$$|\psi \left(z\right)⟩=exp\left(-2i{g}_{0}z\right)\sum _{n=-\infty }^{\infty }{i}^n{J}_n(-2g_{k}z, k=1,2,\dots ,N;{(-i)}^k, k=1,2,\dots ,N-1){\widehat{V}}^{†n}|\psi \left(0\right)⟩.$$

(18)

Let us take $|\psi \left(0\right)⟩=|m⟩$ with m as an integer; as ${\widehat{V}}^{†n}|m⟩=|m+n⟩$,

$$|\psi \left(z\right)⟩=exp\left(-2i{g}_{0}z\right)\sum _{n=-\infty }^{\infty }{i}^n{J}_n(-2g_{k}z, k=1,2,3,\dots ,N;{(-i)}^k, k=1,2,3,\dots ,N-1)|m+n⟩,$$

(19)

and finally, we arrive at

$$E_j\left(z\right)=exp\left(-2i{g}_{0}z\right)i^{j-m}{J}_{j-m}(-2g_{k}z, k=1,2,3,\dots ,N;{(-i)}^k, k=1,2,3,\dots ,N-1)$$

(20)

which is the solution to our problem in Equation (11).

Figure 1 presents the intensity distribution in the waveguides as a function of the propagation distance z, described by Equation (11) for different values of N. The assumption $g_1>g_2>g_3>g_4$ is physically justified by the natural decrease in the coupling strength as light propagates through the array. Panel (a) illustrates the interaction limited to first-neighbor coupling ($N=1$) with $g_1=0.8$. Panel (b) extends this to second-neighbor interactions ($N=2$), incorporating $g_1=0.8$ and $g_2=0.6$. In panel (c), the third-neighbor coupling ($N=3$) is considered, adding $g_3=0.4$. Finally, panel (d) considers up to fourth-neighbor interactions ($N=4$), where the coupling constants are $g_1=0.8$, $g_2=0.6$, $g_3=0.4$, and $g_4=0.2$. It should be noted that in actual photonic systems, the evanescent coupling strength between the waveguides tends to decrease exponentially as distance increases. However, Figure 1 employs linearly decreasing values for $g_k$ to illustrate a potential light behavior within the array, as the variances would be too small in a specific physical model to be noticed in a graphic; nevertheless, that does not mean that in a properly designed experimental setup these intensity variations cannot be measured. This configuration can be achieved using the femtosecond laser writing technique [49,50]. A remarkable observation is that the propagation pattern does not simply broaden; rather, it undergoes qualitative changes due to higher-order coupling effects. In particular, while the side lobes exhibit increased divergence, the main portion of the propagating light remains increasingly concentrated around the initially excited waveguide as higher-order coupling effects become more pronounced.

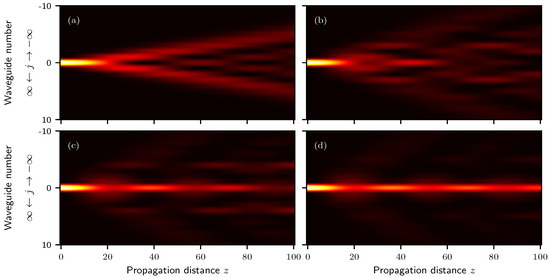
Figure 1. The evolution of the squared amplitude modulus in each waveguide is shown for an infinite waveguide array governed by Equation (11), considering interactions up to the fourth neighbor. In panels (a–d), the central waveguide ($j=0$) is initially excited. The coupling constants decrease progressively, taking the values $g_1=0.8$, $g_2=0.6$, $g_3=0.4$, and $g_4=0.2$.

Using the fourth-order Runge–Kutta method, Figure 2 demonstrates that the analytical results agree closely with the numerical simulations presented above, showing an excellent match between both approaches. To keep the presentation focused, we display only two plots. Panel (a) shows how the intensity evolves in the central waveguide $(j=0)$ along the propagation direction z; the solid blue curve represents the analytical result, while the black dots indicate the numerical data. Panel (b) provides a snapshot of the intensity distribution across all waveguides at a fixed propagation distance $(z=100)$. Here, the solid blue bars correspond to the analytical results, and the black diagonal lines represent the numerical results.

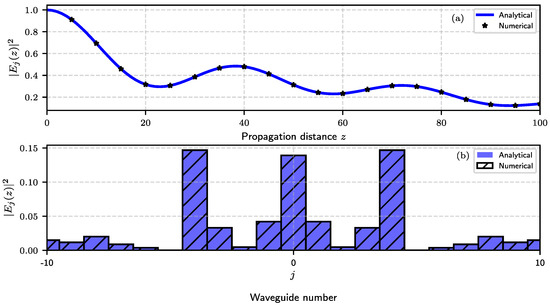
Figure 2. The Schrödinger equation with the Hamiltonian of Equation (2) is numerically solved and compared with the analytical solution in Equation (11), accounting for interactions to third neighbors ($N=3$). The coupling parameters are chosen as $g_1=0.8$, $g_2=0.6$, and $g_3=0.4$. Panel (a) shows how the intensity evolves in the central waveguide $(j=0)$ along the propagation direction z; the solid blue curve represents the analytical result, while the black dots indicate the numerical data. Panel (b) provides a snapshot of the intensity distribution across all waveguides at a fixed propagation distance $(z=100)$. Here, the solid blue bars correspond to the analytical results, and the black diagonal lines represent the numerical results.

4. From Discrete to Continuous Models

Now, we examine the transition from the discrete regime to the continuum limit. As mentioned in Section 2, in the limit $N\to \infty$, the sum in the Hamiltonian (2) can define a function. To illustrate this, we assume a propagator of the form $\widehat{U}\left(z\right)=exp(-iz[f(\widehat{V})+f({\widehat{V}}^{†})])$, where $f(.)$ is an arbitrary well-behaved function and admits a Taylor series expansion of the form $f\left(x\right)={\sum }_{k=0}^{\infty }{a}_k{x}^k$. Comparison of this last expression with the propagator in Equation (14) makes it clear that we can directly identify the set $a_k,k=0,1,2,\dots ,\infty$ with the set $g_k,k=0,1,2,\dots ,\infty$; thus, we may obtain an analytical and exact solution to the system of equations for the waveguides. Given this identification of the as with the gs, we must impose certain requirements on the properties of the former: they must be non-negative (zero or positive) and must decay rapidly enough to ensure that the series converges, allowing the gs to behave like interaction constants. Hence, one can easily verify that the propagation of an arbitrary state in terms of phase states is given by

$$|\psi \left(z\right)⟩={\int }_0^{2\pi }{C}_{\psi }(\Phi )exp\left(-iz\left[f\left(\widehat{V}\right)+f\left({\widehat{V}}^{†}\right)\right]\right)|\Phi ⟩d\Phi .$$

(21)

Using the fact that the operators $\widehat{V}$, ${\widehat{V}}^{†}$ commute and the fact that ${\widehat{V}}^k|\Phi ⟩=e^{ik\Phi }|\Phi ⟩$ and ${\widehat{V}}^{†k}|\Phi ⟩=e^{-ik\Phi }|\Phi ⟩$, we can apply the operator to obtain

$$|\psi \left(z\right)⟩={\int }_0^{2\pi }{C}_{\psi }(\Phi )exp\left(-iz\left[f\left(e^{i\Phi }\right)+f\left(e^{-i\Phi }\right)\right]\right)|\Phi ⟩d\Phi .$$

(22)

Next, we project the above state on the bra $⟨l|$, with l an integer, and we can write

$$⟨l|\psi \left(z\right)⟩={\displaystyle \frac{1}{\sqrt{2\pi }}}{\int }_0^{2\pi }{C}_{\psi }(\Phi )exp\left(-iz\left[f\left(e^{i\Phi }\right)+f\left(e^{-i\Phi }\right)\right]\right)e^{il\Phi }d\Phi , l\in \mathbb{Z}.$$

(23)

Finally, taking $|\psi \left(0\right)⟩=|m⟩$, with m being an integer, as an initial condition, we get

$$E_l\left(z\right)=⟨l|\psi \left(z\right)⟩={\displaystyle \frac{1}{2\pi }}{\int }_0^{2\pi }exp\left(-iz\left[f\left(e^{i\Phi }\right)+f\left(e^{-i\Phi }\right)\right]\right)e^{i(l-m)\Phi }d\Phi , l\in \mathbb{Z}.$$

(24)

It is crucial to emphasize that the functions $E_l\left(z\right)$ in Equation (24) are precisely the Fourier series coefficients of $exp\left(-iz\left[f\left(e^{i\Phi }\right)+f\left(e^{-i\Phi }\right)\right]\right)$. By expanding in the phase basis, we directly obtain these coefficients, leading to a solution expressed as a Fourier series. Essentially, this process corresponds to performing a Fourier transform of the function that defines the coupling between the waveguides, providing both a mathematical and a physical interpretation of the system’s evolution.

In the next subsections, we analyze particular functions from Equation (24) that allow an explicit computation of the coefficients $E_l$.

4.1. Natural Logarithm Function

We now examine the case where the function is given by $f\left(x\right)=-ln\left(1-\alpha x\right)$, resulting in the coupling constants in Propagator (14) being $g_0=0$ and $g_k={\displaystyle \frac{{\alpha }^k}{k}}$. Under this assumption, Equation (24) can be rewritten as

$$E_l\left(z\right)={\displaystyle \frac{1}{2\pi }}{\int }_0^{2\pi }{\left[1+{\alpha }^2-2\alpha cos(\Phi )\right]}^{iz}{e}^{i(l-m)\Phi }d\Phi , l\in \mathbb{Z}.$$

(25)

4.2. Exponential Function

Considering the function $f\left(x\right)=exp\left(\alpha x\right)$, we find that the propagator coefficients in (14) are given by $g_k={\displaystyle \frac{{\alpha }^k}{k!}}$. Consequently, Equation (24) can be expressed as

$$E_l\left(z\right)={\displaystyle \frac{1}{2\pi }}{\int }_0^{2\pi }exp\left(-iz\left[exp\left(\alpha e^{i\Phi }\right)+exp\left(\alpha e^{-i\Phi }\right)\right]\right)e^{i(l-m)\Phi }d\Phi , l\in \mathbb{Z}.$$

(26)

4.3. Polylogarithm Function

Consider the polylogarithm function, defined as ${\mathrm{Li}}_n\left(x\right)={\sum }_{k=1}^{\infty }{\displaystyle \frac{x^k}{k^n}}$. Since this function is explicitly given by its Taylor series, the coefficients $a_k$, and consequently the coupling coefficients $g_k={\displaystyle \frac{1}{k^n}}$, are inherently determined. It is also important to note that all the coefficients in the Taylor series expansion of the polylogarithm function are positive. Substituting ${\mathrm{Li}}_2\left(x\right)$ into (24), simplifying the expressions, and evaluating the integral, we obtain

$$\begin{array}{c}{E}_l\left(z\right)={\displaystyle \frac{{(-1)}^{3/4}}{2\sqrt{z}}}exp\left({\displaystyle \frac{i}{6}}\left[{\displaystyle \frac{3{(l-m)}^2}{z}}+6\pi (l-m)+{\pi }^{2}z\right]\right)\hfill \\ \hfill \\ \times \left[\mathrm{erf}\left({\displaystyle \frac{1}{2}}\left(1+i\right){\displaystyle \frac{l-m+\pi z}{\sqrt{z}}}\right)+\mathrm{erf}\left({\displaystyle \frac{1}{2}}\left(1+i\right){\displaystyle \frac{m-l+\pi z}{\sqrt{z}}}\right)\right], l\in \mathbb{Z}.\hfill \end{array}$$

(27)

4.4. Quadratic Polynomial

Consider a second-degree polynomial $f\left(x\right)=g_0+g_{1}x+g_2{x}^2$, and from Equation (24), we have

$$E_l\left(z\right)={\displaystyle \frac{exp\left(-2i{g}_{0}z\right)}{2\pi }}{\int }_0^{2\pi }exp\left(-2iz\left[g_{1}cos(\Phi )+g_{2}cos(2\Phi )\right]\right)e^{i(l-m)\Phi }d\Phi , l\in \mathbb{Z}.$$

(28)

Now using the Jacobi–Anger expansion [51] $e^{izcos\theta }={\sum }_{n=-\infty }^{\infty }{i}^n{J}_n\left(z\right)e^{in\theta }$, the above equation may be written as

$$E_l\left(z\right)={\displaystyle \frac{exp\left(-2i{g}_{0}z\right)}{2\pi }}{\int }_0^{2\pi }\sum _{n_1,n_2=-\infty }^{\infty }{i}^{n_1+n_2}{J}_{n_1}(-2g_{1}z)J_{n_2}(-2g_{2}z)e^{n_1\Phi +2n_2\Phi }d\Phi , l\in \mathbb{Z},$$

(29)

and integrated to obtain $E_l\left(z\right)=exp\left(-2i{g}_{0}z\right){\sum }_{n_2=-\infty }^{\infty }{i}^{m-l-n_2}{J}_{m-l-2n_2}(-2g_{1}z)J_{n_2}(-2g_{2}z)$; finally, we can recognize the generalized Bessel functions with two variables and one parameter (GBF2-1) making $s\to -i$, to obtain

$$E_l\left(z\right)=i^{m-l}exp\left(-2iz{g}_0\right)J_{m-l}\left(-2g_{1}z,-2g_{2}z;-i\right), l\in \mathbb{Z}.$$

(30)

Equation (24) reveals that when $f\left(x\right)$ is a polynomial of degree N, the resulting equation coincides with (8), which describes the interaction with multiple neighbors; additionally, this equation can be rewritten using the generalized Bessel functions (GBF-N). Thus, the integral of the exponential of an arbitrary polynomial admits a solution in terms of these functions.

4.5. Geometric Series

Finally, we analyze the case where $f\left(x\right)={\displaystyle \frac{\alpha }{1-x}}={\sum }_{k=0}^{\infty }\alpha x^k$, leading to constant and equal coupling coefficients $g_k$. Substituting this expression into Equation (24), we obtain

$$E_l\left(z\right)={\displaystyle \frac{exp\left(-iz\right)}{2\pi }}{\int }_0^{2\pi }{e}^{i(l-m)\Phi }d\Phi =\left\{\begin{array}{cc}exp\left(-iz\right),\hfill & l=m,\hfill \\ 0,\hfill & l\ne m.\hfill \end{array}\right.$$

(31)

Figure 3 illustrates the light intensity distribution as a function of the propagation distance z for different coupling functions applied in Equation (24). Panels (a) and (b) correspond to cases where the coupling is defined by natural logarithm and exponential functions, respectively, leading to a slight concentration of light in the central waveguide. Panel (c) exhibits a propagation pattern similar to that observed under nearest-neighbor interactions. Finally, panel (d) describes a nonphysical configuration with zero losses, highlighting the tendency of light to remain localized in the central region.

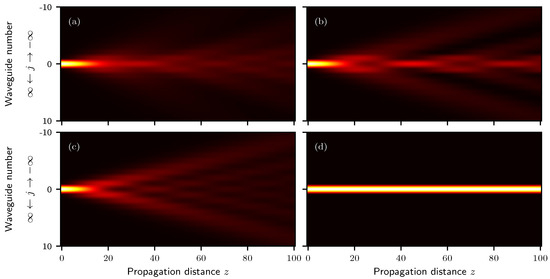
Figure 3. The intensity evolution of the field in an infinite waveguide array described by Equation (24) is shown for different functions when the central waveguide is illuminated; (a) corresponds to (25) with $\alpha =0.8$, (b) corresponds to (26) with the same parameter value, (c) represents (27), and (d) illustrates (26) again with $\alpha =0.8$.

As in the previous section, Schrödinger’s equation is numerically solved using the fourth-order Runge–Kutta method. Figure 4 shows a strong agreement between the numerical and analytical results. To avoid overwhelming the reader with excessive figures, we only present the case in which the function in Equation (24) is defined as $f\left(x\right)=exp\left(\alpha x\right)$. Panel (a) illustrates the intensity evolution in the central waveguide $(j=0)$ along the propagation direction z; the solid blue curve represents the analytical result, while the black dots denote the numerical data. Panel (b) displays the intensity distribution at a fixed distance $z=100$, where blue bars and black diagonal lines indicate analytical and numerical results, respectively.

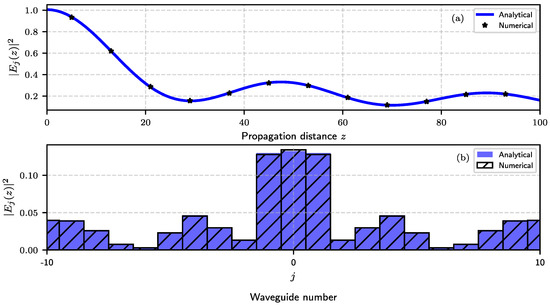
Figure 4. The numerical solution of the Schrödinger equation, using the Hamiltonian defined in Equation (2) is obtained in the limit $N\to \infty$ and compared against the semi-analytical expression of Equation (26) with the parameter $\alpha =0.8$. Panel (a) illustrates the intensity evolution in the central waveguide $(j=0)$ along the propagation direction z; the solid blue curve represents the analytical result, while the black dots denote the numerical data. Panel (b) displays the intensity distribution at a fixed distance $z=100$, where blue bars and black diagonal lines indicate analytical and numerical results, respectively.

5. Conclusions

This work investigates the complex dynamics in waveguide arrays by extending the analysis beyond nearest-neighbor interactions to include higher-order couplings. We derive an analytical expression in terms of a generalized Bessel-like function, structurally analogous to the first-neighbor case in an infinite array. Our results show that, for sufficiently strong higher-order coupling, a significant fraction of the propagating light remains localized around the initially excited waveguide. Finally, we discuss the passage from discrete to continuous formulations relating the field amplitudes and the Fourier-series coefficients of a specified function and illustrate these concepts with figures depicting intensity distributions under varied coupling scenarios.