Dynamics of Interacting Colloidal Particles Using the IIR Recursive Digital Filter Method
Abstract
1. Introduction
2. Resolution Method
2.1. The Non-Hydrodynamic Forces
2.2. The Hydrodynamic Interactions
2.3. Expressions of the Mobility Matrix Coefficients
2.3.1. The Quasi-Point Approximation (QPA)
2.3.2. Rotne–Prager–Yamakawa (RPY) Approximation
- At the limit where , the Rotne–Prager–Yamakawa mobility matrix tends to be the mobility matrix of the point approximation. This turns out to be legitimate and corresponds to the so-called far-field hypothesis.
- When both spheres have the same radius, the following expression for the generalized mobility matrix is obtained:
2.4. Equations of Motion
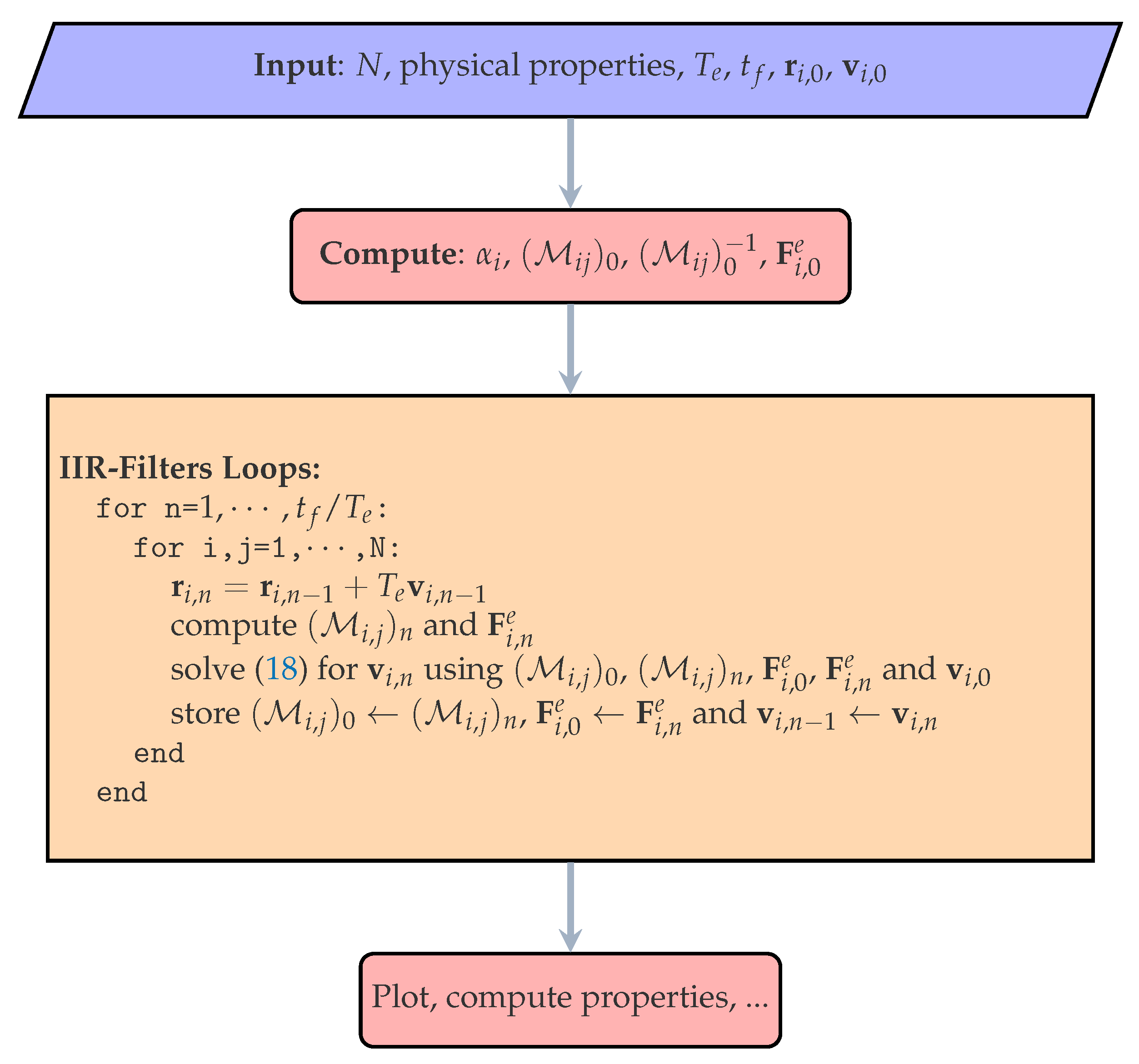
2.5. Numerical Resolution Using the IIR-Filter Method
2.6. Full Dynamics versus Long-Time Dynamics
3. Sedimentation of Two Identical Colloidal Particles
3.1. Presentation
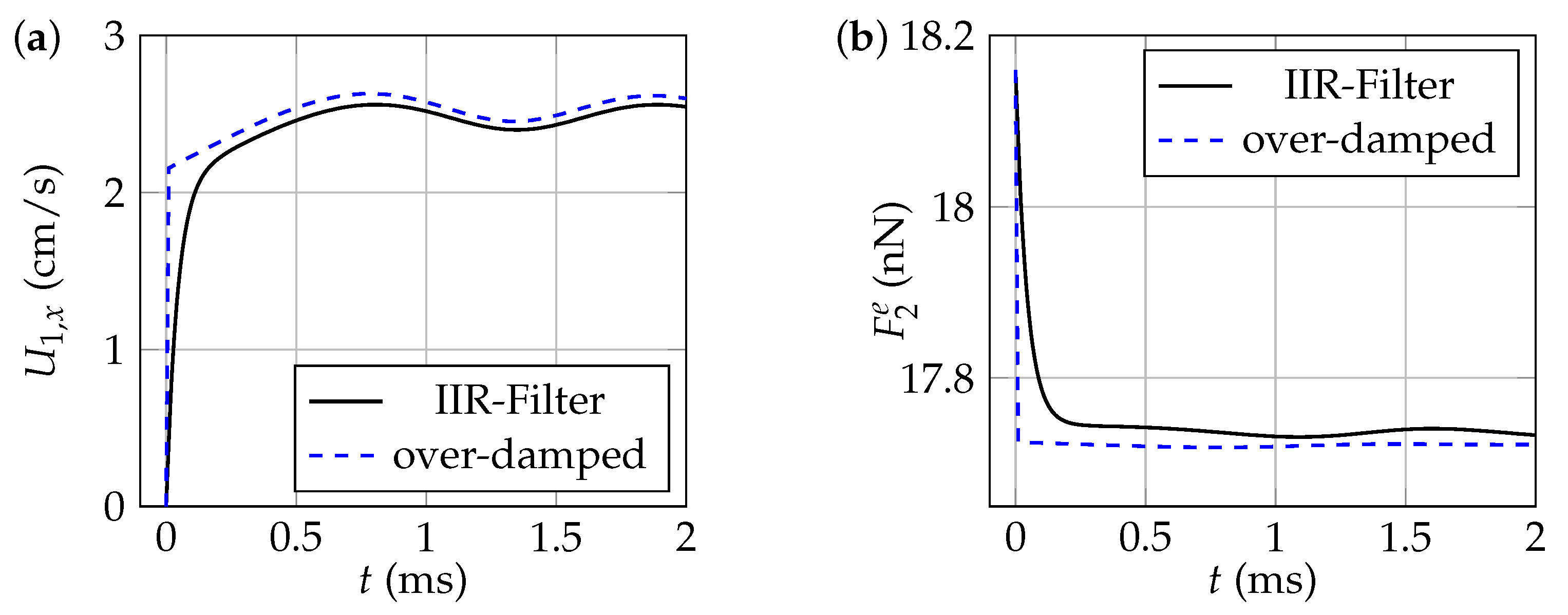
3.2. The Results
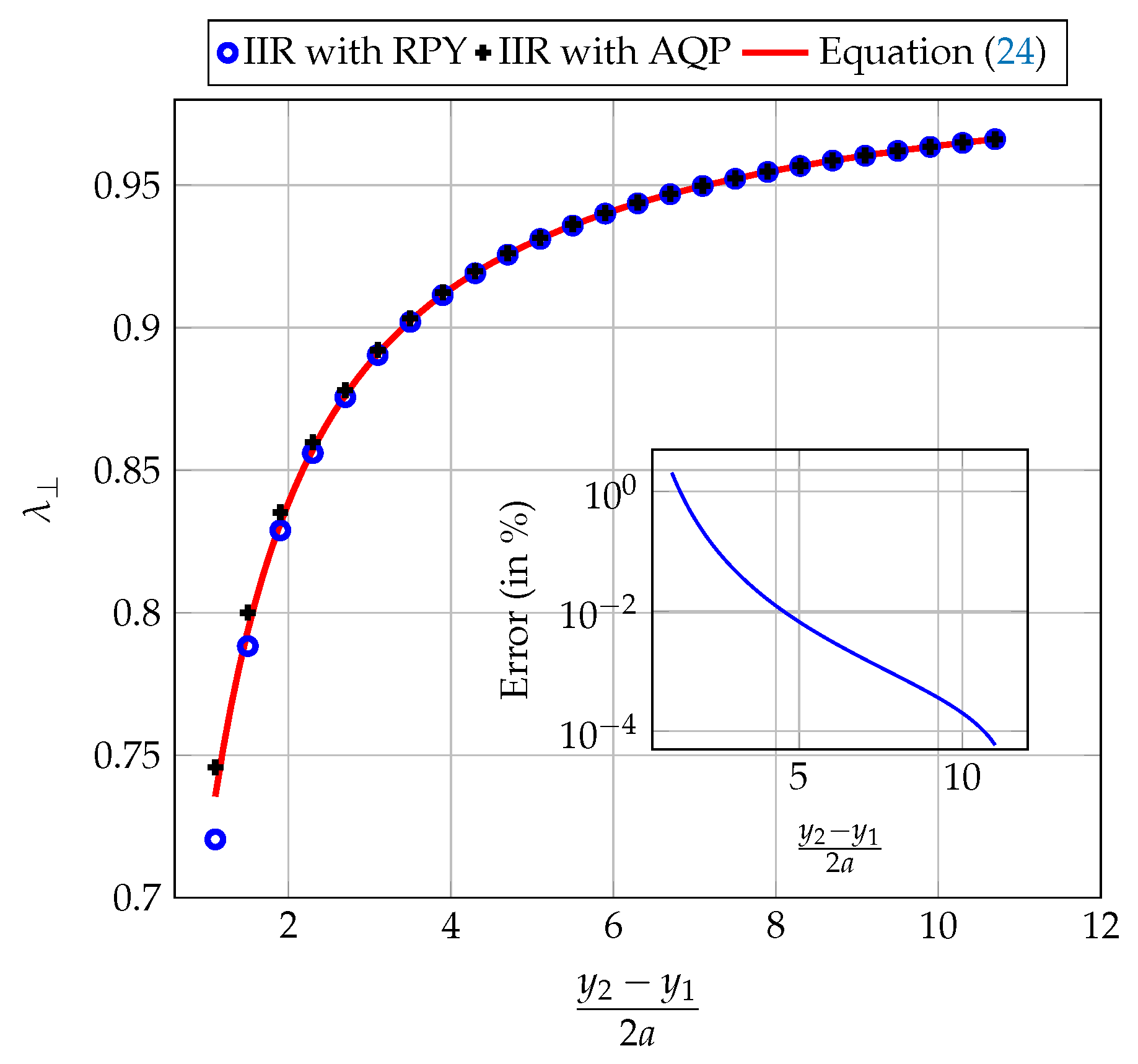
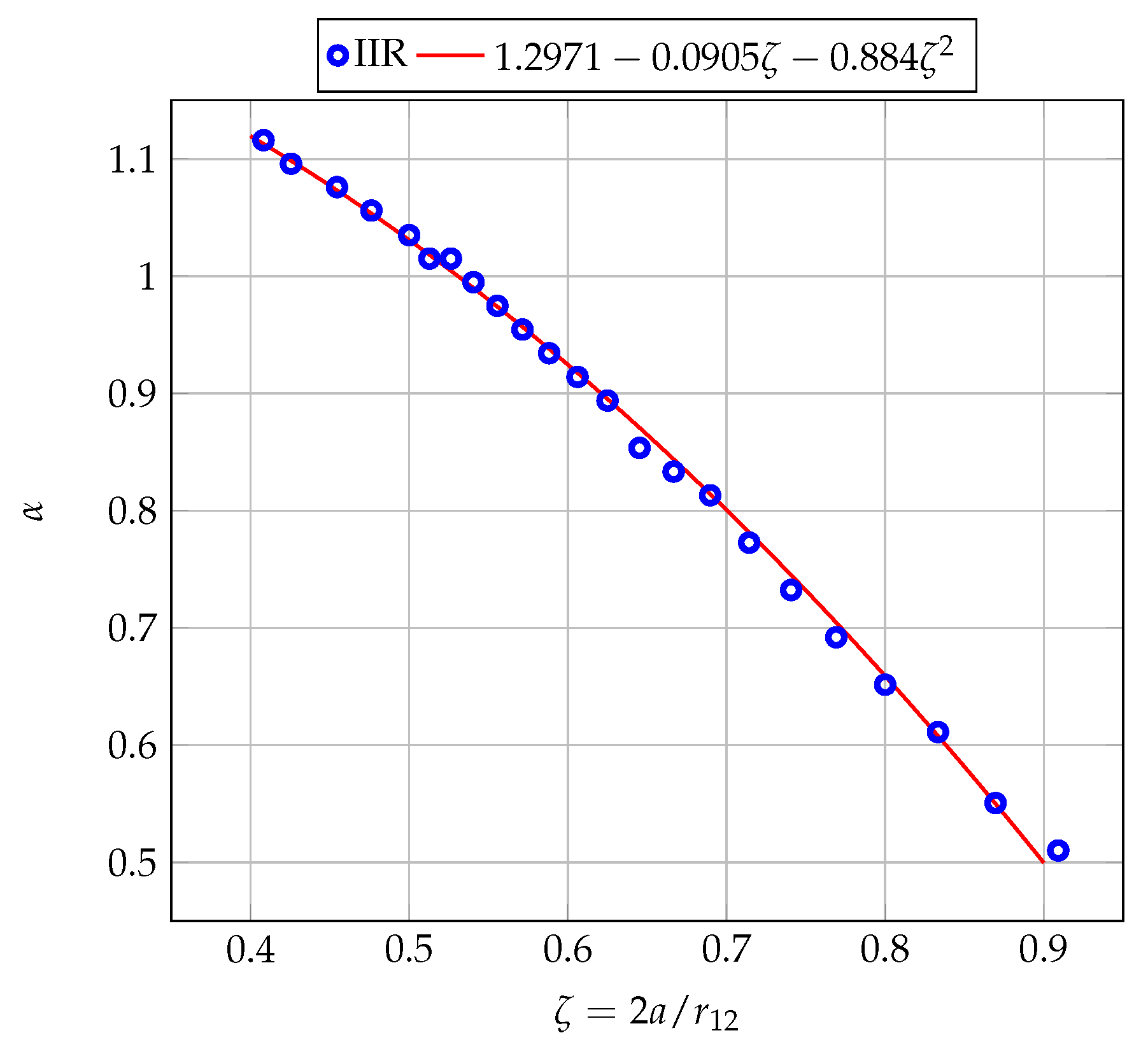
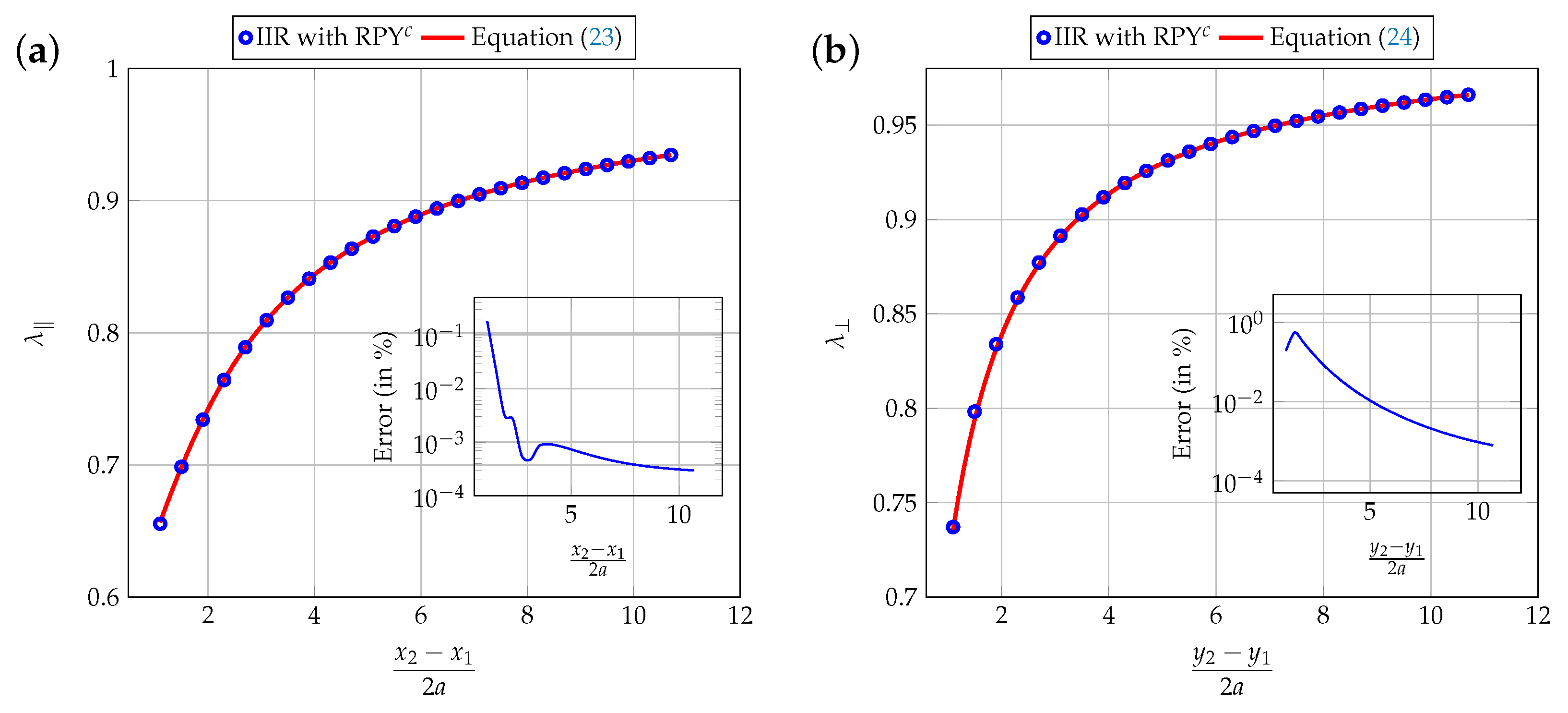
3.3. Correction to the RPY Mobility Matrix
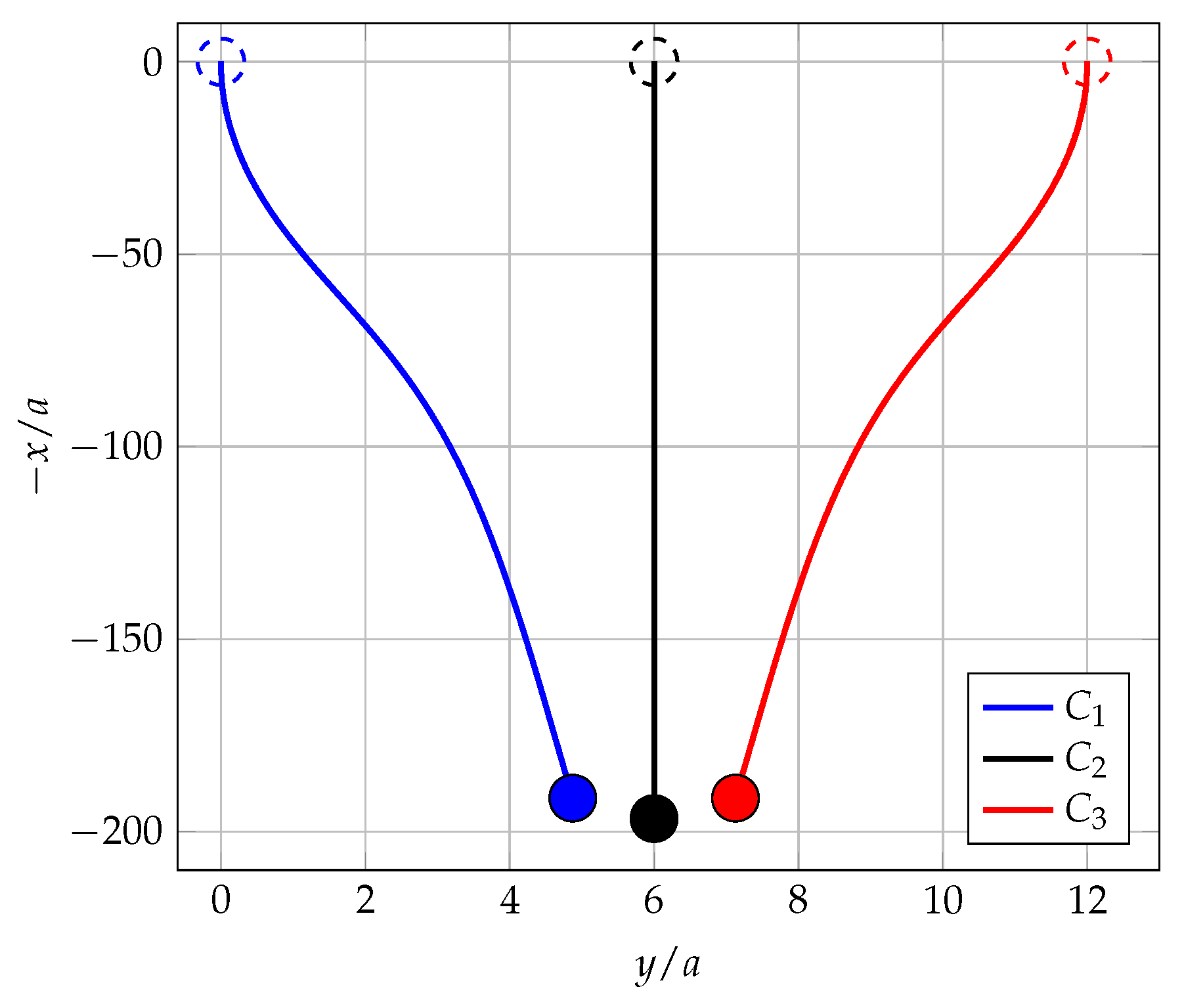
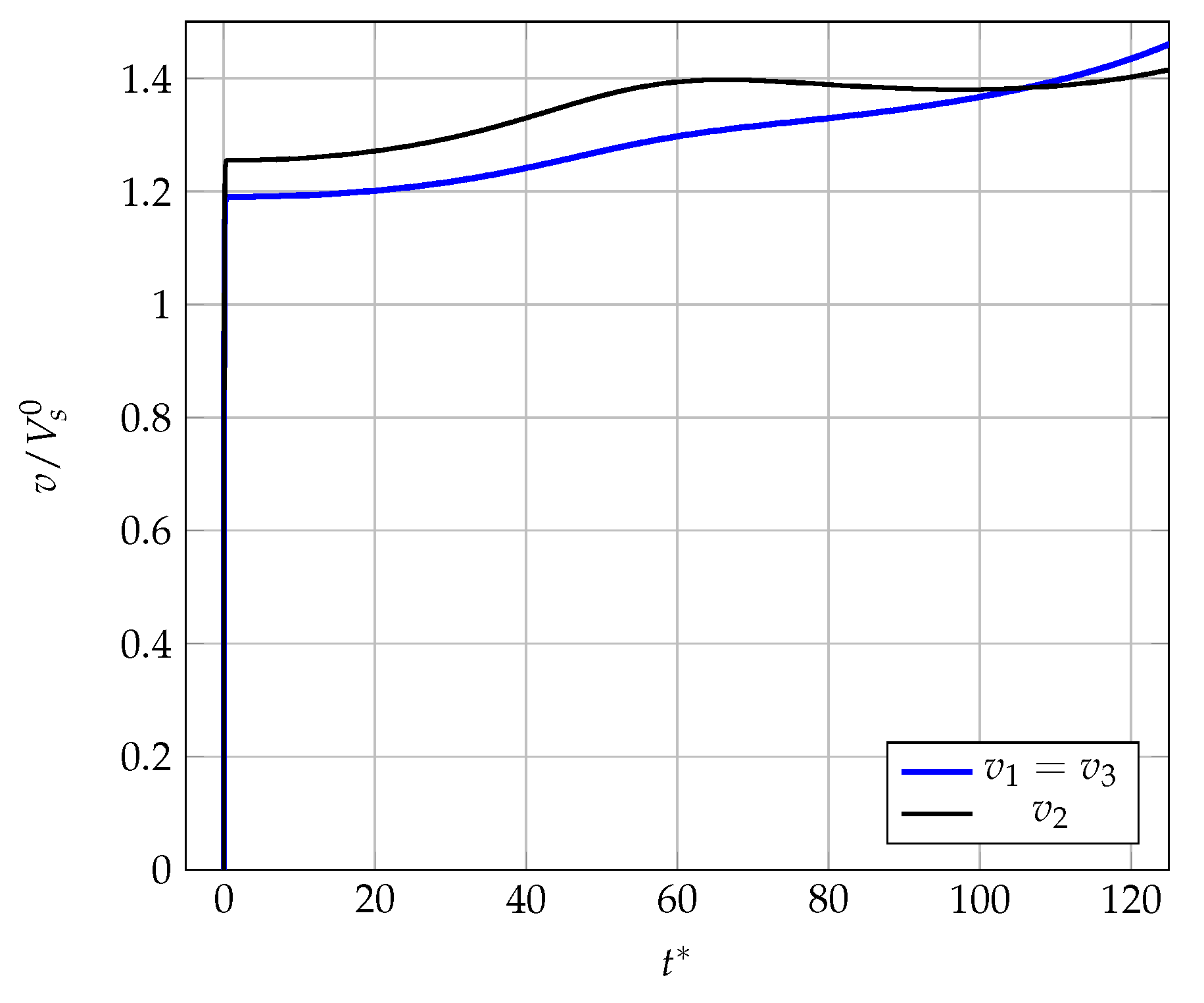
4. Sedimentation of Three Particles
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B

References
- Wacholder, E.; Sather, N.F. The hydrodynamic interaction of two unequal spheres moving under gravity through quiescent viscous fluid. J. Fluid Mech. 1974, 65, 417–437. [Google Scholar] [CrossRef]
- Brady, J.F.; Bossis, G. Stokesian Dynamics. Annu. Rev. Fluid Mech. 1988, 20, 111–157. [Google Scholar] [CrossRef]
- Sierou, A. Handbook of Materials Modeling; Chapter Stokesian Dynamics Simulations for Particle Laden Flows; Springer: Berlin/Heidelberg, Germany, 2005; pp. 2607–2617. [Google Scholar]
- Laura, S.; Paul, B. Colloidal dynamics in polymer solutions: Optical two-point microrheology measurements. Faraday Discuss. 2003, 123, 323–334. [Google Scholar] [CrossRef][Green Version]
- Waigh, T.A. Microrheology of complex fluids. Rep. Prog. Phys. 2005, 68, 685. [Google Scholar] [CrossRef]
- Lahboub, D.; Heyd, R.; Bakak, A.; Lotfi, M.; Koumina, A. Solution of Basset integro-differential equations by IIR digital filters. Alex. Eng. J. 2022, 61, 11899–11911. [Google Scholar] [CrossRef]
- Margaret, S.; George, B.J. The Motion of Two Spheres in a Viscous Fluid. Proc. R. Soc. A Math. Phys. Eng. Sci. 1926, 111, 110–116. [Google Scholar]
- Goldman, A.J.; Cox, R.G.; Brenner, H. The slow motion of two identical arbitrarily oriented spheres through a viscous fluid. Chem. Eng. Sci. 1966, 21, 1151–1170. [Google Scholar] [CrossRef]
- Brenner, H. The slow motion of a sphere through a viscous fluid towards a plane surface. Chem. Eng. Sci. 1961, 16, 242–251. [Google Scholar] [CrossRef]
- Guyon, E.; Hulin, J.P.; Petit, L.; Mitescu, C. Physical Hydrodynamics, 2nd ed.; Oxford University Press: Oxford, UK, 2015. [Google Scholar] [CrossRef]
- O’Neill, M. Some Motions in Incompressible Liquid Generated by the Movement of Spheres; University of London: London, UK, 2013. [Google Scholar]
- Wakiya, S. Slow Motions of a Viscous Fluid around Two Spheres. J. Phys. Soc. Jpn. 1967, 22, 1101–1109. [Google Scholar] [CrossRef]
- Ganatos, P.; Pfeffer, R.; Weinbaum, S. A numerical-solution technique for three-dimensional Stokes flows, with application to the motion of strongly interacting spheres in a plane. J. Fluid Mech. 1978, 84, 79–111. [Google Scholar] [CrossRef]
- Gluckman, M.J.; Pfeffer, R.; Weinbaum, S. A new technique for treating multiparticle slow viscous flow: Axisymmetric flow past spheres and spheroids. J. Fluid Mech. 1971, 50, 705–740. [Google Scholar] [CrossRef]
- Leichtberg, S.; Pfeffer, R.; Weinbaum, S. Stokes flow past finite coaxial clusters of spheres in a circular cylinder. Int. J. Multiph. Flow 1976, 3, 147–169. [Google Scholar] [CrossRef]
- Dhont, J.K.G. An Introduction to Dynamics of Colloids; Elsevier: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Davies, C.N.L. Low Reynolds Number Hydrodynamics, with Special Applications to Particulate Media: John Happel and Howard Brenner; Second revised Edition; Noordhoff International Publishing: Leyden, IL, USA, 1973. [Google Scholar]
- O’neill, M.E.; Majumdar, R. Asymmetrical slow viscous fluid motions caused by the translation or rotation of two spheres. Part I: The determination of exact solutions for any values of the ratio of radii and separation parameters. Z. Angew. Math. Phys. ZAMP 1970, 21, 164–179. [Google Scholar] [CrossRef]
- Shing, B.C.; Xiangnan, Y. Faxen’s Laws of a Composite Sphere under Creeping Flow Conditions. J. Colloid Interface Sci. 2000, 221, 50–57. [Google Scholar] [CrossRef]
- Wajnryb, E.; Mizerski, K.A.; Zuk, P.J.; Szymczak, P. Generalization of the Rotne–Prager–Yamakawa mobility and shear disturbance tensors. J. Fluid Mech. 2013, 731, R3. [Google Scholar] [CrossRef]
- Zuk, P.J.; Wajnryb, E.; Mizerski, K.A.; Szymczak, P. Rotne–Prager–Yamakawa approximation for different-sized particles in application to macromolecular bead models. J. Fluid Mech. 2014, 741, R5. [Google Scholar] [CrossRef]
- Kim, S.; Mifflin, R.T. The resistance and mobility functions of two equal spheres in low-Reynolds-number flow. Phys. Fluids 1985, 28, 2033–2045. [Google Scholar] [CrossRef]
- Jeffrey, D.J.; Onishi, Y. Calculation of the resistance and mobility functions for two unequal rigid spheres in low-Reynolds-number flow. J. Fluid Mech. 1984, 139, 261–290. [Google Scholar] [CrossRef]
- Lamb, H. Hydrodynamics; Cambridge University Press: Cambridge, UK, 1932. [Google Scholar]
- Perkins, G.S.; Jones, R.B. Hydrodynamic interaction of a spherical particle with a planar boundary: II. Hard wall. Phys. A Stat. Mech. Its Appl. 1992, 189, 447–477. [Google Scholar] [CrossRef]
- Beenakker, C.W.J.; Van Saarloos, W.; Mazur, P. Many-sphere hydrodynamic interactions: III. The influence of a plane wall. Phys. A Stat. Mech. Its Appl. 1984, 127, 451–472. [Google Scholar] [CrossRef]
- van Saarloos, W.; Mazur, P. Many-sphere hydrodynamic interactions: II. Mobilities at finite frequencies. Phys. A Stat. Mech. Its Appl. 1983, 120, 77–102. [Google Scholar] [CrossRef]
- Heyd, R. Real-time heat conduction in a self-heated composite slab by Padé filters. Int. J. Heat Mass Transf. 2014, 71, 606–614. [Google Scholar] [CrossRef]
- Lotfi, M.; Mezrigui, L.; Heyd, R. Study of heat conduction through a self-heated composite cylinder by Laplace transfer functions. Appl. Math. Model. 2016, 40, 10360–10376. [Google Scholar] [CrossRef]
- Ambardar, A. Analog and Digital Signal Processing, 2nd ed.; Brooks/Cole: Pacific Grove, CA, USA, 1999. [Google Scholar]
- Durlofsky, L.; Brady, J.F.; Bossis, G. Dynamic simulation of hydrodynamically interacting particles. J. Fluid Mech. 1987, 180, 21–49. [Google Scholar] [CrossRef]
- Chauvin, C. Influence des Forces D’interactions Particulaires dans la Simulation Lagrangienne du Comportement de Particules en Sédimentation et Écoulements Turbulents. Ph.D. Dissertation, University of Rouen, Rouen, France, 1991. [Google Scholar]









Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lahboub, D.; Heyd, R.; Lotfi, M.; Bakak, A.; Koumina, A. Dynamics of Interacting Colloidal Particles Using the IIR Recursive Digital Filter Method. Dynamics 2024, 4, 506-525. https://doi.org/10.3390/dynamics4030027
Lahboub D, Heyd R, Lotfi M, Bakak A, Koumina A. Dynamics of Interacting Colloidal Particles Using the IIR Recursive Digital Filter Method. Dynamics. 2024; 4(3):506-525. https://doi.org/10.3390/dynamics4030027
Chicago/Turabian StyleLahboub, Driss, Rodolphe Heyd, Mohamed Lotfi, Abderrahim Bakak, and Abdelaziz Koumina. 2024. "Dynamics of Interacting Colloidal Particles Using the IIR Recursive Digital Filter Method" Dynamics 4, no. 3: 506-525. https://doi.org/10.3390/dynamics4030027
APA StyleLahboub, D., Heyd, R., Lotfi, M., Bakak, A., & Koumina, A. (2024). Dynamics of Interacting Colloidal Particles Using the IIR Recursive Digital Filter Method. Dynamics, 4(3), 506-525. https://doi.org/10.3390/dynamics4030027







