Auto-Correlation Functions of Chaotic Binary Sequences Obtained by Alternating Two Binary Functions
Abstract
1. Introduction
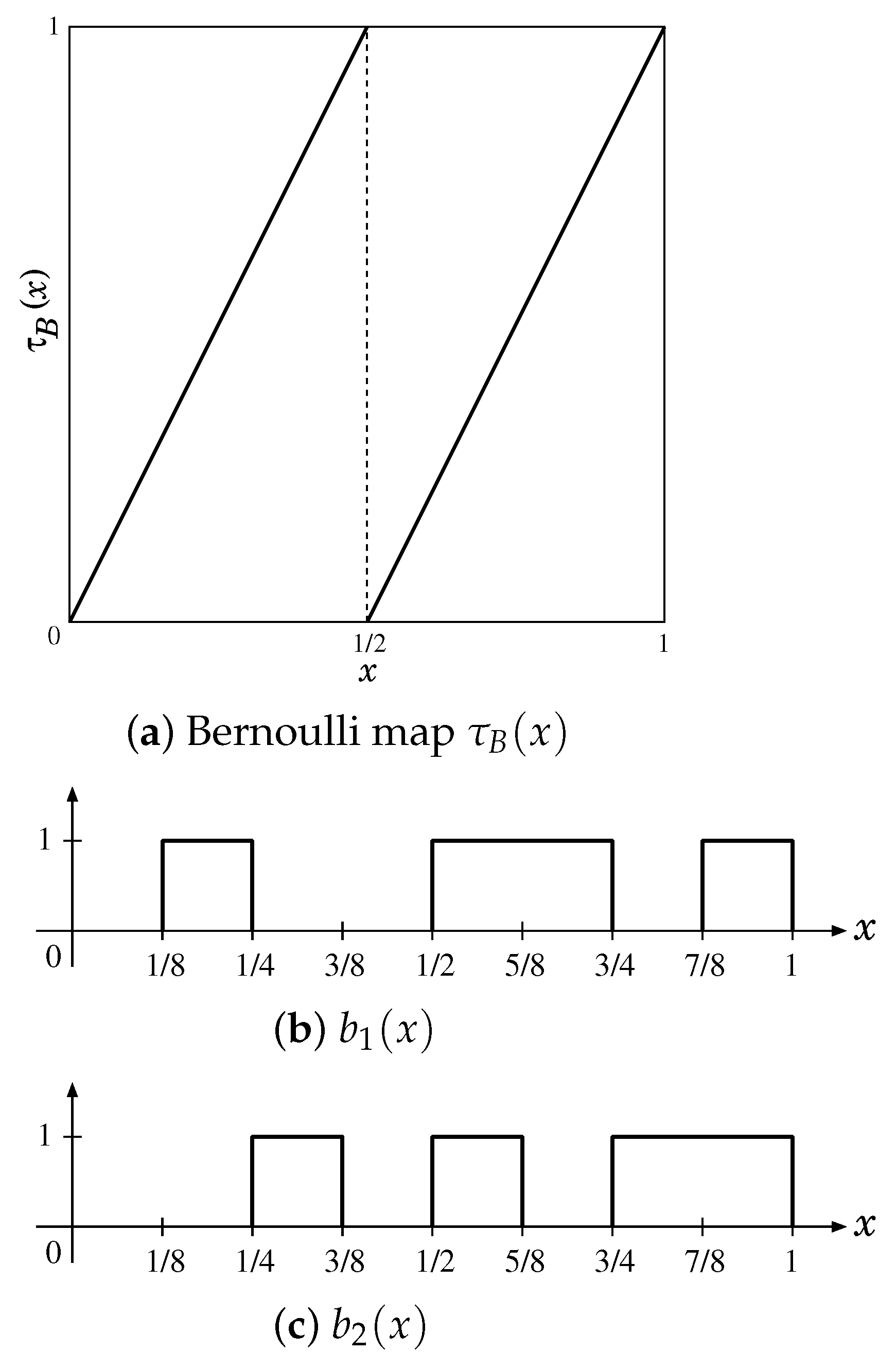
2. Chaotic Binary Sequences Based on a One-Dimensional Map and a Binary Function
3. Chaotic Binary Sequences Obtained by Alternating Two Binary Functions
3.1. Method 1
3.2. Method 2
4. Numerical Experiments
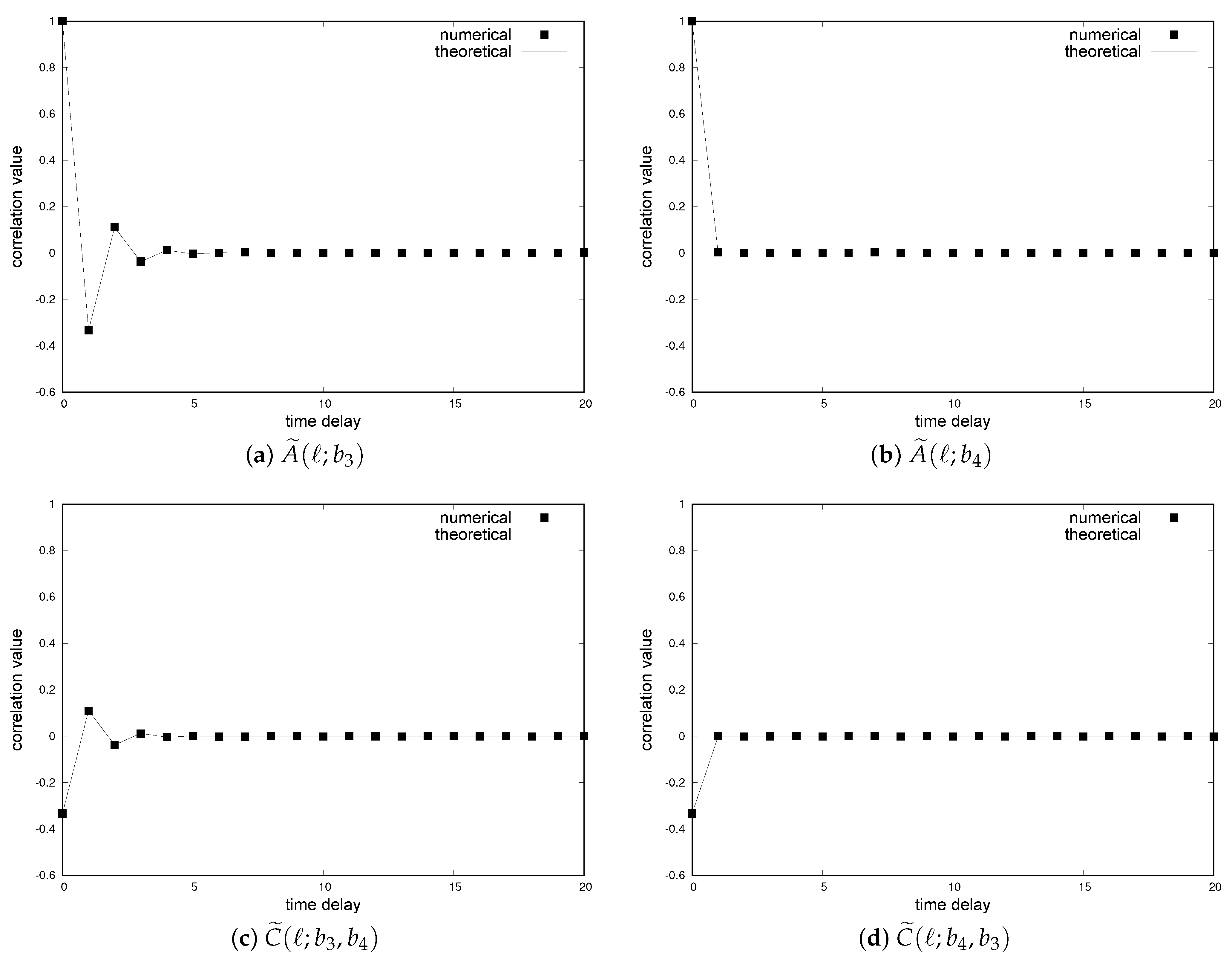
4.1. Bernoulli Map and Binary Functions
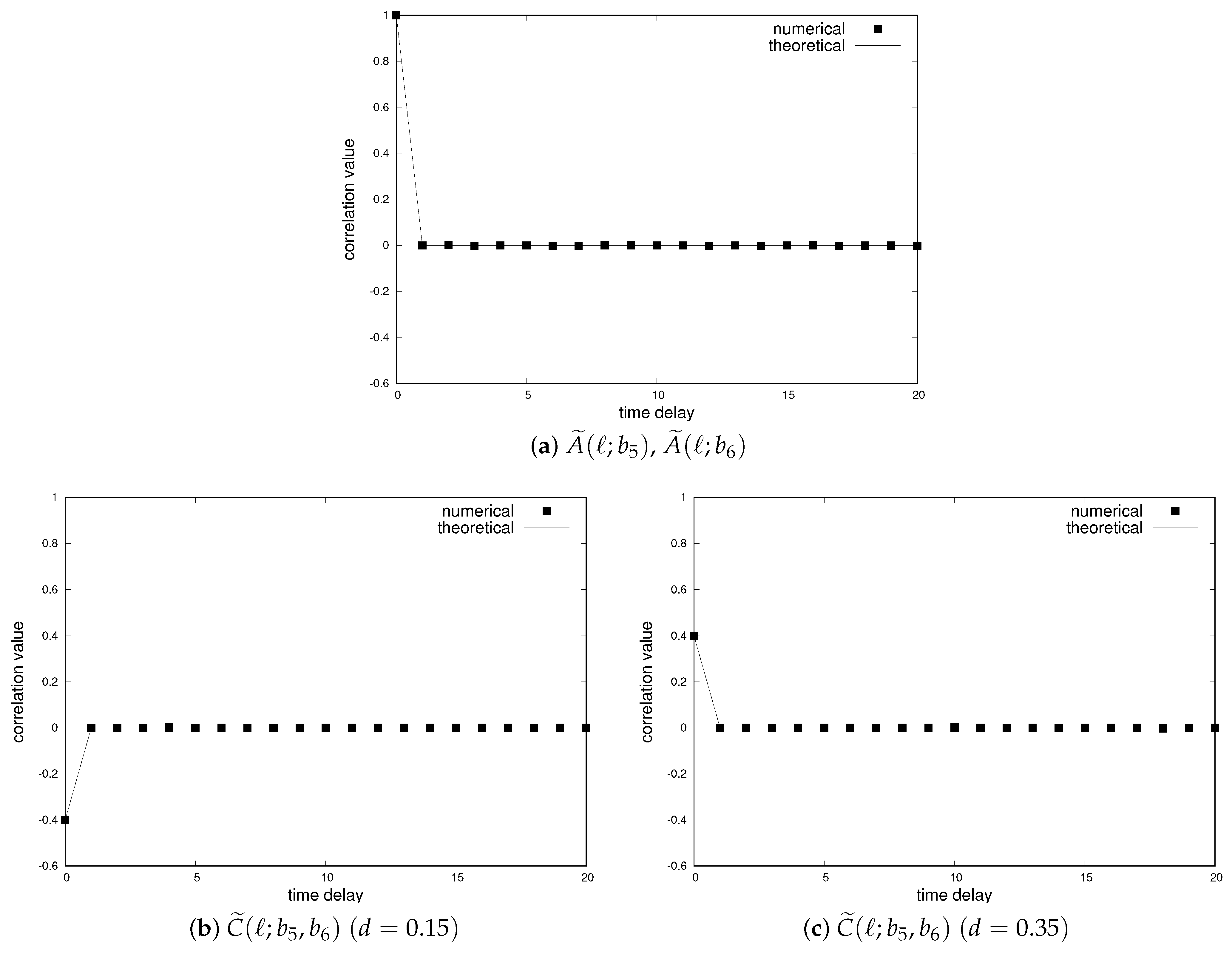
4.2. Piecewise Linear Map with Three Sections and Binary Functions
4.3. Tent Map and Binary Functions
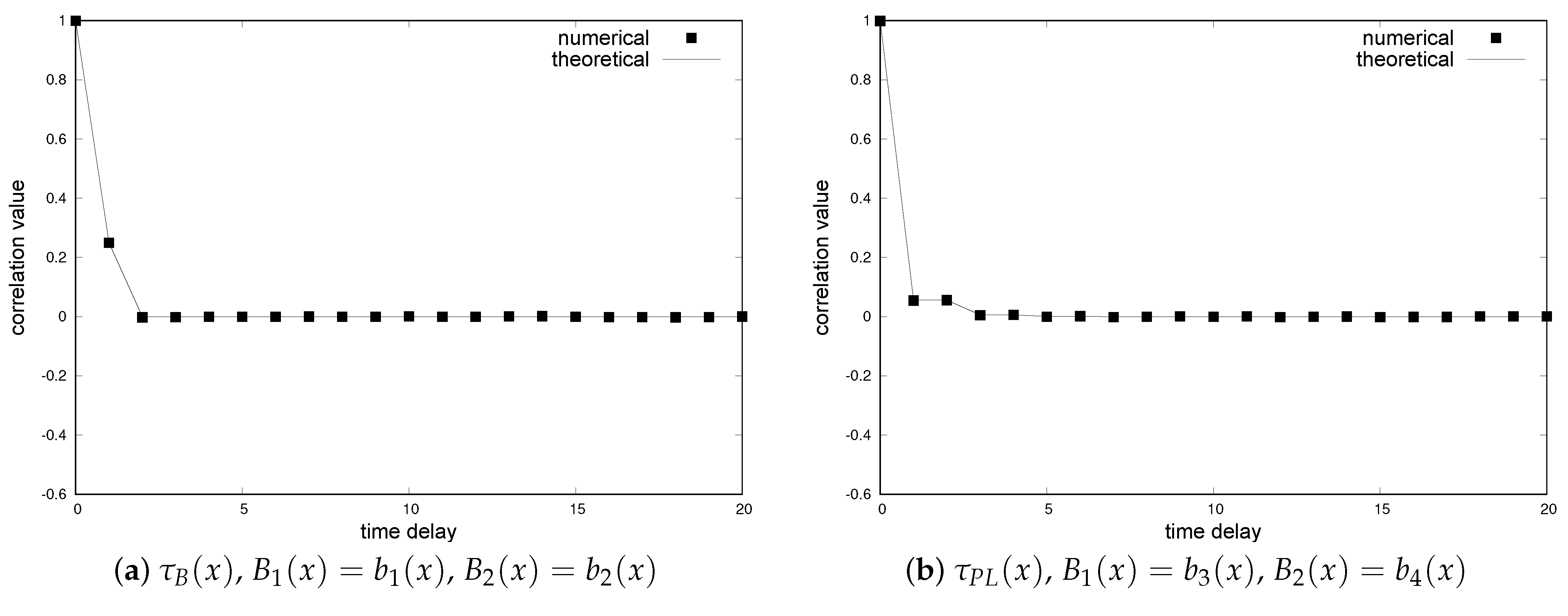
4.4. Auto-Correlation Functions of New Binary Sequences by Method 1 and Method 2
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Derivation of Auto-/Cross-Correlation Functions of Chaotic Binary Sequences Used in Numerical Experiments
Appendix A.1. Correlation Functions of Chaotic Binary Sequences Generated by Bernoulli Map
Appendix A.2. Correlation Functions of Chaotic Binary Sequences Generated by PL Map Defined by (28)
Appendix A.3. Correlation Functions of Chaotic Binary Sequences Generated by Tent Map
References
- Lasota, A.; Mackey, M.C. Chaos, Fractals, and Noise; Springer: New York, NY, USA, 1994. [Google Scholar]
- Boyarsky, A.; Góra, P. Laws of Chaos; Birkhäuser Boston: Boston, MA, USA, 1997. [Google Scholar]
- Gerosa, A.; Bernardini, R.; Pietri, S. A fully integrated chaotic system for the generation of truly random numbers. IEEE Trans. Circuits Syst. I 2001, 49, 993–1000. [Google Scholar] [CrossRef]
- Stojanovski, T.; Kocarev, L. Chaos-based random number generators—Part I: Analysis. IEEE Trans. Circuits Syst. I 2001, 48, 281–288. [Google Scholar] [CrossRef]
- Cicek, I.; Pusane, A.E.; Dundar, G. A novel design method for discrete time chaos based true random number generators. Integr. VLSI J. 2014, 47, 38–47. [Google Scholar] [CrossRef]
- Li, C.; Feng, B.; Li, S.; Kurths, J.; Chen, G. Dynamic analysis of digital chaotic maps via state-mapping networks. IEEE Trans. Circuits Syst. I 2019, 66, 2322–2335. [Google Scholar] [CrossRef]
- Kennedy, M.P.; Rovatti, R.; Setti, G. (Eds.) Chaotic Electronics in Telecommunications; CRC: Boca Raton, FL, USA, 2000. [Google Scholar]
- Liu, Z.; Tang, J.; Yu, J. An application of chaos: Generating binary pseudo-random sequences. In Proceedings of the 1988 IEEE International Symposium on Circuits and Systems, Espoo, Finland, 7–9 June 1988; pp. 1–3. [Google Scholar]
- Kohda, T.; Tsuneda, A. Statistics of chaotic binary sequences. IEEE Trans. Inf. Theory 1997, 43, 104–112. [Google Scholar] [CrossRef]
- Sakai, H.; Tokumaru, H. Autocorrelations of a certain chaos. IEEE Trans. Acoust. Speech Signal Process 1980, 28, 588–590. [Google Scholar] [CrossRef]
- Rovatti, R.; Mazzini, G. Interference in DS-CDMA systems with exponentially vanishing autocorrelations: Chaos-based spreading is optimal. Electron. Lett. 1998, 34, 1911–1913. [Google Scholar] [CrossRef]
- Mazzini, G.; Rovatti, R.; Setti, G. Interference minimization by autocorrelation shaping in asynchronous DS-CDMA systems: Chaos-based spreading is nearly optimal. Electron. Lett. 1999, 35, 1054–1055. [Google Scholar] [CrossRef]
- Tsuneda, A. Design of binary sequences with tunable exponential autocorrelations and run statistics based on one-dimensional chaotic maps. IEEE Trans. Circuits Syst. I 2005, 52, 454–462. [Google Scholar] [CrossRef]
- Yang, C.A.; Yao, K.; Umeno, K.; Biglieri, E. Using deterministic chaos for superefficient Monte-Carlo simulations. IEEE Circuits Syst. Mag. 2013, 13, 26–35. [Google Scholar] [CrossRef]
- Souza, C.E.C.; Chaves, D.P.B.; Pimentel, C. One-dimensional pseudo-chaotic sequences based on the discrete Arnold’s cat map over Z3m. IEEE Trans. Circuits Syst. II 2021, 68, 491–495. [Google Scholar]
- Paul, P.S.; Sadia, M.; Hossain, M.R.; Muldrey, B.; Hasan, M.S. Cascading CMOS-based chaotic maps for improved performance and its application in efficient RNG design. IEEE Access 2022, 10, 33758–33770. [Google Scholar] [CrossRef]
- Tang, J.; Zhang, Z.; Chen, P.; Huang, Z.; Huang, T. A simple chaotic model with complex chaotic behaviors and its hardware implementation. IEEE Trans. Circuits Syst. I 2023, 70, 3676–3688. [Google Scholar] [CrossRef]
- Tsuneda, A. Various Auto-correlation functions of m-bit random numbers generated from chaotic binary sequences. Entropy 2021, 23, 1295. [Google Scholar] [CrossRef]





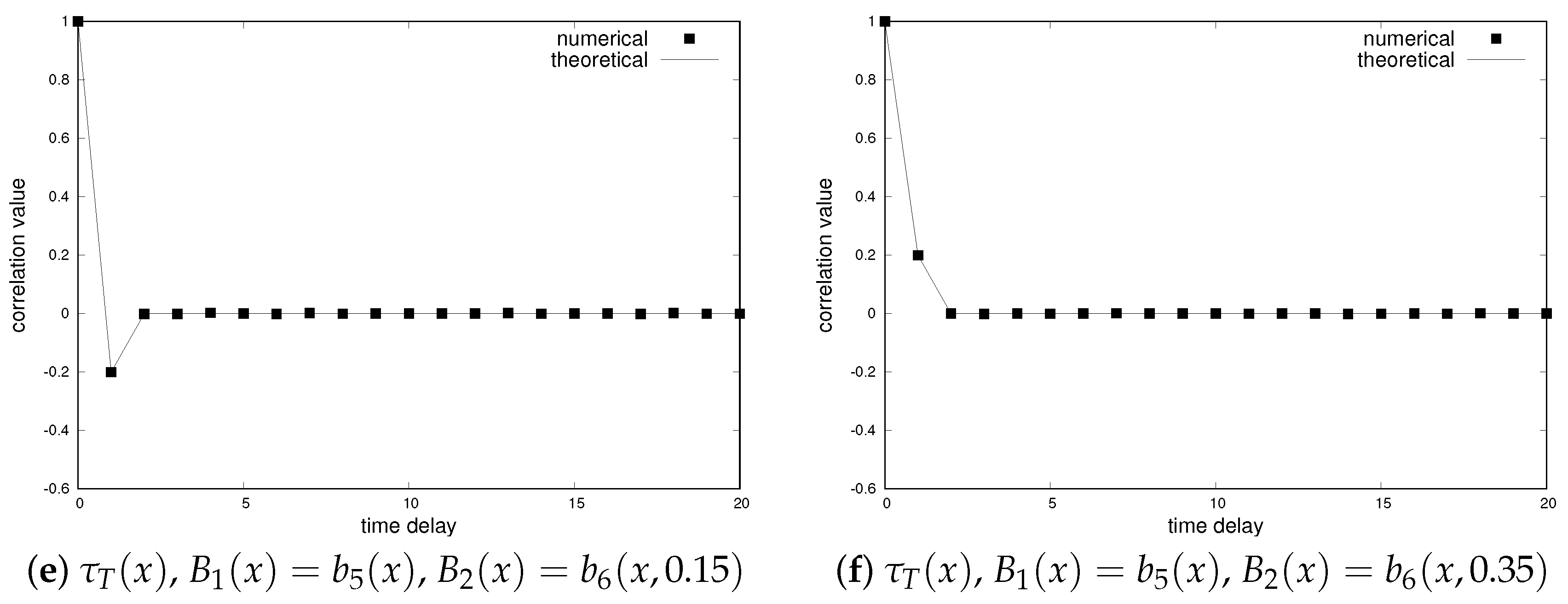
| 1 | 0 | |||
| 1 | 0 | 0 | ||
| 0 | 0 | 0 | ||
| 0 | 0 |
| 1 | 0 | 0 | 0 | |
| 0 | 0 | 0 | ||
| 1 | 0 | |
| 1 | 0 | |
| 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsuneda, A. Auto-Correlation Functions of Chaotic Binary Sequences Obtained by Alternating Two Binary Functions. Dynamics 2024, 4, 272-286. https://doi.org/10.3390/dynamics4020016
Tsuneda A. Auto-Correlation Functions of Chaotic Binary Sequences Obtained by Alternating Two Binary Functions. Dynamics. 2024; 4(2):272-286. https://doi.org/10.3390/dynamics4020016
Chicago/Turabian StyleTsuneda, Akio. 2024. "Auto-Correlation Functions of Chaotic Binary Sequences Obtained by Alternating Two Binary Functions" Dynamics 4, no. 2: 272-286. https://doi.org/10.3390/dynamics4020016
APA StyleTsuneda, A. (2024). Auto-Correlation Functions of Chaotic Binary Sequences Obtained by Alternating Two Binary Functions. Dynamics, 4(2), 272-286. https://doi.org/10.3390/dynamics4020016










