Author Contributions
Conceptualization, T.O. and J.G.R.; methodology, T.O. and J.G.R.; software, J.G.R.; validation, J.G.R.; formal analysis, J.G.R., T.O. and O.J.U.; investigation, J.G.R.; resources, T.O. and C.Q.Z.; data curation, J.G.R.; writing—original draft preparation, J.G.R.; writing—review and editing, O.J.U., T.O. and J.G.R.; visualization, J.G.R.; supervision, T.O.; project administration, T.O. and C.Q.Z.; funding acquisition, T.O. and C.Q.Z. All authors have read and agreed to the published version of the manuscript.
Figure 1.
Example of 6800 simulated pellets being dropped in the drop test set up and coming to rest with red highlighted angle of repose.
Figure 1.
Example of 6800 simulated pellets being dropped in the drop test set up and coming to rest with red highlighted angle of repose.
Figure 2.
Left angle of repose vs. pellet diameter trendline comparing simulation and experimental results.
Figure 2.
Left angle of repose vs. pellet diameter trendline comparing simulation and experimental results.
Figure 3.
Right angle of repose vs. pellet diameter trendline comparing simulation and experimental results.
Figure 3.
Right angle of repose vs. pellet diameter trendline comparing simulation and experimental results.
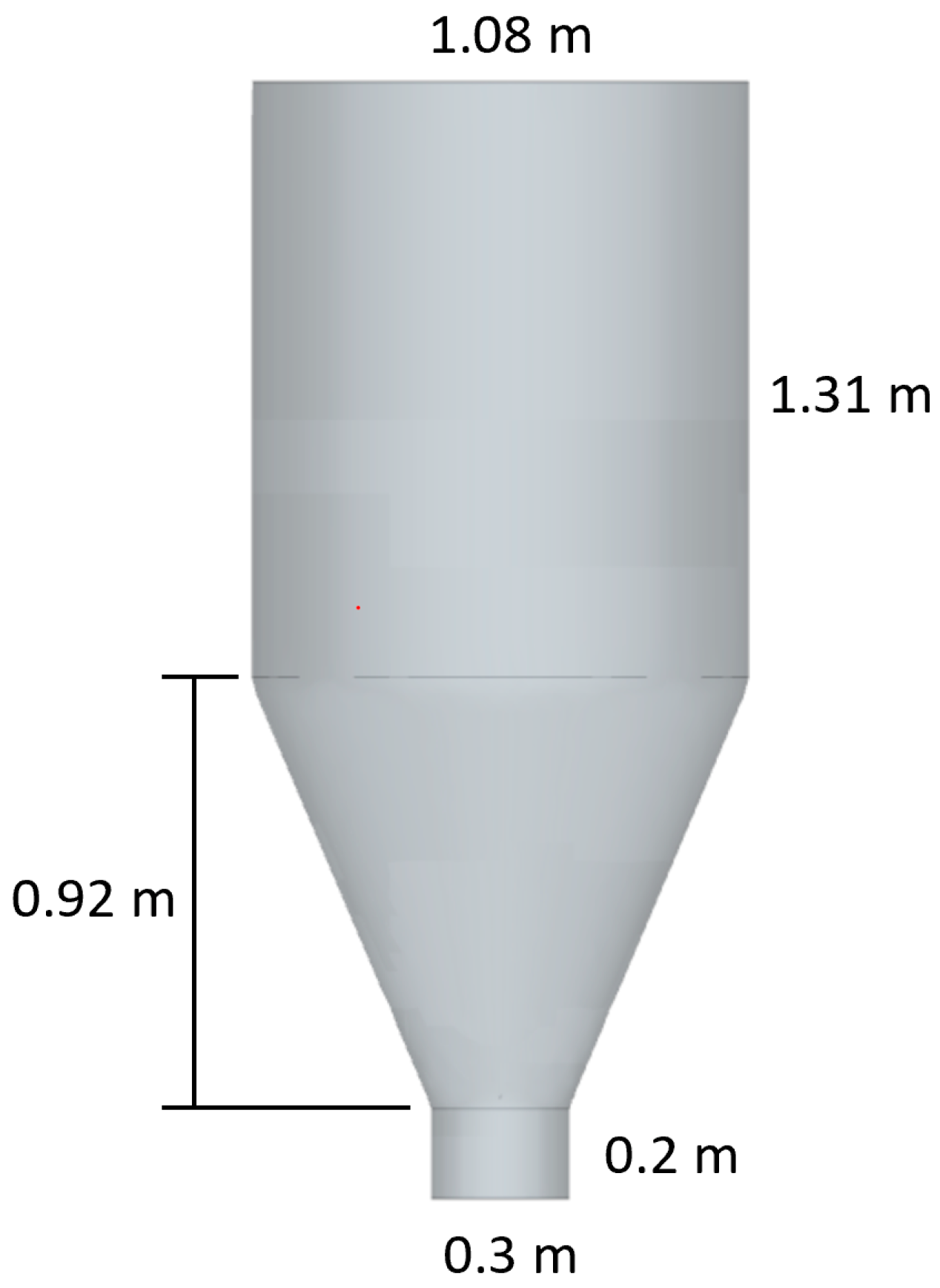
Figure 4.
Full hopper geometry (A) and computational domain geometry and boundary conditions (B).
Figure 4.
Full hopper geometry (A) and computational domain geometry and boundary conditions (B).
Figure 5.
Full meshed domain of the feed system hopper (A) and cross-sections of the mesh (B).
Figure 5.
Full meshed domain of the feed system hopper (A) and cross-sections of the mesh (B).
Figure 6.
Outer, side, and inner views (from left to right) of the feed system hopper filled with iron ore pellets (grey), heavy pellets to replicate fill height (red), and highlighted upper and lower regions where metrics are tracked.
Figure 6.
Outer, side, and inner views (from left to right) of the feed system hopper filled with iron ore pellets (grey), heavy pellets to replicate fill height (red), and highlighted upper and lower regions where metrics are tracked.
Figure 7.
Dimensions of the small hopper used for the computational cost reduction study.
Figure 7.
Dimensions of the small hopper used for the computational cost reduction study.
Figure 8.
Simplified hopper domain to gather pellet bulk flow metrics for actual and modified pellet size distributions (A); reduced hopper domain with symmetry conditions applied to compare bulk flow impact (B).
Figure 8.
Simplified hopper domain to gather pellet bulk flow metrics for actual and modified pellet size distributions (A); reduced hopper domain with symmetry conditions applied to compare bulk flow impact (B).
Figure 9.
Force distribution on the surface of the flow aid insert during baseline operation with an arrow pointing to the widest part of flow aid where the flow aid begins to narrow (A); force distribution on the hopper walls during baseline operation (B).
Figure 9.
Force distribution on the surface of the flow aid insert during baseline operation with an arrow pointing to the widest part of flow aid where the flow aid begins to narrow (A); force distribution on the hopper walls during baseline operation (B).
Figure 10.
Contour of the void fraction within the hopper during baseline operation.
Figure 10.
Contour of the void fraction within the hopper during baseline operation.
Figure 11.
Pellet velocity during baseline operation.
Figure 11.
Pellet velocity during baseline operation.
Figure 12.
Average forces on flow aid for the baseline (A) and 5.5% moisture (B) cases with arrows pointing to the widest portion of the flow aid.
Figure 12.
Average forces on flow aid for the baseline (A) and 5.5% moisture (B) cases with arrows pointing to the widest portion of the flow aid.
Figure 13.
Average wall forces for the baseline (A) and 5.5% moisture (B) cases, with dotted horizontal lines added to highlight differences in force distribution shape and location.
Figure 13.
Average wall forces for the baseline (A) and 5.5% moisture (B) cases, with dotted horizontal lines added to highlight differences in force distribution shape and location.
Figure 14.
Average force on hopper walls vs. normalized hopper height for the baseline and 5.5% moisture pellet flow.
Figure 14.
Average force on hopper walls vs. normalized hopper height for the baseline and 5.5% moisture pellet flow.
Figure 15.
Contours of the void fraction in the baseline (A) and 5.5% moisture (B) cases.
Figure 15.
Contours of the void fraction in the baseline (A) and 5.5% moisture (B) cases.
Figure 16.
Void fraction vs. normalized height of the hopper for baseline and 5.5% moisture pellet flow.
Figure 16.
Void fraction vs. normalized height of the hopper for baseline and 5.5% moisture pellet flow.
Figure 17.
Pellet velocity profile for the baseline (A) and 5.5% moisture (B) cases.
Figure 17.
Pellet velocity profile for the baseline (A) and 5.5% moisture (B) cases.
Figure 18.
Pellet velocity vs. normalized height of hopper for both baseline operation and 5.5% moisture pellet flow.
Figure 18.
Pellet velocity vs. normalized height of hopper for both baseline operation and 5.5% moisture pellet flow.
Figure 19.
Temperature of pellets as they exit the domain.
Figure 19.
Temperature of pellets as they exit the domain.
Figure 20.
Visual aid to show which pellets bond together.
Figure 20.
Visual aid to show which pellets bond together.
Figure 21.
Feed system filled with 5 additional discrete phases (shown in blue) above flow aid to control bonding and parameterize the percent icy and wet pellets charged in this region, along with dry pellets (shown in grey) and heavy pellets to replicate the fill height of the hopper (shown in red).
Figure 21.
Feed system filled with 5 additional discrete phases (shown in blue) above flow aid to control bonding and parameterize the percent icy and wet pellets charged in this region, along with dry pellets (shown in grey) and heavy pellets to replicate the fill height of the hopper (shown in red).
Figure 22.
Baseline flow (A) compared to jammed flow with 33% wet, 33% icy, and 33% dry (B), and jammed with 5% wet, 10% icy, 85% dry (C).
Figure 22.
Baseline flow (A) compared to jammed flow with 33% wet, 33% icy, and 33% dry (B), and jammed with 5% wet, 10% icy, 85% dry (C).
Figure 23.
Velocity of the pellets in the baseline vs. jammed with 33% icy, wet, and dry pellets, and jammed with 10% icy, 5% wet, and 85% dry pellets.
Figure 23.
Velocity of the pellets in the baseline vs. jammed with 33% icy, wet, and dry pellets, and jammed with 10% icy, 5% wet, and 85% dry pellets.
Table 1.
Static and rolling friction coefficients that reproduced experimental angle of repose.
Table 1.
Static and rolling friction coefficients that reproduced experimental angle of repose.
| | Pellet–Pellet | Steel–Pellet [20] |
|---|
| Coefficient of Static Friction | 0.50 | 0.40 |
| Coefficient of Rolling Friction | 0.20 | 0.25 |
Table 2.
Simulation and experimental angle of repose results for differing pellet diameters.
Table 2.
Simulation and experimental angle of repose results for differing pellet diameters.
| | Experiment | Simulation |
|---|
| Diameter (mm) | Left | Right | Left | Right |
|---|
| 5.0 | 36.66 | 36.48 | --- | --- |
| 5.5 | --- | --- | 37.03 | 36.84 |
| 7.0 | 34.96 | 34.75 | 34.94 | 35.69 |
| 9.0 | 33.55 | 33.39 | 33.19 | 33.12 |
Table 3.
Iron ore material and thermal properties [
20,
34,
35].
Table 3.
Iron ore material and thermal properties [
20,
34,
35].
| Iron Ore Pellet Material Properties |
|---|
| Density (kg/m3) | 3948 |
| Poison’s Ratio | 0.25 |
| Young’s Modulus (MPa) | 40 |
| Thermal Conductivity (W/m K) | 1.2 |
| Specific Heat (J/kg K) | 560 |
Table 4.
Properties of operating gas.
Table 4.
Properties of operating gas.
| Gas Properties |
|---|
| Density (kg/m3) | 1.26 |
| Dynamic Viscosity (Pa-s) | 1.788 × 10−5 |
Table 5.
Pellet and steel contact parameters used in DEM model.
Table 5.
Pellet and steel contact parameters used in DEM model.
| | Pellet–Pellet Contact for Baseline and Wet/Icy Charged Pellet Cases | Pellet–Pellet Contact for the High Moisture Case | Pellet–Steel Contact for All Cases [20] |
|---|
| Static Friction Coefficient | 0.50 | 0.90 | 0.40 |
| Coefficient of Restitution [20] | 0.48 | 0.48 | 0.39 |
| Coefficient of Rolling Friction | 0.20 | 0.90 | 0.25 |
Table 6.
Resultant computationally efficient case conditions from the parametric investigation of iron ore pellets flowing through a hopper vs. the original case conditions.
Table 6.
Resultant computationally efficient case conditions from the parametric investigation of iron ore pellets flowing through a hopper vs. the original case conditions.
| | Geometry | Particle Size
Distribution | Particle Diameter Scaling Factor | Normalized Total Particle Number |
|---|
| Reduced baseline | Full | Normal | 1.0 | 1.00 |
| Reduced computational cost | Third | Normal | 2.0 | 0.07 |
Table 7.
Average void, average pellet velocity, and time per iteration for both the reduced baseline case and the computationally efficient case along with percent changes.
Table 7.
Average void, average pellet velocity, and time per iteration for both the reduced baseline case and the computationally efficient case along with percent changes.
| | Average Void
Fraction | Average Pellet
Velocity | Time Elapsed per Iteration |
|---|
| Reduced baseline | 0.365 | 0.339 m/s | 627.78 s |
| Reduced computational cost | 0.376 | 0.295 m/s | 13.44 s |
| Percent change | 3.17% | −12.85% | −97.9% |
Table 8.
Average void fraction and average pellet velocity in upper and lower flow aid regions during baseline operation.
Table 8.
Average void fraction and average pellet velocity in upper and lower flow aid regions during baseline operation.
| | Average Pellet Velocity (m/s) | Average Void Fraction |
|---|
| Upper Flow Aid Region | 0.13 | 0.33 |
| Lower Flow Aid Region | 0.36 | 0.37 |
Table 9.
Percent change in bulk flow properties near the flow aid insert due to assumed increase in friction from moist pellets.
Table 9.
Percent change in bulk flow properties near the flow aid insert due to assumed increase in friction from moist pellets.
| | Average Pellet Velocity% Change | Average Void Fraction% Change |
|---|
| Upper Flow Aid Region | −46.2 | 22.2 |
| Lower Flow Aid Region | −49.5 | 23.1 |
Table 10.
Shear and tensile strength of bonds between pellets.
Table 10.
Shear and tensile strength of bonds between pellets.
| Bond Shear Strength (kPa) | Bond Tensile Strength (kPa) |
|---|
| 600 | 500 |
Table 11.
Minimal amount of icy and wet pellets charged and percent moisture of total charge.
Table 11.
Minimal amount of icy and wet pellets charged and percent moisture of total charge.
| Icy Pellets Charged (5.5% Moisture, Frozen) | Wet Pellets Charged (5.5% Moisture, Liquid) | Dry Pellets
Charged | Mass Percent Moisture of Total Charge (%) |
|---|
| 15% | 0% | 85% | 0.818 |
| 10% | 5% | 85% | 0.818 |