Chaotic van der Pol Oscillator Control Algorithm Comparison
Abstract
1. Introduction
1.1. Novelties Presented
1.2. Main Conclusion of the Study
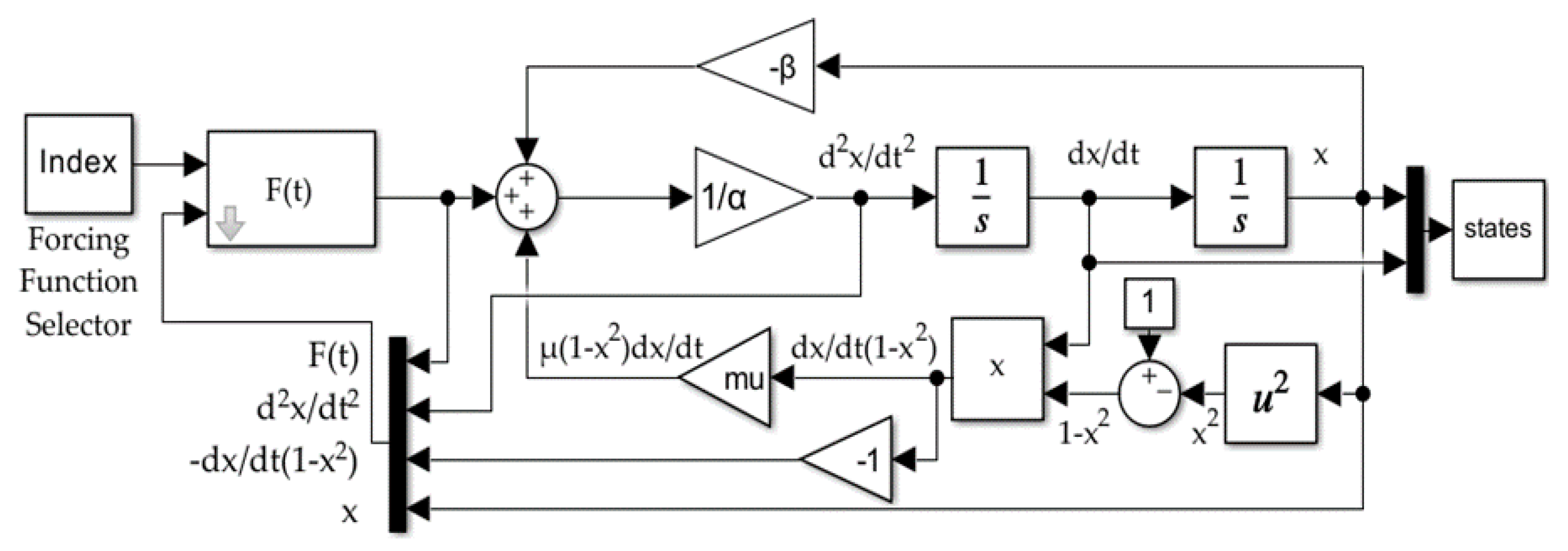
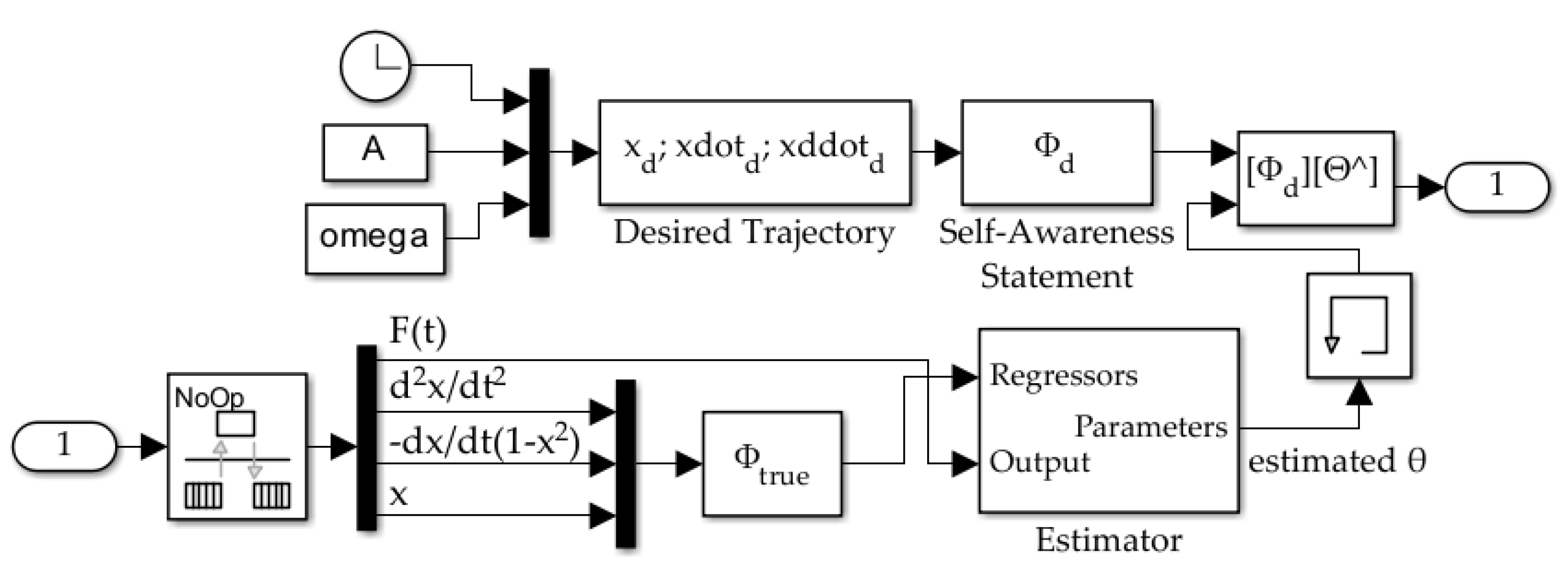
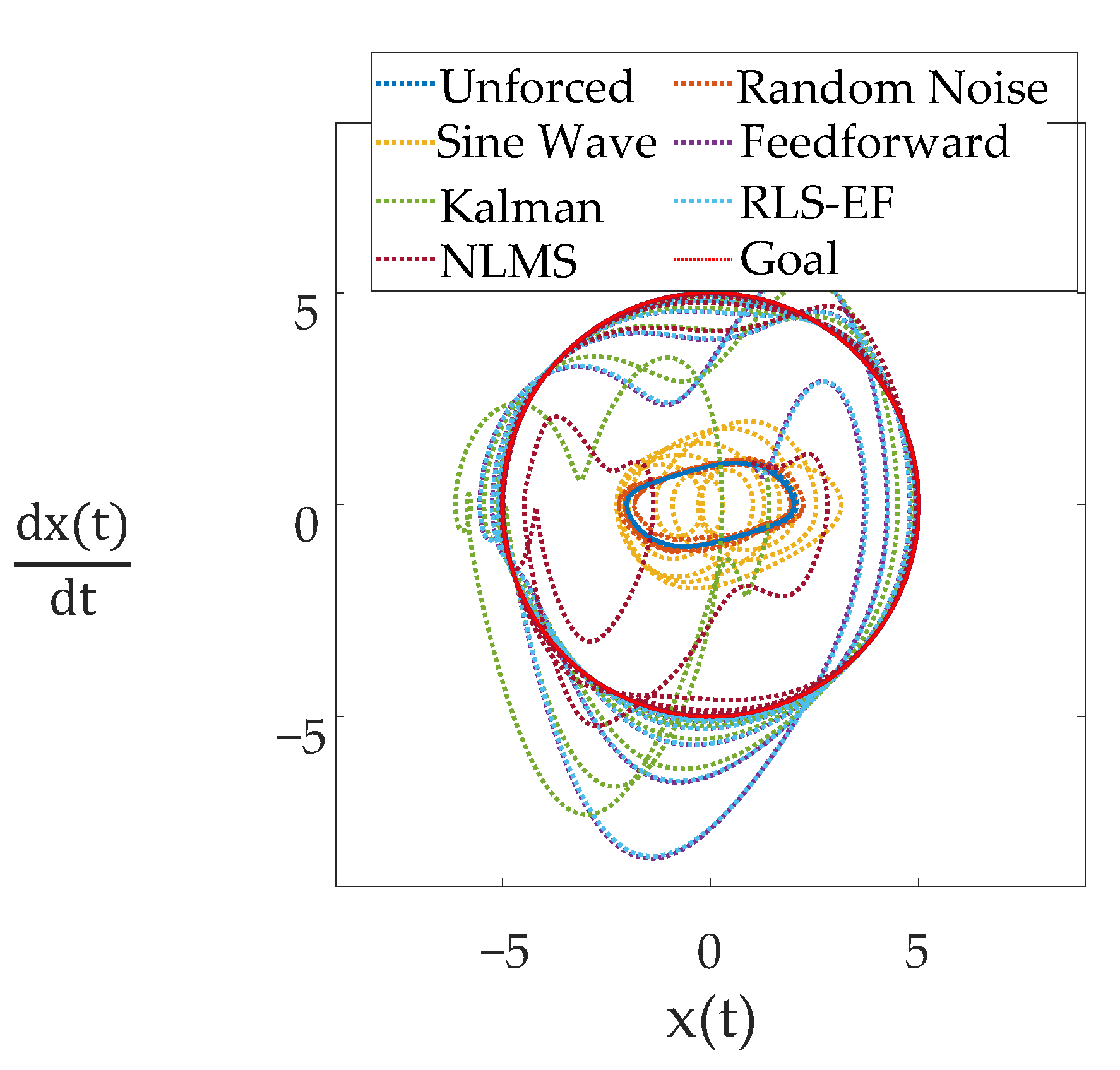
- Using a Kalman filter for online estimation in a deterministic AI architecture exhibited worse performance than the Cooper–Heidlauf baseline [10]. Both recursive least squares with exponential forgetting and least mean squares performed better than baseline. Figure 4, Figure 5 and Figure 6 show the implementation of the forced van der Pol oscillator simulation in SIMULINK® with modular forcing function components. These figures in conjunction with MATLAB® code in the Appendix A facilitate extension of results.
- 2.
- An optimal approach to online estimation for deterministic artificial intelligence may involve using more than one algorithm. The authors found that one algorithm may exhibit superior performance when the error between predicted chaotic trajectories and observed trajectories is greatest, while another may have lower error when the system approaches the limit cycle, or steady state. The authors propose this as a direction for future research.
2. Materials and Methods
3. Results
- Unforced
- Uniform noise
- Sine wave
- Feedforward
- Deterministic artificial intelligence (DAI)—Kalman filter estimator
- Deterministic artificial intelligence (DAI)—recursive least squares with exponential forgetting estimator.
- Deterministic artificial intelligence (DAI)—normalized gradient least mean squares estimator
4. Discussion
5. Conclusions
Future Research
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| MATLAB® Code: |
| %% |
| clear all; close all; clc; |
| headless = 1; |
| RngSeed = 1; |
| % Oscillator Parameters |
| alpha = 5; |
| mu = 1; |
| beta = 1; |
| % RLS Parameters |
| rls_sample_time = 0.01; |
| alpha_i = 0.1; |
| mu_i = 0.1; |
| beta_i = 0.1; |
| % Desired Trajectory Parameters |
| A = 5; |
| omega = 1; |
| SampleTime = 0.01; |
| % Initial Conditions |
| x0 = 1; |
| v0 = 1; |
| %% |
| figure(1); |
| hold on; |
| errors = []; |
| errors2 = []; |
| episodes = 6001; |
| forgetting_factor = 1; |
| noise_covariance = 80; |
| adaption_gain = 0.9277; |
| grab_index = 1000; |
| for Index = 1:1:3 |
| sim(‘SimVanDerPol’); |
| errors = [errors; mean(abs(states–desiredstates(1:2,:)’))] |
| errors2 = [errors2; mean(abs(states(grab_index:end,:)–desiredstates(1:2,grab_index:end)’))] |
| figure(1); |
| plot(states(:,1), states(:,2),’:’, ‘Linewidth’,2);hold on; |
| end |
| for Index = 4:1:7 |
| sim(‘SimVanDerPol’); |
| errors = [errors; mean(abs(states–desiredstates(1:2,:)’))] |
| errors2 = [errors2; mean(abs(states(grab_index:end,:)–desiredstates(1:2,grab_index:end)’))] |
| figure(1); |
| plot(states(:,1), states(:,2),’:’, ‘Linewidth’,2);hold on; |
| figure(2); |
| subplot(1,4,Index-3);plot(states(grab_index:end,1)–desiredstates(1,grab_index:end)’);axis([0,length(desiredstates(1,grab_index:end)),-0.025,0.025]); |
| end |
| figure(1); |
| plot(desiredstates(1,:), desiredstates(2,:),’:’, ‘Linewidth’,1, ‘Color’, ‘red’);hold off; |
| legend(“Unforced”, “Random Noise”, “Sine Wave”, “Feedforward”, “RLS Kalman”, “RLS-EF”, “Norm’d LMS”, “Goal”,’fontname’,’Palatino’, ‘fontsize’,22,’NumColumns’,2,’Location’,’northeast’,’Orientation’,’horizontal’); |
| set(gca,’fontname’,’Palatino’, ‘fontsize’,26); |
| axis([-9,9,-9,9]); |
| xlabel(“x(t)”,’fontname’,’Palatino’, ‘fontsize’,32); ylabel(“dx(t)/dt”,’fontname’,’Palatino’, ‘fontsize’,26); |
| figure(3); |
| subplot(1,2,1);plot(abs(errors(:,1))); |
| subplot(1,2,2);plot(abs(errors(:,2))); |
References
- File: Strange Attractor of van der Pol and Duffing Mixed Type Equation.svg. Available online: https://commons.wikimedia.org/wiki/File:Strange_attractor_of_van_der_Pol_and_Duffing_mixed_type_equation.svg (accessed on 27 February 2023).
- CC0 1.0 Universal (CC0 1.0) Public Domain Dedication. Available online: https://creativecommons.org/publicdomain/zero/1.0/deed.en (accessed on 27 February 2023).
- Cassady, J.; Maliga, K.; Overton, S.; Martin, T.; Sanders, S.; Joyner, C.; Kokam, T.; Tantardini, M. Next Steps in the Evolvable Path to Mars. In Proceedings of the International Astronautical Congress, Jerusalem, Israel, 12–16 October 2015. [Google Scholar]
- Song, Y.; Li, Y.; Li, C. Ott-Grebogi-Yorke controller design based on feedback control. In Proceedings of the 2011 International Conference on Electrical and Control Engineering, Yichang, China, 24 October 2011; pp. 4846–4849. [Google Scholar]
- Pyragas, K. Continuous control of chaos by self-controlling feedback. Phys. Lett. A 1992, 170, 421–428. [Google Scholar] [CrossRef]
- Slotine, J.; Li, W. Applied Nonlinear Control; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1991; pp. 392–436. [Google Scholar]
- Osburn, J.; Whitaker, H.; Kezer, A. New Developments in the Design of Model Reference Adaptive Control Systems; Institute of the Aerospace Sciences: Reston, VA, USA, 1961; Volume 61. [Google Scholar]
- Fossen, T. Handbook of Marine Craft Hydrodynamics and Motion Control, 2nd ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2021. [Google Scholar]
- Fossen, T. Guidance and Control of Ocean Vehicles; John Wiley & Sons Inc.: Chichester, UK, 1994. [Google Scholar]
- Cooper, M.; Heidlauf, P.; Sands, T. Controlling Chaos—Forced van der Pol Equation. Mathematics 2017, 5, 70. [Google Scholar] [CrossRef]
- van der Pol, B. A note on the relation of the audibility factor of a shunted telephone to the antenna circuit as used in the reception of wireless signals. Philos. Mag. 1917, 34, 184–188. [Google Scholar] [CrossRef]
- van der Pol, B. On “relaxation-oscillations”. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1926, 2, 978–992. [Google Scholar] [CrossRef]
- van der Pol, B.; van der Mark, J. Frequency Demultiplication. Nature 1927, 120, 363–364. [Google Scholar] [CrossRef]
- van der Pol, B.; van der Mark, J. The heartbeat considered as a relaxation-oscillation, and an electrical model of the heart. Philos. Mag. 1929, 6, 673–675. [Google Scholar] [CrossRef]
- van der Pol, B. The nonlinear theory of electric oscillations. Proc. IRE 1934, 22, 1051–1086. [Google Scholar] [CrossRef]
- Smeresky, B.; Rizzo, A.; Sands, T. Optimal Learning and Self-Awareness Versus PDI. Algorithms 2020, 13, 23. [Google Scholar] [CrossRef]
- Zhai, H.; Sands, T. Controlling Chaos in Van Der Pol Dynamics Using Signal-Encoded Deep Learning. Mathematics 2022, 10, 453. [Google Scholar] [CrossRef]
- Zhai, H.; Sands, T. Comparison of Deep Learning and Deterministic Algorithms for Control Modeling. Sensors 2022, 22, 6362. [Google Scholar] [CrossRef] [PubMed]
- Plackett, R. Some Theorems in Least Squares. Biometrika 1950, 37, 149–157. [Google Scholar] [CrossRef] [PubMed]
- Astrom, K.; Wittenmark, B. Adaptive Control, 2nd ed.; Addison Wesley Longman: Boston, MA, USA, 1995. [Google Scholar]
- Patra, A.; Unbehauen, H. Nonlinear modeling and identification. In Proceedings of the IEEE/SMC’93 Conference System Engineering in Service of Humans, Le Touquet, France, 17–20 October 1993. [Google Scholar]
- Martinek, R.; Kahankova, R.; Nedoma, J.; Fajkus, M.; Skacel, M. Comparison of the LMS, NLMS, RLS, and QR-RLS algorithms for vehicle noise suppression. In Proceedings of the 10th International Conference on Computer Modeling and Simulation, Sydney, Australia, 8–10 January 2018; pp. 23–27. [Google Scholar]
- Welch, G.; Bishop, G. An introduction to the Kalman filter. In UNC Chapel Hill, Department of Computer Science Technical Report, 95-041; University of North Carolina at Chapel Hill: Chapel Hill, NC, USA, 1995. [Google Scholar]
- Ramirez, P.S. The Least-Mean-Square (LMS) Algorithm. In Adaptive Filtering; The Kluwer International Series in Engineering and Computer Science, 694; Springer: Boston, MA, USA, 2002. [Google Scholar]
- Pateria, S.; Subagdja, B.; Tan, A.H.; Quek, C. Hierarchical Reinforcement Learning: A Comprehensive Survey. ACM Comput. Surv. 2021, 54, 109. [Google Scholar] [CrossRef]
- Fawzi, A.; Balog, M.; Huang, A.; Hubert, T.; Romera-Paredes, B.; Barekatain, M.; Novikov, A.; RRuiz, F.J.; Schrittwieser, J.; Swirszcz, G.; et al. Discovering faster matrix multiplication algorithms with reinforcement learning. Nature 2022, 610, 47–53. [Google Scholar] [CrossRef] [PubMed]
- McClement, D.G.; Lawrence, N.P.; Forbes, M.G.; Loewen, P.D.; Backström, J.U.; Gopaluni, R.B. Meta-Reinforcement Learning for Adaptive Control of Second Order Systems. In Proceedings of the 2022 IEEE International Symposium on Advanced Control of Industrial Processes (AdCONIP), Vancouver, BC, Canada, 7–9 August 2022; pp. 78–83. [Google Scholar]




| Method | Method | ||
|---|---|---|---|
| 1 | 3.3234 | 1 | 3.2031 |
| 2 | 3.3334 | 2 | 3.2110 |
| 3 | 3.9843 | 3 | 3.9275 |
| 4 | 0.2091 | 4 | 0.2284 |
| 5 | 0.4975 | 5 | 0.3927 |
| 6 | 0.2041 | 6 | 0.2237 |
| 7 | 0.3089 | 7 | 0.2877 |
| Method | Method | ||
|---|---|---|---|
| 1 | 3.3218 | 1 | 3.1891 |
| 2 | 3.3262 | 2 | 3.1941 |
| 3 | 4.0150 | 3 | 3.9487 |
| 4 | 0.0642 | 4 | 0.0743 |
| 5 | 0.1220 | 5 | 0.1379 |
| 6 | 0.0629 | 6 | 0.0728 |
| 7 | 0.0329 | 7 | 0.0599 |
| Method | Starting at t = 1 MAE (% ± Rel. Method 4) | Starting at t = 1 MAE (% ± Rel. Method 4) | Starting at t = 1000 MAE (% ± Rel. Method 4) | Starting at t = 1000 MAE (% ± Rel. Method 4) |
|---|---|---|---|---|
| Feedforward Only (Method 4) | – | – | – | – |
| DAI with Kalman filter (Method 5) | −137.86 | −71.93 | −90.1 | −85.7 |
| DAI with RLS-EF (Method 6) | 2.41 | 2.04 | 1.97 | 1.93 |
| DAI with NLMS (Method 7) | −47.69 | −25.98 | 48.70 | 19.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ribordy, L.; Sands, T. Chaotic van der Pol Oscillator Control Algorithm Comparison. Dynamics 2023, 3, 202-213. https://doi.org/10.3390/dynamics3010012
Ribordy L, Sands T. Chaotic van der Pol Oscillator Control Algorithm Comparison. Dynamics. 2023; 3(1):202-213. https://doi.org/10.3390/dynamics3010012
Chicago/Turabian StyleRibordy, Lauren, and Timothy Sands. 2023. "Chaotic van der Pol Oscillator Control Algorithm Comparison" Dynamics 3, no. 1: 202-213. https://doi.org/10.3390/dynamics3010012
APA StyleRibordy, L., & Sands, T. (2023). Chaotic van der Pol Oscillator Control Algorithm Comparison. Dynamics, 3(1), 202-213. https://doi.org/10.3390/dynamics3010012






