Role of Mixing Dynamics on Mass Convection-Diffusion in Sparkling Wines: A Laboratory Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Physical Evidence of Mass Transfer Processes in Sparkling Wines
- (a)
- Evaporation: it is the passage from the liquid phase of a substance to its gaseous phase. In champagne wine (and other sparkling wines), evaporation will mainly involve ethanol, water, and to a lesser extent, some volatile compounds.
- (b)
- Diffusion: When the liquid releases 10 g of dissolved CO2 molecules per liter of champagne, this is equivalent to a volume of carbon dioxide gas of 6 L at 20 °C. In an effervescent wine, the carbon dioxide, in a state of supersaturation in wine, is evacuated by:
- –
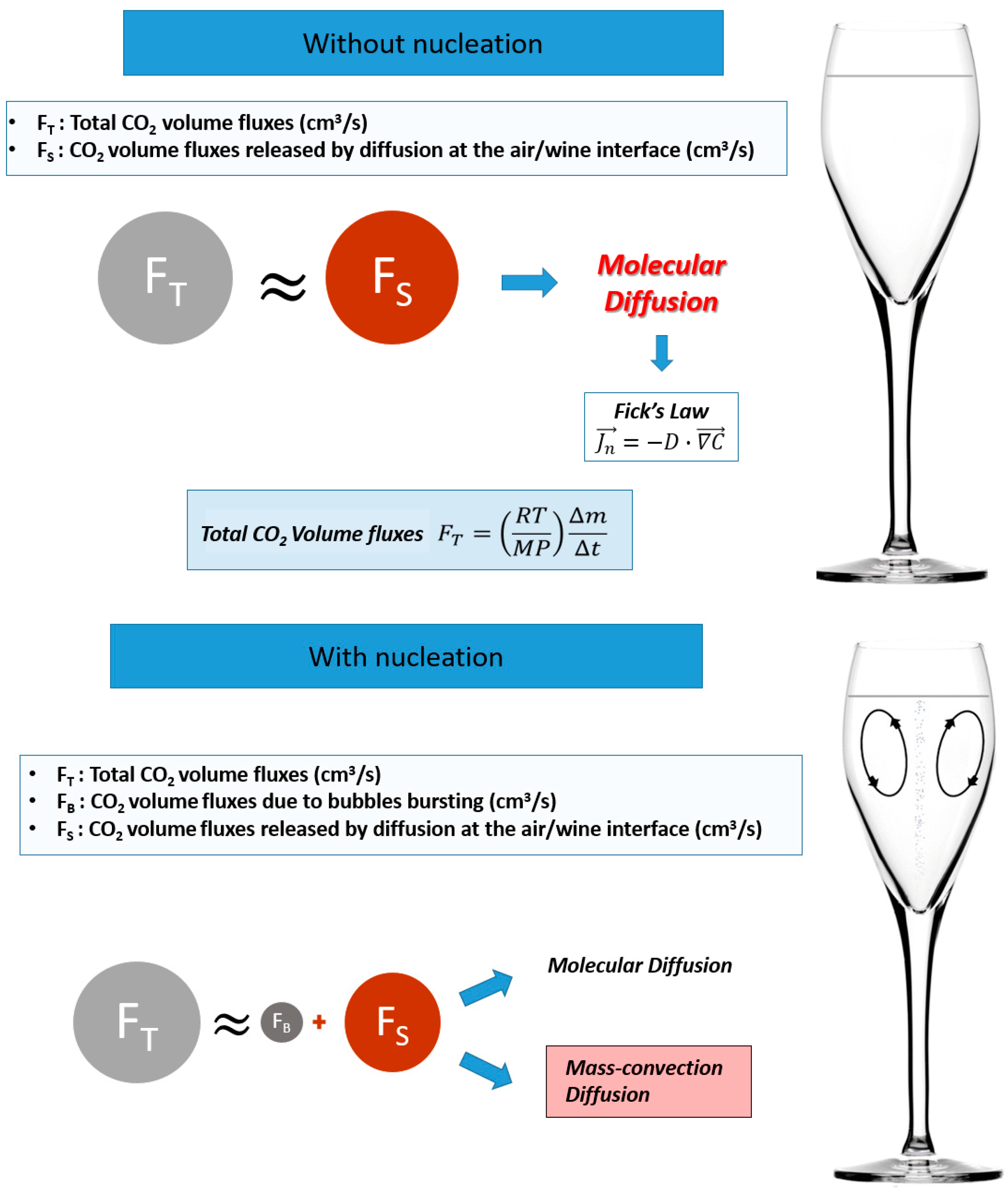
- Molecular diffusion: In the absence of effervescence in the glass, the mass transfer of CO2 occurs solely by molecular diffusion. According to Fick’s law (Equation (1)), CO2 molecules will progressively move from the liquid matrix, where they are contained in excess, to the air where CO2 molecules are in the minority [19,20]. This process, which tends towards equilibrium between the two zones (wine and air), can last several days.
- –
- Mass convection-diffusion: With effervescence, the mass transfer of CO2 occurs by mass convection-diffusion. This is the superposition of two transfer mechanisms, molecular diffusion (Fick’s law), and transport due to the mass transfer (convective transport) induced by effervescence (Figure 1) [15].
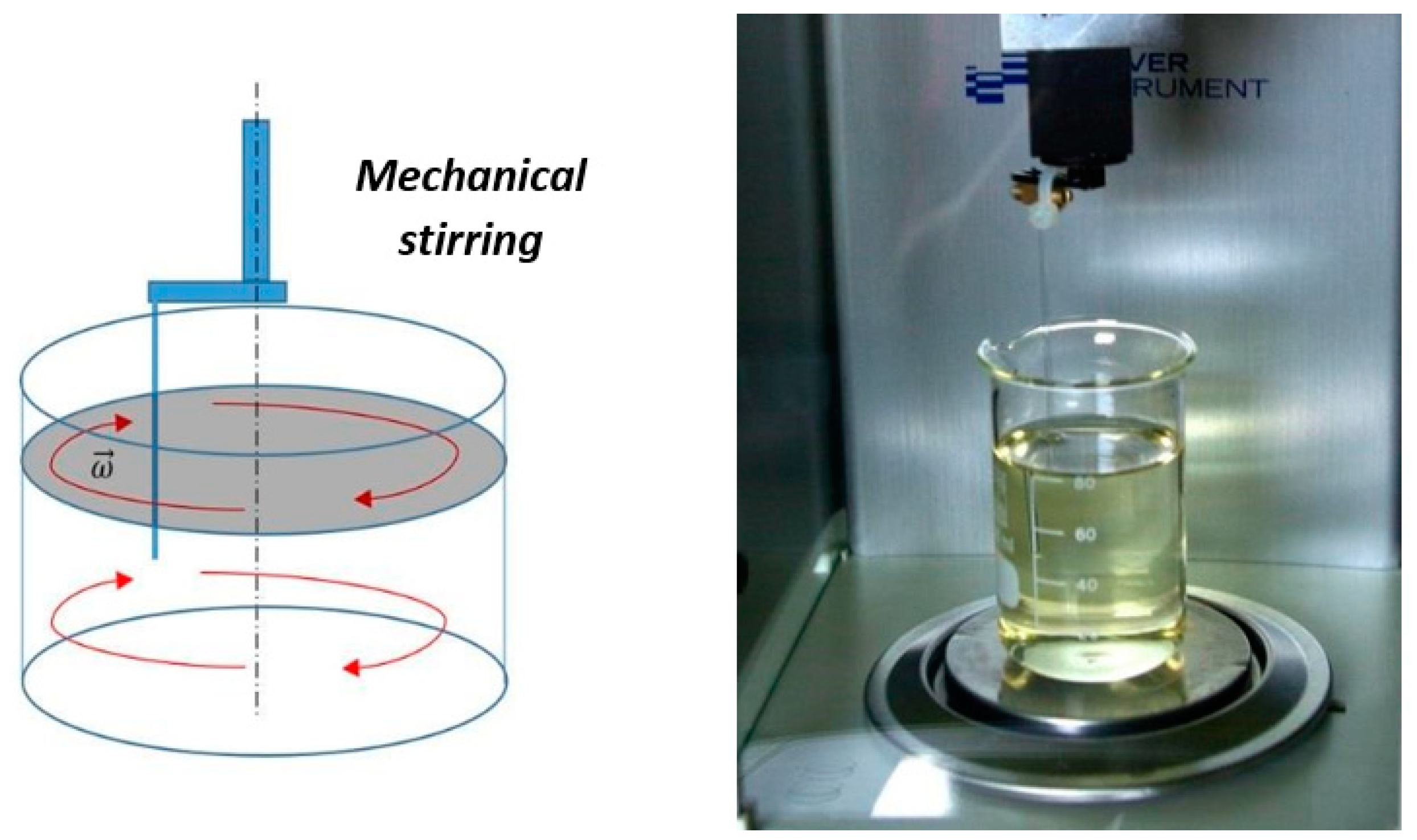
2.2. Experimental Process
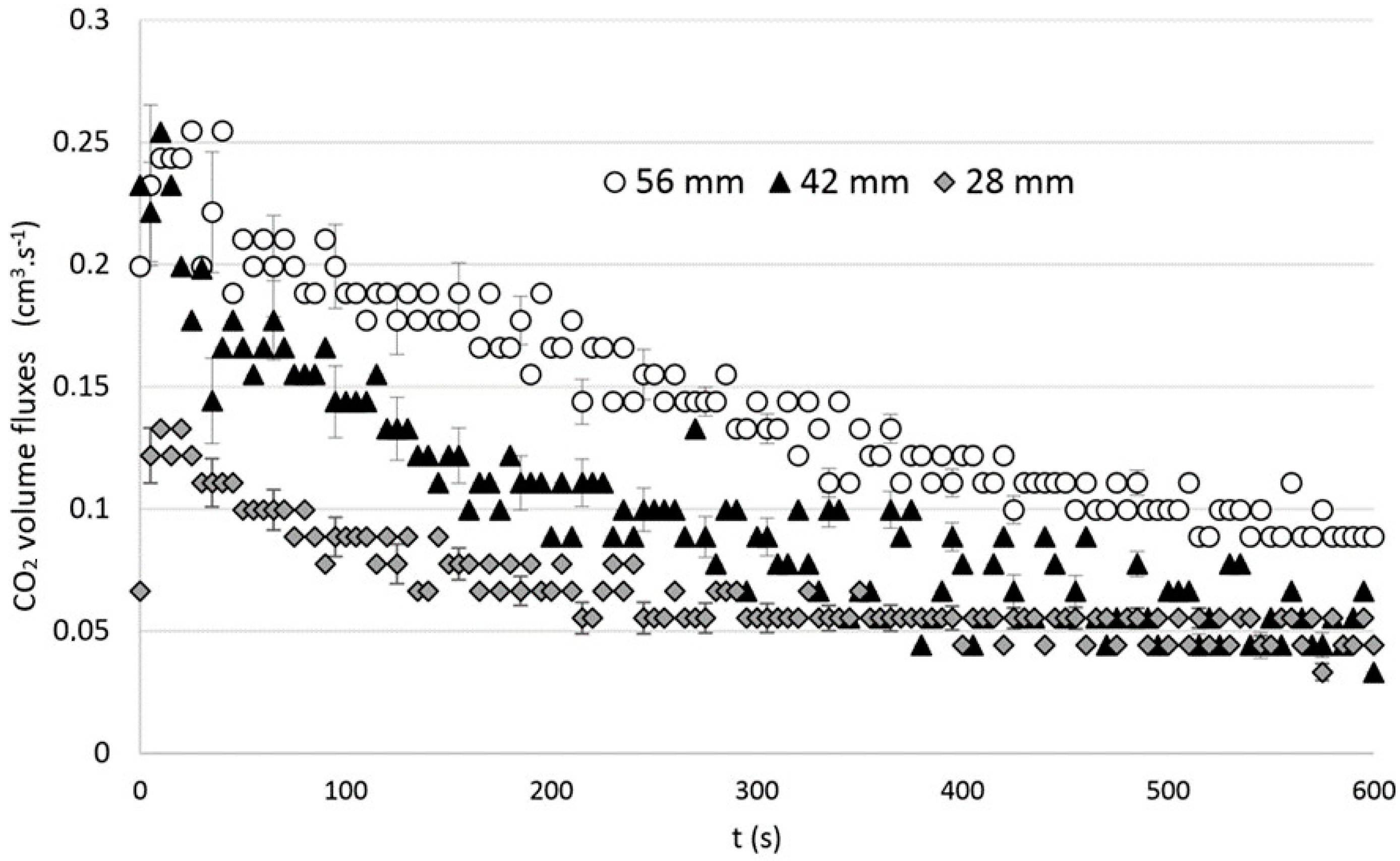
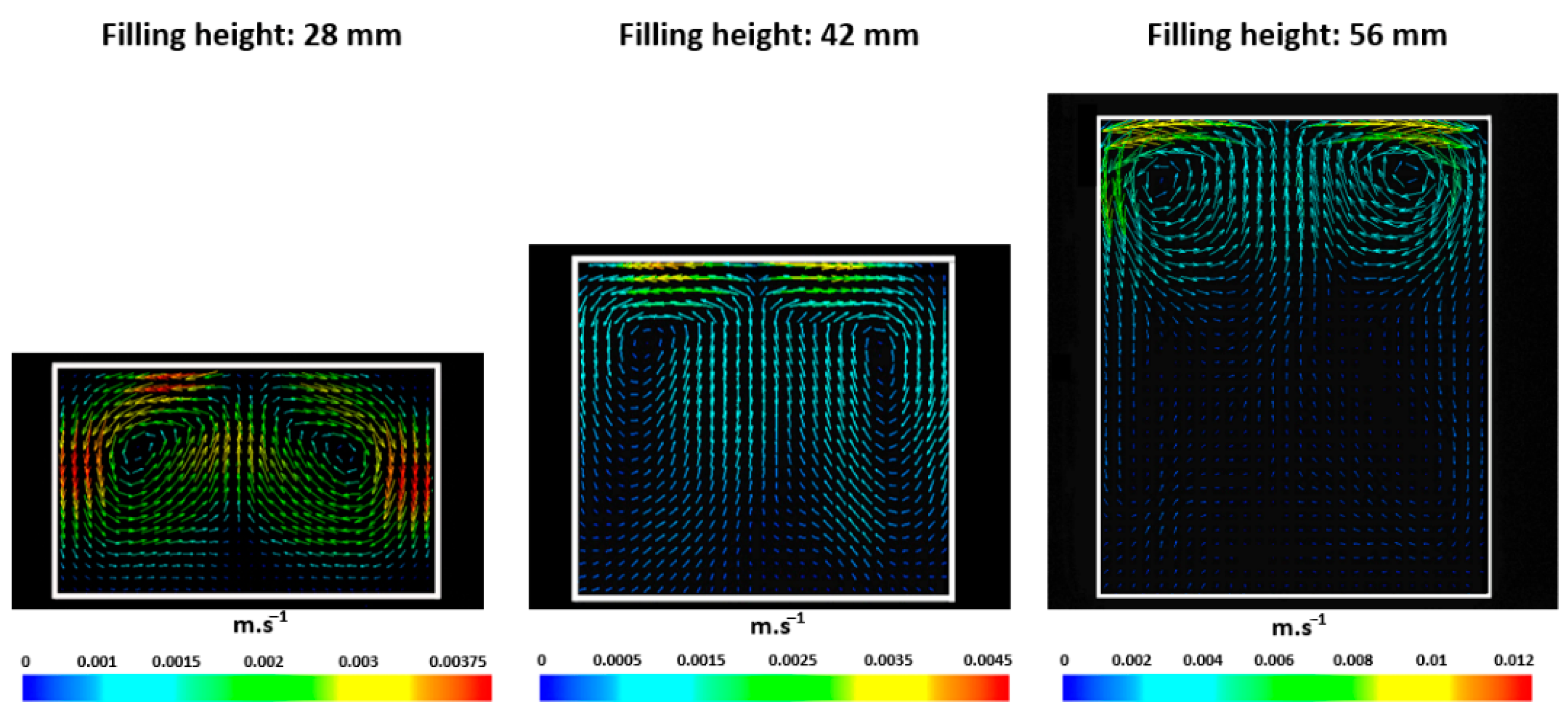
2.3. Influence of the Filling Height
2.4. Influence of Wine Brewing
3. Results
Role of Mixing Dynamics on Mass Convection-Diffusion
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Duteurtre, B. Le Champagne, de la Tradition à la Science; Tec & Doc Lavoisier: Paris, France, 2010. [Google Scholar]
- Liger-Belair, G. Effervescence in champagne and sparkling wines: From grape harvest to bubble rise. Eur. Phys. J. Spec. Top. 2017, 226, 3–116. [Google Scholar] [CrossRef]
- Lubetkin, S.D. Why Is It Much Easier To Nucleate Gas Bubbles than Theory Predicts? Langmuir 2003, 19, 2575–2587. [Google Scholar] [CrossRef]
- Bisperink, C.G.J.; Prins, A. Bubble growth in carbonated liquids. Colloids Surf. A Physicochem. Eng. Asp. 1994, 85, 237–253. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Z. “Fizzics” of Bubble Growth in Beer and Champagne. Elements 2008, 4, 47–49. [Google Scholar] [CrossRef]
- Ruocco, G. Mass Transfer by Diffusion and Convection. In Introduction to Transport Phenomena Modeling; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Ottino, J.M. The Kinematics of Mixing: Stretching, Chaos, and Transport; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 6th ed.; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Polidori, G.; Beaumont, F.; Jeandet, P.; Liger-Belair, G. Visualization of swirling flows in champagne glasses. J. Vis. 2008, 11, 184. [Google Scholar] [CrossRef]
- Polidori, G.; Beaumont, F.; Jeandet, P.; Liger-Belair, G. Ring vortex scenario in engraved champagne glasses. J. Vis. 2009, 12, 275–282. [Google Scholar] [CrossRef]
- Polidori, G.; Jeandet, P.; Liger-Belair, G. Bubbles and flow patterns in champagne. Am. Sci. 2009, 97, 294–301. [Google Scholar] [CrossRef]
- Beaumont, F.; Cilindre, C.; Abdi, E.; Maman, M.; Polidori, G. The Role of Glass Shapes on the Release of Dissolved CO2 in Effervescent Wine. Curr. Res. Nutr. Food Sci. J. 2019, 7, 227–235. [Google Scholar]
- Beaumont, F.; Liger-Belair, G.; Polidori, G. Flow analysis from PIV in engraved champagne tasting glasses: Flute versus coupe. Exp. Fluids 2015, 56, 170. [Google Scholar] [CrossRef]
- Beaumont, F.; Liger-Belair, G.; Bailly, Y.; Polidori, G. A synchronized particle image velocimetry and infrared thermography technique applied to convective mass transfer in champagne glasses. Exp. Fluids 2016, 57, 85. [Google Scholar] [CrossRef]
- Padet, J. Convection Thermique et Massique; Ed. Techniques de l’Ingénieur: Saint Denis De Palin, France, 2005. [Google Scholar]
- Perret, A.; Bonhommeau, D.A.; Liger-Belair, G.; Cours, T.; Alijah, A. CO2 Diffusion in Champagne Wines: A Molecular Dynamics Study. J. Phys. Chem. B 2014, 118, 1839–1847. [Google Scholar] [CrossRef]
- Liger-Belair, G.; Villaume, S.; Cilindre, C.; Jeandet, P. Kinetics of CO2 fluxes outgassing from champagne glasses in tasting conditions: The role of temperature. J. Agric. Food Chem. 2009, 57, 1997–2003. [Google Scholar] [CrossRef]
- Agabaliantz, G. Bases scientifiques de la technologie des vins mousseux. Bull. OIV 1963, 36, 703–714. [Google Scholar]
- Liger-Belair, G. Nucléation, ascension et éclatement d’une bulle de champagne. Ann. Phys. 2006, 31, 1–133. [Google Scholar] [CrossRef]
- Liger-Belair, G.; Cilindre, C.; Beaumont, F.; Jeandet, P.; Polidori, G. Evidence for ascending bubble-driven flow patterns in champagne glasses, and their impact on gaseous CO2 and ethanol release under standard tasting conditions. Bubble Sci. Eng. Technol. 2012, 4, 35–48. [Google Scholar] [CrossRef]
- Liger-Belair, G.; Villaume, S.; Cilindre, C.; Polidori, G.; Jeandet, P. CO2 volume fluxes outgassing from champagne glasses in tasting conditions: Flute versus coupe. J. Agric. Food Chem. 2009, 57, 4939–4947. [Google Scholar] [CrossRef] [PubMed]
- Liger-Belair, G.; Parmentier, M.; Jeandet, P. Modeling the Kinetics of Bubble Nucleation in Champagne and Carbonated Beverages. J. Phys. Chem. B 2006, 110, 21145–21151. [Google Scholar] [CrossRef]
- Brogioli, D.; Vailati, A. Diffusive mass transfer by non-equilibrium fluctuations: Fick’s law revisited. Phys. Rev. E 2000, 63, 012105. [Google Scholar] [CrossRef]
- Buch, A.; Rakib, M.; Stambouli, M. Transfert de Matière—Cinétique du Transfert de Matière Entre Deux Phases; Techniques de l’Ingénieur: Saint Denis De Palin, France, 2008. [Google Scholar]

| Filling Height (mm) | Capacity (mL) | Interface Area (cm2) |
|---|---|---|
| 28 | 40 | 16 |
| 42 | 60 | 16 |
| 56 | 80 | 16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beaumont, F.; Bogard, F.; Murer, S.; Polidori, G. Role of Mixing Dynamics on Mass Convection-Diffusion in Sparkling Wines: A Laboratory Study. Dynamics 2022, 2, 326-335. https://doi.org/10.3390/dynamics2040018
Beaumont F, Bogard F, Murer S, Polidori G. Role of Mixing Dynamics on Mass Convection-Diffusion in Sparkling Wines: A Laboratory Study. Dynamics. 2022; 2(4):326-335. https://doi.org/10.3390/dynamics2040018
Chicago/Turabian StyleBeaumont, Fabien, Fabien Bogard, Sebastien Murer, and Guillaume Polidori. 2022. "Role of Mixing Dynamics on Mass Convection-Diffusion in Sparkling Wines: A Laboratory Study" Dynamics 2, no. 4: 326-335. https://doi.org/10.3390/dynamics2040018
APA StyleBeaumont, F., Bogard, F., Murer, S., & Polidori, G. (2022). Role of Mixing Dynamics on Mass Convection-Diffusion in Sparkling Wines: A Laboratory Study. Dynamics, 2(4), 326-335. https://doi.org/10.3390/dynamics2040018







