Comprehensive Analysis of the Genetic Variation in the LPA Gene from Short-Read Sequencing
Abstract
1. Introduction
2. Materials and Methods
2.1. Cohort
2.2. Measurement of Lp(a)
2.3. Sequencing
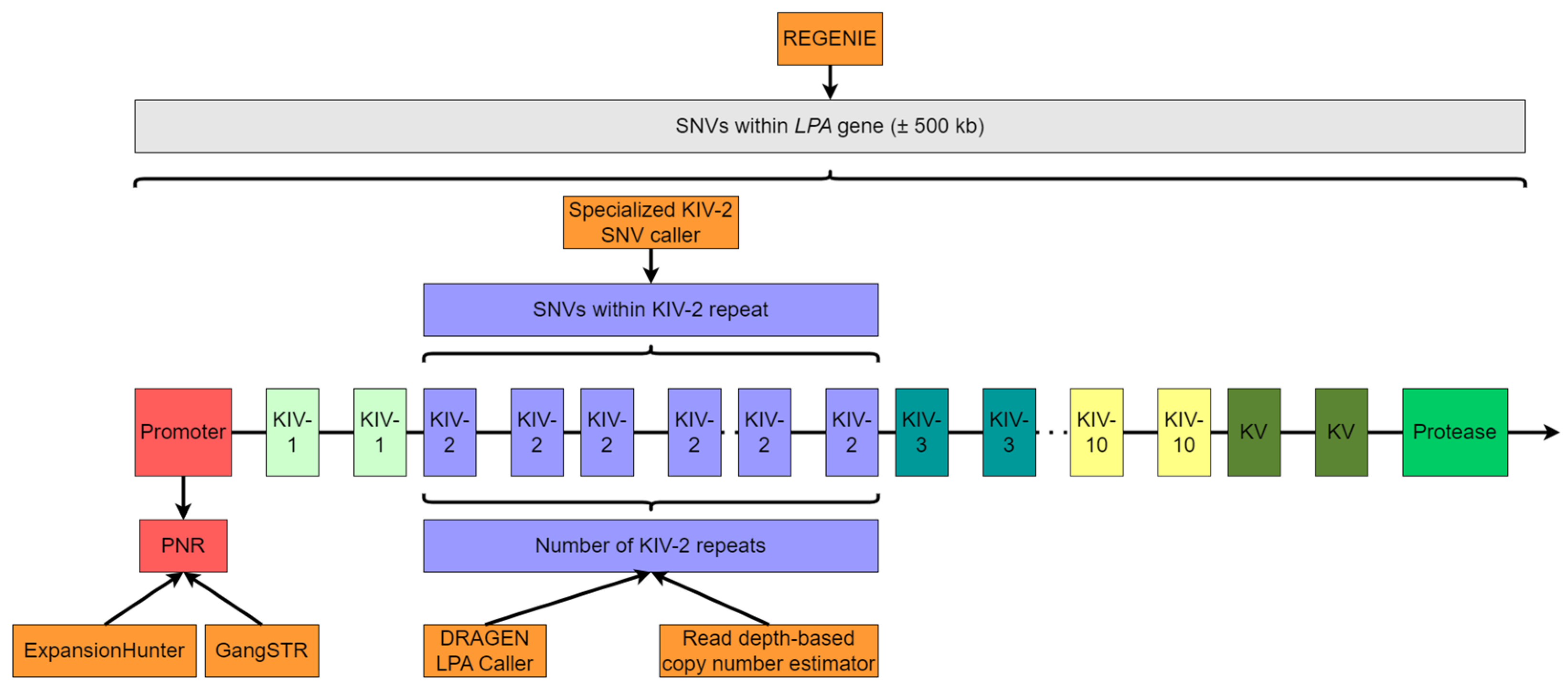
2.4. Pre-Processing, Quality Control, and Multi-Sample Calling of WGS Data
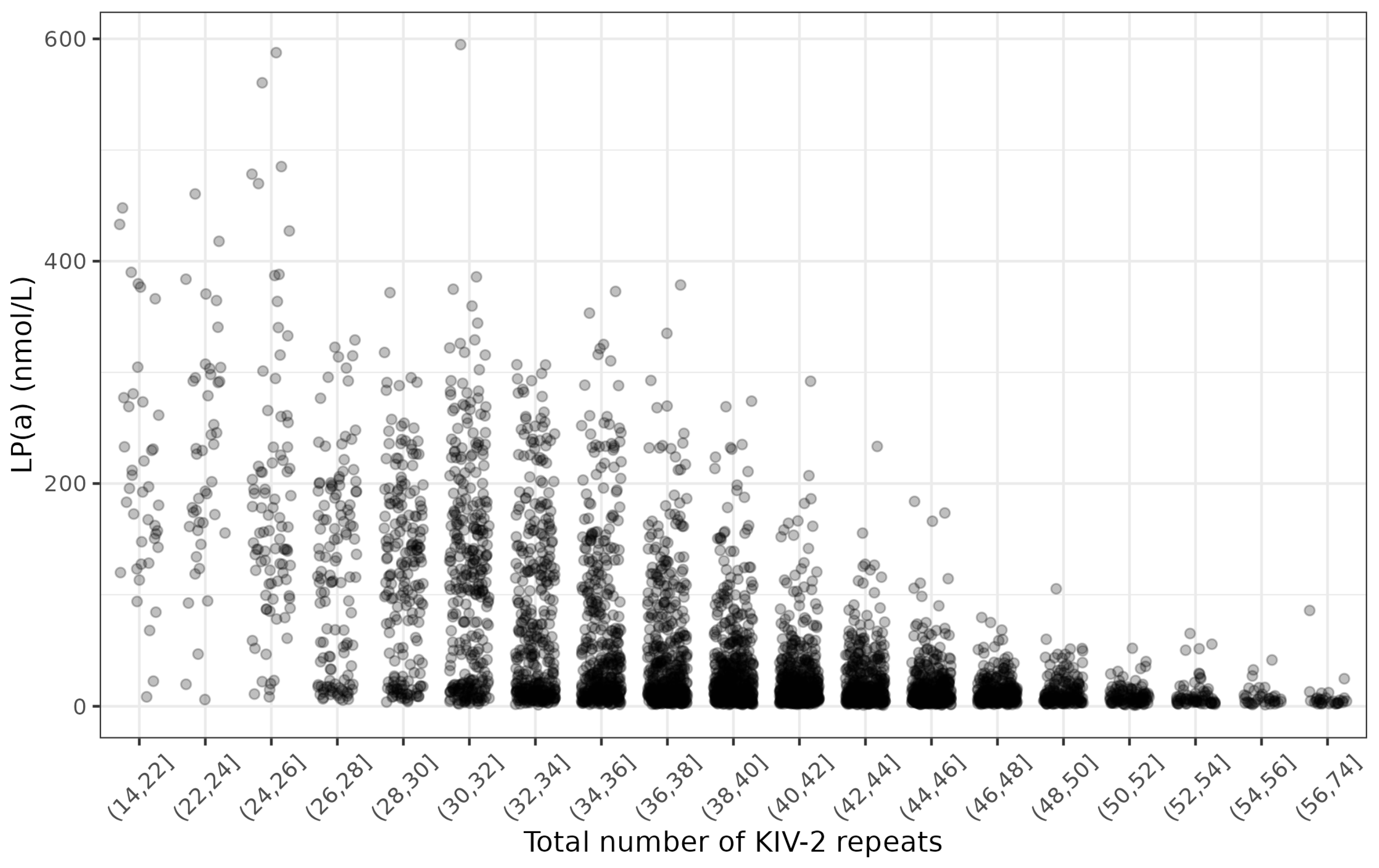
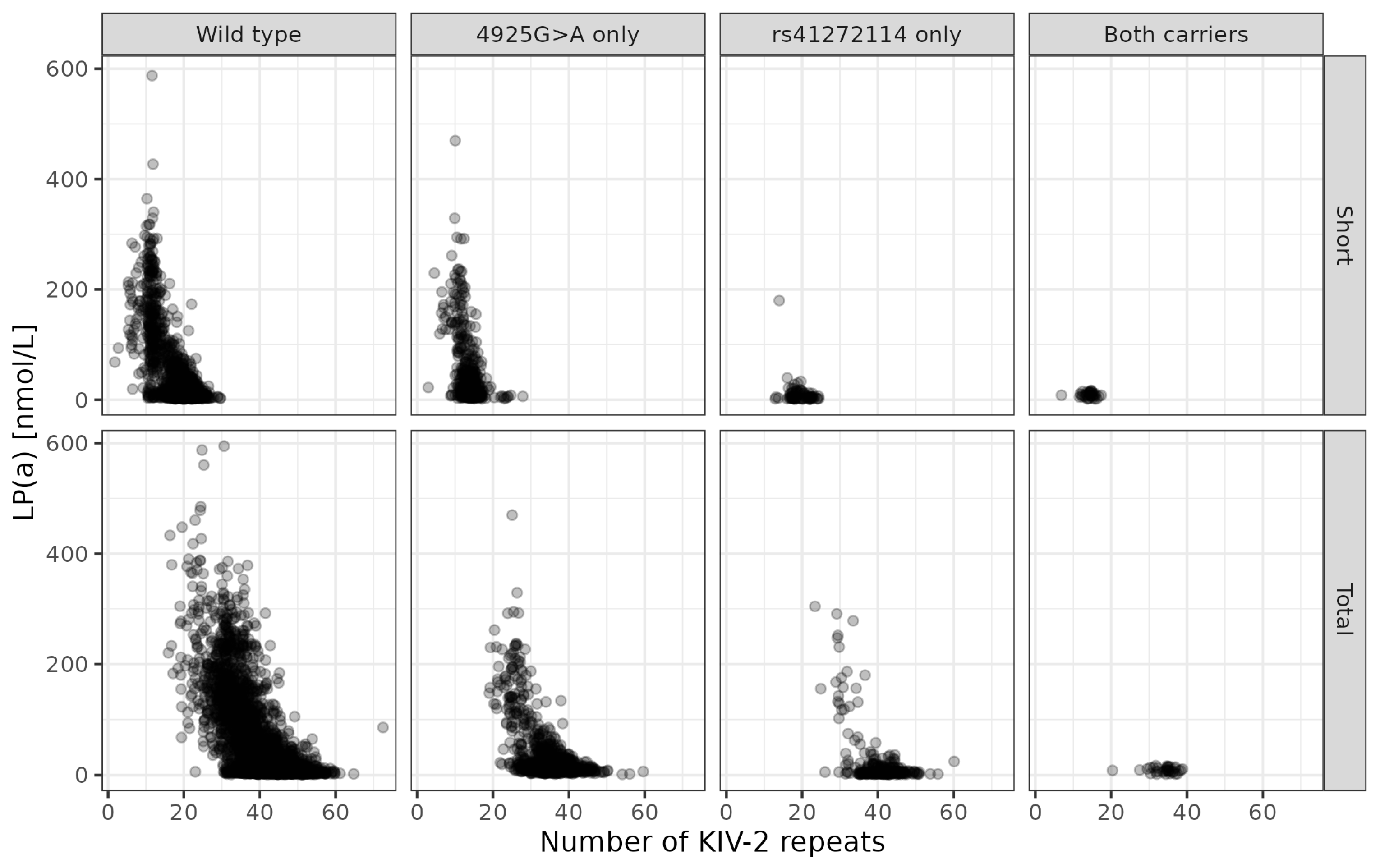
2.5. Measurement of Number of KIV-2 Repeats
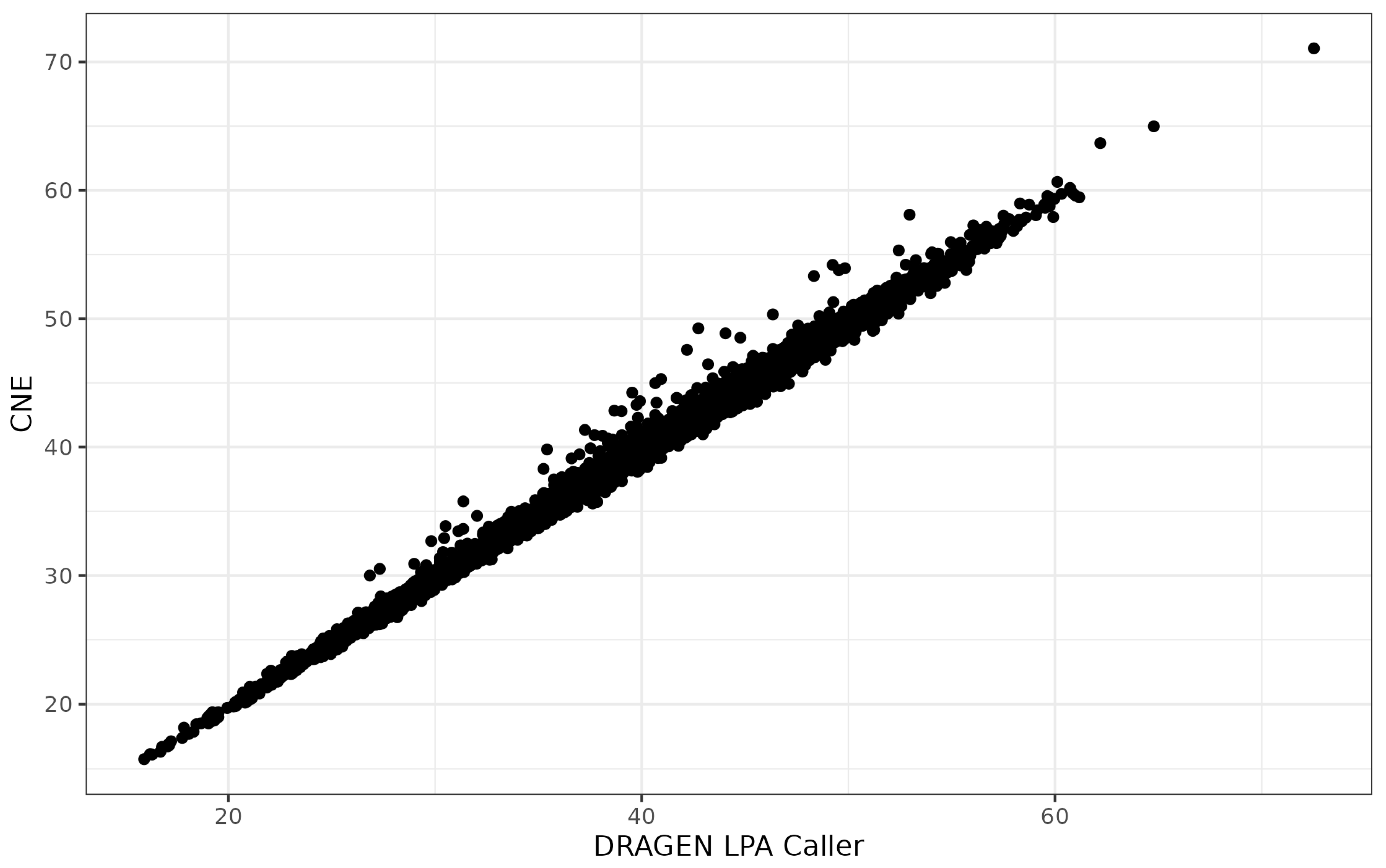
2.5.1. Read Depth-Based Copy Number Estimator (CNE)
2.5.2. DRAGEN LPA Caller
2.6. Analysis of the Pentanucleotide Repeat (PNR)
2.7. Analysis of the KIV-2 Single Nucleotide Variations (SNVs)
2.8. Statistical Analysis
2.8.1. Descriptive Statistics
2.8.2. Genome-Wide Association Study (GWAS)
2.8.3. Predictive Model for Lp(a) Levels Using Random Forests
- Full model: inclusion of all available genetic variation plus
- the total number of KIV-2 repeats
- the allele-specific number of KIV-2 repeats
- KIV-2 RF1: inclusion of genetic variation with CPI p < 0.05 from RF1 plus
- the total number of KIV-2 repeats
- the allele-specific number of KIV-2 repeats
- KIV-2 RF2: inclusion of genetic variation with CPI p < 0.05 from RF2 plus
- the total number of KIV-2 repeats
- the allele-specific number of KIV-2 repeats
- Hypothesis 1: The full model shows the highest predictive performance.
- Hypothesis 2: RF1 is sparser than RF2.
- Hypothesis 3: Model KIV-2 RF1 b performs better than KIV-2 RF1 a.
- Hypothesis 4: Model KIV-2 RF2 b performs better than KIV-2 RF2 a.
- Hypothesis 5: Full models a and b show similar performance, because proxy SNVs from the LPA gene should compensate for the additional information for the allele-specific number of KIV-2 repeats.
2.8.4. Software and Hardware
3. Results
3.1. Study Characteristics
3.2. Agreement between Specialized Variant Callers
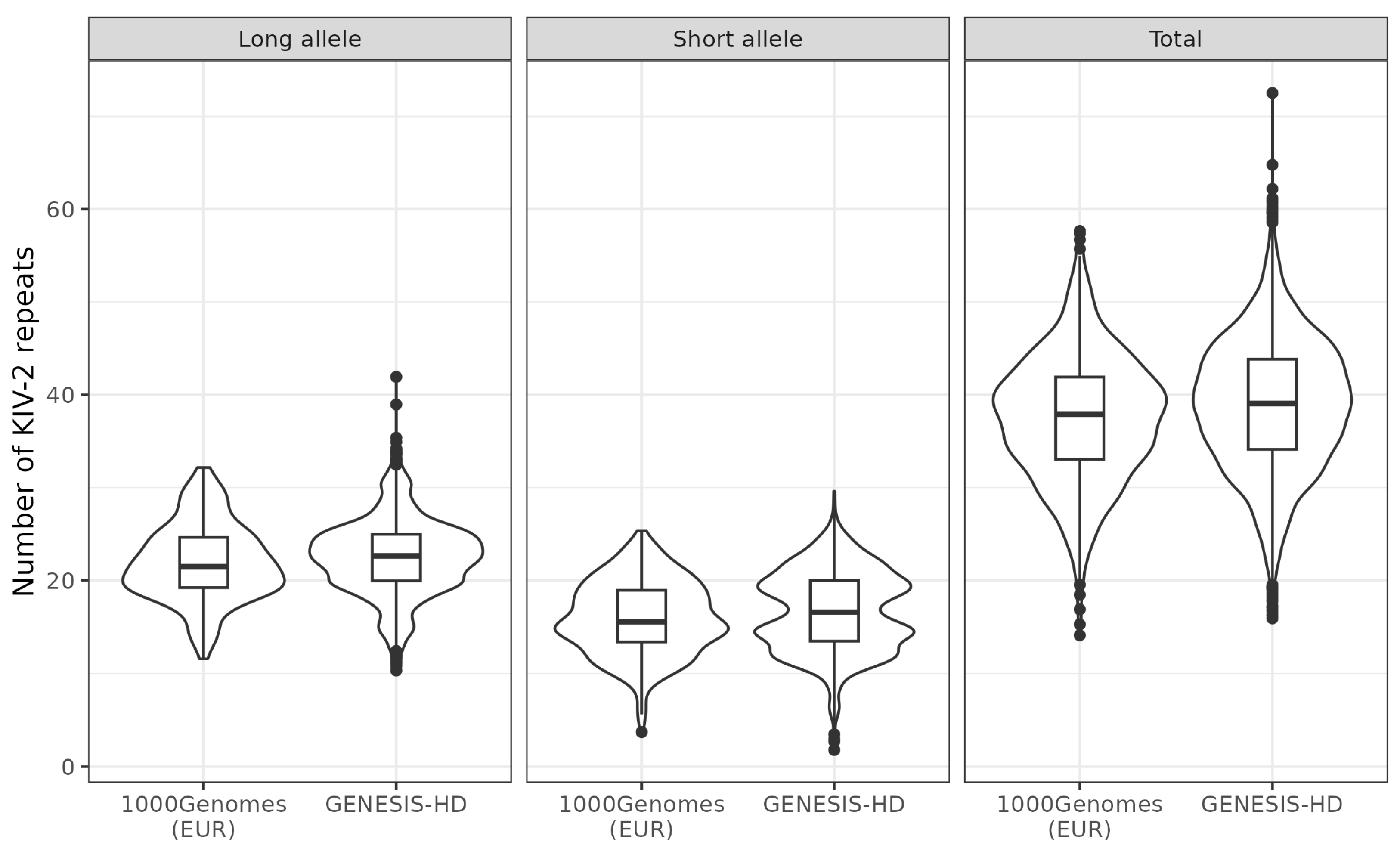
3.3. Agreement of Allele-Specific Number of KIV-2 Repeats with Results from 1000 Genomes Project
3.4. Genome-Wide Association Study for Lp(a) Concentration
3.5. Genetic Variants Selected by Conditional Predictive Impact (CPI)
3.6. Comparison of Predictive Performances for Lp(a) Concentrations
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Koschinsky, M.L.; Marcovina, S.M. Structure-function relationships in apolipoprotein(a): Insights into lipoprotein(a) assembly and pathogenicity. Curr. Opin. Lipidol. 2004, 15, 167–174. [Google Scholar] [CrossRef] [PubMed]
- Berg, K. A new serum type system in man—The Ld system. Vox Sang. 1965, 10, 513–527. [Google Scholar] [CrossRef] [PubMed]
- Kronenberg, F.; Utermann, G. Lipoprotein(a): Resurrected by genetics. J. Intern. Med. 2013, 273, 6–30. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, K.; Noureen, A.; Kronenberg, F.; Utermann, G. Structure, function, and genetics of lipoprotein (a). J. Lipid Res. 2016, 57, 1339–1359. [Google Scholar] [CrossRef] [PubMed]
- Kamstrup, P.R.; Tybjaerg-Hansen, A.; Steffensen, R.; Nordestgaard, B.G. Genetically elevated lipoprotein(a) and increased risk of myocardial infarction. JAMA 2009, 301, 2331–2339. [Google Scholar] [CrossRef] [PubMed]
- McLean, J.W.; Tomlinson, J.E.; Kuang, W.J.; Eaton, D.L.; Chen, E.Y.; Fless, G.M.; Scanu, A.M.; Lawn, R.M. cDNA sequence of human apolipoprotein(a) is homologous to plasminogen. Nature 1987, 330, 132–137. [Google Scholar] [CrossRef] [PubMed]
- Hancock, M.A.; Boffa, M.B.; Marcovina, S.M.; Nesheim, M.E.; Koschinsky, M.L. Inhibition of plasminogen activation by lipoprotein(a): Critical domains in apolipoprotein(a) and mechanism of inhibition on fibrin and degraded fibrin surfaces. J. Biol. Chem. 2003, 278, 23260–23269. [Google Scholar] [CrossRef] [PubMed]
- Nordestgaard, B.G.; Chapman, M.J.; Ray, K.; Boren, J.; Andreotti, F.; Watts, G.F.; Ginsberg, H.; Amarenco, P.; Catapano, A.; Descamps, O.S.; et al. Lipoprotein(a) as a cardiovascular risk factor: Current status. Eur. Heart J. 2010, 31, 2844–2853. [Google Scholar] [CrossRef]
- Brown, M.S.; Goldstein, J.L. Plasma lipoproteins: Teaching old dogmas new tricks. Nature 1987, 330, 113–114. [Google Scholar] [CrossRef]
- Gaubatz, J.W.; Ghanem, K.I.; Guevara, J.; Nava, M.L.; Patsch, W.; Morrisett, J.D. Polymorphic forms of human apolipoprotein[a]: Inheritance and relationship of their molecular weights to plasma levels of lipoprotein[a]. J. Lipid Res. 1990, 31, 603–613. [Google Scholar] [CrossRef]
- Jawi, M.M.; Frohlich, J.; Chan, S.Y. Lipoprotein(a) the Insurgent: A New Insight into the Structure, Function, Metabolism, Pathogenicity, and Medications Affecting Lipoprotein(a) Molecule. J. Lipids 2020, 2020, 3491764. [Google Scholar] [CrossRef] [PubMed]
- Mack, S.; Coassin, S.; Rueedi, R.; Yousri, N.A.; Seppala, I.; Gieger, C.; Schonherr, S.; Forer, L.; Erhart, G.; Marques-Vidal, P.; et al. A genome-wide association meta-analysis on lipoprotein (a) concentrations adjusted for apolipoprotein (a) isoforms. J. Lipid Res. 2017, 58, 1834–1844. [Google Scholar] [CrossRef] [PubMed]
- Coassin, S.; Erhart, G.; Weissensteiner, H.; Eca Guimaraes de Araujo, M.; Lamina, C.; Schonherr, S.; Forer, L.; Haun, M.; Losso, J.L.; Kottgen, A.; et al. A novel but frequent variant in LPA KIV-2 is associated with a pronounced Lp(a) and cardiovascular risk reduction. Eur. Heart J. 2017, 38, 1823–1831. [Google Scholar] [CrossRef] [PubMed]
- Coassin, S.; Kronenberg, F. Lipoprotein(a) beyond the kringle IV repeat polymorphism: The complexity of genetic variation in the LPA gene. Atherosclerosis 2022, 349, 17–35. [Google Scholar] [CrossRef] [PubMed]
- Mukamel, R.E.; Handsaker, R.E.; Sherman, M.A.; Barton, A.R.; Zheng, Y.; McCarroll, S.A.; Loh, P.R. Protein-coding repeat polymorphisms strongly shape diverse human phenotypes. Science 2021, 373, 1499–1505. [Google Scholar] [CrossRef] [PubMed]
- Mahmoud, M.; Harting, J.; Corbitt, H.; Chen, X.; Jhangiani, S.N.; Doddapaneni, H.; Meng, Q.; Han, T.; Lambert, C.; Zhang, S.; et al. Closing the gap: Solving complex medically relevant genes at scale. medRxiv 2024. [Google Scholar] [CrossRef] [PubMed]
- Warburton, P.E.; Sebra, R.P. Long-Read DNA Sequencing: Recent Advances and Remaining Challenges. Annu. Rev. Genomics. Hum. Genet. 2023, 24, 109–132. [Google Scholar] [CrossRef] [PubMed]
- Behera, S.; Belyeu, J.R.; Chen, X.; Paulin, L.F.; Nguyen, N.Q.H.; Newman, E.; Mahmoud, M.; Menon, V.K.; Qi, Q.; Joshi, P.; et al. Identification of allele-specific KIV-2 repeats and impact on Lp(a) measurements for cardiovascular disease risk. bioRxiv 2023. [Google Scholar] [CrossRef] [PubMed]
- Garg, P.; Jadhav, B.; Lee, W.; Rodriguez, O.L.; Martin-Trujillo, A.; Sharp, A.J. A phenome-wide association study identifies effects of copy-number variation of VNTRs and multicopy genes on multiple human traits. Am. J. Hum. Genet. 2022, 109, 1065–1076. [Google Scholar] [CrossRef]
- Lu, W.; Cheng, Y.C.; Chen, K.; Wang, H.; Gerhard, G.S.; Still, C.D.; Chu, X.; Yang, R.; Parihar, A.; O’Connell, J.R.; et al. Evidence for several independent genetic variants affecting lipoprotein (a) cholesterol levels. Hum. Mol. Genet. 2015, 24, 2390–2400. [Google Scholar] [CrossRef]
- Mooser, V.; Mancini, F.P.; Bopp, S.; Petho-Schramm, A.; Guerra, R.; Boerwinkle, E.; Muller, H.-J.; H.Hobbs, H. Sequence polymorphisms in the apo(a) gene associated with specific levels of Lp(a) in plasma. Hum. Mol. Genet. 1995, 4, 173–181. [Google Scholar] [CrossRef] [PubMed]
- Prins, J.; Leus, F.R.; Bouma, B.N.; van Rijn, H.J. The identification of polymorphisms in the coding region of the apolipoprotein (a) gene–association with earlier identified polymorphic sites and influence on the lipoprotein (a) concentration. Thromb. Haemost. 1999, 82, 1709–1717. [Google Scholar] [PubMed]
- Grüneis, R.; Weissensteiner, H.; Lamina, C.; Schönherr, S.; Forer, L.; Di Maio, S.; Streiter, G.; Peters, A.; Gieger, C.; Kronenberg, F.; et al. The kringle IV type 2 domain variant 4925G>A causes the elusive association signal of the LPA pentanucleotide repeat. J. Lipid Res. 2022, 63, 100306. [Google Scholar] [CrossRef] [PubMed]
- Jagodzinski, A.; Johansen, C.; Koch-Gromus, U.; Aarabi, G.; Adam, G.; Anders, S.; Augustin, M.; der Kellen, R.B.; Beikler, T.; Behrendt, C.A.; et al. Rationale and design of the Hamburg City Health Study. Eur. J. Epidemiol. 2020, 35, 169–181. [Google Scholar] [CrossRef] [PubMed]
- The 1000 Genomes Project Consortium. A global reference for human genetic variation. Nature 2015, 526, 68–74. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, B.S.; Quinlan, A.R. Mosdepth: Quick coverage calculation for genomes and exomes. Bioinformatics 2018, 34, 867–868. [Google Scholar] [CrossRef]
- Mousavi, N.; Shleizer-Burko, S.; Yanicky, R.; Gymrek, M. Profiling the genome-wide landscape of tandem repeat expansions. Nucleic Acids Res. 2019, 47, e90. [Google Scholar] [CrossRef]
- Dolzhenko, E.; van Vugt, J.; Shaw, R.J.; Bekritsky, M.A.; van Blitterswijk, M.; Narzisi, G.; Ajay, S.S.; Rajan, V.; Lajoie, B.R.; Johnson, N.H.; et al. Detection of long repeat expansions from PCR-free whole-genome sequence data. Genome Res. 2017, 27, 1895–1903. [Google Scholar] [CrossRef]
- Oketch, J.W.; Wain, L.V.; Hollox, E.J. A comparison of software for analysis of rare and common short tandem repeat (STR) variation using human genome sequences from clinical and population-based samples. bioRxiv 2023. [Google Scholar] [CrossRef]
- Zook, J.M.; McDaniel, J.; Olson, N.D.; Wagner, J.; Parikh, H.; Heaton, H.; Irvine, S.A.; Trigg, L.; Truty, R.; McLean, C.Y.; et al. An open resource for accurately benchmarking small variant and reference calls. Nat. Biotechnol. 2019, 37, 561–566. [Google Scholar] [CrossRef]
- Danecek, P.; Bonfield, J.K.; Liddle, J.; Marshall, J.; Ohan, V.; Pollard, M.O.; Whitwham, A.; Keane, T.; McCarthy, S.A.; Davies, R.M.; et al. Twelve years of SAMtools and BCFtools. Gigascience 2021, 10, giab008. [Google Scholar] [CrossRef] [PubMed]
- Weissensteiner, H.; Forer, L.; Fuchsberger, C.; Schöpf, B.; Kloss-Brandstätter, A.; Specht, G.; Kronenberg, F.; Schönherr, S. mtDNA-Server: Next-generation sequencing data analysis of human mitochondrial DNA in the cloud. Nucleic Acids Res. 2016, 44, W64–W69. [Google Scholar] [CrossRef]
- Mbatchou, J.; Barnard, L.; Backman, J.; Marcketta, A.; Kosmicki, J.A.; Ziyatdinov, A.; Benner, C.; O’Dushlaine, C.; Barber, M.; Boutkov, B.; et al. Computationally efficient whole-genome regression for quantitative and binary traits. Nat. Genet. 2021, 53, 1097–1103. [Google Scholar] [CrossRef] [PubMed]
- Manichaikul, A.; Mychaleckyj, J.C.; Rich, S.S.; Daly, K.; Sale, M.; Chen, W.M. Robust relationship inference in genome-wide association studies. Bioinformatics 2010, 26, 2867–2873. [Google Scholar] [CrossRef] [PubMed]
- Gogarten, S.M.; Sofer, T.; Chen, H.; Yu, C.; Brody, J.A.; Thornton, T.A.; Rice, K.M.; Conomos, M.P. Genetic association testing using the GENESIS R/Bioconductor package. Bioinformatics 2019, 35, 5346–5348. [Google Scholar] [CrossRef] [PubMed]
- Gogarten, S.M.; Zheng, X.; Stilp, A. SeqVarTools: Tools for Variant Data, R package version 1.42.0. 2023. [CrossRef]
- Wright, M.N.; Ziegler, A. ranger: A fast implementation of random forests for high dimensional data in C++ and R. J. Stat. Softw. 2017, 77, 1–17. [Google Scholar] [CrossRef]
- Watson, D.S.; Wright, M.N. Testing conditional independence in supervised learning algorithms. Mach. Learn 2021, 110, 2107–2129. [Google Scholar] [CrossRef]
- Lang, M.; Binder, M.; Richter, J.; Schratz, P.; Pfisterer, F.; Coors, S.; Au, Q.; Casalicchio, G.; Kotthoff, L.; Bischl, B. mlr3: A modern object-oriented machine learning framework in R. J. Open Source Softw. 2019, 4, 1903. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 13 March 2024).
- Landau, W.M. The targets R package: A dynamic make-like function-oriented pipeline toolkit for reproducibility and high-performance computing. J. Open Source Softw. 2019, 6, 2959. [Google Scholar] [CrossRef]
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis; Springer International Publishing: Basel, Switzerland, 2016. [Google Scholar] [CrossRef]
- Solomon, T.; Smith, E.N.; Matsui, H.; Braekkan, S.K.; Consortium, I.; Wilsgaard, T.; Njolstad, I.; Mathiesen, E.B.; Hansen, J.B.; Frazer, K.A. Associations between common and rare exonic genetic variants and serum levels of 20 cardiovascular-related proteins: The Tromsø Study. Circ. Cardiovasc. Genet. 2016, 9, 375–383. [Google Scholar] [CrossRef]
- Ronald, J.; Rajagopalan, R.; Cerrato, F.; Nord, A.S.; Hatsukami, T.; Kohler, T.; Marcovina, S.; Heagerty, P.; Jarvik, G.P. Genetic variation in LPAL2, LPA, and PLG predicts plasma lipoprotein(a) level and carotid artery disease risk. Stroke 2011, 42, 2–9. [Google Scholar] [CrossRef] [PubMed]
- Schachtl-Riess, J.F.; Kheirkhah, A.; Grüneis, R.; Di Maio, S.; Schoenherr, S.; Streiter, G.; Losso, J.L.; Paulweber, B.; Eckardt, K.U.; Köttgen, A.; et al. Frequent LPA KIV-2 variants lower lipoprotein(a) concentrations and protect against coronary artery disease. J. Am. Coll. Cardiol. 2021, 78, 437–449. [Google Scholar] [CrossRef] [PubMed]
- Kraft, H.G.; Lingenhel, A.; Pang, R.W.; Delport, R.; Trommsdorff, M.; Vermaak, H.; Janus, E.D.; Utermann, G. Frequency distributions of apolipoprotein(a) kringle IV repeat alleles and their effects on lipoprotein(a) levels in Caucasian, Asian, and African populations: The distribution of null alleles is non-random. Eur. J. Hum. Genet. 1996, 4, 74–87. [Google Scholar] [CrossRef]
- van der Hoek, Y.Y.; Wittekoek, M.E.; Beisiegel, U.; Kastelein, J.J.; Koschinsky, M.L. The apolipoprotein(a) kringle IV repeats which differ from the major repeat kringle are present in variably-sized isoforms. Hum. Mol. Genet. 1993, 2, 361–366. [Google Scholar] [CrossRef] [PubMed]
| Demographics | n = 4861 |
|---|---|
| Age (years) | 63 (56, 70) |
| Sex (male) | 2425 (49.9%) |
| Lp(a) (nmol/L) | 16.7 (7.50, 59.0) |
| Total number of KIV-2 repeats | 39.0 (34.1, 43.9) |
| Number of KIV-2 repeats long allele | 22.7 (20.0, 25.0) |
| Number of KIV-2 repeats short allele | 16.6 (13.4, 19.9) |
| Allele-specific number of KIV-2 repeats available | 2274 (47.0%) |
| 4925G>A carrier | 1124 (23.1%) |
| rs41272114 carrier | 283 (5.8%) |
| RF1 (Allele-Specific) | RF2 (Total) | |||||
|---|---|---|---|---|---|---|
| Variable | CPI | 95% CI | p-Value | CPI | 95% CI | p-Value |
| Short KIV-2 | 97.7 | 77.8–117.7 | 5.5 × 10−16 | – | – | – |
| Long KIV-2 | 22.6 | 14.3–30.9 | 3.8 × 10−6 | – | – | – |
| Total KIV-2 | – | – | – | 58.9 | 43.6–70.1 | 1.2 × 10−10 |
| 4925G>A | 9.9 | 4.3–15.5 | 1.8 × 10−3 | 8.7 | 2.0–15.3 | 1.6 × 10−2 |
| rs41272114 | 3.6 | 1.0–6.3 | 1.3 × 10−2 | 4.4 | 0.6–8.1 | 2.7 × 10−2 |
| rs9347465 | – | – | – | 9.6 × 10−4 | 1.2 × 10−6–1.9 × 10−3 | 4.9 × 10−2 |
| rs2489959 | – | – | – | 8.6 × 10−4 | 5.6 × 10−6–1.7 × 10−3 | 4.9 × 10−2 |
| rs2457567 | – | – | – | 8.4 × 10−4 | 3.2 × 10−5–1.6 × 10−3 | 4.4 × 10−2 |
| rs41272114 | ||||
|---|---|---|---|---|
| 4925G>A | CC | CT | TT | Total |
| GG | 3490 (71.8%) | 244 (5.0%) | 3 (0.1%) | 3737 (76.9%) |
| GA/AA | 1088 (22.4%) | 36 (0.7%) | 0 | 1124 (23.1%) |
| Total | 4578 (94.2%) | 280 (5.8%) | 3 (0.1%) | 4861 (100%) |
| Model | KIV-2 | R2 | CI | Difference | CI of Difference | p-Value |
|---|---|---|---|---|---|---|
| Full | Total | 0.6855 | 0.6109–0.7601 | 0.0098 | −0.0163–0.0359 | 0.4620 |
| Allele-specific | 0.6953 | 0.6414–0.7492 | ||||
| RF1 | Total | 0.4290 | 0.3086–0.5494 | 0.0540 | 0.0116–0.0965 | 0.0126 |
| Allele-specific | 0.4830 | 0.3806–0.5855 | ||||
| RF2 | Total | 0.4788 | 0.3978–0.5599 | 0.0413 | 0.0000–0.0826 | 0.0496 |
| Allele-specific | 0.5201 | 0.4054–0.6350 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Betschart, R.O.; Koliopanos, G.; Garg, P.; Guo, L.; Rossi, M.; Schönherr, S.; Blankenberg, S.; Twerenbold, R.; Zeller, T.; Ziegler, A. Comprehensive Analysis of the Genetic Variation in the LPA Gene from Short-Read Sequencing. BioMed 2024, 4, 156-170. https://doi.org/10.3390/biomed4020013
Betschart RO, Koliopanos G, Garg P, Guo L, Rossi M, Schönherr S, Blankenberg S, Twerenbold R, Zeller T, Ziegler A. Comprehensive Analysis of the Genetic Variation in the LPA Gene from Short-Read Sequencing. BioMed. 2024; 4(2):156-170. https://doi.org/10.3390/biomed4020013
Chicago/Turabian StyleBetschart, Raphael O., Georgios Koliopanos, Paras Garg, Linlin Guo, Massimiliano Rossi, Sebastian Schönherr, Stefan Blankenberg, Raphael Twerenbold, Tanja Zeller, and Andreas Ziegler. 2024. "Comprehensive Analysis of the Genetic Variation in the LPA Gene from Short-Read Sequencing" BioMed 4, no. 2: 156-170. https://doi.org/10.3390/biomed4020013
APA StyleBetschart, R. O., Koliopanos, G., Garg, P., Guo, L., Rossi, M., Schönherr, S., Blankenberg, S., Twerenbold, R., Zeller, T., & Ziegler, A. (2024). Comprehensive Analysis of the Genetic Variation in the LPA Gene from Short-Read Sequencing. BioMed, 4(2), 156-170. https://doi.org/10.3390/biomed4020013






