Abstract
The reproduction number, , is an important parameter in epidemic models. It is interpreted as the average number of new cases resulted from each infected individual during the course of infection. In this paper, the estimates since the outbreak of COVID-19 till 10 August 2020 for eight countries were computed using the package R{eSIR}. The computed values were examined and compared with the daily estimates obtained by a static SIR model by aligning the days of infection, assuming a fixed number of days for the infected person to become confirmed/recover/die. The results showed that running R{eSIR} to obtain estimates provided an easy mean of exploring epidemic data. Care must be taken in the interpretation of as a measure of severity of the spread of an epidemic. Other factors, such as imported cases, need to be considered.
1. Introduction
Since the outbreak of COVID-19 cases in Wuhan, China in December 2019, the disease has swept through over 50 countries in the world, affecting the lives and activities of at least half of its population. As of 5:01 p.m. CEST, 18 July 2020, the number of confirmed cases and deaths were 13,876,441 and 593,087, respectively (https://www.who.int/emergencies/diseases/novel-coronavirus-2019 (accessed on 22 June 2024)). Although the death rates were not high for the young, the infectivity of the virus was exceptionally high compared with other diseases caused by coronaviruses like SARS. Moreover, some young patients with good health history suddenly experienced severe symptoms in around 2 weeks’ time. To combat the pandemic, many countries had to lock down cities, stop transports, close schools and shops, etc. Social distancing, hand washing, and wearing masks were practised. These measures were shown to be effective in lowering the transmission rate, albeit at a great cost to the economy and the normal living of people. Up to the present moment, no effective treatments for the severe COVID-19 cases has been documented, although in some research, Remdesivir and a few other anti-inflammatory drugs, and some anti-virus drugs have been found to have beneficial effects in severe cases. The hope for the epidemic to stop lies on the successful production of vaccines and/or effective treatments.
Data on the daily reported number of confirmed, recovered, and death cases in many countries are available from the World Health Organization (https://www.who.int/ (accessed on 22 June 2024)), though there are discrepancies on the exact methods or tests for diagnosis and the definition of death cases. There may also be a time lag between the occurrence and the confirmation of diagnosis. Due to the lack of resources for diagnostic tests, the number of cases may have been under-estimated or confirmed with much time delay in some regions. The death cases could possibly be over-estimated. Patients might have died of other conditions like heart diseases, although they had COVID-19. This may possibly cause an over-estimation of death cases. On the other hand, some patients might have died at home or in nursery without being diagnosed with COVID-19, and this might have caused an under-estimation of death cases for some age groups.
When will the pandemic ends? Will it cause as severe consequences as the 1918 Spanish flu pandemic?
There has been much research on modelling the epidemic data of COVID-19. The data for some countries/cities have been analysed. The reproduction number (), average transmission rate (), average removal rate (), and other parameters in infection models have been found to be varying quite a lot from regions to regions, and so have the predictions of their courses of outbreak [1]; for instance, the estimation of the asymptomatic proportion of cases on board the Diamond Princess cruise ship, Yokohama, Japan [2], report on the pandemic in Italy [3], the prediction of COVID-19 spreading profiles in South Korea, Italy, and Iran by data-driven coding [4], the assessment of the lockdown effect in India [5], an epidemiological forecast model and software assessing interventions on COVID-19 epidemic in China [6], the COVID-19 epidemic trend in Malaysia under movement control order (MCO) [7], the case of Ethiopia [8], controlling the COVID-19 pandemic in Vietnam [9], analysing South Korean recovered and death data [10], overall statistics and research on COVID-19 data [11], predicting the COVID-19 epidemic in Algeria [12], assessing the effects of interventions [13,14,15], etc. All these efforts in modelling and predicting the pandemic are valuable tools in helping governments to set up effective measures to get the COVID-19 pandemic, as well as future epidemics, under control.
How to model epidemic data?
At the very early stage of the outbreak of COVID-19 in Wuhan, China in December 2019, with data only up to 31 January 3020, Liu et al. [16] built an SIR model with the compartment infected (I) going through two stages: asymptomatic and symptomatic. Further, for those cases with symptoms, some were reported (R) while some were not reported (U). Together with susceptible (S), it formed a four-compartment SIRU model. By numerical simulation using data on symptomatic infected cases, they estimated f, the fraction of asymptomatic infectious that became reported symptomatic infectious cases, , the average time during which asymptomatic infectious were asymptomatic, and , the average time during which the symptomatic infectious had symptoms. Assuming that f = 0.8, they estimated that = 7 days and = 7 days. These values were useful in the early-stage prevention and control of COVID-19 in Wuhan.
Again using the SIRU model, Liu et al. [17] estimated the parameters which best fit the data available from January 2022 to March or April 2022. (Note: the data available from different countries have different start and end dates). For instance, for China, the estimated parameters were = 5 days, = 6 days, and f = 0.6; for South Korea, the estimated parameters were = 4 days, = 16 days, and f = 0.9; and so on. The results were compatible with results from the WHO: the estimated latent period for the asymptomatic phase was around 5–6 days but could be up to 14 days.
Using a similar SIRU model, Griette et al. [18] estimated the instantaneous reproduction number for eight geographic areas: California, France, India, Israel, Japan, Peru, Spain, and the UK, using data till January 2021. They started by defining the epidemic model SEIRU (S: susceptible, E: exposed, I: infected, R: reported infectious, U: unreported infectious), then fit the data to Bernoulli–Verhulst curves [19], using the Levenberg–Marquardt algorithm [20]. In order for their model not to just fit any value of ascertainment rate (i.e., the proportions of infectious that were reported through diagnostic testing) and transmission rate, they needed to pre-set some parameters, using estimates from other sources. These included:
- (1)
- The average length of the non-infectious incubation period: 1 day;
- (2)
- The average length of the infectious incubation period: 3 days;
- (3)
- The average length of the symptomatic period: 7 days;
- (4)
- The ascertainment rate: 0.8.
Then, the transmission rate was computed, which was then used to estimate the instantaneous reproduction number . They found that the instantaneous reproduction number was dominated by 3.5. With this result, they postulated that when the portion of vaccinated or immunized population reached , the instantaneous reproduction numbers would become less than one. The epidemic would then be contained.
Based on the SI model, they started by fitting the early cumulative number of confirmed cases using the exponential function. But soon, they found that they could neither estimate the duration of infectiousness nor the fraction of infected cases reported. The reason was obvious: there were always many possible combinations of parameter values which would give an exact fit to the data.
Later, they used the Bernoulli–Verhulst model as a phenomenological model and obtained and expressed as a function of the parameter of the Bernoulli–Verhulst model. Assuming a day-by-day piecewise constant rate of transmission, they could reproduce well the number of reported cases by simulation using the following set of parameters: f = 0.5, = 0.1 or = 0.2 with the cumulative number of reported cases = 67,102, the number of susceptible cases at start = the total population of China , and the initial number of reported cases = 954. The daily reproduction number could be obtained by .
They highlighted in the conclusion that there were four challenges in epidemic modelling: (1) the estimation of the average transmission rate; (2) the estimation of the mean duration of the infectious period for the infected; (3) the quality of the reported cases; and (4) the estimation of the average transmission rate for each day of the infectious period.
In 2021, the SIRU model was also adopted by Griette et al. [21] to model early data in France. They used the data between February 2020 and January 2021. During the period, there were two obvious epidemic waves. They divided the epidemic waves into two phases: (1) the endemic phase, when the number of new cases fluctuated around an average value; and (2) the epidemic phase, when the number of new cases changed with time. They used a standard curve-fitting algorithm to find the parameters which would fit the data best. Their estimated duration for infectious period was (1) = 12.5 days during the first epidemic wave and (2) = 3.5 days during the second epidemic wave. By assuming the average length of asymptotic infectious period to 3 days, they fit the time-dependent reproduction number . At the first epidemic wave, decreased from around three to 3 than 1, and in the first part of the second epidemic wave, was almost constant and equalled 1.11. Nevertheless, they found that obtained in their model was too sensitive to the number of active cases and was not a reliable indicator of the severity of the epidemic.
In the meantime, more mathematical models were built [22]. Starting from the modelling of a single epidemic wave, modelling multiple epidemic waves became important. More compartments were introduced in the SI models. For instance, the infected (I) component could further be split into various components, such as reported (R)/unreported (U). Whatever the model, the estimation of the reproduction number and the transmission rate were always of core importance.
Among the most common epidemic models are the SIR [23] and SEIR models [24,25]. Other methods include a time series analysis of the infection curve [26], network-inference-based prediction [27], generalized epidemic modelling framework [28], a double epidemic SEIRP model [29], etc.
Most of the time, numerical methods have been used to estimate the parameters of the models. However, analytical solutions or exact solutions for the models under specific conditions are possible. Schlickeriser et al. [30] provided the detailed construction of general solutions for some of these SIR derived models. Also, an analytical solution of the SIRV-Model (where V stands for vaccinated) was provided by Kroger et al. [31].
The comparison and evaluation of methods have been prevalent. In 2021, Yang et al. [32] conducted an evaluation of various epidemic models based on COVID-19 data from China. They compared the forecasting performance based on (1) the model evaluation criteria used, the Akaike information criteria (AIC)/root mean square error (RMSE)/robustness coefficient(RC); (2) the mathematical functions used for model fitting; (3) the statistical inference methods used; (4) the underlying dynamical models used.
Concerning model evaluation methods, AIC and its various modified versions are widely used in comparing SIR and SEIR models, and researchers have found that the model with the least RMSE can be picked out based on AIC and RC. Moreover, researchers have found that among different mathematical functions, the sigmoid function is a good choice for epidemic modelling. Apart from that, it is always difficult to make long-term forecast at an early stage; while in later stages, sequential Bayesian and time-dependent reproduction number can provide useful predictions.
In this analysis, the focus was on the reproduction number. The changes in for the COVID-19 pandemic in the period from 22 January 2020 to 10 August 2020 for eight countries/cities, including Brazil, China, India, Italy, South Korea, Singapore, the United Kingdom, and the United States of America were analysed. These countries/cities were selected because there experienced outbreaks as well as changes in the control measures during the selected periods. was estimated for comparison.
An SIR model with time-dependent transmission rate was adopted by using the R{eSIR} package, assuming no prior knowledge on the different phases of quarantine measures and no prior value for the transmission rate, except that it was between zero and one. An exponential distribution for the transmission rate was not adopted. Instead, parameter estimates were obtained for four different time frames for comparison.
2. The SIR Model
The SIR model [23,24,25] is one of the simplest model for epidemic modelling. There are many variant forms of the SIR model, such as the SEIR and double epidemic models [33]. Such models are built on the daily number or proportion of confirmed cases, deaths, and recovered, with the assumption of a constant/varying transmission rate and removal rate, where removal can be from deaths or from recovery.
, which is equal to the ratio of the transmission rate to the removal rate, is an indicator of the direction of an epidemic: if , the epidemic is in the outbreak stage; on the other hand, if , the epidemic is under control.
How to estimate from daily figures? One simple way is to use packages like R{eSIR} [34]. output figures can provide insights for the stage of outbreak for a particular country/city. As R{eSIR} is easy to use, it provides a user-friendly exploratory tool for the public. While direct plots of the figures can provide visible trends, estimates provide a snapshot of the hidden underlying trend.
3. SIR Modelling
Based on a Dirichlet distribution [35] and assuming a constant population of size N, at any time t (in days, without loss of generality), define
- N: Population size;
- : Susceptible (the number of cases in the population who are without immunity against the infection);
- : Infected (the number of cases in the population who are infected);
- : Removed (the number of cases in the population who died or recovered from the infection, or vaccinated with immunity).
where .
In the SIR model, = / is the average number of new cases resulted from an infected individual throughout his/her course of infection, where
- is the transmission rate (the number of effective contacts per day made by an individual);
- is the removal rate (on average, an infected will recover or die in days after infection).
For instance, if is 0.2, then the number of effective contacts per day per infected (which means once infected, a individual will on average infect 0.2 others per day since the time he/she became infected and before the time he/she dies/recovers. If is 0.1 = 1/10 (which means on average an infected will have 10 “actively infective” days to infect others before he/she dies/recovers. Then, it is easy to obtain = 0.2 ∗ 10 = 2. Thus, on average, each infected individual will infect two others during his/her course of infection.
The dynamics of , , and are given by the three differential equations:
is an important parameter in predicting the direction of the epidemic.
- Case 1: : the epidemic will go on with more and more infected;
- Case 2: : The epidemic will maintain its present condition, with number of infected = number of removed. However, will not stay at one during the course of the epidemic.
- Case 3: : the epidemic will be contained with fewer and fewer cases.
Note that in order to control an epidemic, the aim is to reduce and to increase , so as to achieve . By measures like lockdown, social distancing, hand washing, wearing masks, the effective number of contacts per individual per day is greatly reduced. Effective treatments like drugs so that patients can recover earlier increase the rate of recovery. Moreover, vaccines which help people to acquire immunity without becoming infected have the effect of directly increasing the removed portion in the SIR model.
3.1. The R{eSIR} Package
The R{eSIR} was built on a state-space SIR model, with an extension of time-dependent transmission rate . It can be a step-wise function or follow an exponential function .
In this analysis, the package R{eSIR} was used. The R{eSIR} was adopted by scholars in predicting the epidemic trend of COVID-19 in Italy and Hunan, China [34]. The basic reproductive numbers for the time-series data of COVID-19 data from 22 January 2020 to 16 March 2020 were found to be 4.10 (95% CI: 2.15–6.77) for Italy and 3.15 (95% CI: 1.71–5.21) for Hunan. They further predicted that with rigorous blockage measures maintained in Italy, there would be 30,086 (95% CI: 7920–81869) infected cases in total, and the epidemic would reach an endpoint by 25 April (30 March–7 August).
The R{eSIR}package is available from https://github.com/lilywang1988/eSIR (accessed on 22 June 2024).
3.2. The tvt.eSIR Method in the R{eSIR} Package
One of the three models in the R{eSIR} package is the tvt.eSIR(). This model was adopted in this analysis. It allows for a time-varying transmission rate, which can be step-wise or exponential. It is the simplest model in the package and requires only the time-series data of the number of confirmed and removed cases. As the other two models would need quarantine or vaccination data, respectively, they were not considered in this analysis.
Compared with the standard SIR model, the tvt.eSIR model introduces a function which reflects time-dependent changes in the transmission function due to public health policies, e.g., quarantine measures, mutation or changes in the virulence of the variants, environmental changes like changes in temperature and humidity, changes in data collection or case definition policies (e.g., how a confirmed or death case is defined), etc.
This modification function can be a step function or a continuous function. In this analysis, a step function approach was adopted.
The dynamics of , , and are given by the three differential equations:
When a step function is assumed, = constant value between zero and one; When a continuous function is assumed, .
Note that the extra functions is providing an extra “factor” for the transmission rate to accommodate the changes in transmission rate over time due to human intervention or virus evolution.
In the demonstration example provided in the package document, a step function of = (1, 0.9, 0.5, 0.1) at change_time = (“01/23/2020”, “02/04/2020”, “02/08/2020”) is used to model early data from China. The change_time variable reflects when there was a major change in quarantine policies in China. The decline in the initial values used reflects the tightening of quarantine measures.
When an exponential function is used, it reflects a gradual decrease in transmission when public awareness, isolation policies, and personal protection measures gradually increase in intensity.
Both and change_points can be set to NULL, reflecting no prior information about the change in quarantine practices in the region.
In this package, the compartments are defined by a time series of proportions, not by counts. Let and denote the proportions of infected and removed at time t, respectively, then the proportion of susceptible cases at time t is given by . Assume that and follows a Beta–Dirichlet state-space model (BDSSM) [36]. [Note: In the formulae below, Beta, Gamma, Dirichlet, LogN stand for the Beta, Gamma, Dirichlet and lognormal distributions, respectively. These are common probability functions used to describe the underlying distributions.] The observations are
and the latent process is
where is the vector of the underlying prevalence of susceptible, infectious, and removed populations, and with , , and are parameters controlling the respective variances for the observation and latent processes, and and denote the transmission and removal rates, respectively.
To solve the derivative functions of the SIR process, we use:
The solution is obtained by the fourth-order Runge–Kutta(RK4) approximation [37].
Initially, the proportions of infected and removed is given by the corresponding first data value from the dataset, denoted by and , respectively, and the initial proportion of susceptible individuals is therefore . The initial parameters and prior distributions were specified according to the SARS data from Hong Kong as follows:
with , ;
with , and ;
JAGS [38] was then be used to run MCMC [39] chains to obtain the posterior estimates of the parameters.
3.3. Initial Values and Hyper-Parameters Used in the tvt.eSIR Function
Some default initial values and hyper-parameters used in the tvt.eSIR function are given as follows:
- (1)
- death_in_R = 0.02(death_in_R refers to the average of cumulative deaths in the removed compartments. When it was within Hubei, 0.4 was used. When it was outside Hubei, 0.02 was used).
- (2)
- beta0 = 0.2586(beta0 refers to , the average transmission rate. The value of 0.2586 was estimated from the SARS first-month outbreak [40].
- (3)
- gamma0 = 0.0821(gamma0 refers to , the average removed rate. The value 0.0821 was estimated from the SARS first-month outbreak).
- (4)
- R0 = beta0/gamma0(R0 refers to , the mean reproduction number. With this set of initial values for beta0 and gamma0, = 3.15).
- (5)
- gamma0_sd = 0.1(gamma0_sd refers to the standard deviation for the prior distribution of the removed rate . This value was chosen as a relatively large variance. This allowed more flexibility at the start so as to achieve an easier fit of the data. When more prior knowledge is available, a smaller value can be used for reaching more accurate estimates of parameters).
- (6)
- R0_sd = 1(R0_sd refers to the standard deviation for the prior distribution of . Similarly, this value was chosen as a relatively large variance).
- (7)
- eps = 1 ×(This is a non-zero controller so that all the input Y and R values would be bounded above 1 × .
- (8)
- time_unit = 1 day (It can be set to other values, e.g., 7 days for weekly data. But as the data used in this analysis were the daily numbers, the default of time_unit = 1 day was appropriate).
As there is sufficient variability allowed for the MCMC chains, the prior distributions and initial values did not restrict the final estimated parameter values obtained.
4. Source of Data
The daily numbers of confirmed, deaths, and recovered cases for the eight countries were obtained from the Coronavirus Disease (COVID-19) Dashboard, WHO (https://covid19.who.int/(accessed on 22 June 2024)).
The data from the sources were packed into three data files (see the three .csv files in the “Supplementary Files”) and processed with R.
The approximate population for the eight countries were estimated from three sources:
- (1)
- Worldmeter (https://www.worldmeters.info/world-population/population-by-country/(accessed on 22 June 2024));
- (2)
- World Health Organization (https://www.who.int/(accessed on 22 June 2024)); and
- (3)
- Wikipedia (https://www.wikipedia.org/(accessed on 22 June 2024)).
As the most updated figures from these three sources for each country varied, an estimate for 2019 taking into account all these three sources was adopted. Only estimated approximate values were used in this analysis, as small differences in the population size would affect the results very little.
5. Method
In this analysis, the R{eSIR} package was used to obtain the estimates. The tvt.eSIR method was adopted.
In the tvb.eSIR method, the time-dependent transmission rate can either be a step function with initial values and change_time specified, or it can follow an exponential function .
As an exploratory analysis, here, was simply assumed to be a constant between 0 and 1. There was no assumption on any known change_time, too. Therefore, both were set to NULL.
In order to compare the changes in the reproduction numbers in the periods from January to July 2020, the data were extracted into 4 datasets with different time frames:
- (i)
- Time frame 1 (dataset labelled as d1): from 22 January 2020 to 21 March 2020;
- (ii)
- Time frame 2 (dataset labelled as d2): from 22 January 2020 to 21 May 2020;
- (iii)
- Time frame 3 (dataset labelled as d3): from 22 January 2020 to 21 July 2020;
- (iv)
- Time frame 4 (dataset labelled as d4): from 22 January 2020 to 10 August 2020.
A sample R code for running Brazil data for time frame 1 (i.e., d1) is included in the Appendix A. Codes for d2, d3, and d4 and those of other countries are similar (see the code samples in the “Supplementary Files”). Each run took around 20 min to one hour and 20 min.
Note that the variable begin_str specified when the period begins (i.e., day 1 in this analysis). Both pi0 and change_time were not specified. This is different from the demonstrated use given in the package R{eSIR}, where the changing_time is specified as 3 dates when the quarantine policies changed, and prior values for function are specified to be 1.0, 0.9, 0.5 and 0.1, respectively, for the four periods concerned. For the method used in this analysis, on the other hand, no prior knowledge or assumption concerning the changes in government policies, quarantine measures, or virus mutation was needed. Thus, the method here can easily be applied to any epidemic data as long as the numbers of confirmed/deaths/recovered are available.
6. Results
The estimated values are summarized in Table 1. For the eight countries concerned, the values changed throughout the four time frames. They ranged from 0.97 to 5.28. The trend was lower values for d2, then there was a gradual increase in values for d3 and d4, showing the pandemic situation was, in general, becoming less serious in April and May 2020, but it gained momentum in May and continued to get worse in June, July and August.

Table 1.
estimates obtained from the eSIR_tvt step for the 8 countries considered.
The estimates were calculated using the beta and gamma estimates in the MCMC chains, using the formula = /. The mean values and the plot on how it changed throughout the iterations were obtained from the outputs every time the R codes was run.
Besides the estimates obtained, the automatic figures generated by the package (see Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 and “sample_outputs” folder in the “Supplementary Files”) provided more insights on the predicted trends. As an illustration, here are some plots obtained from analysing the Brazil data.
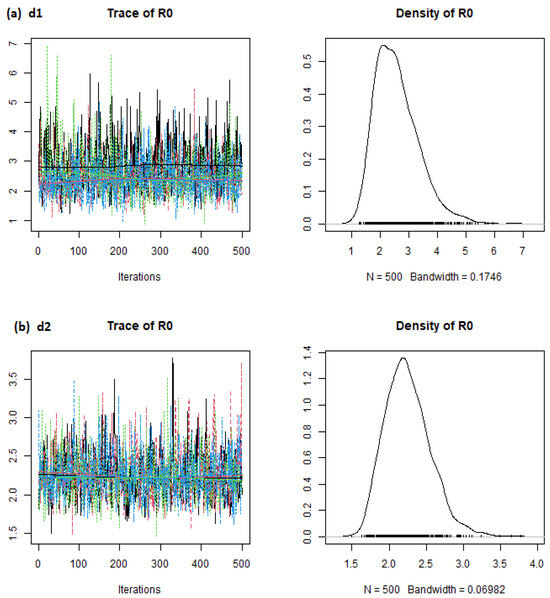
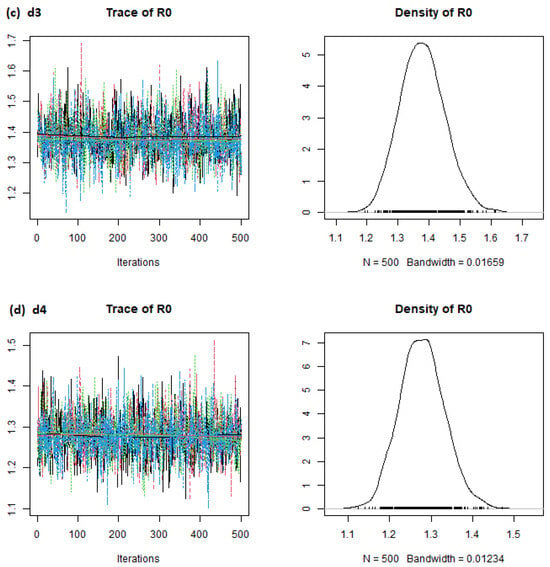
Figure 1.
estimates (Brazil) from the eSIR_tvt step for data from 22 January to 10 August 2020.
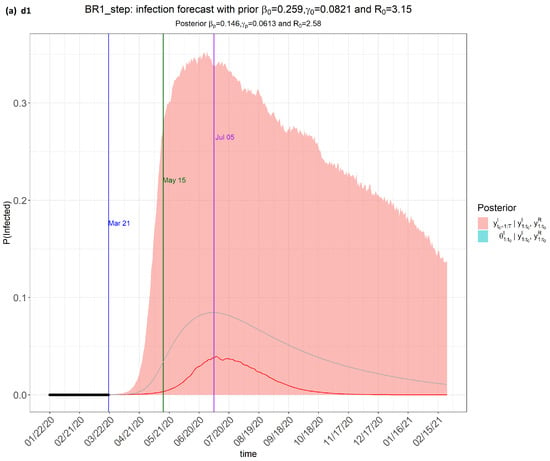
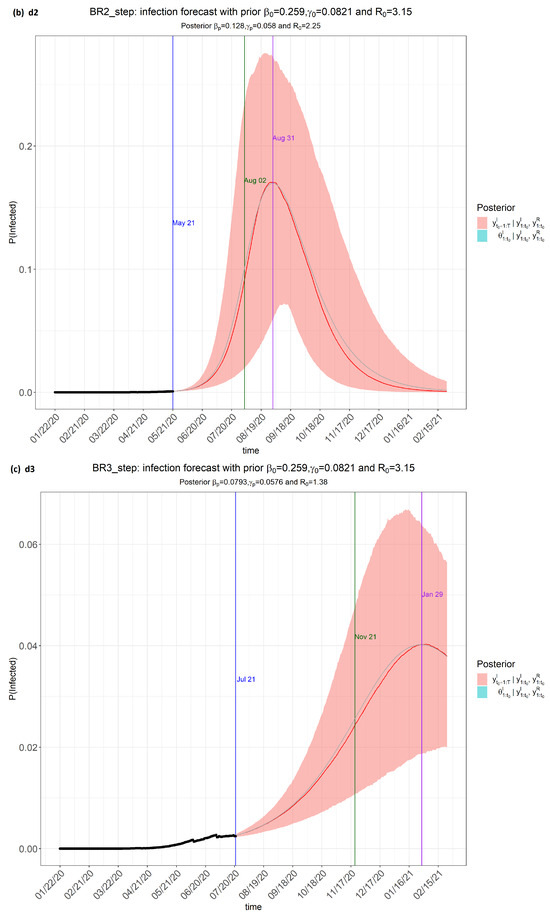
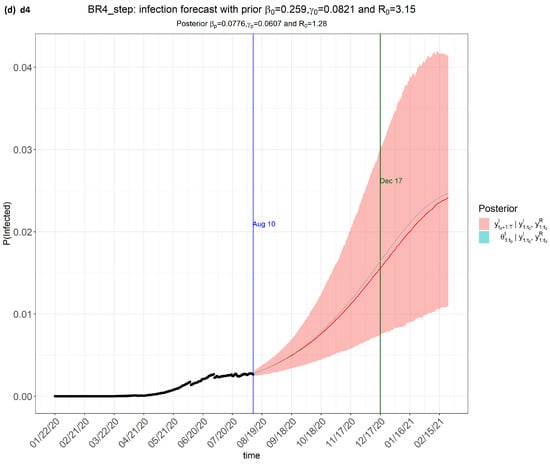
Figure 2.
step_forecast (Brazil) from the eSIR_tvt step for data from 22 January to 10 August 2020.

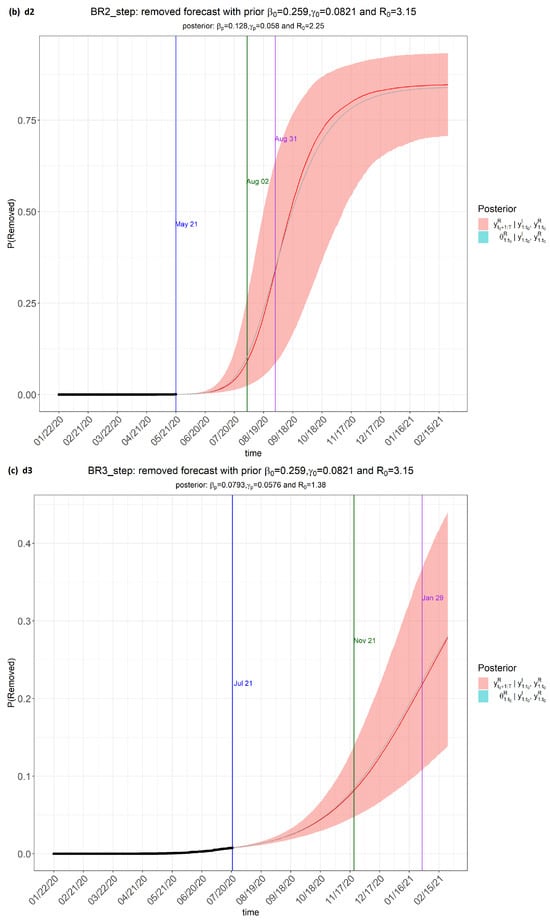
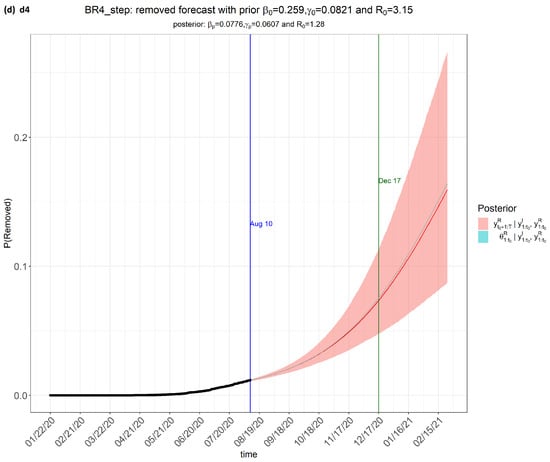
Figure 3.
step_forecast2 (Brazil) from the eSIR_tvt step for data from 22 January to 10 August 2020.
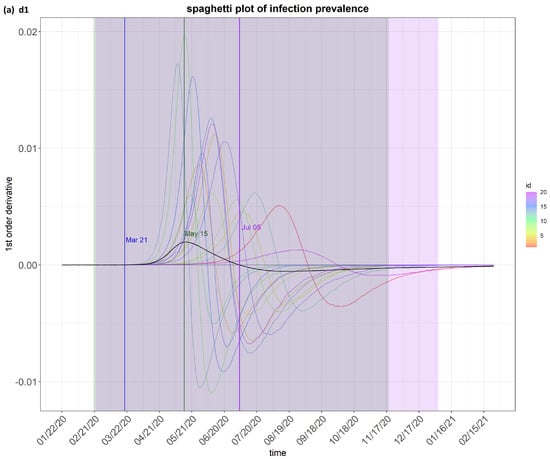
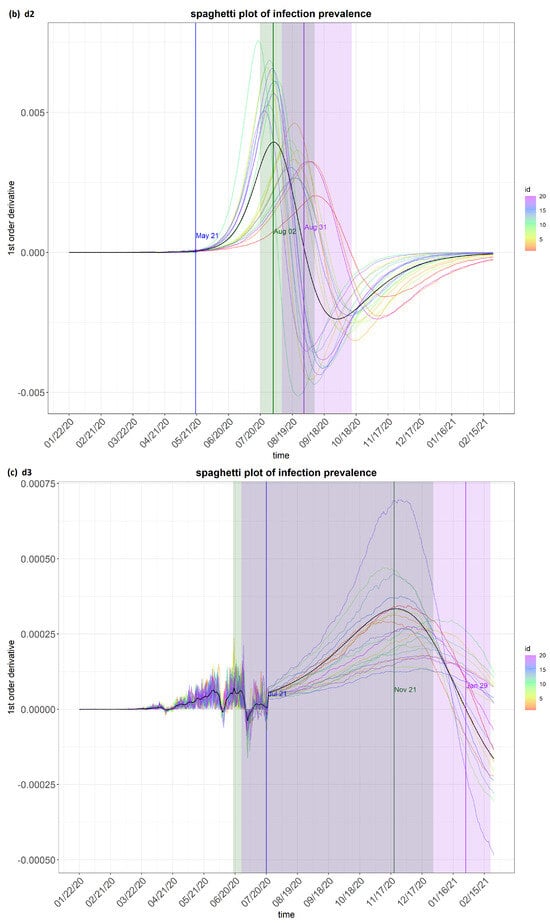
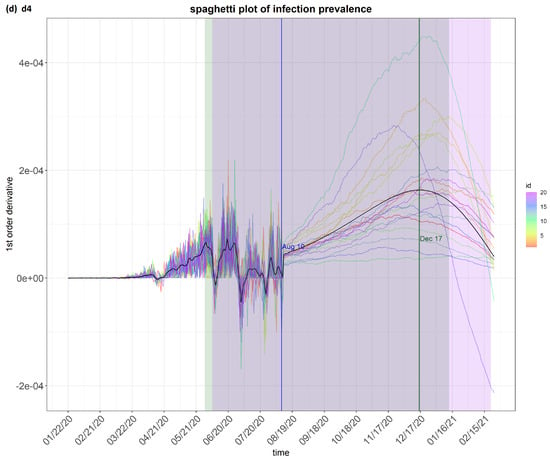
Figure 4.
step_spaghetti (Brazil) from the eSIR_tvt step for data from 22 January to 10 August 2020.
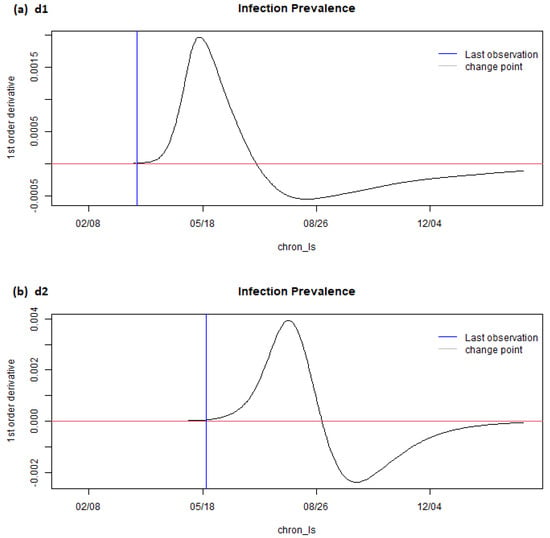

Figure 5.
stepderiv (Brazil) from the eSIR_tvt step for data from 22 January to 10 August 2020.
From Figure 1, the mean estimates for Brazil were around 1.3, 1.2, 1.3, and 1.4 for d1, d2, d3, and d4, respectively. Similarly, the mean estimates for other countries can be obtained visually from the stepR0_p charts.
From Figure 2, the pink regions show the projected regions of possible outcomes of the proportions of population infected at future dates, as generated by the model.
From Figure 3, the pink regions show the projected regions of possible outcomes of the proportions of population removed (i.e., either dead or recovered) at future dates, as generated by the model.
Figure 4 shows the spaghetti plots of infection prevalence as generated by the model. The infection prevalence is the proportion of people infected in the population at a specific time. It is a useful indicator to predict how the epidemic may evolve and for making comparisons on the survival and impact of a transmission disease. The value of its first-order derivative indicates the direction and momentum of change. The spaghetti plots show the possible “flows” of the first derivative of the infection prevalence. This first derivatives is important. A high positive value means the epidemic is getting worse quickly, e.g., due to the emergence of a new variant. On the other hand, a high negative value means the situation is improving quickly, e.g., due to quarantine measures or effective drugs.
Figure 5 shows the estimated and projected first-order derivative of the infection prevalence. For Brazil, a positive predicted value for most of the time from February to August 2020 meant that the percentage of population becoming infected was getting higher and higher with positive momentum. With the projected value even higher after August 2020, it meant the speed for the rate of increase would be even higher in the following months.
7. Discussion
What did the estimated from the eSIR_tvt step reflect? Why was the estimates in China and South Korea as high as 3.66 or 3.41? COVID-19 was well under control in these countries by 10 August, 2020. Why was the estimates in Brazil as low as 1.39? The daily numbers of confirmed cases were high in early August in Brazil. Does the estimate comply with the results from other studies? Are the estimates from the eSIR_tvt step model to be trusted?
First of all, there are many relevant studies on data over similar periods, with a whole range of estimates obtained. A review from February 2020 by the WHO showed that the initial estimates of R0 ranged from 1.5 to 6.68 [41]. For studies on individual country/region, an estimate of 3.1 was obtained for Brazil using data up to 31 May 2020 [42]. For China, an early-stage value was estimated to be 5.7 from data in late January 2020, while studies using different models and methods for data till 7 February 2020 from China resulted in estimates ranging from 1.5 to 6.49 [43]. For India, research on data from February 2020 to March 2021 by districts resulted in estimates varying from two to three (in most districts) to over seven (in eight districts) [44]. In a study on data till 31 March 2020 from the United States and eight European countries, values for Italy, the United Kingdom, and the US were estimated to be 4.6, 3.9, and 5.9, respectively [45]. For Singapore, an estimate from a study using local data up until 17 March 2020 was 0.7 [46]. For Korea, a study from data as of 6 March 2020 resulted in a estimate of 1.5 [47].
The estimates from this study are similar in range to those obtained from other studies except for China and South Korea. Actually, the resulting estimates for China and Korea from this analysis seem to be against the “intuitive” belief that a high means an “uncontrolled” condition, while a low means a “controlled” condition. What is wrong?
In this study, estimates fluctuated with time. The fluctuation is greater when the numbers of new infected, new dead, and new recovered individuals are comparatively low. This was the case for China and South Korea. In late 2020, the situations in these two countries were more or less under control, and there were a lower number of active cases as compared with before. Examining the data revealed that for these two countries, there were often days when the number of removed cases (i.e., deaths + recovered) exceeded the number of newly confirmed cases. The “negative” or “near zero” new active cases might be due to delays, say, around 30 days for deaths and around 21 days after the infection day. Moreover, there might be the issue of undiscovered cases in the background, which affected estimates significantly when the number of confirmed cases were very low.
These “negative” or “near zero” new cases might be affecting both the transmission rate and the removal rate estimation. Both the rate of transmission and the rate of removal were subjected to high variability. High variability for the removal rate is especially troublesome. As it is the denominator in the calculation of , any slight error would affect the model and the estimates significantly.
The number of new cases in China and South Korea were comparatively very low on the days before 10 August 2020. It was of the order of around 100 for China and 50 for South Korea and remained around the same level for many days. Compared with the data in earlier days, the number of confirmed cases in China was in the thousands in February 2020, while the number of confirmed cases for South Korea was in the hundreds in April 2020. In the SIR model, the estimated value from a comparatively low and flat number of new confirmed cases may not be low. Moreover, it is highly unstable. If the number of new confirmed cases randomly drifts to a slightly larger number for a few days, then could appear even higher.
Further, in this analysis, local and “imported” cases were not analysed separately. In a real situation, “imported” cases are not “infected” from the local cases and should be excluded from the estimates or analysed separately.
On the other hand, for Brazil, although the epidemic was growing at a fast rate with the number of new cases per day around 20,000 or more, the number of new cases “infected” from the large number of active cases of around 3,000,000 resulted in a comparatively stable value.
It is obvious that the estimates vary greatly from time to time, and from places to places. Moreover, the complexity of estimated values also depends on model structures and assumptions [48]. The operational definitions are not always identical. The interpretation of estimates from data with a comparatively low number of cases need to be taken with care. Comparison is best made with the same model, so that changes in values over time can be observed, compared, and interpreted. This will give important clues about the status of the epidemic for intelligent decisions on public health policies.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/covid4070065/s1.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article and supplementary materials.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
#################################################################################
library(eSIR)
set.seed(12082020+11)
#####################
# row1 Brazil (BR): 11 #seed 12082020+11
# row2 China (CN): 35
# row3 India (IN): 86
# row4 Italy (IT): 32
# row5 Korea, South (KR): 16
# row6 Singapore (SG): 09
# row7 United Kingdom (GB): 64
# row8 United States of America (US): 28
######################
# populations as at 31 December 2019
# Brazil (BR): 212.6e6
# China (CN): 1439.3e6
# India (IN): 1380.0e6
# Italy (IT): 60.5e6
# Korea, South (KR): 51.3e6
# Singapore (SG): 5.9e6
# United Kingdom (GB): 67.9e6
# United States of America (US): 331.0e6
######################
setwd(“C:/Users/user”)
getwd()
data1 <- read.csv(“confirmeddata.csv”)
data2 <- read.csv(“deathsdata.csv”)
data3 <- read.csv(“recovereddata.csv”)
##########################################
# data up to 21 March 2020
# BR: Brazil
####################################
NI_complete_BR1 <- c(t(data1[1,2:61]))
Deaths_BR1 <- c(t(data2[1,2:61]))
Recovered_BR1 <- c(t(data3[1,2:61]))
RI_complete_BR1 <- c(t(data2[1,2:61]+data3[1,2:61]))
N_BR1 <- 212.6e6
R_BR1 <- RI_complete_BR1/N_BR1
Y_BR1 <- NI_complete_BR1/N_BR1 - R_BR1
N_BR1
NI_complete_BR1
Deaths_BR1
Recovered_BR1
RI_complete_BR1
###################################
# tvt step
###################################
## Model 1 using tvt.eSIR(): an SIR model with a time-varying transmission rate
###################################
### Step function of pi(t)
###################################
change_time <- NULL
pi0 <- NULL
res.step <- tvt.eSIR(Y_BR1, R_BR1, begin_str = “1/22/2020”, T_fin = 400,
pi0 = pi0, change_time = change_time, dic = T,
casename = “BR1_step”, save_files = T, save_mcmc=T,
save_plot_data = T, M = 5e3, nburnin = 2e2)
res.step$dic_val
###############################################################################
References
- Atkeson, A.; Kopecky, K.A.; Zha, T.A. Estimating and Forecasting Disease Scenarios for COVID-19 with an SIR Model; NBER Working Paper: Cambridge, MA, USA, 2020; p. w27335. [Google Scholar]
- Mizumoto, K.; Kagaya, K.; Zarebski, A.; Chowell, G. Estimating the asymptomatic proportion of coronavirus disease 2019 (COVID-19) cases on board the Diamond Princess cruise ship, Yokohama, Japan, 2020. Eur. Cent. Dis. Prev. Control Eurosurveillance 2020, 25, 2000180. [Google Scholar] [CrossRef]
- Donida, B.M. Report on the New Coronavirus COVID-19 Pandemic in Italy; JSciMed Central: Hyderabad, India, 2020. [Google Scholar]
- Zhan, C.; Chi, K.T.; Lai, Z.; Hao, T.; Su, J. Prediction of COVID-19 Spreading Profiles in South Korea, Italy and Iran by Data-Driven Coding; Cold Spring Harbor Laboratory Press: Cold Spring Harbor, NY, USA, 2020. [Google Scholar]
- Sardar, T.; Nadim, S.S.; Rana, S.; Chattopadhyay, J. Assessment of lockdown effect in some states and overall India: A predictive mathematical study on COVID-19 outbreak. Chaos Solitons Fractals 2020, 139, 110078. [Google Scholar] [CrossRef]
- Song, P.X.; Wang, L.; Zhou, Y.; He, J.; Zhu, B.; Wang, F.; Tang, L.; Eisenberg, M. An Epidemiological Forecast Model and Software Assessing Interventions on COVID-19 Epidemic in China; Cold Spring Harbor Laboratory Press: Cold Spring Harbor, NY, USA, 2020. [Google Scholar]
- Arifin, W.N.; Chan, W.H.; Amaran, S.; Musa, K.I. A Susceptible-Infected-Removed (SIR) Model of COVID-19 Epidemic Trend in Malaysia under Movement Control Order (MCO) Using a Data Fitting Approach; Cold Spring Harbor Laboratory Press: Cold Spring Harbor, NY, USA, 2020. [Google Scholar]
- Tolu, L.B.; Ezeh, A.; Feyissa, G.T. How Prepared Is Africa for the COVID-19 Pandemic Response? The Case of Ethiopia. Dove Press Risk Manag. Healthc. Policy 2020, 13, 771. [Google Scholar] [CrossRef] [PubMed]
- Dao, T.L.; Nguyen, T.D. Controlling the COVID-19 pandemic: Useful lessons from Vietnam. Travel Med. Infect. Dis. 2020, 37, 101822. [Google Scholar] [CrossRef] [PubMed]
- Al-Rousan, N.; Al-Najjar, H. Data Analysis of Coronavirus CoVID-19 Epidemic in South Korea Based on Recovered and Death Cases. J. Med. Virol. 2020, 92, 1603–1608. [Google Scholar] [CrossRef] [PubMed]
- Roser, M.; Ritchie, H.; Ortiz-Ospina, E.; Hasell, J. Coronavirus disease (COVID-19)–Statistics and research. Our World Data 2020, 4, 1–45. [Google Scholar]
- Boudrioua, M.S.; Boudrioua, A. Predicting the COVID-19 Epidemic in Algeria Using the SIR Model; Cold Spring Harbor Laboratory Press: Cold Spring Harbor, NY, USA, 2020. [Google Scholar]
- Deo, V.; Chetiya, A.R.; Deka, B.; Grover, G. Forecasting Transmission Dynamics of COVID-19 in India Under Containment Measures-A Time-Dependent State-Space SIR Approach. Stat. Appl. 2020, 18, 157–180. [Google Scholar]
- Juni, P.; Rothenbuhler, M.; Bobos, P.; Thorpe, K.E.; da Costa, B.R.; Fisman, D.N.; Slutsky, A.S.; Gesink, D. Impact of climate and public health interventions on the COVID-19 pandemic: A prospective cohort study. Can. Med. Assoc. J. 2020, 192, E566–E573. [Google Scholar] [CrossRef]
- Bagal, D.K.; Rath, A.; Barua, A.; Patnaik, D. Estimating the Parameters of SIR Model of COVID-19 Cases in India during Lock Down Periods; Cold Spring Harbor Laboratory Press: Cold Spring Harbor, NY, USA, 2020. [Google Scholar]
- Liu, Z.; Magal, P.; Seydi, O.; Webb, G. Understanding unreported cases in the COVID-19 epidemic outbreak in Wuhan, China, and the importance of major public health interventions. Biology 2020, 9, 50. [Google Scholar] [CrossRef]
- Liu, Z.; Magal, P.; Webb, G. Predicting the number of reported and unreported cases for the COVID-19 epidemics in China. arXiv 2020, arXiv:10:2020.04. [Google Scholar]
- Griette, Q.; Demongeot, J.; Magal, P. What can we learn from COVID-19 data by using epidemic models with unidentified infectious cases? medRxiv 2021. 2021-06. Available online: https://www.medrxiv.org/content/10.1101/2021.06.16.21259019v1 (accessed on 6 September 2023).
- Dietz, K.; Heesterbeek, J.A.P. Daniel Bernoulli’s epidemiological model revisited. Math. Biosci. 2002, 180, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Sapna, S.; Tamilarasi, A.; Kumar, M.P. Backpropagation learning algorithm based on Levenberg Marquardt Algorithm. Comp. Sci. Inf. Technol. 2012, 2, 393–398. [Google Scholar]
- Griette, Q.; Demongeot, J.; Magal, P. A robust phenomenological approach to investigate COVID-19 data for France. medRxiv 2021. 2021-02. Available online: https://www.medrxiv.org/content/10.1101/2021.02.10.21251500v1.full (accessed on 6 September 2023). [CrossRef]
- Demongeot, J.; Magal, P. Data-Driven Mathematical Modeling Approaches for COVID-19: A survey. arXiv 2023, arXiv:2309.17087. [Google Scholar]
- Howard, W. The SIR Model and the Foundations of Public Health. 1887. Available online: https://mat.uab.cat/~matmat/ebook2013/V2013n03-ebook.pdf (accessed on 6 September 2023).
- Roberts, M.G.; Heesterbeek, J. Mathematical Models in Epidemiology; EOLSS: Abu Dhabi, United Arab Emirates, 2003. [Google Scholar]
- Brauer, F. Compartmental models in epidemiology. Math. Epidemiol. 2008, 1945, 19–79. [Google Scholar]
- Jiang, F.; Zhao, Z.; Shao, X. Time series analysis of COVID-19 infection curve: A change-point perspective. J. Econom. 2020, 232, 1–17. [Google Scholar] [CrossRef]
- Prasse, B.; Achterberg, M.A.; Ma, L.; Van, M.P. Network-inference-based prediction of the COVID-19 epidemic outbreak in the Chinese province Hubei. Appl. Netw. Sci. 2020, 5, 1–11. [Google Scholar] [CrossRef]
- Sahneh, F.D.; Vajdi, A.; Shakeri, H.; Fan, F.; Scoglio, C. GEMFsim: A stochastic simulator for the generalized epidemic modeling framework. J. Comput. Sci. 2017, 22, 36–44. [Google Scholar] [CrossRef]
- Ng, T.W.; Turinici, G.; Danchin, A. A double epidemic model for the SARS propagation. BMC Infect. Dis. 2003, 3, 19. [Google Scholar] [CrossRef]
- Schlickeiser, R.; Kröger, M. Mathematics of Epidemics: On the General Solution of SIRVD, SIRV, SIRD, and SIR Compartment Models. Mathematics 2024, 12, 941. [Google Scholar] [CrossRef]
- Kröger, M.; Schlickeiser, R. On the Analytical Solution of the SIRV-Model for the Temporal Evolution of Epidemics for General Time-Dependent Recovery, Infection and Vaccination Rates. Mathematics 2024, 12, 326. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, D.; Peng, L.; Zhuge, C.; Hong, L. Rational evaluation of various epidemic models based on the COVID-19 data of China. Epidemics 2021, 37, 100501. [Google Scholar] [CrossRef]
- Meng, X.; Zhao, S.; Feng, T.; Zhang, T. Dynamics of a novel nonlinear stochastic SIS epidemic model with double epidemic hypothesis. J. Math. Anal. Appl. 2016, 433, 227–242. [Google Scholar] [CrossRef]
- Wangping, J.; Ke, H.; Yang, S.; Wenzhe, C.; Shengshu, W.; Shanshan, Y.; Yao, H. Extended SIR prediction of the epidemics trend of COVID-19 in Italy and compared with Hunan, China. Front. Front. Med. 2020, 7, 169. [Google Scholar]
- Lin, J. On the Dirichlet Distribution; Department of Mathematics and Statistics, Queens University: Kingston, ON, Canada, 2016. [Google Scholar]
- Manouchehri, N.; Bouguila, N. Multivariate Beta-Based Hierarchical Dirichlet Process Hidden Markov Models in Medical Applications. In Hidden Markov Models and Applications; Springer International Publishing: Cham, Switzerland, 2022; pp. 235–261. [Google Scholar]
- Rößler, A. Runge–Kutta methods for the strong approximation of solutions of stochastic differential equations. SIAM J. Numer. Anal. 2010, 48, 922–952. [Google Scholar] [CrossRef]
- Plummer, M. JAGS, Version 3.3; 0 User Manual; 2012. Available online: https://www.stat.cmu.edu/~brian/463-663/week10/articles (accessed on 6 September 2023).
- Chernozhukov, V.; Hong, H. An MCMC approach to classical estimation. J. Econom. 2003, 115, 293–346. [Google Scholar] [CrossRef]
- Riley, S.; Fraser, C.; Donnelly, C.A.; Ghani, A.C.; Abu-Raddad, L.J.; Hedley, A.J.; Anderson, R.M. Transmission dynamics of the etiological agent of SARS in Hong Kong: Impact of public health interventions. Science 2003, 300, 1961–1966. [Google Scholar] [CrossRef]
- Achaiah, N.C.; Subbarajasetty, S.B.; Shetty, R.M. R0 and re of COVID-19: Can we predict when the pandemic outbreak will be contained? Indian Soc. Crit. Care Med. Indian J. Crit. Care Med.-Peer-Rev. Off. Publ. Indian Soc. Crit. Care Med. 2020, 24, 1125. [Google Scholar] [CrossRef] [PubMed]
- de Souza, W.M.; Buss, L.F.; Candido, D.S.; Carrera, J.P.; Li, S.; Zarebski, A.E.; Pereira, R.H.M.; Prete, C.A., Jr.; de Souza-Santos, A.A.; Parag, K.V.; et al. Epidemiological and clinical characteristics of the COVID-19 epidemic in Brazil. Nat. Hum. Behav. 2020, 4, 856–865. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Gayle, A.A.; Wilder-Smith, A.; Rocklöv, J. The Reproductive Number of COVID-19 is Higher Compared to SARS Coronavirus; Oxford University Press (OUP): Oxford, UK, 2020. [Google Scholar]
- Shil, P.; Atre, N.M.; Patil, A.A.; Tandale, B.V.; Abraham, P. District-wise estimation of Basic reproduction number (R 0) for COVID-19 in India in the initial phase. Spat. Inf. Res. 2021, 30, 1–9. [Google Scholar] [CrossRef]
- Ke, R.; Romero-Severson, E.; Sanche, S.; Hengartner, N. Estimating the reproductive number R0 of SARS-CoV-2 in the United States and eight European countries and implications for vaccination. J. Theor. Biol. 2021, 517, 110621. [Google Scholar] [CrossRef] [PubMed]
- Tariq, A.; Lee, Y.; Roosa, K.; Blumberg, S.; Yan, P.; Ma, S.; Chowell, G. Real-time monitoring the transmission potential of COVID-19 in Singapore, March 2020. BioMed Cent. BMC Med. 2020, 18, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Shim, E.; Tariq, A.; Choi, W.; Lee, Y.; Chowell, G. Transmission potential and severity of COVID-19 in South Korea. Int. J. Infect. Dis. 2020, 93, 339–344. [Google Scholar] [CrossRef]
- Delamater, P.L.; Street, E.J.; Leslie, T.F.; Yang, Y.T.; Jacobsen, K.H. Complexity of the basic reproduction number (R0). Centers Dis. Control Prev. Emerg. Infect. Dis. 2019, 25, 1. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).