Using Two Group-Contribution Methods to Calculate Properties of Liquid Compounds Involved in the Cyclohexanone Production Operations
Abstract
1. Introduction
2. Two Group-Contribution Methods for Estimating Properties of Pure Substances
2.1. The Joback Method
2.2. Marrero–Gani Method
3. Evaluation of Estimates for the Selected Substances
3.1. Evaluation of Temperatures and Enthalpies of Phase Transition
3.2. Critical Properties
3.3. Estimation of Enthalpies of Formation and Thermal Capacities
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Compounds Present in the Streams of the Cyclohexanone Production Process
- Cyclohexane feeding; cyclohexane, hydrocarbons.
- Oxidant supply; air.
- Entrance to oxidation; cyclohexane, hydrocarbons, cyclohexanone, cyclohexanol, light oxides.
- Nitrogen.
- Oxidation effluent; cyclohexane, cyclohexanone, cyclohexanol, light and heavy oxidized, peroxides, formic acid, acetic acid, other monocarboxylic acids, dicarboxylic acids, esters, butanol, pentanol, cyclopentanone, cyclopentanol, 2-pentanone, 2-cyclo-hexen-1-one, cyclohexene, 2-methylcyclopentanone, methylcyclopentanol, heptanones, 2-methyl-3-heptanone, 1,3-cyclohexanedione, 1,2-cyclohexanediol, methylcyclohexanols, ethers.
- Washing water; water.
- Washing emulsion; water, cyclohexane, cyclohexanone, cyclohexanol, light and heavy oxidized, peroxides, formic acid, acetic acid, other monocarboxylic acids, dicarboxylic acids, esters, butanol, pentanol, cyclopentanone, cyclopentanol, 2-pentanone, 2-cyclo hexen-1-one, cyclohexene, 2-methylcyclopentanone, 1-methylcyclopentanol, heptanones, 2-methyl-3-heptanone, 1,3-cyclohexanedione, 1,2-cyclohexanediol, methylcyclohexanols, ethers.
- Acid water; water, formic acid, acetic acid, other monocarboxylic acids.
- Oxidized product; cyclohexane, cyclohexanone, cyclohexanol, light and heavy oxidized, peroxides, monocarboxylic acids, dicarboxylic acids, esters, butanol, pentanol, cyclopentanone, cyclopentanol, 2-pentanone, 2-cyclohexen-1-one, cyclohexene, 2-methyl cyclopentanone, 1-methylcyclopentanol, heptanones, 2-methyl-3-heptanone, 1,3-cyclo hexanedione, 1,2-cyclohexanediol, methylcyclohexanols, ethers.
- Alkali; water, sodium hydroxide.
- Saponification emulsion; water, sodium hydroxide, cyclohexane, cyclohexanone, cyclohexanol, light and heavy oxidized, peroxides, monocarboxylic acids, dicarboxylic acids, esters, butanol, pentanol, cyclopentanone, cyclopentanol, 2-pentanone, cyclohexenone, cyclohexene, methylcyclopentanone, methylcyclopentanol, heptanones, methylheptanone, cyclohexanedione, cyclohexanediol, methylcyclohexanols, ethers.
- Sodium salts; sodium hydroxide, sodium salts.
- Saponified product; sodium hydroxide, cyclohexanone, cyclohexanol, light oxidized.
- Cx I recycle; cyclohexanone, cyclohexanol, light oxides.
- KA-Oil; cyclohexanone, cyclohexanol, oxides, alcohols, aldehydes and ketones.
- Purified cyclohexanone; butanol, pentanol, cyclopentanol, cyclopentanone, 5-hexenal, hexanal, 2-hexanone, cyclohexanone, cyclohexanol, 2-cyclohexen-1-one, heptanones, methylcyclohexanones, butylcyclohexane, cyclohexyl-butyl-ether.
- Residue from the purification of cyclohexanone; cyclohexanol, 2-cyclohexen-1-one, 2-cyclohexen-1-ol, heptanones, methylcyclohexanones, butylcyclohexane, cyclohexyl-butyl-ether, cyclohexene oxides, cyclohexylidene-cyclohexanone, cyclohexanone oligo mers, pentylcyclohexane, cyclohexyl acetate, other light/heavy condensation products.
- Heavy-residue; cyclohexylidene-cyclohexanone, cyclohexanone oligomers, heavy condensation products.
- Cyclohexanol for dehydrogenation; cyclohexanone, cyclohexanol, 2-cyclohexen-1-one, 2-cyclohexen-1-ol, heptanones, methylcyclohexanones, butylcyclohexane, cyclohexyl-butyl-ether, cyclohexene oxides, cyclohexylidene-cyclohexanone, cyclohexa-none oligomers, n-pentylcyclohexane, cyclohexyl acetate, other light/heavy condensation products.
- Cyclohexanol recycle; cyclopentanol, hexanal, 2-hexanone, cyclohexanone, cyclo-hexanol, cyclohexenone, cyclohexenol, heptanones, methylcyclohexanone, cyclohexyl-butyl ether.
- Hydrogen.
Appendix B. Compounds Involved in the Production Process of Cyclohexanone
| No. | Compound | Formula | Chemical Structure | CAS# |
| 1 | acetic acid | C2H4O2 | 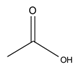 | 64-19-7 |
| 2 | 1,1′-bicyclohexyl | C12H22 | 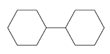 | 92-51-3 |
| 3 | [1,1′-bicyclohexyl]-2,3′-dione | C12H18O2 |  | 55265-34-4 |
| 4 | 1-butanol | C4H10O | 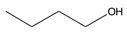 | 71-36-3 |
| 5 | butoxycyclohexane | C10H20O | 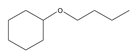 | 24072-44-4 |
| 6 | butylcyclohexane | C10H20 | 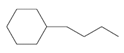 | 1678-93-9 |
| 7 | 2-butylcyclohexanone | C10H18O | 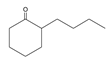 | 1126-18-7 |
| 8 | cycloheptanone | C7H12O | 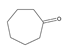 | 502-42-1 |
| 9 | 1,2-cyclohexanediol | C6H12O2 | 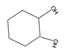 | 931-17-9 |
| 10 | 1,3-cyclohexanedione | C6H8O2 | 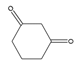 | 504-02-9 |
| 11 | cyclohexanol | C6H12O |  | 108-93-0 |
| 12 | cyclohexanone | C6H10O |  | 108-94-1 |
| 13 | 2-cyclohexen-1-ol | C6H8O |  | 822-67-3 |
| 14 | 2-cyclohexen-1-one | C6H8O | 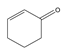 | 930-68-7 |
| 15 | 1-(1-cyclohexen-1-yl)-2-propanone | C9H14O | 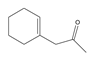 | 768-50-3 |
| 16 | cyclohexene | C6H10 | 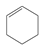 | 110-83-8 |
| 17 | cyclohexyl acetone | C9H16O |  | 103-78-6 |
| 18 | cyclohexyl butanoate | C10H18O2 |  | 1551-44-6 |
| 19 | cyclohexyl ethanone | C8H14O | 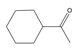 | 823-76-7 |
| 20 | cyclohexyl ethanoate | C8H14O2 |  | 622-45-7 |
| 21 | cyclohexyl ether | C12H22O | 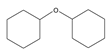 | 4645-15-2 |
| 22 | cyclohexyl hexanoate | C12H22O2 | 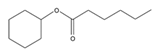 | 6243-10-3 |
| 23 | cyclohexyl pentanoate | C11H20O2 |  | 1551-43-5 |
| 24 | 2-cyclohexylidencyclohexanone | C12H18O | 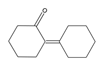 | 1011-12-7 |
| 25 | cyclopentanol | C5H10O | 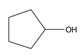 | 96-41-3 |
| 26 | cyclopentanone | C7H8O | 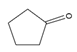 | 120-92-3 |
| 27 | 3,3-dimethylhexane | C8H18 |  | 563-16-6 |
| 28 | 4-(1,1-dimethylpropyl)cyclohexanone | C11H20O | 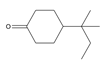 | 16587-71-6 |
| 29 | 2-ethylidenecyclohexanone | C8H12O |  | 1122-25-4 |
| 30 | formic acid | CH2O2 | 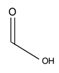 | 64-18-6 |
| 31 | 2-heptanone | C7H14O |  | 110-43-0 |
| 32 | 3-heptanone | C7H14O | 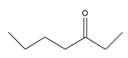 | 106-35-4 |
| 33 | hexanal | C6H12O | 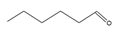 | 66-25-1 |
| 34 | 2-hexanone | C6H12O | 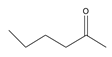 | 591-78-6 |
| 35 | 5-hexenal | C6H10O | 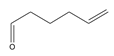 | 764-59-0 |
| 36 | 1-methoxycyclohexane | C7H14O | 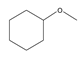 | 931-56-6 |
| 37 | 5-methyl-2-isopropylidenecyclohexanone | C10H16O |  | 15932-80-6 |
| 38 | 2-methyl-3-heptanone | C8H16O | 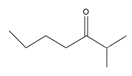 | 13019-20-0 |
| 39 | methylcyclohexane | C7H14 | 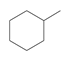 | 108-87-2 |
| 40 | 2-methylcyclohexanone | C7H12O | 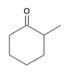 | 583-60-8 |
| 41 | 3-methylcyclohexanone | C7H12O | 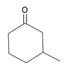 | 591-24-2 |
| 42 | methylcyclopentane | C6H12 | 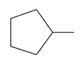 | 96-37-7 |
| 43 | 1-methylcyclopentanol | C6H12O | 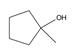 | 1462-03-9 |
| 44 | (1-methylethyl)cyclohexane | C9H18 | 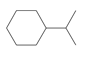 | 696-29-7 |
| 45 | 2-methylcyclopentanone | C6H10O | 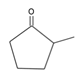 | 1120-72-5 |
| 46 | 1-pentanol | C5H12O |  | 71-41-0 |
| 47 | 2-pentanone | C5H10O | 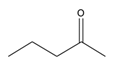 | 107-87-9 |
| 48 | 3-pentyl-1-cyclohexene | C11H20 | 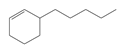 | 15232-92-5 |
| 49 | pentylcyclohexane | C11H22 | 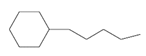 | 4292-92-6 |
| 50 | phenol | C6H6O | 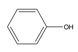 | 108-95-2 |
| 51 | p-tert-butylcyclohexanol | C10H20O | 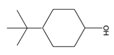 | 98-52-2 |
| 52 | 2-tetrahydrofurylmethanol | C5H10O2 | 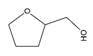 | 97-99-4 |
| 53 | 1,2,3,4-tetrahydronaphthalene | C10H12 | 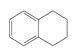 | 119-64-2 |
| 54 | toluene | C7H8 |  | 108-88-3 |
Appendix C. Mathematics of the Joback Method
| Property | Parameter | Equation |
|---|---|---|
| Boiling temperature/K | ||
| Melting temperature/K | ||
| Critical temperature/K | ||
| Critical pressure/bar | ||
| Critical volume/cm3·mol−1 | ||
| Gibbs energy of formation/kJ·kmol−1 | ||
| Enthalpy of formation/kJ·kmol−1 | ||
| Enthalpy of vaporization/kJ·kmol−1 | ||
| Enthalpy of melting/kJ·kmol−1 | ||
| Isobaric thermal capacity/kJ·kmol−1·K−1 | ; ; |
| No. | Compound | K | K | Tc K | pc bar | vc m3/kmol | cp (298 K) J/(molK) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | acetic acid | 390.7 | 272.9 | 587.3 | 57.31 | 0.171 | −434.8 | −377.9 | 40.67 | 11.08 | 65.7 |
| 2 | 1,1′-bicyclohexyl | 544.3 | 262.8 | 782.6 | 27.35 | 0.587 | −320.5 | 0.8 | 47.85 | 16.39 | 275.0 |
| 3 | [1,1′-bicyclohexyl]-2,3′-dione | 648.7 | 376.2 | 909.1 | 27.99 | 0.588 | −457.8 | −146.1 | 63.11 | 9.53 | 219.2 |
| 4 | 1-butanol | 406.7 | 190.1 | 571.1 | 39.76 | 0.344 | −354.6 | −198.0 | 43.25 | 12.87 | 138.0 |
| 5 | butoxycyclohexane | 470.2 | 232.1 | 665.9 | 25.25 | 0.547 | −327.6 | −47.2 | 40.69 | 14.68 | 238.0 |
| 6 | butylcyclohexane | 447.8 | 209.8 | 644.6 | 25.69 | 0.529 | −195.4 | 57.8 | 38.28 | 13.49 | 223.0 |
| 7 | 2-butylcyclohexanone | 515.6 | 278.1 | 729.1 | 26.63 | 0.536 | −333.1 | −64.8 | 42.53 | 13.00 | 228.0 |
| 8 | cycloheptanone | 455.9 | 245 | 689.2 | 39.46 | 0.361 | −257.0 | −94.5 | 36.33 | 2.06 | 123.0 |
| 9 | 1,2-cyclohexanediol | 502.8 | 358.9 | 720.4 | 34.8 | 0.342 | −464.9 | −273.6 | 53.77 | 16.55 | 195.0 |
| 10 | 1,3-cyclohexanedione | 496.5 | 305.4 | 743.3 | 45.29 | 0.319 | −367.9 | −213.3 | 48.19 | 1.08 | 114.7 |
| 11 | cyclohexanol | 431.9 | 264 | 654.6 | 49.25 | 0.270 | −278.7 | −120.9 | 41.73 | 9.30 | 147.0 |
| 12 | cyclohexanone | 428.7 | 237.2 | 656.0 | 43.23 | 0.313 | −230.2 | −90.8 | 33.94 | 1.57 | 105.0 |
| 13 | 2-cyclohexen-1-ol | 431.0 | 264.7 | 656.2 | 62.89 | 0.257 | −220.9 | −90.9 | 42.02 | 10.53 | 140.0 |
| 14 | 2-cyclohexen-1-one | 427.9 | 238 | 654.8 | 45.35 | 0.299 | −172.4 | −60.8 | 34.23 | 2.79 | 97.5 |
| 15 | 1-(1-cyclohexen-1-yl)-2-propanone | 488.6 | 271.8 | 707.4 | 34.04 | 0.458 | −180.8 | 12.0 | 43.46 | 14.40 | 190.0 |
| 16 | cyclohexene | 360.1 | 169.8 | 566.9 | 43.28 | 0.292 | −34.7 | 61.8 | 29.98 | 3.28 | 92.6 |
| 17 | cyclohexylacetone | 478.7 | 248.5 | 689.0 | 30.39 | 0.479 | −287.4 | −79.6 | 42.80 | 12.50 | 201.0 |
| 18 | cyclohexyl butanoate | 506.0 | 252.2 | 708.4 | 25.82 | 0.555 | −512.7 | −252.6 | 45.69 | 17.86 | 239.0 |
| 19 | cyclohexylethanone | 455.9 | 237.2 | 669.2 | 33.88 | 0.423 | −266.7 | −88.0 | 40.58 | 9.91 | 178.0 |
| 20 | cyclohexyl ethanoate | 460.2 | 229.1 | 668.4 | 41.52 | 0.443 | −471.4 | −269.4 | 40.94 | 14.44 | 169.0 |
| 21 | cyclohexyl ether | 544.3 | 262.8 | 782.6 | 26.46 | 0.587 | −320.5 | 0.8 | 47.85 | 16.39 | 275.0 |
| 22 | cyclohexyl hexanoate | 551.7 | 274.7 | 748.6 | 21.43 | 0.667 | −554.0 | −235.8 | 50.14 | 23.04 | 285.0 |
| 23 | cyclohexyl pentanoate | 528.9 | 263.4 | 728.5 | 23.47 | 0.611 | −533.3 | −244.2 | 47.92 | 20.45 | 262.0 |
| 24 | 2-cyclohexylidencyclohexanone | 621.1 | 362.1 | 872.0 | 27.33 | 0.606 | −235.8 | 43.5 | 59.44 | 11.56 | 220.1 |
| 25 | cyclopentanol | 404.7 | 256.2 | 621.0 | 54.55 | 0.223 | −251.9 | −117.2 | 39.33 | 8.81 | 129.0 |
| 26 | cyclopentanone | 401.6 | 229.5 | 622.3 | 47.56 | 0.265 | −203.4 | −87.1 | 31.54 | 1.08 | 87.0 |
| 27 | 3,3-dimethylhexane | 379.2 | 182.3 | 553.4 | 25.85 | 0.473 | −217.2 | 19.3 | 34.77 | 14.67 | 184.0 |
| 28 | 4-(1,1-dimethylpropyl)cyclohexanone | 535.2 | 291.8 | 758.9 | 24.63 | 0.581 | −362.5 | −53.6 | 46.13 | 13.79 | 251.0 |
| 29 | 2-ethylidenecyclohexanone | 481.1 | 270.1 | 709.8 | 35.26 | 0.408 | −195.5 | −28.5 | 39.62 | 7.07 | 142.0 |
| 30 | formic acid | 363.1 | 203.8 | 534.4 | 75.88 | 0.127 | −301.8 | −278.6 | 43.65 | 4.72 | 46.1 |
| 31 | 2-heptanone | 413.4 | 218.58 | 590.0 | 29.96 | 0.434 | −300.4 | −120.9 | 39.08 | 15.49 | 167.3 |
| 32 | 3-heptanone | 413.4 | 218.58 | 590.0 | 29.96 | 0.434 | −300.4 | −120.9 | 39.08 | 15.49 | 167.3 |
| 33 | hexanal | 385.3 | 198.9 | 557.8 | 36.47 | 0.389 | −252.8 | −99.9 | 35.37 | 15.35 | 148.0 |
| 34 | 2-hexanone | 390.6 | 206.8 | 568.1 | 35.99 | 0.378 | −279.8 | −129.3 | 35.30 | 14.66 | 144.0 |
| 35 | 5-hexenal | 382.0 | 197.1 | 558.1 | 35.52 | 0.370 | −127.3 | −12.0 | 34.70 | 14.07 | 137.0 |
| 36 | 1-Methoxycyclohexane | 374.4 | 190.5 | 569.6 | 33.53 | 0.331 | −238.9 | −68.8 | 31.62 | 6.42 | 151.0 |
| 37 | 5-methyl-2-isopropylidenecyclohexanone | 522.1 | 274.5 | 755.1 | 27.58 | 0.520 | −266.9 | −27.9 | 43.40 | 12.01 | 219.0 |
| 38 | 2-methyl-3-heptanone | 435.8 | 214.8 | 615.2 | 27.27 | 0.483 | −326.3 | −114.8 | 40.96 | 14.55 | 189.2 |
| 39 | Methylcyclohexane | 379.1 | 176 | 581.6 | 35.22 | 0.361 | −133.5 | 32.5 | 31.61 | 5.72 | 155.0 |
| 40 | 2-methylcyclohexanone | 352.0 | 168.28 | 546.9 | 38.39 | 0.313 | −106.7 | 36.2 | 29.40 | 5.23 | 112.6 |
| 41 | 3-methylcyclohexanone | 352.0 | 168.28 | 546.9 | 38.39 | 0.313 | −106.7 | 36.2 | 29.40 | 5.23 | 112.6 |
| 42 | 1-methylcyclopentanol | 427.8 | 291.4 | 651.6 | 50.66 | 0.277 | −257.3 | −114.3 | 40.41 | 5.11 | 121.0 |
| 43 | 2-methylcyclopentanone | 419.8 | 236.5 | 637.4 | 40.11 | 0.320 | −244.4 | −86.4 | 37.61 | 4.74 | 117.5 |
| 44 | (1-methylethyl)cyclohexane | 424.4 | 183.6 | 628.2 | 28.63 | 0.467 | −180.1 | 46.9 | 35.67 | 7.38 | 200.0 |
| 45 | methylcyclopentanone | 351.9 | 168.2 | 546.9 | 38.39 | 0.312 | −106.6 | 36.1 | 29.40 | 5.23 | 111.7 |
| 46 | 1-pentanol | 406.0 | 206.9 | 567.6 | 38.77 | 0.335 | −298.8 | −145.6 | 43.40 | 12.79 | 131.0 |
| 47 | 2-pentanone | 367.6 | 196 | 545.9 | 37.41 | 0.321 | −259.1 | −137.7 | 33.96 | 10.30 | 120.7 |
| 48 | 3-pentyl-1-cyclohexene | 469.8 | 221.9 | 666.3 | 24.19 | 0.571 | −158.3 | 96.2 | 40.80 | 17.30 | 239.0 |
| 49 | pentylcyclohexane | 470.6 | 221.1 | 665.2 | 23.36 | 0.585 | −216.1 | 66.2 | 40.51 | 16.08 | 246.0 |
| 50 | phenol | 439.0 | 283 | 671.0 | 59.26 | 0.230 | −96.5 | −32.9 | 43.58 | 11.51 | 95.2 |
| 51 | p-tert-butylcyclohexanol | 523.6 | 271.8 | 729.8 | 25.77 | 0.576 | −270.8 | −32.7 | 50.04 | 18.90 | 214.3 |
| 52 | 2-tetrahydrofurylmethanol | 449.3 | 235.8 | 635.2 | 48.29 | 0.315 | −399.6 | −227.7 | 48.45 | 14.06 | 125.0 |
| 53 | 1,2,3,4-tetrahydronaphthalene | 475.5 | 260.1 | 708.1 | 35.69 | 0.438 | 62.3 | 192.5 | 41.19 | 10.27 | 144.0 |
| 54 | toluene | 386.2 | 195.1 | 597.8 | 41.14 | 0.320 | 48.7 | 120.5 | 33.45 | 7.93 | 102.0 |
Appendix D. Mathematics of the Marrero–Gani Method
| Property | f= | Right-Hand Side of Equation (A1) |
|---|---|---|
| Melting temperature/K | ||
| Boiling temperature/K | ||
| Critical temperature/K | ||
| Critical pressure/bar | ||
| Critical volume/cm3·mol−1 | ||
| Gibbs energy of formation/kJ·kmol−1 | ||
| Enthalpy of formation/kJ·kmol−1 | ||
| Enthalpy of vaporization/kJ·kmol−1 | ||
| Enthalpy of melting/kJ·kmol−1 |
| Generic Constants | |
|---|---|
| /K | 147.450 |
| /K | 222.543 |
| Tc0/K | 231.239 |
| pc1/bar | 5.9827 |
| pc2/bar−0.5 | 0.108998 |
| vc0/cm3·mol−1 | 7.95 |
| /kJ·mol−1 | −34.967 |
| /kJ·mol−1 | 5.549 |
| /kJ·mol−1 | 11.733 |
| /kJ·mol−1 | −2.806 |
| No. | Compound | K | Tc K | pc bar | vc m3/kmol | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | acetic acid | 397.3 | 308.4 | 646.20 | 58.88 | 0.159 | −369.2 | −426.9 | 28.95 | 9.55 |
| 2 | 1,1′-bicyclohexyl | 511.7 | 271.7 | 727.00 | 25.60 | 0.598 | 42.6 | −272.0 | 57.98 | 12.91 |
| 3 | [1,1′-bicyclohexyl]-2,3′-dione | 579.8 | 354.2 | 867.22 | 30.29 | 0.599 | −528.3 | −229.8 | 85.54 | 23.04 |
| 4 | 1-butanol | 381.7 | 213.0 | 553.80 | 43.70 | 0.276 | −277.8 | −151.9 | 50.83 | 10.93 |
| 5 | Butoxycyclohexane | 464.5 | 231.5 | 676.94 | 22.89 | 0.610 | −40.9 | −357.0 | 59.80 | 19.52 |
| 6 | butylcyclohexane | 454.1 | 199.4 | 650.20 | 25.40 | 0.533 | 70.0 | −200.3 | 49.37 | 13.49 |
| 7 | 2-Butylcyclohexanone | 493.3 | 286.4 | 762.27 | 27.58 | 0.544 | −105.3 | −366.3 | 63.58 | 19.70 |
| 8 | cycloheptanone | 451.7 | 278.9 | 734.20 | 41.37 | 0.361 | −111.9 | −286.1 | 48.90 | 9.75 |
| 9 | 1,2-cyclohexanediol | 504.2 | 349.0 | 714.14 | 44.00 | 0.341 | −263.8 | −466.5 | 90.63 | 16.06 |
| 10 | 1,3-cyclohexanedione | 493.4 | 331.6 | 807.20 | 51.56 | 0.312 | −295.2 | −429.1 | 58.73 | 13.74 |
| 11 | cyclohexanol | 434.0 | 287.8 | 650.00 | 42.60 | 0.322 | −109.5 | −286.2 | 61.20 | 9.84 |
| 12 | cyclohexanone | 431.2 | 265.7 | 715.26 | 45.93 | 0.312 | −125.2 | −267.5 | 45.56 | 8.68 |
| 13 | 2-cyclohexen-1-ol | 437.2 | 288.9 | 648.32 | 45.39 | 0.307 | −49.6 | −189.2 | 62.29 | 8.88 |
| 14 | 2-cyclohexen-1-one | 443.2 | 267.8 | 714.00 | 49.12 | 0.297 | −59.2 | −183.0 | 53.06 | 10.23 |
| 15 | 1-(1-cyclohexen-1-yl)-2-propanone | 470.7 | 262.3 | 685.83 | 31.52 | 0.460 | −27.4 | −205.9 | 52.37 | 14.73 |
| 16 | cyclohexene | 356.1 | 183.6 | 558.00 | 43.92 | 0.289 | 104.7 | −8.9 | 32.86 | 2.66 |
| 17 | cyclohexylacetone | 473.7 | 266.4 | 679.01 | 29.83 | 0.483 | −75.0 | −301.2 | 54.96 | 15.75 |
| 18 | cyclohexyl butanoate | 486.2 | 237.2 | 683.41 | 25.83 | 0.545 | −245.5 | −543.1 | 61.08 | 18.83 |
| 19 | cyclohexylethanone | 453.7 | 278.5 | 662.05 | 33.33 | 0.427 | −83.1 | −280.4 | 49.43 | 13.11 |
| 20 | cyclohexyl ethanoate | 441.0 | 225.4 | 639.90 | 31.20 | 0.448 | −481.9 | −267.1 | 53.53 | 12.88 |
| 21 | cyclohexyl ether | 515.7 | 281.6 | 732.56 | 26.16 | 0.608 | −3.9 | −342.5 | 64.85 | 16.71 |
| 22 | cyclohexyl hexanoate | 515.7 | 257.9 | 727.13 | 20.21 | 0.713 | −221.3 | −605.5 | 75.81 | 26.75 |
| 23 | cyclohexyl pentanoate | 497.7 | 244.4 | 698.92 | 23.63 | 0.601 | −237.4 | −563.9 | 65.99 | 21.47 |
| 24 | 2-cyclohexylidencyclohexanone | 565.4 | 323.2 | 783.20 | 31.56 | 0.501 | −72.1 | −341.8 | 58.93 | 12.95 |
| 25 | cyclopentanol | 413.4 | 275.3 | 622.23 | 47.41 | 0.273 | −122.8 | −267.6 | 57.86 | 11.73 |
| 26 | cyclopentanone | 403.8 | 251.1 | 694.64 | 51.44 | 0.262 | −138.5 | −248.9 | 42.22 | 7.61 |
| 27 | 3,3-dimethylhexane | 385.1 | 187.3 | 555.14 | 25.68 | 0.466 | 17.2 | −217.9 | 38.06 | 10.52 |
| 28 | 4-(1,1-dimethylpropyl)cyclohexanone | 503.9 | 298.3 | 776.91 | 27.06 | 0.575 | −90.3 | −392.6 | 65.55 | 16.86 |
| 29 | 2-ethylidenecyclohexanone | 478.4 | 276.7 | 737.22 | 33.74 | 0.448 | −47.1 | −211.7 | 63.55 | 11.38 |
| 30 | formic acid | 362.8 | 259.4 | 554.90 | 83.20 | 0.102 | −279.9 | −303.6 | 48.32 | 13.31 |
| 31 | 2-heptanone | 426.7 | 223.8 | 611.13 | 29.34 | 0.417 | −300.8 | −122.0 | 46.38 | 17.58 |
| 32 | 3-heptanone | 417.1 | 227.2 | 596.91 | 29.44 | 0.418 | −305.0 | −125.4 | 46.29 | 17.26 |
| 33 | hexanal | 407.6 | 228.8 | 591.00 | 33.10 | 0.373 | −251.1 | −100.7 | 43.90 | 20.10 |
| 34 | 2-hexanone | 400.8 | 215.1 | 589.20 | 32.47 | 0.373 | −278.6 | −127.6 | 41.82 | 14.20 |
| 35 | 5-hexenal | 405.6 | 232.5 | 594.10 | 34.76 | 0.359 | −128.8 | −14.9 | 42.80 | 17.07 |
| 36 | 1-Methoxycyclohexane | 408.2 | 203.4 | 607.23 | 32.33 | 0.406 | −63.2 | −279.8 | 37.51 | 10.73 |
| 37 | 5-methyl-2-isopropylidenecyclohexanone | 497.2 | 299.0 | 753.09 | 28.05 | 0.558 | −33.8 | −255.2 | 77.19 | 11.98 |
| 38 | 2-methyl-3-heptanone | 431.2 | 233.0 | 613.20 | 26.78 | 0.470 | −122.8 | −334.2 | 49.16 | 16.81 |
| 39 | Methylcyclohexane | 374.2 | 182.4 | 577.23 | 35.07 | 0.370 | 44.6 | −137.8 | 35.17 | 6.74 |
| 40 | 2-methylcyclohexanone | 448.3 | 266.3 | 723.99 | 38.52 | 0.370 | −299.4 | −125.3 | 48.95 | 11.81 |
| 41 | 3-methylcyclohexanone | 448.3 | 266.3 | 723.99 | 38.52 | 0.370 | −299.4 | −125.3 | 48.95 | 11.81 |
| 42 | 1-methylcyclopentanol | 409.2 | 283.5 | 580.05 | 44.29 | 0.325 | −142.0 | −313.4 | 57.35 | 5.99 |
| 43 | 2-methylcyclopentanone | 422.4 | 251.8 | 704.16 | 42.52 | 0.321 | −280.8 | −138.6 | 45.61 | 10.74 |
| 44 | (1-methylethyl)cyclohexane | 427.9 | 191.4 | 621.05 | 28.42 | 0.481 | 57.3 | −196.4 | 43.00 | 11.32 |
| 45 | methylcyclopentanone | 340.4 | 155.8 | 538.30 | 38.44 | 0.313 | 31.3 | −119.2 | 31.83 | 5.64 |
| 46 | 1-pentanol | 410.9 | 221.5 | 580.32 | 38.12 | 0.332 | −143.9 | −298.6 | 55.80 | 14.20 |
| 47 | 2-pentanone | 362.1 | 210.4 | 544.80 | 37.06 | 0.306 | −141.6 | −263.3 | 36.47 | 11.98 |
| 48 | 3-pentyl-1-cyclohexene | 473.2 | 180.7 | 652.99 | 25.51 | 0.559 | 128.8 | −109.7 | 59.95 | 16.49 |
| 49 | pentylcyclohexane | 476.9 | 208.7 | 668.01 | 23.27 | 0.590 | 78.0 | −221.2 | 54.28 | 16.13 |
| 50 | phenol | 455.0 | 308.0 | 687.06 | 59.65 | 0.271 | −32.6 | −94.3 | 64.25 | 15.36 |
| 51 | p-tert-butylcyclohexanol | 494.8 | 240.6 | 694.60 | 24.12 | 0.595 | 216.4 | −43.5 | 58.23 | 13.72 |
| 52 | 2-tetrahydrofurylmethanol | 451.2 | 258.3 | 641.69 | 48.15 | 0.305 | −239.0 | −399.2 | 64.17 | 14.14 |
| 53 | 1,2,3,4-tetrahydronaphthalene | 480.8 | 241.7 | 664.03 | 31.37 | 0.521 | 110.1 | −61.3 | 77.10 | 11.86 |
| 54 | toluene | 383.8 | 202.1 | 604.05 | 42.18 | 0.317 | 123.6 | 50.6 | 38.43 | 9.90 |
References
- Sosa, A.; Ortega, J.; Fernández, L.; Romero, A.; Santos, A.; Lorenzo, D. Evaluation of VLEs for Binary Compounds Involved in the Production Process of Cyclohexanone. ChemEngineering 2022, 6, 42. [Google Scholar] [CrossRef]
- Ritz, J.; Fuchs, H.; Kieczka, H.; Moran, W.C. Caprolactam. In Ullmann’s Encyclopedia of Industrial Chemistry; Cambell, F.T., Pfefferkorn, R., Rounsaville, J.R., Eds.; Wiley-VCH: Weinheim, Germany, 1986; Volume A5, pp. 31–50. [Google Scholar]
- Zhu, Z.; Li, G.; Yang, J.; Dai, Y.; Cui, P.; Wang, Y.; Xu, D. Improving the energy efficiency and production performance of the cyclohexanone ammoximation process via thermodynamics, kinetics, dynamics, and economic analyses. Energy Convers. Manag. 2019, 192, 100–113. [Google Scholar] [CrossRef]
- Matshwele, J.; Mmusi, K.; Vishwanathan, V. A single step low cost production of cyclohexanone from phenol hydrogenation. Sreyas Int. J. Sci. Technol. 2019, 3, 1–6. [Google Scholar] [CrossRef]
- Jodra, L.G.; Romero, A.; García-Ochoa, F.; Aracil, J. Analysis of the Impurities in Industrial Epsilon-Caprolactam—Hypothesis of Formation. J. Appl. Polym. Sci. 1981, 26, 3271–3282. [Google Scholar] [CrossRef]
- Jodra, L.G.; Romero, A.; García-Ochoa, F.; Aracil, J. Impurity Content and Quality Definition of Commercial Epsilon-Caprolactam. Ind. Eng. Chem. Prod. Res. Dev. 1981, 20, 562–566. [Google Scholar] [CrossRef]
- Romero, A.; Yustos, P.; Santos, A. Dehydrogenation of cyclohexanol to cyclohexanone: Influence of methylcyclopentanols on the impurities obtained in epsilon-caprolactam. Ind. Eng. Chem. Res. 2003, 42, 3654–3661. [Google Scholar] [CrossRef]
- Romero, A.; Yustos, P.; Santos, A.; Rodríguez, S. Kinetic study of the oxidation of epsilon-caprolactam impurities with permanganate for PZ estimation. J. Ind. Eng. Chem. 2005, 11, 88–95. [Google Scholar]
- Romero, A.; Santos, A.; Escrig, D.; Simón, E. Comparative dehydrogenation of ciclohexanol to cyclohexanone with commercial copper catalysts: Catalytic activity and impurities formed. Appl. Cat. A Gen. 2011, 392, 19–27. [Google Scholar] [CrossRef]
- Lorenzo, D.; Santos, A.; Simon, E.; Romero, A. Kinetics of Alkali-Catalyzed Condensation of Impurities in the Cyclohexanone Purification Process. Ind. Eng. Chem. Res. 2013, 52, 15780–15788. [Google Scholar] [CrossRef]
- Lydersen, A.L.; Greenkorn, R.A.; Hougen, O.A. Generalized Thermodynamic Properties of Pure Fluids; Engineering Experiment Station Report 4; University of Wisconsin: Madison, WI, USA, 1955. [Google Scholar]
- Poling, B.E.; Prausnitz, J.M.; O’Connell, J.P. The Properties of Gases and Liquids, 5th ed.; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Simmrock, K.H.; Janowsly, R.; Ohnsorge, A. Critical Data of Pure Substances; Chemistry Data Series; DECHEMA: Frankfurt, Germany, 1986; Volume II. [Google Scholar]
- Joback, K.G.; Reid, R.C. Estimation of pure-component properties from group-contributions. Chem. Eng. Commun. 1987, 57, 233–243. [Google Scholar] [CrossRef]
- Marrero, J.; Gani, R. Group-contribution based estimation of pure component. Fluid Phase Equilib. 2001, 183–184, 183–208. [Google Scholar] [CrossRef]
- Riddick, J.A.; Bunger, W.B.; Sakano, T.K. Organic Solvents: Physical Properties and Methods of Purification, 4th ed.; Wiley-Interscience: New York, NY, USA, 1986. [Google Scholar]
- Steele, W.V.; Chirico, R.D.; Knipmeyer, S.E.; Nguyen, A. Vapor Pressure, Heat Capacity, and Density along the Saturation Line, Measurements for Cyclohexanol, 2-Cyclohexen-1-one, 1,2-Dichloropropane, 1,4-Di-tert-butylbenzene, (±)-2-Ethylhexanoic Acid, 2-(Methylamino)ethanol, Perfluoro-n-heptane, and Sulfolane. J. Chem. Eng. Data 1997, 42, 1021–1036. [Google Scholar] [CrossRef]
- Weast, R.C.; Grasselli, J.G. (Eds.) CRC Handbook of Data on Organic Compounds, 2nd ed.; CRC Press: Boca Raton, FL, USA, 1989; Volume 1. [Google Scholar]
- Forziati, A.F.; Rossini, F.D. Physical properties of sixty API-NBS hydrocarbons. J. Res. Natl. Bur. Stand. 1949, 43, 473–476. [Google Scholar] [CrossRef]
- Markovnik, V.S.; Sachek, A.I.; Peshchenko, A.D.; Shvaro, O.V.; Andreevskii, D.N.; Olizarevich, N.M. Temperature Dependence of Pressure for a Few Aldehydes. Termodin. Org. Soedin. 1979, 8, 107–110. [Google Scholar]
- Mears, T.W.; Stanley, C.L.; Compere, E.L.; Howard, F.L. Synthesis, purification, and physical properties of seven twelve-carbon hydrocarbons. J. Res. Natl. Bur. Stand. A Phys. Chem. 1963, 67, 475–479. [Google Scholar] [CrossRef]
- Moshkin, P.A. Vpr. Isolz. Pentozansoderzh. Syrya. Tr. Vses. Soveshch. Riga 1958, 1955, 225. [Google Scholar]
- Olson, W.T.; Hipsher, H.F.; Buess, C.M.; Goodman, I.A.; Hart, I.; Lamneck, J.H.; Gibbons, L.C. The Synthesis and Purification of Ethers. J. Am. Chem. Soc. 1947, 69, 2451–2454. [Google Scholar] [CrossRef]
- Reid, R.C.; Prausnitz, J.M.; Sherwood, T.K. The Properties of Gases and Liquids, 3rd ed.; McGraw-Hill: New York, NY, USA, 1977. [Google Scholar]
- Sayar, A.A.; Tatli, B.; Dramur, U. Liquid-Liquid Equilibria of the Water + Acetic Acid + Cyclohexyl Acetate Ternary. J. Chem. Eng. Data 1991, 36, 378–382. [Google Scholar] [CrossRef]
- Smith, H.A.; Pennekamp, E.F.H. The Catalytic Hydrogenation of the Benzene Nucleus II. The Hydrogenation of Benzene and Mono-alkylkbenzenes. J. Am. Chem. Soc. 1945, 67, 276–278. [Google Scholar] [CrossRef]
- Timmermans, J.; Hennaut-Roland, M. Works from International Bureau at Physical-Chemical Standards. VIII. Physical constants of 20 organic compounds. J. Chim. Phys. Phys.-Chim. Biol. 1937, 34, 693–735. [Google Scholar] [CrossRef]
- Walling, C.; Padwa, A. Positive Halogen Compounds. VI. Effects of Structure and Medium on the β-Scission of Alkoxy Radicals. J. Am. Chem. Soc. 1963, 85, 1593–1597. [Google Scholar] [CrossRef]
- White, A.H.; Bishop, W.S. Dielectric Evidence of Molecular Rotation in the Crystals of Certain Non-aromatic Compounds. J. Am. Chem. Soc. 1940, 62, 8–16. [Google Scholar] [CrossRef]
- Bridson-Jones, F.S.; Buckley, G.D.; Cross, L.H.; Driver, A.P. Oxidation of organic compounds by nitrous oxide: Part I. J. Chem. Soc. 1951, 2999–3008. [Google Scholar] [CrossRef]
- Adkins, H.; Pavlic, A.A. Hydrogenation of Esters to Alcohols over Raney Nickel. I. J. Am. Chem. Soc. 1947, 69, 3039–3041. [Google Scholar] [CrossRef] [PubMed]
- Gonthier-Vassal, A.; Szwarc, H. Thermodynamic properties of cycloketones: A DSC study. Thermochim. Acta 1998, 320, 141–154. [Google Scholar] [CrossRef]
- Kabo, G.J.; Kozyro, A.A.; Frenkel, M.; Blokhin, A.V. Solid Phase Transitions of the Cyclohexane Derivatives and the Model of Energy States of Molecules in Plastic Crystals. Mol. Cryst. Liq. 1999, 326, 333–355. [Google Scholar] [CrossRef]
- Streiff, A.J.; Hulme, A.R.; Cowie, P.A.; Krouskop, N.C.; Rossini, F.D. Purification, Purity, and Freezing Points of Sixty-four American Petroleum Institute Standard and Research Hydrocarbons. Anal. Chem. 1955, 27, 411–415. [Google Scholar] [CrossRef]
- Timmermans, J. Freezing points of organic compounds. VVI New determinations. Bull. Soc. Chim. Belg. 1952, 61, 393–402. [Google Scholar] [CrossRef]
- Timmermans, J. Physical Constants of Crystalline Organic Compounds; Mass on & Cie: Paris, France, 1953. [Google Scholar]
- Timmermans, J.; Mattaar, J.F. The Freezing Points of Organic Substances IV. New Exp. Determinations. Bull. Soc. Chim. Belg. 1921, 30, 62–71. [Google Scholar]
- Fiege, C.; Joh, R.; Petri, M.; Gmehling, J. Solid-Liquid Equilibria for Different Heptanones with Benzene, Cyclohexane, and Ethanol. J. Chem. Eng. Data 1996, 41, 1431–1433. [Google Scholar] [CrossRef]
- Wibaut, J.P.; Hoog, H.; Langedijk, S.L.; Overhoff, J.; Smittenberg, J. A study on the preparation and the physical constants of a number of alkanes and cycloalkanes. Recl. Trav. Chim. Pays-Bas 1939, 58, 329–377. [Google Scholar] [CrossRef]
- Wolfrom, M.L.; Bobbitt, J.M. Periodate Oxidation of Cyclic 1,3-Diketones. J. Am. Chem. Soc. 1956, 78, 2489–2493. [Google Scholar] [CrossRef]
- Ambrose, D.; Ghiassee, N.B. Vapour pressures and critical temperatures and critical pressures of C5 and C6 cyclic alcohols and ketones. J. Chem. Thermodyn. 1987, 19, 903–909. [Google Scholar] [CrossRef]
- Fuchs, R.; Peacock, L.A. Heats of vaporization of monoalkylcyclohexanes by the gas chromatography-calorimetry method. Can. J. Chem. 1978, 56, 2493–2498. [Google Scholar] [CrossRef]
- Landrieu, P.; Baylocq, F.; Johnson, J.R. Etude thermochimique dans la serie furanique. Bull. Soc. Chim. France 1929, 45, 36–49. [Google Scholar]
- Lee, C.H.; Dempsey, D.M.; Mohamed, R.S.; Holder, G.D. Vapor-liquid equilibria in the systems of n-decane/tetralin, n-hexadecane/tetralin, n-decane/1-methylnaphthalene, and 1-methylnaphthalene/tetralin. J. Chem. Eng. Data 1992, 37, 183–186. [Google Scholar] [CrossRef]
- Majer, V.; Svoboda, V. Enthalpies of Vaporization of Organic Compounds: A Critical Review and Data Compilation; Blackwell Scientific Publications: Oxford, UK, 1985. [Google Scholar]
- Paulechka, Y.U.; Zaitsau, D.H.; Kabo, G.J. On the difference between isobaric and isochoric heat capacities of liquid cyclohexyl esters. J. Mol. Liq. 2004, 115, 105–111. [Google Scholar] [CrossRef]
- Stephenson, R.M.; Malanowski, S. Handbook of the Thermodynamics of Organic Compounds, 1st ed.; Springer: Dordrecht, The Netherlands, 1987. [Google Scholar]
- Teodorescu, M.; Barhala, A.; Dragoescu, D. Isothermal (vapour+liquid) equilibria for the binary (cyclopentanone or cyclohexanone with 1,1,2,2-tetrachloroethane) systems at temperatures of (343.15, 353.15, and 363.15) K. J. Chem. Thermodyn. 2006, 38, 1432–1437. [Google Scholar] [CrossRef]
- Domalski, E.S.; Hearing, E.D. Heat Capacities and Entropies of Organic Compounds in the Condensed Phase. Volume III. J. Phys. Chem. Ref. Data 1996, 25, 1–523. [Google Scholar] [CrossRef]
- McCullough, J.P.; Finke, H.L.; Messerly, J.F.; Kincheloe, T.C.; Waddington, G. The low temperature thermodynamic properties of naphthalene, 1-methylnaphthalene, 2-methylnaphthalene, 1,2,3,4-tetrahydronaphthalene, trans-decahydronaphthalene and cis-decahydronaphthalene. J. Phys. Chem. 1957, 61, 1105–1116. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Krasnykh, E.L.; Vasiltsova, T.V.; Koutek, B.; Doubsky, J.; Heintz, A. Vapor pressures and enthalpies of vaporization of a series of the linear aliphatic aldehydes. Fluid Phase Equilib. 2003, 206, 331–339. [Google Scholar] [CrossRef]
- Wiberg, K.B.; Wasserman, D.J.; Martin, E.J.; Murcko, M.A. Enthalpies of hydration of alkenes. 3. Cycloalkenes. J. Am. Chem. Soc. 1985, 107, 6019–6022. [Google Scholar] [CrossRef]
- Pulliam, M.K.; Gude, M.T.; Teja, A.S. The Critical Properties of Twelve Isomeric n-Alkanones with Six to Nine Carbon Atoms. In Experimental Results for DIPPR 1990–91 Projects on Phase Equilibria and Pure Component Properties; DIPPR Data Series; American Institute of Chemical Engineers: New York, NY, USA, 1994; pp. 184–187. [Google Scholar]
- Teja, A.S.; Rosenthal, D.J. The critical pressures and temperatures of twelve substances using a low residence time flow apparatus. AIChE Symp. Ser. 1990, 86, 133–137. [Google Scholar]
- Tsonopoulos, C.; Ambrose, D. Vapor-Liquid Critical Properties of Elements and Compounds. 3. Aromatic Hydrocarbons. J. Chem. Eng. Data 1995, 40, 547–558. [Google Scholar] [CrossRef]
- Ambrose, D.; Broderick, B.E.; Townsend, R. The Critical Temperatures and Pressures of Thirty Organic Compounds. J. Appl. Chem. Biotechnol. 1974, 24, 359–372. [Google Scholar] [CrossRef]
- Wilson, L.C.; Wilson, H.L.; Wilding, W.V.; Wilson, G.M. Critical Point Measurements for Fourteen Compounds by a Static Method and a Flow Method. J. Chem. Eng. Data 1996, 41, 1252–1254. [Google Scholar] [CrossRef]
- Prosen, E.J.; Johnson, W.H.; Rossini, F.D. Heats of formation and combustion of the normal alkylcyclopentanes and cyclohexanes and the increment per CH2 group for several homologous series of hydrocarbons. J. Res. Natl. Bur. Stand. 1946, 37, 51–56. [Google Scholar] [CrossRef]
- Wiberg, K.B.; Crocker, L.S.; Morgan, K.M. Thermochemical studies of carbonyl compounds. 5. Enthalpies of reduction of carbonyl groups. J. Am. Chem. Soc. 1991, 113, 3447–3450. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Beckhaus, H.D.; Belen’kaja, R.S.; Rakus, K.; Rüchardt, C. Geminal substituent effects Part 9. Standard enthalpies of formation and strain free increments of branched esters and ethers. Thermochim. Acta 1996, 279, 47–64. [Google Scholar] [CrossRef]
- Blokhin, A.V.; Kabo, G.J.; Kozyro, A.A.; Ivashkevich, L.S.; Krasulin, A.P.; Diky, V.V.; Maksimuk, Y.V. Thermodynamic properties of 1-methylcyclopentanol and 1-chloro-1-methylcyclopentane in the ideal gas state. Thermochim. Acta 1997, 292, 19–29. [Google Scholar] [CrossRef]
- Wolf, G. Thermochemische Untersuchungen an cyclischen Ketonen. Helv. Chim. Acta 1972, 55, 1446–1459. [Google Scholar] [CrossRef]
- Good, W.D.; Lee, S.H. The enthalpies of formation of selected naphthalenes, diphenylmethanes, and bicyclic hydrocarbons. J. Chem. Thermodyn. 1976, 8, 643–650. [Google Scholar] [CrossRef]
- Harrop, D.; Head, A.J.; Lewis, G.B. Thermodynamic properties of organic oxygen compounds. 22. Enthalpies of combustion of some aliphatic ketones. J. Chem. Thermodyn. 1970, 2, 203–210. [Google Scholar] [CrossRef]
- Simirskii, V.V.; Kozyro, A.A.; Kabo, G.Y.; Yursha, I.A.; Marachuk, L.I. Thermodynamic properties and saponification kinetics of cyclohexyl acetate. J. Appl. Chem. USSR 1993, 65, 1348–1353. [Google Scholar]
- Pilcher, G.; Parchment, O.G.; Hillier, I.H.; Heatley, F.; Fletcher, D.; Ribeiro da Silva, M.A.V.; Ferrao, M.L.C.C.H.; Monte, M.J.S.; Jiye, F. Thermochemical and theoretical studies on cyclohexanediones. J. Phys. Chem. 1993, 97, 243–247. [Google Scholar] [CrossRef]
- Marachik, L.I.; Kozyro, A.A.; Simirskii, V.V.; Kabo, G.Y.; Yursha, I.A.; Krasulin, A.P.; Sevruk, V.M. Thermodynamic characteristics of by-products from caprolactam synthesis. J. Appl. Chem. USSR 1992, 65, 710–715. [Google Scholar]
- Benson, G.C.; D’Arcy, P.J. Excess isobaric heat capacities of some binary mixtures: (a C5-alkanol + n-heptane) at 298.15 K. J. Chem. Thermodynam. 1986, 18, 493–498. [Google Scholar] [CrossRef]
- Finke, H.L.; Messerly, J.F.; Todd, S.S. Thermodynamic properties of n-propyl-, n-butyl-, and n-decyl-substituted cyclohexane from 10 to 370 K. J. Phys. Chem. 1965, 69, 2094–2100. [Google Scholar] [CrossRef]
- Mayer, J.; Rachwalska, M.; Sciesinska, E.; Sciesinski, J. On the polymorphism of solid cyclohexanol by adiabatic calorimetry and far infrared methods. J. Phys. France 1990, 51, 857–867. [Google Scholar] [CrossRef][Green Version]
- Nakamura, N.; Suga, H.; Seki, S. Calorimetric study on orientationally disordered crystals. Cyclohexene oxide and cyclohexanone. Bull. Chem. Soc. Japan 1980, 53, 2755–2761. [Google Scholar] [CrossRef]
- Osborne, N.S.; Ginnings, D.C. Measurements of heat of vaporization and heat capacity of a number of hydrocarbons. J. Res. Natl. Bur. Stand. 1947, 39, 453–477. [Google Scholar] [CrossRef] [PubMed]
- Siddiqi, M.A.; Svejda, P.; Kohler, F. A generalized van der Waals equation of state II. Excess heat capacities of mixtures containing cycloalkanes (C5,C6), methylcycloalkanes (C5,C6) and n-decane. Ber. Bunsenges. Phys. Chem. 1983, 87, 1176–1181. [Google Scholar] [CrossRef]


 ) and Marrero–Gani (
) and Marrero–Gani ( ). (b) Analogous comparison for the melting temperatures. Labels correspond to the order of compounds established in Appendix B.
). (b) Analogous comparison for the melting temperatures. Labels correspond to the order of compounds established in Appendix B.
 ) and Marrero–Gani (
) and Marrero–Gani ( ). (b) Analogous comparison for the melting temperatures. Labels correspond to the order of compounds established in Appendix B.
). (b) Analogous comparison for the melting temperatures. Labels correspond to the order of compounds established in Appendix B.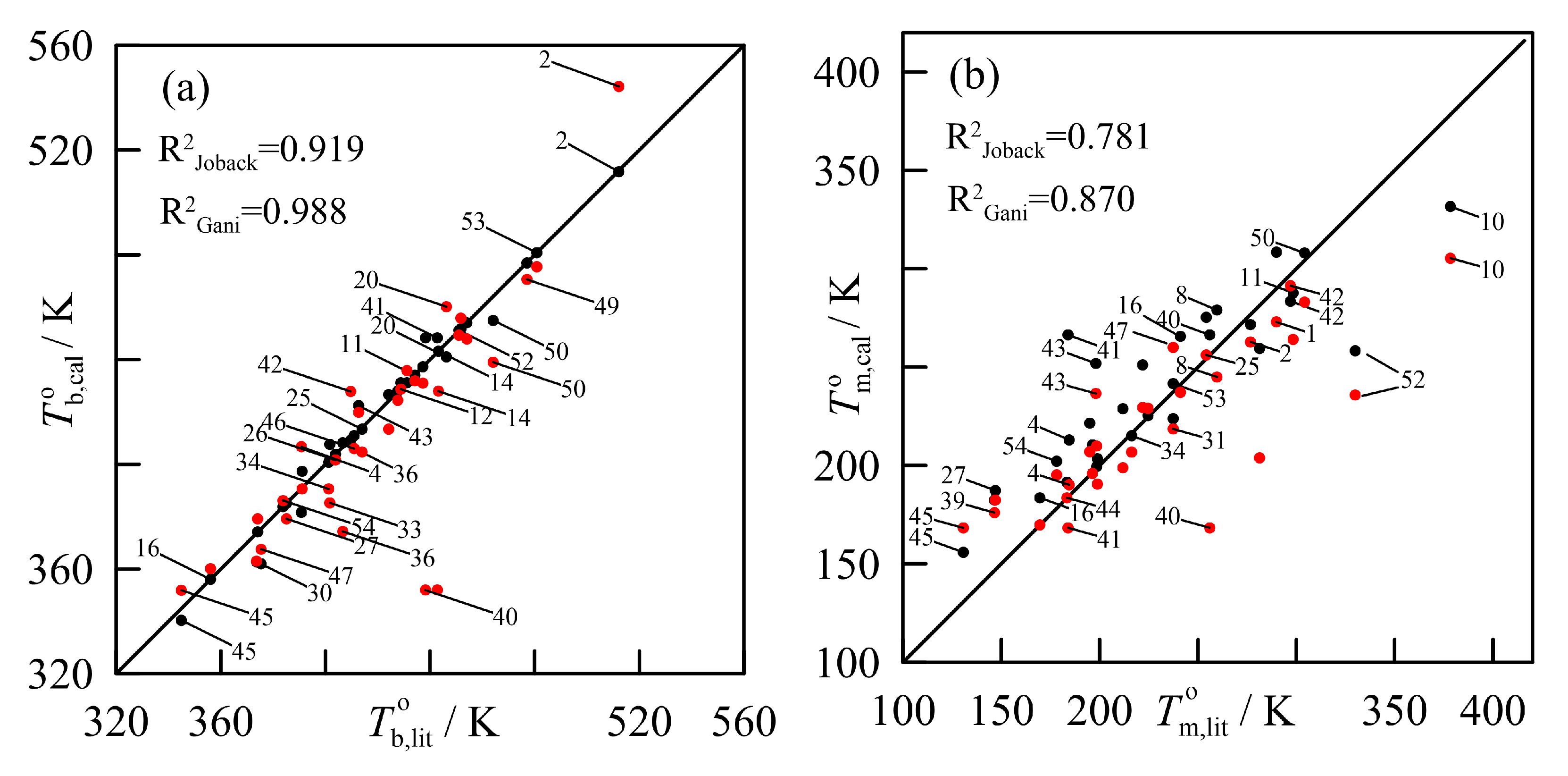
 ) and Marrero–Gani (
) and Marrero–Gani ( ) and those from the literature: (a) vaporization enthalpies; (b) melting enthalpies. Labels correspond to the order of compounds, as shown in Appendix B.
) and those from the literature: (a) vaporization enthalpies; (b) melting enthalpies. Labels correspond to the order of compounds, as shown in Appendix B.
 ) and Marrero–Gani (
) and Marrero–Gani ( ) and those from the literature: (a) vaporization enthalpies; (b) melting enthalpies. Labels correspond to the order of compounds, as shown in Appendix B.
) and those from the literature: (a) vaporization enthalpies; (b) melting enthalpies. Labels correspond to the order of compounds, as shown in Appendix B.
 ) and Marrero–Gani (
) and Marrero–Gani ( ): (a) critical temperature; (b) critical pressure; (c) critical volume. Labels correspond to the order of compounds, as shown in Appendix B.
): (a) critical temperature; (b) critical pressure; (c) critical volume. Labels correspond to the order of compounds, as shown in Appendix B.
 ) and Marrero–Gani (
) and Marrero–Gani ( ): (a) critical temperature; (b) critical pressure; (c) critical volume. Labels correspond to the order of compounds, as shown in Appendix B.
): (a) critical temperature; (b) critical pressure; (c) critical volume. Labels correspond to the order of compounds, as shown in Appendix B.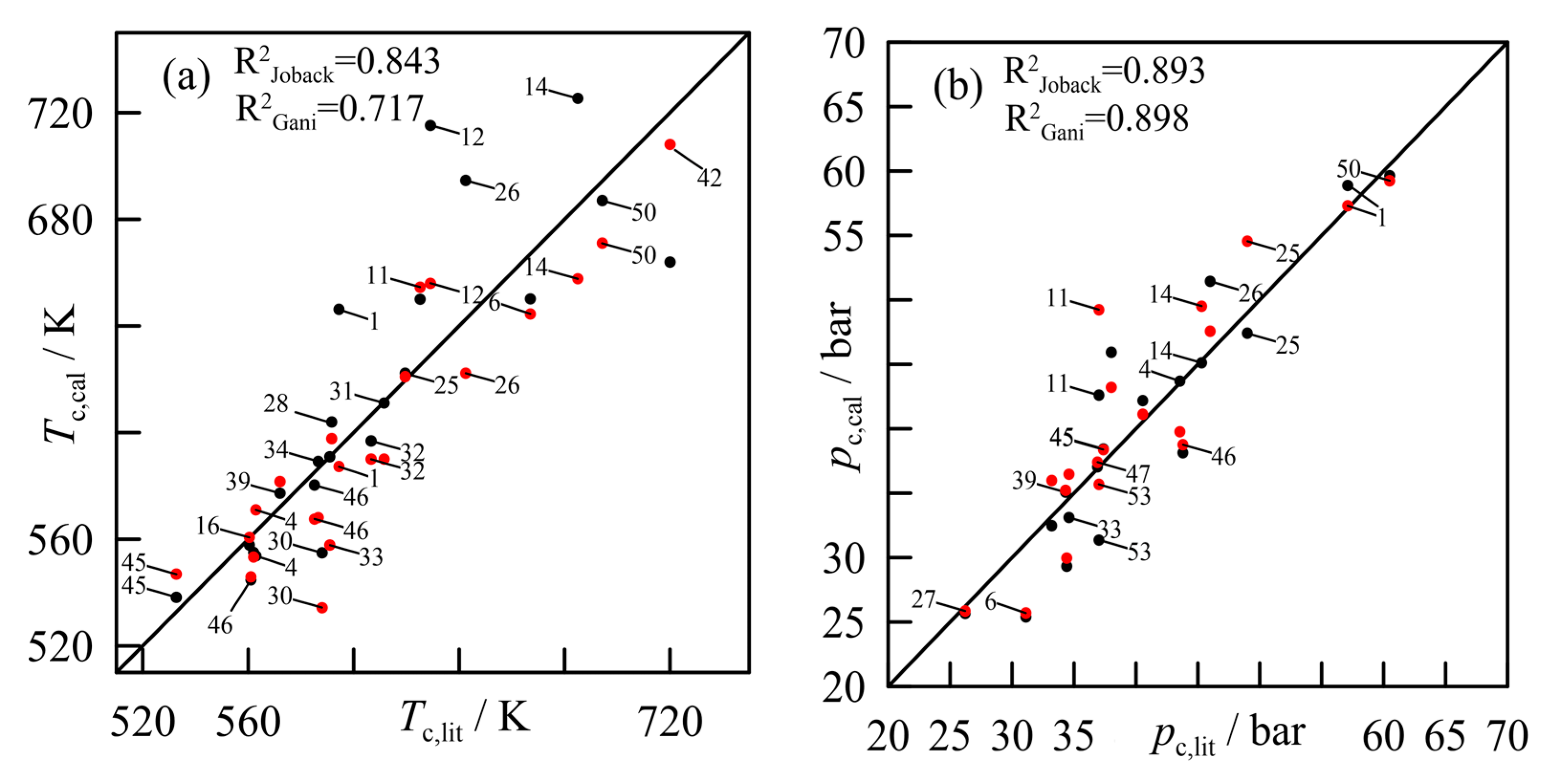

 ) and Marrero–Gani (
) and Marrero–Gani ( ). (b) Comparison between the thermal capacities obtained from literature and those calculated by the Joback method. Labels correspond to the order of compounds, as shown in Appendix B.
). (b) Comparison between the thermal capacities obtained from literature and those calculated by the Joback method. Labels correspond to the order of compounds, as shown in Appendix B.
 ) and Marrero–Gani (
) and Marrero–Gani ( ). (b) Comparison between the thermal capacities obtained from literature and those calculated by the Joback method. Labels correspond to the order of compounds, as shown in Appendix B.
). (b) Comparison between the thermal capacities obtained from literature and those calculated by the Joback method. Labels correspond to the order of compounds, as shown in Appendix B.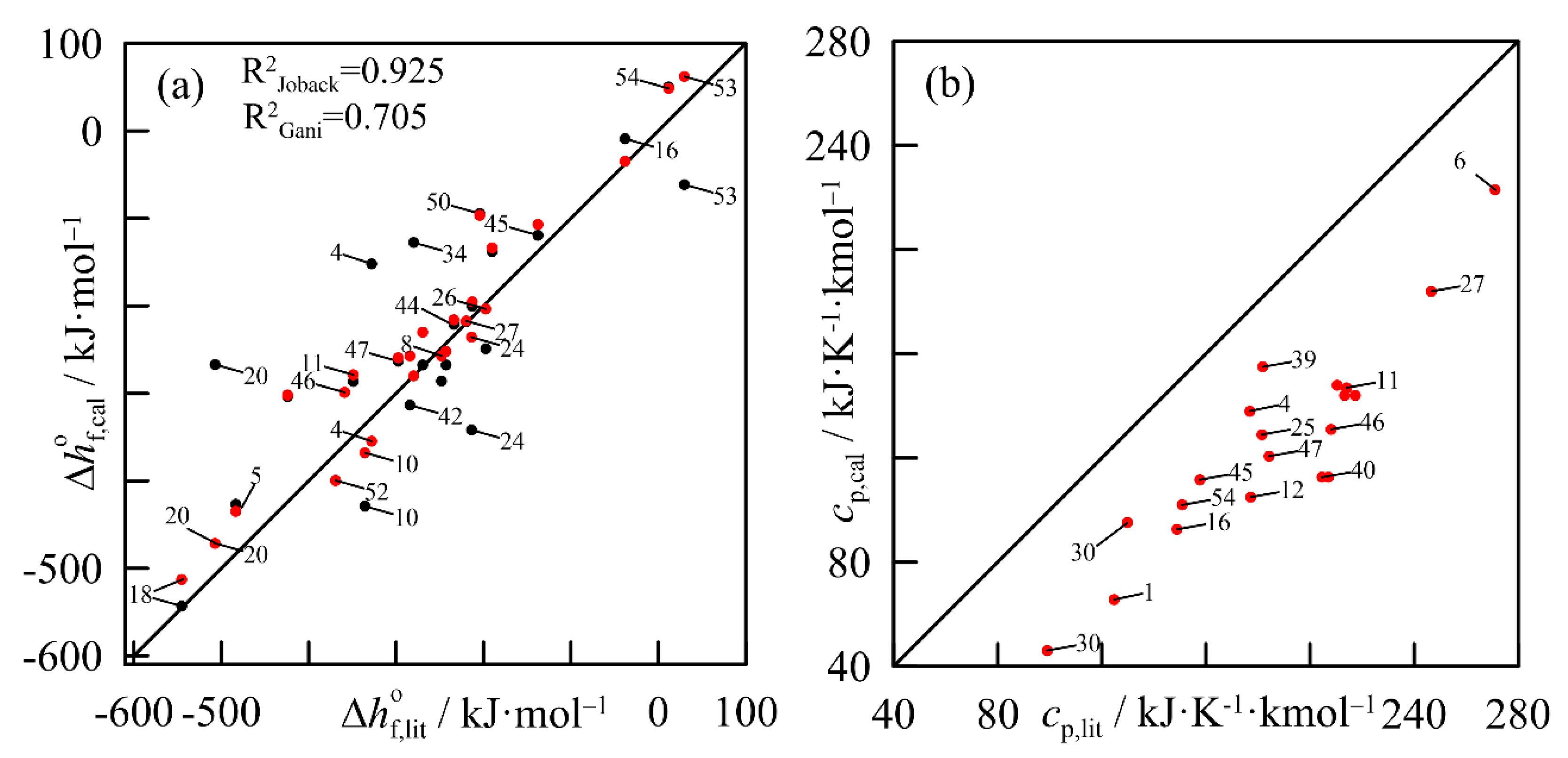
| Compounds | Groups | Nk | |||
|---|---|---|---|---|---|
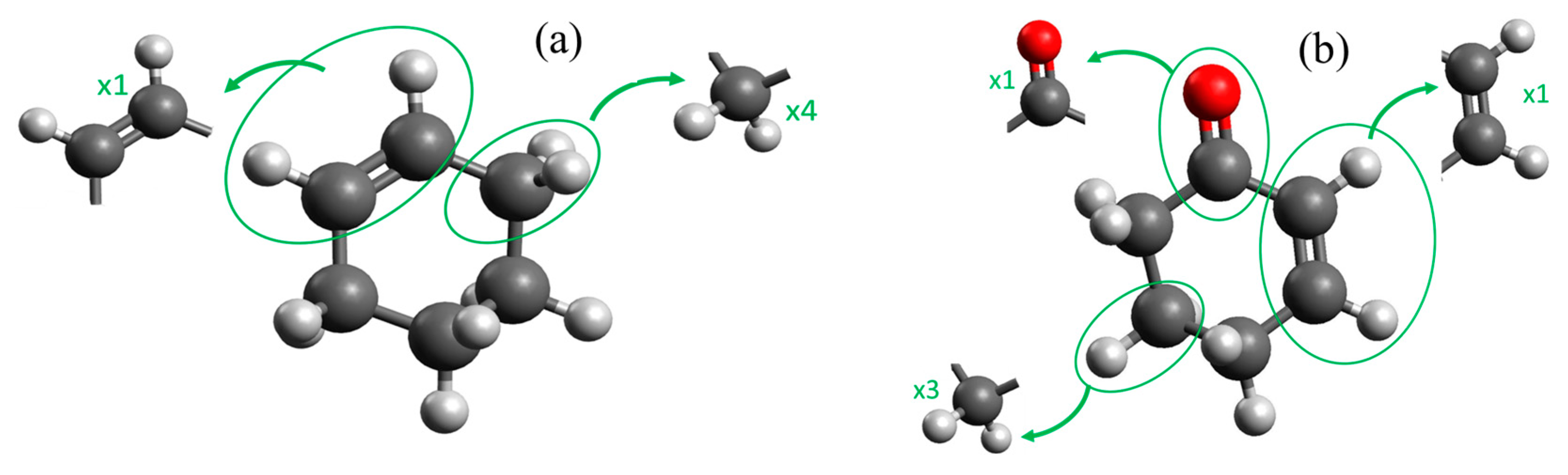
| Cyclohexene | –CH2– | 4 | 0.0100 | 0.0025 | 48 |
| =CH– | 2 | 0.0082 | 0.0011 | 41 | |
| total: | 0.0564 | 0.0122 | 274 | ||
| estimated→ | Tc/K = 567 | pc/bar = 43.3 | vc/cm3·mol−1 = 291 | ||
| from ref. [16] | Tc/K = 560.4 | pc/bar = 48.41 | vc/cm3·mol−1 = 377.4 | ||
| 2-Cyclohexen-1-one | –CH2– | 3 | 0.0100 | 0.0025 | 48 |
| =CH– | 2 | 0.0082 | 0.0011 | 41 | |
| >C=O | 1 | 0.0284 | 0.0028 | 55 | |
| total: | 0.0784 | 0.0125 | 281 | ||
| estimated→ | Tc/K = 655 | pc/bar = 45.3 | vc/cm3·mol−1 = 298 | ||
| from ref. [17] | Tc/K = 685.0 | pc/bar = 45.30 | vc/cm3·mol−1 = 304.9 |
| Compounds | Groups | j | Nk | |||
|---|---|---|---|---|---|---|
| Cyclohexene | CH2 (cyc) | 1º | 4 | 1.8815 | 0.009884 | 49.24 |
| CH=CH (cyc) | 1º | 1 | 3.6426 | 0.013815 | 83.91 | |
| total: | 11.1686 | 0.053351 | 280.87 | |||
| estimated→ | Tc/K = 558 | pc/bar = 43.9 | vc/cm3·mol−1 = 289 | |||
| from ref. [16] | Tc/K = 560.4 | pc/bar = 48.41 | vc/cm3·mol−1 = 377.4 | |||
| 2-Cyclohexen-1-one | CH2 (cyc) | 1º | 3 | 1.8815 | 0.009884 | 49.24 |
| CH=CH (cyc) | 1º | 1 | 3.6426 | 0.013815 | 83.91 | |
| CO (cyc) | 1º | 1 | 12.6396 | −0.000207 | 57.38 | |
| total: | 21.9267 | 0.043260 | 289.01 | |||
| estimated→ | Tc/K = 714 | pc/bar = 49 | vc/cm3·mol−1 = 297 | |||
| from ref. [17] | Tc/K = 685.0 | pc/bar = 45.30 | vc/cm3·mol−1 = 304.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández, L.; Ortega, J.; Domínguez, L.; Lorenzo, D.; Santos, A.; Romero, A. Using Two Group-Contribution Methods to Calculate Properties of Liquid Compounds Involved in the Cyclohexanone Production Operations. Liquids 2022, 2, 413-431. https://doi.org/10.3390/liquids2040024
Fernández L, Ortega J, Domínguez L, Lorenzo D, Santos A, Romero A. Using Two Group-Contribution Methods to Calculate Properties of Liquid Compounds Involved in the Cyclohexanone Production Operations. Liquids. 2022; 2(4):413-431. https://doi.org/10.3390/liquids2040024
Chicago/Turabian StyleFernández, Luis, Juan Ortega, Leandro Domínguez, David Lorenzo, Aurora Santos, and Arturo Romero. 2022. "Using Two Group-Contribution Methods to Calculate Properties of Liquid Compounds Involved in the Cyclohexanone Production Operations" Liquids 2, no. 4: 413-431. https://doi.org/10.3390/liquids2040024
APA StyleFernández, L., Ortega, J., Domínguez, L., Lorenzo, D., Santos, A., & Romero, A. (2022). Using Two Group-Contribution Methods to Calculate Properties of Liquid Compounds Involved in the Cyclohexanone Production Operations. Liquids, 2(4), 413-431. https://doi.org/10.3390/liquids2040024








