You are currently viewing a new version of our website. To view the old version click .
MDPIMDPI
Search all articles
Liquids
Download PDF
  • Article
  • Open Access

24 July 2022

Abraham Solvation Parameter Model: Examination of Possible Intramolecular Hydrogen-Bonding Using Calculated Solute Descriptors

,
,
and
Department of Chemistry, University of North Texas, Denton, TX 76203, USA
*
Author to whom correspondence should be addressed.
Liquids2022, 2(3), 131-146;https://doi.org/10.3390/liquids2030009
This article belongs to the Section Molecular Liquids
Version Notes
Order Reprints

Abstract

Published solubility data for 4,5-dihydroxyanthraquinone-2-carboxylic acid dissolved in several organic solvents of varying polarity and hydrogen-bonding character are used to calculate the Abraham model solute descriptors. Calculated descriptor values suggest that 4,5-dihydroxyanthraquinone-2-carboxylic acid engages in intramolecular hydrogen formation between the two phenolic hydrogens and the proton acceptor sites (the lone electron pairs) on the neighboring quinone oxygen atom. Our study further shows that existing group contribution and machine learning methods provide rather poor estimates of the experimental-based solute descriptors of 4,5-dihydroxyanthraquinone-2-carboxylic acid, in part because the estimation methods to not account for the likely intramolecular hydrogen-bonds. The predictive aspect of the Abraham model is illustrated by predicting the solubility of 4,5-dihydroxyanthraquinone-2-carboxylic acid in 28 additional organic mono-solvents for which experimental data does not exist.

1. Introduction

Hydrogen-bonding plays an important role in many chemical and biological processes, and affects the arrangement of molecules in liquid mixtures and the molecular packing in crystalline materials. Both experimental and computational methods have been successfully employed in studying the dynamic and static nature of hydrogen-bond formation, as well as examining how the H-bond strength and H-bond length determine the mixture’s/material’s spectral, physical, and thermodynamic properties. Hydrogen-bond formation often results in significant changes in the observed vibrational infrared and proton NMR spectrum, as manifested by large wavelength shifts in the infrared absorption band, or by large chemical shifts in the NMR signal of the H-bonded proton(s). Spectral data provides a convenient means to obtain the association constant of both homogeneous and heterogeneous hydrogen-bonded complexes. Through the variation of the natural logarithm of the association constant with the reciprocal of the Kelvin temperature, the accompanying standard enthalpy of H-bond formation can be obtained.
Solution calorimetric methods provide a more direct means for obtaining the standard molar hydrogen-bond enthalpy, though one may have to separate the specific interactions associated with H-bond formation from the enthalpic contributions due to the nonspecific dispersion interactions that also are present in the liquid mixtures. Calorimetric measurements using “model” probe compounds lacking the ability to engage in hydrogen-bond formation have proved useful in quantifying the much smaller nonspecific interactions. The pure base method developed by Arnett and coworkers [1] is an early calorimetric application of the utilization of “model” probe compounds to separate the contributions of hydrogen-bond formation from nonspecific interactions, which are present in all liquid mixtures. The authors determined the enthalpies of hydrogen-bond formation of 4-fluorophenol with 35 different bases from measured enthalpies of solution of both 4-fluorophenol and 4-fluoroanisole in each pure base solvent. Measured solution enthalpies of the 4-fluoroanisole “model” compound were used to correct for 4-fluorophenol-base interactions other than H-bond formation. More involved correction procedures [2,3,4,5,6] have involved experimental determinations of enthalpies of solution of H-bond donors, H-bond acceptors and/or model probe compounds in saturated hydrocarbon solvents like cyclohexane and heptane, or in weakly interacting solvents like benzene and tetrachloromethane. Measurements in slightly interacting solvents, though not ideal, might be needed in instances where a given H-bond donor/acceptor molecule fails to sufficiently dissolve the saturated hydrocarbon solvent.
To reduce the number of experimental measurements predictive group contribution methods [7,8,9], as well as quantitative structure-property relationships (QSPR) [10,11,12] and linear solvation energy relationships (LSER) [13,14,15,16,17], have been reported for predicting enthalpies of solvation of organic solutes in more than 40 different organic solvents of varying polarity and hydrogen-bonding character. The complete solvent dataset includes five saturated hydrocarbons (hexane, heptane, octane, hexadecane, and cyclohexane), carbon tetrachloride, and four alkylbenzenes (benzene, toluene, 1,4-dimethylbenzene, and 1,3,5-trimethylbenzene), plus numerous alcohols, chloroalkanes, ketones, esters, and other common miscellaneous organic solvents used in commercial manufacturing processes. Each published correlation is based on calorimetric and activity coefficient measurements for more than 40 different solutes, and can back-calculate the experimental enthalpy of solvation data used in determining group values and/or correlation coefficients to within 3.5 kJ mol−1 (or less).
One of the predictive correlations based on the Abraham solvation parameter model [18]:
∆Hsolv = a1 · A + bk · B + e1 · E + s1 · S + l1 · L + c1
enables estimation of the standard enthalpy of hydrogen-bond formation, ∆HH-bond, from
∆HH-bond = a1 · A + b1 · B
known A and B solute descriptors and calculated a1 and b1 equation coefficients according to Equation (2). Solute descriptors A and B refer to the overall H-bond donating and H-bond accepting character of the given solute, and the lowercase equation coefficients, a1 and b1, denote the complimentary solvent properties. When multiplied together, as in Equation (2), the summed product corresponds to the enthalpy of hydrogen-bond formation. The remaining three solute descriptors in Equation (1) denote the solute’s excess molar refraction, E; the combination of the solute’s dipolarity and polarizability, S; and the logarithm of the solute’s gas-to-hexadecane partition coefficient measured at 298.15 K, L. The remaining lowercase coefficients (e1, s1, l1, and c1) in Equation (2) represent the complimentary solvent properties. Wilson et al. [18] have used Equation (2) (with b1 set equal to zero as 1,4-dioxane lacks an acidic hydrogen and thus cannot serve as an H-bond donor) in estimating the strength of hydrogen-bonding interactions between acid solutes and 1,4-dioxane, which were in the order of ∆HH-bond ≈ −5.5 kJ mol−1 (for chloroform) to ∆HH-bond ≈ −22 kJ mol−1 (for phenol). The numerical values of ∆HH-bond calculated in this fashion were found to be well in agreement with the available literature data. The preceding paragraphs are not intended to provide a complete review of the published literature pertaining to hydrogen-bonding. Rather, we wish to briefly mention the difficulty in determining the thermodynamic properties associated with hydrogen-bond formation, and how predictive group contribution methods and linear solvation energy expressions can assist in such determinations.
The Abraham model solute descriptors and complimentary solvent properties are not simply curve-fitting parameters. Rather, the quantities encode valuable chemical information regarding the properties of the solute and solvent. For example, very small or near zero A-solute descriptor values calculated from published molar solubilities and water-to-organic solvent partition coefficients, alone or in combination with measured proton NMR chemical shift data, have been used to establish the likely presence of intramolecular hydrogen-bonding in both 1,4-dihydroxyanthraquinone and 1,8-dihydroxyanthraquinone [19], in 2-nitrophenol and 2,4-dinitrophenol [20], and in select hydroxyflavones and hydroxyisoflavones [21]. Functional group activity models would estimate much larger A-solute descriptor values. For example, estimation of the A solute descriptor of 1,4-dihydroxyanthraquinone using the predictive software on the UFZ-LSER [22] and the compound’s canonical SMILES code, C1=CC=C2C(=C1)C(=O)C3=C(C=CC(=C3C2=O)O)O, gives A = 0.82, which is considerably larger than the experimental-based value of A = −0.121 obtained by analyzing published solubility data in accordance with the Abraham model. Negative values of the A solute descriptor are meaningless, so the value was set equal to zero with no loss in descriptive ability [19].
Recent publication [23,24] of mole fraction solubilities for 4,5-dihydroxyanthraquinone-2-carboxylic acid (molecular structure given in Figure 1) dissolved in several organic solvents provides the opportunity to: (1) calculate experimental-based solute descriptors for one additional compound; (2) assess the likelihood of hydrogen-bond formation; (3) further assess the limitations and applications of existing group contribution [25,26,27,28] and machine learning [27,28] methods in terms of estimating solute descriptors for more complex, multi-functional group molecules; and (4) illustrate the predictive aspects of the Abraham model. An important facet of the model is that a common set of solute descriptors, either (E, S, A, B, and V) or (E, S, A, B and L), can predict so many important chemical and thermodynamic properties needed in the design of industrial manufacturing processes. Many other QSPRs and LSERs require a different set of solute descriptors for each property to be predicted. In other words, one set of solute descriptors would be needed to predict enthalpies of solvation in 1,4-dioxane, and a completely different set of descriptor values would be needed to predict practical water-to-ethyl acetate partition coefficients. In the present communication we determine experimental-based solute descriptors for 4,5-dihydroxyanthraquinone-2-carboxylic acid, which are then used to estimate the solubility of the carboxylic acid in an additional 28 organic solvents for which experimental data are not available. Solubility is an important consideration in identifying a suitable solvent for chemical purification through recrystallization. 4,5-Dihydroxyanthraquinone-2-carboxylic acid, whose molecular structure is given in Figure 1, has been shown to exhibit select antimicrobial, anticancer, and anti-inflammatory activities.
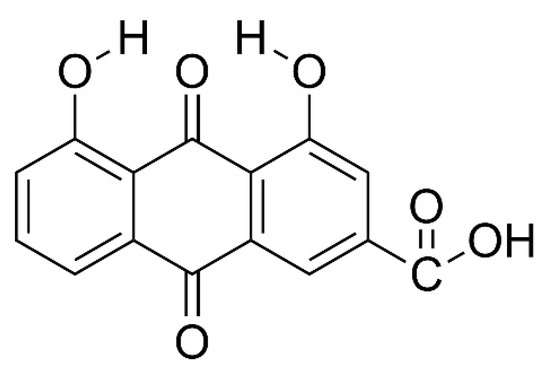
Figure 1. Molecular structure of 4,5-dihydroxyanthraquinone-2-carboxylic acid, having two hydroxyl, one carboxylic and two carbonyl function groups, in additional to the two aromatic and one cyclic ring backbone.

2. Solute Descriptor Computations

As noted above, the calculated A solute descriptor can provide an indication regarding whether not intramolecular hydrogen-bond formation occurs in 4,5-dihydroxyanthraquinone-2-carboxylic acid. Based upon the three proton-donating groups present in the molecule one would expect the A solute descriptor to exceed unity. In fact, three estimation methods that use the molecule’s canonical SMILES code: C1=CC2=C(C(=C1)O)C(=O)C3=C(C2=O)C=C(C=C3O)C(=O)O as the structural input information:
  • UFZ-LSER estimation [28]: E = 2.34; S = 2.46; A = 1.28; B = 1.14; V = 1.8615; and L = 11.352
  • Group contribution estimation [27]: E = 2.32; S = 2.37; A = 1.44; B = 0.96; V = 1.8615; and L = 11.368
  • Machine learning estimation [27]: E = 2.49; S = 2.17; A = 1.11; B = 0.87; V = 1.8615; and L = 11.327
give numerical values of the A solute descriptor in the range of A = 1.11 to A = 1.44. Significantly smaller values would be expected if intramolecular hydrogen-bond formation occurred as the two phenolic hydrogens would not be available to interact with surrounding solvent molecules. As shown in Figure 2, both phenolic hydrogens would interact with the proton acceptor sites (the lone electron pairs) on the neighboring quinone oxygen atom as depicted in Figure 2. Only the carboxylic acid functional group would contribute to the H-bond character. The A solute descriptors of benzoic acid (A = 0.59) and substituted-benzoic acids like 4-chlorobenzoic acid (A = 0.63), 4-nitrobenzoic acid (A = 0.68); and 4-chloro-3-nitrobenzoic acid (A = 0.70) typically fall somewhere around A = 0.65 ± 0.10, depending on the substituent(s) and its(their) placement on the aromatic ring. As an informational note, estimation methods also calculate the numerical value of the V solute descriptor, which corresponds to the characteristic McGowan volume. The V solute descriptor appears in Abraham model correlations that describe solute transfer between two condensed. This solute descriptor will be used shortly when experimental-based solute descriptors of 4,5-dihydroxyanthraquinone-2-carboxylic acid are calculated.
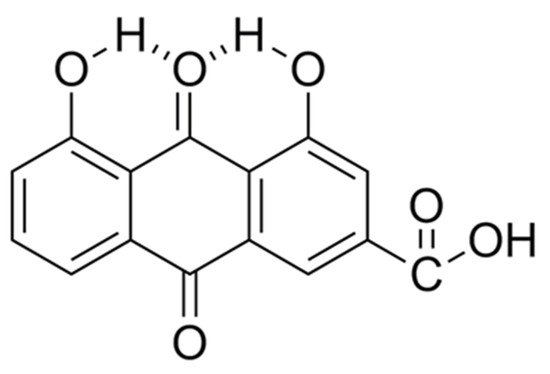
Figure 2. Pictorial depiction showing the possible intramolecular H-bond formation, that results in 4,5-dihydroxyanthraquinone-2-carboxylic acid, from interactions between the acidic hydrogen on the two -OH functional groups and the neighboring quinone oxygen atom on the >C=O functional group.
The calculation of Abraham model solute descriptors begins by constructing mathematical Abraham molar solubility ratio equations:
log P and log (CS,organic/CS,water) = e3 · E + s3 · S + a3 · A + b3 · B + v3 · V + c3
log K and log (CS,organic/CS,gas) = e4 · E + s4 · S + a4 · A + b4 · B + l4 · L + c4
for each solvent which both experimental solubility data and solvent/process coefficients are known. The three concentrations denote the molar solubility of the solute in the respective organic solvent, CS,organic, and in water, CS,water, and a gas-phase concentration of the solute, CS,gas, respectively. The published mole fraction solubility, xS,organic, determined by Wu et al. [23] and by Cheng et al. [24] are converted to molar solubilities:
CS,organic = xS,organic/Vsolvent
by dividing by the molar volume of the respective organic solvent, Vsolvent. The mole fraction solubility is sufficiently small that only the solvent contributes to the total volume of the solution.
We use in the solute descriptor computation only those organic solvents in which dimerization of 4,5-dihydroxyanthraquinone-2-carboxylic acid is minimal. We note that, for dimerization to occur, two carboxylic acid monomers must be in close proximity to each other. In the case of 4,5-dihydroxyanthraquinone-2-carboxylic acid this is highly unlikely given its very small molar solubility in each of the organic solvents listed in Table 1. From a simple probability standpoint, 4,5-dihydroxyanthraquinone-2-carboxylic acid is more likely to be surrounded by organic solvent molecules having the ability to form heterogeneous hydrogen-bonded association complexes. For example, in an aqueous-organic two-phase extraction study involving benzoic acid, Yamada et al. [29] found that the dimerization constant of benzoic acid decreased in the 1-octanol-benzene organic phase with increasing alcohol concentration. The molarity-based dimerization constant was less than unity at 1-octanol concentrations of 0.40 Molar or larger. The published partitioning studies were performed at benzoic acid concentrations of 0.05 to 1.4 Molar. Carboxylic acids exist predominantly in dimeric form in nonpolar solvents. Solute descriptors of the monomeric and cyclic dimeric form of carboxylic acids are different in that the hydrogen of the –COOH groups is not available to hydrogen-bond with surrounding solvent molecules. In Table 1 we list the molar solubility data used in the solute descriptor computation.
Table 1. Logarithms of the published experimental molar solubilities, log CS,organic, and logarithms of the water-to-1-octanol partition coefficient, log P, for 4,5-dihydroxyanthraquinone-2-carboxylic acid dissolved in organic solvents at 298.15 K.
For the convenience of journal readers, we have assembled in Table 2 the numerical values of the solvent coefficients that pertain to both water-to-organic solvent partition coefficients, log P, gas-to-water partition coefficients, log K, and molar solubility ratios. The equation coefficients have been published in small subsets in many of our earlier publications that have described the calculation of solute descriptors of a specific solute. Normally, we report only those equation coefficients that are used in the solute descriptor computation. A complete listing of solvent equations has not been published until now. As an informational note, the coefficients denoted by the word “wet” after the organic solvent name pertain to practical, direct partition coefficients where the organic solvent phase is in direct contact with the aqueous phase. In other words, the solute partitioning process is between the organic solvent that is saturated with water, and the aqueous phase that is saturated with the organic solvent. For these solvents, the presence of water in the organic solvent affects its solubilizing ability as evidenced by the difference in the partition coefficients for ethyl acetate (wet) versus ethyl acetate. Practical partition coefficients are used in designing chemical extraction processes where the goal is to separate the desired chemical product/analyte from impurities and other reaction products that might be present in the reaction mixture (or chemical sample). For solvents that are fully miscible with water, such as methanol, no confusion is possible, because log P must refer to the “hypothetical partitioning process” between the two pure solvents. For solvents that are almost completely immiscible with water, such as saturated alkanes, 1,2-dichloroethane, and many aromatic solvents, there should be no confusion because hypothetical partition coefficients expressed through the solubility ratio, CS,organic/CS,water, will be nearly the same as the measured direct partition coefficient. The very small amount of water in the organic solvent does not affect its solubilizing character.
Table 2. Equation coefficients for water solvent partition coefficients and air solvent partition coefficients, as log P and log K, and for molar solubility ratios, as log (CS,org/CS,water) and log (CS,org/CS,gas), at 298 K.
Once the Abraham model equations have been constructed, they are solved simultaneously for the optimal set of solute descriptors that minimizes the summed squared deviation between the experimental data and values back-calculated based on the computed solute descriptors. In the current study we have 26 equations counting the two gas-to-water equations in Table 2 to use in calculating the six solute descriptors (E, S, A, B, V, and L), as well as the values of log CS,organic and log CS,gas needed to calculate the solubility ratios. The log K value for “wet” 1-octanol is calculated as:
log K = log P + log CS,water − log CS,gas
Fortunately, the excess molar refraction and McGowan volume solute descriptors can be calculated solely based on molecular structure considerations. The numerical value of E solute descriptor can be obtained using either the UFZ-LSER or PharmaAlgorithm software [31]. Both software programs estimate E by fragmenting the molecule into functional groups. The characteristic McGowan volume, V, can be computed from the molecular structure, atomic sizes, and number of bonds as described in an earlier paper by Abraham and McGowan [32]. The values of V and E that we calculate are V = 1.8615 and E = 2.340 for 4,5-dihydroxyanthraquinone-2-carboxylic acid. Simultaneous solution of the 14 Abraham model equations for 4,5-dihydroxyanthraquinone-2-carboxylic acid gave numerical values of S = 2.195, A = 0.755, B = 0.596, L = 11.073, log CS,water = −7.767 and log CS,gas = −17.865, with an overall standard error being SE = 0.148 log units. The very small, calculated A solute descriptor is comparable to experimental-based values for substituted-benzoic acids, thus suggesting the formation of intramolecular H-bonds involving both phenolic hydrogens as depicted in Figure 2. Intramolecular hydrogen-bond formation is further supported by experimental NMR chemical shift data [21,33,34,35] for 5,2′-dihydroxyflavone, 5,3′-dihydroxyflavone, 5-hydroxyflavone, 5,4′-dihydroxyflavone, 5,4′-dihydroxy-7-methoxyflavone, 5-hydroxy-1,4-naphthenedione, and 5-hydroxy-2-methyl-1,4-naphthenedione, which have -OH and >C=O functional group arrangements very similar to that in 4,5-dihydroxyanthraquinone-2-carboxylic acid. The molar structures of the fore-mentioned compounds are depicted in Figure 3. Existing group contribution and machine learning provide poor estimates of the experimental-based solute descriptors 4,5-dihydroxyanthraquinone-2-carboxylic acid. The poor estimated values likely result from not accounting for the likely intramolecular hydrogen-bonding within the solute molecule.
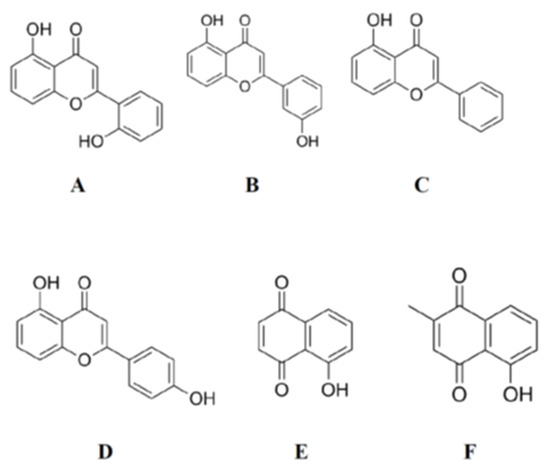
Figure 3. Molecular structures of 5,2′-dihydroxyflavone (A), 5,3′-dihydroxyflavone (B), 5-hydroxyflavone (C), 5,4′-dihydroxyflavone (D), 5,4′-dihydroxy-7-methoxyflavone, 5-hydroxy-1,4-naphthenedione (E), and 5-hydroxy-2-methyl-1,4-naphthenedione (F) which have –OH and >C=O functional group arrangements very similar to that in 4,5-dihydroxyanthraquinone-2-carboxylic acid.

3. Solubility Predictions in Additional Organic Mono-Solvents

The driving force behind many of the published experimental solubility studies is to assist process design engineers in identifying suitable organic mono-solvents and solvent mixtures for use in chemical purification through recrystallization. It is not possible to identify all potential suitable solvent candidates as measurements are performed on only limited number of solvents. What one must do is to use the knowledge gained from the limited experimental measurements to estimate the compound’s solubility in additional organic mono-solvents and solvent mixtures. This requires that the measured solubility data be analyzed using a model, such as the Abraham solvation parameter model, that is capable of making further predictions.
We illustrate in this communication the predictive nature of the Abraham model by estimating solubility of 4,5-dihydroxyanthraquinone-2-carboxylic acid in an additional 28 organic mono-solvents. Theoretically, one can make predictions in the more than 130 different organic mono-solvents and binary aqueous-organic solvent mixtures for which Abraham model correlations have been developed. Table 2 provides the equation coefficients needed for such predictions. The nature of 4,5-dihydroxyanthraquinone-2-carboxylic acid will limit our illustrative predictions to those solvents in which dimerization is not likely to occur. The solute descriptors that were calculated in the preceding section pertain to the monomeric form of the solute. The solute descriptors of the dimeric form are completely different, and could be perhaps calculated from the compound’s solubility in nonpolar organic solvents as was done previously for the trans-cinnamic acid molecule [36]. Moreover, the measured solubility in nonpolar solvents may include contributions from both the monomeric and dimeric forms of the carboxylic acid. We give in Table 3 the predicted solubilities of 4,5-dihydroxyanthraquinone-2-carboxylic acid based on Equation (3), Equation (4) and the solute descriptors obtained in the preceding section for several alcoholic, alkanenitrile, alkyl acetate, dialkyl carbonate, and alkoxyalcohol solvents for which dimerization is expected to be minimal. Numerical values log CS,water = −7.767 and log CS,gas = −17.865 were used to convert the predicted molar solubility ratios to the molar solubility in each of the listed organic mono-solvents. Also included in Table 3 are the back-calculated molar solubilities for those organic mono-solvents used in calculating the solute descriptor values.
Table 3. Prediction of the logarithm of the molar solubilities of 4,5-dihydroxyanthraquinone-2-carboxylic acid in various organic solvents at 298 K based on the Abraham solvation parameter model.

4. Concluding Remarks

Abraham model solute descriptors are calculated for 4,5-dihydroxyanthraquinone-2-carboxylic acid based on published solubility data retrieved from the published chemical literature [23,24]. The numerical values obtained from our analysis, E = 2.340; S = 2.195; A = 0.755; B = 0.596; V = 1.8615; and L = 11.073, are found to differ significantly from estimated values based upon published group contribution and machine methods. The very small, calculated A solute descriptor is comparable to experimental-based values for substituted-benzoic acids, thus suggesting the formation of intramolecular H-bonds between both phenolic hydrogens and the lone electron pairs of the quinone oxygen atom as depicted in Figure 2. The poor estimated values likely result from not accounting for the likely intramolecular hydrogen-bonding within the solute molecule. The predictive nature of the Abraham solvation parameter model is illustrated by using the experimental-based solute descriptors to predict the solubility of 4,5-dihydroxyanthraquinone-2-carboxylic acid in 28 additional alcoholic, alkanenitrile, alkyl acetate, dialkyl carbonate, and alkoxyalcohol solvents for which dimerization is expected to be minimal.
Intramolecular hydrogen-bonding does not prevent 4,5-dihydroxyanthraquinone-2-carboxylic acid from serving as a H-bond acceptor. Our predictive computations show that the positive coefficients on the a4 · A and b4 · B terms of Equation (4) will facilitate the dissolution if the solute engages in intermolecular H-bond formation with surrounding solvent molecules, as would be expected for all of the solvents listed in Table 3. The enthalpy and Gibbs energy contributions of H-bond formation can be estimated through Equation (2) and through:
∆GH-bond = − RT (a4 · A + b4 · B)
where R and T denote the universal gas constant and solution temperature, respectively. In the case of 4,5-dihydroxyanthraquinone-2-carboxylic acid, it is doubtful if ∆HH-bond could be determined by experimental calorimetric measurements. The solubility of the crystalline compound in organic solvents is very small and would not be amenable to direct solution calorimetric measurements.

Author Contributions

Conceptualization, writing—original draft preparation, W.E.A.J.; formal data analysis, S.S., C.Y., and E.W.; writing—review and editing, S.S., C.Y., and E.W. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Data is contained within the article.

Acknowledgments

Sneha Sinha, Chelsea Yang, and Emily Wu thank the University of North Texas’s Texas Academy of Mathematics & Science (TAMS) program for providing a summer research scholarship to each student.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Arnett, E.M.; Joris, L.; Mitchell, E.; Murty, T.S.S.R.; Gorrie, T.M.; Schleyer, P.v.R. Hydrogen-bonded complex formation. III. Thermodynamics of complexing by infrared spectroscopy and calorimetry. J. Am. Chem. Soc. 1970, 92, 2365–2377. [Google Scholar] [CrossRef]
  2. Spencer, J.N.; Wolbach, W.S.; Hovick, J.W.; Ansel, L.; Modarress, K.J. Hydrogen bonding by alcohols and amines. J. Solut. Chem. 1985, 14, 805–814. [Google Scholar] [CrossRef]
  3. Spencer, J.N.; Campanella, C.L.; Harris, E.M.; Wolbach, W.S. Solvent effects on hydrogen-bond formation. J. Phys. Chem. 1985, 89, 1888–1891. [Google Scholar] [CrossRef]
  4. Solomonov, B.N.; Novikov, V.B.; Varfolomeev, M.A.; Mileshko, N.M. A new method for the extraction of specific interaction enthalpy from the enthalpy of solvation. J. Phys. Org. Chem. 2005, 18, 49–61. [Google Scholar] [CrossRef]
  5. Varfolomeev, M.A.; Abaidullina, D.I.; Solomonov, B.N.; Verevkin, S.P.; Emel’Yanenko, V.N. Pairwise substitution effects, inter- and intramolecular hydrogen bonds in methoxyphenols and dimethoxybenzenes. Thermochemistry, calorimetry, and first-principles calculations. J. Phys. Chem. B 2010, 114, 16503–16516. [Google Scholar]
  6. Zaitseva, K.V.; Varfolomeev, M.A.; Solomonov, B.N. Thermodynamics of hydrogen bonding of weak bases in alcohol solutions: Calorimetry of solution, IR-spectroscopy and vapor pressure analysis. J. Mol. Struct. 2012, 1018, 14–20. [Google Scholar] [CrossRef]
  7. Solomonov, B.N.; Nagrimanov, R.N.; Mukhametzyanov, T.A. Additive scheme for calculation of solvation enthalpies of heterocyclic aromatic compounds. Sublimation/vaporization enthalpy at 298.15 K. Thermochim. Acta 2016, 633, 37–47. [Google Scholar] [CrossRef]
  8. Nagrimanov, R.N.; Samatov, A.A.; Solomonov, B.N. Additive scheme of solvation enthalpy for linear, cyclic and branched-chain aliphatic compounds at 298.15 K. J. Mol. Liq. 2019, 292, 111365/1–111365/7. [Google Scholar] [CrossRef]
  9. Solomonov, B.N.; Varfolomeev, M.A.; Nagrimanov, R.N.; Novikov, V.B.; Buzyurov, A.V.; Fedorova, Y.V.; Mukhametzyanov, T.A. New method for determination of vaporization and sublimation enthalpy of aromatic compounds at 298.15 K using solution calorimetry technique and group-additivity scheme. Thermochim. Acta 2015, 622, 88–96. [Google Scholar] [CrossRef]
  10. Golmohammadi, H.; Dashtbozorgi, Z.; Gholam Samani, M.; Acree, W.E., Jr. QSPR prediction of gas-to-methanol solvation enthalpy of organic compounds using replacement method and support vector machine. Phys. Chem. Liq. 2015, 53, 46–66. [Google Scholar] [CrossRef]
  11. Toubaei, A.; Golmohammadi, H.; Dashtbozorgi, Z.; Acree, W.E., Jr. QSPR studies for predicting gas to acetone and gas to acetonitrile solvation enthalpies using support vector machine. J. Mol. Liq. 2012, 175, 24–32. [Google Scholar] [CrossRef]
  12. Fariba, S.; Dakhel, A.A.; Shariati, S. Predictive artificial neural network model for solvation enthalpy of organic compounds in N,N-dimethylformamide. Russ. J. Phys. Chem. A 2019, 93, 2661–2668. [Google Scholar] [CrossRef]
  13. Magsumov, T.I.; Sedov, I.A.; Acree, W.E., Jr. Development of Abraham model correlations for enthalpies of solvation of solutes dissolved in N-methylformamide, 2-pyrrolidone and N-methylpyrrolidone. J. Mol. Liq. 2021, 323, 114609/1–114609/10. [Google Scholar] [CrossRef]
  14. Huang, J.; Eddula, S.; Tirumala, P.; Casillas, T.; Acree, W.E., Jr.; Abraham, M.H. Updated Abraham model correlations to describe enthalpies of solvation of solutes dissolved in heptane, cyclohexane and N,N-dimethylformamide. Phys. Chem. Liq. 2021, 59, 442–453. [Google Scholar] [CrossRef]
  15. Lu, J.Z.; Acree, W.E., Jr.; Abraham, M.H. Abraham model correlations for enthalpies of solvation of organic solutes dissolved in methyl acetate and octane. Phys. Chem. Liq. 2020, 58, 18–30. [Google Scholar] [CrossRef]
  16. Stolov, M.A.; Zaitseva, K.V.; Varfolomeev, M.A.; Acree, W.E. Enthalpies of solution and enthalpies of solvation of organic solutes in ethylene glycol at 298.15 K: Prediction and analysis of intermolecular interaction contributions. Thermochim. Acta 2017, 648, 91–99. [Google Scholar] [CrossRef]
  17. Hart, E.; Grover, D.; Zettl, H.; Koshevarova, V.; Acree, W.E., Jr.; Abraham, M.H. Development of Abraham model expressions for predicting the enthalpies of solvation of solutes dissolved in acetic acid. Phys. Chem. Liq. 2016, 54, 141–154. [Google Scholar] [CrossRef]
  18. Wilson, A.; Tian, A.; Dabadge, N.; Acree, W.E., Jr.; Varfolomeev, M.A.; Rakipov, I.T.; Arkhipova, S.M.; Abraham, M.H. Enthalpy of solvation correlations for organic solutes and gases dissolved in dichloromethane and 1,4-dioxane. Struct. Chem. 2013, 24, 1841–1853. [Google Scholar] [CrossRef]
  19. Acree, W.E., Jr.; Smart, K.; Abraham, M.H. Abraham model solute descriptors reveal strong intramolecular hydrogen bonding in 1,4-dihydroxyanthraquinone and 1,8-dihydroxyanthraquinone. Phys. Chem. Liq. 2018, 56, 416–420. [Google Scholar] [CrossRef]
  20. Abraham, M.H.; Du, C.M.; Platts, J.A. Lipophilicity of the nitrophenols, J. Org. Chem. 2000, 65, 7114–7118. [Google Scholar] [CrossRef]
  21. Abraham, M.H.; Acree, W.E., Jr.; Earp, C.E.; Vladimirova, A.; Whaley, W.L. Studies on the hydrogen bond acidity, and other descriptors and properties for hydroxyflavones and hydroxyisoflavones. J. Mol. Liq. 2015, 208, 363–372. [Google Scholar] [CrossRef]
  22. Ulrich, N.; Endo, S.; Brown, T.N.; Watanabe, N.; Bronner, G.; Abraham, M.H.; Goss, K.-U. UFZ-LSER Database v 3.2.1 [Internet]. Leipzig (Germany): Helmholtz Centre for Environmental Research-UFZ. 2017. Available online: http://www.ufz.de/lserd (accessed on 17 June 2022).
  23. Wu, Y.; Xie, Y.; Shi, H. Determination and model correlation of rhein in 12 pure solvents from 283.15 K to 323.15 K. J. Chem. Eng. Data 2022, in press. [CrossRef]
  24. Cheng, Y.; Wang, D.; Zhang, Z.; Wang, Z. Solubility and solution thermodynamics of rhein in eight pure solvents from (288.15 to 313.15) K. RSC Adv. 2015, 5, 80548–80552. [Google Scholar] [CrossRef]
  25. Platts, J.A.; Butina, D.; Abraham, M.H.; Hersey, A. Estimation of molecular linear free energy relation descriptors using a group contribution approach. J. Chem. Inf. Comp. Sci. 1999, 39, 835–845. [Google Scholar] [CrossRef]
  26. Platts, J.A.; Abraham, M.H.; Butina, D.; Hersey, A. Estimation of molecular linear free energy relationship descriptors by a group contribution approach. 2. Prediction of partition coefficients. J. Chem. Inf. Comp. Sci. 2000, 40, 71–80. [Google Scholar] [CrossRef]
  27. Chung, Y.; Vermeire, F.H.; Wu, H.; Walker, P.J.; Abraham, M.H.; Green, W.H. Group contribution and machine learning approaches to predict Abraham solute parameters, solvation free energy, and solvation enthalpy. J. Chem. Inf. Model. 2022, 62, 433–446. [Google Scholar] [CrossRef]
  28. Ulrich, N.; Ebert, A. Can deep learning algorithms enhance the prediction of solute descriptors for linear solvation energy relationship approaches? Fluid Phase Equilib. 2022, 555, 113349/1–113349/7. [Google Scholar] [CrossRef]
  29. Yamada, H.; Yajima, K.; Wada, H.; Nakagawa, G. Effects of solvation on partition and dimerization of benzoic acid in mixed solvent systems. Talanta 1995, 42, 789–795. [Google Scholar] [CrossRef]
  30. Strickland, S.; Ocon, L.; Zhang, A.; Wang, S.; Eddula, S.; Liu, G.; Tirumala, P.; Huang, J.; Dai, J.; Jiang, C.; et al. Abraham model correlations for describing dissolution of organic solutes and inorganic gases in dimethyl carbonate. Phys. Chem. Liq. 2021, 59, 181–195. [Google Scholar] [CrossRef]
  31. PharmaAlgorithms. ADME Boxes, Version 3.0; PharmaAlgorithms Inc.: Toronto, ON, Canada.
  32. Abraham, M.H.; McGowan, J.C. The use of characteristic volumes to measure cavity terms in reversed phase liquid chromatography. Chromatographia 1987, 23, 243–246. [Google Scholar] [CrossRef]
  33. Abraham, M.H.; Abraham, R.J.; Acree, W.E.; Aliev, A.E.; Leo, A.J.; Whaley, W.L. An NMR method for the quantitative assessment of intramolecular hydrogen bonding; Application to physicochemical, environmental, and biochemical properties. J. Org. Chem. 2014, 79, 11075–11083. [Google Scholar] [CrossRef] [PubMed]
  34. Whaley, W.L.; Okoso-amaa, E.M.; Womack, C.L.; Vladimirova, A.; Rogers, L.B.; Risher, M.J.; Abraham, M.H. Summation solute hydrogen bonding acidity values for hydroxyl substituted flavones determined by NMR spectroscopy. Nat. Prod. Comm. 2013, 8, 85–98. [Google Scholar] [CrossRef] [Green Version]
  35. Padhye, S.B.; Kulkarni, B.A. PMR evidence for hydrogen bonding in naturally occurring isomeric juglones. J. Mag. Res. 1974, 16, 150–152. [Google Scholar] [CrossRef]
  36. Bradley, J.-C.; Abraham, M.H.; Acree, W.E., Jr.; Lang, A.S.I.D.; Beck, S.N.; Bulger, D.A.; Clark, E.A.; Condron, L.N.; Costa, S.T.; Curtin, E.M.; et al. Determination of Abraham model solute descriptors for the monomeric and dimeric forms of trans-cinnamic acid using measured solubilities from the Open Notebook Science Challenge. Chem. Cent. J. 2015, 9, 1–6. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Article Metrics

Citations

Article Access Statistics

Journal Statistics
Multiple requests from the same IP address are counted as one view.
Download PDF
Solute-Induced Perturbation of the Solvent Microstructure in Aqueous Electrolyte Solutions: Some Uses and Misuses of Structure Making/Breaking Criteria
Previous
Development of Machine Learning Flood Model Using Artificial Neural Network (ANN) at Var River
Next