Predicting Plant Breeder Decisions Across Multiple Selection Stages in a Wheat Breeding Program
Abstract
1. Introduction
2. Materials and Methods
2.1. Plant Material, Classification of Breeder’s Decisions, and Genotypic Data
- Selection decisions in concerning lines that were forwarded to s , with a classification of non-selected lines () versus lines that were selected once () as well as twice ().
- Selection decisions in s concerning lines that were tested again in s , with a classification of lines that were selected once () versus lines that were selected twice ().
- Selection decisions concerning all lines tested in s and the subset of twice-selected lines () that finally entered s after passing s , with a classification of non-selected lines () as well as lines that were selected once ( versus lines that were selected twice ().
2.2. Prediction of the Breeder’s Multi-Stage Selection Decisions by Elastic Net
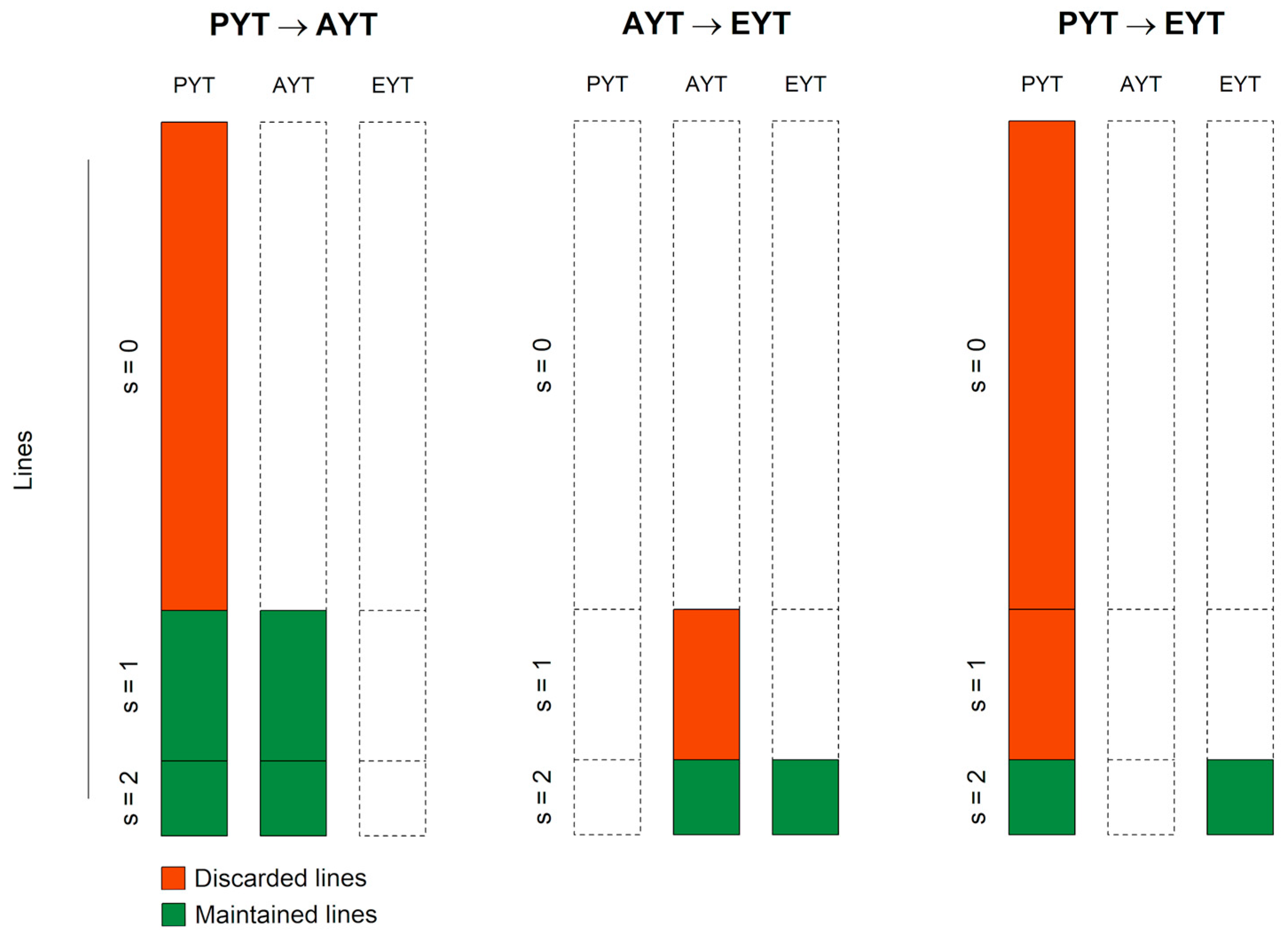
- The 50 lines in the validation population with the highest probability of falling into the class of once- and twice-selected lines ( and ) were accordingly labeled with ‘maintain’, and the other 350 lines were labeled as ‘discard’ in the scheme .
- The 10 lines in the validation population with the highest probability of falling into the class of twice-selected lines () were accordingly labeled with ‘maintain’, and the other 40 lines were labeled as ‘discard’ in the scheme
- The 10 lines in the validation population with the highest probability of falling into the class of twice-selected lines () were accordingly labeled with ‘maintain’, and the other 390 lines were labeled as ‘discard’ in the scheme
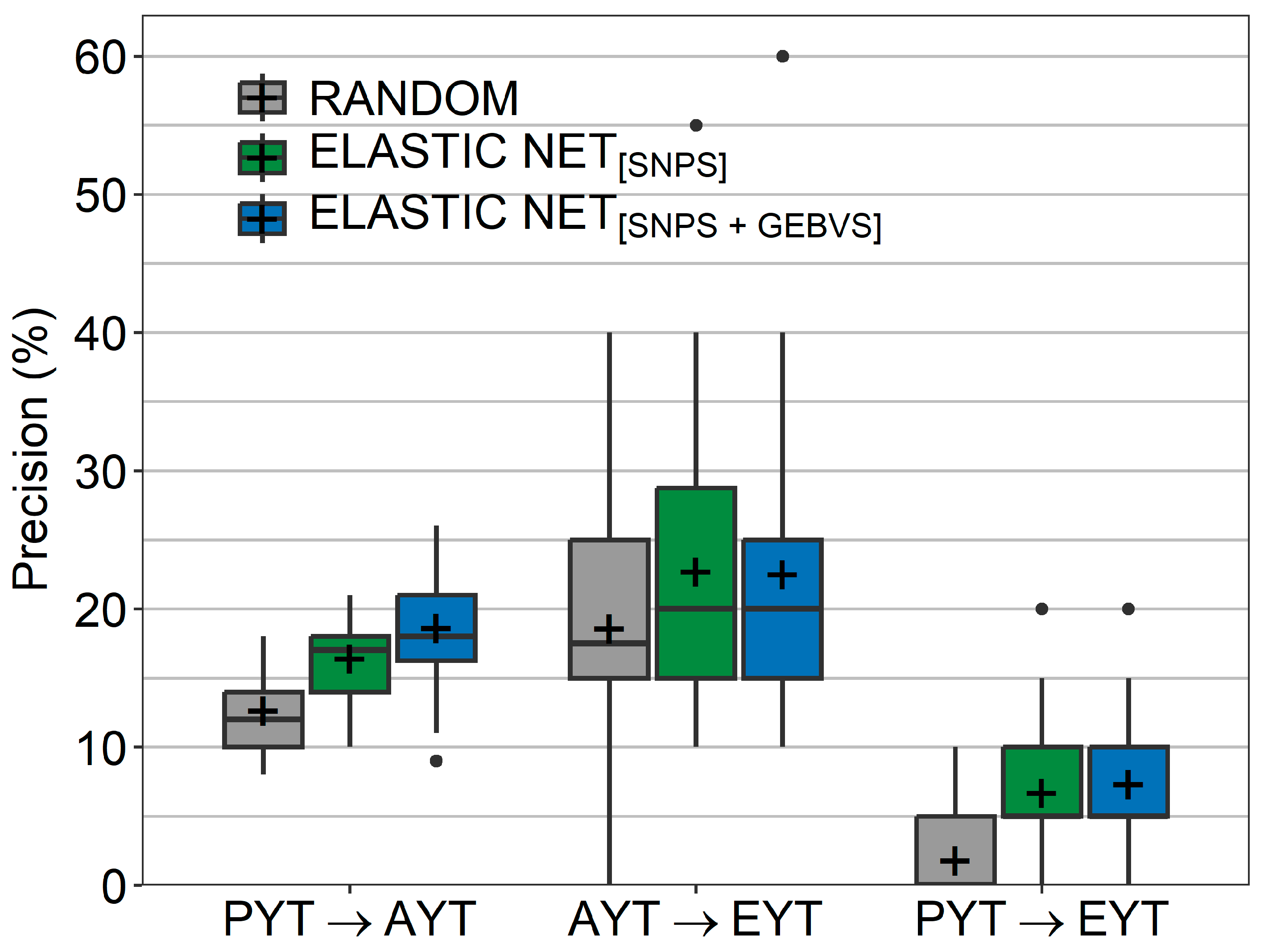
- The precision of this classification into ‘maintained’ and ‘discarded’ lines in the different selection schemes was finally estimated by:where is the number of true positive- and is the number of false positive-classified lines in the validation population based on a confusion matrix. refers to lines that were predicted as being ‘maintained’ and were actually selected by the breeder, whereas refers to lines that were wrongly classified by elastic net as falling into the class of ‘maintained’ lines. The precision was lastly compared to a random choice from among the lines in the validation population in the above-outlined scenarios.
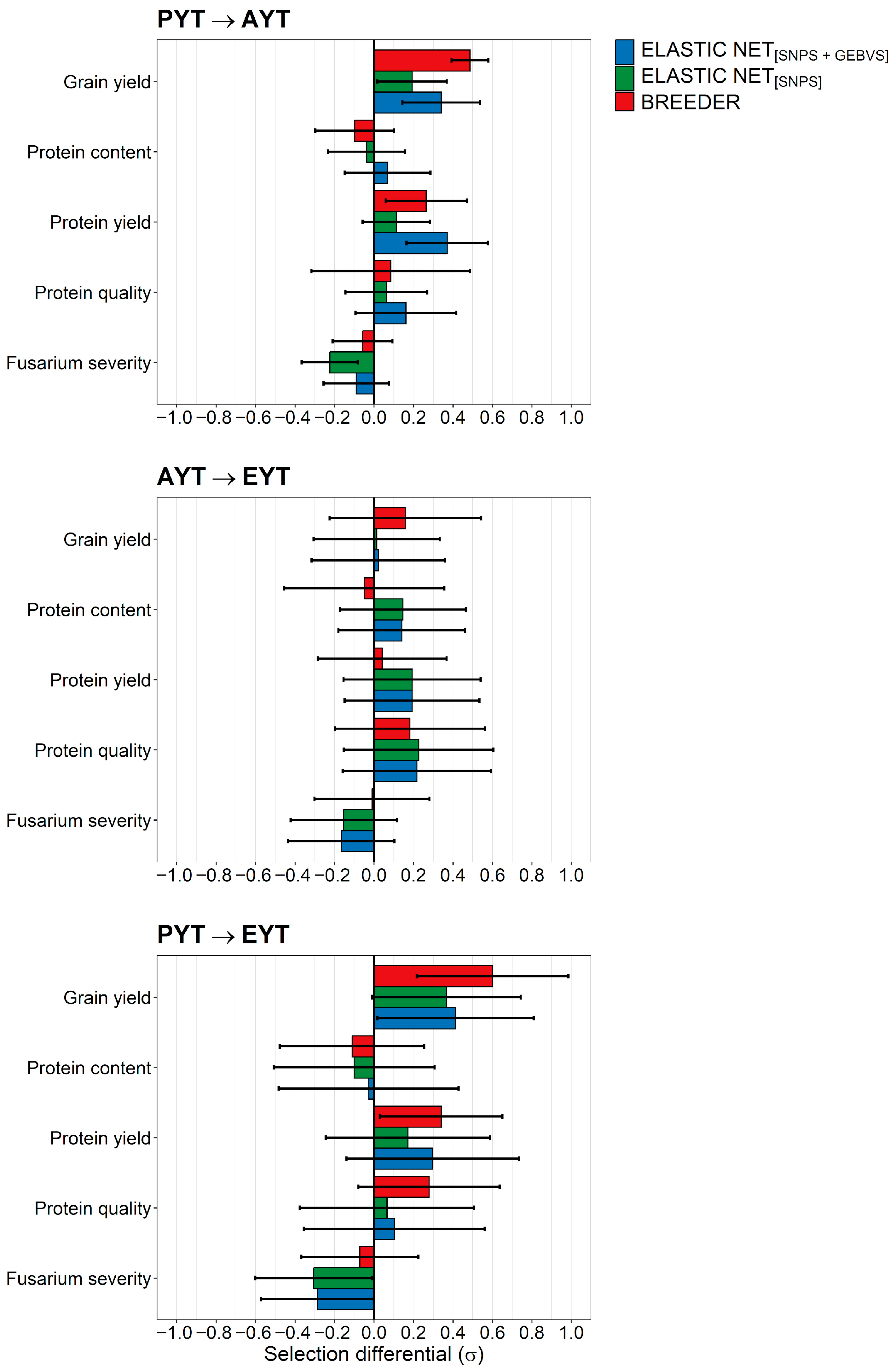
2.3. Comparison of the Breeder’s Selection Decisions and Elastic Net’s Recommendations
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bernardo, R. Reinventing Quantitative Genetics for Plant Breeding: Something Old, Something New, Something Borrowed, Something BLUE. Heredity 2020, 125, 375–385. [Google Scholar] [CrossRef]
- Duvick, D.N. Theory, Empiricism and Intuition in Professional Plant Breeding. In Farmers, Scientists and Plant Breeding: Integrating Knowledge and Practice; CABI Publishing: Wallingford, UK, 2002; pp. 189–211. [Google Scholar]
- Batista, L.G.; Gaynor, R.C.; Margarido, G.R.A.; Byrne, T.; Amer, P.; Gorjanc, G.; Hickey, J.M. Long-Term Comparison between Index Selection and Optimal Independent Culling in Plant Breeding Programs with Genomic Prediction. PLoS ONE 2021, 16, e0235554. [Google Scholar] [CrossRef]
- Akdemir, D.; Beavis, W.; Fritsche-Neto, R.; Singh, A.K.; Isidro-Sánchez, J. Multi-Objective Optimized Genomic Breeding Strategies for Sustainable Food Improvement. Heredity 2019, 122, 672–683. [Google Scholar] [CrossRef]
- Guzmán, C.; Peña, R.J.; Singh, R.; Autrique, E.; Dreisigacker, S.; Crossa, J.; Rutkoski, J.; Poland, J.; Battenfield, S. Wheat Quality Improvement at CIMMYT and the Use of Genomic Selection on It. Appl. Transl. Genom. 2016, 11, 3–8. [Google Scholar] [CrossRef]
- Gorjanc, G.; Gaynor, R.C.; Hickey, J.M. Optimal Cross Selection for Long-Term Genetic Gain in Two- Part Programs with Rapid Recurrent Genomic Selection. Theor. Appl. Genet. 2018, 131, 1953–1966. [Google Scholar] [CrossRef]
- Vanavermaete, D.; Fostier, J.; Maenhout, S.; De Baets, B. Adaptive Scoping: Balancing Short- and Long-Term Genetic Gain in Plant Breeding. Euphytica 2022, 218, 109. [Google Scholar] [CrossRef]
- Repinski, S.L.; Hayes, K.N.; Miller, J.K.; Trexler, C.J.; Bliss, F.A. Plant Breeding Graduate Education: Opinions about Critical Knowledge, Experience, and Skill Requirements from Public and Private Stakeholders Worldwide. Crop Sci. 2011, 51, 2325–2336. [Google Scholar] [CrossRef]
- Sangjan, W.; Kick, D.R.; Washburn, J.D. Improving Plant Breeding through AI-Supported Data Integration. Theor. Appl. Genet. 2025, 138, 132. [Google Scholar] [CrossRef] [PubMed]
- Farooq, M.A.; Gao, S.; Hassan, M.A.; Huang, Z.; Rasheed, A.; Hearne, S.; Prasanna, B.; Li, X.; Li, H. Artificial Intelligence in Plant Breeding. Trends Genet. 2024, 40, 891–908. [Google Scholar] [CrossRef]
- Roth, L.; Fossati, D.; Krähenbühl, P.; Walter, A.; Hund, A. Image-Based Phenomic Prediction Can Provide Valuable Decision Support in Wheat Breeding. Theor. Appl. Genet. 2023, 136, 162. [Google Scholar] [CrossRef] [PubMed]
- Moeinizade, S.; Hu, G.; Wang, L. A Reinforcement Learning Approach to Resource Allocation in Genomic Selection. Intell. Syst. with Appl. 2022, 14, 200076. [Google Scholar] [CrossRef]
- Robertsen, C.; Hjortshøj, R.; Janss, L. Genomic Selection in Cereal Breeding. Agronomy 2019, 9, 95. [Google Scholar] [CrossRef]
- Robert, P.; Brault, C.; Rincent, R.; Segura, V. Phenomic Selection: A New and Efficient Alternative to Genomic Selection. In Methods in Molecular Biology; Springer Nature: Berlin, Germany, 2022; Volume 2467, pp. 397–420. ISBN 9781071622056. [Google Scholar]
- Borrenpohl, D.; Huang, M.; Olson, E.; Sneller, C. The Value of Early-Stage Phenotyping for Wheat Breeding in the Age of Genomic Selection. Theor. Appl. Genet. 2020, 133, 2499–2520. [Google Scholar] [CrossRef]
- Robert, P.; Auzanneau, J.; Goudemand, E.; Oury, F.-X.; Rolland, B.; Heumez, E.; Bouchet, S.; Le Gouis, J.; Rincent, R. Phenomic Selection in Wheat Breeding: Identification and Optimisation of Factors Influencing Prediction Accuracy and Comparison to Genomic Selection. Theor. Appl. Genet. 2022, 135, 895–914. [Google Scholar] [CrossRef]
- Meyenberg, C.; Braun, V.; Longin, C.F.H.; Thorwarth, P. Feature Engineering and Parameter Tuning: Improving Phenomic Prediction Ability in Multi-Environmental Durum Wheat Breeding Trials. Theor. Appl. Genet. 2024, 137, 188. [Google Scholar] [CrossRef]
- Belamkar, V.; Guttieri, M.J.; Hussain, W.; Jarquín, D.; El-basyoni, I.; Poland, J.; Lorenz, A.J.; Baenziger, P.S. Genomic Selection in Preliminary Yield Trials in a Winter Wheat Breeding Program. G3 Genes|Genomes|Genet. 2018, 8, 2735–2747. [Google Scholar] [CrossRef] [PubMed]
- Desta, Z.A.; Ortiz, R. Genomic Selection: Genome-Wide Prediction in Plant Improvement. Trends Plant Sci. 2014, 19, 592–601. [Google Scholar] [CrossRef] [PubMed]
- Meuwissen, T.H.E.; Hayes, B.J.; Goddard, M.E. Prediction of Total Genetic Value Using Genome-Wide Dense Marker Maps. Genetics 2001, 157, 1819–1829. [Google Scholar] [CrossRef]
- Rincent, R.; Charpentier, J.-P.; Faivre-Rampant, P.; Paux, E.; Le Gouis, J.; Bastien, C.; Segura, V. Phenomic Selection Is a Low-Cost and High-Throughput Method Based on Indirect Predictions: Proof of Concept on Wheat and Poplar. G3 Genes|Genomes|Genet. 2018, 8, 3961–3972. [Google Scholar] [CrossRef] [PubMed]
- Tschermak, E. Ein Leben Fuer Die Zuechtung. Aus Der Werkstatt Eines Alten Pflanzenzuechter. Odal 1941, 10, 768–777. [Google Scholar]
- Timmermann, M. The Breeder’s Eye—Theoretical Aspects of the Breeder’s Decision-Making. In Proceedings of the COST SUSVAR Workshop on Cereal Crop Diversity: Implications for Production and Products; Ostergard, H., Fontaine, L., Eds.; Institut Technique de l’Agriculture Biologique: Paris, France, 2006; pp. 118–123. ISBN 2-9515855-7-8 9782951585577. [Google Scholar]
- Crossa, J.; Montesinos-Lopez, O.A.; Costa-Neto, G.; Vitale, P.; Martini, J.W.R.; Runcie, D.; Fritsche-Neto, R.; Montesinos-Lopez, A.; Pérez-Rodríguez, P.; Gerard, G.; et al. Machine Learning Algorithms Translate Big Data into Predictive Breeding Accuracy. Trends Plant Sci. 2024, 30, 167–184. [Google Scholar] [CrossRef]
- Michel, S.; Löschenberger, F.; Ametz, C.; Bistrich, H.; Bürstmayr, H. Can We Teach Machines to Select Like a Plant Breeder? A Recommender System Approach to Support Early Generation Selection Decisions Based on Breeders’ Preferences. Crops 2025, 5, 31. [Google Scholar] [CrossRef]
- Diversity Arrays Technology Pty Ltd. DArT P/L. 2020. Available online: https://www.diversityarrays.com/ (accessed on 1 October 2025).
- Stekhoven, D.J.; Bühlmann, P. Missforest-Non-Parametric Missing Value Imputation for Mixed-Type Data. Bioinformatics 2012, 28, 112–118. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learing 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Rutkoski, J.E.; Poland, J.; Jannink, J.-L.; Sorrells, M.E. Imputation of Unordered Markers and the Impact on Genomic Selection Accuracy. G3 Genes|Genomes|Genet. 2013, 3, 427–439. [Google Scholar] [CrossRef]
- Moreno-Amores, J.; Michel, S.; Löschenberger, F.; Buerstmayr, H. Dissecting the Contribution of Environmental Influences, Plant Phenology, and Disease Resistance to Improving Genomic Predictions for Fusarium Head Blight Resistance in Wheat. Agronomy 2020, 10, 2008. [Google Scholar] [CrossRef]
- Michel, S.; Löschenberger, F.; Ametz, C.; Pachler, B.; Sparry, E.; Bürstmayr, H. Combining Grain Yield, Protein Content and Protein Quality by Multi—Trait Genomic Selection in Bread Wheat. Theor. Appl. Genet. 2019, 132, 2767–2780. [Google Scholar] [CrossRef]
- Tay, J.K.; Narasimhan, B.; Hastie, T. Elastic Net Regularization Paths for All Generalized Linear Models. J. Stat. Softw. 2023, 106, 1–31. [Google Scholar] [CrossRef] [PubMed]
- Reif, J.C.; Melchinger, A.E.; Frisch, M. Genetical and Mathematical Properties of Similarity and Dissimilarity Coefficients Applied in Plant Breeding and Seed Bank Management. Crop Sci. 2005, 45, 1–7. [Google Scholar] [CrossRef]
- Sneller, C.; Ignacio, C.; Ward, B.; Rutkoski, J.; Mohammadi, M. Using Genomic Selection to Leverage Resources among Breeding Programs: Consortium-Based Breeding. Agronomy 2021, 11, 1555. [Google Scholar] [CrossRef]
- Tsai, H.-Y.Y.; Janss, L.L.; Andersen, J.R.; Orabi, J.; Jensen, J.J.D.; Jahoor, A.; Jensen, J.J.D. Genomic Prediction and GWAS of Yield, Quality and Disease-Related Traits in Spring Barley and Winter Wheat. Sci. Rep. 2020, 10, 3347. [Google Scholar] [CrossRef]
- Adunola, P.; Ferrão, L.F.V.; Benevenuto, J.; Azevedo, C.F.; Munoz, P.R. Genomic Selection Optimization in Blueberry: Data-driven Methods for Marker and Training Population Design. Plant Genome 2024, 17, e20488. [Google Scholar] [CrossRef]
- Bandillo, N.B.; Jarquin, D.; Posadas, L.G.; Lorenz, A.J.; Graef, G.L. Genomic Selection Performs as Effectively as Phenotypic Selection for Increasing Seed Yield in Soybean. Plant Genome 2022, 16, e20285. [Google Scholar] [CrossRef]
- Burke, R.; Felfernig, A.; Göker, M.H. Recommender Systems: An Overview. AI Mag. 2011, 32, 13–18. [Google Scholar] [CrossRef]
- Roy, D.; Dutta, M. A Systematic Review and Research Perspective on Recommender Systems. J. Big Data 2022, 9, 59. [Google Scholar] [CrossRef]
- Batmaz, Z.; Yurekli, A.; Bilge, A.; Kaleli, C. A Review on Deep Learning for Recommender Systems: Challenges and Remedies. Artif. Intell. Rev. 2019, 52, 1–37. [Google Scholar] [CrossRef]
- Jugovac, M.; Jannach, D. Interacting with Recommenders—Overview and Research Directions. ACM Trans. Interact. Intell. Syst. 2017, 7, 10. [Google Scholar] [CrossRef]
- Michel, S.; Löschenberger, F.; Ametz, C.; Bistrich, H.; Bürstmayr, H. Towards Streamlining the Choice of Crossing Combinations in Plant Breeding by Integrating Model-Based Recommendations and Plant Breeder’s Preferences. Crops 2025, 5, 5. [Google Scholar] [CrossRef]
- Gesesse, C.A.; Nigir, B.; de Sousa, K.; Gianfranceschi, L.; Gallo, G.R.; Poland, J.; Kidane, Y.G.; Abate Desta, E.; Fadda, C.; Pè, M.E.; et al. Genomics-Driven Breeding for Local Adaptation of Durum Wheat Is Enhanced by Farmers’ Traditional Knowledge. Proc. Natl. Acad. Sci. USA 2023, 120, 2017. [Google Scholar] [CrossRef] [PubMed]
- Mancini, C.; Kidane, Y.G.; Mengistu, D.K.; Melfa and Workaye Farmer Community; Pè, M.E.; Fadda, C.; Dell, M. Joining Smallholder Farmers’ Traditional Knowledge with Metric Traits to Select Better Varieties of Ethiopian Wheat. Sci. Rep. 2017, 7, 9120. [Google Scholar] [CrossRef]
- Teeken, B.; Olaosebikan, O.; Haleegoah, J.; Oladejo, E.; Madu, T.; Bello, A.; Parkes, E.; Egesi, C.; Kulakow, P.; Kirscht, H.; et al. Cassava Trait Preferences of Men and Women Farmers in Nigeria: Implications for Breeding. Econ. Bot. 2018, 72, 263–277. [Google Scholar] [CrossRef] [PubMed]
- Rattunde, H.F.W.; Michel, S.; Leiser, W.L.; Piepho, H.P.; Diallo, C.; Vom Brocke, K.; Diallo, B.; Haussmann, B.I.G.; Weltzien, E. Farmer Participatory Early-Generation Yield Testing of Sorghum in West Africa: Possibilities to Optimize Genetic Gains for Yield in Farmers’ Fields. Crop Sci. 2016, 56, 2493–2505. [Google Scholar] [CrossRef]
- Jin, H.; Tross, M.C.; Tan, R.; Newton, L.; Mural, R.V.; Yang, J.; Thompson, A.M.; Schnable, J.C. Imitating the “Breeder’s Eye”: Predicting Grain Yield from Measurements of Non-yield Traits. Plant Phenome J. 2024, 7, e20102. [Google Scholar] [CrossRef]
- Löschenberger, F.; Fleck, A.; Grausgruber, H.; Hetzendorfer, H.; Hof, G.; Lafferty, J.; Marn, M.; Neumayer, A.; Pfaffinger, G.; Birschitzky, J. Breeding for Organic Agriculture: The Example of Winter Wheat in Austria. Euphytica 2008, 163, 469–480. [Google Scholar] [CrossRef]
- Cowling, W.A. Sustainable Plant Breeding. Plant Breed. 2013, 132, 1–9. [Google Scholar] [CrossRef]
- Ceccarelli, S.; Grando, S. Return to Agrobiodiversity: Participatory Plant Breeding. Diversity 2022, 14, 126. [Google Scholar] [CrossRef]
- Reif, J.C.; Zhang, P.; Dreisigacker, S.; Warburton, M.L.; Van Ginkel, M.; Hoisington, D.; Bohn, M.; Melchinger, A.E. Wheat Genetic Diversity Trends during Domestication and Breeding. Theor. Appl. Genet. 2005, 110, 859–864. [Google Scholar] [CrossRef]
- Louwaars, N.P. Plant Breeding and Diversity: A Troubled Relationship? Euphytica 2018, 214, 114. [Google Scholar] [CrossRef]
- Swarup, S.; Cargill, E.J.; Crosby, K.; Flagel, L.; Kniskern, J.; Glenn, K.C. Genetic Diversity Is Indispensable for Plant Breeding to Improve Crops. Crop Sci. 2021, 61, 839–852. [Google Scholar] [CrossRef]
- Bernardo, R. Retrospective Index Weights Used in Multiple Trait Selection in a Maize Breeding Program. Crop Sci. 1991, 31, 1174–1179. [Google Scholar] [CrossRef]
- Akata, Z.; Balliet, D.; De Rijke, M.; Dignum, F.; Dignum, V.; Eiben, G.; Fokkens, A.; Grossi, D.; Hindriks, K.; Hoos, H.; et al. A Research Agenda for Hybrid Intelligence: Augmenting Human Intellect with Collaborative, Adaptive, Responsible, and Explainable Artificial Intelligence. Computer 2020, 53, 18–28. [Google Scholar] [CrossRef]
- Kamar, E. Directions in Hybrid Intelligence: Complementing AI Systems with Human Intelligence. In Proceedings of the 25th International Joint Conference on Artificial Intelligence, New York, NY, USA, 9–15 July 2016; pp. 4070–4073. [Google Scholar]
- Nyholm, S. Artificial Intelligence and Human Enhancement: Can AI Technologies Make Us More (Artificially) Intelligent? Cambridge Q. Healthc. Ethics 2024, 33, 76–88. [Google Scholar] [CrossRef] [PubMed]
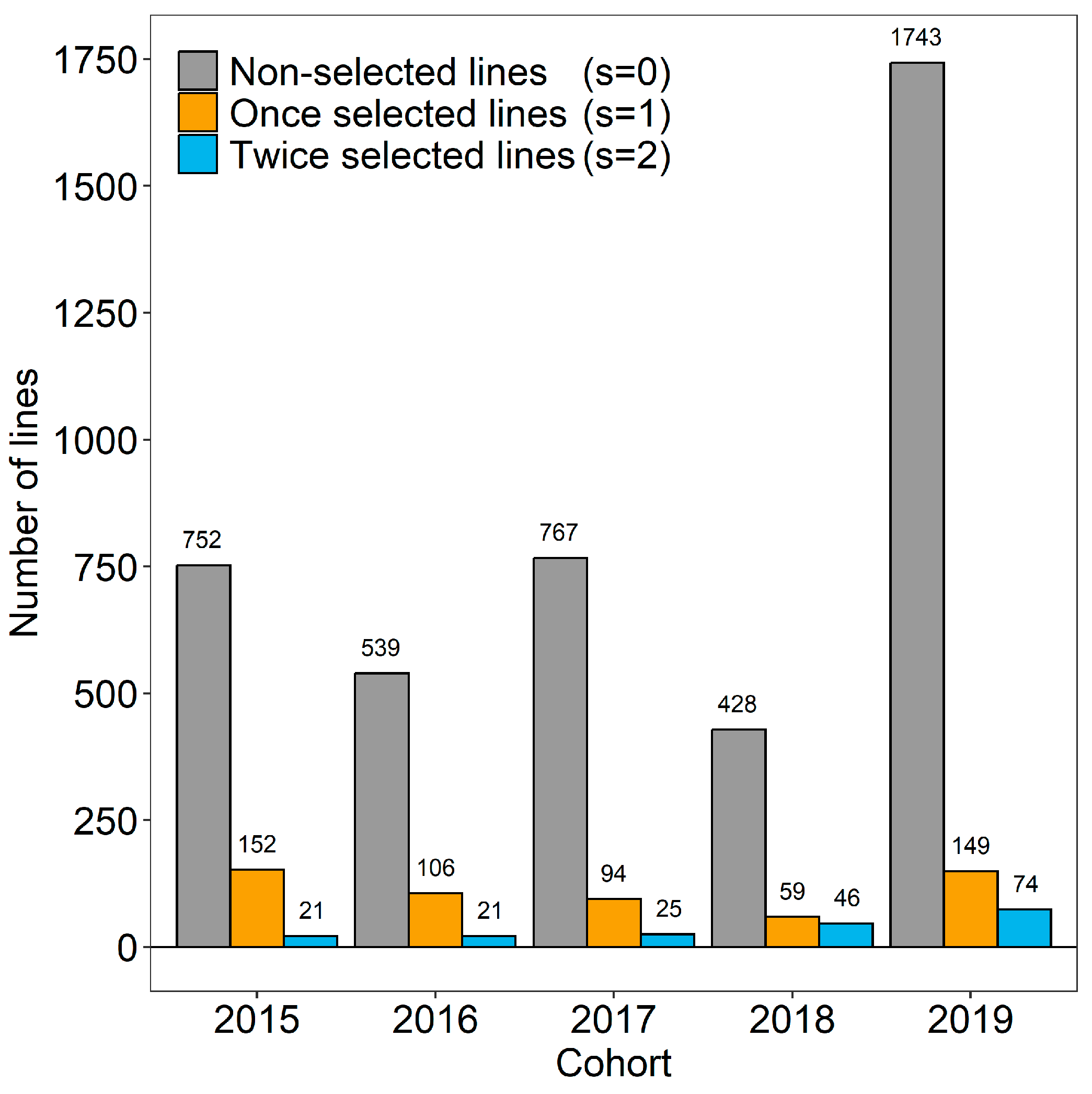

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Michel, S.; Löschenberger, F.; Ametz, C.; Bistrich, H.; Bürstmayr, H. Predicting Plant Breeder Decisions Across Multiple Selection Stages in a Wheat Breeding Program. Crops 2025, 5, 69. https://doi.org/10.3390/crops5050069
Michel S, Löschenberger F, Ametz C, Bistrich H, Bürstmayr H. Predicting Plant Breeder Decisions Across Multiple Selection Stages in a Wheat Breeding Program. Crops. 2025; 5(5):69. https://doi.org/10.3390/crops5050069
Chicago/Turabian StyleMichel, Sebastian, Franziska Löschenberger, Christian Ametz, Herbert Bistrich, and Hermann Bürstmayr. 2025. "Predicting Plant Breeder Decisions Across Multiple Selection Stages in a Wheat Breeding Program" Crops 5, no. 5: 69. https://doi.org/10.3390/crops5050069
APA StyleMichel, S., Löschenberger, F., Ametz, C., Bistrich, H., & Bürstmayr, H. (2025). Predicting Plant Breeder Decisions Across Multiple Selection Stages in a Wheat Breeding Program. Crops, 5(5), 69. https://doi.org/10.3390/crops5050069






