Towards Streamlining the Choice of Crossing Combinations in Plant Breeding by Integrating Model-Based Recommendations and Plant Breeder’s Preferences

Abstract

Selecting crossing combinations crucial for successfully developing new improved crop varieties and genomic data from DNA markers have become invaluable for guiding plant breeders in evaluating and choosing promising crosses between potential parents. However, navigating the vast array of thousands of possible parental combinations, even with extensive genomic information, can be challenging, even for experienced breeders with deep knowledge of their crop’s gene pool. This case study aimed to evaluate the effectiveness of a recommender system to support plant breeders in this complex decision-making process. It took a retrospective approach, analyzing selection decisions made by an experienced breeder across several thousand potential crossing combinations over six years. The results indicated that a recommender system could significantly reduce the time and effort needed to identify promising crosses aligned with the breeder’s preferences. However, active feedback from the breeder to the recommender system appeared to be essential for achieving a satisfactory prediction. Integrating model-based recommendations and plant breeder’s preferences in a recommender system featuring such a reciprocal fine-tuning scheme, where the breeder actively provides feedback to the machine in the style of hybrid human–artificial intelligence, represents one step towards streamlining the choice of crossing combinations in plant breeding programs.

1. Introduction

Creating new genetic variations by crossing two or more parents is the initial and often most important step in plant breeding programs before evaluating the performance of progenies across multiple environments and several stages of selections, aiming to finally release the most promising as novel cultivars. The choice of parents is thus a decisive matter, which is complemented by decisions concerning the specific crosses among the multitude of possible parental combinations when breeding, for example, line varieties. Some breeders conduct few crosses with a restricted number of parents to achieve this goal during variety development, while others stratify their resources on the progeny from many different crosses among a diverse set of parents [1,2].

There is admittedly no consensus on which strategy is preferable and with a limited budget in breeding programs; however, predicting the outcome of crossing combinations is of utmost interest in applied plant breeding programs in order to achieve a high rate of genetic improvement. Although metrics like the general and specific combining ability can be useful for choosing cross combinations in line breeding programs, they would, in most cases, require conducting some extensive progeny tests [3]. A convenient alternative is given by the mid-parent value, which has been shown to be a good predictor of the progeny population average of bi-parental crosses in this context [4,5,6], and crossing the best with the best by using the aforementioned mid-parent value for selecting specific crosses can lead to a high short-term selection gain [7,8]. Additionally, an appropriate management of diversity and genetic variation when choosing crosses can be considered as pivotal for safeguarding a high long-term selection gain [9,10,11]. The inclusion of the amount of inbreeding [10,12] or the estimated genetic variance of progeny populations [7,13,14,15,16] based on genome-wide distributed DNA markers to obtain genomic cross predictions for various agronomic relevant traits has thus gained large popularity for further informing breeders about the outcome of potential crossing combinations. Genome-wide distributed DNA markers are specific sequences of DNA that can be used to identify and analyze genetic variations between individuals within and across gene pools. They commonly serve as biological tags that help researchers and plant breeders to trace inheritance patterns and assess genetic diversity and explanatory variables in prediction models for major agronomic traits like grain yield [17]. However, choosing the most promising crosses among the plethora of possible crossing combinations enriched with the vast information coming from genomic fingerprints is oftentimes a very difficult endeavor, even for experienced breeders who possess a profound knowledge of their crop’s gene pool. Assuming, for example, an array of 100 parental lines, the number of all possible bi-parental crossing combination already amounts to 4950, of which a plant breeder has to choose around 200 combinations due to cost restrictions when screening several thousand progenies of such crosses in field experiments. Since the aim of a plant breeding program is the development of new, improved plant varieties, a plant breeder additionally has to consider dozens of agronomic traits simultaneously for each of the many possible crossing combinations, like grain yield and different aspects of quality, as well as resistances against multiple diseases and pests. Although the above-mentioned genomic mating indices [7,13,14,15,16] provide performance predictions for individual traits, the task of choosing crossing combinations based on these predictions remains with the plant breeder.

One approach to streamlining this process and potentially reducing a plant breeder’s time and effort for finding the most interesting crossing combinations is the implementation of a recommender system. The basis of such a recommender system is classically given by training a prediction model based on the preferences of a user among an array of possible items [18], which, in the case of plant breeding, would, for example, be the differentiation between the selected and non-selected crosses among all possible crossing combinations based on a breeder’s preferences in previous years. Such a recommender system would subsequently suggest selecting an array of specific crosses among all the possible crossing combinations that are given in the present year with pending selection decisions. The recommendations derived in this way would accordingly be based on the characteristics of previously chosen crossing combinations by the breeder and thus reflect the breeder’s preferences and breeding goals of the plant breeding program. Hence, the potential value of such a recommender system is given by the fact that the plant breeder most likely does not have to screen all the available data for hundreds or thousands of possible crossing combinations and multiple agronomic traits but only part of this vast information. Extending this concept further, it is possible to imagine a reciprocal fine-tuning scheme, where the breeder actively provides feedback to the machine in the style of hybrid human–artificial intelligence. For example, the initial recommendations of 200 among 4950 possible crossing combinations are screened by the breeder with respect to their potential performance with regards to grain yield, quality, disease resistance, and other agronomic important characteristics. Based on this screening, the plant breeder might retain the labeling (“select”) or relabel the recommended crosses (“not select”), followed by augmenting the training population and updating the prediction models underlying the recommender system and then screening the next batch of recommended crosses among the set of not yet labeled crossing combinations. Since plant breeders implicitly influence different genomic regions when conducting such selection decisions, for example, increasing the frequency of a favorable yield by increasing the allele of a gene, it appears reasonable to employ genome-wide distributed DNA markers as underlying predictor variables for such a recommender system. The aim of this case study was thus to assess the merit of such a recommender system to support plant breeders in choosing crosses based on the described reciprocal fine-tuning scheme, where a plant breeder actively provides feedback to the recommender system with subsequent prediction model updating in the style of hybrid human–artificial intelligence.

2. Materials and Methods

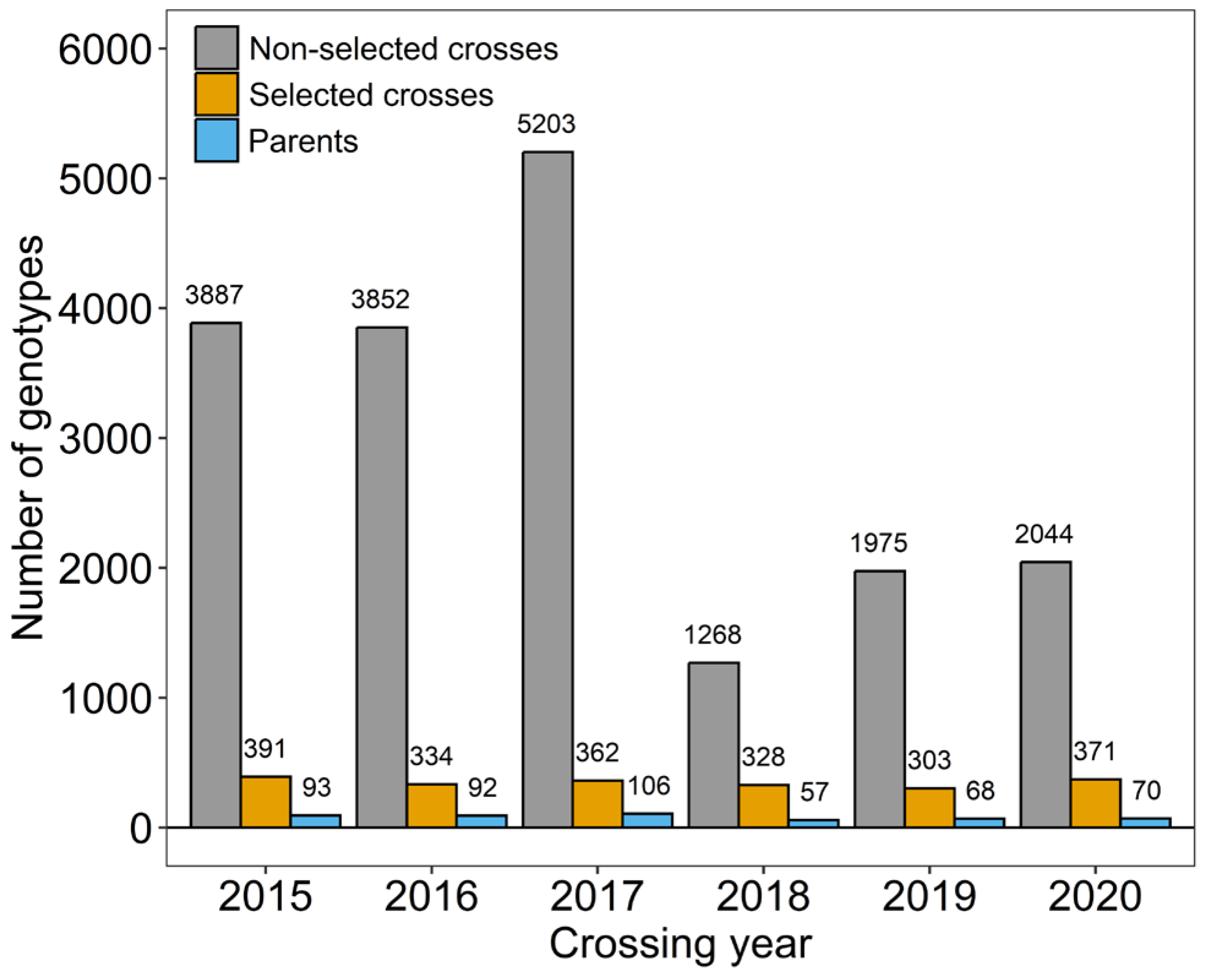
2.1. Plant Material, Classification of Breeder’s Decisions, and Genotypic Data

This study focused on a set of 388 winter wheat (Triticum aestivum L.) parental lines from the commercial plant breeding program of Saatzucht Donau GesmbH & CoKG, which were used as crossing partners in the six distinct crossing years 2015–2020. Different subsets of 57–106 parental lines were considered for conducting crosses within each of these years, resulting in 1596–5565 possible combinations within each crossing year, of which 303–391 were actually selected by the plant breeder (Franziska Löschenberger) (Figure 1). The total number of all potential bi-parental crosses that were used to the train prediction models amounted thus to 20,318, with 2089 falling into the class of selected crosses $(\mathrm{s}\mathrm{e}\mathrm{l}=1)$ and 18,229 into the class of non-selected crosses $(\mathrm{s}\mathrm{e}\mathrm{l}=0)$. The sole target trait used in the study at hand was furthermore the mentioned classification into selected $(\mathrm{s}\mathrm{e}\mathrm{l}=1)$ and non-selected crosses $(\mathrm{s}\mathrm{e}\mathrm{l}=0)$.

The parental lines were genotyped with the DArTcap targeted genotyping-by-sequencing approach [19]. The resulting DNA markers possessed two alleles, i.e., states, and served as predictor variables for the recommender system in the study at hand. For this purpose, the DNA marker genotypes for each parental line and DNA marker were coded as “+1” for homozygous major (AA), “0” for heterozygous (Aa), and “−1” for homozygous minor (aa). DNA markers with more than 10% missing data and a minor allele frequency smaller than 5% were filtered out. This filtering resulted in a final dataset of 2295 DNA markers after the imputation of missing data points with the missForest algorithm [20]. A principal component analysis with these DNA markers did not reveal a clear population structure in the studied set of winter wheat parental lines (Figure S1). The DNA marker profiles of all potential bi-parental crosses, i.e., the F₁ generation, were lastly inferred from the parental DNA marker profiles analogous to the routine procedures used for the genomic prediction of single cross-hybrid varieties [21]. This is feasible, as the F₁ generation of a cross between two parents is expected to inherit half of its genome from each of the parents.

It should firstly be noticed that the selection decisions reached by the plant breeder were largely based on superior progeny values [14,22] for a multitude of individual agronomic traits related to grain yield, baking quality, and disease resistance. Hence, the conducted selection decisions that were used for training the prediction models already integrated the information coming from these different genomic mating indices.

It should also be noticed that the underlying agronomic data for reaching the selection decisions were not included, since the aim of this study was to assess the quality of a recommender system in terms of congruency with the actual decisions by the plant breeder. Although these selection decisions by a breeder, i.e., a human, can be considered to be partly of a subjective nature, they can be still considered the “golden standard”, as there is currently no other option in plant variety development. The value of these decisions is thus given by the continuous and successful release of novel varieties, i.e., products, by the plant breeder and winter wheat breeding program in the study at hand. The objectively superior agronomic performance of the chosen crossing combinations was thus merely implicitly considered in this study.

2.2. Forward Prediction of the Breeder’s Choice of Crosses

Training and validation populations for fitting models to predict the breeder’s choice of crosses were built by 100 times repeatedly and randomly sampling 200 selected crosses, as well as 1200 non-selected crosses, from each of the individual years 2015–2020. Hence, merely subsets of all possible crossing combinations, i.e., partial diallels, were used in this case study in order to homogenize the sizes of the different training and validation populations. The individual years 2018, 2019, and 2020 served as validation populations, each with a size of 1400 crosses, whereas the three respective previous years 2015–2017, 2016–2018, and 2017–2019 served as training populations, each with a size of 4200 crosses. This allowed to test the prediction models under different environmental conditions. The selected crosses were labeled as $\mathrm{s}\mathrm{e}\mathrm{l}=1$ and the non-selected crosses as $\mathrm{s}\mathrm{e}\mathrm{l}=0$ in this forward prediction scheme, where the R package glmnet [23,24] was used for predicting the breeder’s choice of crosses with a binomial logistic regression based on

$$\widehat{\mathbf{u}}=\underset{\mathbf{u}}{\mathrm{argmin}}({‖\mathbf{y}-\mathbf{Z}\mathbf{u}‖}^2+\mathsf{\lambda }(\mathsf{\alpha }{‖\mathbf{u}‖}_1^{}+0.5\left(1-\mathsf{\alpha }\right){‖\mathbf{u}‖}_2^2))$$

(1)

where $\widehat{\mathbf{u}}$ is the vector of SNP DNA marker effects, $\mathbf{y}$ the vector with the above-described labeling, $\mathbf{Z}$ the SNP DNA marker matrix, and $\mathsf{\lambda }$ the penalty parameter that determines the amount of shrinkage. Elastic net (ENET) models were fitted by balancing the ${\mathrm{L}}_1$ and ${\mathrm{L}}_2$ regularization with the hyperparameter $\mathsf{\alpha }=0.5$, while this hyperparameter was set at $\mathsf{\alpha }=0$ for conducting a ridge regression (RIDGE) and to $\mathsf{\alpha }=1$ for obtaining the least absolute shrinkage and selection operator (LASSO). These regression-based models are commonly used in many plant breeding programs to obtain predictions for various agronomic traits based on genomic fingerprints [17], making them a familiar tool for plant breeders, and were thus used in the study at hand instead of more complex models like neural networks.

The predictions from each of the models were expressed in terms of the probability for each of the 1400 crosses in the respective validation populations to be part of the class of the selected crosses ($\mathrm{s}\mathrm{e}\mathrm{l}=1$). The 200 crosses in the validation population with the highest probability were subsequently labeled to fall into the mentioned class of selected crosses ($\mathrm{s}\mathrm{e}\mathrm{l}=1$) in order to reflect a recommender system in which the most promising crosses are suggested to a plant breeder. The performance of the models to predict the actual plant breeder’s choice was estimated by using the accuracy of this classification:

$$\mathrm{A}\mathrm{c}\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{y}={\displaystyle \frac{\mathrm{T}\mathrm{P}+\mathrm{T}\mathrm{N}}{\mathrm{T}\mathrm{P}+\mathrm{T}\mathrm{N}+\mathrm{F}\mathrm{P}+\mathrm{F}\mathrm{N}}}$$

(2)

where $\mathrm{T}\mathrm{P}$ is the number of true positives, $\mathrm{T}\mathrm{N}$ is the number of true negatives, $\mathrm{F}\mathrm{P}$ is the number of false positives, and $\mathrm{F}\mathrm{N}$ is the number of false negatives of classified crosses in the validation population of non-labeled cross combinations based on a confusion matrix. The recommendations made by the different prediction models were, in this way, compared between each other, as well as to a random choice of 200 crosses among all possible crossing combinations in the validation populations.

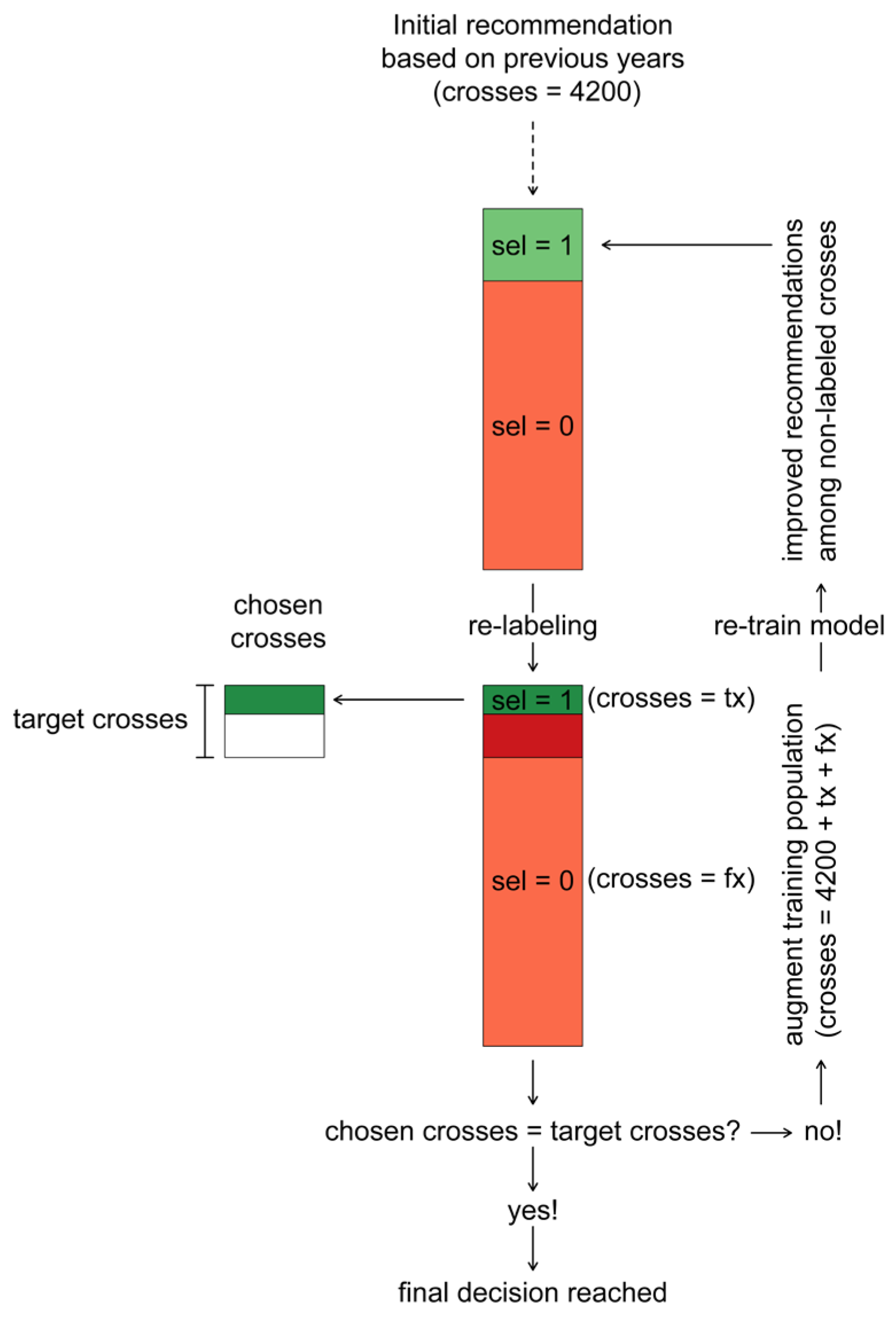
2.3. Integrating Model-Based Recommendations and Breeder’s Preferences

The merit of integrating the recommendations made by the different prediction models and the breeder’s preferences was assessed in a reciprocal fine-tuning algorithm, which aimed to synthesize artificial and human intelligence (Figure 2). The retrospective assessment used in this case study followed the same forward prediction scheme outlined above. The algorithm was initiated by obtaining recommendations for the validation populations in 2018, 2019, and 2020 based on model training with the respective three previous, years while aiming to reach a target number of ${\mathrm{x}}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}=200$ selected crosses after several iterations:

• In the first iteration $\left(\mathrm{i}=1\right),$ the ${\mathrm{r}\mathrm{x}}_{\mathrm{i}=1}={\mathrm{x}}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}=200$ crosses with the highest probability of selection were recommended and labeled to fall into the class of selected crosses $(\mathrm{s}\mathrm{e}\mathrm{l}=1)$ and all the other 1200 crosses to fall into the class of non-selected crosses $(\mathrm{s}\mathrm{e}\mathrm{l}=0)$.
• Based on the actual breeder’s choice among these recommended crosses, this labeling of $\mathrm{s}\mathrm{e}\mathrm{l}=1$ was retained for a number of ${\mathrm{t}\mathrm{x}}_{\mathrm{i}=1}$ crosses corresponding to the true positives, while it was changed to $\mathrm{s}\mathrm{e}\mathrm{l}=0$ for a number of ${\mathrm{f}\mathrm{x}}_{\mathrm{i}=1}$ crosses corresponding to the false positives.
• The ${\mathrm{t}\mathrm{x}}_{\mathrm{i}=1}$ true positive crosses were then added to the pool of chosen crosses ${\mathrm{x}}_{\mathrm{c}\mathrm{h}\mathrm{o}\mathrm{s}\mathrm{e}\mathrm{n}}$.
• After (re)-labeling the crosses in the validation population in this way, they were used to augment the initial training population of ${\mathrm{c}}_{\mathrm{i}=1}=4200$ crosses to a size of ${\mathrm{c}}_{\mathrm{i}=2}={\mathrm{c}}_{\mathrm{i}=1}+{\mathrm{t}\mathrm{x}}_{\mathrm{i}=1}+{\mathrm{f}\mathrm{x}}_{\mathrm{i}=1}$.
• Prediction models were then re-trained with this augmented training population to obtain recommendations for the remaining not yet labeled crosses.
• In the second iteration $\left(\mathrm{i}=2\right),$ the ${\mathrm{r}\mathrm{x}}_{\mathrm{i}=2}={\mathrm{x}}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}-{\mathrm{x}}_{\mathrm{c}\mathrm{h}\mathrm{o}\mathrm{s}\mathrm{e}\mathrm{n}}$ crosses with the highest probability of selection were recommended and labeled to fall into the class of selected crosses $(\mathrm{s}\mathrm{e}\mathrm{l}=1)$, reducing the number of recommended crosses to the remaining difference towards the target of ${\mathrm{x}}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}=200$ crosses.
• Steps 2–6 were repeated for $\mathrm{i}=20$ iterations or until the target number of crosses ${\mathrm{x}}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}=200$ was reached in the pool of chosen crosses ${\mathrm{x}}_{\mathrm{c}\mathrm{h}\mathrm{o}\mathrm{s}\mathrm{e}\mathrm{n}}.$

The performance of the elastic net, ridge regression, and the least absolute shrinkage and selection operator was finally compared to a random choice among the crossing combinations in terms of the accuracy (2), as well as the average percentage of totally labeled crosses, and found target crosses in each iteration across the 100 times repeated random sampling described in the previous section.

Figure 2. Schematic representation of the suggested dynamic reciprocal fine-tuning algorithm where the plant breeder actively provides feedback to the machine in the style of hybrid human–artificial intelligence. The initial recommendations of selected (light green) and non-selected crosses (light red) based on a training population of labeled 4200 crosses are screened by the breeder, who retains the labeling (dark green) or re-labels the recommended crosses (dark red). The initial training population of 4200 crosses is subsequently augmented by these labeled and re-labeled crosses for updating the predictions models and screening the next batch of recommended crosses among the set of not yet labeled crossing combinations. The recommendations in the subsequent iterations are likewise screened by the breeder, followed by further augmenting the training population. The pool of chosen crosses is furthermore enlarged in each iteration of the algorithm until reaching the target number of crosses in the pool of chosen crosses and thus the final selection decision.

Figure 2. Schematic representation of the suggested dynamic reciprocal fine-tuning algorithm where the plant breeder actively provides feedback to the machine in the style of hybrid human–artificial intelligence. The initial recommendations of selected (light green) and non-selected crosses (light red) based on a training population of labeled 4200 crosses are screened by the breeder, who retains the labeling (dark green) or re-labels the recommended crosses (dark red). The initial training population of 4200 crosses is subsequently augmented by these labeled and re-labeled crosses for updating the predictions models and screening the next batch of recommended crosses among the set of not yet labeled crossing combinations. The recommendations in the subsequent iterations are likewise screened by the breeder, followed by further augmenting the training population. The pool of chosen crosses is furthermore enlarged in each iteration of the algorithm until reaching the target number of crosses in the pool of chosen crosses and thus the final selection decision.

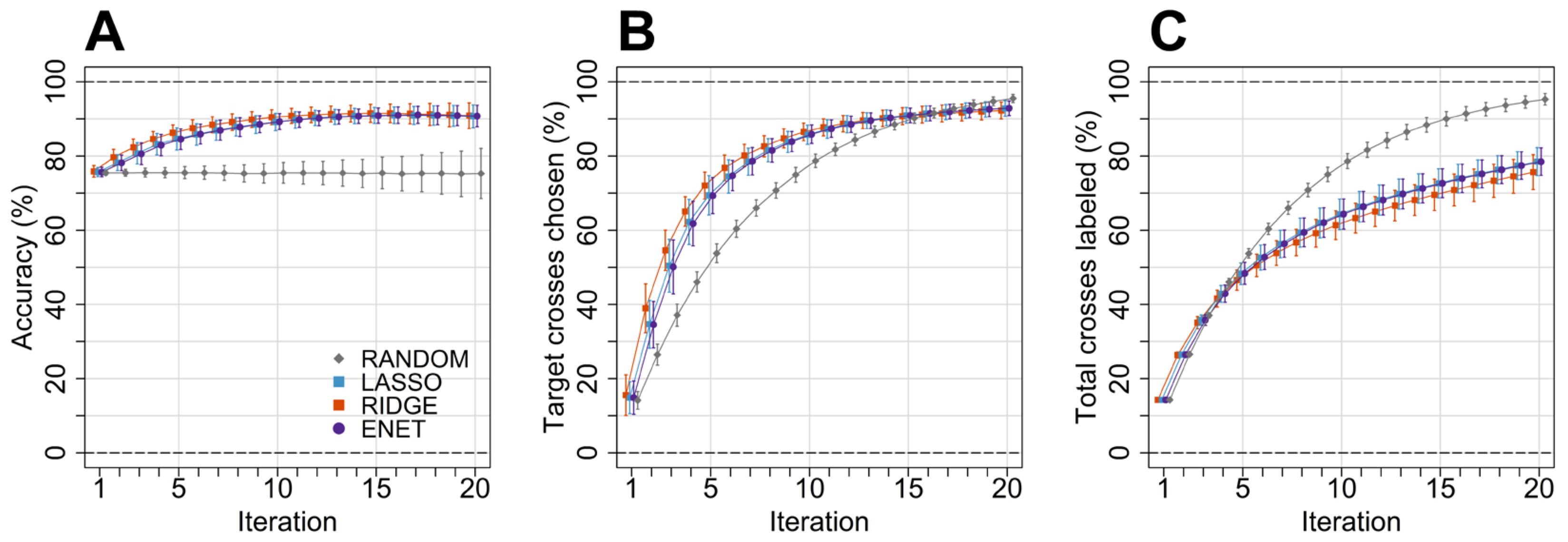
3. Results

The average accuracy in the forward prediction of the plant breeder’s choice of crosses was only marginally higher in comparison to a random choice of crosses (75.5%) when merely the previous three years were used for model training (Figure 3A). The highest accuracy for recommending crosses was, in this case, achieved with the ridge regression model (75.9%), followed by the elastic net (75.7%) and the least absolute shrinkage and selection operator (75.7%). This also resulted in a similar number of identified target crosses in the first iteration of the reciprocal fine-tuning algorithm (Figure 3B). The accuracy of the prediction models increased markedly up to 84.6% (iteration five) and even 90.5% (iteration ten) in subsequent iterations when the training population was gradually augmented by already labeled or re-labeled crosses in the validation population (Figure 3A).

This led moreover to a higher percentage of found target crosses by the recommender system, as, for example, the percentage of found target crosses by employing the ridge regression model (72%) strongly surpassed a non-systematic random choice of crosses (54%) after five iterations (Figure 3B). Noticeably, the percentage of found target crosses amounted to more than 80% after ten iterations when following the recommendations of the ridge regression model (Figure 3B), whereas only about 60% of the total number of crosses under consideration had to be labeled for this purpose (Figure 3C). Stopping the reciprocal fine-tuning algorithm after 20 iterations revealed that all tested methods of choosing crosses were able to identify, on average, more than 90% of the target crosses. However, when using the recommendations by the ridge regression model, only 71% of all crosses under consideration had to be labeled in order to reach this goal of almost finalizing the selection decisions. Following, on the other hand, the non-systematic approach of randomly choosing crosses, 94% of the crosses under consideration had to be screened for this purpose, i.e., basically the entire array of all possible crossing combinations (Figure 3C).

4. Discussion

Plant breeders aim to conduct the most promising crosses among a large number of possible combinations based on their experience, knowledge of the germplasm, or complementary performance of the parents. Although genomic cross predictions for agronomic traits represent a promising approach to inform breeders about the potential outcome of specific crosses [7,25,26], breeders oftentimes face the challenge of choosing among hundreds or thousands of possible crossing combinations for dozens of agronomic traits simultaneously. The usage of a recommender system might thus be a promising approach to reduce the time and effort that is required to fulfill this inherently difficult task and streamline the search and choice of crosses that appear to be most promising to a breeder. Testing such a recommender system in this case study by training regression-based prediction models with a wheat breeder’s decisions concerning the choice of crosses showed an accuracy that was merely marginally higher than a random choice of crosses, however, at least when the model training was solely conducted with past selection decision made in years preceding the present year in which selection decisions are pending. Since these recommendations were based on genome-wide distributed DNA markers, this result indicated a varying importance of genomic regions among the six different years in which the breeder made the selection decisions. Approximating the genetic correlations by the correlation of DNA marker effects showed an accordingly low relationship between the different years of r = −0.08–0.11 for the ridge regression models, r = −0.03–0.06 for elastic nets, and r = −0.03–0.08 for the least absolute shrinkage and selection operator (Figure S2). One possible reason could be the targeted diversification of the program by the breeder, who aimed to introduce new genetic variations every year and used merely a few common parental lines in multiple years for crossing.

The simple usage of such recommendations similar to predictions of crossing combinations for agronomic traits [27,28], where models are only fitted once to derive DNA marker effects, followed by deriving predictions for all possible crossing combinations, appeared accordingly to not be a promising approach. Hence, a more interactive approach aiming to integrate the model-based recommendations and breeder’s preferences in a specific crossing year with pending selection decisions was tested for its merit as a decision support tool. Such an approach would furthermore take into account that the target environment for which a breeder is selecting is changing over time, for example, with respect to temperature and precipitation [29], since the current and past climatic prerequisites are implicitly considered when choosing crossing combinations based on predictions made for agronomic traits supported by the model-based recommendations. The suggested dynamic recommender approach showed a marked increase in accuracy of the prediction models when the training population was stepwise augmented by crosses which label of “select” was kept or which were re-labeled to “non-select” based on the plant breeder’s preferences (Figure 2). It should be noticed, though, that the breeder used some parental lines more often as crossing partners, as they were successful varieties from the international seed market, whereas other parental lines were just used in few crossing combinations. The prediction models most likely benefitted from this circumstance due to a closer genetic relationship between the already labeled crosses in the training population and their as yet non-labeled half-sib crosses, which might partially explain this increase in accuracy after some iterations of the reciprocal fine-tuning scheme. Although a retrospective perspective was taken for this reciprocal fine-tuning scheme in the case study at hand, the results suggested that the practical application of this approach would allow to screen the available data, e.g., cross predictions for multiple agronomic traits, more systematically and efficiently without being overwhelmed by the vast amount information from all the selection candidates at once. Indeed, a reduction of about a quarter in the effort of finding the most promising crosses was achieved by integrating the model-based recommendations and breeder’s preferences in the mentioned reciprocal fine-tuning.

Alternatively to the dynamic approach where fewer crosses are being recommended with an increasing pool of chosen crosses after each iteration, a static approach can likewise be imagined where, in each iteration, a fixed number of crosses, e.g., 200, 100, 50, or only 20, are recommended by the prediction model. The advantage of such a static recommender approach lies especially early on in the process of decision-making, as, for example, in this approach, instead of 200, merely 20 crosses are recommended and have to be re-labeled by the breeder before updating prediction models. One reason is that it would probably be easier for a breeder, i.e., a human user, to screen a lower number of crosses in one iteration and provide feedback to the prediction models that are used for obtaining recommendations. However, more iterations of a reciprocal fine-tuning algorithm are necessary when following such a static approach with a low batch size of 20 recommended crosses in comparison to a dynamic approach in order to reach a selection decision with a high percentage of chosen target number of crosses (Figure S3). Implementing such a static or dynamic regression-based recommender system with SNP DNA marker data appears furthermore convenient, as the underlying tools are already commonly employed for the purpose of deriving genomic estimated breeding values or genomic cross-predictions in many plant breeding programs [7,25,30,31,32,33]. These relatively simple models furthermore possess a low computational burden and converge rather fast, which makes them readily applicable in the currently available standard computational resources, such as an Intel Core i9 machine with 3.3 GHz and 32 GB RAM, as used in this case study. For example, training the elastic net model with 4200 crosses took approximately 3 s, while upscaling the training population size to 8400 crosses required approximately 9 s for model fitting. Notwithstanding, the application of more sophisticated machine learning and deep learning models can likewise be considered, as such models have been used for recommending music and movies on entertainment platforms or job announcements on career network websites [34,35]. Nevertheless, these recommender systems were based on a much lower number of predictor variables like movie genres or music interpretations instead of thousands of DNA markers that are commonly used in plant breeding and genetic studies. Hence, testing, for example, neural network architectures like multi-layer perceptrons [36] or decision tree models [37] with the available data in this case study revealed that these more complex models are converging too slowly with standard resources like the above-mentioned single core machine, especially when aiming to implement a dynamic selection decision support tool like the suggested reciprocal fine-tuning algorithm (Figure 2). Nevertheless, given the availability of computational resources like a computational server with several dozen cores, the integration of model-based recommendations and a breeder’s current preferences by using the latest developments in artificial intelligence might also be interesting and lead to more versatile applications of recommender systems in plant breeding [38,39]. These approaches might be further extended by a finer separation into crossing recommendations made specially for certain target regions and production systems such as organic farming while additionally integrating more objective meta-data like quality classes into the prediction models.

5. Conclusions

This case study investigated the potential of using a recommender system based on DNA marker data to support breeders in the choice of crossing combinations. A retrospective perspective was thereby taken to investigate a reciprocal fine-tuning scheme based on actual selection decisions made by an experienced breeder. The results suggested that the effort to find the most interesting crossing combinations suiting a breeder’s preferences can be markedly reduced by a recommender system, even if it is based on relatively simple prediction models like ridge regression. For the purpose of a successful implementation, it appeared however to be pivotal to apply a scheme where the breeder actively provides feedback to the recommender system, with subsequent model updating in the style of hybrid human–artificial intelligence. Lastly, it should be noticed that the decisions made by an experienced winter wheat breeder were merely used as an example in this study, and although different breeders might come to different selection decisions, the outlined methodology might be used by any other plant breeder in order to obtain personalized recommendations for choosing crossing combinations.