Self-AdaptIve LOcal Relief Enhancer (SAILORE): A New Filter to Improve Local Relief Model Performances According to Local Topography
Abstract
:1. Introduction
2. Materials and Methods
2.1. Airbone Laser Scanning Data and Derived Dataset
2.2. Principle of the Local Relief Model and of the SAILORE Method
2.2.1. The LRM Principles
2.2.2. The SAILORE Approach
2.3. Description of the SAILORE Algorithm
- (a)
- Realization of a sliding average smoothing with a very large filter buffer (100 cells, or 50 m in our case, the DTM resolution being 0.5 m).
- (b)
- Calculation of the slope of this global relief, from which will be determined the size of the filtering buffer applied to each zone. The slope is calculated with the default procedure proposed in ArcGis®, with a neighborhood of 3 × 3 cells. It was calculated from the previously smoothed DTM, and thus gives us information on the steepest slope around each pixel, expressed in degrees. This local slope value must be related to the size of the filtering kernel. The simplest way to proceed would be to adapt the size of the filtering area proportionally to the slope. If we look at the slope distribution from a statistical perspective (Figure 5), we can see that it logically follows a Weibull distribution, with a high occurrence of low slopes and very few values beyond 45°.
- (c)
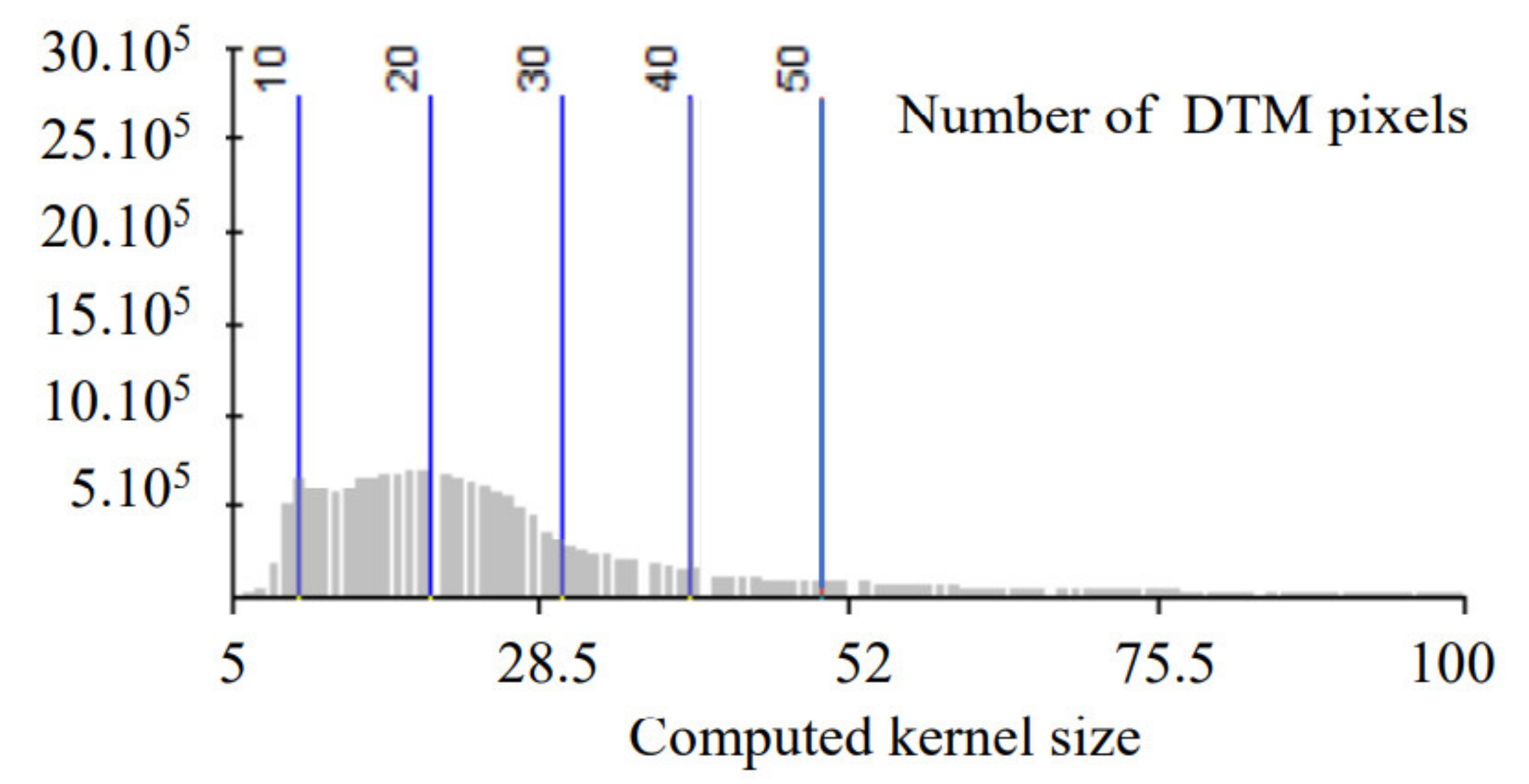
- Differential smoothing of the original DTM. For this phase, in order to reduce the complexity of the model, 5 thresholds were chosen (see Figure 4 and Figure 6). The maximum kernel size was set at 50 pixels (25 m), which corresponds to half of the kernel chosen in the first phase to restore the global relief of the site by removing all medium and high-frequency components. Values of 60 and 80 pixels, respectively, were tested, and they led to very similar results, which is logical because this kernel size will be used on very flat areas, for which the quality of the filtering was not very sensitive to the size of the kernel, the pixels having all a similar value. The interest of the 50-pixel kernel was then to be less demanding in terms of computing time. The minimum kernel size was set to 10 pixels (5m), which also corresponds to the values classically used to highlight micro-variations of the relief. Indeed, from a practical point of view, a sliding average filtering does not make sense if it is performed at the scale of a few pixels, knowing that for a structure to be identified, even by an expert eye, it must include several 10s of pixels. Finally, 3 intermediate filtering levels, corresponding, respectively, to 20, 30, and 40 pixels, were defined (10, 15, and 20 m, respectively). These values were chosen to allow for a gradual transition between minimum and maximum kernel sizes and to accommodate areas of intermediate slopes. In the absolute, we could consider 40 successive levels, allowing to go from the filtering on 10 pixels to the filtering on 50 pixels with a step of 1, but this configuration, which complicates the model, does not bring a significant gain in terms of resolution, as we could notice it in our tests. The step of 10 pixels was thus chosen as the best compromise between the resolution obtained and the necessary computing time. It is important to note that the choice of these thresholds was independent of the calculation principle of our Self-AdaptIve LOcal Relief Enhancer and that they can be adapted if particular study contexts require it.
- (d)
- Finally, each pixel is associated with the filtering result of the threshold to which it corresponds, and the global filtered DTM is thus generated, pixel by pixel and then subtracted from the initial DTM, to provide the final visualization (Figure 4).
2.4. Testing the Performance of the SAILORE Approach
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Crutchley, S.; Crow, P. The Light Fantastic: Using Aiborne Lidar in Archaeological Survey; English Heritage: Swindon, UK, 2009. [Google Scholar]
- Masini, N.; Coluzzi, R.; Lasaponara, R. On the Airborne Lidar Contribution in Archaeology: From Site Identification to Landscape Investigation; Wang, C.-C., Ed.; Laser Scanning, Theory and Applications; InTech Online Publishers: Rijeka, Croatia, 2011. [Google Scholar]
- Lozić, E.; Štular, B. Documentation of Archaeology-Specific Workflow for Airborne LiDAR Data Processing. Geosciences 2021, 11, 26. [Google Scholar] [CrossRef]
- Opitz, R.S.; Cowley, D.C. (Eds.) Interpreting Archaeological Topography: Airborne Laser Scanning, 3D Data and Ground Observation; Occasional Publication of the Aerial Archaeology Research Group; Oxbow Books: Oxford, UK, 2013. [Google Scholar]
- Doneus, M.; Briese, C. Airborne Laser Scanning in forested areas–Potential and limitations of an archaeological prospection technique. In Remote Sensing for Archaeological Heritage Management; Cowley, D.C., Ed.; Europae Archaeologia Consilium (EAC): Brussels, Belgium, 2011; pp. 59–76. [Google Scholar]
- Siart, C.; Forbriger, M.; Bubenzer, O. Digital Geoarchaeology: New Techniques for Interdisciplinary Human-Environmental Research; Springer: Cham, Switzerland, 2018. [Google Scholar]
- De Matos-Machado, R.; Toumazet, J.P.; Bergès, J.C.; Amat, J.P.; Arnaud-Fassetta, G.; Bétard, F.; Jacquemot, S. War landform mapping and classification on the Verdun battlefield (France) using airborne LiDAR and multivariate analysis. Earth Surf. Process. Landf. 2019, 44, 1430–1448. [Google Scholar] [CrossRef]
- Masini, N.; Gizzi, F.T.; Biscione, M.; Fundone, V.; Sedile, M.; Sileo, M.; Lasaponara, R. Medieval archaeology under the canopy with lidar. the (re) discovery of a medieval fortified settlement in southern Italy. Remote Sens. 2018, 10, 1598. [Google Scholar] [CrossRef] [Green Version]
- Jones, A.F.; Brewer, P.A.; Johnstone, E.; Macklin, M.G. High-Resolution Interpretative Geomorphological Mapping of River Valley Environments Using Airborne LiDAR Data. Earth Surf. Process. Landf. 2007, 32, 1574–1592. [Google Scholar] [CrossRef]
- Migoń, P.; Jancewicz, K.; Kasprzak, M. Inherited periglacial geomorphology of a basalt hill in the Sudetes, Central Europe: Insights from LiDAR-aided landform mapping. Permafr. Periglac. Process. 2020, 31, 587–597. [Google Scholar] [CrossRef]
- González-Díez, A.; Barreda-Argüeso, J.A.; Rodríguez-Rodríguez, L.; Fernández-Lozano, J. The use of filters based on the Fast Fourier Transform applied to DEMs for the objective mapping of karstic features. Geomorphology 2021, 385, 107724. [Google Scholar] [CrossRef]
- Lasaponara, R.; Masini, N. Beyond modern landscape features: New insights in the archaeological area of Tiwanaku in Bolivia from satellite data. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 464–471. [Google Scholar] [CrossRef]
- Vosselman, G. Slope based filtering of laser altimetry data. Int. Arch. Photogramm. Remote Sens. 2000, 33, 935–942. [Google Scholar]
- Zakšek, K.; Pfeifer, N. An Improved Morphological Filter for Selecting Relief Points from a LIDAR Point Cloud in Steep Areas with Dense Vegetation; Technical Report; Institute of Anthropological and Spatial Studies: Ljubljana, Solvenia, 2006; Available online: https://iaps.zrc-sazu.si/sites/default/files/Zaksek_Pfeifer_ImprMF.pdf (accessed on 1 November 2021).
- McCoy, M.D.; Asner, G.P.; Graves, M.W. Airborne lidar survey of irrigated agricultural landscapes: An application of the slope contrast method. J. Archaeol. Sci. 2011, 38, 2141–2154. [Google Scholar] [CrossRef]
- Hesse, R. LiDAR-derived Local Relief Models—A new tool for archaeological prospection. Archaeol. Prospect. 2010, 17, 67–72. [Google Scholar] [CrossRef]
- Moyes, H.; Montgomery, S. Locating cave entrances using lidar-derived local relief modeling. Geosciences 2019, 9, 98. [Google Scholar] [CrossRef] [Green Version]
- Kokalj, Ž.; Zakšek, K.; Oštir, K. Application of sky-view factor for the visualisation of historic landscape features in LiDAR-derived relief models. Antiquity 2011, 85, 263–273. [Google Scholar] [CrossRef]
- Devereux, B.J.; Amable, G.S.; Crow, P. Visualisation of LiDAR terrain models for archaeological feature detection. Antiquity 2008, 82, 470–479. [Google Scholar] [CrossRef]
- Bennett, R.; Welham, K.; Hill, R.A.; Ford, A. A Comparison of Visualization Techniques for Models Created from Airborne Laser Scanned Data. Archaeol. Prospect. 2012, 19, 41–48. [Google Scholar] [CrossRef]
- Doneus, M. Openness as vizualisation technique for interpretative mapping of airborne LiDAR derived Digital Terrain Models. Remote Sens. 2013, 5, 6427–6442. [Google Scholar] [CrossRef] [Green Version]
- Stular, B.; Kokalj, Z.; Ostir, K.; Nuninger, L. Visualization of Lidar-Derived Relief Models for Detection of Archaeological Features. J. Archaeol. Sci. 2012, 39, 3354–3360. [Google Scholar] [CrossRef]
- Mayoral, A.; Toumazet, J.-P.; Simon, F.-X.; Vautier, F.; Peiry, J.-L. The Highest Gradient Model: A New Method for Analytical Assessment of the Efficiency of LiDAR-Derived Visualization Techniques for Landform Detection and Mapping. Remote Sens 2017, 9, 120. [Google Scholar] [CrossRef] [Green Version]
- Simon, F.X.; Pascual, A.M.; Vautier, F.; Miras, Y. Premiers résultats des volets géoarchéologie et géomatique du programme interdisciplinaire AYPONA (Paysages et visages d’une agglomération clermontoise: Approche intégrée et diachronique de l’occupation de l’oppidum de Corent, Auvergne, France). In Proceedings of the Journée Régionale de L’archéologie Auvergne, Clermont-Ferrand, France, 17 May 2015. [Google Scholar]
- Mayoral, A. Analyse de Sensibilité Aux Forçages Anthropo-Climatiques des Paysages Protohistoriques et Antiques du Plateau Volcanique de Corent (Auvergne) et de Ses Marges par une Approche Géoarchéologique Pluri-Indicateurs; Université Clermont Auvergne: Clermont-Ferrand, France, 2018. [Google Scholar]
- Poux, M. Corent, Voyage au Coeur d’une Ville Gauloise; Editions Errance: Paris, France, 2012. [Google Scholar]
- Poux, M.; Milcent, P.-Y.; Pranyies, A.; Mader, S.; Laurenson, R.; Courtot, A.; Dubreu, N.; Brossard, C.; Chorin, A.; Evrard, M.; et al. Corent, Fouille Pluriannuelle 2014–2016; Rapport Final d’Opération; Université de Lyon: Lyon, France, 2018; Available online: http://www.luern.fr/rapports/2015.pdf (accessed on 9 September 2021).
- LiDAR Litemapper 7800 Technical Documentation. Available online: https://www.igi-systems.com/files/IGI/Brochures/LiteMapper/LiteMapper_spec.pdf (accessed on 1 November 2021).
- Evans, J.S.; Hudak, A.T. A multiscale curvature algorithm for classifying discrete return LiDAR in forested environments. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1029–1038. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toumazet, J.-P.; Simon, F.-X.; Mayoral, A. Self-AdaptIve LOcal Relief Enhancer (SAILORE): A New Filter to Improve Local Relief Model Performances According to Local Topography. Geomatics 2021, 1, 450-463. https://doi.org/10.3390/geomatics1040026
Toumazet J-P, Simon F-X, Mayoral A. Self-AdaptIve LOcal Relief Enhancer (SAILORE): A New Filter to Improve Local Relief Model Performances According to Local Topography. Geomatics. 2021; 1(4):450-463. https://doi.org/10.3390/geomatics1040026
Chicago/Turabian StyleToumazet, Jean-Pierre, François-Xavier Simon, and Alfredo Mayoral. 2021. "Self-AdaptIve LOcal Relief Enhancer (SAILORE): A New Filter to Improve Local Relief Model Performances According to Local Topography" Geomatics 1, no. 4: 450-463. https://doi.org/10.3390/geomatics1040026
APA StyleToumazet, J.-P., Simon, F.-X., & Mayoral, A. (2021). Self-AdaptIve LOcal Relief Enhancer (SAILORE): A New Filter to Improve Local Relief Model Performances According to Local Topography. Geomatics, 1(4), 450-463. https://doi.org/10.3390/geomatics1040026





