Abstract
Thermophysiological comfort is a crucial aspect of human life, contributing to health and work performance. The current paper aims to enhance the understanding of current research, progress, and remaining challenges regarding clothing thermophysiological comfort from a textile science perspective. It provides a comprehensive review of several facets of clothing thermophysiological comfort, focusing on the history of thermophysiological comfort prediction models, heat and moisture transfer mechanisms in the skin–clothing–environment system, controlling factors of thermophysiological comfort, textile materials for superior thermophysiological comfort, and thermal comfort assessment techniques. The paper shows that previously developed thermophysiological comfort models were mainly based on the human thermoregulation process. However, the effect of the air gap size between the human skin and the cloth layer, i.e., the microclimate, on the heat and moisture transfer in the skin–clothing–environment system has been largely overlooked. In addition, thermophysiological comfort models of skin–clothing–environment systems generally only considered dry thermal resistance and evaporative resistance, yet many other fabric properties have effects on human thermophysiological comfort. Potential future directions are identified to fill some of the current gaps. A conceptual model of clothing comfort to contribute to a better understanding of thermophysiological comfort is also proposed.
1. Introduction
The term “thermophysiological comfort” is often used in textile science research to define the ability of a garment to maintain the thermal balance of a human body under various environmental conditions [1]. Human thermophysiological comfort is associated with the human body’s physiological characteristics and processes, clothing heat and moisture transport properties, and environmental conditions [2]. The air gap distance between the human skin and the cloth layer (referred to as the microclimate) is one of the dominant factors affecting thermophysiological comfort [3,4]. Parsons [1] identified seven factors that contribute to human thermophysiological comfort: metabolic heat production, adaptive responses (e.g., thermoregulation process), clothing insulation, air temperature, relative humidity, air velocity, and radiant temperature. It is important to note that the term “thermal comfort” is often used interchangeably with thermophysiological comfort in scholarly works, as the thermal properties of fabrics affect the human thermophysiological process [2].
Attaining thermophysiological comfort is essential to maintain the well-being of the human body [1,2]. Poor heat and moisture transfer properties of fabrics cause an increase in core body temperature in warm conditions, which can lead to heat strain [5,6,7]. The possible physiological responses associated with heat strain can be divided into three stages [8]: heat loss, temperature re-increase, and cardiac system failure. In ideal conditions, the amount of metabolic heat produced by the human body equals the amount of heat lost from the human body to the environment. This loss of heat may become lower than metabolic heat production, e.g., due to poor heat and moisture management properties of the clothing ensemble. As a result, an increase in core temperature occurs in the human body system. The first stage of heat stress causes vasodilation (i.e., the body expands the diameter of the blood vessels to increase the blood flow) and sweating in response to the rising core body temperature. This vasodilation and sweat evaporation foster initial heat loss. In the next stage, vital organs receive insufficient blood flow and the fatigue of the sweat glands generates less perspiration. This causes an increase in core body temperature, leading to heatstroke in the third stage.
A comparison of the level of heat strain generated by clothing made of a selectively permeable membrane (SPM) and a textile fabric with a similar level of heat and water vapor resistance evidenced a greater increase in core body temperature and heart rate over time with the SPM-based clothing, in addition to a higher amount of sweat production and accumulation in the clothing [9]. This was attributed to the poor air permeability and lower ventilation with the SPM-based clothing. In another study, Holmer [10] showed that the water vapor pressure in the microclimate increased more over time while wearing an impermeable overall compared to a microporous overall. The increase in the heart rate, rectal temperature, and skin temperature measured was attributed to the limited permeability of the fabric material under various ambient temperatures.
On the other hand, cold strain is caused by exposure to low temperatures while wearing garments with poor clothing insulation [11]. Even though physical activity increases metabolic heat generation, it might not be sufficient to mitigate the effect of cold weather conditions in the long run [12]. The human body responds to cold mainly in four ways: (a) vasoconstriction (i.e., reduction in the diameter of blood vessels, which reduces the blood flow to extremities and minimizes heat loss) [13], (b) shivering (i.e., systematic muscle contraction to increase metabolic heat production) [14], (c) non-shivering thermogenesis (i.e., heat production by the metabolism of brown fat) [15], and (d) piloerection [16]. Pisacane et al. [17] mentioned that long-term cold exposure can cause muscle hardening, heart fibrillation, unconsciousness, and cardiac and respiratory failure.
The study of thermophysiological comfort involves the use of thermophysiological comfort models, human subject assessment, and investigation of clothing heat and moisture transport properties [1]. Several models and indices have been developed to predict human thermophysiological comfort [18]. Among these, Fanger’s model [19], Gagge’s model [20], and Stolwijk’s model [21] are widely used in the construction, automotive, medical, and aerospace industries [22]. More sophisticated models have built upon these early thermophysiological comfort models to predict the local skin and core body temperature under various exposure conditions [23]. Models derived from Stolwijk’s model are Fiala’s model [24], UC Berkeley’s model [25], Tanabe’s model [26], and ThermoSEM [27].
Fanger’s and Fiala’s models are most frequently used by clothing comfort researchers because they can be combined with standard test methods of fabric/clothing to determine human thermophysiological comfort [1,18,28,29]. Fanger’s model is considered the first comprehensive model for thermophysiological comfort prediction [23]. It is based on a heat balance equation to estimate the net heat loss or gain in a skin–cloth–environment system (Section 2.1). Fanger’s model was adopted by the ASHRAE 55 [30] and ISO 7730 [31] standards to assess the thermophysiological comfort of the human body. On the other hand, Fiala’s model is based on Pennes’s bioheat equation, which includes heat conduction within nodes/tissue layers, metabolic heat generation, and heat transfer due to arterial blood flow [24]. Fiala’s model can be coupled with ISO 18640-1 [32] when determining the clothing thermophysiological comfort using a sweating cylindrical torso [29].
The existing problem with these thermophysiological comfort prediction models is that they include only two fabric properties: dry thermal and evaporative resistance [18,28]. However, other fabric properties may also affect human thermophysiological comfort, such as moisture wicking, drying rate, wet conduction, and heat of sorption [33,34,35,36]. Noman and Petru [37] indicated that the water vapor transmission rate, air permeability, moisture wicking, and thermal effusivity are the main thermophysiological comfort properties of fabrics. Hes [38] constructed a comfort index that listed nine different fabric properties that affect overall comfort perception. These fabric properties are dry thermal resistance, evaporative resistance, moisture absorptivity, dry thermal absorptivity, wet friction coefficient, dry friction coefficient, bending rigidity, shearing rigidity, and compression work.
Another aspect of thermophysiological comfort is the assessment of the human body’s psychophysical (i.e., subjective) and physiological (i.e., objective) responses under various exposure conditions [39]. Subjective assessment requires human subjects to determine their comfort level using a rating scale, for example, a 7-point Likert scale [1]. Likert scales quantify comfort perception, functional effectiveness, preference, acceptance, and tolerance of a particular clothing system [40]. On the other hand, objective assessment measures human physiological responses, such as core body temperature, skin temperature, heart rate, and sweat loss [41]. These subjective and objective responses can then be associated with the heat and moisture management properties of fabrics (also referred to as the thermal comfort properties of fabrics) to construct the thermophysiological comfort model. Some common standard test methods for assessing the heat and moisture management properties of fabrics are dry thermal and evaporative resistance [42], water vapor transmission rate [43], liquid moisture management test [44], air permeability [45], and thermal effusivity [46].
The human thermophysiological comfort models thus depend on a wide variety of interconnected factors, which makes it difficult to predict the precise level of thermal comfort of an individual under a given condition [28]. The next sections describe several aspects of thermophysiological comfort modeling, including the conceptual ground for model development, the physics of heat and moisture transfer in the skin–clothing–environment system, factors controlling thermophysiological comfort, and assessment techniques.
2. Thermophysiological Comfort Prediction Models
Thermophysiological comfort models can be classified into two main categories depending on the number of segments representing the body parts [18]: (a) single-segment and (b) multi-segment. The single-segment predictive model considers the entire human body as a whole. In contrast, the multi-segment model considers different body parts separately. Another way to classify thermophysiological comfort models is based on the number of concentric layers: (a) single-node, (b) two-node, and (b) multi-node. A single-node model only considers the core to represent the cross-section of a human body, whereas a two-node model considers the core and skin to represent the cross-section of the human body. In contrast, the multi-node model considers the core, muscles, fat, and skin layers separately. Figure 1 shows the chronology of the development of the different types of thermophysiological comfort prediction models.
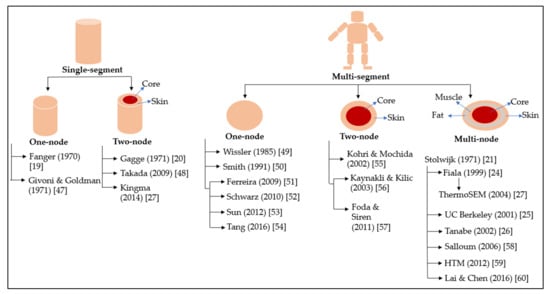
Figure 1.
Chronology of the development of thermophysiological comfort models [19,20,21,24,25,26,27,47,48,49,50,51,52,53,54,55,56,57,58,59,60] (inspired by [18]).
Thermophysiological comfort prediction models are mainly constructed using physiological variables (e.g., heat and sweat generation within the human body, skin temperature, and core body temperature), clothing insulation properties, and environmental conditions [24,31,61]. For instance, Kang et al. [62] developed an advanced thermophysiological comfort model to predict the human core body and skin temperature. The model employed a three-dimensional approach and divided the human body into 15 different segments, mimicking the cylindrical geometry of the body parts. First, it determined the heat transfer inside a human body, which included basal metabolism, shivering, and external work as heat generation sources. The study calculated the thermal conductivity of the body segments, including when vasodilation and vasoconstriction occur, depending on the skin temperature. Next, the model determined the amount of convective and radiative heat transfer from the human body to the environment, assuming the human skin and cloth as a single layer (i.e., no air gap between the skin and clothing). The model also included evaporative heat dissipation (i.e., both for insensible and sensible sweating) to estimate the total evaporative heat loss from the human skin.
Fanger’s thermophysiological comfort prediction model consists of three steps [1]: (a) determination of the thermal stress level using the predicted mean vote (PMV) and predicted percentage of dissatisfied (PPD), (b) calculation of the equivalent temperature, and (c) evaluation of thermal comfort based on subjective assessment. The PMV and PPV indices are estimated from the basal metabolism (M), heat produced by work (W), clothing surface temperature (tcl), clothing insulation (Icl), clothing cover factor (fcl), air temperature (Ta), relative humidity of air (RHa), mean radiant temperature (Tmr), and convective heat transfer coefficient (hr). The PMV values range from −3 to +3, mimicking a 7-point Likert scale, where −3 represents very cold, −2 represents cold, −1 represents slightly cold, 0 represents neutral, 1 represents slightly warm, 2 represents warm, and 3 represents very warm. When the PMV is −0.5 to +0.5, the PPD is 10%. This indicates that 10% of the participants are in discomfort. It is to be noted that discrepancies have been documented between PMV results and thermal sensation from wear trials [63]. They are possibly due to issues with the determination of tcl.
Fiala et al. [24,64] developed a thermophysiological comfort prediction model for different environmental conditions considering the passive and active thermoregulatory systems. The passive system involves the functions of human body attributes (e.g., bone, muscle, fat, and skin), such as the basal metabolism, arterial blood flow, and metabolic heat. On the other hand, the active system includes human thermoregulatory responses like vasodilation, vasoconstriction, shivering, and sweating. The passive model was developed in three different steps: (a) modeling the human body, (b) modeling the heat transfer between the nodes or periphery, and (c) numerical simulation. First, the human body was divided into 15 segments and 7 tissue layers or nodes. Next, the heat transfer between the nodes was derived from Pennes’s bioheat equation. This step also includes heat exchange between the human body and the environment through clothing. In the third step, numerical simulations were performed to predict the tissue temperature. Fiala et al. [64] combined active thermoregulatory responses with the passive model [24] to construct an overall thermophysiological comfort prediction model. The simulation started by exposing the passive system to predefined boundary conditions when no active system was running. The active regulatory responses that had been obtained experimentally were then added to the model. The results of numerical simulations using the model were in good agreement with experimentally obtained results.
The thermophysiological comfort prediction models described above did not consider the effect of the air gap thickness between the human skin and the cloth, which is called the microclimate. However, studies investigating the effect of this air gap thickness on heat and moisture transport phenomena in the skin–cloth–environment system found that it significantly affects the amount of heat and moisture transfer from the human body to the environment through the cloth layer, which eventually contributes to the thermal balance of the human body [4,65]. Ding et al. [3] showed that an air gap distance greater than 12 mm between the sweating-guarded hot plate (i.e., simulating the human skin) and the clothing layer allowed the occurrence of natural convection in the microclimate. In contrast, when the air gap between the sweating-guarded hot plate and the cloth layer was lower than 12 mm, the heat transfer mechanism in the microclimate only involved conduction and radiation. Joshi [28] developed a thermophysiological comfort prediction model that included the effect of the air gap on heat and moisture transfer in a skin–clothing–environment system. Awais et al. [66] described a modeling and simulation procedure to predict the thermophysiological comfort of clothing ensembles for various values of the air gap. First, the physical, mechanical, and thermal properties of the fabrics were added to the simulation software Modaris (V8) for creating realistic clothing simulations. Next, human body scanned data were added to the Modaris software for conducting the fit simulation. Finally, these data were imported in finite-element software for thermophysiological comfort simulation of the clothing ensemble. The thermophysiological comfort simulations were conducted for different physical activities and air gap distributions.
2.1. Heat Balance Equation
Another aspect of thermophysiological comfort prediction models is the heat balance in the human body. Fanger [61] stated that thermophysiological comfort can be achieved by balancing the amount of heat produced within the human body and the amount of heat transferred from the human body to the environment through clothing. The heat balance equation was described as follows [1]:
H − Ed − Esw − Eres − Cres = K = R + C
Here, H is the internal heat production within the human body, Ed is the heat loss due to water-vapor diffusion through the skin, Esw is the heat loss due to sweat evaporation, Eres is the latent respiratory heat loss, Cres is the dry respiratory heat loss, K is the net heat loss by clothing, R is the radiative heat loss from the outer cloth surface, and C is the convective heat loss from the outer cloth surface. Fanger estimated the internal heat production by subtracting the mechanical energy spent in work (W) from the total metabolic heat production (M) [1]. Thus, H = M − W. However, W is considered to be 0 in most cases. Therefore, the expression can be written as H = M. Later, they developed another expression to estimate the metabolic heat production based on the human body surface area. The surface area of the human body (AD) was estimated using the Du Bois equation, where AD = 0.202 (weight)0.425 × (height)0.725. Fanger created a database of metabolic heat production for various physical activities in order to estimate the heat balance of the human body. For instance, the normalized metabolic rate estimated for seated people was 58.15 Wm−2. It gave a normalized metabolic rate of 116.3 W for a person with a body surface area of 2 m2.
Water vapor diffusion occurs through the skin due to the difference in vapor pressure at the interior skin and the outer air layer, which causes heat loss [1]. Mathematically, the heat loss due to water vapor diffusion through the skin (Ed) is related to the vapor diffusion coefficient (d) of the skin, the latent heat of vaporization (λ) at the skin temperature (tsk), and the difference between the interior skin vapor pressure (which is always wet) and the air layer vapor pressure (∆P) according to the following equation:
Ed = d · λ · ∆P
Heat loss also occurs at the outer surface of the skin due to the evaporation of sweat [1]. During extreme physical activity, the sweat rate increases. Research has shown that the evaporative heat loss (Esw.req) required to maintain thermophysiological comfort increases with increasing physical activity. Simultaneously, the required skin temperature (tsk.req) decreases with an increase in intensity of physical activity.
Heat loss from the human body also occurs due to breathing [1]. When a person inhales moist air from the ambient air, it travels through the lungs and respiratory tract. The temperatures of the lungs and respiratory tract are usually higher than the ambient temperature, which increases the temperature of the inhaled moist air. There might also be some heat gain due to the inhalation process itself, as the inhaled moisture vapor is condensed inside the body. On the other hand, when a person exhales, the moist air exhaled carries more heat and vapor than the inhaled moist air, which causes both evaporative and dry heat loss. In this case, heat transfer occurs via evaporation and convection. The evaporative heat loss depends on the difference between the water vapor concentrations in exhaled air (Dex) and inhaled air (Din) [1]. Conversely, convective heat transfer depends on the temperature difference between exhaled air (tex) and inhaled air (tin).
In the heat balance equation (Equation (1)), K refers to the net heat exchange between the human body and the environment through the cloth layer [1]. The estimation of K is complex, as many other factors are involved in this heat exchange process, such as the thickness of the air gap between the skin and the cloth, clothing contact area, the presence of uncovered body parts, and human body movement. The heat transfer mechanism in the skin–cloth–environment may involve conduction, convection, radiation, and evaporative cooling [4]. Fanger proposed that K can be estimated from the temperature difference between the skin (tsk) and the air layer adjacent to the outer fabric surface (ta) divided by the fabric’s dry thermal resistance (Rcl) [1]. The unit of dry thermal resistance is m2KW−1. This unit is generally used for the thermal resistance of fabrics. Gagge et al. [67] devised another unit, clo, for thermal resistance (called thermal insulation, Icl). The clo unit is generally used for the overall thermal resistance of the clothing based on how much area of the body is covered by the cloth [1]. The expression to estimate the heat transfer through the cloth is K = (tsk − ta)/Rcl and 1 clo = 0.155 m2KW−1. Thus, K= (tsk − ta)/0.155Icl. It is important to note that the dry thermal resistance value obtained from the sweating-guarded hot plate/manikin/torso corresponds to the total thermal resistance (Rct) of the fabric and the air layer adjacent to the outer fabric surface. Thus, Rct = Rcf + Rc0, with Rcf the thermal resistance of the fabric and Rc0 the thermal resistance of the air layer adjacent to the outer fabric surface. In the case of thermal insulation, the expression can be written as Icl = IT − Ia/fcl. Here, Icl refers to the clothing thermal resistance, IT is the total thermal resistance, Ia is the thermal resistance of the air layer, and fcl (=Acl/Abody) is the clothing cover factor. Ia is divided by fcl because the thermal insulation of the cloth is determined based on how much area of the body is covered by the cloth. Here, Acl is the surface area of the body that is covered by the cloth and Abody is the whole-body surface area.
The outer surface of clothing loses heat to the environment through radiation and convection [1,68]. The radiative heat transfer depends on the difference in the fourth power of difference in temperature between the two surfaces. The heat loss by convection between the clothing’s outer surface and the environment can be categorized into (a) free or natural convection (when no external force is working on heat flow) and (b) forced convection (when an external force causes heat flow) [1]. An example of natural convection is when light warm air is substituted by heavier chilled air due to gravity acting on the air. On the other hand, forced convection may occur due to human body movement, heavy winds, etc. Fanger expressed the heat balance equation (Equation (1)) in terms of the PMV and PPD indices to predict the human thermophysiological comfort level (Figure 2).
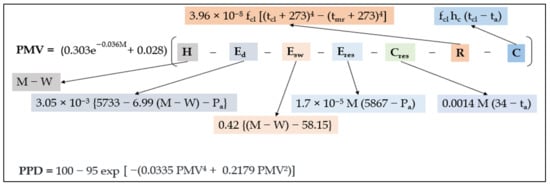
Figure 2.
PMV and PPD equations based on the heat balance equation [1,69]. The different parameters are described in Section 2.
2.2. Thermoregulation in a Human Body
Human body thermophysiological comfort arises from the thermoregulation process [2]. Thermoregulation causes the generation of heat and sweat to maintain a constant core body temperature of 37.0 ± 0.5 °C under various exposure conditions [8]. The thermoregulation process is complex and depends on various physiological and environmental parameters. The main thermoregulation-controlling point of the human body is the hypothalamus [2]. It is a gland in the brain that receives signals from (a) peripheral nerves and (b) blood particles (due to their movement in the hypothalamus area) [8]. The peripheral nerves collect signals from warm and cold receptors of the cutaneous sensory layer. The warm and cold receptors can sense temperature changes as little as 0.007 °C and 0.012 °C, respectively.
When the human body is exposed to cold weather conditions, it begins to lose heat [2]. Concurrently, the hypothalamus in the brain receives signals about this temperature drop and attempts to counterbalance the effect of cold weather conditions by implementing vasoconstriction, shivering, and piloerection. The vasoconstriction process compresses the blood vessels and decreases blood flow, which lowers the amount of heat loss from the body. The shivering process generates heat in the body. Piloerection creates a thin insulating layer of air around the human skin, which helps to prevent the loss of body heat [16]. Unfortunately, all these processes cannot counter the effect of cold weather conditions forever if appropriate clothing ensembles are not worn. Thus, the human body’s core temperature might fall below the normal range, which causes hypothermia [70].
When the human body is exposed to hot weather conditions, the core body temperature starts to rise [2]. At the same time, the hypothalamus in the human brain receives signals about the temperature increase and attempts to counterbalance the effect of hot weather conditions by vasodilation and sweating. The vasodilation process increases the circumference of the blood vessels, which augments blood flow. Increased blood flow enhances heat loss to the environment, which helps lower the core temperature. In addition, the human body starts sweating. This sweat eventually evaporates into the environment and causes heat loss (known as evaporative cooling) [71]. When the thermoregulation processes (e.g., sweating and vasodilation) are unable to lower the core body temperature as needed, heat stress occurs.
3. Physics of Heat and Moisture Transfer in the Skin–Clothing–Environment System
3.1. Heat and Sweat Generation in the Human Body
The human body generates heat and sweat in response to the clothing worn, exposure to the environment, and level of physical activity [28]. Heat generation in the human body involves basal metabolism, shivering, and metabolic heat due to physical activity [24,62]. The total heat generation within human body parts or tissue layers can be estimated from Equation (3) in Table 1. Equation (3) assumes that there is a temperature variation along the radial directions of the tissue layer for the estimation of conductive heat transfer [24]. No angular heat flow within the tissues is considered. Even though there might be temperature variations in the angular direction, the total amount of angular heat transfer is considered to be negligible compared to the radial direction.

Table 1.
Heat and sweat generation within the human body.
The thermal conductivity (K) of tissue in a local body part takes the highest value (Kmax) of 2.8 Wm−1K−1 when TSkin ≥ 37 °C during the vasodilation process [62]. In contrast, the minimum thermal conductivity (Kmin) is achieved when the skin temperature falls below 27.9 °C. Different body parts have different values of Kmin [4]. Finally, when TSkin is between 27.9 and 37 °C, the thermal conductivity (K) of the tissue of a certain body part can be estimated from Equation (4) (Table 1). In this equation, the thermal conductivity of the tissue layer in a particular body segment is assumed to have a linear correlation with the skin temperature of that body segment [62].
The basal metabolic heat can be estimated from previous studies, such as Kang et al.’s [62] work, where they provided tables that contain the value of total basal metabolic heat (Qtbm) of different body parts. Equation (5) can be used to compute the local basal metabolic heat (Table 1).
Like the thermal conductivity of the tissue layer, heat generation by shivering (QSh) can be estimated from the body segment skin temperature [62]. When TSkin ≥ 36.4 °C, QSh is 0 Wm−3. Maximum shivering occurs when TSkin ≤ 34.1 °C. Eyolfson et al. [72] reported that the maximum shivering heat generation could become 3.9 times the basal metabolic heat generation when the core body temperature and mean skin temperature reach 35.2 °C and 22.1 °C, respectively. Therefore, at TSkin ≤ 34.1 °C, the shivering heat generation would be QSh = 3.9 × QBasic. Lastly, when the skin temperature is between 34.1 and 36.4 °C, the amount of shivering heat generation is estimated using Equation (6) (Table 1).
Finally, the metabolic heat due to physical activity can be estimated from Tanabe et al.’s model [26]. If wi is the heat distribution factor of labor work (value in [62]) and Qtotal is the total heat generation from Tanabe et al.’s model [26], then the metabolic heat loss due to physical activity (without considering shivering) can be estimated using Equation (7) (Table 1).
The skin sweat rate can also be estimated based on the tissue temperature [4]. When the core body temperature exceeds 37 °C, the human body starts to sweat. The sweat rate of a body segment (msw) can be theoretically calculated from Equation (8) (Table 1). In this equation, fsw is the sweat factor and fmin is the minimum sweat rate (value in [62]).
3.2. Heat and Moisture Transfer in the Skin–Clothing–Environment System
The heat transfer mechanism from the human body to the skin through clothing can be divided into two categories: (a) sensible heat transfer and (b) latent heat transfer [4]. Sensible heat transfer refers to the conductive, convective, and radiative heat transfer from human skin to the environment through the clothing layer. On the other hand, latent heat transfer refers to evaporative cooling that occurs due to sweat evaporation.
3.2.1. Sensible Heat Transfer
The sensible heat transfer (Qsensible) in the skin–clothing–environment system can be estimated from the difference between the skin temperature (Ts) and the air layer temperature (Ta) adjacent to the outer cloth surface divided by the total thermal resistance (Rct) of the skin–clothing–environment system (Equation (9)) [28]. Joshi et al. [4] reported that sensible heat transfer in the skin–clothing–environment system can be divided into three regions: (a) from the skin to the inner surface of the cloth, which can be termed the enclosed air layer (EAL), (b) through the cloth, and (c) from the outer surface of the cloth to the environment, which can be termed the boundary air layer (BAL). If the dry thermal resistance of the enclosed air layer, cloth layer, and boundary air layer are labeled REAL_cf, Rcf, and RBAL_cf, respectively, the sensible heat transfer in the skin–cloth–environment system can be written as the right side of Equation (9) [4].
Qsensible = (Ts − Ta)/Rct = (Ts − Ta)/(REAL_cf + Rcf + RBAL_cf)
Sensible Heat Transfer in the Enclosed Air Layer (or Microclimate)
The dominant sensible heat transfer mechanisms in the enclosed air layer between the skin and the cloth are conduction, convection, and radiation [68]. If the thickness of the microclimate or enclosed air layer is lower than a certain value, no convection occurs, and the heat transfer mechanisms in the microclimate solely involve conduction and radiation [3]. On the other hand, when the microclimate thickness surpasses the value that corresponds to the onset of natural convection, conduction becomes negligible, and the heat transfer in the microclimate is convection- and radiation-driven. The density of the air enclosed in the microclimate layer varies locally due to the temperature difference between the two boundaries of the microclimate layer [73]. If they defeat the viscous force of the fluid, the buoyancy force causes the upward movement of the less dense warm air, while gravity causes the downward movement of the heavier cool air. The moment when the buoyancy force overcomes the viscous resistance of the fluid corresponds to the onset of natural convection. Lord Rayleigh, who was particularly interested in the convection phenomenon in the early 20th century, developed a dimensionless parameter, the Rayleigh number, that characterizes the effect of the buoyancy force over the viscous force [74]. The Rayleigh number for heat transfers can be estimated from Equation (10) in Table 2 [68]. When the Rayleigh number value is greater than or equal to 1708, natural convection is observed [3]. On the other hand, when the value of the Rayleigh number is less than 1708 in a heat transfer system, the heat transfer is conduction-driven. The amount of sensible heat transfer in the enclosed air layer can be estimated using Equations (14) and (15) (Table 2).

Table 2.
Sensible heat transfer mechanisms in the enclosed air layer.
Sensible Heat Transfer through the Clothing Layer
The amount of heat transfer through the clothing layer can be obtained experimentally using advanced instruments, such as a sweating-guarded hot plate, sweating cylindrical torso, and thermal manikin [28]. The standard test method ISO 11092 requires direct contact between the skin-simulating hot surface and the fabric layer for the measurement of the dry thermal resistance of fabric (Rcf) (Equation (19)) [42].
Rcf = (TSkin − TAir)/Qcf
Here, TSkin is the surface temperature of the guarded hot plate, TAir is the air temperature inside the guarded hot plate chamber, and Qcf is the heat transfer through the fabric layer.
Sensible Heat Transfer in the Boundary Air Layer
The heat transfer from the outer surface of cloth to the environment involves convection and radiation [68]. Both natural and forced convection, i.e., mixed convection, may occur depending on the conditions. The radiative and mixed convective heat transfer from the outer surface of the clothing to the environment are calculated using Equation (20) to Equation (22) in Table 3.

Table 3.
Sensible heat transfer mechanisms in the boundary air layer.
3.2.2. Latent Heat Transfer
The latent heat transfer (Qlatent) in the skin–clothing–environment system can be estimated from the difference between the saturated vapor pressure at the skin (Ps) and the partial vapor pressure at the air layer adjacent to the outer cloth surface (Pa) divided by the total evaporative resistance (Ret) of the skin–clothing–environment system (Equation (24)) [28]. Like sensible heat transfer, the latent heat transfer in the skin–clothing–environment system can be divided into three regions: (a) the enclosed air layer between the skin and the inner surface of the cloth (EAL), (b) the cloth, and (c) the boundary air layer from the outer surface of the cloth to the environment (BAL) [4]. Thus, if the evaporative resistance of the enclosed air layer, cloth layer, and boundary air layer are labelled REAL_ef, Ref, and RBAL_ef, respectively, the latent heat transfer in the skin–cloth–environment system can be written as the right side of Equation (24) [4].
Qlatent = (Ps − Pa)/Ret = (Ps − Pa)/(REAL_ef + Ref + RBAL_ef)
The latent heat transfer in the skin–clothing–environment system due to sweat evaporation depends on the sweat vapor transmission of the vapor transfer medium (e.g., enclosed air layer and fabric) [68,76]. The sweat vapor transmission rate in the skin–clothing–environment system can be theoretically calculated using Fick’s law of vapor diffusion. For instance, if the vapor pressure at the inner surface of the fabric is C1, the vapor pressure at the outer surface of the fabric is C2, the fabric thickness is L, and the vapor diffusion coefficient fabric is D, the sweat vapor transmission rate through the fabric (mDiff) can be estimated using Equation (25) [75].
When the thickness of the vapor transfer medium (i.e., the microclimate) corresponds to a Rayleigh number less than 1708, the vapor transfer mechanism obeys Fick’s law of vapor diffusion [3,75]. On the other hand, when the Rayleigh number is equal to or greater than 1708, the vapor transfer mechanism is convection-driven. The convective vapor transfer (mcon) in a medium is calculated from Equation (26) [62]. The evaporative heat loss (QEVAP) due to sweat evaporation or moisture-vapor transfer (i.e., mDiff/mcon) is estimated from Equation (27) [28]. Here, λ is the latent heat of water vaporization (2257 J/g).
The evaporation rate or vapor transfer rate in the enclosed air layer depends on the difference between the saturated vapor concentration on the skin and the water vapor partial pressure at the inner surface of the clothing layer [75]. In this case, the vapor transfer mechanism can be either diffusion-driven or convection-driven. The evaporative heat transfer in the enclosed air layer can be estimated from either Equation (28) or Equation (29) (Table 4). The water vapor transmission rate for the enclosed air layer is determined from either Equation (30) or Equation (31) (Table 4). The evaporative resistance is computed according to Equation (32) or Equation (33) (Table 4). The evaporative resistance of the clothing layer can be experimentally obtained using advanced instruments, such as the sweating-guarded hot plate, sweating cylindrical torso, and thermal manikin (Equation (34) in Table 4). Parsons [8] showed an estimation of the evaporative heat loss from the boundary air layer using the Lewis ratio (LR) and vapor convection coefficient (). The evaporative heat transfer of the boundary air layer is calculated using Equation (35) in Table 4.

Table 4.
Latent heat transfer mechanisms in the skin–cloth–environment system.
4. Factors Controlling Thermophysiological Comfort
The discussion above identified five factors that affect human thermophysiological comfort. These factors are (a) the physiological characteristics and processes, (b) microclimate layer, (c) clothing properties, (d) ambient conditions, and (e) body motion. The current section describes the effect of these factors on thermophysiological comfort based on the information found in scholarly works.
4.1. Effect of the Physiological Characteristics and Processes
Human physiological characteristics (such as age, sex, and body composition) contribute to the variation in thermophysiological comfort [77,78]. Firstly, the thermoregulatory process of the human body varies with age. This variation results from structural changes in the body parameters (e.g., skin, muscles, bones, and blood flow) [79]. Blatteis [80] found that the thermoregulatory processes of humans decline with age due to the reduction in fitness. Fanger [61] observed a lower rate of metabolic heat production by older people. Hoof [81] reported that older people prefer higher temperatures compared to young people in order to perceive a similar level of thermal comfort.
Human thermophysiological comfort also varies depending on the sex of a person. Fanger [61] found that women produce less metabolic heat compared to men, which translates into a lower skin temperature and lower heat loss due to sweat evaporation. Other research studies suggested that women possess a higher surface-to-volume ratio, resulting in increased heat dissipation through the skin [77,82]. Hoof [81] found that women are more sensitive to temperature changes and feel colder than men in the same ambient conditions. Rupp et al. [83] reported that boys are sensitive to warm temperatures, whereas girls are sensitive to cold temperatures. This finding was later attributed to the metabolic rate of the corresponding sexes.
Body composition and fitness are also essential factors for thermophysiological comfort. The presence of fat in the subcutaneous region helps maintain the thermal balance of the human body in a colder environment [84]. The greater thickness of the fat layer provides more insulation to limit heat loss from the body. However, in hot conditions, the thermal insulation characteristic of the fat layer causes poor thermophysiological comfort due to the lack of heat transfer from the human body to the environment [85].
Like physiological characteristics, the human body’s physiological processes, such as vasodilation, vasoconstriction, shivering, breathing, and metabolism, also contribute to thermophysiological comfort. Heat and sweat generation in the human body due to the thermoregulation process have been described in Section 3.1.
4.2. Effect of the Microclimate Layer
The air gap distance between the human skin and the cloth layer impacts the heat and sweat transfer in the skin–clothing–environment system [4]. Ding et al. [3,86] studied the effect of different microclimate thicknesses on the heat and sweat transfer through firefighter fabric systems using both experimental methods and numerical simulation. They showed that the total dry thermal resistance (Rct) and total evaporative resistance (Ret) vary with the microclimate thickness and ambient temperature. The Rct and Ret increased with an increase in the microclimate thickness up to 12 mm at an ambient temperature of approximately 20 °C. Below 12 mm, the heat and water-vapor transfer mechanisms in the microclimate were considered to be conduction and diffusion, respectively, due to the absence of air movement. The poor thermal conductivity of immobile microclimate air caused an increase in the total dry thermal resistance. Similarly, water-vapor diffusivity in the immobile microclimate air was low, causing an increase in evaporative resistance. When the microclimate thickness was greater than 12 mm, Rct and Ret values started decreasing and appeared to eventually reach a plateau for a microclimate thickness greater than approximately 18 mm. This might have happened as the enclosed air in the microclimate had sufficient space to experience natural convection, which eventually increased the transfer of heat and sweat vapor in the microclimate. Radiative heat transfer was also present in the microclimate; however, it was not affected by the microclimate thickness or the movement of the microclimate air.
Ding et al. [86] also showed that the microclimate thickness for the onset of natural convection increased with the increase in the ambient temperature between −50 and 60 °C for Rct and between 0 and 30 °C for Ret. At higher ambient temperatures (i.e., TE > 60 °C for Rct and TE > 30 °C for Ret, approximately), the Rct and Ret values did not decrease at higher air gap thicknesses due to natural convection and appeared to follow a logarithmic curve. The Rct and Ret results obtained by Ding et al. [86] in their simulations were experimentally validated by Ding et al. [3] for air gap values of up to 12 mm.
While the microclimate discussed in Ding et al.’s [3,86] work was horizontal and homogeneous, the microclimate formed between the human skin and the cloth layer is usually heterogeneous and vertical in orientation [28]. Mert et al. [65] investigated the total heat flux in the skin–cloth–environment system using a vertical microclimate. Both homogeneous and heterogeneous microclimates were created to conduct the study. In the case of the homogeneous vertical microclimate, the distance between the single-sector sweating cylindrical torso (i.e., skin) and the surrounding cloth layer was kept the same (Figure 3a). On the other hand, the heterogeneous air gap was created by folding the fabric at various frequencies (Figure 3b). The study found that the total heat of the system decreased with the increase in microclimate thickness. Neither their experimental results nor theoretical calculations showed any clear evidence of the onset of natural convection. Natural convection in a vertical microclimate starts when the buoyancy force overcomes the fluid resistance [75]. Mert et al.’s [65] study also found that the number of folds increased the amount of total heat loss in the skin–clothing–environment system. Santos et al. [87] developed a numerical heat transfer model in 2D cylindrical microclimates implementing forced convection from the ambient air to the cloth outer surface for a Reynold number of 3900. They suggested that the airflow inside the microclimate regime depended on the air velocity of the ambient air, a characteristic length corresponding to the microclimate thickness, and the porosity of the fabric. The airflow inside the microclimate was estimated to be laminar when the fabric porosity was such that it kept the microclimate air velocity < 0.16 m/s and the characteristic length of the fluid flow < 20 mm.
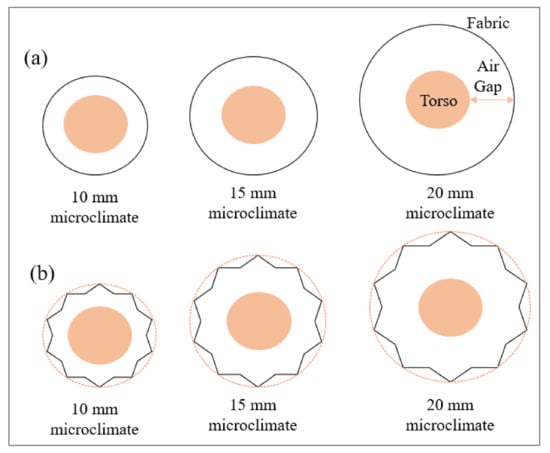
Figure 3.
Schematic representations of cross-sections of (a) homogeneous and (b) heterogeneous vertical microclimate (inspired by [65]).
4.3. Effect of Clothing Properties
The clothing properties that impact human thermophysiological comfort can be divided into three categories: (a) fiber, (b) yarn, and (c) fabric properties [11]. Fibers are small hair-like structures whose length is generally thousands of times greater than the width [88]. The final properties of textile materials partly depend on the chemical and structural features (i.e., crystallinity) of the fibers of which they are comprised [89,90]. Next, a yarn is a continuous strand-like form that is produced by twisting fibers together [88]. When a yarn is produced from filament fibers, it requires low twist/no twist to create the continuous strand [91]. The final properties of textile materials depend on the yarn fineness, number of twists per inch of yarn (TPI), cross-section, production technique, etc. [92,93]. Lastly, the fabric is a 3D structure produced by the interlacement or interloping of yarns or chemical and mechanical bonding of fibers [94]. The functionality of textile materials greatly depends on the fabric’s structural features, physical and mechanical properties, and surface finish [95]. The next sections describe the fiber, yarn, and fabric characteristics that contribute to human thermophysiological comfort.
4.3.1. Effect of the Fiber Properties
The fiber properties that can contribute to human thermophysiological comfort include their moisture absorption and transmission properties, heat of sorption, thermal conductivity, and specific heat capacity [11]. These properties mainly depend on the chemical and structural features (i.e., the fine structure of fiber) of the constituent fibers [36]. For instance, Fourt and Harrist [96] and Badr et al. [97] reported that the type of fibers in fabrics influences the water vapor transmission rate regardless of the fabric structure. When talking about fibers, the term “fine structure” refers to the way the fiber is formed by the linear arrangement of polymer chains, how the crystallites are oriented and ordered, the structure of the crystalline and amorphous regions, the degree of crystallinity, and the size of the crystallites [98].
Moisture is absorbed in textiles as either a liquid or vapor [1]. When moisture (both liquid and vapor phases) is absorbed by fibers, heat is either absorbed or released into the system [36]. This heat is called heat of sorption. A general tendency of molecules is to stay at a low chemical potential (i.e., the condition at which a substance stays at low energy). When moisture absorption occurs into the fiber, the fiber reaches a low chemical potential due to heat release. The water molecule absorbed by the fiber can be attached to the polymer structure either directly or indirectly, i.e., it can be directly attached to the polymer structure or attached to another water molecule connected to the polymer structure. Several studies reported that heat of sorption is released when moisture is absorbed by fibers, which keeps the microclimate warmer than when the moisture is not absorbed by the fibers [99,100].
The crystallinity of fibers plays a large role in moisture absorption [36]. For instance, cotton fibers absorb less moisture than regenerated cellulosic fibers (e.g., rayon and lyocell). The crystalline regions in cotton are tightly packed and experience no moisture absorption. On the other hand, the crystalline regions in rayon and lyocell are less compact, causing some level of moisture absorption in the crystalline region. Morton and Hearle [36] also reported that the moisture regain, a parameter that is used to describe the moisture-vapor absorption of fibers from the ambient air, largely depends on the degree of crystallinity of fibers. A high degree of crystallinity usually causes a low moisture regain and vice versa.
Some studies explored the effect of crystallinity on the water vapor transmission rate, but these studies mainly focused on polymer composites. For instance, Trifol et al. [101] investigated the effect of crystallinity on the water vapor transmission rate through a cellulose polymer matrix. The study found a higher water vapor transmission rate through amorphous specimens than crystalline specimens. Duan and Thomas [102] investigated the water vapor transmission rate of PLA (polylactic acid) specimens with different crystallinity percentages. The study showed a decline in the water vapor transmission rate with an increase in crystallinity percentage.
The crystallinity of fibers also affects their thermal properties, such as thermal conductivity, specific heat capacity, and heat of sorption [36]. The heat transfer through the crystalline regions of a fiber occurs through crystal lattice vibrations [103]. For the amorphous regions, the conductive heat transfer mainly involves the intrachain axial conduction mechanism [104]. A polymer with a higher degree of crystallinity exhibits a higher thermal conductivity than a polymer with a lower degree of crystallinity [105]. For instance, the thermal conductivity of polyester fibers is usually lower than that of cotton, which has been attributed to the lower degree of crystallinity of the PET polymer [36]. In addition, the free volume in the amorphous regions of low-density polymers causes their low thermal conductivity. Figure 4 provides a comparison of the thermal conductivity of different textile fibers.
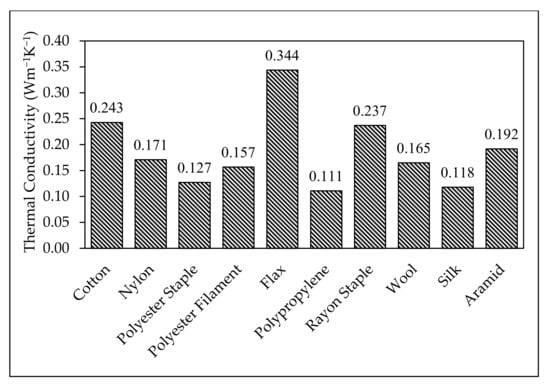
Figure 4.
Thermal conductivity of different fibers [106].
The presence of amorphous regions in the fiber structure increases the thermal insulation of textile materials [36]. The specific heat capacity refers to the amount of heat that can be stored per unit mass and the associated change in the temperature of fibers [62]. The specific heat capacity thus has a negative correlation with the crystallinity percentage [107]. However, the number of studies that have analyzed the relationship between the thermal conductivity or specific heat capacity of fibers and their crystalline structure is limited.
The chemical groups present in the polymer, both side groups and the backbone, also affect the moisture absorption behavior of fibers [36]. Based on the chemical groups present, textile fibers can be categorized into two classes: (a) hydrophilic and (b) hydrophobic. Hydrophilic fibers contain polar groups (such as -OH, -NH3, -COO−, and -CO-NH2) in their chemical structure, resulting in higher moisture absorption. On the other hand, hydrophobic fibers contain relatively inert groups and have poor moisture absorption. For instance, the chemical composition of polyester includes a benzene ring, —CH2—, and —CO.O—. None of these groups has a strong affinity toward water molecules. As a result, polyester fiber is considered a hydrophobic fiber.
4.3.2. Effect of Yarn Properties
Yarn characteristics that affect thermophysiological comfort include the yarn linear density, yarn fiber content, yarn twist, and yarn tightness [92,108,109]. The term “linear density” (sometimes called yarn count/numbering) expresses the fineness of the yarn [88]. Özdil et al. [92] investigated the thermal resistance of 1 × 1 rib structures manufactured in a 28-gauge and 30-inch circular knitting machine using 100% cotton yarns with different linear densities. The thermal resistance of rib fabrics decreased with the decrease in linear density (i.e., finer yarns). The authors attributed this decrease to the fact that finer yarns might trap less air in their structure compared to bulkier yarns, causing low thermal resistance of fabrics. Conversely, the water-vapor permeability of fabrics increased with the increase in yarn fineness, as finer yarns create more open channels in fabric structures for moisture-vapor transport.
Yarn fiber content plays an important role in human thermophysiological comfort [110]. Hydrophilic and hydrophobic fiber types function differently in terms of heat (e.g., the heat of sorption) and moisture (e.g., moisture regain and wicking) management. Therefore, several studies suggested fiber blending techniques to create yarns that give better performance in warm and sweaty conditions [111,112]. Prakash and Ramakrishnan [113] investigated the thermal comfort properties of fabrics made of yarns produced by blending cotton and bamboo-based regenerated fibers. The study found an increase in air permeability and water-vapor permeability of fabrics with the increase in bamboo fiber content in the yarn. In contrast, the thermal conductivity of fabrics had a decreasing trend with the increasing proportion of bamboo fibers in the yarn.
There are two types of yarns: (a) staple and (b) filament [88]. Staple yarns are produced from short fibers by twisting them together, whereas filament yarns are produced with little or no twist. The level of twist applied to fibers or filaments to create yarns significantly impacts the thermal comfort properties of fabrics [114]. A higher number of twists per unit length of yarn decreases the volume of void spaces in the yarn, causing a decrease in the thermal resistance of the corresponding fabric. Özdil et al. [92] also showed that the thermal resistance of fabrics decreased with the increase in the yarn twist while the water-vapor permeability increased. Similarly, Atalie et al. [114] reported that as the number of twists per unit length in the weft yarn increased, the thermal resistance of a 100% cotton fabric decreased.
The spinning technique used is also one of the determinants of the contribution of yarns to the thermal comfort properties provided by the fabric. The ring-spinning process produces the finest yarns compared to all other techniques [88]. Indeed, it involves multiple steps to remove short and unnecessary fibers and creates slivers with parallel fibers using the combing process [115]. On the other hand, other yarn manufacturing techniques, such as the air jet technique, focus on quick production and do not have multiple refining steps [116]. The air jet spinning technique applies twists on the slivers using a pneumatic air flow mechanism, which provides a bulky cross-section to the final yarn. The bulkiness in the yarn cross-section traps air and increases the thermal insulation of the final product [117]. Moreover, the texturization process is used in the filament yarn production to improve the bulkiness and elasticity of yarns. The bulkiness in the texturized yarns influences the thermal insulation and moisture transport properties of fabrics [109].
4.3.3. Effect of Fabric Properties
Fabric physical properties (thickness, weight, count, structure, porosity, etc.) and surface properties (e.g., surface finish) can affect thermophysiological comfort [11]. First, the fabric thickness impacts its thermal resistance and water-vapor transmission rate [28]. As the fabric’s dry thermal resistance is given by the fabric thickness divided by its thermal conductivity, the thermal resistance of the fabric increases with the fabric thickness for the same thermal conductivity. On the other hand, the water-vapor transmission rate through a fabric structure (J) is equal to the product of the water-vapor diffusion coefficient (DF) and the water-vapor concentration difference (ΔC) between both sides of the fabric, divided by the fabric thickness (L), as described by Fick’s law [75]. If DF and ΔC are kept constant, the water-vapor transmission rate will decrease with the increase in fabric thickness. An experimental study by Stoffberg et al. [118] found that the fabric thickness had a positive correlation with the dry thermal resistance and a negative correlation with the water-vapor transmission rate. In another study, Dalbaşı et al. [119] reported an increase in fabric dry thermal resistance with the number of washing cycles due to an increase in the fabric thickness. In addition, fabric weight and thickness are positively correlated when the fabric density remains constant [75]. Fabric weight (or mass per unit area) thus also affects thermal comfort properties [11]. Guan et al. [33] investigated the sweat absorption behaviors of cloth using a sweating cylindrical torso. The results showed that fabrics with higher weight and thickness absorb more sweat than lighter and thinner fabrics.
Fabric count, structure, and porosity are interrelated fabric parameters [120]. Fabric count refers to the number of threads per unit length in the longitudinal direction and transverse direction of the fabric [88]. When the fabric count is low, the fabric structure is loose and has high porosity [121,122]. Several studies have reported how fabric count, structure, and porosity impact thermal comfort properties [95,123]. Limeneh et al. [124] investigated the thermal comfort properties of different weave structures (i.e., plain, twill, and satin) made of 100% cotton yarns. The fabrics had the same fabric count and yarn linear density. The results showed that the satin and twill structures exhibited higher water-vapor permeability, water absorption rate, and air permeability than the plain structure. This result was attributed by the authors to the amount of yarn interlacements in the fabric structure. They suggested that, since the satin structure has a lower number of interlacements, the length of void channels through the fabric structure where air and water vapor can travel increases. On the other hand, the plain structure had the highest number of interlacements, which caused poor moisture vapor and air transport properties through the fabric.
Lastly, the surface finish of the fabric may also affect the thermal comfort properties of clothing [11,109]. Surface-finishing techniques can be either (a) chemical or (b) mechanical. Chemical surface finishes can enhance the cool touch feeling, radiative cooling, and solar heat reflection of fabrics [125]. Dalbaşı et al. [119] treated fabrics made of regenerated bamboo fibers and regenerated bamboo–cotton blends with softeners made of poly-amino siloxane to improve the fabrics’ cool touch or thermal absorptivity. The experimental results showed higher thermal absorptivity in the treated fabrics compared to the untreated fabrics. The use of a solar radiation-reflective chemical finish on the outer surface of cloth limits the penetration of solar radiation through the fabric and keeps the body cool [126]. In addition, hydrophilic finishes improve the moisture-wicking performance of clothes [11]. On the other hand, water-repellent finishes prevent the wetting of fabrics by water and block its penetration through the fabric. When a fabric is wet, its thermal conductivity increases, which can cause excessive heat loss from the human body [28]. For their part, mechanical finishes are applied to enhance the warmth, bulkiness, and smoothness of the fabric surface [11,88]. Raising and shearing are two mechanical finishing techniques that cut the loops from one side of the fabric and create a fleecy surface. The fleecy surface improves the thermal insulation property of fabrics [88].
4.4. Effect of Ambient Conditions
Human body thermophysiological comfort depends also on environmental parameters [8]. Previous scholarly works identified four essential environmental parameters of thermophysiological comfort: air temperature, air velocity, relative humidity, and mean radiant temperature [2]. Sometimes, the air temperature is different from the “feels like” temperature because the sensation of warmth and coolness also depends on air velocity, relative humidity, and mean radiant temperature at the same time. This feel-like temperature is referred to as the apparent temperature [127].
The psychometric chart is a graphical representation of moisture air thermal and physical (i.e., amount of vapor present in air) properties [128]. The vertical axis of the psychometric chart on the right side is the specific humidity, the bottom horizontal axis is the dry-bulb temperature, and the curvature on the left side indicates the dew-point temperature (Figure 5a). The dry-bulb temperature is the actual air temperature in dry conditions [8,129]. The dew-point temperature is the temperature at which moisture vapor starts condensing—the air is at full saturation. The specific humidity is different from the relative humidity and can be defined as the amount of vapor per unit mass of dry air. The wet-bulb globe temperature and relative humidity are derived from the dry bulb temperature, specific humidity, and dew-point temperature (Figure 5a). The wet-bulb temperature is the minimum temperature at which water evaporates in the atmosphere and cools air at a steady pressure [8]. It is measured using a wet wick wrapped around the bulb of the thermometer. The wet-bulb globe temperature is positioned along the curve of the dew-point temperature in the top-left corner (Figure 5a). The wet-bulb globe temperature is determined by drawing a diagonal line along the top-left corner direction, which creates a 45-degree angle (approximately) from the perpendicular crossing point of dry-bulb temperature and specific humidity. When the specific humidity is extended in the exact opposite direction horizontally (from right to left), it can determine the dew-point temperature. The curvature lines inside the graph represent different relative humidity values.
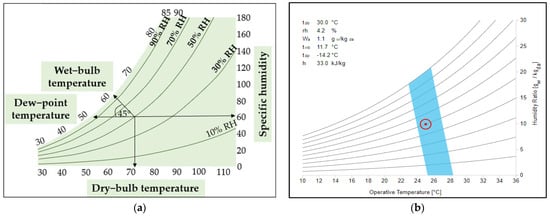
Figure 5.
(a) Schematic diagram of a psychometric chart (inspired by [129]), and (b) CBE thermal comfort tool (reproduced from [130], available through the Creative Commons license: http://creativecommons.org/licenses/by/4.0/ (accessed on 8 July 2023).
Tartarini et al. [130] developed a thermal comfort prediction tool (called CBE thermal comfort tool) using a psychometric chart. The tool uses the operative temperature, air velocity, relative humidity, metabolic rate, and clothing insulation as inputs to predict whether the human subject is within or outside the comfort zone (Figure 5b). The red point located within the blue comfort zone in Figure 5b indicates the operative temperature (which depends on the dry-bulb temperature, mean radiant temperature, and air velocity) and relative humidity of the environment. Teitelbaum et al. [131] applied contour shading in the psychometric chart to define the comfort zone using comfort parameters, such as mean radiant temperature, air velocity, metabolism, skin wetness, and physical activity of occupants.
Based on the discussion above, it is evident that human thermophysiological comfort depends on multiple environmental parameters. Huang and Chen [132] investigated the effect of air temperature, air velocity, and relative humidity on the water-vapor transmission rate through the fabric structure. They found that the water-vapor transmission of the fabric increased with the air temperature and velocity, while it had a negative correlation with the relative humidity of the air flowing over the fabric surface. The numerical simulation of the heat transfer in a 2D cylindrical microclimate showed that the ambient air velocity increased the convective heat transfer coefficient from the outside of the fabric to the ambient [87]. Guan et al. [110] investigated the radiant heat gain (RHG) with or without the presence of a radiant heat source, including a continuous sweat supply at different rates. The study found that the hygroscopic fabrics tested exhibited a high RHG compared to the hydrophobic fabrics. The study also showed that RHG increased with the incident radiation intensity.
4.5. Effect of Body Movement
Several researchers explored the effect of human body movement on human thermophysiological comfort [28,133,134,135]. Belding et al. [133] investigated the effect of different levels of physical activities (e.g., sitting, standing, and walking) on the human body’s thermal energy balance and clothing insulation while closing the opening at the wrists, ankles, waist, etc. The results showed that the lower-level activities (i.e., sitting and standing) produced a metabolic heat of 50 to 70 cal·m−2·h−1, while the higher-level activities produced 300 to 500 cal·m−2·h−1. The heat loss from the human body at a lower level of physical activity occurs by convection and radiation through the cloth layer. On the contrary, at a higher level of physical activity, the heat-loss mechanism includes sweat evaporation and other external mechanisms. In the case of clothing insulation, the study found that the clothing insulation varied depending on the intensity of the physical activity. The thermal insulation of the same clothing ensemble at standing, walking at 2.25 m/h, and running at 6 m/h were 2.7 clo, 1.6 clo, and 1.2 clo, respectively. The reduction in clothing thermal insulation was caused by the forced convection of air in the enclosed microclimate caused by human movement.
The forced convection caused by human movement in the enclosed microclimate between the human body and the cloth layer is sometimes referred to as the pumping effect [28]. Vogt et al. [134] investigated the influence of the pumping effect on the thermal insulation of the cloth layer. The authors assumed that the pumping effect would be minimal when the mean skin temperature and ambient air temperature have the same value. In this situation, most of the heat transfer is through radiation in addition to forced convection. On the other hand, when the mean skin temperature and mean radiant temperature (temperature of the chamber wall) are the same, the pumping effect is expected to be maximal. The results showed up to 75% of loss in the thermal insulation of the cloth layer was due to the pumping effect. Nielsen et al. [135] analyzed the effect of various physical activities, body shapes, sex, and air velocity on the thermal insulation of clothing. The study found that the clothing insulation is maximum in the standing position compared to a seated position, bicycling, and walking. The clothing insulation decreased by 8–18% in a seated position and 30–50% while bicycling and walking. An air velocity of 1.1 ms−1 decreased the thermal insulation of clothing by 18% in a standing position, while it did not affect the thermal insulation of clothing in a seated position. The decline in clothing insulation was higher for male participants compared to female participants due to a higher pumping effect.
Another way to lose body heat through movements is called ventilation. Ventilation occurs when the garment openings are not sealed and fabric pores are large so that they allow the movement of microclimate air through the fabric structure [136]. External wind and human body motion cause the ventilation effect in the clothing system [137]. Zhu et al. [138] reported that fabrics’ air permeability significantly increased with the porosity, which causes the ventilation of air through the fabric structure due to human body movement [139]. However, there are a limited number of studies that have explored the ventilation effect due to pore structure and garment openings.
Researchers have developed empirical models to estimate the heat and moisture transfer due to the movement of body parts [68,136]. However, these models exhibit limited predictability in terms of estimating the thermophysiological comfort of any local body parts due to the complex nature of the fabric draping and human movement with different garment fits. Moreover, very few thermophysiological comfort prediction models have incorporated the pumping effect with realistic microclimate air gap values.
5. Materials and Advanced Technologies for Superior Thermophysiological Comfort
Techniques have been developed by researchers and garment manufacturers to improve the thermophysiological comfort of fabrics and garments. The next four sections cover the strategies based on fiber selection and engineering, moisture management finishes, radiative cooling and heating, and the use of smart textiles.
5.1. Fiber Selection and Engineering
Evidence of the use of textile fibers, namely, flax, has been found dating back to 35,000 BC [140]. Natural fibers (e.g., flax, cotton, wool, and silk) were the major sources for clothing applications until the nineteenth century. Hydrocarbon-based and regenerated cellulose fibers were invented throughout the late nineteenth century and twentieth century [141]. Advances in textile fibers in the late twentieth century and early twenty-first century were motivated by considerations related to sustainability and improved functionality [142]. Fibers used in clothing for superior thermophysiological comfort include cotton, wool, polyester, nylon, regenerated cellulose (rayon, modal, lyocell), elastane, channeled-cross-section fibers (e.g., Coolmax®), and fibers containing phase-change materials (e.g., Outlast®). They are described in the sections below, with the exception of fibers containing phase-change materials which are covered in Section 5.4. Table 5 provides the chemical nature, structural features, and functionality of some commercial fibers that have been used in clothing application for superior thermophysiological comfort.

Table 5.
Commercial fibers for superior thermophysiological comfort properties [143,144].
Cotton fiber has been widely used in the clothing industry for centuries as it has excellent thermal conductivity and moisture absorption properties [36]. The high thermal conductivity of cotton fibers comes from their polymeric structure [145]. The polymeric structure of cotton is highly crystalline, which makes it possible to transfer heat easily. On the other hand, the tightly packed crystalline structure of cotton makes cotton fiber less permeable to water vapor [36]. However, due to the presence of hydrophilic groups at the polymer backbone of the cellulose polymer, cotton fibers show excellent water absorbency. Studies have shown that the use of cotton fibers reduces the damp feeling of the wearer due to superior moisture absorption ability [99,146]. However, cotton fabrics show poor moisture-wicking ability, which leads to long drying times [147,148]. Plante et al. [146] explored the moisture dampness perception of clothing with varying fiber contents (i.e., cotton, wool, polyester, and a wool/cotton blend) in different RH values. The moisture dampness perception had a negative correlation with fiber hygroscopicity at 25% RH; the difference in dampness perception with different fiber contents decreased with the increase in ambient RH. Kim and Spivak [99] investigated the dynamic moisture-vapor transfer through bilayer fabrics made of cotton (C) and polyester (P) in various combinations, such as C/C, P/C, C/P, and P/P. The study found that the partial moisture-vapor pressure at the inner surface of the hydrophilic fiber-containing layer was lower due to the high absorption of moisture vapor, while for the hydrophobic fiber-containing inner layer, the partial moisture-vapor pressure was higher at the inner surface due to low absorption rate. Moreover, the inner surface temperature of the hydrophilic inner layer was higher compared to the hydrophobic inner layer because of the heat released during moisture absorption, which provided a warm feeling. Cotton fiber is usually blended with other fibers (i.e., moisture-wicking fibers) to improve the overall wicking performance of the fabric [111,112,149].
Wool fiber is extracted from the fur of sheep, camels, goats, rabbits, etc. [150,151]. Wool is well known for its thermal insulation, hygroscopic (i.e., moisture-vapor absorption) ability, air permeability, and water-vapor transmission. The concentric layer in the wool cross-section (from outer to inner) includes the cuticle layers (endocuticle, exocuticle, and epicuticle) layers, cortical cell, macro-fibrils, matrix, micro-fibrils, and twisted chains of proteins [152]. The epicuticle layer has microscopic pores that act as channels for water-vapor diffusion. Due to this, water vapor is easily absorbed by wool. However, the wool fiber surface usually repeals water droplets that come into contact and takes time to absorb liquid water. Wool is considered a hydrophilic fiber, as its monomer (a protein) contains (-COOH) carboxylic and (-NH2) on the ends [36]. As a result, wool fabrics dry slowly [153]. The scaly surface of the fiber helps to trap air in the fabric as well as provide a passage for moisture vapor to be transported [154]. Merino wool is one of the finest sheep wools and exhibits excellent thermal resistance and moisture absorption behaviors [155]. Merino wool forms natural crimps in the fabric structure, which improve the bulkiness and thermal insulation of the fabrics [156]. Kumar et al. [154] explored the thermal resistance and water-vapor transmission rate of fabrics made of merino wool, silk, and bamboo fibers with different fabric structures. The study found that fabrics with merino wool exhibited a higher thermal resistance and water-vapor transmission rate than fabrics made of silk and bamboo fibers, owing to the bulkiness of the wool fabrics.
Polyester fiber is produced from the reaction between ethylene glycol and terephthalic acid [145]. Polyester fibers are hydrophobic and usually more amorphous than cotton [36]. Thus, polyester fiber has a lower thermal conductivity than cotton [106]. On the other hand, the poor moisture absorption behavior of polyester may increase the moisture-wicking rate in polyester fabrics [157]. However, the wicking rate also depends on the yarn structure, fabric structure, and surface finish [158,159,160]. As polyester lacks moisture absorption properties, it minimizes the release of the heat of water sorption in the microclimate and causes a lower temperature at the inner fabric surface [99]. However, this process leaves the human skin wet, which causes discomfort [100]. The thermal properties of polyester fabrics can be improved by playing with the fiber fineness and cross-section. Varshney et al. [161] investigated the thermophysiological comfort of polyester fabrics with varying degrees of fiber fineness and different cross-sections (i.e., circular, triangular, four-channel propeller, and tetrakelion). The study found that the thermal resistance and air permeability of fabrics increased with the fiber fineness, while the wicking rate of fabrics with fibers with round cross-sections was lower than the other three types of cross-sections displaying receding or outward acute angles. Different commercial products have been developed where the cross-section of polyester fibers is deliberately altered to create capillary wicking channels along the fiber, such as Coolmax® and Octa® [144].
Nylon fiber (nylon 6,6) was invented in 1930 by Wallace H. Carothers, who was looking for a synthetic alternative to silk fibers [162]. Nylon is a polyamide fiber typically produced by the polymerization reaction of adipic acid and hexamethylenediamine; it contains the amide linkage (-CO-NH-) in its polymer structure [163]. The polymer backbone of the nylon fiber contains the hydrophilic -NH2 group, which leads to a high moisture absorption ability [36]. Moreover, nylon is less crystalline than cotton, which makes nylon fiber a good candidate for thermally insulating fabric [106,163]. Adamu and Gao [164] investigated the thermal comfort properties of woven fabrics made of cotton, nylon, and cotton–nylon blends. The results showed that the fabrics’ wicking increased with the proportion of nylon in the cotton–nylon blend, whereas the air permeability and moisture-vapor transmission rate decreased. The study also found that coarser yarns with the cotton–nylon blend increased the vertical and horizontal wicking rate. Anas et al. [165] explored the thermal comfort properties of weft-knitted fabrics made of nylon, polyester, cotton, and acrylic fibers. The results showed that fabrics made of nylon and polyester blends had higher air permeability than cotton and acrylic blends.
Rayon, modal, and lyocell fibers are man-made cellulose fibers or regenerated cellulose fibers [36]. These fibers are produced using wood pulp or other sources of cellulose. However, their production processes are slightly different, which affects the final thermal and moisture absorption behavior. The first generation of regenerated cellulose fiber is called viscose rayon and was invented in 1938 to replace silk [166]. The viscose rayon manufacturing process is complex, involves NaOH and CS2 solvent treatments, and generates a large amount of toxic chemical waste. Because the cellulose polymer is regenerated in a chemical process, the resulting viscose rayon has a lower crystallinity than cotton, which affects the final strength and thermal comfort behavior of fibers [163]. Viscose rayon fiber is comparatively less strong and shows superior moisture absorption [163,167] and thermal insulation [168] compared to cotton because of its reduced crystallinity. Prakash et al. [169] explored the moisture management behavior of a blend of cotton and regenerated cellulose fibers from bamboo. The study found that when the proportion of regenerated bamboo fibers increased, the wetting time and maximum wetted radius decreased, and the moisture absorption rate increased.
The second generation of regenerated cellulose fiber is called modal rayon or HWM rayon for “high wet modulus” [170]. It was developed to improve the wet strength of viscose rayon, which was a great concern for the dyeing process. However, the manufacturing process of modal fibers is still somewhat similar to the viscose process. The degree of crystallinity is moderate in modal fibers, which causes comparatively less moisture absorption than viscose rayon, but still more than cotton [171].
The third generation of regenerated cellulose fibers is called lyocell [166]. It is produced using the environmentally friendly N-methyl morpholine N-oxide (NMMO) solvent [172]. It has the highest degree of crystallinity among the three generations of regenerated cellulosic fibers [173]. It is 43% higher than that of viscose rayon and 16% higher than that of modal [174]. The higher degree of crystallinity of the lyocell fiber reduces its moisture absorption [167,172]. Chen [163] reported that the moisture regain of lyocell fibers is around 11%, while the moisture regain of viscose rayon is between 12% and 14%. However, lyocell fibers have some drawbacks. The lateral chemical bond between the crystallites in the lyocell fiber is weak, causing fibrillation on the fiber surface [175]. As a result, they have a lower resistance to pilling, which impacts the thermal comfort properties of the corresponding fabrics. Ozdemir [176] investigated the permeability to air and water vapor and the wicking behavior of woven fabrics with varying weave patterns using both modal and lyocell fibers. The study found that the use of lyocell fibers led to a higher permeability and wicking for all different woven structures compared with the modal fibers due to the fringed fibrillary structure in both the crystalline and amorphous regions of lyocell.
Elastane fiber is widely blended with other fibers in activewear to produce tight-fitting garments [177]. Elastane fiber is made from polyurethane, which is typically produced by the polymerization reaction of a diisocyanate and a diol [163]. It contains urethane groups (-NH-CO-O-) in the polymer structure. The resulting polymer is then extruded through a spinneret by melt spinning. Manshahia and Das [178] investigated the thermophysiological comfort properties of knitted fabrics made of polyester staple fiber yarns and elastane monofilaments. The results showed that the air permeability and moisture-vapor permeability index of the fabrics were negatively influenced by the increase in linear density of the elastane filaments, possibly due to the associated increase in fabric tightness and density. Shobanasree et al. [179] studied the effect of elastane plating on lyocell-based single jersey knit structures. The study found that fabrics’ thickness, mass per unit area, and density had a positive correlation with the elastane content, while the thermal resistance, air permeability, and water-vapor transmission rate had a negative correlation with the elastane content. These relationships were attributed to the fact that the presence of elastane in the fabric structures increases the fabrics’ tightness.
Coolmax® is an example of fibers that have a propeller-shaped cross-section [144]. It is made out of polyester. The propeller-shaped cross-section helps these fibers wick moisture more efficiently than traditional polyester fibers. Several studies blended Coolmax® with moisture-absorbing hydrophilic fibers to improve the moisture absorption and wicking in clothing. Öner and Okur [180] investigated the thermal comfort properties of six knitted fabrics with different fiber contents (cotton, viscose, soybean, Tencel LF, cotton–Coolmax®, and polyester) and knit structures. The study found that the cotton–Coolmax® blends had a better moisture-wicking performance than the other fabrics tested. Atasağun et al. [181] conducted a comprehensive study of the moisture management behavior of knitted fabrics with various fiber contents. They showed that fabrics made of 100% Coolmax® fibers and a 50/50 Viloft®–Coolmax® fiber blend exhibited higher one-way moisture transport behavior (AOTI) and overall moisture management capability (OMMC) compared to the other fiber blends tested.
5.2. Finishes for Improved Thermophysiological Comfort
Moisture management finishes are often applied to fabrics to improve moisture absorption and water-spreading ability. For instance, Krithika et al. [182] applied amino silicone polyether copolymer (ASPC) and hydrophilic polymer (HP) finishes to four different sportswear fabrics made of micro-denier polyester, cotton, cotton/polyester blend, and nylon fibers. The results showed that after the treatment, the rate of water spreading in the four fabrics increased due to capillary action. The water-vapor transmission rate through the fabrics also increased, while the wetting time (i.e., the time taken by a fabric specimen to sink in water completely) was found to decrease. In another study, Sampath and Senthilkumar [183] measured the vertical wicking, water absorbency, wetting time, and water-vapor transmission rate of knitted fabrics made of micro-denier polyester treated with ASPC and HP. They found that the moisture management ability of the treated fabrics significantly improved without impacting their air permeability. Sampath et al. [184] treated fabrics made of various cotton and polyester blends with a dispersion containing a polysiloxane with hydrophilic and hydrophobic groups, and a hydrophilic nonionic surfactant for polyester fibers. The researchers found that the finishing treatment significantly improved the moisture-wicking, moisture-absorption, wetting time, and water-vapor transmission of the tested fabrics. Liu et al. [185] treated polyester woven fabric specimens using a 3-mercaptopropyltrimethoxysilane and potassium 3-sulfopropyl acrylate-based durable moisture-wicking finish. The findings showed that the treated fabrics exhibited excellent moisture-wicking and fast-drying properties.
Water-repellent finishes may also be applied to fabrics to prevent the absorption of water by the fabric and/or its passage through it [186]. The presence of a water repellent positively affects human thermophysiological comfort in some sports activities, such as canoeing, rafting, kayaking, and rowing in rivers or lakes, as well as for protection against bad weather. There are several types of water-repellent finishes, such as paraffin, stearic acid–melamine, fluorocarbon, and silicone-based finishes [187]. Paraffin-based water-repellent finishes are nonpolar and can create polar–nonpolar junctions with polar fibers [188]. They create a hydrophobic layer over the fabric surface, which prevents the penetration of water droplets in the fabric. However, paraffin-based water-repellent finishes do not perform well in terms of durability and flammability. The reaction of stearic acid and formaldehyde with melamine creates another kind of water-repellent finish for fabrics [187]. However, this type of finish adversely affects fabrics’ tearing strength and abrasion resistance [188]. Fluorocarbon-based water-repellent finishes are common for fabrics made of synthetic fibers and their blends with natural fibers [187]. Tama et al. [188] treated woven fabrics made of cotton, polyester, polyamide, and polypropylene fibers with a fluorocarbon-based finishing chemical (commercial name: Imofob FMU). The results showed that the water repellency and thermal insulation of the fabrics significantly increased after the water-repellent treatment. Previous studies reported that fluorocarbon-based (e.g., perfluorochemicals and per/poly-fluoroalkyl substances) water-repellent finishes are the most durable. However, these chemicals have adverse effects on both human health and the environment [189,190,191]. For this reason, silicon-based water-repellent finishes are progressively replacing fluorocarbon-based finishes. Silicone-based finishes can rely on different compounds, such as silane, siloxane, and silicone rubber [192]. These finishes are harmless to the human body and the environment [193,194]. In addition, they are durable to washing and abrasion [195]. However, it is important that for the thermophysiological comfort of the wearer, the water-repellent clothing still allows evaporated sweat from the inside of the garment to transfer to the environment [188,196]. For instance, Mohseni et al. [195] developed a breathable and non-fluorinated superhydrophobic fabric produced by two sequential spraying using a silica nanoparticle-containing solution (spraying 1) and an optimized mixture of polydimethylsiloxane and alkyl silane (spraying 2), respectively. The study found that the surface treatment significantly improved the water repellency of the fabric. On the other hand, the air permeability of the treated fabric remained the same as the untreated fabric.
Finally, to combine the desired moisture absorption of fabrics while avoiding the clammy feeling that sometimes appears due to the long-term presence of sweat in the cloth [197], researchers have developed a technique called the one-way moisture transport mechanism [198]. This mechanism involves having the inner surface of the cloth being hydrophobic while the outer surface is hydrophilic. The hydrophobic inner surface wicks human sweat from the skin through capillary channels of fabric. The hydrophilic outer surface absorbs the sweat away from the inner surface and causes rapid evaporation in the environment [199,200]. Prabu et al. [201] developed a Janus moisture management fabric made of cotton with a fluorocarbon-based hydrophobic finish sprayed on the inner side; the outer side of the fabric was unfinished. The researchers found that the overall moisture management ability (OMMC) of the treated cotton fabric significantly increased from 2.5 (for untreated fabric) to 4.0 (on a scale of 5). Guan et al. [199] developed Janus fabrics made of cotton, flax, and polyester fibers. They treated them with hydrophilic graphene oxide (GO) on the outer surface and hydrophobic reduced graphene oxide (rGO) on the inner surface. The results showed that the treated fabrics exhibited an excellent one-way moisture transport from the inner surface to the outer surface and a quick evaporation of water to the outside environment.
5.3. Radiative Cooling and Heating Technologies
Infrared (IR)-transparent materials can be used to help cool the human body [126]. IR radiation emitted from the human body (at wavelengths from 7 to 14 μm with a peak intensity at 9 μm) is transferred to the indoor environment through the cloth layer. This process is known as radiative cooling. Tong et al. [202] developed a virtual IR-transparent visible opaque fabric (ITVOF) using a highly IR-transparent polymer—polyethylene (PE). Finite element simulation showed that the woven fabric made of PE yarns exhibited an IR transmittance of 0.97 (i.e., near to completely transparent). IR-transparent polymeric materials can also be artificially engineered by altering their thermal and optical properties [203]. Hsu et al. [204] developed a nanoporous PE membrane for radiative cooling of the human body (Figure 6a). The pore size of the nanoporous PE textile ranged between 50 and 1000 nm, which covered the whole range of the visible spectrum, making the PE substrate opaque. This happened because the C-H and C-C bonds in aliphatic PE absorb smaller wavelengths (in the range of the visible spectrum), a phenomenon called mie scattering. On the other hand, the fabric was transparent to the mid-infrared radiation (MIR) released from the human body. When the nanoporous membrane was laminated on a cotton mesh, the results showed that the final textile material had sufficient air permeability, wicking, and mechanical properties to be considered wearable. Figure 6a illustrates how human body radiation cannot pass through clothing made of traditional textile fibers (left part of Figure 6a), whereas it can pass through nanoporous PE membrane (central part of Figure 6a) and PE sheet (right part of Figure 6a). Because it is a solid film, the PE sheet prevents convection across the film while the nanoporous PE membrane allows it. Ke et al. [205] developed women’s regular-fit shirts using a nanoporous PE-based fabric and compared this with a cotton fabric. The results of wear trials showed that the female participants had a significantly lower mean skin temperature when wearing the nanoporous PE-based shirts than the regular cotton shirts at ambient temperature between 23 and 27 °C. Other polymers, such as polyamide (PA) and polyvinylidene fluoride (PVDF), can be artificially designed to be IR-transparent [126]. This can be achieved by creating a hierarchical structure or incorporating nanostructure features in the polymer substrate. It is important to note that traditional textile fibers, such as cotton, polyester, flax, and hemp, are IR-absorbing fibers because their thermal radiation absorption peaks match the wavelength of the IR radiation released from the human body [206]. However, these fibers can be blended with PE and IR-transparent nylon in specific proportions to improve the overall IR-transparent properties of the corresponding fabrics [24,206].
Figure 6.
(a) Radiative cooling mechanism of PE-based nanoporous membrane (inspired by [204]), (b) IR transmission and solar reflective radiative cooling mechanism (reproduced from [207] with permission from John Wiley and Sons), and (c) Janus fabric heating and cooling techniques (reproduced from [208] with permission from Elsevier).
Radiative cooling textiles for the outdoor environment can be divided into three categories: (a) solar reflection (SR), (b) solar reflection and IR emission (SRIE), and (c) solar-reflection and IR transmission (SRIT) [126,209]. SR fabrics can reflect solar radiation within the visible and IR wavelength range, which limits the heat transfer to the human body [210]. The solar reflection function can be incorporated into textiles in three ways: (a) by applying metal coatings [211,212], (b) by creating air voids [114], and (c) by altering the fiber cross-sections [213,214]. On the other hand, SRIE fabrics absorb the human body’s thermal radiation and emit it to the environment while reflecting the sun’s radiation back to the environment, thus preventing it from heating the human body [215]. For instance, Zhang and Yu [216] developed a radiative cooling polyester fabric by treating it with a tetraethyl orthosilicate (TEOS) solution. The chemical treatment caused the in situ formation of SiO2 microspheres, which created bonds with the polyester fibers. Results showed that the fabrics exhibited a high emissivity greater than 95% in the near- to mid-infrared region while blocking the sun’s radiation near the visible region. Finally, SRIT fabrics perform radiative cooling by transmitting IR radiation from the human body through the clothing layer as well as by reflecting the sun’s radiation on the outer clothing surface [209]. For instance, Cai et al. [207] developed nanoporous PE textiles embedded with ZnO nanoparticles for radiative cooling in outdoor conditions (Figure 6b). PE is IR-transparent to the human body’s thermal radiation, but when embedded with ZnO nanoparticles provides both IR transmission (up to 80%) and reflection (up to 90%).
Radiative thermal management clothing can also be used to prevent the loss of heat from the human body, and is mainly based on two principles: (a) reflective heating and (b) radiative heating [126]. The reflective heating mechanism involves allowing the heat radiated from the human body to bounce back towards the body. Studies have used a metallic coating on the inner surface of clothing to generate reflective heating [126,217]. For instance, a commercially available blanket is made of a Mylar (biaxially oriented PET) sheet that is coated with aluminum on one side [218,219]. However, such products lack breathability due to the metal coating, which causes poor wearing comfort. Another reflective heating technology, omni-heating, has metallic printed dots on the inner side of the fabric [220]. However, these reflective heating textiles display poor heating performance. Another strategy is to combine IR-transparent, IR-absorbing, and low-IR-emissivity materials with reflective heating to enhance the heating performance. Cai et al. [221] developed a nanostructured heating textile made of IR-transparent nanoporous PE coated with IR-reflective silver on one side. The textile had a low emissivity of about 10% on the PE side. On the other hand, when the metallic-coated side of the textile was exposed to direct sunlight, it showed an excellent heat-reflective performance. The set-point temperature decreased by 7.1 °C, surpassing the performance of other radiative thermal management textiles. Yue et al. [222] created a nanoporous cellulose-based multilayer radiative heating textile. One side of the cellulose membrane was coated with carbon nanotubes (CNTs) using foam finishing, while the other was coated with Ag nanoparticles by magnetron sputtering. The results showed that the outer CNT layer demonstrated solar radiation absorption greater than 90%, while the inner Ag-coated layer exhibited solar radiation reflectivity greater than 80%. The smart heating textile developed also showed excellent water vapor transmission, wicking, and flexibility, which suggests a large potential as an outdoor thermal management clothing.
Another type of radiative thermal management textile, called Janus, can provide both warming and cooling effects utilizing the solar radiation [210,223]. The Janus fabric is created in such a way that the two sides of the fabric can provide two different effects (i.e., warming and cooling) (Figure 6c): one side of the fabric shows high emissivity, while the other side shows low emissivity. In one configuration, the high-emissivity outer layer of the Janus fabric releases body heat to the environment in hot weather, whereas in the other configuration, the low-emissivity outer layer limits body heat loss in cold weather. Yue et al. [224] created a Janus fibrous membrane using a cellulose-based material. One side of the membrane was coated with ZnO nanorods for high solar radiation reflectivity and high IR emissivity, while the other side was coated with ultralong MnO2 nanowires and Ag nanowires for high solar radiation absorption and low emissivity. In another study, Abebe et al. [223] simulated the performance of a fabric made of an asymmetrical yarn composition using metallic and dielectric fibers. They calculated a difference in emissivity of Δε = 0.72 between the two sides of the fabric, with a temperature window of more than 13 °C when flipping the double-sided fabric.
5.4. Smart Textiles for Superior Thermophysiological Comfort
Various smart materials have been incorporated into clothing as an integral part to actively increase human thermophysiological comfort when needed. This includes phase-change materials, shape-memory polymers, electroactive materials, thermoelectric materials, and so on [125,126,225,226].
Phase-change materials (PCMs) have reached the commercial clothing market to improve human thermophysiological comfort [227]. PCM microcapsules can be incorporated into textiles by a wide variety of techniques, such as wet spinning, melt spinning, electro-spinning, pad-dry-cure, and printing [125]. For instance, the Outlast® fiber, which was invented by NASA in the early 1980s to improve the regulation of human body temperature in space [143,228], is used in activewear apparel for superior thermophysiological comfort. The fiber contains PCM microcapsules (known as thermocules), which absorb and release latent heat when they change phase between solid and liquid. The Outlast® fiber is generally blended with regular fibers to produce clothes with improved thermophysiological comfort [227]. Wang et al. [229] developed a thermoregulating alginate fiber by incorporating PCMs from a microemulsion using wet spinning. The microemulsion of PCMs was prepared by mixing paraffin wax and emulsifiers (alkylphenol polyoxyethylene ether and sodium dodecyl sulfate). The study found that the alginate PCM fibers retained 97.3% of their latent heat after 100 heating and cooling cycles. The fibers also displayed smooth surfaces and porous cross-sections. Tran et al. [230] developed a bi-component fiber by melt spinning using polypropylene (PP) as the sheath and a mixture of PP and PCM as the core material. The study reported that the core–sheath fiber developed has a latent heat of up to 22.2 J/g, which is three times higher than traditional fibers. Ding and Yu [231] developed a PCM-based composite fiber by electrospinning of organic PCMs (paraffin wax, fatty acid, and polyethylene glycol mixtures) encapsulated in cellulose acetate/polyethylene terephthalate/polyvinylpyrrolidone. The study concluded that the thermal properties of the PCM-based fiber composite depended on the PCM vs. polymer ratio. Shin et al. [232] incorporated eicosane-containing melamine–formaldehyde PCM microcapsules in a polyester fabric with the aid of polyurethane binders using the pad-dry-cure method. The study showed that the moisture regain and heat storage capacity of the polyester fabric increased with the amount of microcapsules added to the fabric while the air permeability and water vapor transmission rate decreased. Choi et al. [233] developed octadecane-containing melamine formaldehyde PCM microcapsules and coated them on a polyester fabric using knife-over-roll (KOR) and screen printing (SP) methods. The study found that the coating technique significantly affected the mechanical and thermal comfort properties of fabrics. Fabrics coated with the SP technique had a lower bending and shearing rigidity than the KOR-enabled fabrics. On the other hand, the KOR fabrics offered a lower air permeability and higher moisture absorption than the SP fabrics. Further investigation on KOR polyester fabrics revealed that the heat capacity of the fabrics increased with the amount of PCM microcapsules [234]. The changes in the skin and microclimate temperatures with PCM-incorporated KOR fabrics were found to be lower during wear trials than with untreated fabrics. However, PCM-based smart materials have some limitations in terms of thermoregulatory response [125]. When incorporated in textiles, PCMs provide a slow response against warm or cold conditions due to their low thermal conductivity. Another phenomenon exhibited by PCMs is supercooling, which keeps PCMs in a liquid state below the solidification temperature and increases the temperature variation between the heating and cooling cycles. Lastly, continuous heating and cooling cycles for prolonged periods can reduce the performance of PCMs over time.
Recently, shape-memory polymers (SMPs) have been spun into fibers and yarns to develop clothes with superior heat and moisture transport properties [226]. SMPs can change shape when exposed to any external stimulus (e.g., heat, moisture, electricity, light, and chemicals) and return to their original shape when the stimulus is removed. An SMP can be programmed into single or multiple temporary shapes [235]. The shape recovery mechanism in one-way SMP works in three steps: (a) from its original shape, the specimen is heated to a temperature T > Ttrans (Ttrans = transition temperature; depending on the case, it can correspond to the polymer glass transition or melting temperature) and programmed in a particular shape, (b) the specimen is cooled down below the transition temperature (T < Ttrans) with or without applied stress, which fixes the temporary shape, and (c) if the specimen is again heated above the transition temperature (T > Ttrans), it will recover its original shape. The shape recovery ability of SMPs comes from their unique molecular features. The molecular structure of SMPs includes switching segments and net points. The switching segment changes between the glassy and rubbery states when exposed to the stimuli. The switching segments can be polymer backbones, side groups or chains, functional groups, ionic groups, etc. The net points are created by covalent bonds or intermolecular bonds (e.g., hydrogen bonds). They are responsible for the “memory” of the original shape of SMPs. SMP fibers can be produced by wet spinning [236], melt spinning [237], and electrospinning [238] using various polymers such as polyurethane, polylactic acid, polycaprolactone, and ethylene–vinyl acetate. The features obtained at the fiber level are microlevel surface roughness and a large surface-to-volume ratio [226].
Apart from synthetic polymers, Xiao and Hu [239] reported that wool fibers exhibited an SME effect when exposed to moisture due to the presence of α-keratin in the fibrous protein structure. The study found that the hydrogen bonds present in the α-keratin structure worked as switching segments, while the disulfide covalent bonds acted as net points. Thanks to this, smart thermoregulatory fabrics have been developed using wool fibers [226]. Hu et al. [240] developed a knitted woolen fabric that could increase and reduce its pore size in response to human body sweat. The results showed that the increase in pore size after moisture actuation positively influenced the moisture absorption, air permeability, water vapor transmission rate, and IR body heat transmission. The fabric temperature also decreased in wet conditions compared to dry conditions. In another study, Wang et al. [241] developed shape-memory smart fabrics by incorporating shape-memory filaments as weft yarns. They managed to control the moisture and thermal management of fabrics. Memiş and Kaplan [242] applied a shape-memory polyurethane (SMPU) finish to a woolen fabric to improve its thermal and moisture management properties. It helped improve the fabric breathability (i.e., air permeability and water-vapor permeability) at high temperatures, while it reduced breathability (due to a reduction in the fabric pore size) at low temperatures. However, SMPs suffer from some limitations in terms of wearability, durability, and functionality [243,244]. The mechanical properties of SMPs degrade over time: they easily tear off and form cracks on the polymer surface. In addition, SMP-based fabrics are generally stiffer, display a slow response, and are expensive. Researchers are still working to overcome these limitations so that SMPs can be used in large-scale textile production for thermal management.
Human thermophysiological comfort can also be enhanced by embedding electroactive (EA) materials in the clothing, for example, to generate joule heating [225]. Joule heating, also referred to as resistive heating, is a technique to produce heat using conductive materials due to the material’s resistance to electric current flow [125,245]. During current flow through the conductive material, electrons collide with other atoms/molecules and vibrate, causing heat generation [246,247]. In 1840, British scientist James Prescott Joule came up with a mathematical formulation for joule heating [248], which is Q = I2Rt, where Q represents the amount of heat generation, I represents the current flow, R represents material resistance, and t represents time [225,245]. Hsu et al. [216] developed a silver nanowire dip-coated cotton fabric for thermal comfort management. The fabric exhibited joule heating ability as well as reflected back IR radiation on the inside, allowing for the preservation of body heat. The fabric also demonstrated excellent air permeability, which remained comparable to the untreated fabric, as the nanowires created a porous network on the surface of the fabric. In another study, Doganay et al. [249] developed a joule heating woven cotton fabric coated using Ag nanowires dispersed in an ethanol solution and applied using the dip-dry method. The results showed that the temperature of the coated fabric could be raised between 30 °C and 125 °C with a current flow between 0.2 and 0.92 A and a voltage between 1 and 6 V. Ahn et al. [250] sprayed a mixture of carbon nanotubes dispersed in isopropyl alcohol and Ag nanowires on a nylon–polyurethane (80/20) blended knit fabric. The operating temperature of the joule heating fabric ranged between 35 and 55 °C for voltages of 3 to 5 V. Joule heating textiles can also be prepared by integrating conductive fibers/filaments/yarns into the fabric structures. Cheng et al. [251] developed composite stretchable heating fibers (SHFs) in a hierarchical structure, where a twisted polyester microfiber core was coated with Cu nanowires and then dip-coated in a silicon-rubbed solution and cured. Prior to weaving, the fibers demonstrated excellent mechanical and heating performance. The temperature of the SHFs increased from 20 to 57 °C within 20 s when supplied with 3 V. The SHF fibers were then integrated into a woven fabric structure for joule heating purposes. The application of SHF-based woven heating textiles as a joule heater was also demonstrated. However, joule heating textiles for clothing applications lack standardization. A group of researchers at the University of Alberta is working on the development of test standards to assess the safety and durability of joule heating textiles [252].
The use of thermoelectric (TE) materials embedded into clothing can warm and cool the human body using the Peltier effect [225]. When electricity passes through the junction of N-type and P-type semiconductors, it causes the creation of a thermal gradient. Depending on whether heating or cooling is needed, the hot and cold sides can be flipped by reversing the voltage. The TE-based heating and cooling mechanism is also referred to as an electrocaloric effect in some studies [253,254]. Hong et al. [255] developed a TE cooling vest using two conductive elastomeric layers, between which high-zT firm TE pillars were sandwiched. In this context, zT is a dimensionless value that indicates the energy conversion efficiency of thermoelectric materials [256]. The results showed that the temperature between the cold and heated sides went from 19 °C to 33 °C, while the neutral temperature was 26 °C. However, TE fabrics developed using coatings or polymeric layers exhibit poor breathability. This has motivated researchers to work on TE yarns that can be used to manufacture woven and knitted fabrics [225]. Lee et al. [257] produced TE yarns by electrospinning polyacrylonitrile (PAN) nanofibers, which were then coated with p-type (Sb2Te3) and n-type (Bi2Te3) semiconductors. They produced knitted fabrics with zigzag and garter stitches where neighboring course yarns were either p-type or n-type alternatively. On the other hand, a plain-woven structure was created by interlacing the TE yarn containing both p-type and n-type coated portions connected by Au-coated junctions between two non-conductive yarns in the warp direction and using non-conductive yarns in the weft direction.
6. Human Thermophysiological Comfort Assessment
Human thermophysiological comfort assessment can be conducted in two ways: (a) subjective and (b) objective [258].
6.1. Subjective Assessment
The subjective assessment of human thermophysiological comfort is generally conducted using surveys and questionnaires based on Likert scales to obtain human thermophysiological comfort perception [258]. Some common scales are the thermal sensation scale, comfort perception scale, wetness perception scale, and stickiness scale [259]. For instance, human subjects perform some specific physical activities (e.g., standing, walking, running, and cycling) for a certain period while wearing clothing ensembles under specific environmental conditions [40]. During and/or after the activity, the participants provide their thermophysiological comfort perceptual responses using Likert scales. Human subjects are selected randomly from the population of interest to prevent bias in the thermophysiological comfort assessments. A repeated-measure design statistical approach is preferable for the subjective study, where all the human subjects will be randomly assigned in all exposure conditions. It is important to note that an individual’s response to the thermophysiological comfort scale can vary depending on their demographic and personal preference. In addition, some individuals, such as babies and people with disabilities, cannot easily differentiate the subjective perception of thermophysiological comfort. The subjective thermophysiological comfort assessment scales are sometimes referred to as psychophysical scales.
Human psychophysics detects the presence of external stimuli and translates it as a psychological experience [260]. In the case of thermophysiological comfort, the human body’s somatosensory system senses external stimuli (i.e., temperature) associated with the exposure conditions and creates a psychological experience of the comfort perception [261]. This process is essential for the survival of animal species, as it contributes to thermoregulatory processes (e.g., blood flow volume and shivering) and thermal behaviors (e.g., donning or doffing clothing layers) [2,62]. The somatosensory system in the human body involves different receptors in the skin layer, such as thermoreceptors (sensitive to a change in temperature) and mechanoreceptors (detecting friction, vibration, and pressure) [260]. Thermo- and mechanoreceptors are located in the dermis layer of the human skin [261].
However, human skin does not have any specific sensory receptors for wetness perception, contrary to insects [262]. Therefore, it has been suggested that humans learn to perceive wetness through the complex interaction between thermoreceptors and mechanoreceptors [263]. Bentley [264] showed that when a human finger was dipped in a sheath-covered (dry surface) cold liquid, the blindfolded human subjects felt wetness even though their fingers were not soaked. Bentley [264] suggested that the wetness perception originated from the cold sensation and light pressure on the skin surface. During the actual wetting, the liquid (i.e., water) evaporates from the skin and provides a cool feeling [265]. It is a process similar to the cool-touch feeling, partially accounting for the wetness perception shown by Bentley [260]. Another study found that the perception of coldness and wetness declines when the contact pressure is high between the skin and the material [266]. It has also been reported that if the temperature of the stimulus is higher than the skin temperature, the wetness perception is suppressed [260]. On the other hand, when the thermoreceptors cannot identify temperature differences, the individual uses the stickiness cue as the wetness perception tool [263].
Studies have also shown that ambient temperature and wetness perception are directly associated with human psychophysics [99,267]. A higher temperature of the ambient environment (over 27 °C) and wetness perception cause an increase in discomfort [260]. In thermophysiological comfort research, skin wetness was introduced by Gagge [268] to estimate the human body’s thermal energy balance. A higher magnitude of skin wetness reduces the sweat output due to the fatigue of the sweat glands as well as the blockage of the sweat gland channels.
6.2. Objective Assessment
The objective assessment of human thermophysiological comfort involves the measurement of local skin temperature, heart rate, core body temperature, sweat rate, and neural responses [1,2,260]. These results are then interpreted in terms of human thermophysiological comfort.
The local skin temperature can mainly be determined in two ways: (a) contact [269] and (b) non-contact methods [270]. The contact method requires temperature-sensing devices such as temperature sensors and thermometers to touch human skin. The non-contact method does not require any contact with the human skin, and instead uses IR technology, such as infrared thermography, to measure human skin temperature. The core body temperature is usually determined using ingestible telemetric pills [271]. The pill contains a temperature sensor and a wireless data transmitting system. When the pill is swallowed, it reaches the human gastrointestinal tract and measures the core body temperature. Meanwhile, the wireless system sends the output to a real-time monitoring device. However, this ingestible telemetric pill might be invasive for some people, and researchers are trying to find alternative techniques.
The heart rate can also be determined using contact and non-contact methods. The contact method includes positioning a heart rate sensor on the skin to measure the electrical activity of the heart, with the recording of electrocardiograms [272]. The non-contact method passes light through the skin to measure the heart rate from the change in blood flow volume (photoplethysmography) [273]. The human body’s sweat rate can be obtained using wearable sensors or patches [274]. External patches are positioned on the skin and absorb sweat, and the weight of the patch is measured at the end of the experiment to estimate the sweat loss from the human body. With wearable sensors, the amount of sweat absorbed affects the conductivity of the sensor, which is measured.
Recently, neurophysiological studies have gained large popularity to complement psychophysical studies (or subjective assessment), as it is sometimes difficult to assess the effect of the external stimulus using psychophysical scales [260]. The technique involves the observation of the electrical and chemical activity of the human brain in response to external stimuli [275,276], which are recorded using various advanced techniques, such as electroencephalography, transcranial magnetic stimulation, positron emission tomography, and functional magnetic resonance imaging. The cutaneous thermal and wetness cues originating at the thermal and mechanoreceptors of the human skin travel through four regions to generate a neural response [2,260]. These regions are (a) the peripheral nervous system (PNS), (b) spinal cord, (c) thalamus, and (c) cerebral cortex (Figure 7). The PNS is responsible for sending somatosensory information to the central nervous system (CNS). There are various types of nerves in the PNS, such as moderately myelinated Aβ fiber (associated with mechanoreceptors), myelinated Aδ fiber (associated with cold-sensitive thermoreceptors), and unmyelinated C fiber (associated with warm-sensitive thermoreceptors) [260,277,278]. The mechanical cues at Aβ fiber peripheral nerves travel through the dorsal-columns pathway in the spinal cord and then reach the human brain. On the other hand, the spinothalamic tract in the spinal cord sends temperature cues to the human brain. Lastly, thermal and mechanical cues reach the thalamus region in the center of the brain and eventually generate neural responses in the cerebral cortex.
Figure 7.
Neurophysiological pathways for cutaneous temperature and wetness sensation (inspired by [260]).
6.3. Relationship between Subjective and Objective Assessment of Thermophysiological Comfort
Thermophysiological comfort models developed before 1990, such as Fanger’s model, mainly applied to steady-state and uniform conditions [18]. However, human thermal environments are usually transient and non-uniform [279]. Thus, recently developed thermophysiological comfort prediction models have incorporated transient and non-uniform thermal environments [24,64,258,280,281]. These models translate local skin and core body temperatures (derived from the objective assessment) into the subjective comfort output. For instance, Zhang et al. [279] developed a local thermal sensation model of various human body parts considering non-uniform and transient conditions. The study found that when the mean skin temperature of the local body part is between 29 and 34 °C, the correlation between the mean skin temperature and the thermal sensation is approximately linear (Figure 8a). If the mean skin temperature falls outside this range, the correlation curve takes a sigmoidal shape, represented by the logistic function in Figure 8b. A mathematical equation (Equation (36)) was proposed to determine the thermal sensation based on the skin temperature of the local body part (Tskin,i) and the set-point skin temperature (Tskin,i,set). In this context, the set-point temperature refers to the optimal temperature at which the thermal sensation of a human body is neutral [282]. The set-point skin temperature (33 °C) is lower than the core body temperature at the neutral thermal sensation point.
Figure 8.
Correlation between the mean skin temperature and the thermal sensation: (a) linear correlation trend for mean skin temperatures of local body parts between 29 and 34 °C, and (b) sigmoidal trend curve outside this mean skin temperature range (reproduced from [279] with permission from Elsevier).
In Equation (36), C1 is the coefficient for the correlation curve between the mean skin temperature and the thermal sensation [279]. Certain body parts have more influence on the overall thermophysiological comfort, such as the chest and back; they have higher C1 values. On the contrary, body parts such as the hands have a lower value of C1 as they do not have a strong effect on the overall thermophysiological comfort. When the skin temperature is close to the set-point skin temperature, the local sensation approaches a neutral point. The study mentioned that when Tskin.i < Tskin.i.set, then the local sensation becomes colder, but when Tskin.i > Tskin.i.set, the effect is not clear.
It is important to note that the local body thermal sensation is also affected by the whole-body thermal sensation [283]. Further developments of Equation (36) added the mean skin temperature and average set-point skin temperature of the whole body to estimate the steady-state local sensation [279]. A dynamic sensation model was developed by introducing the time derivative of the skin temperature and the time derivative of the core body temperature. Finally, the transient thermal sensation was estimated from the summation of the steady-state thermal sensation and dynamic thermal sensation.
In another study, Zhang et al. [284] developed a thermal comfort model from the local thermal sensation for non-uniform and transient conditions. The study showed that the thermal sensation (along the X-axis) and comfort responses (along the Y-axis) created a saddle-shaped curve (Figure 9a). When the whole body became hypothermic, the scatter plot had a positive slope; contrarily, when the whole body became hyperthermic, the scatter plot had a negative slope (Figure 9b). For instance, in a hypothermic body, a local body part feels very pleasant in warm conditions, which is also the least pleasant situation for a hyperthermic body part. Zhang et al. [284] developed a mathematical model (Equation (37)) to predict the local thermal comfort of the human body from local thermal sensations.
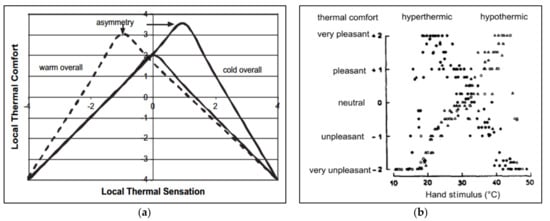
Figure 9.
(a) Saddle-shaped curve produced by the local thermal comfort and local thermal sensation, and (b) scatter plot of the thermal comfort of hyperthermic and hypothermic human bodies (reproduced from [284] with permission from Elsevier).
When x is large, Equation (37) approaches −b (leading to a negative slope) [284]. On the other hand, when x is small, comfort perception = (a − b) (i.e., a positive slope). These two slopes meet close to the neutral intersection point of the thermal sensation and thermal comfort perception scales and create a saddle shape. C indicates the stiffness of the intersection of the two slopes. The offset value moves the maximum comfort left (for warm) or right (for cold) from the neutral zone (Figure 9a).
Finally, the local thermal sensation and thermal comfort of various body parts were incorporated together to create overall thermal sensation and thermal comfort models. Zhang et al. [283] developed global or overall thermal sensation and thermal comfort models using results from local thermal (Slocal) sensations under non-uniform and transient conditions. The study showed that the overall thermal sensation is impacted predominantly by the back, chest, and pelvis. These three body parts are very susceptible to cool sensation. Even though the other body parts have a warm sensation, the overall sensation will be cool if the back, chest, and pelvis have a cold thermal sensation. This is called a complaint pattern. However, under a neutral environment, the overall sensation does not have a complaint pattern. The head, neck, face, and hands are considered the lowest cool perception zones. Results showed that the overall thermal sensation was governed by the cooling and recovery (or warming up) of the back (dorsal part) skin, as it is a dominant body part. However, the hand did not strongly contribute to the overall thermal sensation because the hand is not a dominant body part. The overall thermal sensation model was developed considering two cases: (a) no opposite sensation condition (when all body parts have the same sensation, either warm or cool, and the local thermal sensations (unitless) of all the body parts are within ±1), and (b) opposite sensation (when a body part significantly feels different than the other body parts). The no-opposite overall thermal sensation model consisted of two cases: (a) high-level thermal sensation (i.e., when more than three body parts have local thermal sensation |Slocal| ≥ 2), (b) low-level thermal sensation model (i.e., when the third-highest local thermal sensation |Slocal, thirdmax| is ≤ 2). It is important to note that when the thermal sensation of the dominant part is slightly cool or ≤ −1, the overall thermal sensation is cool. For two groups of opposite sensations, the larger group follows the no-opposite sensation rule, and the smaller group follows the combined force rule. The combined force rule estimates the overall thermal sensation effect of the smaller group from the thermal sensation of two local body parts with extreme values. Finally, the overall thermal sensation is estimated from the summation of the local overall thermal sensation of the larger group (Soverall bigger group) and the combined force. The second part of the study constructed models for overall thermal comfort depending on a criterion of whether the subject has control over the thermal environment was used. The models were validated using experimental data from published research articles. Figure 10 shows the overall workflow of thermophysiological comfort model development using the subjective and objective assessment results.
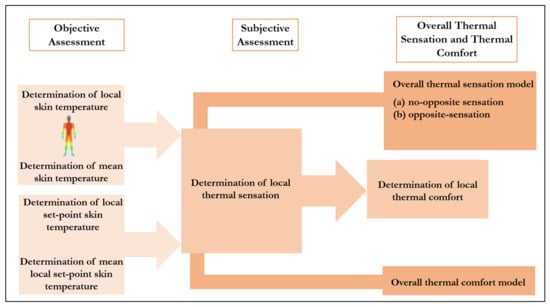
Figure 10.
Overall workflow of thermophysiological comfort model development.
7. Clothing Thermophysiological Comfort Assessment
The thermal comfort provided by fabrics can be assessed by subjective and objective approaches [285].
7.1. Subjective Assessment
The subjective thermal comfort assessment of clothing relies on human subjects’ wear trials [259]. During a wear trial, participants are asked for feedback on the thermal comfort perception of clothing. The subjective assessment of clothing uses Likert scales, similar to subjective assessment of the human thermophysiological comfort (mentioned in Section 6.1). ISO 10551 [286] provides guidelines on how to construct thermal comfort assessment Likert scales. The questions for the Likert scales should be specific, clear, non-leading, unbiased, and impersonal. Several studies conducted subjective thermal assessment trials of clothing following the guidelines of ISO 10551. For instance, Grujic and Geršak [287] performed a subjective thermal comfort assessment of women’s summer clothing (including woven dresses, blouses, and shorts) using a 5-point Likert scale. The rating points ranged from 0 to 4, where 0 corresponded to dry, 1 to slightly humid, 2 to humid, 3 to wet, and 4 to very wet. The study found that the subjective assessment results had a strong correlation with human thermophysiological variables such as skin temperature and amount of excreted sweat. In another study, Celcar [288] investigated the subjective thermal comfort of clothing made for cold environments using the guidelines of ISO 10551. The study found that the perception of clothing thermal comfort by human subjects was strongly influenced by the environmental conditions and the clothing system. It is important to note that most of the scholarly works have used the wording subjective thermal comfort of humans and subjective thermal comfort of clothing interchangeably, as the subjective thermal comfort assessment is conducted when the clothing is worn [287,288].
7.2. Objective Assessment
A series of laboratory-scale equipment has also been developed over the years to assess the thermophysiological comfort of fabrics and clothing: the sweating-guarded hot plate, sweating manikin, and sweating torso.
7.2.1. Sweating-Guarded Hot Plate
A sweating-guarded hot plate is an advanced instrument for the thermal comfort assessment of fabrics used by standard test methods such as ISO 11092 [42] and ASTM F1868 [289] to characterize the dry thermal and evaporative resistance of fabrics. Also called the skin model, it provides a two-dimensional representation of the heat and moisture transfer between the skin (simulated by the hot plate), the fabric, and the environment [290].
The sweating-guarded hot plate consists of a test plate, a thermal guard, a lower guard, a temperature-controlling device, a heat-supplying device, and a water-dosing system. The surface area of the test plate in ISO 11092 is 0.04 m2 (200 mm × 200 mm) [42]. Other sizes of the sweating-guarded hot plate have also been used by researchers [291]. For instance, a larger sweating-guarded hot plate with a test plate surface area of 0.065 m2 is available [292]. The test plate is equipped with a heating element and a water supply system. The test plate is surrounded by a thermal guard to prevent parasitic heat loss on the sides. Both the test plate and the thermal guard are surrounded by a lower guard for further thermal insulation. There is a rotating wheel outside the lower guard, which is used to move up/down the test plate and thermal guard to create an air gap between the sweating-guarded hot plate and the fabric layer. To create this air gap, a spacer is inserted between the test plate and the fabric layer [3]. The sweating-guarded hot plate is kept inside an environmental chamber to conduct the experiments under controlled environment conditions.
For the estimation of the dry thermal resistance of the fabric specimen, the dry thermal resistance of the bare test plate is determined first using a surface temperature of 35 ± 0.1 °C for the hot plate (i.e., the test plate and thermal guard) [42]. The rest of the conditions are an ambient temperature of 20 ± 0.1 °C, a relative humidity of 65 ± 3%, and an air velocity of 1 ± 0.05 m/s. Then the fabric specimen is placed on the hot plate surface. The total dry thermal resistance of the fabric and air layer is determined under the same experimental conditions. The fabric’s dry thermal resistance is determined by subtracting the dry thermal resistance for the bare test plate from the total dry thermal resistance of the fabric and air system. Other values may be used for the experimental parameters depending on the study plan.
The fabric’s evaporative resistance is determined in a similar fashion. However, in this case, the test plate surface is covered with a film of cellophane or another liquid-tight/water-vapor-permeable material, and water (to simulate sweat) is supplied to the instrument to determine the bare test plate’s evaporative resistance [42]. Next, the fabric specimen is placed on the hot plate surface covered with the cellophane film, and the total evaporative resistance of the fabric and air layer is determined. The fabric’s evaporative resistance is calculated by subtracting the bare test plate evaporative resistance from the total evaporative resistance of the fabric and air system. The experimental conditions for the evaporative resistance test are an ambient temperature of 35 ± 0.1 °C, a hot plate surface temperature of 35 ± 0.1 °C, a relative humidity of 40 ± 3%, and an air velocity of 1 ± 0.05 m/s.
Most sweating-guarded hot plates are horizontal in orientation, but some models allow making the measurement at an angle or vertically, which may better simulate the configuration of fabrics when worn on the body and allow observing the chimney effect, as described in [290] for the vertical cylindrical microclimate. However, the regular version of the sweating-guarded hot plate instrument may suffer from some limitations. First, it generally does not provide information about the sweating rate. However, this information is critical to estimate the heat loss from the amount of evaporated sweat, the amount of sweat absorbed by the fabric, and the amount of sweat present on the hot plate simulating the skin [33]. In addition, the flat layout of the fabric on the hot plate does not correspond to the somewhat cylindrical shape taken by clothing parts when worn. This limitation has been overcome with the development of sweating manikins and sweating cylindrical torsos described in the following sections [18]. Thermophysiological models have also been incorporated into the software system of sweating manikins and sweating cylindrical torsos to predict thermophysiological parameters, such as skin temperature, core body temperature, and comfort sensations [66].
7.2.2. Thermal Sweating Manikins
Thermal sweating manikins have been in use in comfort-related research for more than 70 years [12,293]. They are employed in the ASTM standard test methods for dry thermal resistance [294] and evaporative resistance [295]. A thermal sweating manikin is a human-shaped instrument that exchanges heat and moisture with the surrounding environment [12]. Various types of manikins (e.g., both male and female) have been developed with different specifications based on the anthropometry of different nations. Some of the most popular manikins are Newton, Norman, Coppelius, SAM, Walter, Ruth, ADAM, TOM, and Wenda [296].
Thermal sweating manikins can be one-segment or multi-segment (e.g., 7, 16, 19, 36) [296]. The manikin contains many body parts, including separated fingers connected to hand palms. The individualized fingers allow gloves to be properly fitted on the manikin hand. The manikin consists of a power supply system (to maintain the skin temperature at a set temperature), a water supply system (to simulate sweat generation), and different sensors for the measurement of the skin temperature, air temperature, and relative humidity. The experiment is conducted within an environmental chamber where the air temperature, air velocity, and relative humidity are controlled. The surface area of the manikin in ASTM F2370 is 1.8 ± 0.3 m2, and the manikin height is 170 ± 10 cm [295]. The manikin can have a single heating zone or multiple heating zones. Each heating zone contains a certain number of water nozzles, which are distributed equally around the body to mimic the human sweating process. Prior to the experiment, the whole body of the sweating manikin is covered by a next-to-skin layer. This next-to-skin layer absorbs the water droplets from the orifices and saturates the surface of the whole next-to-skin layer. The overall saturation of the next-to-skin layer is confirmed by thermal imaging.
The dry thermal resistance of the clothing ensemble is conducted in a similar way to that using the sweating-guarded hot plate [294]. First, the dry thermal resistance of the nude manikin is assessed, followed by the total dry thermal resistance of the clothing ensemble and air layer system. The dry thermal resistance of the clothing ensemble is computed by subtracting the ratio of the nude manikin dry thermal resistance by the clothing cover factor from the total dry thermal resistance of the clothing ensemble and air layer system.
The process of estimating the evaporative resistance is slightly different. In this case, the manikin is dressed with a next-to-skin layer (e.g., a tight-fit knitted suit) to help saturate the manikin surface homogeneously with water [295]. The manikin is then brought to an equilibrium state where the saturated manikin skin temperature stays at 35 ± 0.1 °C for at least 30 min. The evaporative resistance of nude manikin is then determined. Next, the test clothing ensemble is worn over the saturated next-to-skin layer. When the system with the test clothing reaches equilibrium, the total evaporative resistance of the clothing ensemble and air layer (Ret) is measured. The evaporative resistance of the clothing ensemble is calculated by subtracting the ratio of the nude manikin evaporative resistance by the clothing cover factor from the total evaporative resistance.
Psikuta [297] coupled Fiala’s thermophysiological comfort model with a multi-sector thermal sweating manikin, called SAM, in their Ph.D. work. The results showed a good agreement between the manikin’s output and human subject results in terms of predicting the thermophysiological comfort. In another study, Psikuta et al. [298] coupled the Manikin PC2 thermophysiological model (ThermoAnalytics, Detroit, MI, USA) with an adaptive sweating manikin named Newton. The term adaptive sweating manikin refers to a manikin that can simulate the heat flux, temperature, and sweat rate at the outer surface, like a human body, when coupled with thermophysiological comfort models depending on the exposure conditions. The results showed a good agreement between the responses of Newton and human subjects to passive heating and cooling. Wang [299] investigated the influence of physical motion on the thermophysiological reactions of the adaptive manikin (Newton) and human subjects. The study found that, for the standing position, Newton overestimated the core body temperature compared to human subjects, while there was no significant difference in the core body temperature between the manikin and human subjects during walking. They suggested that the adaptive thermal manikin should only be used while simulating human activities. More recently, Martinez-Albert et al. [300] developed a new test method to assess the thermophysiological comfort of cooling vests, which combined both subjective and objective evaluation. The objective evaluation used a Newton manikin in conjugation with the Manikin PC2 software. The manikin was powered at different rates corresponding on the level of physical activity independently of the surface temperature. The manikin output variables were the thermal comfort based on the ASHRAE-7 point scale, thermal sensation scale, hypothalamus temperature, and skin temperature. The researchers concluded that the newly proposed method did not accurately represent the human thermal comfort perception for the high levels of physical activity or very high metabolic heat. However, the predicted results were found to be consistent with the data generated following the ASTM 2371 standard for low-level physical activity.
Sweating thermal manikins are generally adult-sized and available both in male and female shapes [18]. There are also a few thermal manikins that are infant-sized [301]. For instance, a baby manikin with thermoregulation was developed at Bunka Women’s University to determine comfort [302]. Golden et al. [303] worked with an infant-sized manikin to create a predictive formula for clothing insulation. The study found that clothing thermal insulation can be predicted from the garment weight and ratio of the body surface area covered by clothing and nude (BSAC).
7.2.3. Sweating Cylindrical Torso
A sweating cylindrical torso determines the coupled heat and moisture transfer properties (i.e., dry thermal insulation, cooling properties, and drying behavior) of fabrics in a vertical cylindrical arrangement, as described in ISO 18640-1 [32]. The sweating cylindrical torso uses a gravimetric system for the supply of sweat-simulating water and measures the amount of water dripping from the torso surface, which makes it possible to estimate the amount of evaporated water from the torso to the environment through the cloth layer [33]. A hollow cylindrical spacer can be placed between the torso and the cloth layer to mimic the air gap between the human body and the cloth [64]. Structurally, the torso has a vertical cylindrical shape with an upper guard and a lower guard on both cylindrical ends, mimicking the human trunk [32]. The torso can either be single-sector or multi-sector [304]. The heat supply and sweat rate are centrally controlled in a single-sector torso, whereas the heat supply and sweat rate are controlled separately in each segment of the multi-sector torso. The experiment is conducted inside a conditioning room, where the air temperature, air velocity, and relative humidity are controlled [32].
The experiment is carried out in three phases [32,305]: (P1) 35 °C constant temperature at the torso surface without sweating for 60 min, (P2) 125 W constant heat supply and 100 g/h constant sweat rate for 60 min, and (P3) 25 W constant heat supply without sweating for 60 min. The torso is wrapped in a wicking layer similar to the manikin to spread the moisture homogeneously over the torso surface. The human body surface contains 50 to 250 sweat glands per cm2 to facilitate sweating. In the case of the torso, there is one sweat nozzle per cm2. An experiment with the succession of the P1, P2, and P3 phases creates two typical curves: (a) temperature (of the torso surface) vs. time, and (b) amount of sweat supplied vs. time (Figure 11).
Figure 11.
Hypothetical curves generated in a typical sweating cylindrical torso experiment: (a) temperature vs. time, and (b) amount of moisture supplied vs. time (inspired by [32]).
In Figure 11a, the P1 phase determines the total dry thermal resistance (Rct) of the system. The curve corresponding to the P2 phase shows a cooling delay (CD), an initial cooling (IC), and a sustained cooling (SC). The curve for the P3 phase starts with post-cooling (PC) [32]. CD occurs due to the release of the heat of sorption by the fabric when it initially absorbs sweat. The released heat of sorption and the absence of initial evaporative cooling increase the total heat of the torso-clothing system, evidenced by an increase in the temperature. Once the fabric is in IC, evaporation cooling kicks in. Moreover, the addition of more sweat does not lead to the generation of the heat of sorption. Therefore, a sharp temperature drop occurs at the skin-simulating cylindrical surface. When the temperature reaches the starting point of SC, the system stabilizes and the torso surface temperature enters a slow decrease regime. During PC, the cooling persists even if the water supply has been stopped as sweat evaporation continues and the heat supplied to the torso is reduced. In Figure 11b, the P2 phase causes moisture dripping or evaporation (represented by “a”) and moisture absorption by the fabric (represented by “b”), while “c” in the P3 phase represents the sweat drying time.
Psikuta et al. [29] investigated the heat and mass transfer phenomena in the skin–cloth–environment system using a single-sector sweating cylindrical torso coupled with Fiala’s thermophysiological comfort model. The instrument sensed the experimental conditions and then generated physiological responses, e.g., skin temperature and body core temperature, based on Fiala’s model. When the skin temperature was used as the controlled parameter, the heat flux from the torso surface was considered a feedback signal. The study investigated the effect of homogeneous heat flux on the skin and core temperature for different exposure conditions. The results revealed that the thermal response of the single sector torso showed a good agreement with human trials (semi-nude) in steady-state and transient conditions. In another study, Psikuta et al. [306] explored the thermal response of the single-sector sweating torso without a physiological control model to simulate the impact of clothing and environment. The findings of this study also showed good agreement with human trial results.
The sweating cylindrical torso makes it possible to determine more precisely the sweat management behavior in the skin–cloth–environment system. For instance, Guan et al. [33] studied the moisture transfer characteristics of human-clothing systems with or without radiant heat exposures. The moisture transfer characteristics were described in terms of the total supplied sweat, evaporated sweat, skin wettedness, and sweat evaporative efficiency. Definitions of these terms are given below. The results showed that the sweat evaporation rate was positively correlated with the sweat rate and amount of moisture absorbed by the fabric. The sweat rate was negatively correlated with the sweat evaporative efficiency. In addition, Candas et al. [307] reported that the sweat evaporative efficiency decreased with an increase in skin wettedness.
- ▪
- Total supplied sweat = (sweat present on the skin + sweat absorbed by the fabric + evaporated sweat + dripped sweat) [33].
- ▪
- Skin wettedness = body surface area covered by sweat/total body surface area.
- ▪
- Sweat evaporative efficiency (ηevap) = total evaporated sweat from the skin and cloth/total supplied sweat.
In another study, Guan et al. [308] investigated the apparent evaporative cooling efficiency of single and multi-layered clothes under a continuous sweating situation. The apparent evaporative cooling efficiency (ηApp) was estimated from the ratio of the apparent evaporative cooling (EApp) and total evaporative heat loss from the skin and environment due to sweat evaporation (estimated from the evaporated mass loss, EMass). EApp is the heat loss determined using the sweating torso during the evaporative resistance test both under iso-thermal and non-iso-thermal conditions. EApp under iso-thermal conditions includes only real evaporative cooling due to sweat evaporation from the skin (EReal), while EApp under non-isothermal conditions includes real evaporative cooling (EReal) and non-evaporative cooling components (e.g., heat pipe effect and wet conduction, Enon-Evap). The heat pipe effect occurs when sweat evaporated on the skin is absorbed by the inner fabric surface and releases heat from the outer fabric surface to the environment [309]. The heat loss of the wet fabric (i.e., when the fabric is saturated with sweat) is called wet conduction. The total evaporative heat loss (EMass) not only comes from the heat by the skin (EReal). Some sweat also absorbs heat from the environment to convert it into vapor (EEnv). Thus, the apparent evaporative cooling efficiency (ηApp) can be estimated from Equation (38).
ηApp = EApp/EMass = (EReal + Enon-Evap)/(EReal + EEnv)
Guan et al. [308] reported an increase in the evaporative cooling efficiency due to the heat pipe effect and wet conduction for hydrophilic fabrics. However, for hydrophobic fabrics, there was no significant increase in the evaporative cooling efficiency. The study also mentioned that hydrophilic fabrics showed an increase in vertical wicking with the sweat rate, which led to higher cooling efficiency.
It is important to note that it was shown that the evaporative heat-loss calculation based on mass loss, which is used in many studies, overestimates the total evaporative heat loss from the human skin under hot conditions because some amount of liquid sweat absorbs heat from the ambient to change the phase into vapor [309].
8. Summary and Key Insights
This review showed that the previously developed thermophysiological comfort prediction models depend on the human body’s physiological characteristics and processes, microclimate properties, clothing heat and moisture transport properties, and environmental conditions. These models have been categorized based on either the segmentation of body parts or the characteristics of the human body’s cross-sections [18]. The thermal comfort of a human body depends on the heat balance, which is controlled by conductive, convective, radiative, and evaporative heat transfer between the human body and the environment. Finally, the heat balance equation incorporating the heat transfer mechanisms is used to construct thermophysiological comfort models [1].
Heat and sweat generation within the human body depend on a person’s age, sex, weight, height, and demographic, as well as on metabolic heat production due to physical activity, basal metabolism, shivering, and vasomotion [8]. The thickness of the microclimate affects the heat and moisture transfer in the skin–clothing–environment system [64]. Moreover, human body movement causes a pumping and ventilation effect in the microclimate, which increases heat and moisture transfer from the human body to the environment [28]. The fabric properties that affect the thermal balance of the human body include thermal resistance, water vapor transmission rate, moisture wicking, and thermal effusivity [37]. Environmental conditions affecting thermophysiological comfort include air temperature, relative humidity, mean radiant temperature, and air velocity [8].
8.1. Research Gaps and Future Directions
Thermophysiological comfort depends on a wide range of variables. Previously developed thermophysiological comfort models suffer from limitations in terms of incorporating all these variables into the model. Fiala et al.’s [24,64] and Fanger’s [19] models do not consider the effect of microclimate thickness on the heat and moisture transfer in the skin–clothing–environment system, which affects the thermal balance of the human body. Some recent models, such as Joshi et al. [4] and Mert et al. [65], took the microclimate thickness into consideration. However, these models only describe the conductive and convective heat transfer into a vertical microclimate without considering the convective transfer of evaporated sweat. Ding et al. [3,86] developed a heat and mass transfer model in the skin–clothing–environment system that includes the microclimate air gap. Their study showed the presence of moisture-vapor convection in the horizontal microclimate. However, Ding et al.’s [3,86] work lacks experimental validation.
Another limitation is that current thermophysiological comfort models only include two fabric properties: (a) dry thermal and (b) evaporative resistance. However, there are other fabric properties (such as moisture absorption and wicking, air permeability, thermal effusivity, water vapor transmission, reflectivity, and emissivity) that can affect the heat and moisture transfer in the skin–clothing–environment system to maintain human thermophysiological comfort [33,37,126]. The relationship between the thermophysiological variables (such as heart rate, skin temperature, and core body temperature) and fabrics’ heat and moisture transport properties (other than dry thermal and evaporative resistance) has not been explored yet.
The existing technology for the thermal comfort assessment of fabrics also suffers from some challenges. The test methods to evaluate the fabric’s heat and moisture transport properties do not assess thermal comfort in a realistic way, i.e., considering when the fabric will be worn as a part of the garment. For instance, the water vapor transmission rate experiment of fabrics based on ASTM E96 is conducted at 23.5 ± 0.5 °C [43]. However, the evaporation of sweat occurs on human skin, and the average skin temperature is around 35 °C [1]. This limitation can be overcome when testing the fabric’s water vapor resistance or evaporative resistance using a sweating-guarded hot plate, where the hot plate surface temperature is maintained at 35 °C throughout the test [42]. However, the surface of the hot plate is flat, and it is usually kept in a horizontal orientation, contrary to human body shape and orientation [65].
On the other hand, when assessing the fabric’s thermal comfort properties using human subjects, the results can vary depending on sex, body type, and demography of subjects [40]. Further, there is a significant research gap in the area of the thermal comfort psychophysical scale. For instance, the thermal effusivity of fabrics has been linked to the thermal sensation scale [283,310], which is generally used for the subjective assessment of clothing thermal insulation. On the other hand, the development of a psychophysical scale to determine the wetness perception of fabrics made of various fibers is critically needed so that the level of physical stimuli that trigger the wetness sensation is determined [143]. For instance, a polyester and a cotton fabric may not give a perception of wetness at the same moisture content.
Advanced instruments such as sweating thermal manikin and sweating cylindrical torso have made it possible to determine clothing thermal comfort properties in a more realistic way [32,294,295]. The sweating thermal manikin can determine the dry thermal and evaporative resistance of clothing while simulating various levels of physical activities. These instruments have also been coupled with thermophysiological comfort models to simulate the human physiological response [29]. One major limitation of these two instruments is that they have a lower number of sweating nozzles than the number of sweat glands present on human skin. To facilitate the even moisture distribution on the surface of the manikin and torso, a quick saturation, moisture-wicking cloth is worn over the manikin or wrapped around the torso [295]. This helps in achieving moisture spreading and evaporation from the manikin and torso surface to proceed similarly to what has been observed with human skin. Another advantage of using these two instruments is that they can assess both heat and moisture transport properties (such as dry thermal resistance, wicking, drying, and heat of sorption) at the same time, which is not possible with the traditional bench scale test methods [306].
Although the assessment of clothing thermal comfort technologies has demonstrated significant progress, some aspects remain underrepresented in the current state of the literature. For instance, very few studies have focused on how fabrics would behave when they are exposed to outside environmental conditions, such as the effect of sun exposure and precipitation. The effect of sun exposure on clothing heat and moisture transport properties has been investigated using radiant heat exposure in a lab setting [110]. It was concluded that, under sweating conditions, the presence of radiant heat leads to a larger human body heat gain when wearing clothing made of hydrophilic fibers compared to hydrophobic fibers. In the case of precipitation, most scholarly works focused on the water-repelling behavior of fabrics treated with a variety of chemicals [189,190,191,192,193,194,195]. However, the human body may also be exposed to rainy conditions while wearing water-absorbing clothes. Wang et al. [311] stated that the spraying of water onto the cloth surface can facilitate heat loss from the human body in a hot climate environment. The statement suggests that when exposed to rain, the human body might lose heat through soaked clothes. In the case of protective clothing, researchers intensively focused on the protective performance against different hazards (such as exposure to high temperature, steam, and hot liquids) over the thermophysiological comfort aspect [312,313]. Only in recent years has the importance of thermophysiological comfort been acknowledged [314].
In addition, when moisture generated on the skin is absorbed by the cloth, questions remain regarding how it will impact the human thermal balance in transient conditions [315]. The wet cloth may release heat in the microclimate due to the latent heat of sorption and in the environment from the outer fabric surface by the heat pipe effect [309]. The wicking and drying of moisture on the fabric surface may also influence the heat loss through the fabric [316]. In-depth investigations of all these parameters using reliable test methods have yet to be reported.
Finally, the discussion in this review has been limited to heat and moisture transfer through single-layer clothing. However, a clothing ensemble can be bilayer or multilayered, and further research can be carried out on that aspect. A few researchers have investigated heat and moisture transfer through multilayered clothes [33,317]. However, the accuracy of the theoretically simulated results is affected by the heterogeneity of the air gaps formed between the fabric layers that vary as a result of human body movement. Moreover, the mechanisms of heat and moisture transfer have been described in this work in a steady state, which might not appropriately depict cases when the human body is exposed to non-uniform and transient conditions. The ability to incorporate the fabric’s thermal and moisture management behavior can improve the predictability of a thermophysiological comfort prediction model.
8.2. Thermophysiological Comfort Conceptual Model
This review has shown the complexity of thermophysiological comfort prediction models and how different controlling factors of these models are interconnected [2]. To represent the multifaceted and interconnected nature of the thermophysiological comfort model, it is proposed to use Bronfenbrenner’s human ecological model as an inspiration. Bronfenbrenner’s model illustrates how child development depends on a multilayer concentric system [318]. Bronfenbrenner placed the child or individual at the center of the model. The following successive layers are defined as the microsystem, mesosystem, exosystem, macrosystem, and chronosystem. Similarly, a human thermal comfort model can be built with the individual at the center (Figure 12). The successive layers of this conceptual model are the physiological characteristics and processes, microclimate, clothing properties, and environmental conditions. All these concentric layers control the human thermal balance [2,4,12,104]. More concentric layers can be added to the model to incorporate the sociocultural effect on overall comfort [1].
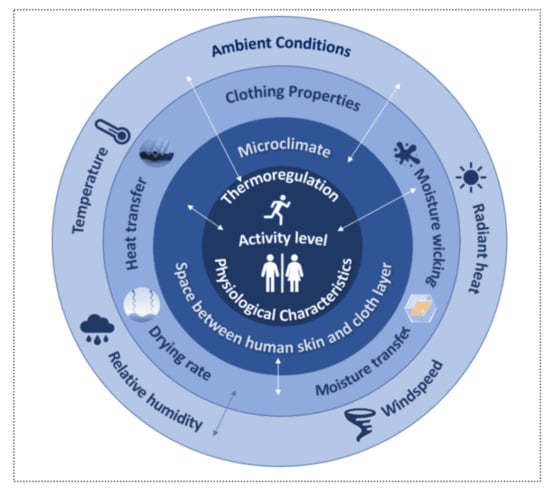
Figure 12.
Proposed thermophysiological comfort model.
As such a model places the human body’s physiological characteristics and processes at the very center of the conceptual model, it signifies that human body weight, height, sex, age, etc. and vasodilation, vasoconstriction, heart rate, shivering, etc. are the most important parameters that affect the human thermophysiological comfort [2]. The second concentric layer is the microclimate [3,86]. It contributes to human thermophysiological comfort by acting as a heat and moisture transfer medium between the human body and the cloth. This layer has been largely neglected in previous studies [3,24,64,86]. Similarly, the fabric properties of the clothing, such as the thermal resistance, moisture-vapor transmission rate, moisture wicking, and drying behavior, impact human thermophysiological comfort [11]. The last layer in the conceptual model corresponds to the ambient conditions, such as the temperature, relative humidity, and wind speed. Exposure to radiant heat from the sun or precipitation will also affect human thermophysiological comfort.
All these layers are connected with one another using double arrows, meaning that they interplay in terms of their effect on the human thermoregulation process and thermal comfort. For instance, the amount of heat and moisture transferred through the cloth depends on the size of the microclimate, as well as the temperature and moisture-vapor concentration gradient between the surface of the human body and the environment [28]. The absorption and wicking of moisture in the cloth depend on how well the garment fits the human body [178]. While sweat evaporation takes place on the cloth surface to facilitate drying, it may cool the human body [315]. Finally, the ambient conditions can significantly impact the factors corresponding to the inner concentric layers in the conceptual model [2].
Author Contributions
Writing—original draft preparation, M.R.I.; writing—review and editing, P.I.D. and K.G.; visualization, M.R.I.; funding acquisition, P.I.D. and K.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by MITACS (Project IT18447) and lululemon athletica (Canada).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
As this is a review paper, data are available in the articles cited.
Acknowledgments
The authors want to thank Jane Batcheller for her feedback on the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Parsons, K.C. Human Thermal Comfort; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Abingdon, UK, 2020. [Google Scholar]
- Angelova, R.A. Textiles and Human Thermophysiological Comfort in the Indoor Environment; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar] [CrossRef]
- Ding, D.; Tang, T.; Song, G.; McDonald, A. Characterizing the Performance of a Single-Layer Fabric System through a Heat and Mass Transfer Model—Part I: Heat and Mass Transfer Model. Text. Res. J. 2011, 81, 398–411. [Google Scholar] [CrossRef]
- Joshi, A.; Wang, F.; Kang, Z.; Yang, B.; Zhao, D. A Three-Dimensional Thermoregulatory Model for Predicting Human Thermophysiological Responses in Various Thermal Environments. Build. Environ. 2022, 207, 108506. [Google Scholar] [CrossRef]
- Havenith, G.; Fiala, D. Thermal Indices and Thermophysiological Modeling for Heat Stress. Compr. Physiol. 2015, 6, 255–302. [Google Scholar] [PubMed]
- Havenith, G. Heat Balance When Wearing Protective Clothing. Ann. Occup. Hyg. 1999, 43, 296–298. [Google Scholar] [CrossRef]
- Holmér, I. Protective Clothing in Hot Environments. Ind. Health 2006, 44, 404–413. [Google Scholar] [CrossRef]
- Havenith, G.; Hartog, E.A.D.; Martini, S. Heat Stress in Chemical Protective Clothing: Porosity and Vapour Resistance. Ergonomics 2011, 54, 497–507. [Google Scholar] [CrossRef]
- Holmér, I. Protective Clothing and Heat Stress. Ergonomics 1995, 38, 166–182. [Google Scholar] [CrossRef]
- Parsons, K.C. Human Thermal Environments; Taylor & Francis: Abingdon, UK, 2002. [Google Scholar]
- Song, G. Improving Comfort in Clothing; Woodhead Publishing Limited: Cambridge, UK, 2011. [Google Scholar]
- Psikuta, A.; Allegrini, J.; Koelblen, B.; Bogdan, A.; Annaheim, S.; Martínez, N.; Derome, D.; Carmeliet, J.; Rossi, R.M. Thermal Manikins Controlled by Human Thermoregulation Models for Energy Efficiency and Thermal Comfort Research—A Review. Renew. Sustain. Energy Rev. 2017, 78, 1315–1330. [Google Scholar] [CrossRef]
- Alba, B.K.; Castellani, J.W.; Charkoudian, N. Cold-induced Cutaneous Vasoconstriction in Humans: Function, Dysfunction and the Distinctly Counterproductive. Exp. Physiol. 2019, 104, 1202–1214. [Google Scholar] [CrossRef]
- Haman, F.; Blondin, D.P. Shivering Thermogenesis in Humans: Origin, Contribution and Metabolic Requirement. Temperature 2017, 4, 217–226. [Google Scholar] [CrossRef]
- Luginbuehl, I.; Bissonnette, B. Thermal Regulation. In Elsevier eBooks; Saunders Elsevier: Philadelphia, PA, USA, 2009; pp. 557–567. [Google Scholar] [CrossRef]
- Chaplin, G.; Jablonski, N.G.; Sussman, R.W.; Kelley, E.A. The Role of Piloerection in Primate Thermoregulation. Folia Primatol. 2013, 85, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Pisacane, V.L.; Kuznetz, L.H.; Logan, J.S.; Clark, J.B.; Wissler, E.H. Thermoregulatory Models of Space Shuttle and Space Station Activities. Aviat. Space Environ. Med. 2007, 78 (Suppl. 4), A48–A55. [Google Scholar]
- Katić, K.; Li, R.; Zeiler, W. Thermophysiological Models and Their Applications: A Review. Build. Environ. 2016, 106, 286–300. [Google Scholar] [CrossRef]
- Fanger, P.O. Thermal Comfort: Analysis and Applications in Environmental Engineering; Danish Technical Press: Copenhagen, Denmark, 1970. [Google Scholar]
- Gagge, A.P.; Stowijk, J.A.J.; Nishi, Y. An Effective Temperature Scale Based on a Simple Model of Human Physiological Regulatory Response. ASHRAE Trans. 1971, 77, 247–262. [Google Scholar]
- Stolwijk, J.A. A Mathematical Model of Physiological Temperature Regulation in Man; National Aeronautics and Space Administration: Washington, DC, USA, 1971. [Google Scholar]
- Guedes, J.C. Mathematical Modelling of Human Thermoregulation in Hot Environments, University of Porto. 2016. Available online: https://core.ac.uk/download/pdf/302916501.pdf (accessed on 7 June 2023).
- Basdanis, T.; Tatsios, G.; Valougeorgis, D. Human Thermophysiological Models: Quantification of Uncertainty in the Output Quantities of the Passive System Due to Uncertainties in the Control Equations of the Active System via the Monte Carlo Method. J. Therm. Biol. 2021, 100, 103045. [Google Scholar] [CrossRef]
- Fiala, D.; Lomas, K.J.; Stohrer, M. A Computer Model of Human Thermoregulation for a Wide Range of Environmental Conditions: The Passive System. J. Appl. Physiol. 1999, 87, 1957–1972. [Google Scholar] [CrossRef]
- Huizenga, C.; Hui, Z.; Arens, E. A Model of Human Physiology and Comfort for Assessing Complex Thermal Environments. Build. Environ. 2001, 36, 691–699. [Google Scholar] [CrossRef]
- Tanabe, S.; Kobayashi, K.; Nakano, J.; Ozeki, Y.; Konishi, M. Evaluation of Thermal Comfort Using Combined Multi-Node Thermoregulation (65MN) and Radiation Models and Computational Fluid Dynamics (CFD). Energy Build. 2002, 34, 637–646. [Google Scholar] [CrossRef]
- Kingma, B.R.M.; Vosselman, M.J.; Frijns, A.J.H.; van Steenhoven, A.A.; van Marken Lichtenbelt, W.D. Incorporating Neurophysiological Concepts in Mathematical Thermoregulation Models. Int. J. Biometeorol. 2014, 58, 87–99. [Google Scholar] [CrossRef]
- Joshi, A. Comprehensive Model for Heat and Mass Transfer in Human Skin-Clothing-Environment System; Université de Haute-Alsace: Mulhouse, France, 2019. [Google Scholar]
- Psikuta, A.; Richards, M.; Fiala, D. Single-Sector Thermophysiological Human Simulator. Physiol. Meas. 2008, 29, 181–192. [Google Scholar] [CrossRef]
- ASHRAE 55; Thermal Environmental Conditions for Human Occupancy. American Society of Heating Refrigerating and Air-Conditioning Engineers: Atlanta, GA, USA, 2017.
- ISO 7730; Ergonomics of the Thermal Environment—Analytical Determination and Interpretation of Thermal Comfort Using Calculation of the PMV and PPD Indices and Local Thermal Comfort Criteria. International Organization for Standardization: Geneva, Switzerland, 2005.
- ISO 18640-1; Protective Clothing for Firefighters—Physiological Impact—Part 1: Measurement of Coupled Heat and Moisture Transfer with the Sweating Torso. International Organization for Standardization: Geneva, Switzerland, 2018.
- Guan, M.; Annaheim, S.; Camenzind, M.; Li, J.; Mandal, S.; Psikuta, A.; Rossi, R.M. Moisture Transfer of the Clothing–Human Body System during Continuous Sweating under Radiant Heat. Text. Res. J. 2019, 89, 4537–4553. [Google Scholar] [CrossRef]
- Guthrie, J.C. The Integral and Differential Heats of Sorption of Water by Cellulose. J. Text. Inst. Trans. 1949, 40, T489–T504. [Google Scholar] [CrossRef]
- Kim, H.-A. Moisture Vapor Permeability and Thermal Wear Comfort of Ecofriendly Fiber-Embedded Woven Fabrics for High-Performance Clothing. Materials 2021, 14, 6205. [Google Scholar] [CrossRef] [PubMed]
- Morton, W.; Hearle, J.S. Physical Properties of Textile Fibres; Heinemann: London, UK, 2008. [Google Scholar]
- Noman, M.T.; Petru, M. Effect of Sonication and Nano TiO 2 on Thermophysiological Comfort Properties of Woven Fabrics. ACS Omega 2020, 5, 11481–11490. [Google Scholar] [CrossRef]
- Hes, L. Non-Destructive Determination of Comfort Parameters during Marketing of Functional Garments and Clothing. Indian J. Fibre Text. Res. 2008, 33, 239–245. [Google Scholar]
- Croitoru, C.; Nastase, I.; Bode, F.; Meslem, A.; Dogeanu, A. Thermal Comfort Models for Indoor Spaces and Vehicles—Current Capabilities and Future Perspectives. Renew. Sustain. Energy Rev. 2015, 44, 304–318. [Google Scholar] [CrossRef]
- ISO 14505-3; Ergonomics of the Thermal Environment—Evaluation of Thermal Environments in Vehicles—Part 3: Evaluation of Thermal Comfort Using Human Subjects. International Organization for Standardization: Geneva, Switzerland, 2006.
- ISO 9886; Ergonomics-Evaluation of Thermal Strain by Physiological Measurements. International Organization for Standardization: Geneva, Switzerland, 2004.
- ISO 11092; Textiles—Physiological Effects—Measurement of Thermal and Water Vapour Resistance under Steady-State Conditions (Sweating Guarded Hotplate Test. International Organization for Standardization: Geneva, Switzerland, 2014.
- ASTM E96/E96M; Standard Test Methods for Water Vapor Transmission of Materials. ASTM International: London, UK, 2017.
- AATCC 195; Test Method for Liquid Moisture Management Properties of Textile Fabrics. American Association of Textile Chemists and Colorists: Research Triangle Park, NC, USA, 2017.
- ASTM D737; Standard Test Method for Air Permeability of Textile Fabrics. ASTM International: London, UK, 2018.
- ASTM D7984; Standard Test Method for Measurement of Thermal Effusivity of Fabrics Using a Modified Transient Plane Source (MTPS) Instrument. ASTM International: London, UK, 2021.
- Givoni, B.; Goldman, R.F. Predicting Metabolic Energy Cost. J. Appl. Physiol. 1971, 30, 429–433. [Google Scholar] [CrossRef]
- Takada, S.; Kobayashi, H.; Matsushita, T. Thermal Model of Human Body Fitted with Individual Characteristics of Body Temperature Regulation. Build. Environ. 2009, 44, 463–470. [Google Scholar] [CrossRef]
- Wissler, E.H. Heat Transfer in Medicine and Biology; Shitzer, A., Eberhart, R.C., Eds.; Plenum Press: New York, USA, 1985; Volume 1, pp. 325–373. [Google Scholar]
- Smith, C.E. A Transient, Three-Dimensional Model of the Human Thermal System; Kansas State University: Kansas, NY, USA, 1991. [Google Scholar]
- Ferreira, M.S.; Yanagihara, J.I. A Transient Three-Dimensional Heat Transfer Model of the Human Body. Int. Commun. Heat Mass Transf. 2009, 36, 718–724. [Google Scholar] [CrossRef]
- Schwarz, M.; Krueger, M.W.; Busch, H.-J.; Benk, C.; Heilmann, C. Model-Based Assessment of Tissue Perfusion and Temperature in Deep Hypothermic Patients. IEEE Trans. Biomed. Eng. 2010, 57, 1577–1586. [Google Scholar] [CrossRef]
- Sun, X.; Eckels, S.J.; Zheng, Z.C. An Improved Thermal Model of the Human Body. Hvac Res. 2012, 18, 323–338. [Google Scholar] [CrossRef]
- Tang, Y.; He, Y.; Shao, H.; Ji, C. Assessment of Comfortable Clothing Thermal Resistance Using a Multi-Scale Human Thermoregulatory Model. Int. J. Heat Mass Transf. 2016, 98, 568–583. [Google Scholar] [CrossRef]
- Kohri, I.; Mochida, T. Evaluation Method of Thermal Comfort in a Vehicle with a Dispersed Two-Node Model Part 1—Development of Dispersed Two-Node Model. J. Human Environ. Syst. 2002, 6, 19–29. [Google Scholar] [CrossRef]
- Kaynakli, O.; Unver, U.; Kilic, M. Evaluating Thermal Environments for Sitting and Standing Posture. Int. Commun. Heat Mass Transf. 2003, 30, 1179–1188. [Google Scholar] [CrossRef]
- Foda, E.; Sirén, K. A New Approach Using the Pierce Two-Node Model for Different Body Parts. Int. J. Biometeorol. 2010, 55, 519–532. [Google Scholar] [CrossRef]
- Salloum, M.; Ghaddar, N.; Ghali, K. A New Transient Bioheat Model of the Human Body and Its Integration to Clothing Models. Int. J. Therm. Sci. 2007, 46, 371–384. [Google Scholar] [CrossRef]
- Dongmei, P.; Mingyin, C.; Shiming, D.; Minglu, Q. A Four-Node Thermoregulation Model for Predicting the Thermal Physiological Responses of a Sleeping Person. Build. Environ. 2012, 52, 88–97. [Google Scholar] [CrossRef]
- Lai, D.; Chen, Q. A Two-Dimensional Model for Calculating Heat Transfer in the Human Body in a Transient and Non-Uniform Thermal Environment. Energy Build. 2016, 118, 114–122. [Google Scholar] [CrossRef]
- Fanger, P.O. Assessment of Man’s Thermal Comfort in Practice. Occup. Environ. Med. 1973, 30, 313–324. [Google Scholar] [CrossRef]
- Kang, Z.; Wang, F.; Udayraj. An Advanced Three-Dimensional Thermoregulation Model of the Human Body: Development and Validation. Int. Commun. Heat Mass Transf. 2019, 107, 34–43. [Google Scholar] [CrossRef]
- Broday, E.; de Paula Xavier, A.; de Oliveira, R. Comparative Analysis of Methods for Determining the Clothing Surface Temperature (TCL) in Order to Provide a Balance between Man and the Environment. Int. J. Ind. Ergon. 2017, 57, 80–87. [Google Scholar] [CrossRef]
- Fiala, D.; Lomas, K.J.; Stohrer, M. Computer Prediction of Human Thermoregulatory and Temperature Responses to a Wide Range of Environmental Conditions. Int. J. Biometeorol. 2001, 45, 143–159. [Google Scholar] [CrossRef] [PubMed]
- Mert, E.; Psikuta, A.; Bueno, M.-A.; Rossi, R.M. Effect of Heterogenous and Homogenous Air Gaps on Dry Heat Loss through the Garment. Int. J. Biometeorol. 2015, 59, 1701–1710. [Google Scholar] [CrossRef]
- Awais, M.; Krzywinski, S.; Wendt, E. A Novel Modeling and Simulation Approach for the Prediction of Human Thermophysiological Comfort. Text. Res. J. 2021, 91, 691–705. [Google Scholar] [CrossRef]
- Gagge, A.P.; Burton, A.C.; Bazett, H.C. A Practical System of Units for the Description of the Heat Exchange of Man with His Environment. Science 1941, 94, 428–430. [Google Scholar] [CrossRef] [PubMed]
- Joshi, A.; Psikuta, A.; Bueno, M.-A.; Annaheim, S.; Rossi, R.M. Analytical Clothing Model for Sensible Heat Transfer Considering Spatial Heterogeneity. Int. J. Therm. Sci. 2019, 145, 105949. [Google Scholar] [CrossRef]
- Ekici, C. A Review of Thermal Comfort and Method of Using Fanger’s PMV Equation. In 5th International Symposium on Measurement, Analysis and Modeling of Human Functions; Curran Associates Inc.: Vancouver, BC, Canada, 2003. [Google Scholar]
- Krucińska, I.; Skrzetuska, E.; Kowalski, K. Application of a Thermal Mannequin to the Assessment of the Heat Insulating Power of Protective Garments for Premature Babies. Autex Res. J. 2019, 19, 134–146. [Google Scholar] [CrossRef]
- Crandall, C.G. Mechanisms and Controllers of Eccrine Sweating in Humans. Front. Biosci. 2010, S2, 94. [Google Scholar] [CrossRef]
- Eyolfson, D.A.; Tikuisis, P.; Xu, X.; Weseen, G.; Giesbrecht, G.G. Measurement and Prediction of Peak Shivering Intensity in Humans. Eur. J. Appl. Physiol. 2001, 84, 100–106. [Google Scholar] [CrossRef]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; DeWitt, D.P. Introduction to Heat and Mass Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Aziz, K.; Holst, P.H.; Karra, P.S. Natural Convection In Porous Media. In Proceedings of the 19th Annual Technical Meeting of the Petroleum Society of Canada, Petroleum Society of Canada. Calgary, AB, Canada, 8 May 1968. [Google Scholar]
- Çengel, Y.A.; Ghajar, A.J. Heat Transfer and Mass Transfer: Fundamentals and Applications; McGraw-Hill Higher Education: New York, USA, 2015. [Google Scholar]
- Hu, Y.; Topolkaraev, V.; Hiltner, A.; Baer, E. Measurement of Water Vapor Transmission Rate in Highly Permeable Films. J. Appl. Polym. Sci. 2001, 81, 1624–1633. [Google Scholar] [CrossRef]
- Schweiker, M.; Huebner, G.M.; Kingma, B.R.M.; Kramer, R.; Pallubinsky, H. Drivers of Diversity in Human Thermal Perception—A Review for Holistic Comfort Models. Temperature 2018, 5, 308–342. [Google Scholar] [CrossRef] [PubMed]
- Rewitz, K.; Müller, D. Influence of Gender, Age and BMI on Human Physiological Response and Thermal Sensation for Transient Indoor Environments with Displacement Ventilation. Build. Environ. 2022, 219, 109045. [Google Scholar] [CrossRef]
- Van Someren, E.J.W. Thermoregulation and Aging. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2007, 292, R99–R102. [Google Scholar] [CrossRef] [PubMed]
- Blatteis, C.M. Age-Dependent Changes in Temperature Regulation–A Mini Review. Gerontology 2012, 58, 289–295. [Google Scholar] [CrossRef] [PubMed]
- van Hoof, J. Forty Years of Fanger’s Model of Thermal Comfort: Comfort for All? Indoor Air 2008, 18, 182–201. [Google Scholar] [CrossRef] [PubMed]
- Kingma, B.; van Marken Lichtenbelt, W. Energy Consumption in Buildings and Female Thermal Demand. Nat. Clim. Chang. 2015, 5, 1054–1056. [Google Scholar] [CrossRef]
- Rupp, R.F.; Vásquez, N.G.; Lamberts, R. A Review of Human Thermal Comfort in the Built Environment. Energy Build. 2015, 105, 178–205. [Google Scholar] [CrossRef]
- Rennie, D.W. Tissue Heat Transfer in Water: Lessons from the Korean Divers. Med. Sci. Sports Exerc. 1988, 20 (Suppl. S1), S177–S184. [Google Scholar] [CrossRef]
- Speakman, J.R. Obesity and Thermoregulation. Handb. Clin. Neurol. 2018, 156, 431–443. [Google Scholar] [CrossRef]
- Ding, D.; Tian Tang, T.; Song, G.; McDonald, A. Characterizing the Performance of a Single-Layer Fabric System through a Heat and Mass Transfer Model—Part II: Thermal and Evaporative Resistances. Text. Res. J. 2011, 81, 945–958. [Google Scholar] [CrossRef]
- Santos, M.S.; Oliveira, D.; Campos, J.B.L.M.; Mayor, T.S. Numerical Analysis of the Flow and Heat Transfer in Cylindrical Clothing Microclimates–Influence of the Microclimate Thickness Ratio. Int. J. Heat Mass Transf. 2018, 117, 71–79. [Google Scholar] [CrossRef]
- Belal, S.A. Understanding Textiles for a Merchandiser; BMN3 Foundation: Dhaka, Bangladesh, 2009. [Google Scholar]
- Hatch, K.L. Textile Science; West Publishing Co.: St Paul, MN, USA, 1993. [Google Scholar]
- Cimilli, S.; Nergis, B.U.; Candan, C.; Özdemir, M. A Comparative Study of Some Comfort-Related Properties of Socks of Different Fiber Types. Text. Res. J. 2010, 80, 948–957. [Google Scholar] [CrossRef]
- Aisyah, H.A.; Paridah, M.T.; Sapuan, S.M.; Ilyas, R.A.; Khalina, A.; Nurazzi, N.M.; Lee, S.H.; Lee, C.H. A Comprehensive Review on Advanced Sustainable Woven Natural Fibre Polymer Composites. Polymers 2021, 13, 471. [Google Scholar] [CrossRef] [PubMed]
- Özdil, N.; Marmaralı, A.; Kretzschmar, S.D. Effect of Yarn Properties on Thermal Comfort of Knitted Fabrics. Int. J. Therm. Sci. 2007, 46, 1318–1322. [Google Scholar] [CrossRef]
- Aydın, İ.S.; Kertmen, M.; Marmarali, A. Evaluating the Effect of Spinning Systems on Thermal Comfort Properties of Modal Fabrics. IOP Conf. Ser. Mater. Sci. Eng. 2017, 254, 182011. [Google Scholar] [CrossRef]
- Spencer, D.J. Knitting Technology: A Comprehensive Handbook and Practical Guide; Woodhead Publishing: Sawston, UK, 2001. [Google Scholar]
- Ahmad, S.; Ahmad, F.; Afzal, A.; Rasheed, A.; Mohsin, M.; Ahmad, N. Effect of Weave Structure on Thermo-Physiological Properties of Cotton Fabrics. Autex Res. J. 2015, 15, 30–34. [Google Scholar] [CrossRef]
- Fourt, L.; Harrist, M. Diffusion of Water Vapor Through Textiles. Text. Res. J. 1947, 17, 256–263. [Google Scholar] [CrossRef]
- Badr, A.A.; Hassanin, A.; Moursey, M. Influence of Tencel/Cotton Blends on Knitted Fabric Performance. Alex. Eng. J. 2016, 55, 2439–2447. [Google Scholar] [CrossRef]
- Ward, K. Crystallinity of Cellulose and Its Significance for the Fiber Properties. Text. Res. J. 1950, 20, 363–372. [Google Scholar] [CrossRef]
- Kim, J.O.; Spivak, S.M. Dynamic Moisture Vapor Transfer Through Textiles. Text. Res. J. 1994, 64, 112–121. [Google Scholar] [CrossRef]
- Li, Y.; Holcombe, B.V.; Apcar, F. Moisture Buffering Behavior of Hygroscopic Fabric During Wear. Text. Res. J. 1992, 62, 619–627. [Google Scholar] [CrossRef]
- Trifol, J.; Plackett, D.; Szabo, P.; Daugaard, A.E.; Giacinti Baschetti, M. Effect of Crystallinity on Water Vapor Sorption, Diffusion, and Permeation of PLA-Based Nanocomposites. ACS Omega 2020, 5, 15362–15369. [Google Scholar] [CrossRef]
- Duan, Z.; Thomas, N.L. Water Vapour Permeability of Poly(Lactic Acid): Crystallinity and the Tortuous Path Model. J. Appl. Phys. 2014, 115, 064903. [Google Scholar] [CrossRef]
- Kwon, Y.-J.; Park, J.-B.; Jeon, Y.-P.; Hong, J.-Y.; Park, H.-S.; Lee, J.-U. A Review of Polymer Composites Based on Carbon Fillers for Thermal Management Applications: Design, Preparation, and Properties. Polymers 2021, 13, 1312. [Google Scholar] [CrossRef] [PubMed]
- Feng, T.; He, J.; Rai, A.; Hun, D.; Liu, J.; Shrestha, S.S. Size Effects in the Thermal Conductivity of Amorphous Polymers. Phys. Rev. Appl. 2020, 14, 044023. [Google Scholar] [CrossRef]
- Bui, H.; Sebaibi, N.; Boutouil, M.; Levacher, D. Determination and Review of Physical and Mechanical Properties of Raw and Treated Coconut Fibers for Their Recycling in Construction Materials. Fibers 2020, 8, 37. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, F. Comfort Management of Fibrous Materials. In Handbook of Fibrous Materials; Wiley: Hoboken, NJ, USA, 2020; pp. 857–887. [Google Scholar] [CrossRef]
- Szurgot, M. On the Specific Heat Capacity and Thermal Capacity of Meteorites. In Proceedings of the 42nd Lunar and Planetary Science Conference, The Woodlands, TX, USA, 7–11 March 2011. [Google Scholar]
- Tyagi, G.; Madhusoodhanan, P. Effect of Fibre Cross-Sectional Shape on Handle Characteristics of Polyester-Viscose and Polyester-Cotton Ring and MJS Yarn Fabrics. Indian J. Fibre Text. Res. (IJFTR) 2006, 31, 496–500. [Google Scholar]
- Ravandi, S.A.H.; Valizadeh, M. Properties of Fibers and Fabrics That Contribute to Human Comfort. In Improving Comfort in Clothing; Elsevier: Amsterdam, The Netherlands, 2011; pp. 61–78. [Google Scholar] [CrossRef]
- Guan, M.; Psikuta, A.; Camenzind, M.; Li, J.; Mandal, S.; Michel Rossi, R.; Annaheim, S. Effect of Perspired Moisture and Material Properties on Evaporative Cooling and Thermal Protection of the Clothed Human Body Exposed to Radiant Heat. Text. Res. J. 2019, 89, 3663–3676. [Google Scholar] [CrossRef]
- Atasağun, H.G.; Okur, A.; Psikuta, A.; Rossi, R.M.; Annaheim, S. Determination of the Effect of Fabric Properties on the Coupled Heat and Moisture Transport of Underwear–Shirt Fabric Combinations. Text. Res. J. 2018, 88, 1319–1331. [Google Scholar] [CrossRef]
- Hussain, U.; Younis, F.B.; Usman, F.; Hussain, T.; Ahmed, F. Comfort and Mechanical Properties of Polyester/Bamboo and Polyester/Cotton Blended Knitted Fabric. J. Eng. Fibers Fabr. 2015, 10, 155892501501000. [Google Scholar] [CrossRef]
- Prakash, C.; Ramakrishnan, G. Effect of Blend Proportion on Thermal Behaviour of Bamboo Knitted Fabrics. J. Text. Inst. 2013, 104, 907–913. [Google Scholar] [CrossRef]
- Atalie, D.; Tesema, A.F.; Rotich, G.K. Effect of Weft Yarn Twist Level on Thermal Comfort of 100 per Cent Cotton Woven Fabrics. Res. J. Text. Appar. 2018, 22, 180–194. [Google Scholar] [CrossRef]
- Majumdar, P.K. Process Control in Ring and Rotor Spinning. In Process Control in Textile Manufacturing; Elsevier: Amsterdam, The Netherlands, 2013; pp. 191–224. [Google Scholar] [CrossRef]
- Basu, A. Progress in air-jet spinning. Text. Prog. 1999, 29, 1–38. [Google Scholar] [CrossRef]
- Das, A.; Alagirusamy, R. Dynamic Heat and Mass Transmission. In Science in Clothing Comfort; Woodhead Publishing India Pvt Limited: New Delhi, India, 2010; pp. 136–138. [Google Scholar] [CrossRef]
- Stoffberg, M.E.; Hunter, L.; Botha, A. The Effect of Fabric Structural Parameters and Fiber Type on the Comfort-Related Properties of Commercial Apparel Fabrics. J. Nat. Fibers 2015, 12, 505–517. [Google Scholar] [CrossRef]
- Dalbaşı, E.S.; Süpüren Mengüç, G.; Özgüney, A.T.; Özdil, N. The Effect of Softeners on Thermal Comfort and Wetting Properties of Bamboo Viscose and Bamboo/Cotton Blended Fabrics. J. Nat. Fibers 2022, 19, 1700–1714. [Google Scholar] [CrossRef]
- Dias, T.; Delkumburewatte, G.B. Changing Porosity of Knitted Structures by Changing Tightness. Fibers Polym. 2008, 9, 76–79. [Google Scholar] [CrossRef]
- Bibi, N.; Abdullah Makhdoom, M.U. Prediction of Fabric Porosity from Yarn Diameter and Effect of Different Spinning Techniques and Process on Porosity. Int. J. Sci. Res. Publ. (IJSRP) 2021, 11, 699–706. [Google Scholar] [CrossRef]
- Hoque, M.S.; Hossain, M.J.; Rahman, M.M.; Rashid, M.M. Fiber Types and Fabric Structures Influence on Weft Knitted Fabrics. Heliyon 2022, 8, e09605. [Google Scholar] [CrossRef] [PubMed]
- Chowdhary, U.; Islam, M.R. Pre-Post Wash Wicking Behavior, Moisture Transfer, and Water Repellency of Plain, Twill and Satin Weaves. J. Text. Sci. Fash. Technol. 2019, 2, 1–13. [Google Scholar] [CrossRef]
- Limeneh, D.Y.; Ayele, M.; Tesfaye, T.; Liyew, E.Z.; Tesema, A.F. Effect of Weave Structure on Comfort Property of Fabric. J. Nat. Fibers 2020, 19, 4148–4155. [Google Scholar] [CrossRef]
- Tabor, J.; Chatterjee, K.; Ghosh, T.K. Smart Textile-Based Personal Thermal Comfort Systems: Current Status and Potential Solutions. Adv. Mater. Technol. 2020, 5, 1901155. [Google Scholar] [CrossRef]
- Zhu, F.L.; Feng, Q.Q. Recent Advances in Textile Materials for Personal Radiative Thermal Management in Indoor and Outdoor Environments. Int. J. Therm. Sci. 2021, 165, 106899. [Google Scholar] [CrossRef]
- Wichmann, J.; Andersen, Z.; Ketzel, M.; Ellermann, T.; Loft, S. Apparent Temperature and Cause-Specific Emergency Hospital Admissions in Greater Copenhagen, Denmark. PLoS ONE 2011, 6, e22904. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.K. Handbook of Air Conditioning and Refrigeration; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Legg, R. Properties of Humid Air. In Air Conditioning System Design; Elsevier: Amsterdam, The Netherlands, 2017; pp. 1–28. [Google Scholar] [CrossRef]
- Tartarini, F.; Schiavon, S.; Cheung, T.; Hoyt, T. CBE Thermal Comfort Tool: Online Tool for Thermal Comfort Calculations and Visualizations. SoftwareX 2020, 12, 100563. [Google Scholar] [CrossRef]
- Teitelbaum, E.; Jayathissa, P.; Miller, C.; Meggers, F. Design with Comfort: Expanding the Psychrometric Chart with Radiation and Convection Dimensions. Energy Build. 2020, 209, 109591. [Google Scholar] [CrossRef]
- Huang, J.; Chen, Y. Effects of Air Temperature, Relative Humidity, and Wind Speed on Water Vapor Transmission Rate of Fabrics. Text. Res. J. 2010, 80, 422–428. [Google Scholar] [CrossRef]
- Belding, H.S.; Russell, H.D.; Darling, R.C.; Folk, G.E. Analysis of Factors Concerned in Maintaining Energy Balance for Dressed Men in Extreme Cold; Effects of Activity on the Protective Value and Comfort of an Arctic Uniform. Am. J. Physiol. Leg. Content 1947, 149, 223–239. [Google Scholar] [CrossRef]
- Vogt, J.J.; Meyer, J.P.; Candas, V.; Libert, J.P.; Sagot, J.C. Pumping Effects on Thermal Insulation of Clothing Worn by Human Subjects. Ergonomics 1983, 26, 963–974. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, R.; Olesen, B.W.; Fanger, P.O. Effect of Physical Activity and Air Velocity on the Thermal Insulation of Clothing. Ergonomics 1985, 28, 1617–1631. [Google Scholar] [CrossRef]
- Ismail, N.; Ghaddar, N.; Ghali, K. Electric Circuit Analogy of Heat Losses of Clothed Walking Human Body in Windy Environment. Int. J. Therm. Sci. 2018, 127, 105–116. [Google Scholar] [CrossRef]
- Ismail, N.; Ghaddar, N.; Ghali, K. Determination of Segmental and Overall Ventilation of Clothed Walking Human by Means of Electric Circuit Analogy. Text. Res. J. 2016, 88, 586–601. [Google Scholar] [CrossRef]
- Zhu, G.; Kremenakova, D.; Wang, Y.; Militky, J. Air Permeability of Polyester Nonwoven Fabrics. Autex Res. J. 2015, 15, 8–12. [Google Scholar] [CrossRef]
- Joshi, A.; Psikuta, A.; Bueno, M.-A.; Annaheim, S.; Rossi, R.M. Effect of Movement on Convection and Ventilation in a Skin-Clothing-Environment System. Int. J. Therm. Sci. 2021, 166, 106965. [Google Scholar] [CrossRef]
- Fisher, C.H. History of Natural Fibers. J. Macromol. Sci. 1981, 15, 1345–1375. [Google Scholar] [CrossRef]
- Cook, J.G. Handbook of Textile Fibres: Man-Made Fibres; Woodhead Pub Limited: Cambridge, UK, 1984. [Google Scholar]
- Ahmad, S.; Rasheed, A.; Nawab, Y. Fibers for Technical Textiles; Springer Nature: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Zhang, Y.F.; Sun, B.K. Development of Outlast Fiber and Study about Its Character of Thermoregulation. Adv. Mater. Res. 2012, 557–559, 979–982. [Google Scholar] [CrossRef]
- Gulhane, S.S.; Raichurkar, P.P. Developments in Profile Filament Yarn for Enhancing Moisture Management Properties of Fabrics. Man Made Text. India 2020, XLVIII, 88–92. [Google Scholar]
- Sperling, L.H. Introduction to Physical Polymer Science; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar] [CrossRef]
- Plante, A.M.; Holcombe, B.V.; Stephens, L.G. Fiber Hygroscopicity and Perceptions of Dampness. Text. Res. J. 1995, 65, 293–298. [Google Scholar] [CrossRef]
- Senthilkumar, M.; Sampath, M.B.; Ramachandran, T. Moisture Management in an Active Sportswear: Techniques and Evaluation—A Review Article. J. Inst. Eng. (India) Ser. E 2012, 93, 61–68. [Google Scholar] [CrossRef]
- Jhanji, Y.; Gupta, D.; Kothari, V.K. Thermo-Physiological Properties of Polyester–Cotton Plated Fabrics in Relation to Fibre Linear Density and Yarn Type. Fash. Text. 2015, 2, 16. [Google Scholar] [CrossRef]
- Islam, M.R.; Chowdhary, U. Relative Color Pickup of Three Different Knits and Predictive Dyeing Recipe Formulation. Int. J. Polym. Text. Eng. 2019, 6, 1–16. [Google Scholar] [CrossRef]
- Laitala, K.; Klepp, I.; Henry, B. Does Use Matter? Comparison of Environmental Impacts of Clothing Based on Fiber Type. Sustainability 2018, 10, 2524. [Google Scholar] [CrossRef]
- Russell, I.M. Sustainable Wool Production and Processing. In Sustainable Textiles; Elsevier: Amsterdam, The Netherlands, 2009; pp. 63–87. [Google Scholar] [CrossRef]
- Allafi, F.; Hossain, M.S.; Lalung, J.; Shaah, M.; Salehabadi, A.; Ahmad, M.I.; Shadi, A. Advancements in Applications of Natural Wool Fiber: Review. J. Nat. Fibers 2022, 19, 497–512. [Google Scholar] [CrossRef]
- Laing, R.M.; Wilson, C.A.; Gore, S.E.; Carr, D.J.; Niven, B.E. Determining the Drying Time of Apparel Fabrics. Text. Res. J. 2007, 77, 583–590. [Google Scholar] [CrossRef]
- Kumar, S.; Boominathan, S.K.; Raj, D.V.K. Comparative Analysis on Thermo-Physiological Behavior of Eri Silk, Wool and Bamboo Knitted Fabrics Toward Sportswear. J. Nat. Fibers 2022, 19, 7702–7713. [Google Scholar] [CrossRef]
- Troynikov, O.; Wardiningsih, W. Moisture Management Properties of Wool/ Polyester and Wool/Bamboo Knitted Fabrics for the Sportswear Base Layer. Text. Res. J. 2011, 81, 621–631. [Google Scholar] [CrossRef]
- Hossaini, F.A. Customer Quality Analysis of Outdoor Clothing, Mälardalen University. 2011. Available online: http://www.diva-portal.org/smash/get/diva2:431565/fulltext01 (accessed on 7 June 2023).
- Jeon, E.; Yoo, S.; Kim, E. Psychophysical Determination of Moisture Perception in High-Performance Shirt Fabrics in Relation to sweating Level. Ergonomics 2011, 54, 576–586. [Google Scholar] [CrossRef]
- Hatch, K.L.; Woo, S.S.; Barker, R.L.; Radhakrishnaiah, P.; Markee, N.L.; Maibach, H.I. In Vivo Cutaneous and Perceived Comfort Response to Fabric. Text. Res. J. 1990, 60, 405–412. [Google Scholar] [CrossRef]
- Adler, M.M.; Walsh, W.K. Mechanisms of Transient Moisture Transport Between Fabrics. Text. Res. J. 1984, 54, 334–343. [Google Scholar] [CrossRef]
- Hsieh, Y.-L. Liquid Transport in Fabric Structures. Text. Res. J. 1995, 65, 299–307. [Google Scholar] [CrossRef]
- Varshney, R.K.; Kothari, V.K.; Dhamija, S. A Study on Thermophysiological Comfort Properties of Fabrics in Relation to Constituent Fibre Fineness and Cross-Sectional Shapes. J. Text. Inst. 2010, 101, 495–505. [Google Scholar] [CrossRef]
- Kohan, M.I. The History and Development of Nylon-66. In High Performance Polymers: Their Origin and Development; Springer: Dordrecht, The Netherlands, 1986; pp. 19–37. [Google Scholar] [CrossRef]
- Chen, J. Synthetic Textile Fibers. In Textiles and Fashion; Elsevier: Amsterdam, The Netherlands, 2015; pp. 79–95. [Google Scholar] [CrossRef]
- Adamu, B.F.; Gao, J. Comfort Related Woven Fabric Transmission Properties Made of Cotton and Nylon. Fash. Text. 2022, 9, 8. [Google Scholar] [CrossRef]
- Anas, M.S.; Awais, H.; Ali Hamdani, S.T.; Shaker, K.; Azam, Z.; Nawab, Y. Investigating the Thermo-Physiological Comfort Properties of Weft-Knitted Smart Structures Having a Negative Poisson’s Ratio. Adv. Mater. Sci. Eng. 2022, 2022, 1896634. [Google Scholar] [CrossRef]
- Kumar, P.S.; Suganya, S. Introduction to Sustainable Fibres and Textiles. In Sustainable Fibres and Textiles; Elsevier: Amsterdam, The Netherlands, 2017; pp. 1–18. [Google Scholar] [CrossRef]
- Colom, X.; Carrillo, F. Crystallinity Changes in Lyocell and Viscose-Type Fibres by Caustic Treatment. Eur. Polym. J. 2002, 38, 2225–2230. [Google Scholar] [CrossRef]
- Kayseri, G.Ö.; Bozdo, F. Performance Properties of Regenerated Cellulose Fibers. Tekst. Ve Konfeksiyon 2010, 20, 208–212. [Google Scholar]
- Prakash, C.; Ramakrishnan, G.; Koushik, C.V. Effect of Blend Proportion on Moisture Management Characteristics of Bamboo/Cotton Knitted Fabrics. J. Text. Inst. 2013, 104, 1320–1326. [Google Scholar] [CrossRef]
- Brito, M.D.; Carbone, V.; Blanquart, C.M. Towards a Sustainable Fashion Retail Supply Chain in Europe: Organisation and Performance. Int. J. Prod. Econ. 2008, 114, 534–553. [Google Scholar] [CrossRef]
- Stana-Kleinschek, K.; Ribitsch, V.; Kreze, T.; Fras, L. Determination of the Adsorption Character of Cellulose Fibres Using Surface Tension and Surface Charge. Mater. Res. Innov. 2002, 6, 13–18. [Google Scholar] [CrossRef]
- Parajuli, P.; Acharya, S.; Rumi, S.S.; Hossain, M.T.; Abidi, N. Regenerated Cellulose in Textiles: Rayon, Lyocell, Modal and Other Fibres. In Fundamentals of Natural Fibres and Textiles; Elsevier: Amsterdam, The Netherlands, 2021; pp. 87–110. [Google Scholar] [CrossRef]
- Smole, M.S.; Peršin, Z.; Kreže, T.; Kleinschek, K.S.; Ribitsch, V.; Neumayer, S. X-Ray Study of Pre-Treated Regenerated Cellulose Fibres. Mater. Res. Innov. 2003, 7, 275–282. [Google Scholar] [CrossRef]
- Kreze, T.; Strnad, S.; Stana-Kleinschek, K.; Ribitsch, V. Influence of Aqueous Medium on Mechanical Properties of Conventional and New Environmentally Friendly Regenerated Cellulose Fibers. Mater. Res. Innov. 2001, 4, 107–114. [Google Scholar] [CrossRef]
- Öztürk, H.B.; Okubayashi, S.; Bechtold, T. Splitting Tendency of Cellulosic Fibers. Part 2: Effects of Fiber Swelling in Alkali Solutions. Cellulose 2006, 13, 403–409. [Google Scholar] [CrossRef]
- Ozdemir, H. Permeability and Wicking Properties of Modal and Lyocell Woven Fabrics Used for Clothing. J. Eng. Fibers Fabr. 2017, 12, 155892501701200. [Google Scholar] [CrossRef]
- Eryuruk, S.H.; Kalaoglu, F. Analysis of the Performance Properties of Knitted Fabrics Containing Elastane. Int. J. Cloth. Sci. Technol. 2016, 28, 463–479. [Google Scholar] [CrossRef]
- Manshahia, M.; Das, A. Thermophysiological Comfort Characteristics of Plated Knitted Fabrics. J. Text. Inst. 2013, 105, 509–519. [Google Scholar] [CrossRef]
- Shobanasree, P.C.; Prakash, C.; Kumar, M.R.; Lokesh, K.V. Effect of Elastane Plating on Physical & Thermal Comfort Properties of Lyocell Single Jersey Knit Fabric with Different Loop Length. J. Nat. Fibers 2022, 19, 11574–11581. [Google Scholar]
- Öner, E.; Okur, A. Thermophysiological Comfort Properties of Selected Knitted Fabrics and Design of T-Shirts. J. Text. Inst. 2015, 106, 1403–1414. [Google Scholar] [CrossRef]
- Atasağun, H.G.; Öner, E.; Okur, A.; Beden, A.R. A Comprehensive Study on the General Performance Properties of Viloft-Blended Knitted Fabrics. J. Text. Inst. 2015, 106, 523–535. [Google Scholar] [CrossRef]
- Krithika, U.S.M.; Sampath, M.B.; Prakash, C.; Senthilkumar, M. Moisture Management Finish on Woven Fabrics. Indian J. Fibre Text. Res. 2019, 44, 486–491. [Google Scholar]
- Sampath, M.B.; Senthilkumar, M. Effect of Moisture Management Finish on Comfort Characteristics of Microdenier Polyester Knitted Fabrics. J. Ind. Text. 2009, 39, 163–173. [Google Scholar] [CrossRef]
- Sampath, M.B.; Prakash, C.; Senthilkumar, M. Influence of Moisture Management Finish on Comfort Characteristics of Knitted Fabrics Made from Different Yarns. Indian J. Fibre Text. Res. 2020, 45, 102–108. [Google Scholar] [CrossRef]
- Liu, J.; Wang, W.; Yu, D.; Zhao, K. Durable Moisture-Wicking and Fast-Dry Polyester Fabric Prepared by UV-Induced Click Reaction. Fibers Polym. 2020, 21, 111–118. [Google Scholar] [CrossRef]
- Holmes, D.A. Waterproof Breathable Fabrics. In Handbook of Technical Textiles; Elsevier: Amsterdam, The Netherlands, 2000; pp. 282–315. [Google Scholar] [CrossRef]
- Schindler, W.D.; Hauser, P.J. Chemical Finishing of Textiles; Woodhead Publishing in Textiles: Cambridge, UK, 2004. [Google Scholar]
- Tama, D.; Catarino, A.; Abreu, M.J. Evaluating the Effect of Water-Repellent Finishing on Thermal Insulation Properties of Rowing Shirts Using a Thermal Manikin. Tekst. Ve Konfeksiyon 2019, 29, 279–288. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, H.; Niu, H.; Gestos, A.; Wang, X.; Lin, T. Fluoroalkyl Silane Modified Silicone Rubber/Nanoparticle Composite: A Super Durable, Robust Superhydrophobic Fabric Coating. Adv. Mater. 2012, 24, 2409–2412. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Liu, W.; Jiang, C.; Liu, C.; He, S.; Xie, Y.; Wang, Z. Robust Fabrication of Superhydrophobic and Photocatalytic Self-Cleaning Cotton Textile Based on TiO2 and Fluoroalkylsilane. J. Mater. Sci. 2019, 54, 2079–2092. [Google Scholar] [CrossRef]
- Hays, H.L.; Mathew, D.; Chapman, J. Fluorides and Fluorocarbons Toxicity. In StatPearls; StatePearls Publishing: Treasure Island, FL, USA, 2022. [Google Scholar]
- Vethandamoorthy, D.; Mandawala, E.; Bandara, W. Development of Silicone-Based Water-Resistant, Chemical Resistant, Moisture Absorbent and Non-Ignitable Fabric. Int. J. Sci. Eng. Res. 2019, 10, 346. [Google Scholar]
- Cheng, X.-W.; Liang, C.-X.; Guan, J.-P.; Yang, X.-H.; Tang, R.-C. Flame Retardant and Hydrophobic Properties of Novel Sol-Gel Derived Phytic Acid/Silica Hybrid Organic-Inorganic Coatings for Silk Fabric. Appl. Surf. Sci. 2018, 427, 69–80. [Google Scholar] [CrossRef]
- Özek, H.Z. Silicone-Based Water Repellents. In Waterproof and Water Repellent Textiles and Clothing; Elsevier: Amsterdam, The Netherlands, 2018; pp. 153–189. [Google Scholar] [CrossRef]
- Mohseni, M.; Far, H.S.; Hasanzadeh, M.; Golovin, K. Non-Fluorinated Sprayable Fabric Finish for Durable and Comfortable Superhydrophobic Textiles. Prog. Org. Coat. 2021, 157, 106319. [Google Scholar] [CrossRef]
- De, P.; Sankhe, M.D.; Chaudhari, S.S.; Mathur, M.R. UV-Resist, Water-Repellent Breathable Fabric as Protective Textiles. J. Ind. Text. 2005, 34, 209–222. [Google Scholar] [CrossRef]
- Yoo, S.; Barker, R.L. Moisture Management Properties of Heat-Resistant Workwear Fabrics— Effects of Hydrophilic Finishes and Hygroscopic Fiber Blends. Text. Res. J. 2004, 74, 995–1000. [Google Scholar] [CrossRef]
- Chen, Q.; Fan, J.T.; Sarkar, M.K.; Bal, K. Plant-Based Biomimetic Branching Structures in Knitted Fabrics for Improved Comfort-Related Properties. Text. Res. J. 2011, 81, 1039–1048. [Google Scholar] [CrossRef]
- Guan, X.; Wang, X.; Huang, Y.; Zhao, L.; Sun, X.; Owens, H.; Lu, J.R.; Liu, X. Smart Textiles with Janus Wetting and Wicking Properties Fabricated by Graphene Oxide Coatings. Adv. Mater. Interfaces 2021, 8, 2001427. [Google Scholar] [CrossRef]
- Zeng, C.; Wang, H.; Zhou, H.; Lin, T. Directional Water Transport Fabrics with Durable Ultra-High One-Way Transport Capacity. Adv. Mater. Interfaces 2016, 3, 1600036. [Google Scholar] [CrossRef]
- Prabu, G.; Chattopadhyay, S.K.; Patil, P.G.; Arputharaj, A.; Mandhyan, P.; Prasad, G.K.; Vivekanandan, M.; Hadge, G.B.; Nadanathangam, V. Moisture Management Finish on Cotton Fabric by Electrospraying. Text. Res. J. 2017, 87, 2154–2165. [Google Scholar] [CrossRef]
- Tong, J.K.; Huang, X.; Boriskina, S.V.; Loomis, J.; Xu, Y.; Chen, G. Infrared-Transparent Visible-Opaque Fabrics for Wearable Personal Thermal Management. ACS Photon. 2015, 2, 769–778. [Google Scholar] [CrossRef]
- Wang, J.; Dai, G.; Huang, J. Thermal Metamaterial: Fundamental, Application, and Outlook. iScience 2020, 23, 101637. [Google Scholar] [CrossRef]
- Hsu, P.-C.; Song, A.Y.; Catrysse, P.B.; Liu, C.; Peng, Y.; Xie, J.; Fan, S.; Cui, Y. Radiative Human Body Cooling by Nanoporous Polyethylene Textile. Science 2016, 353, 1019–1023. [Google Scholar] [CrossRef]
- Ke, Y.; Wang, F.; Xu, P.; Yang, B. On the Use of a Novel Nanoporous Polyethylene (NanoPE) Passive Cooling Material for Personal Thermal Comfort Management under Uniform Indoor Environments. Build. Environ. 2018, 145, 85–95. [Google Scholar] [CrossRef]
- Catrysse, P.B.; Song, A.Y.; Fan, S. Photonic Structure Textile Design for Localized Thermal Cooling Based on a Fiber Blending Scheme. ACS Photonics 2016, 3, 2420–2426. [Google Scholar] [CrossRef]
- Cai, L.; Song, A.Y.; Li, W.; Hsu, P.; Lin, D.; Catrysse, P.B.; Liu, Y.; Peng, Y.; Chen, J.; Wang, H.; et al. Spectrally Selective Nanocomposite Textile for Outdoor Personal Cooling. Adv. Mater. 2018, 30, 1802152. [Google Scholar] [CrossRef]
- Yue, X.; Zhang, T.; Yang, D.; Qiu, F.; Wei, G.; Zhou, H. Multifunctional Janus Fibrous Hybrid Membranes with Sandwich Structure for On-Demand Personal Thermal Management. Nano Energy 2019, 63, 103808. [Google Scholar] [CrossRef]
- Liang, J.; Wu, J.; Guo, J.; Li, H.; Zhou, X.; Liang, S.; Qiu, C.-W.; Tao, G. Radiative Cooling for Passive Thermal Management towards Sustainable Carbon Neutrality. Natl. Sci. Rev. 2023, 10, nwac208. [Google Scholar] [CrossRef]
- Simms, D.L.; Hinkley, P.L. Protective Clothing Against Flames and Heat; Fire Research Notes 324; Fire Research Station: Boreham Wood, Herts, UK, 1959. [Google Scholar]
- Cai, G.; Wang, H.; Luo, Z.; Wang, X. Study on Thermal Insulation Properties of Aluminised Aramid Fabrics. Fibres Text. East. Eur. 2015, 23, 52–56. [Google Scholar]
- Zhu, F.; Feng, Q. Preparation, Thermal Properties and Permeabilities of Aluminum-coated Fabrics Destined for Thermal Radiation Protective Clothing. Fire Mater. 2020, 44, 844–853. [Google Scholar] [CrossRef]
- Shi, N.N.; Tsai, C.-C.; Camino, F.; Bernard, G.D.; Yu, N.; Wehner, R. Keeping Cool: Enhanced Optical Reflection and Radiative Heat Dissipation in Saharan Silver Ants. Science 2015, 349, 298–301. [Google Scholar] [CrossRef]
- Yamada, J. Radiative Properties of Fibers with Non-Circular Cross Sectional Shapes. J. Quant. Spectrosc. Radiat. Transf. 2002, 73, 261–272. [Google Scholar] [CrossRef]
- Sun, Y.; Ji, Y.; Javed, M.; Li, X.; Fan, Z.; Wang, Y.; Cai, Z.; Xu, B. Preparation of Passive Daytime Cooling Fabric with the Synergistic Effect of Radiative Cooling and Evaporative Cooling. Adv. Mater. Technol. 2022, 7, 2100803. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, J. In Situ Formation of SiO 2 Nanospheres on Common Fabrics for Broadband Radiative Cooling. ACS Appl. Nano Mater. 2021, 4, 11260–11268. [Google Scholar] [CrossRef]
- Hsu, P.-C.; Liu, X.; Liu, C.; Xie, X.; Lee, H.R.; Welch, A.J.; Zhao, T.; Cui, Y. Personal Thermal Management by Metallic Nanowire-Coated Textile. Nano Lett. 2015, 15, 365–371. [Google Scholar] [CrossRef]
- Mccann, J. Build the Perfect Survival Kit: Custom Kits for Adventure, Sport, and Travel; Krause Publications: Iola, Wisconsin, USA, 2005. [Google Scholar]
- Kosiński, S.; Podsiadło, P.; Darocha, T.; Pasquier, M.; Mendrala, K.; Sanak, T.; Zafren, K. Prehospital Use of Ultrathin Reflective Foils. Wilderness Environ. Med. 2022, 33, 134–139. [Google Scholar] [CrossRef]
- Hayes, S.G.; Venkatraman, P. Materials and Technology for Sportswear and Performance Apparel; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Cai, L.; Song, A.Y.; Wu, P.; Hsu, P.-C.; Peng, Y.; Chen, J.; Liu, C.; Catrysse, P.B.; Liu, Y.; Yang, A.; et al. Warming up Human Body by Nanoporous Metallized Polyethylene Textile. Nat. Commun. 2017, 8, 496. [Google Scholar] [CrossRef]
- Yue, X.; He, M.; Zhang, T.; Yang, D.; Qiu, F. Laminated Fibrous Membrane Inspired by Polar Bear Pelt for Outdoor Personal Radiation Management. ACS Appl. Mater. Interfaces 2020, 12, 12285–12293. [Google Scholar] [CrossRef]
- Abebe, M.G.; De Corte, A.; Rosolen, G.; Maes, B. Janus-Yarn Fabric for Dual-Mode Radiative Heat Management. Phys. Rev. Appl. 2021, 16, 054013. [Google Scholar] [CrossRef]
- Yue, X.; Zhang, T.; Yang, D.; Qiu, F.; Wei, G.; Lv, Y. A Robust Janus Fibrous Membrane with Switchable Infrared Radiation Properties for Potential Building Thermal Management Applications. J. Mater. Chem. A Mater. 2019, 7, 8344–8352. [Google Scholar] [CrossRef]
- Fang, Y.; Chen, G.; Bick, M.; Chen, J. Smart Textiles for Personalized Thermoregulation. Chem. Soc. Rev. 2021, 50, 9357–9374. [Google Scholar] [CrossRef] [PubMed]
- Wei, W.; Liu, J.; Huang, J.; Cao, F.; Qian, K.; Yao, Y.; Li, W. Recent Advances and Perspectives of Shape Memory Polymer Fibers. Eur. Polym. J. 2022, 175, 111385. [Google Scholar] [CrossRef]
- Chen, W.L.; He, M.M.; Gao, Y.; Wu, X. Temperature-Regulating Properties of Phase Change Fiber Blended Knitted Fabrics after Laundering. Adv. Mater. Res. 2011, 393–395, 397–400. [Google Scholar] [CrossRef]
- Mondal, S. Phase Change Materials for Smart Textiles—An Overview. Appl. Therm. Eng. 2008, 28, 1536–1550. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, J.; Zhu, G.; Militky, J.; Marek, J.; Venkataraman, M.; Zhang, G. A Novel Method for Producing Bi-Component Thermo-Regulating Alginate Fiber from Phase Change Material Microemulsion. Text. Res. J. 2020, 90, 1038–1044. [Google Scholar] [CrossRef]
- Tran, N.H.A.; Kirsten, M.; Cherif, C. New Fibers from PCM Using the Conventional Melt Spinning Process. In Proceedings of the Europe/Africa conference Dresden 2017—Polymer Processing Society PPS; AIP Publishing: College Park, Maryland, USA, 2019; p. 060002. [Google Scholar] [CrossRef]
- Ding, B.; Yu, J. Electrospun Nanofibers for Energy and Environmental Applications; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Shin, Y.; Yoo, D.-I.; Son, K. Development of Thermoregulating Textile Materials with Microencapsulated Phase Change Materials (PCM). IV. Performance Properties and Hand of Fabrics Treated with PCM Microcapsules. J. Appl. Polym. Sci. 2005, 97, 910–915. [Google Scholar] [CrossRef]
- Choi, K.; Cho, G.; Kim, P.; Cho, C. Thermal Storage/Release and Mechanical Properties of Phase Change Materials on Polyester Fabrics. Text. Res. J. 2004, 74, 292–296. [Google Scholar] [CrossRef]
- Kim, J.; Cho, G. Thermal Storage/Release, Durability, and Temperature Sensing Properties of Thermostatic Fabrics Treated with Octadecane-Containing Microcapsules. Text. Res. J. 2002, 72, 1093–1098. [Google Scholar] [CrossRef]
- Mazumder, J. Functional Polymers; Springer International Publishing: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Zhu, Y.; Hu, J.; Lu, J.; Yeung, L.Y.; Yeung, K. Shape Memory Fiber Spun with Segmented Polyurethane Ionomer. Polym. Adv. Technol. 2008, 19, 1745–1753. [Google Scholar] [CrossRef]
- Kaursoin, J.; Agrawal, A.K. Melt Spun Thermoresponsive Shape Memory Fibers Based on Polyurethanes: Effect of Drawing and Heat-Setting on Fiber Morphology and Properties. J. Appl. Polym. Sci. 2007, 103, 2172–2182. [Google Scholar] [CrossRef]
- Xia, Y.; Zhang, F.; Wang, L.; Liu, Y.; Leng, J. Electrospun Shape-Memory Polymer Fibers and Their Applications. In Electrospun Polymers and Composites; Elsevier: Amsterdam, The Netherlands, 2021; pp. 567–596. [Google Scholar] [CrossRef]
- Xiao, X.; Hu, J. Animal Hairs as Water-Stimulated Shape Memory Materials: Mechanism and Structural Networks in Molecular Assemblies. Sci. Rep. 2016, 6, 26393. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Irfan Iqbal, M.; Sun, F. Wool Can Be Cool: Water-Actuating Woolen Knitwear for Both Hot and Cold. Adv. Funct. Mater. 2020, 30, 2005033. [Google Scholar] [CrossRef]
- Wang, L.; Pan, M.; Lu, Y.; Song, W.; Liu, S.; Lv, J. Developing Smart Fabric Systems with Shape Memory Layer for Improved Thermal Protection and Thermal Comfort. Mater. Des. 2022, 221, 110922. [Google Scholar] [CrossRef]
- Memiş, N.K.; Kaplan, S. Wool Fabric Having Thermal Comfort Management Function via Shape Memory Polyurethane Finishing. J. Text. Inst. 2020, 111, 734–744. [Google Scholar] [CrossRef]
- Rousseau, I.A. Challenges of Shape Memory Polymers: A Review of the Progress toward Overcoming SMP’s Limitations. Polym. Eng. Sci. 2008, 48, 2075–2089. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, X.; Liu, R.; Zhi, C.; Liu, Y.; Fan, W.; Meng, J. Shape Memory Active Thermal-Moisture Management Textiles. Compos. Part A Appl. Sci. Manuf. 2022, 160, 107037. [Google Scholar] [CrossRef]
- Shahzad, A.; Jabbar, A.; Irfan, M.; Qadir, M.B.; Ahmad, Z. Electrical Resistive Heating Characterization of Conductive Hybrid Staple Spun Yarns. J. Text. Inst. 2020, 111, 1481–1488. [Google Scholar] [CrossRef]
- Pillai, A.S.; Chandran, A.; Peethambharan, S.K. Joule Heating Fabrics. In Advances in Healthcare and Protective Textiles; Elsevier: Amsterdam, The Netherlands, 2023; pp. 387–421. [Google Scholar] [CrossRef]
- Wu, B.Y.; Alam, M.O.; Chan, Y.C.; Zhong, H.W. Joule Heating Enhanced Phase Coarsening in Sn37Pb and Sn3.5Ag0.5Cu Solder Joints during Current Stressing. J. Electron. Mater. 2008, 37, 469–476. [Google Scholar] [CrossRef]
- Martins, R.d.A. Joule’s 1840 Manuscript on the Production of Heat by Voltaic Electricity. Notes Rec. R. Soc. J. Hist. Sci. 2022, 76, 117–154. [Google Scholar] [CrossRef]
- Doganay, D.; Coskun, S.; Genlik, S.P.; Unalan, H.E. Silver Nanowire Decorated Heatable Textiles. Nanotechnology 2016, 27, 435201. [Google Scholar] [CrossRef] [PubMed]
- Ahn, J.; Gu, J.; Hwang, B.; Kang, H.; Hwang, S.; Jeon, S.; Jeong, J.; Park, I. Printed Fabric Heater Based on Ag Nanowire/Carbon Nanotube Composites. Nanotechnology 2019, 30, 455707. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.; Zhang, H.; Wang, R.; Wang, X.; Zhai, H.; Wang, T.; Jin, Q.; Sun, J. Highly Stretchable and Conductive Copper Nanowire Based Fibers with Hierarchical Structure for Wearable Heaters. ACS Appl. Mater. Interfaces 2016, 8, 32925–32933. [Google Scholar] [CrossRef]
- Mahmud, S.; Forcier, P.; Decaens, J.; Dolez, P.I. Controlling the Variability in the Measurement of the Efficiency of Joule Heating Textiles; Institute of Textile Science (ITS) Symposium: Edmonton, AB, Canada, 2023. [Google Scholar]
- Ma, R.; Zhang, Z.; Tong, K.; Huber, D.; Kornbluh, R.; Ju, Y.S.; Pei, Q. Highly Efficient Electrocaloric Cooling with Electrostatic Actuation. Science 2017, 357, 1130–1134. [Google Scholar] [CrossRef]
- Wang, H.; Meng, Y.; Zhang, Z.; Gao, M.; Peng, Z.; He, H.; Pei, Q. Self-Actuating Electrocaloric Cooling Fibers. Adv. Energy Mater. 2020, 10, 1903902. [Google Scholar] [CrossRef]
- Hong, S.; Gu, Y.; Seo, J.K.; Wang, J.; Liu, P.; Meng, Y.S.; Xu, S.; Chen, R. Wearable Thermoelectrics for Personalized Thermoregulation. Sci. Adv. 2019, 5, eaaw0536. [Google Scholar] [CrossRef]
- Snyder, G.J.; Snyder, A.H. Figure of Merit ZT of a Thermoelectric Device Defined from Materials Properties. Energy Environ. Sci 2017, 10, 2280–2283. [Google Scholar] [CrossRef]
- Lee, J.A.; Aliev, A.E.; Bykova, J.S.; de Andrade, M.J.; Kim, D.; Sim, H.J.; Lepró, X.; Zakhidov, A.A.; Lee, J.; Spinks, G.M.; et al. Woven-Yarn Thermoelectric Textiles. Adv. Mater. 2016, 28, 5038–5044. [Google Scholar] [CrossRef]
- Zhang, H.; Huizenga, C.; Arens, E.; Wang, D. Thermal Sensation and Comfort in Transient Non-Uniform Thermal Environments. Eur. J. Appl. Physiol. 2004, 92, 728–733. [Google Scholar] [CrossRef]
- West, A.M.; Havenith, G.; Hodder, S. Are Running Socks Beneficial for Comfort? The Role of the Sock and Sock Fiber Type on Shoe Microclimate and Subjective Evaluations. Text. Res. J. 2021, 91, 1698–1712. [Google Scholar] [CrossRef]
- Filingeri, D.; Havenith, G. Human Skin Wetness Perception: Psychophysical and Neurophysiological Bases. Temperature 2015, 2, 86–104. [Google Scholar] [CrossRef] [PubMed]
- Periyaswamy, T.; Islam, M.R. Tactile Rendering of Textile Materials. J. Text. Sci. Fash. Technol. 2022, 9, 1–10. [Google Scholar] [CrossRef]
- Tichy, H.; Kallina, W. Insect Hygroreceptor Responses to Continuous Changes in Humidity and Air Pressure. J. Neurophysiol. 2010, 103, 3274–3286. [Google Scholar] [CrossRef] [PubMed]
- Tiest, W.M.B.; Kosters, N.D.; Kappers, A.M.L.; Daanen, H.A.M. Haptic Perception of Wetness. Acta Psychol. 2012, 141, 159–163. [Google Scholar] [CrossRef] [PubMed]
- Bentley, I.M. The Synthetic Experiment. Am. J. Psychol. 1900, 11, 405. [Google Scholar] [CrossRef]
- Ackerley, R.; Olausson, H.; Wessberg, J.; McGlone, F. Wetness Perception across Body Sites. Neurosci. Lett. 2012, 522, 73–77. [Google Scholar] [CrossRef]
- Filingeri, D.; Redortier, B.; Hodder, S.; Havenith, G. Thermal and Tactile Interactions in the Perception of Local Skin Wetness at Rest and during Exercise in Thermo-Neutral and Warm Environments. Neuroscience 2014, 258, 121–130. [Google Scholar] [CrossRef]
- Li, Y. Perceptions of Temperature, Moisture and Comfort in Clothing during Environmental Transients. Ergonomics 2005, 48, 234–248. [Google Scholar] [CrossRef]
- Gagge, A.P. A New Physiological Variable Associated with Sensible and Insensible Perspiration. Am. J. Physiol. Leg. Content 1937, 120, 277–287. [Google Scholar] [CrossRef]
- MacRae, B.A.; Annaheim, S.; Spengler, C.M.; Rossi, R.M. Skin Temperature Measurement Using Contact Thermometry: A Systematic Review of Setup Variables and Their Effects on Measured Values. Front. Physiol. 2018, 9, 29. [Google Scholar] [CrossRef] [PubMed]
- Kateb, B.; Yamamoto, V.; Yu, C.; Grundfest, W.; Gruen, J.P. Infrared Thermal Imaging: A Review of the Literature and Case Report. Neuroimage 2009, 47, T154–T162. [Google Scholar] [CrossRef] [PubMed]
- Bongers, C.C.W.G.; Hopman, M.T.E.; Eijsvogels, T.M.H. Using an Ingestible Telemetric Temperature Pill to Assess Gastrointestinal Temperature During Exercise. J. Vis. Exp. 2015, 53258. [Google Scholar] [CrossRef]
- Koo, H.R.; Lee, Y.-J.; Gi, S.; Khang, S.; Lee, J.H.; Lee, J.-H.; Lim, M.-G.; Park, H.-J.; Lee, J.-W. The Effect of Textile-Based Inductive Coil Sensor Positions for Heart Rate Monitoring. J. Med. Syst. 2014, 38, 2. [Google Scholar] [CrossRef]
- Temko, A. Accurate Heart Rate Monitoring During Physical Exercises Using PPG. IEEE Trans. Biomed. Eng. 2017, 64, 2016–2024. [Google Scholar] [CrossRef]
- Chung, M.; Fortunato, G.; Radacsi, N. Wearable Flexible Sweat Sensors for Healthcare Monitoring: A Review. J. R. Soc. Interface 2019, 16, 20190217. [Google Scholar] [CrossRef]
- Mekjavic, I.B.; Yogev, D.; Ciuha, U. Perception of Thermal Comfort during Skin Cooling and Heating. Life 2021, 11, 681. [Google Scholar] [CrossRef]
- Pao, S.-L.; Wu, S.-Y.; Liang, J.-M.; Huang, I.-J.; Guo, L.-Y.; Wu, W.-L.; Liu, Y.-G.; Nian, S.-H. A Physiological-Signal-Based Thermal Sensation Model for Indoor Environment Thermal Comfort Evaluation. Int. J. Environ. Res. Public Health 2022, 19, 7292. [Google Scholar] [CrossRef]
- Schepers, R.J.; Ringkamp, M. Thermoreceptors and Thermosensitive Afferents. Neurosci. Biobehav. Rev. 2010, 34, 177–184. [Google Scholar] [CrossRef]
- Campero, M.; Bostock, H. Unmyelinated Afferents in Human Skin and Their Responsiveness to Low Temperature. Neurosci. Lett. 2010, 470, 188–192. [Google Scholar] [CrossRef]
- Zhang, H.; Arens, E.; Huizenga, C.; Han, T. Thermal Sensation and Comfort Models for Non-Uniform and Transient Environments: Part I: Local Sensation of Individual Body Parts. Build. Environ. 2010, 45, 380–388. [Google Scholar] [CrossRef]
- Guan, Y.; Hosni, M.H.; Jones, B.W.; Gielda, T.P. Investigation of Human Thermal Comfort under Highly Transient Conditions for Automobile Applications–Part 2: Thermal Sensation Modeling. ASHRAE Trans. 2003, 109, 898–907. [Google Scholar]
- Wang, X.L.; Peterson, F.K. Estimating Thermal Transient Comfort. ASHRAE Trans. 1992, 98, 182–188. [Google Scholar]
- Briese, E. Normal Body Temperature of Rats: The Setpoint Controversy. Neurosci. Biobehav. Rev. 1998, 22, 427–436. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Arens, E.; Huizenga, C.; Han, T. Thermal Sensation and Comfort Models for Non-Uniform and Transient Environments, Part III: Whole-Body Sensation and Comfort. Build. Environ. 2010, 45, 399–410. [Google Scholar] [CrossRef]
- Zhang, H.; Arens, E.; Huizenga, C.; Han, T. Thermal Sensation and Comfort Models for Non-Uniform and Transient Environments, Part II: Local Comfort of Individual Body Parts. Build. Environ. 2010, 45, 389–398. [Google Scholar] [CrossRef]
- Raccuglia, M.; Hodder, S.; Havenith, G. Human Wetness Perception in Relation to Textile Water Absorption Parameters under Static Skin Contact. Text. Res. J. 2017, 87, 2449–2463. [Google Scholar] [CrossRef]
- ISO 10551; Ergonomics of the Physical Environment—Subjective Judgement Scales for Assessing Physical Environments. International Organization for Standardization: Geneva, Switzerland, 2019.
- Grujic, D.; Geršak, J. Examination of the Relationships between Subjective Clothing Comfort Assessment and Physiological Parameters with Wear Trials. Text. Res. J. 2017, 87, 1522–1537. [Google Scholar] [CrossRef]
- Celcar, D. A Subjective Evaluation of the Thermal Comfort of Clothing Evaluated in Cold Environment. Glas. Hemičara Tehnol. I Ekol. Repub. Srp. 2014, 5, 65–71. [Google Scholar] [CrossRef]
- ASTM F1868; Standard Test Method for Thermal and Evaporative Resistance of Clothing Materials Using a Sweating Hot Plate. ASTM International: London, UK, 2017.
- Rossi, R. Interactions between Protection and Thermal Comfort. In Textiles for Protection; Elsevier: Amsterdam, The Netherlands, 2005; pp. 233–260. [Google Scholar] [CrossRef]
- Huang, J. Sweating Guarded Hot Plate Test Method. Polym. Test. 2006, 25, 709–716. [Google Scholar] [CrossRef]
- Thermetrics. Sweating Guarded Hotplate. Available online: https://thermetrics.com/wp-content/uploads/2020/09/SGHP-Hotplate-Thermetrics.pdf (accessed on 6 June 2023).
- McCullough, E.A. The Use of Thermal Manikins to Evaluate Clothing and Environmental Factors. Elsevier Ergon. Book Ser. 2005, 3, 403–407. [Google Scholar] [CrossRef]
- ASTM F1291; Standard Test Method for Measuring the Thermal Insulation of Clothing Using a Heated Manikin. ASTM International: London, UK, 2016.
- ASTM F2370; Standard Test Method for Measuring the Evaporative Resistance of Clothing Using a Sweating Manikin. ASTM International: London, UK, 2016.
- Lei, Z. Review of Application of Thermal Manikin in Evaluation on Thermal and Moisture Comfort of Clothing. J. Eng. Fibers Fabr. 2019, 14, 155892501984154. [Google Scholar] [CrossRef]
- Psikuta, A. Development of an “Artificial Human” for Clothing Research; De Montfort University: Leicester, UK, 2009. [Google Scholar]
- Psikuta, A.; Weibel, M.; Burke, R.; Hepokoski, M.; Schwenn, T.; Annaheim, S.; Rossi, R.M. A Systematic Approach to the Development and Validation of Adaptive Manikins. Extrem. Physiol. Med. 2015, 4, A15. [Google Scholar] [CrossRef]
- Wang, F. Effect of Body Movement on the Thermophysiological Responses of an Adaptive Manikin and Human Subjects. Measurement 2018, 116, 251–256. [Google Scholar] [CrossRef]
- Albert, M.M.; García, P.D.; Belda, E.B. Development of a new testing protocol to evaluate cooling systems. EXCLI J. 2023, 22, 583–594. [Google Scholar]
- Ostrowski, Z.; Rojczyk, M. Natural Convection Heat Transfer Coefficient for Newborn Baby. Heat Mass Transf. 2018, 54, 2395–2403. [Google Scholar] [CrossRef]
- Kang, I.-H.; Tamura, T. A Study on the Development of an Infant-Sized Movable Sweating Thermal Manikin. J. Hum. Environ. Syst. 2001, 5, 49–56. [Google Scholar] [CrossRef]
- Golden, J.; Brown, T.; Domina, T.; Wroblewski, S.; Kumphai, P. Utilisation of an Infant Sweating Thermal Manikin to Determine Clo Values for Infant Clothing: A Comparison of Predictive Formulas. Int. J. Fash. Des. Technol. Educ. 2021, 14, 272–283. [Google Scholar] [CrossRef]
- Richards, M.; Alison, J.; Devarajan, S.; Bussoli, M.; Gathercole, R.; Jack, A. A Multi-Sector Cylinder For Iso 18640-1, Specially Designed For Studying Clothing Sweat Management, Working in Hot Climates and Dynamic Physiological Control. In Proceedings of the 12th International Manikin and Modelling Meeting (12i3m), St. Gallen, Switzerland, 29–31 August 2018. [Google Scholar]
- Fontana, P.; Saiani, F.; Grütter, M.; Croset, J.-P.; Capt, A.; Camenzind, M.; Morrissey, M.; Rossi, R.M.; Annaheim, S. Exercise Intensity Dependent Relevance of Protective Textile Properties for Human Thermo-Physiology. Text. Res. J. 2017, 87, 1425–1434. [Google Scholar] [CrossRef]
- Psikuta, A.; Wang, L.-C.; Rossi, R.M. Prediction of the Physiological Response of Humans Wearing Protective Clothing Using a Thermophysiological Human Simulator. J. Occup. Environ. Hyg 2013, 10, 222–232. [Google Scholar] [CrossRef]
- Candas, V.; Libert, J.P.; Vogt, J.J. Human Skin Wettedness and Evaporative Efficiency of Sweating. J. Appl. Physiol. 1979, 46, 522–528. [Google Scholar] [CrossRef] [PubMed]
- Guan, M.; Annaheim, S.; Li, J.; Camenzind, M.; Psikuta, A.; Rossi, R.M. Apparent Evaporative Cooling Efficiency in Clothing with Continuous Perspiration: A Sweating Manikin Study. Int. J. Therm. Sci. 2019, 137, 446–455. [Google Scholar] [CrossRef]
- Havenith, G.; Richards, M.G.; Wang, X.; Bröde, P.; Candas, V.; den Hartog, E.; Holmér, I.; Kuklane, K.; Meinander, H.; Nocker, W. Apparent Latent Heat of Evaporation from Clothing: Attenuation and “Heat Pipe” Effects. J. Appl. Physiol. 2008, 104, 142–149. [Google Scholar] [CrossRef] [PubMed]
- Barndt, H.J.; Pierce, J.D., Jr.; Pa, P.U. QMax Relationship to Perceived Comfort as Measured by the Calm Scale; Laboratory for Engineered Human Protection: Philadelphia, PA, USA, 2022. [Google Scholar]
- Wang, F.; Annaheim, S.; Morrissey, M.; Rossi, R.M. Real Evaporative Cooling Efficiency of One-Layer Tight-Fitting Sportswear in a Hot Environment. Scand. J. Med. Sci. Sports 2013, 24, e129–e139. [Google Scholar] [CrossRef]
- McLellan, T.; Selkirk, G. Heat Stress While Wearing Long Pants or Shorts under Firefighting Protective Clothing. Ergonomics 2004, 47, 75–90. [Google Scholar] [CrossRef]
- Lu, Y.; Song, G.; Ackerman, M.Y.; Paskaluk, S.A.; Li, J. A New Protocol to Characterize Thermal Protective Performance of Fabrics against Hot Liquid Splash. Exp. Therm. Fluid Sci. 2013, 46, 37–45. [Google Scholar] [CrossRef]
- Dolez, P.I.; Marsha, S.; McQueen, R.H. Fibers and Textiles for Personal Protective Equipment: Review of Recent Progress and Perspectives on Future Developments. Textiles 2022, 2, 349–381. [Google Scholar] [CrossRef]
- Abedin, F.; DenHartog, E. The Exothermic Effects of Textile Fibers during Changes in Environmental Humidity: A Comparison between ISO:16533 and Dynamic Hot Plate Test Method. Fibers 2023, 11, 47. [Google Scholar] [CrossRef]
- Gao, H.; Deaton, A.S.; Barker, R. A New Test Method for Evaluating the Evaporative Cooling Efficiency of Fabrics Using a Dynamic Sweating Hot Plate. Meas. Sci. Technol. 2022, 33, 125601. [Google Scholar] [CrossRef]
- Renard, M.; Puszkarz, A.K. Modeling of Heat Transfer through Firefighters Multilayer Protective Clothing Using the Computational Fluid Dynamics Assisted by X-Ray Microtomography and Thermography. Materials 2022, 15, 5417. [Google Scholar] [CrossRef]
- Hamilton, S.F.; Luster, T. Bronfenbrenner, Urie. In Encyclopedia of Human Ecology; Miller, J.R., Lerner, R.M., Schiamberg, L.B., Anderson, P.M., Eds.; ABC-CLIO: Santa Barbara, CA, USA, 2003; Volume 1, pp. 84–89. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).