Rotational vs. Vibrational Excitations in a Chemical Laser

Abstract

The research reviews and contrasts two studies based on the gas-phase reaction OH + D₂(v, j). In these studies, Quasi-Classical Trajectory (QCT) calculations and the Gaussian Binning (GB) technique were used on the Wu–Schatz–Lendvay–Fang–Harding (WSLFH) potential energy surface. Large sample sizes allow for precise energy state distribution analysis across translational, vibrational, and rotational components in the products. A key observation is the influence of the vibrational and rotational excitation of D₂ on the total angular momentum (J′) of the HOD* product. This study reveals that increasing the vibrational level, vD₂, significantly shifts P(J′) distributions toward higher values, broadening them due to increased isotropy. In contrast, increasing the rotational level, jD₂, results in a smaller shift but introduces greater anisotropy, leading to a more selective distribution of J′ values. The dual Gaussian Binning selection—Vibrational-GB followed by Rotational-GB—further highlights a preference for either odd or even J′ values, depending on the specific excitation conditions. These findings have implications for the development of chemical lasers, as the excitation and emission properties of HOD* can be leveraged in the laser design. Future research aims to extend this study to a broader range of initial conditions, refining the understanding of reaction dynamics in controlled gas-phase environments.

1. Introduction

The investigation of gas-phase polyatomic reactions has been a cornerstone of modern reaction dynamics, offering insights into the intricate mechanisms governing energy transfer, product formation, and isotopic effects. Among these, the reaction between the hydroxyl radical (OH) and deuterium (D₂) to form the excited product HOD* and an ejected deuterium atom (D) represents a model system. This reaction, often described as a benchmark for tetratomic dynamics, exemplifies the complexity and beauty of chemical processes, merging theoretical precision with experimental feasibility. By comparing the thematic foci of two pivotal studies [1,2], the author suggests exploring advances in the understanding of this reaction system, its methodologies and its potential applications, including the development of the chemical laser.

The OH + D₂ reaction has long served as a prototypical system for examining atomic abstraction mechanisms, in which the OH radical removes a D atom from D₂ to form HOD*. Its relevance extends beyond fundamental science, underpinning processes in atmospheric chemistry and combustion. As a counterpart to the OH + H₂ reaction, which produces water (H₂O) as the product, the OH + D₂ system offers unique opportunities to study isotopic effects and energy distribution due to the heavier mass of deuterium. Alagia et al. [3,4] conducted pioneering molecular beam experiments on OH + D₂, showing that about 64% of the total available energy is transferred to the internal excitation of the HOD product. While these experiments were unable to resolve specific vibrational levels, subsequent studies using advanced techniques such as D-atom Rydberg tagging [5,6] confirmed and expanded upon these findings, providing detailed vibrational state distributions and highlighting the importance of backward scattering in the reaction dynamics.

A critical component of understanding reaction dynamics is the development of accurate potential energy surfaces (PES), which model the interactions between reactants and products. Early efforts, such as the Walch–Dunning–Schatz–Elgersma (WDSE) PES [7], laid the foundation for theoretical studies of OH + D₂. Subsequent surfaces, including the Ochoa–Clary (OC) [8,9] and Wu–Schatz–Lendvay–Fang–Harding (WSLFH) PES [10], provided an enhanced accuracy and resolution, allowing for more reliable simulations of reaction pathways and energy distributions.

Recent innovations in PES development have embraced machine learning approaches, exemplified by Neural Network (NN) PES models. Chen et al. [11] demonstrated the potential of NN PES to capture complex energy landscapes with improved efficiency. However, discontinuities in the transition state region identified by prior studies [12] underscore the need for continued refinement. Non-analytical PESs, such as the Yang–Zhang–Collins–Lee (YZCL2) [13] and Xiao–Xu–Zhang (XXZ) surfaces [14], have also contributed to the field, offering alternative methodologies for studying reaction dynamics. These surfaces have been instrumental in elucidating the interplay between vibrational excitation, rotational effects, and energy partitioning.

The Quasi-Classical Trajectory (QCT) methodology has emerged as a powerful tool for studying polyatomic reactions, providing a balance between the computational efficiency and physical accuracy. By sampling a large number of trajectories on a given PES, QCT simulations yield statistically robust insights into reaction dynamics. The Gaussian Binning (GB) approach, particularly when applied in a two-step process involving vibrational (V-GB) and rotational (R-GB) selections, enhances the resolution of vibro-rotational energy distributions [15,16]. This methodology, employed in both studies under comparison, underscores its versatility and importance in analyzing large datasets generated by QCT simulations. For a triatomic system (C + H₂), a study [17] demonstrated the first successful application of GB to QCT calculations, providing a comparison with quantum mechanical scattering results. Moreover, for the polyatomic reaction, F + CHD₃, [18] the GB method confirmed this through direct comparison to data obtained from crossed molecular beam experiments.

Both articles emphasize the significance of energy distribution in the OH + D₂ → HOD + D reaction, albeit with distinct approaches. The first study [1] focuses on the influence of several initial rotational excitations (jD₂ = 0, 2, 4, 6, 8), examining how these factors shape the internal energy distribution of the HOD product. By leveraging the WSLFH PES and QCT-GB methodologies, this study provides a detailed analysis of product state distributions, revealing trends that align with experimental observations. This work highlights the anisotropic nature of the reaction, particularly in the context of vibrational excitation, which preferentially channels energy into specific modes of the HOD molecule.

In contrast, the second study [2] explores the isotropic effects of initial vibrational excitations (jD₂ = 0, 1, 2, 3, 4) and their implications for reaction dynamics. By comparing the OH + D₂ system to its OH + H₂ counterpart, the author identifies subtle differences in the energy partitioning and scattering behavior.

The translational, vibrational, and rotational state distributions for the products of the {OH (vOH = 0; jOH = 2) + D₂ (vD₂ = 0, 1, 2, 3, 4; jD₂ = 2)} [1] and {OH (vOH = 0; jOH = 2) + D₂ (vD₂ = 0; jD₂ = 0, 2, 4, 6, 8)} [2] gas-phase reactions under initial conditions at a collision energy of 0.28 eV were calculated and analyzed [1,2]. The calculations were performed exclusively using the WSLFH analytical PES, due to its superior performance compared to a more recent PES, NN, [11] as noted in previous research on OH + D₂ [12,19]. Notably, the results obtained for both surfaces (WSLFH and NN) showed excellent agreement with experimental data from high-resolution molecular beam studies [5,6]. This agreement surpassed the results obtained when using the standard Quasi-Classical Trajectory methodology (e.g., histogram binning).

The integration of theoretical and experimental approaches is central to advancing our understanding of polyatomic reaction dynamics [20,21,22,23,24,25,26]. While both studies provide valuable insights, gaps remain in the experimental validation, particularly concerning the resolution of higher vibrational states and the influence of rotational excitation. Recent advancements in experimental techniques [5,6], such as crossed molecular beams with velocity map imaging, hold promise for addressing these challenges. Additionally, the development of ultrafast laser spectroscopy offers new opportunities for probing reaction intermediates and products in real-time, providing a complementary perspective to theoretical simulations.

One of the most intriguing applications of the OH + D₂ reaction is its potential use in chemical lasers. The high internal excitation of the HOD* product, coupled with its anisotropic energy distribution, makes this reaction a promising candidate for laser development. Chemical lasers based on reactions like OH + D₂ could enable the precise control of emitted wavelengths, with applications ranging from materials processing to molecular spectroscopy. Both studies contribute to this vision by elucidating the fundamental dynamics that govern energy transfer and emission processes in this reaction system.

In summary, this research offers an in-depth examination of the gas-phase reaction OH + D₂ → HOD* + D, considered a benchmark system in polyatomic reaction dynamics. It compares two studies that investigate how different initial conditions—rotational and vibrational excitations—affect energy distribution in the reaction products. Both studies apply the Quasi-Classical Trajectory method combined with Gaussian Binning on the WSLFH potential energy surface, which has demonstrated higher accuracy than newer neural network-based PES models. The findings align well with high-resolution molecular beam experiments, confirming the method’s reliability. Key insights include the role of molecular asymmetry, energy partitioning, and the observed anisotropy or isotropy in product distributions depending on the type of excitation. The research also highlights the potential of the OH + D₂ reaction for future chemical laser development due to the high internal excitation and directional energy release in the HOD* product. Lastly, the research emphasizes the importance of integrating theoretical simulations with experimental techniques, such as ultrafast laser spectroscopy and velocity-map imaging, to deepen our understanding of the energy transfer and reaction mechanisms in polyatomic systems.

2. Computational Method

As already stated in the introduction, in the first article [1], the computational method consists of the rotational and vibrational state distributions (in addition to the translational one) for the products of the OH (vOH = 0; jOH = 2) + D₂ (vD₂ = 0; jD₂ = 0, 2, 4, 6, 8) gas-phase reaction’s initial conditions. These have been simulated under a relative translational energy between the reactive molecules, OH and D₂, of 0.28 eV. For these initial conditions, samples were increased so the QCT-GB methodologies could be used efficiently in the analysis. Exclusively the WSLFH PES, due to its reliable performance, was better than a most recent PES, NN, as the author researched [12,19]. Nevertheless, results obtained for both surfaces (WSLFH and NN) showed a strong correlation with the findings from high-detail molecular beam experiments [5,6], better than when the standard Quasi-Classical Trajectory methodology (i.e., histogram binning) was used.

And, in the second one [2], the study focuses on the initial conditions OH (vOH = 0; jOH = 2) + D₂ (vD₂ = 0, 1, 2, 3, 4; jD₂ = 2) at the same initial collision energy, 0.28 eV, with plans to expand the research to encompass broader initial condition samples to enhance the understanding of potential chemical laser applications.

Large samples of these conditions were generated using QCT calculations and analyzed with the GB methodology. The WSLFH analytical PES was exclusively employed due to its excellent chemical-physical properties and efficiency, allowing the generation of extensive, high-quality data samples within shorter computation times. The vibrational states of the HOD* product molecule, and then, the rotational states, were analyzed using the GB methodology, which has proven highly effective, as demonstrated in the author’s previous works [12,16,19]. These results align closely with high-resolution molecular beam experiments [5,6], further validating the superiority of GB over traditional histogram binning methods.

After a second rotational-GB (R-GB) selection, an important property was calculated: the rotational state-specific distribution for the HOD product molecule, P(J′, R-GB). This study was possible thanks to the improvement of the statistics (

Table 1. Number of trajectories (N_R-GB) analyzed after the R-GB selection (2ª) [1,2].

OH + D2 (v = 0, j)	NR-GB (j)	OH + D2 (v, j = 2)	NR-GB (v)
0	195	0	224
2	224	1	206
4	246	2	216
6	239	3	197
8	224	4	146

) [1,2].

Starting with the real number fsj′, the closest natural number to fsj′ represents the natural angular action (J′) of the HOD product molecule. In this second selection, R-GB, only trajectories that meet the following condition are selected: |fsj′ − J′| < epsilon, with epsilon = 0.05.

3. Results and Discussions

The selection of only the most relevant reactive trajectories (Total Reactive Trajectories: TRT) is essential for accurately analyzing reaction dynamics. By applying the Good Reactive Trajectories (GRT) criterion [1,2], which ensures energy conservation within a strict threshold, and utilizing the GB methodology, a more precise and reliable interpretation of the results is achieved. This approach focuses on high-quality data, filtering out less significant trajectories that could introduce inaccuracies.

In the first selection step, Vibrational-GB (V-GB) was applied to determine the vibrational state populations of the HOD product molecule [1,2]. This is achieved by assigning Gaussian statistical weights to each trajectory, ensuring that only those with vibrational actions close to integer values are considered. Traditional QCT methods process all trajectories indiscriminately, often leading to broad and less accurate distributions. In contrast, the GB methodology enhances the resolution by selecting only the most relevant trajectories, reducing the dataset by three orders of magnitude while maintaining statistical reliability.

The second selection step, Rotational-GB (R-GB), refines the dataset further by focusing on rotational-state distributions [1,2]. This step applies a slightly less restrictive Gaussian criterion, ensuring that only trajectories with total angular momentum values closely matching integer quantum numbers are selected. While this reduces the dataset by another order of magnitude, it significantly improves the accuracy of the rotational-state analysis.

By implementing this two-step selection process, this study achieves a more detailed and precise representation of the reaction dynamics. The GB methodology ensures that vibrational and rotational energy distributions align closely with experimental findings, providing deeper insights into the molecular behavior of reaction products. This method represents a substantial improvement over standard QCT approaches, making it a powerful tool for studying polyatomic reaction dynamics.

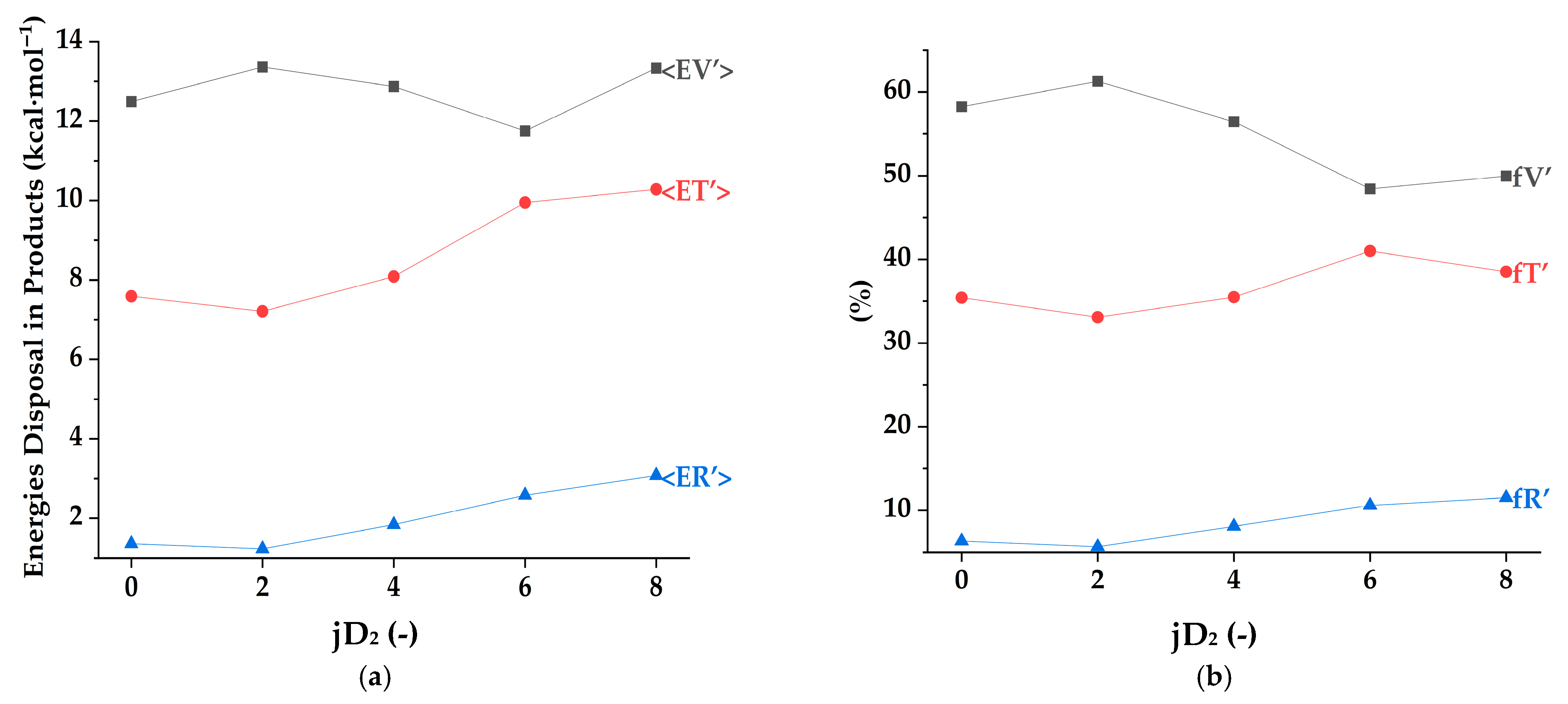
3.1. Energies in “HOD + D” Products

Table 2. Energies in products, “HOD + D”, from the second selection of trajectories, N_R-GB. For the following initial conditions, D₂ (vD₂ = 0; jD₂ = 0, 2, 4, 6, 8). These energies, Vibrational (V), Translational (T), and Rotational (R) ones, are shown as average values, <E> (kcal·mol⁻¹), and their corresponding fractions, (%).

jD2	<EV′> and (fV′)	<ET′> and (fT′)	<ER′> and (fR′)
0	12.49 (58.24%)	7.59 (35.41%)	1.36 (6.34%)
2	13.36 (61.27%)	7.21 (33.08%)	1.23 (5.66%)
4	12.87 (56.45%)	8.09 (35.47%)	1.84 (8.09%)
6	11.75 (48.41%)	9.95 (40.99%)	2.58 (10.61%)
8	13.33 (49.96%)	10.28 (38.52%)	3.08 (11.53%)

and Figure 1 show the distributions of vibrational, translational and rotational energies from the second selection of trajectories, N_R-GB. The total number of reactive trajectories was obtained from the simulation using the QCT methodology on the WSLFH PES, following the initial conditions, (OH + D₂ (vD₂ = 0; jD₂ = 0, 2, 4, 6, 8)) [1].

Similar to the Table 2 and Figure 1, but now (OH + D₂ (vD₂ = 0, 1, 2, 3, 4; jD₂ = 2)) [2],

Table 3. Energies in products, “HOD + D”, from the second selection of trajectories, N_R-GB. For the following initial conditions, D₂ (vD₂ = 0, 1, 2, 3, 4; jD₂ = 2). These energies, Vibrational (V), Translational (T), and Rotational (R) ones, are shown as average values, <E> (kcal·mol⁻¹), and their corresponding fractions, (%).

vD2	<EV′> and (fV′)	<ET′> and (fT′)	<ER′> and (fR′)
0	13.36 (61.27%)	7.21 (33.08%)	1.23 (5.66%)
1	18.38 (60.10%)	9.26 (30.29%)	2.94 (9.61%)
2	25.60 (64.66%)	9.64 (24.36%)	4.35 (10.99%)
3	31.53 (65.46%)	10.11 (20.99%)	6.53 (13.55%)
4	37.95 (67.63%)	10.98 (19.57%)	7.19 (12.81%)

and Figure 2 show the corresponding distributions of vibrational, translational, and rotational energies from the second selection of trajectories, N_R-GB.

Articles [1,2] analyze (for the following four statistical samples: 1. Total Reactive Trajectories (TRT). 2. Good Reactive Trajectories (GRT). 3. First vibrational-GB (V-GB) selection on GRT. 4. Second rotational-GB (R-GB) selection on V-GB trajectories) how changes in the initial conditions of the OH + D₂ reaction influence the distribution of energy among the products, specifically in terms of vibrational, translational, and rotational energy fractions. While the first article [1] focuses on the impact of increasing jD₂, the second article [2] examines the effects of increasing vD₂. A comparison of their findings reveals notable differences in the energy redistribution trends.

However, in this article, only the main statistical samples of both articles [1,2] will be comparatively analyzed: 4. Second rotational-GB (R-GB) selection on V-GB trajectories of both articles [1,2].

The first article states that increasing jD₂ leads to a slight decrease in the vibrational energy fraction (from 58% to 50%), a minor fluctuation in the translational energy fraction (from 35% to 39%), and a significant increase in the rotational fraction (from 6% to 12%). In contrast, in the second article indicates that increasing vD₂ results in a noticeable rise in the vibrational energy fraction (from 61% to 68%), a significant decrease in the translational fraction (from 33% to 20%), and a significant increase in the rotational fraction (from 6% to 13%). This suggests that while increasing jD₂ primarily enhances the rotational energy distribution, increasing vD₂ has a more pronounced effect on the vibrational energy distribution, with a significant reduction in translational energy.

In terms of absolute energy values, both modifications result in an increase in vibrational and rotational energies, but with different magnitudes. The first article [1] notes that increasing jD₂ leads to a small rise in the vibrational energy (from 12.5 to 13.3 kcal·mol⁻¹) and translational energy (from 7.6 to 10.3 kcal·mol⁻¹), but a dramatic increase in the rotational energy (from 1.4 to 3.1 kcal·mol⁻¹), more than doubling its initial value. On the other hand, the second article [2] states that increasing vD₂ causes a substantial rise in the vibrational energy (from 13 to 38 kcal·mol⁻¹) and rotational energy (from 1 to 7 kcal·mol⁻¹), while translational energy experiences only a slight increase (from 7 to 11 kcal·mol⁻¹). Thus, while increasing jD₂ favors rotational excitation with a limited impact on vibrational energy, increasing vD₂ drastically enhances vibrational excitation while significantly reducing the translational energy.

Both articles [1,2] highlight the redistribution of energy in the HOD product. The first article [1] emphasizes that increasing jD₂ leads to a considerable increase in the rotational energy of HOD, causing greater anisotropy in the reaction outcome. The second one [2], however, suggests that increasing vD₂ enhances both vibrational and rotational energies, contributing to an overall rise in the internal energy of the product. This implies that the method of excitation—whether rotational (jD₂) or vibrational (vD₂)—determines the way energy is partitioned among the reaction products, with vibrational excitation playing a more dominant role in boosting internal energy.

Overall, the key difference between the two cases lies in the extent and nature of the energy redistribution. Increasing jD₂ mainly affects rotational energy levels and leads to a modest rise in vibrational and translational energies. In contrast, increasing vD₂ substantially boosts the vibrational energy, considerably diminishes the translational energy, and moderately raises the rotational energy. These findings provide crucial insights into energy disposal mechanisms in polyatomic reaction dynamics, emphasizing the importance of initial conditions in determining reaction outcomes.

3.2. P(J′) for the Product Molecule, HOD

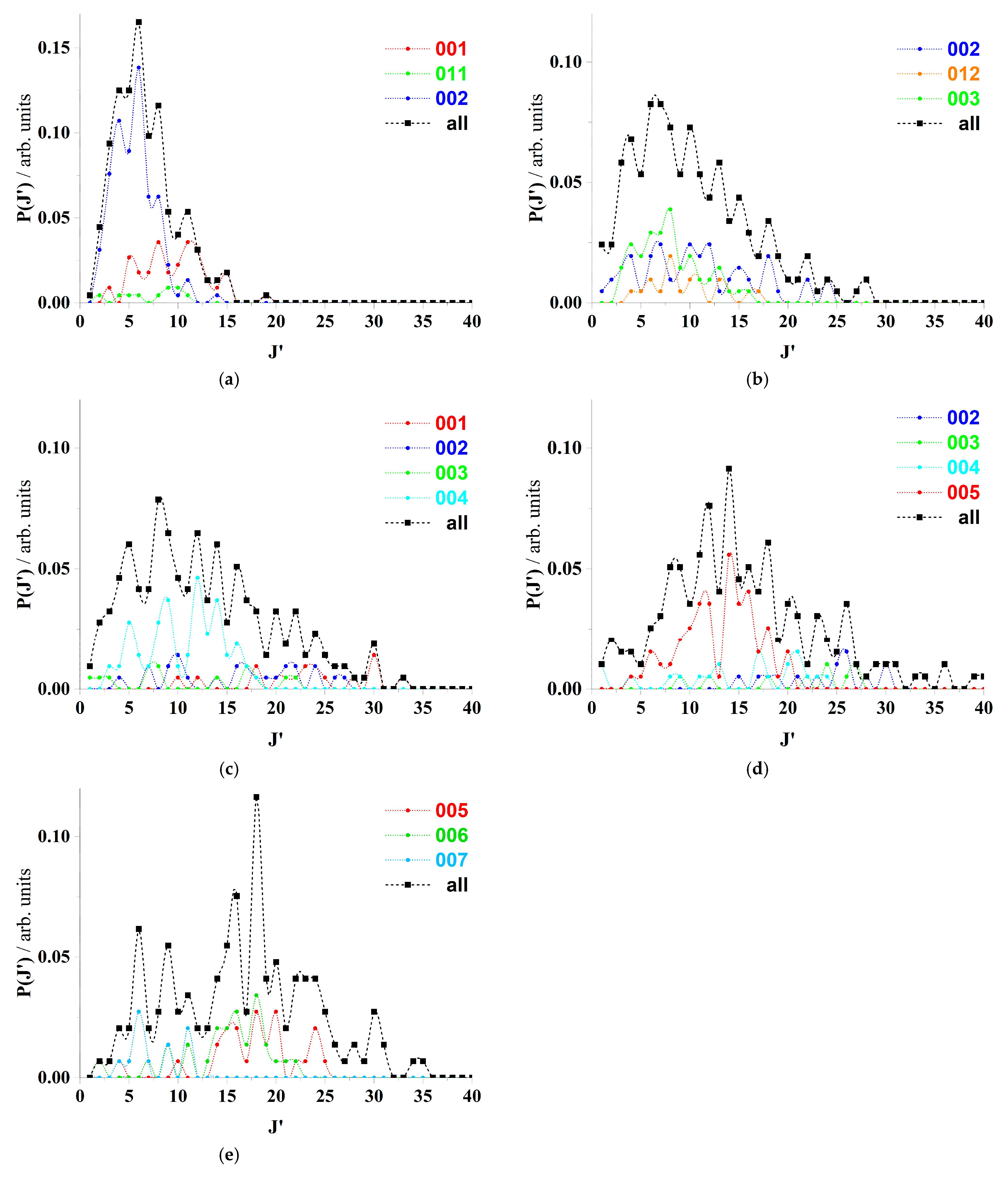
In this section, author makes a comparative analysis of the rotational angular momentum distributions, P(J′), of the HOD product molecule for reactive trajectories after the second selection, R–GB, of both studies, OH (vOH = 0; jOH = 2) + D₂ (vD₂ = 0; jD₂ = 0, 2, 4, 6, 8) and OH (vOH = 0; jOH = 2) + D₂ (vD₂ = 0, 1, 2, 3, 4; jD₂ = 2).

Tables and figures below, present some of the numerical data, P(J′)(ALL) (

Table 4. Numerical values of P(J′)(ALL) after the second selection, R-GB, is analyzed for the following initial conditions, D₂ (vD₂ = 0; jD₂ = 0, 2, 4, 6, 8). The P(J′) distributions are divided into 25 bins and normalized so that the total sum of all probability distributions equals one. The overall distribution, P(J′)(ALL), represents the sum of all individual distributions, P(J′)(v_HO′, v_HOD′, v_OD′) [1]. The author could provide the rest of the huge amount of numerical data shown visually in the Figure 3.

J′/au	jD2 = 0	jD2 = 2	jD2 = 4	jD2 = 6	jD2 = 8
1	0.021	0.004	0.008	0.013	0.004
2	0.087	0.045	0.028	0.025	0.013
3	0.103	0.094	0.081	0.071	0.018
4	0.097	0.125	0.061	0.063	0.045
5	0.097	0.125	0.077	0.067	0.045
6	0.097	0.165	0.089	0.054	0.013
7	0.082	0.098	0.089	0.063	0.080
8	0.062	0.116	0.106	0.067	0.098
9	0.092	0.054	0.069	0.063	0.067
10	0.082	0.040	0.142	0.054	0.094
11	0.062	0.054	0.065	0.067	0.080
12	0.062	0.031	0.061	0.075	0.071
13	0.036	0.013	0.045	0.100	0.063
14	0.005	0.013	0.020	0.042	0.076
15	0	0.018	0.024	0.038	0.067
16	0.015	0	0.008	0.071	0.054
17	0	0	0.016	0.038	0.036
18	0	0	0.004	0.013	0.031
19	0	0.004	0.004	0.004	0.036
20	0	0	0	0.013	0
21	0	0	0	0	0.004
22	0	0	0	0	0
23	0	0	0	0	0.004
24	0	0	0	0	0
25	0	0	0	0	0

and

Table 5. Numerical values of P(J′)(ALL) after the second selection, R-GB, is analyzed for the following initial conditions, D₂ (vD₂ = 0, 1, 2, 3, 4; jD₂ = 2). The P(J′) distributions are divided into 40 bins and normalized so that the total sum of all probability distributions equals one. The overall distribution, P(J′)(ALL), represents the sum of all individual distributions, P(J′)(v_HO′, v_HOD′, v_OD′) [2]. The author could provide the rest of the huge amount of numerical data shown visually in the Figure 4.

J′/au	vD2 = 0	vD2 = 1	vD2 = 2	vD2 = 3	vD2 = 4
1	0.004	0.024	0.009	0.010	0
2	0.045	0.024	0.028	0.020	0.007
3	0.094	0.058	0.032	0.015	0.007
4	0.125	0.068	0.046	0.015	0.021
5	0.125	0.053	0.060	0.010	0.021
6	0.165	0.083	0.042	0.025	0.062
7	0.098	0.083	0.042	0.030	0.021
8	0.116	0.073	0.079	0.051	0.027
9	0.054	0.053	0.065	0.051	0.055
10	0.040	0.073	0.046	0.036	0.027
11	0.054	0.053	0.042	0.056	0.034
12	0.031	0.044	0.065	0.076	0.021
13	0.013	0.058	0.037	0.041	0.021
14	0.013	0.034	0.060	0.091	0.041
15	0.018	0.044	0.028	0.046	0.055
16	0	0.029	0.051	0.051	0.075
17	0	0.019	0.037	0.041	0.027
18	0	0.034	0.032	0.061	0.116
19	0.004	0.019	0.014	0.020	0.041
20	0	0.010	0.032	0.036	0.048
21	0	0.010	0.019	0.030	0.021
22	0	0.019	0.032	0.010	0.041
23	0	0.005	0.014	0.030	0.041
24	0	0.010	0.023	0.020	0.041
25	0	0.005	0.014	0.015	0.027
26	0	0	0.009	0.036	0.014
27	0	0.005	0.009	0.010	0.007
28	0	0.010	0.005	0.005	0.014
29	0	0	0.005	0.010	0.007
30	0	0	0.019	0.010	0.027
31	0	0	0	0.010	0.014
32	0	0	0	0	0
33	0	0	0.005	0.005	0
34	0	0	0	0.005	0.007
35	0	0	0	0	0.007
36	0	0	0	0.010	0
37	0	0	0	0	0
38	0	0	0	0	0
39	0	0	0	0.005	0
40	0	0	0	0.005	0

), and the most important distributions, P(J′)(v_HO′, v_HOD′, v_OD′) (Figure 3 and Figure 4). From the selected GB analyses (following V-GB and R-GB selections) from the QCT calculations performed for the aforementioned initial conditions on the WSLFH PES.

Between both sets of images, Figure 3 and Figure 4, the author analyzes the impact of varying the initial conditions on the energy distribution of the reaction products, particularly focusing on the OH + D₂ reaction and the resulting HOD molecule. While they share a common focus on how rotational (jD₂) and vibrational (vD₂) excitation levels influence the final state distributions, they differ in their emphasis and interpretation of the results.

The first set of images (Figure 3) highlights how the selection of specific vibrational states (V-GB) in conjunction with rotational states (R-GB) leads to a preference for either odd or even rotational quantum numbers (J′). This phenomenon is attributed to the molecular symmetry conditions, specifically comparing the behavior of HOD with that observed in triatomic molecules used in CO₂ gas lasers [27]. Moreover, it suggests that an increase in the rotational quantum number of D₂ (jD₂) results in higher rotational levels in the HOD product and shifts the probability distributions P(J′) toward larger J′ values. However, this shift is described as being more pronounced when vibrational excitation levels increase, and it is noted that this change leads to greater anisotropy in the rotational distributions.

The second set of images (Figure 4), on the other hand, reinforces the idea that similar effects occur in another triatomic molecule used in CO₂ gas lasers [27], but provides a broader discussion on the oscillatory nature of global distributions across different initial conditions. While both sets of images acknowledge the qualitative similarities in the behaviors of these distributions, the second one places greater emphasis on the quantitative differences observed between global and specific distributions P(J′). Furthermore, it underscores the importance of the experimental validation to refine the findings.

A significant point of contrast between the two sets of images (Figure 3 and Figure 4) is their focus on the impact of vibrational versus rotational excitation. The first one (Figure 3) suggests that an increase in jD₂ contributes to higher rotational excitation in the HOD molecule, with only a moderate shift in the P(J′) distributions compared to vibrational excitation. In contrast, the second one (Figure 4) emphasizes that increasing vibrational excitation (vD₂) leads to a more substantial displacement of P(J′) toward much higher J′ values. Additionally, the second one (Figure 4) notes that this shift in J′ values is accompanied by greater dispersion in the rotational distributions, which is attributed to an increase in the isotropic behavior induced by higher vibrational excitation in the initial conditions.

From the comparison between both sets of images (Figure 3 and Figure 4), the author can conclude that the redistribution of energy among vibrational, rotational, and translational degrees of freedom is highly dependent on the initial excitation conditions of the D₂ reactant. The first set of images stresses the anisotropic nature of the resulting distributions when rotational excitation increases, while the second one highlights the enhanced isotropic character introduced by vibrational excitation. The interplay between these factors influences the overall energy disposal in reaction products and their final state distributions.

Despite their differing perspectives, both sets of images (Figure 3 and Figure 4) align on the necessity of further experimental research to validate these theoretical predictions. The first one expresses a desire for experimental data to compare with the calculated results, while the second one explicitly suggests that future experimental studies would be beneficial in verifying the observed trends.

While both sets of images (Figure 3 and Figure 4) explore the effects of rotational and vibrational excitation on the reaction dynamics of OH + D₂, they differ in their emphasis on the mechanisms driving these changes. The first set of images (Figure 3) focuses more on rotational excitation and its contribution to anisotropy, whereas the second one (Figure 4) emphasizes vibrational excitation and its role in enhancing isotropy and dispersion in rotational state distributions. Ultimately, they complement each other by offering a more comprehensive understanding of how different initial conditions impact the final energy distribution of the reaction products.

As a comparative conclusion between both sequences of images/distributions P(J′), (jD₂ = 0, 2, 4, 6, 8) vs. (vD₂ = 0, 1, 2, 3, 4) (Figure 3 and Figure 4), several observations can be drawn.

Starting with the second study [2], some distributions, P(J′)(v_HO′, v_HOD′, v_OD′) (Figure 4), were not visualized due to their broad dispersion of J′ values (significantly homogeneous throughout the possible J′ range, from 1 to 40). As a result, these distributions had low P(J′) values, making them barely visible in the corresponding figures. This lack of visual appreciation partly contributed to the decision not to include them in the P(J′) figures of this study [2].

Regarding the physical explanation for this dispersion of J′ values for certain excitations (v_HO′, v_HOD′, v_OD′) of the HOD product molecule, the dispersive and isotropic influence of vibrational excitation, vD₂, in the reactants OH (vOH = 0; jOH = 2) + D₂ (vD₂ = 0, 1, 2, 3, 4; jD₂ = 2) is evident (Figure 4). This effect becomes more pronounced as vD₂ increases from 0 to 4.

However, increasing rotational excitation, jD₂, in the reactants OH (vOH = 0; jOH = 2) + D₂ (vD₂ = 0; jD₂ = 0, 2, 4, 6, 8) [1] produces different effects. Although a shift of the P(J′) (Figure 3) distributions toward higher J′ values is observed, these distributions are more selective regarding J′ values, showing less tendency for dispersion compared to when vD₂ increases [2]. Therefore, an anisotropic effect of increasing jD₂ on the lower dispersion of J′ values within each P(J′) distribution is evident.

Thus, it can be stated that the distributions P(J′)(v_HO′, v_HOD′, v_OD′) evolve in such a way that they become less dispersed when excitation variation (increase) in reactants occurs over jD₂ = 0, 2, 4, 6, 8 (Figure 3) [1], whereas they evolve toward greater dispersion when excitation variation (increase) occurs over vD₂ = 0, 1, 2, 3, 4 (Figure 4) [2].

3.3. Discussion About a Possible Chemical Laser Based in This Research

The study of the dynamics and kinetics of chemical reactions, such as the polyatomic reaction, OH + D₂ → HOD* + D and its isotopic variations, is essential for the advancement of future gas and chemical lasers. Both theoretical and experimental approaches contribute to this field, providing essential insights into excitation and emission processes that occur within these laser systems. By analyzing these reactions, the author aims to understand the underlying mechanisms that govern the behavior of excited molecular species, thereby enabling more efficient laser technologies based on controlled chemical reactions.

One of the fundamental aspects of this research is the theoretical modeling of reaction dynamics, which has been carried out using quasi-classical trajectory (QCT) calculations. In particular, two selection methodologies, V-GB and R-GB, have been employed to enhance the precision of the simulations. These theoretical techniques will allow scientists to predict how the energy of reactants is distributed among the products, ultimately influencing the efficiency of excitation and emission processes in gas-phase reactions. The significance of these methodologies lies in their ability to provide a more detailed understanding of the interaction between molecular species, energy transfer mechanisms, and the anisotropic nature of the reaction product molecule, HOD.

Experimental validation must play an important role in the advancement of this field. The development of gas and chemical laser prototypes could enable researchers to observe and measure the excitation and emission processes directly. By constructing controlled reaction chambers, scientists could test theoretical predictions and refine their models based on real-world data. This interplay between theory and experimentation could foster a deeper comprehension of the kinetic and dynamic properties of the investigated system (and other equally interesting systems), thereby facilitating advancements in the corresponding laser technologies.

Both studies [1,2] emphasize the strong connection between theoretical calculations and possible experimental applications. The author suggests that a significant portion of the research effort is directed toward understanding the excitation and emission mechanisms in possible chemical lasers. The QCT calculations, along with the V-GB and R-GB selections, provide valuable theoretical insights that could help experimental designs. The ultimate goal is to achieve a seamless integration of theory and experimentation, leading to improved laser systems that leverage chemical reactions for an enhanced performance.

Similarly, those studies [1,2] highlight the importance of the gas-phase reaction dynamics in the context of chemical lasers, particularly those based on water vapor semi-deuterated molecules such as HOD*. The author suggests that these reactions hold potential for both current and future laser technologies. These theoretical studies provide a foundation for experimental works, which in turn can validate and refine theoretical models (e.g., new and better PESs). This constructive interaction between theory and experimentation is crucial for advancing the knowledge of reaction dynamics and optimizing the excitation and emission processes in gas-phase chemical lasers.

A key difference between the two studies [1,2] lies in their emphasis on specific aspects of the research. The first study [1] focuses more on the methodological approach, detailing the use of QCT calculations and selection methodologies to study reaction dynamics. It highlights how these techniques contribute to a comprehensive understanding of energy distribution among reaction products. In contrast, the second study [2] places greater emphasis on the practical implications of this research for laser technology. It discusses how theoretical insights can be applied to the development of chemical laser prototypes, underscoring the potential for real-world applications.

Despite these differences, both studies [1,2] converge on the idea that a synergistic relationship between theory and experimentation is essential for progress in this field. Theoretical models provide predictive power and help identify key factors that influence reaction dynamics, while experimental studies could offer empirical validation and practical insights. By combining these approaches, researchers could refine their understanding of polyatomic reaction kinetics and develop more efficient chemical laser systems, based on the current system, OH + D₂ → HOD* + D, or other equally interesting ones.

One of the most intriguing aspects of this research is its potential impact on future laser technologies. Gas and chemical lasers based on controlled molecular reactions could offer several advantages over traditional laser systems. By harnessing the energy released during specific chemical reactions, these lasers could achieve higher efficiency, greater tunability, and an improved performance in various applications, including spectroscopy, telecommunications, and defense technologies.

Moreover, the study of reaction dynamics in the context of laser development provides valuable insights into fundamental molecular processes. Understanding how energy is transferred between reactants and products, how vibrational and rotational states influence reaction outcomes, and how anisotropic effects shape molecular interactions can have far-reaching implications beyond laser technology.

In conclusion, the research on polyatomic reaction dynamics, particularly in the context of chemical lasers [28], represents a vital area of study with both theoretical and practical significance. The integration of QCT calculations, V-GB and R-GB selection methodologies, and experimental validation could create a comprehensive framework for understanding and optimizing excitation and emission processes in gas-phase reactions. While the first study [1] emphasizes the methodological and theoretical aspects of this research, the second study [2] highlights its practical implications for laser development. Together, they provide a holistic perspective on the importance of studying reaction dynamics to advance gas and chemical laser technologies. By fostering a strong interaction between theoretical modeling and experimental investigations, this research paves the way for future innovations in laser science and molecular reaction dynamics.

4. Conclusions

This study provides a comparative analysis of two distinct sets of initial conditions for the OH + D₂ → HOD + D reaction: OH (vOH = 0; jOH = 2) + D₂ (vD₂ = 0; jD₂ = 0, 2, 4, 6, 8) and OH (vOH = 0; jOH = 2) + D₂ (vD₂ = 0, 1, 2, 3, 4; jD₂ = 2). The results offer important insights into the energy disposal mechanisms in the reaction products, with direct implications for theoretical modeling and potential experimental validation, particularly in the context of chemical laser development.

The analysis reveals that rotational excitation (increasing jD₂) induces moderate shifts in the P(J′) distributions toward higher J′ values, while maintaining relatively narrow distributions, highlighting an anisotropic effect. In contrast, vibrational excitation (increasing vD₂) leads to a significant increase in vibrational energy, larger shifts in P(J′), and greater dispersion, indicating a pronounced isotropic behavior in product formation.

Additionally, the influence of HOD molecular asymmetry is confirmed, as the R-GB selection demonstrates a systematic preference for even or odd J′ values depending on the prior V-GB selection. This phenomenon aligns with similar observations in triatomic molecules like CO₂, reinforcing the broader relevance of the findings.

Overall, this comparative investigation underscores the distinct roles of rotational and vibrational excitation in shaping product energy distributions and highlights the critical importance of molecular symmetry effects. These results contribute to a deeper understanding of reaction dynamics and provide a theoretical foundation for future applications in gas-phase chemical control and laser technologies.