Artificial Neural Networks for the Simulation and Modeling of the Adsorption of Fluoride Ions with Layered Double Hydroxides
Abstract
1. Introduction
2. Materials and Methods
2.1. Synthesis and Characterization of LDH
2.2. Adsorption Experiments in Batch System
2.3. Fitting of Theoretical Kinetic Adsorption Model Experiment Data
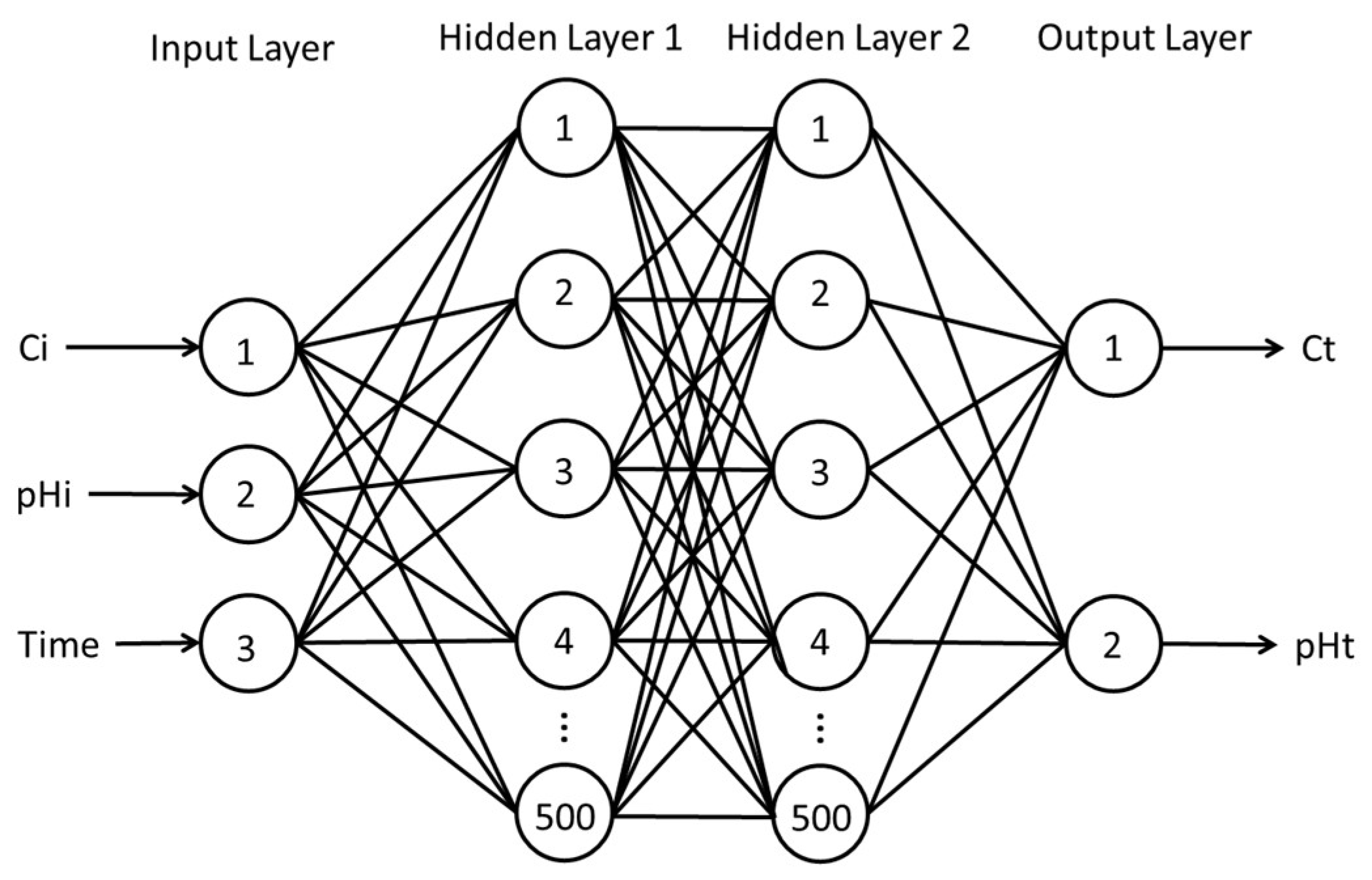
2.4. Fitting of ANN Adsorption Experiment Data
3. Results and Discussion
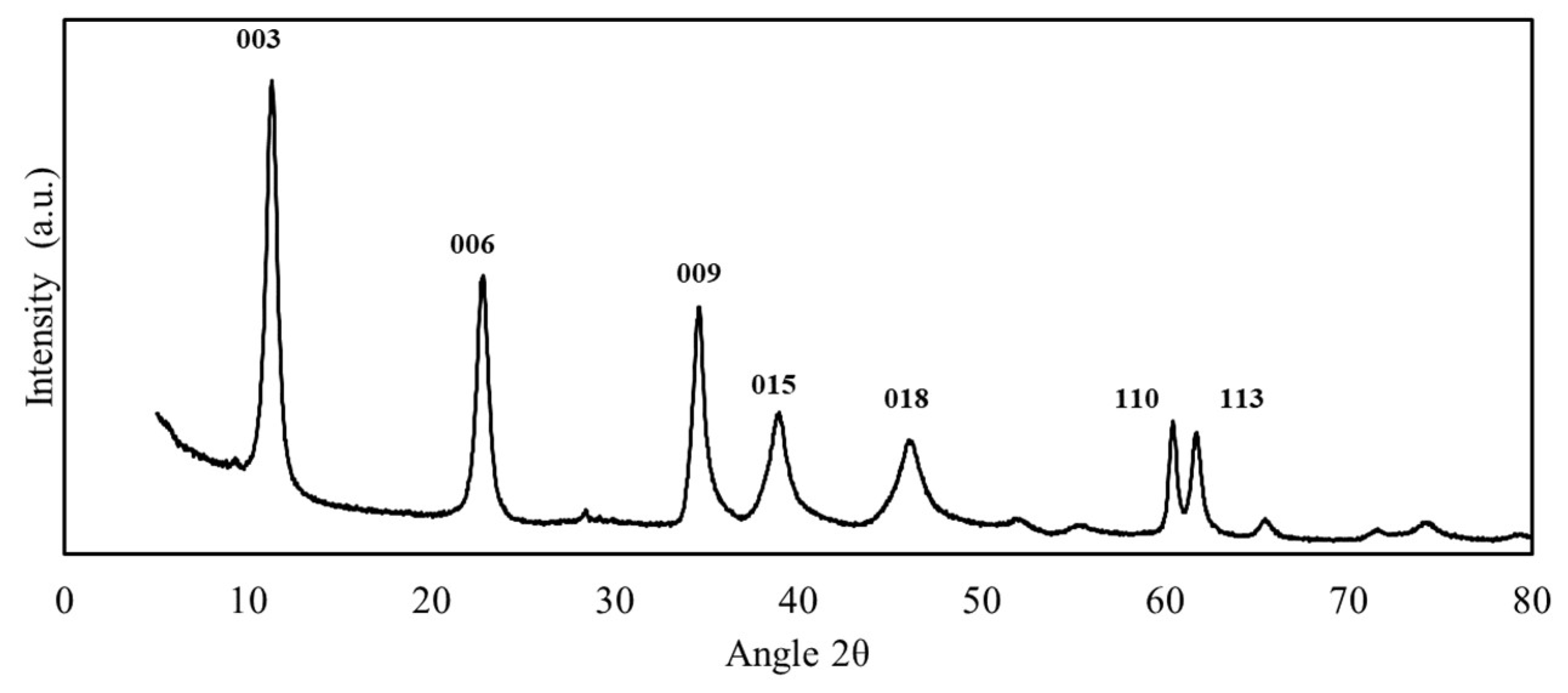
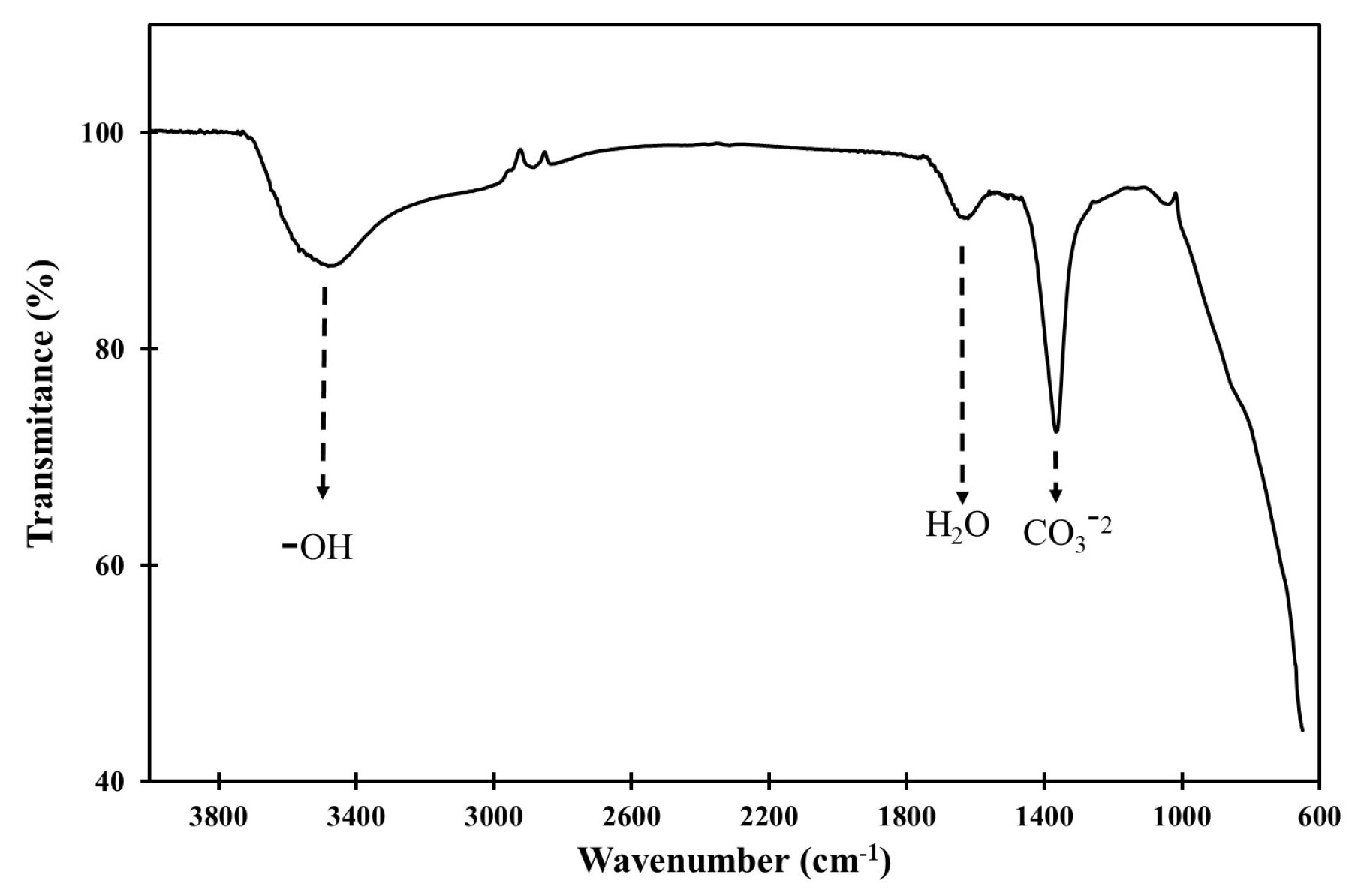
3.1. Synthesis and Characterization of LDH
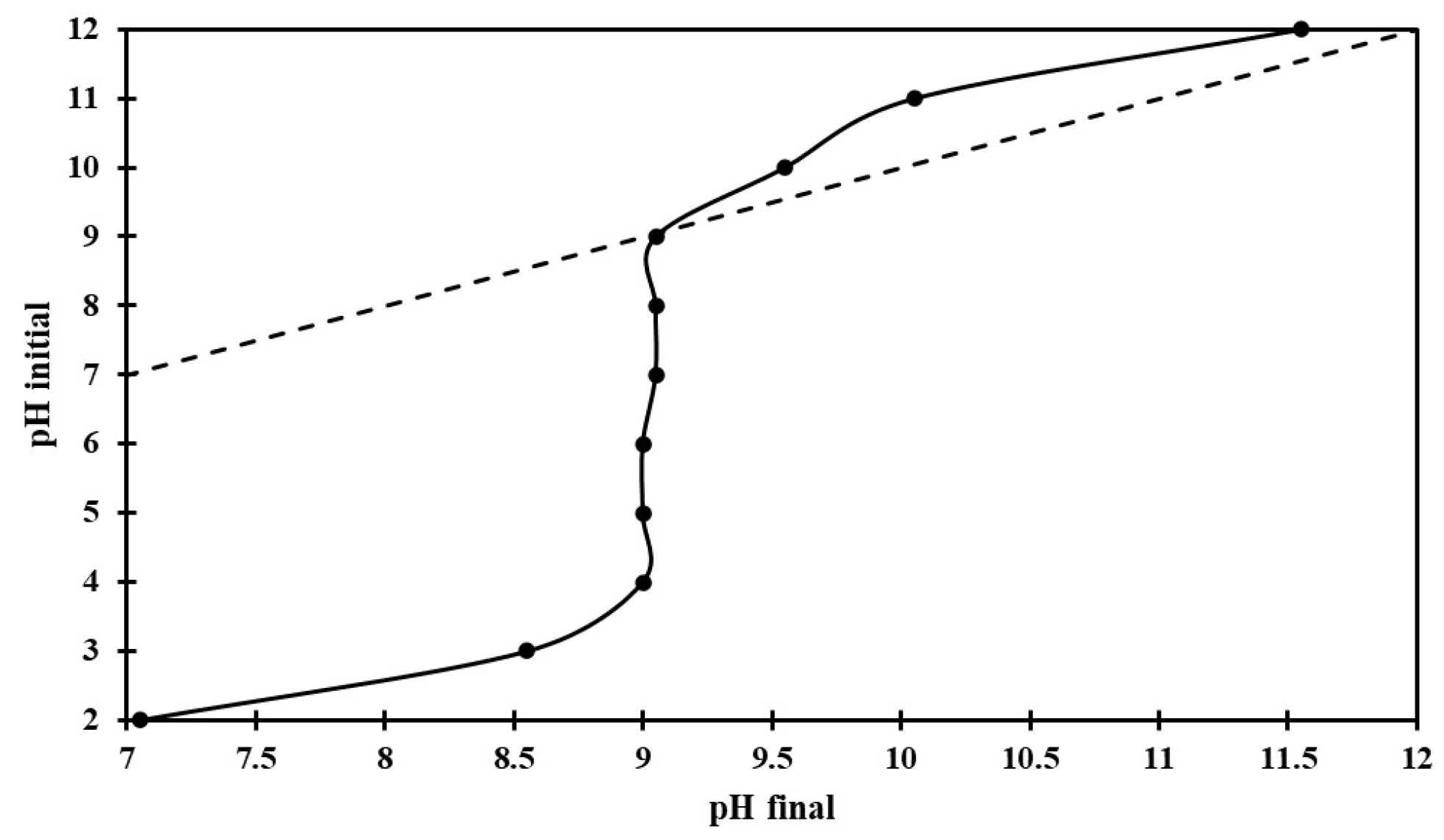
3.2. Adsorption Experiments in a Batch System
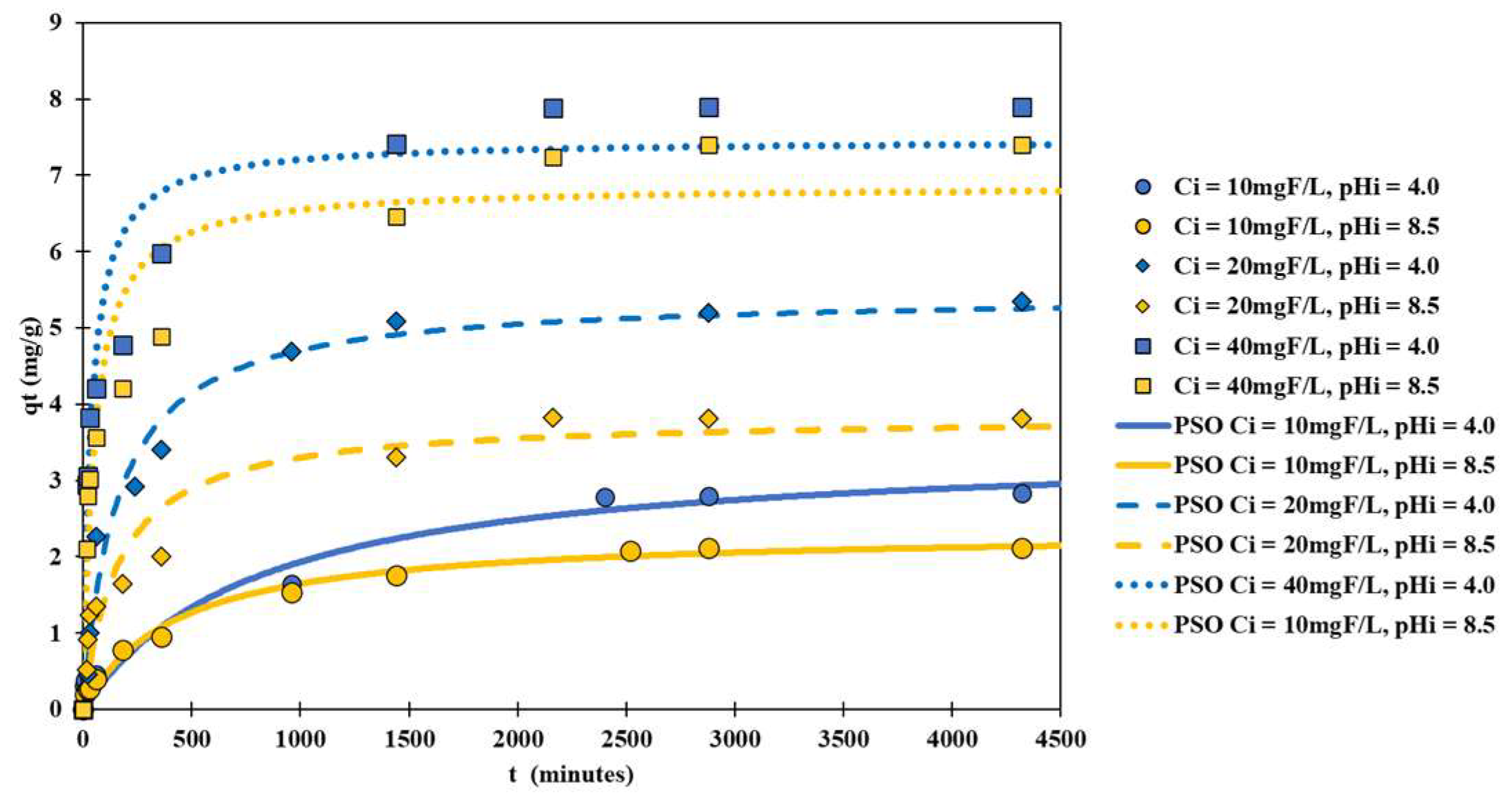
3.3. Fitting of Results of Theoretical Kinetic Adsorption Model Experiments
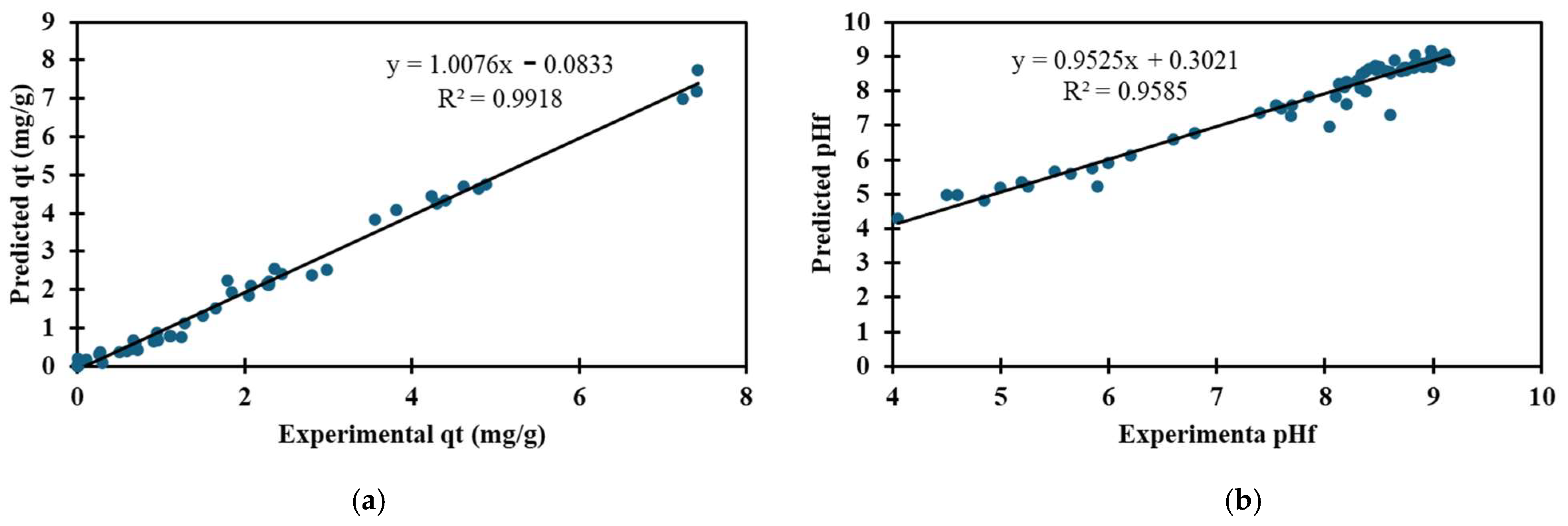
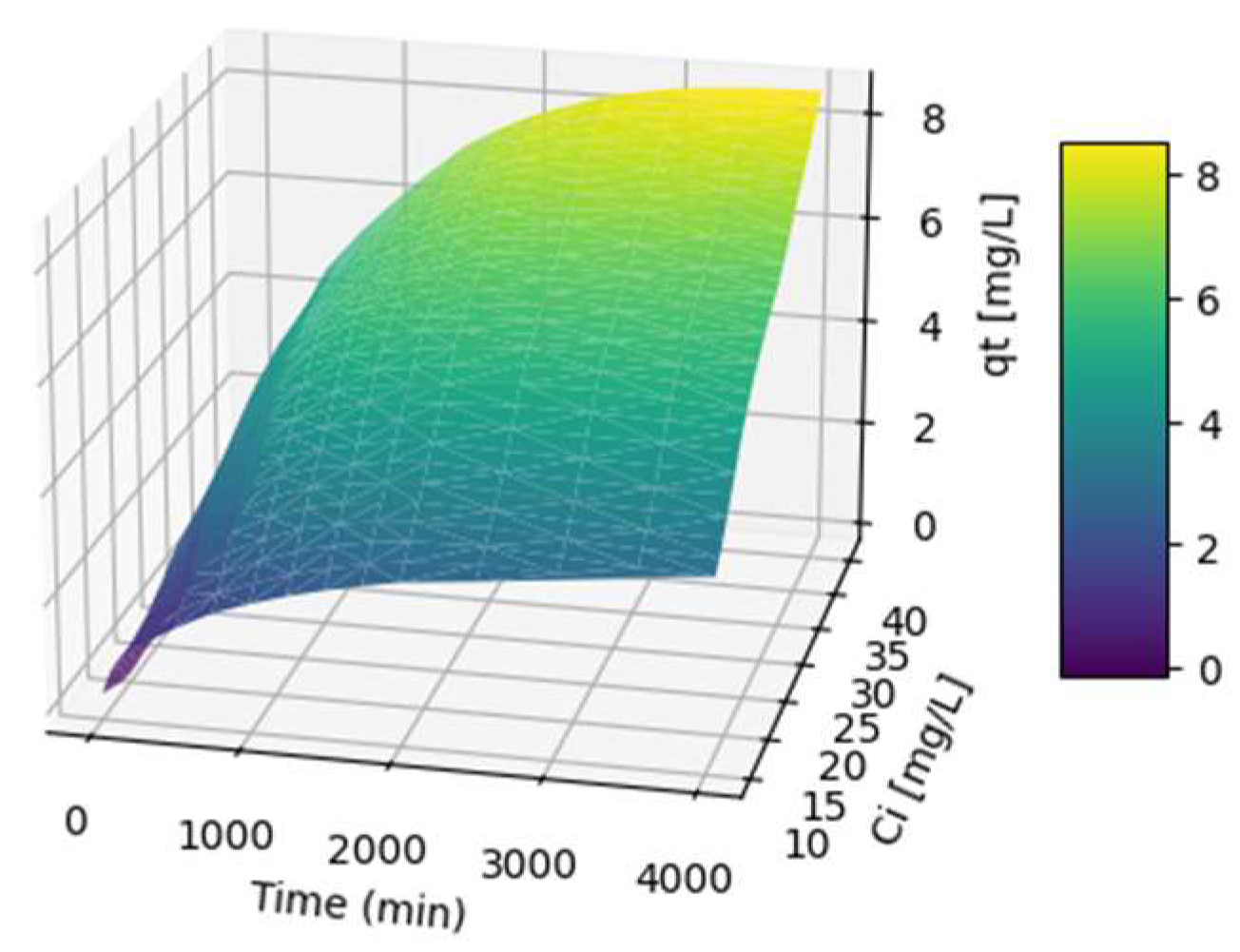
3.4. Fitting of ANN Adsorption Experimental Data
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sahoo, T.R.; Prelot, B. Adsorption processes for the removal of contaminants from wastewater. In Nanomaterials for the Detection and Removal of Wastewater Pollutant; Elsevier: Amsterdam, The Netherlands, 2020; pp. 161–222. [Google Scholar] [CrossRef]
- Gutkoski, J.P.; Schneider, E.E.; Michels, C. How effective is biological activated carbon in removing micropollutants? A comprehensive review. J. Environ. Manag. 2024, 349, 119434. [Google Scholar] [CrossRef] [PubMed]
- Rathi, B.S.; Kumar, P.S. Application of adsorption process for effective removal of emerging contaminants from water and wastewater. Environ. Pollut. 2021, 280, 116995. [Google Scholar] [CrossRef] [PubMed]
- Ebelegi, A.N.; Ayawei, N.; Wankasi, D. Interpretation of Adsorption Thermodynamics and Kinetics. Open J. Phys. Chem. 2020, 10, 166–182. [Google Scholar] [CrossRef]
- Musah, M.; Azeh, Y.; Mathew, J.; Umar, M.; Abdulhamid, Z.; Muhammad, A. Adsorption Kinetics and Isotherm Models: A Review. Caliphate J. Sci. Technol. 2022, 4, 20–26. [Google Scholar] [CrossRef]
- Wang, J.; Guo, X. Adsorption isotherm models: Classification, physical meaning, application and solving method. Chemosphere 2020, 258, 127279. [Google Scholar] [CrossRef]
- Kajjumba, G.W.; Emik, S.; Öngen, A.; Özcan, H.K.; Aydın, S. Modelling of Adsorption Kinetic Processes—Errors, Theory and Application. In Advanced Sorption Process Applications; IntechOpen: London, UK, 2019. [Google Scholar]
- Khan, S.; Ajmal, S.; Hussain, T. Clay-based materials for enhanced water treatment: Adsorption mechanisms, challenges, and future directions. J. Umm Al-Qura Univ. Appl. Sci. 2023, 1–16. [Google Scholar] [CrossRef]
- Shaji, E.; Sarath, K.; Santosh, P.K.M.; Arya, B.; Babu, M.S. Fluoride contamination in groundwater: A global review of the status, processes, challenges, and remedial measures. Geosci. Front. 2024, 15, 101734. [Google Scholar] [CrossRef]
- Dar, F.A.; Kurella, S. Recent advances in adsorption techniques for fluoride removal—An overview. Groundw. Sustain. Dev. 2023, 23, 101017. [Google Scholar] [CrossRef]
- Huiyuan, T.; Yang, L.; Mengyan, X.; Baoyu, C.; Chang, L.; Xiuhong, D.; Zehua, W.; Xianying, D.; Jiehu, C. The enhanced adsorption of layered double hydroxides modification from single to ternary metal for fluoride by TEA-assisted hydrothermal method. Arab. J. Chem. 2024, 17, 105645. [Google Scholar] [CrossRef]
- Ramírez-Llamas, L.; Leyva-Ramos, R.; Jacobo-Azuara, A.; Martínez-Rosales, J.; Isaacs-Paez, E. Adsorption of Fluoride from Aqueous Solution on Calcined and Uncalcined Layered Double Hydroxide. Adsorpt. Sci. Technol. 2015, 33, 393–410. [Google Scholar] [CrossRef]
- Sarma, G.K.; Rashid, H. Synthesis of Mg/Al Layered Double Hydroxides for Adsorptive Removal of Fluoride from Water: A Mechanistic and Kinetic Study. J. Chem. Eng. Data 2018, 63, 2957–2965. [Google Scholar] [CrossRef]
- Li, Y.; Narducci, R.; Varone, A.; Kaciulis, S.; Bolli, E.; Pizzoferrato, R. Zn–Al Layered Double Hydroxides Synthesized on Aluminum Foams for Fluoride Removal from Water. Processes 2021, 9, 2109. [Google Scholar] [CrossRef]
- Qi, C.; Wu, M.; Li, K.; Hu, T.; Armaghani, D.J.; Chen, Q.; Yilmaz, E. Identifying mining-induced chromium contamination in soil through visible-near infrared spectroscopy and machine learning. Green Smart Min. Eng. 2024, 1, 132–139. [Google Scholar] [CrossRef]
- Reynel-Ávila, H.E.; Aguayo-Villarreal, I.A.; Diaz-Muñoz, L.L.; Moreno-Pérez, J.; Sánchez-Ruiz, F.J.; Rojas-Mayorga, C.K.; Mendoza-Castillo, D.I.; Bonilla-Petriciolet, A. A Review of the Modeling of Adsorption of Organic and Inorganic Pollutants from Water Using Artificial Neural Networks. Adsorpt. Sci. Technol. 2022, 2022, 9384871. [Google Scholar] [CrossRef]
- Goel, A.; Goel, A.; Kumar, A. The role of artificial neural network and machine learning in utilizing spatial information. Spat. Inf. Res. 2023, 31, 275–285. [Google Scholar] [CrossRef]
- Estrada-Moreno, J.C.; Rendon-Lara, E.; de la Luz Jiménez-Núñez, M. Combination of Artificial Neural Networks and Principal Component Analysis for the Sim-ultaneous Quantification of Dyes in Multi-Component Aqueous Mixtures. Appl. Sci. 2024, 14, 809. [Google Scholar] [CrossRef]
- Paul, A.; Prasad, A.; Kumar, A. Review on Artificial Neural Network and its Application in the Field of Engineering. J. Mech. Eng. 2022, 1, 53–61. [Google Scholar] [CrossRef]
- Prasad, K.; Kumar, V.R.; Kumar, R.S.; Rajesh, A.S.; Rai, A.K.; Al-Ammar, E.A.; Wabaidur, S.M.; Iqbal, A.; Kefyalew, D. Predicting the Adsorption Efficiency Using Machine Learning Framework on a Carbon-Activated Nanomaterial. Adsorpt. Sci. Technol. 2023, 2023, 4048676. [Google Scholar] [CrossRef]
- Cristea, V.-M.; Baigulbayeva, M.; Ongarbayev, Y.; Smailov, N.; Akkazin, Y.; Ubaidulayeva, N. Prediction of Oil Sorption Capacity on Carbonized Mixtures of Shungite Using Artificial Neural Networks. Processes 2023, 11, 518. [Google Scholar] [CrossRef]
- El Bey, A.; Laidi, M.; Yettou, A.; Hanini, S.; Ibrir, A.; Hentabli, M.; Ouldkhaoua, H. Practical Artificial Neural Network Tool for Predicting the Competitive Adsorption of Dyes on Gemini Polymeric Nanoarchitecture. Kem. Ind. Časopis Kemičara Kem. Inženjera Hrvat. 2021, 70, 481–488. [Google Scholar] [CrossRef]
- Lagergren, S. About the Theory of So-Called Adsorption of Soluble Substances. K. Sven. Vetenskapsakademiens Handl. 1898, 24, 1–39. [Google Scholar]
- Ho, Y.S.; McKay, G. Pseudo-second order model for sorption processes. Process Biochem. 1999, 34, 451–465. [Google Scholar] [CrossRef]
- SElovich, Y.; Larinov, O.G. Theory of adsorption from solutions of non electrolytes on solid (I) equation adsorption from solutions and the analysis of its simplest form,(II) verification of the equation of adsorption isotherm from solutions. Izv. Akad. Nauk. SSSR Otd. Khimicheskikh Nauk. 1962, 2, 209–216. [Google Scholar]
- Weber, W.; Morris, J.C. Intraparticle diffusion during the sorption of surfactants onto activated carbon. J. Sanit. Eng. Div. Am. Soc. Civ. Eng. 1963, 89, 53–61. [Google Scholar] [CrossRef]
- Leyva-Ramos, R.; Geankoplis, C. Model simulation and analysis of surface diffusion of liquids in porous solids. Chem. Eng. Sci. 1985, 40, 799–807. [Google Scholar] [CrossRef]
- Revellame, E.D.; Fortela, D.L.; Sharp, W.; Hernandez, R.; Zappi, M.E. Adsorption kinetic modeling using pseudo-first order and pseudo-second order rate laws: A review. Clean. Eng. Technol. 2020, 1, 100032. [Google Scholar] [CrossRef]
- Wang, J.; Guo, X. Adsorption kinetic models: Physical meanings, applications, and solving. J. Hazard. Mater. 2020, 390, 122156. [Google Scholar] [CrossRef]
- Guo, X.; Wang, J. A general kinetic model for adsorption: Theoretical analysis and modeling. J. Mol. Liq. 2019, 288, 111100. [Google Scholar] [CrossRef]
- Fiyadh, S.S.; Alardhi, S.M.; Al Omar, M.; Aljumaily, M.M.; Al Saadi, M.A.; Fayaed, S.S.; Ahmed, S.N.; Salman, A.D.; Abdalsalm, A.H.; Jabbar, N.M.; et al. A comprehensive review on modelling the adsorption process for heavy metal removal from waste water using artificial neural network technique. Heliyon 2023, 9, e15455. [Google Scholar] [CrossRef]
- Khan, T.; Manan, T.B.A.; Isa, M.; Ghanim, A.; Beddu, S.; Jusoh, H.; Iqbal, M.; Ayele, G.; Jami, M. Modeling of Cu(II) Ad-sorption from an Aqueous Solution Using an Artificial Neural Network (ANN). Molecules 2020, 24, 3263. [Google Scholar] [CrossRef]
- Pérez-Enciso, M.; Zingaretti, L. A Guide for Using Deep Learning for Complex Trait Genomic Prediction. Genes 2019, 10, 553. [Google Scholar] [CrossRef] [PubMed]
- Meyer-Baese, A.; Schmid, V. Foundations of Neural Networks. In Pattern Recognition and Signal Analysis in Medical Imaging; Academic Press: Oxford, UK, 2014; pp. 197–243. [Google Scholar] [CrossRef]
- Giola, C.; Danti, P.; Magnani, S. Learning Curves: A Novel Approach for Robustness Improvement of Load Forecasting. Eng. Proc. 2021, 5, 38. [Google Scholar] [CrossRef]
- Nejati, K.; Keypour, H.; Nezhad, P.D.K.; Asadpour-Zeynali, K.; Rezvani, Z. Experimental Design for the Optimization of the Synthesis Conditions of Zn-Al-Layered Double Hydroxides Nanoparticles Based on X-ray Diffraction Data. Mol. Cryst. Liq. Cryst. 2015, 608, 177–189. [Google Scholar] [CrossRef]
- Ahmad, N.; Arsyad, F.S.; Royani, I.; Lesbani, A. Charcoal activated as template Mg/Al layered double hydroxide for selective adsorption of direct yellow on anionic dyes. Results Chem. 2023, 5, 100766. [Google Scholar] [CrossRef]
- Zhang, W.; Liang, Y.; Wang, J.; Zhang, Y.; Gao, Z.; Yang, Y.; Yang, K. Ultrasound-assisted adsorption of Congo red from aqueous solution using MgAlCO3 layered double hydroxide. Appl. Clay Sci. 2019, 174, 100–109. [Google Scholar] [CrossRef]
- Johnston, A.-L.; Lester, E.; Williams, O.; Gomes, R.L. Understanding Layered Double Hydroxide properties as sorbent materials for removing organic pollutants from environmental waters. J. Environ. Chem. Eng. 2021, 9, 105197. [Google Scholar] [CrossRef]
- Ion, R.-M.; Rizescu, C.E.; Vasile, D.A.; Vasilievici, G.; Atkinson, I.; Rusu, A.; Predoana, L.; Miculescu, F. Layered Double Hydroxides (LDHs) as New Consolidants for Cultural Heritage Masonry. Crystals 2022, 12, 490. [Google Scholar] [CrossRef]
- Estrada-Moreno, J.C.; Jiménez-Núñez, M.L.; Zavala-Arce, R.E.; Norma-Aurea, R.-V.; Garcia-Gaitan, B. X-ray diffraction and FTIR analysis on effect of time and temperature layered double hydroxides synthesis. MRS Adv. 2021, 6, 980–984. [Google Scholar] [CrossRef]
- Mercado-Borrayo, B.M.; Schouwenaars, R.; Litter, M.I.; Montoya-Bautista, C.V.; Ramírez-Zamora, R.M. Metallurgical Slag as an Efficient and Economical Adsorbent of Arsenic. In Water Reclamation and Sustainability; Elsevier: Amsterdam, The Netherlands, 2014; pp. 95–114. [Google Scholar] [CrossRef]
- Plazinski, W.; Rudzinski, W.; Plazinska, A. Theoretical models of sorption kinetics including a surface reaction mechanism: A review. Adv. Colloid Interface Sci. 2009, 152, 2–13. [Google Scholar] [CrossRef]




| Model | Nonlinear Form | Description |
|---|---|---|
| Pseudo-first-order (PFO) | adsorption capacity at time t () equilibrium adsorption capacity () time (min) first-order rate coefficient () | |
| Pseudo-second-order (PSO) | adsorption capacity at time t () equilibrium adsorption capacity () time ( second-order rate coefficient () |
| Experimental Conditions | PFO | PSO | ||||
|---|---|---|---|---|---|---|
| () | () | |||||
| = 4.0 | 0.987 | 2.94 | 0.9709 | 0.362 | 3.4748 | 0.9708 |
| = 7.0 | 3.02 | 2.25 | 0.9438 | 1.83 | 2.4554 | 0.9635 |
| = 7.5 | 3.01 | 2.23 | 0.9398 | 1.83 | 2.4421 | 0.9611 |
| = 8.0 | 2.86 | 2.17 | 0.9202 | 2.01 | 2.3448 | 0.9404 |
| = 8.3 | 3.37 | 2.02 | 0.9020 | 2.69 | 2.1371 | 0.9214 |
| = 8.5 | 1.82 | 2.05 | 0.9751 | 1.01 | 2.3461 | 0.9863 |
| = 4.0 | 4.09 | 5.06 | 0.9553 | 1.18 | 5.4430 | 0.9762 |
| = 6.0 | 1.96 | 5.10 | 0.9550 | 0.437 | 5.7774 | 0.9519 |
| = 6.5 | 2.16 | 4.94 | 0.9810 | 0.480 | 5.6050 | 0.9816 |
| = 7.0 | 2.13 | 4.92 | 0.9680 | 0.506 | 5.5429 | 0.9701 |
| = 7.5 | 2.26 | 4.91 | 0.9784 | 0.537 | 5.5203 | 0.9774 |
| = 8.0 | 4.34 | 4.17 | 0.9458 | 1.53 | 4.4231 | 0.9653 |
| = 8.3 | 4.21 | 3.99 | 0.9217 | 1.67 | 4.2096 | 0.9489 |
| = 8.5 | 3.56 | 3.64 | 0.9175 | 1.58 | 3.8420 | 0.9393 |
| = 4.0 | 22.8 | 6.98 | 0.8645 | 3.71 | 7.4678 | 0.9358 |
| = 8.5 | 17.6 | 6.36 | 0.8522 | 2.96 | 6.8707 | 0.9260 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Estrada-Moreno, J.C.; Rendón-Lara, E.; Jiménez-Núñez, M.d.l.L.; Salazar Rábago, J.J. Artificial Neural Networks for the Simulation and Modeling of the Adsorption of Fluoride Ions with Layered Double Hydroxides. Physchem 2025, 5, 5. https://doi.org/10.3390/physchem5010005
Estrada-Moreno JC, Rendón-Lara E, Jiménez-Núñez MdlL, Salazar Rábago JJ. Artificial Neural Networks for the Simulation and Modeling of the Adsorption of Fluoride Ions with Layered Double Hydroxides. Physchem. 2025; 5(1):5. https://doi.org/10.3390/physchem5010005
Chicago/Turabian StyleEstrada-Moreno, Julio Cesar, Eréndira Rendón-Lara, María de la Luz Jiménez-Núñez, and Jacob Josafat Salazar Rábago. 2025. "Artificial Neural Networks for the Simulation and Modeling of the Adsorption of Fluoride Ions with Layered Double Hydroxides" Physchem 5, no. 1: 5. https://doi.org/10.3390/physchem5010005
APA StyleEstrada-Moreno, J. C., Rendón-Lara, E., Jiménez-Núñez, M. d. l. L., & Salazar Rábago, J. J. (2025). Artificial Neural Networks for the Simulation and Modeling of the Adsorption of Fluoride Ions with Layered Double Hydroxides. Physchem, 5(1), 5. https://doi.org/10.3390/physchem5010005







