Atomic-Scale Study of NASICON Type Electrode Material: Defects, Dopants and Sodium-Ion Migration in Na3V2(PO4)3
Abstract
:1. Introduction
2. Computational Methods
3. Results
3.1. Crystal Structure of NVP
3.2. Intrinsic Defects
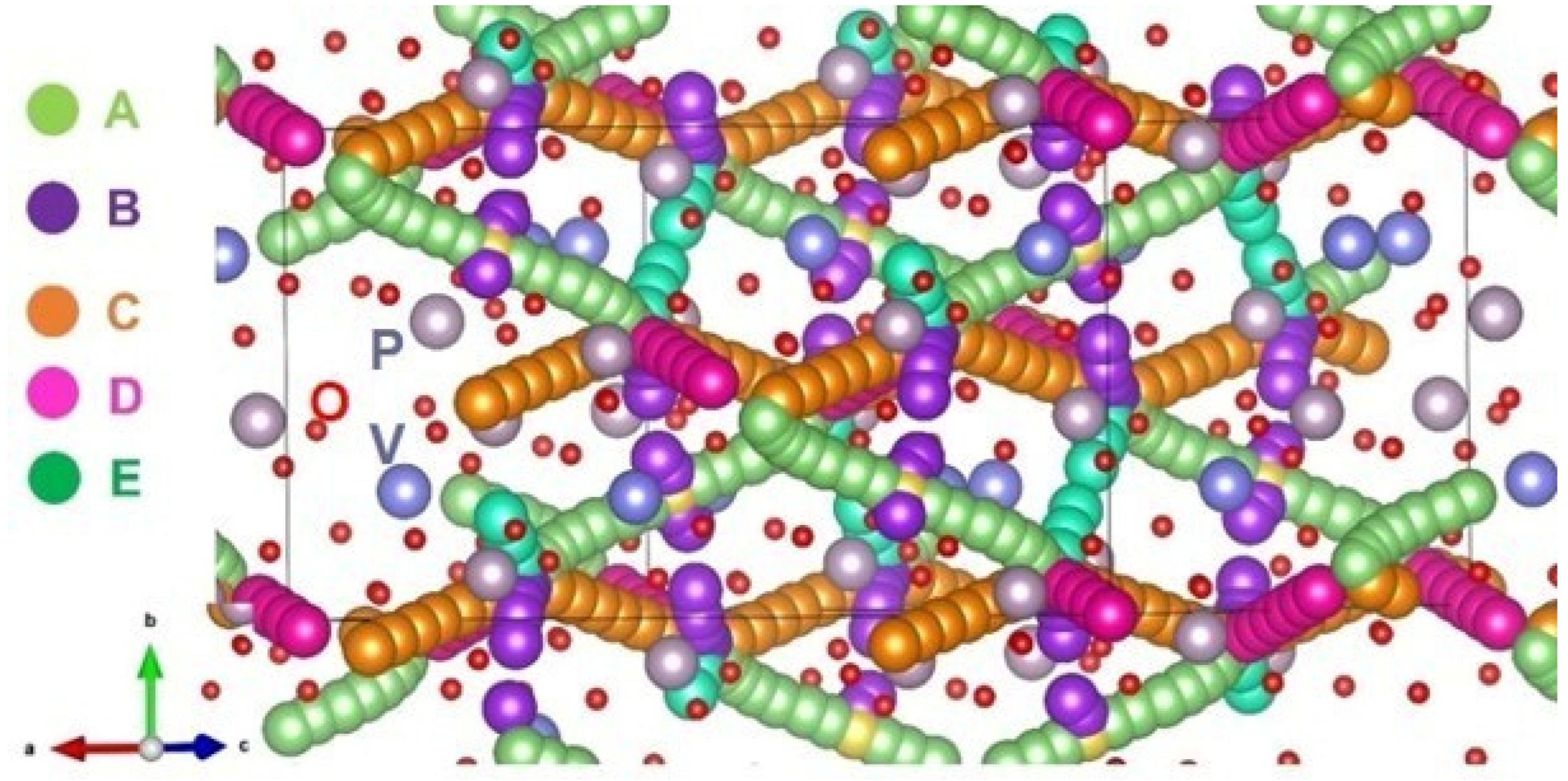
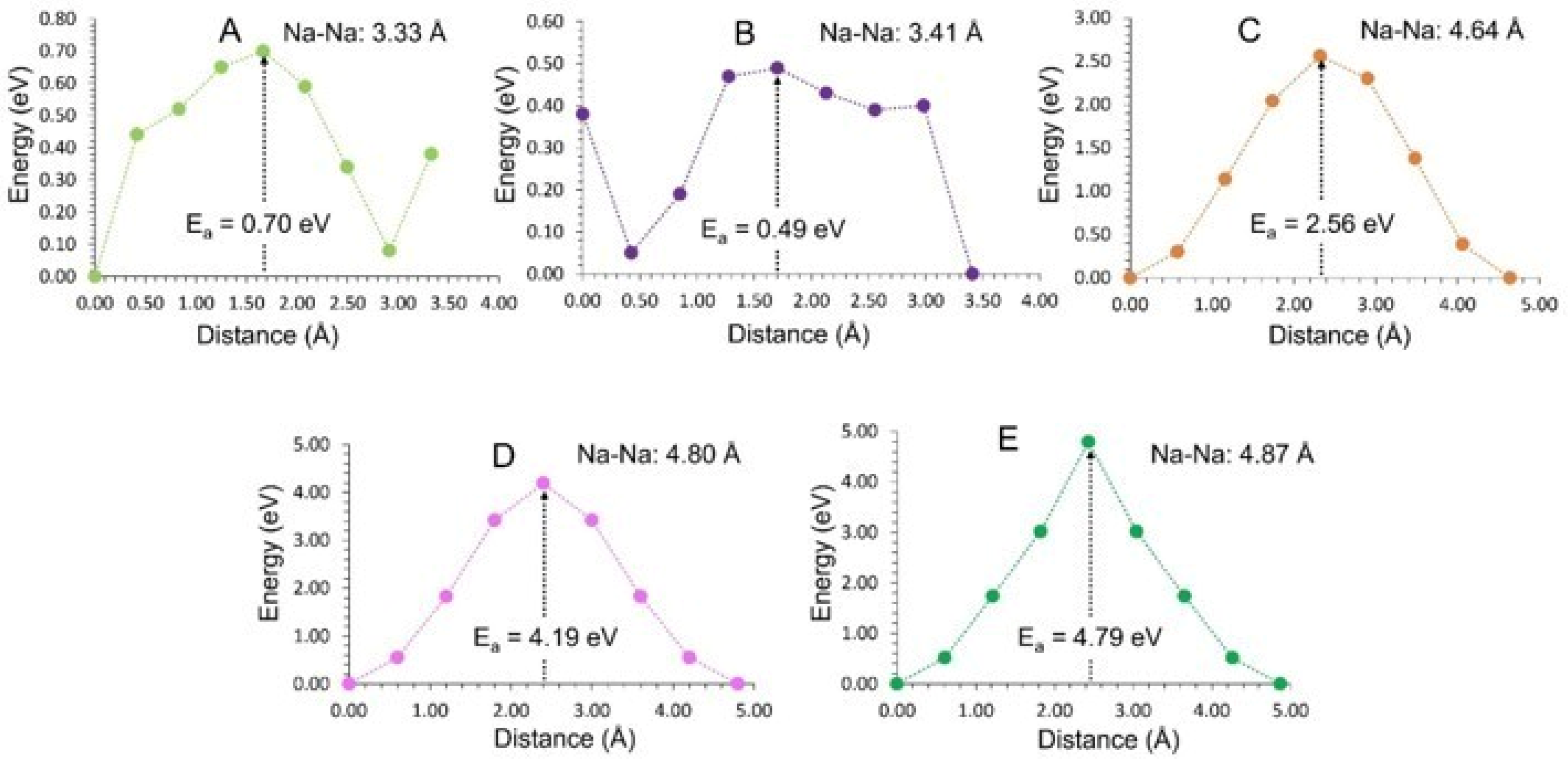
3.3. Diffusion of Na-Ions
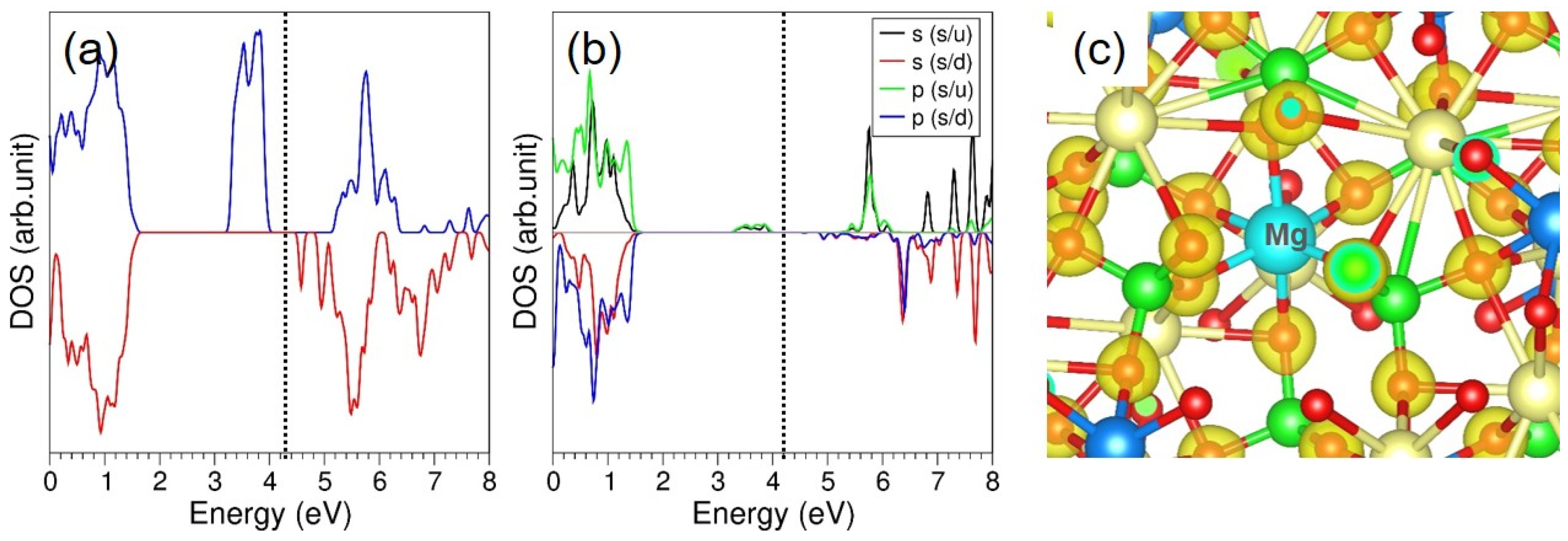
3.4. Solution of Dopants
3.4.1. Monovalent Dopants
3.4.2. Divalent Dopants
3.4.3. Trivalent Dopants
3.4.4. Tetravalent Dopants
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goodenough, J.B.; Park, K.-S. The Li-Ion Rechargeable Battery: A Perspective. J. Am. Chem. Soc. 2013, 135, 1167–1176. [Google Scholar] [CrossRef] [PubMed]
- Khan, T.; Garg, A.K.; Gupta, A.; Madan, A.K.; Jain, P.K. Comprehensive review on latest advances on rechargeable batteries. J. Energy Storage 2023, 57, 106204. [Google Scholar] [CrossRef]
- Berg, E.J.; Villevieille, C.; Streich, D.; Trabesinger, S.; Novák, P. Rechargeable Batteries: Grasping for the Limits of Chemistry. J. Electrochem. Soc. 2015, 162, A2468. [Google Scholar] [CrossRef]
- Nitta, N.; Wu, F.; Lee, J.T.; Yushin, G. Li-ion battery materials: Present and future. Mater. Today 2015, 18, 252–264. [Google Scholar] [CrossRef]
- Manthiram, A. An Outlook on Lithium Ion Battery Technology. ACS Cent. Sci. 2017, 3, 1063–1069. [Google Scholar] [CrossRef]
- Grey, C.P.; Hall, D.S. Prospects for lithium-ion batteries and beyond—A 2030 vision. Nat. Commun. 2020, 11, 6279. [Google Scholar] [CrossRef]
- Singh, B.; Wang, Z.; Park, S.; Gautam, G.S.; Chotard, J.-N.; Croguennec, L.; Carlier, D.; Cheetham, A.K.; Masquelier, C.; Canepa, P. A chemical map of NaSICON electrode materials for sodium-ion batteries. J. Mater. Chem. A 2021, 9, 281–292. [Google Scholar] [CrossRef]
- Qiu, S.; Wu, X.; Wang, M.; Lucero, M.; Wang, Y.; Wang, J.; Yang, Z.; Xu, W.; Wang, Q.; Gu, M.; et al. NASICON-type Na3Fe2(PO4)3 as a low-cost and high-rate anode material for aqueous sodium-ion batteries. Nano Energy 2019, 64, 103941. [Google Scholar] [CrossRef]
- Zhang, H.; Qin, B.; Buchholz, D.; Passerini, S. High-Efficiency Sodium-Ion Battery Based on NASICON Electrodes with High Power and Long Lifespan. ACS Appl. Energy Mater. 2018, 1, 6425–6432. [Google Scholar] [CrossRef]
- Li, C.; Li, R.; Liu, K.; Si, R.; Zhang, Z.; Hu, Y.-S. NaSICON: A promising solid electrolyte for solid-state sodium batteries. Interdiscip. Mater. 2022, 1, 396–416. [Google Scholar] [CrossRef]
- Zhang, X.; Rui, X.; Chen, D.; Tan, H.; Yang, D.; Huang, S.; Yu, Y. Na3V2(PO4)3: An advanced cathode for sodium-ion batteries. Nanoscale 2019, 11, 2556–2576. [Google Scholar] [CrossRef] [PubMed]
- Samigullin, R.R.; Zakharkin, M.V.; Drozhzhin, O.A.; Antipov, E.V. Thermal Stability of NASICON-Type Na3V2(PO4)3 and Na4VMn(PO4)3 as Cathode Materials for Sodium-ion Batteries. Energies 2023, 16, 3051. [Google Scholar] [CrossRef]
- Chen, G.; Huang, Q.; Wu, T.; Lu, L. Polyanion Sodium Vanadium Phosphate for Next Generation of Sodium-Ion Batteries—A Review. Adv. Funct. Mater. 2020, 30, 2001289. [Google Scholar] [CrossRef]
- Kanwade, A.; Gupta, S.; Kankane, A.; Srivastava, A.; Yadav, S.C.; Shirage, P.M. Phosphate-based cathode materials to boost the electrochemical performance of sodium-ion batteries. Sustain. Energy Fuels 2022, 6, 3114–3147. [Google Scholar] [CrossRef]
- Cheng, Q.; Zhao, X.; Yang, G.; Mao, L.; Liao, F.; Chen, L.; He, P.; Pan, D.; Chen, S. Recent advances of metal phosphates-based electrodes for high-performance metal ion batteries. Energy Storage Mater. 2021, 41, 842–882. [Google Scholar] [CrossRef]
- El Aggadi, S.; Ennouhi, M.; Boutakiout, A.; El Hourch, A. Progress towards efficient phosphate-based materials for sodium-ion batteries in electrochemical energy storage. Ionics 2023, 29, 2099–2113. [Google Scholar] [CrossRef]
- Zhu, Y.; Xu, H.; Ma, J.; Chen, P.; Chen, Y. The recent advances of NASICON-Na3V2(PO4)3 cathode materials for sodium-ion batteries. J. Solid State Chem. 2023, 317, 123669. [Google Scholar] [CrossRef]
- Akçay, T.; Häringer, M.; Pfeifer, K.; Anhalt, J.; Binder, J.R.; Dsoke, S.; Kramer, D.; Mönig, R. Na3V2(PO4)3—A Highly Promising Anode and Cathode Material for Sodium-Ion Batteries. ACS Appl. Energy Mater. 2021, 4, 12688–12695. [Google Scholar] [CrossRef]
- Duan, W.; Zhu, Z.; Li, H.; Hu, Z.; Zhang, K.; Cheng, F.; Chen, J. Na3V2(PO4)3@C core–shell nanocomposites for rechargeable sodium-ion batteries. J. Mater. Chem. A 2014, 2, 8668–8675. [Google Scholar] [CrossRef]
- Stüble, P.; Müller, C.; Klemens, J.; Scharfer, P.; Schabel, W.; Häringer, M.; Binder, J.R.; Hofmann, A.; Smith, A. Enabling Long-term Cycling Stability of Na3V2(PO4)3/C vs. Hard Carbon Full-cells. Batter. Supercaps 2024, 7, e202300375. [Google Scholar] [CrossRef]
- Wu, T.; Sun, J.; Yap, Z.Q.J.; Ke, M.; Lim, C.Y.H.; Lu, L. Substantial doping engineering in Na3V2-xFex(PO4)3 (0 ≤ x ≤ 0.15) as high-rate cathode for sodium-ion battery. Mater. Des. 2020, 186, 108287. [Google Scholar] [CrossRef]
- Pal, S.K.; Thirupathi, R.; Chakrabarty, S.; Omar, S. Improving the Electrochemical Performance of Na3V2(PO4)3 Cathode in Na-Ion Batteries by Si-Doping. ACS Appl. Energy Mater. 2020, 3, 12054–12065. [Google Scholar] [CrossRef]
- Shen, W.; Li, H.; Wang, C.; Li, Z.; Xu, Q.; Liu, H.; Wang, Y. Improved electrochemical performance of the Na3V2(PO4)3 cathode by B-doping of the carbon coating layer for sodium-ion batteries. J. Mater. Chem. A 2015, 3, 15190–15201. [Google Scholar] [CrossRef]
- Lee, J.; Park, S.; Park, Y.; Song, J.; Sambandam, B.; Mathew, V.; Hwang, J.-Y.; Kim, J. Chromium doping into NASICON-structured Na3V2(PO4)3 cathode for high-power Na-ion batteries. Chem. Eng. J. 2021, 422, 130052. [Google Scholar] [CrossRef]
- Cushing, B.L.; Goodenough, J.B. Li2NaV2(PO4)3: A 3.7 V Lithium-Insertion Cathode with the Rhombohedral NASICON Structure. J. Solid State Chem. 2001, 162, 176–181. [Google Scholar] [CrossRef]
- Song, W.; Ji, X.; Wu, Z.; Yang, Y.; Zhou, Z.; Li, F.; Chen, Q.; Banks, C.E. Exploration of ion migration mechanism and diffusion capability for Na3V2(PO4)2F3 cathode utilized in rechargeable sodium-ion batteries. J. Power Sources 2014, 256, 258–263. [Google Scholar] [CrossRef]
- Song, W.; Ji, X.; Wu, Z.; Zhu, Y.; Yang, Y.; Chen, J.; Jing, M.; Li, F.; Banks, C.E. First exploration of Na-ion migration pathways in the NASICON structure Na3V2(PO4)3. J. Mater. Chem. A 2014, 2, 5358–5362. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, Q.; Zhang, M.; Han, B.; Zhou, C.; Chen, Y.; Lv, G. A first-principles investigation of the influence of polyanionic boron doping on the stability and electrochemical behavior of Na3V2(PO4)3. J. Mol. Model. 2019, 25, 96. [Google Scholar] [CrossRef]
- Clarke, M.J.; Dawson, J.A.; Mays, T.J.; Islam, M.S. Atomistic Insights into the Effects of Doping and Vacancy Clustering on Li-Ion Conduction in the Li3OCl Antiperovskite Solid Electrolyte. ACS Appl. Energy Mater. 2021, 4, 5094–5100. [Google Scholar] [CrossRef]
- Famprikis, T.; Dawson, J.A.; Fauth, F.; Clemens, O.; Suard, E.; Fleutot, B.; Courty, M.; Chotard, J.-N.; Islam, M.S.; Masquelier, C. A New Superionic Plastic Polymorph of the Na+ Conductor Na3PS4. ACS Mater. Lett. 2019, 1, 641–646. [Google Scholar] [CrossRef]
- Fisher, C.A.J.; Prieto, V.M.H.; Islam, M.S. Lithium Battery Materials LiMPO4 (M = Mn, Fe, Co, and Ni): Insights into Defect Association, Transport Mechanisms, and Doping Behavior. Chem. Mater. 2008, 20, 5907–5915. [Google Scholar] [CrossRef]
- Kuganathan, N.; Kordatos, A.; Anurakavan, S.; Iyngaran, P.; Chroneos, A. Li3SbO4 lithium-ion battery material: Defects, lithium-ion diffusion and tetravalent dopants. Mater. Chem. Phys. 2019, 225, 34–41. [Google Scholar] [CrossRef]
- Kuganathan, N.; Chroneos, A. Na3V(PO4)2 cathode material for Na ion batteries: Defects, dopants and Na diffusion. Solid State Ion. 2019, 336, 75–79. [Google Scholar] [CrossRef]
- Famprikis, T.; Bouyanfif, H.; Canepa, P.; Zbiri, M.; Dawson, J.A.; Suard, E.; Fauth, F.; Playford, H.Y.; Dambournet, D.; Borkiewicz, O.J.; et al. Insights into the Rich Polymorphism of the Na+ Ion Conductor Na3PS4 from the Perspective of Variable-Temperature Diffraction and Spectroscopy. Chem. Mater. 2021, 33, 5652–5667. [Google Scholar] [CrossRef] [PubMed]
- Treacher, J.C.; Wood, S.M.; Islam, M.S.; Kendrick, E. Na2CoSiO4 as a cathode material for sodium-ion batteries: Structure, electrochemistry and diffusion pathways. Phys. Chem. Chem. Phys. 2016, 18, 32744–32752. [Google Scholar] [CrossRef]
- Gale, J.D.; Rohl, A.L. The General Utility Lattice Program (GULP). Mol. Simul. 2003, 29, 291–341. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Bush, T.S.; Gale, J.D.; Catlow, C.R.A.; Battle, P.D. Self-consistent interatomic potentials for the simulation of binary and ternary oxides. J. Mater. Chem. 1994, 4, 831–837. [Google Scholar] [CrossRef]
- Lewis, G.V.; Catlow, C.R.A. Potential models for ionic oxides. J. Phys. C Solid State Phys. 1985, 18, 1149. [Google Scholar] [CrossRef]
- Sauer, J.; Schröder, K.P.; Termath, V. Comparing the acidities of microporous aluminosilicate and silico-aluminophosphate catalysts: A combined quantum mechanics-interatomic potential function study. Collect. Czech. Chem. Commun. 1998, 63, 1394–1408. [Google Scholar] [CrossRef]
- Bispo, G.F.D.C.; Jackson, R.A.; Valerio, M.E.G. Modelling of Intrinsic Defects in CaYAl3O7. Acta Phys. Pol. A 2018, 133, 781–784. [Google Scholar] [CrossRef]
- Gale, J.D. GULP: A computer program for the symmetry-adapted simulation of solids. J. Chem. Soc. Faraday Trans. 1997, 93, 629–637. [Google Scholar] [CrossRef]
- Mott, N.F.; Littleton, M.J. Conduction in polar crystals. I. Electrolytic conduction in solid salts. Trans. Faraday Soc. 1938, 34, 485–499. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C, 2nd ed.; The Art of Scientific Computing, Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Henkelman, G.; Arnaldsson, A.; Jónsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
- Chotard, J.-N.; Rousse, G.; David, R.; Mentré, O.; Courty, M.; Masquelier, C. Discovery of a Sodium-Ordered Form of Na3V2(PO4)3 below Ambient Temperature. Chem. Mater. 2015, 27, 5982–5987. [Google Scholar] [CrossRef]
- Rao, X.; Wang, J.; Yang, M.-A.; Zhao, H.; Li, Z. A superior Na3V2(PO4)3-based cathode enhanced by Nb-doping for high-performance sodium-ion battery. APL Mater. 2022, 10, 010701. [Google Scholar] [CrossRef]
- Zhou, M.; Zhou, X.; Li, L.; Chen, X.; Qiao, Z.; Chou, S. Emerging high voltage V4+/V5+ redox reactions in Na3V2(PO4)3-based cathodes for sodium-ion batteries. Chem. Sci. 2024, 15, 8651–8663. [Google Scholar] [CrossRef]
- Aragón, M.J.; Lavela, P.; Ortiz, G.F.; Tirado, J.L. Benefits of Chromium Substitution in Na3V2(PO4)3 as a Potential Candidate for Sodium-Ion Batteries. ChemElectroChem 2015, 2, 995–1002. [Google Scholar] [CrossRef]
- Liu, X.; Feng, G.; Wang, E.; Chen, H.; Wu, Z.; Xiang, W.; Zhong, Y.; Chen, Y.; Guo, X.; Zhong, B. Insight into Preparation of Fe-Doped Na3V2(PO4)3@C from Aspects of Particle Morphology Design, Crystal Structure Modulation, and Carbon Graphitization Regulation. ACS Appl. Mater. Interfaces 2019, 11, 12421–12430. [Google Scholar] [CrossRef] [PubMed]
- Park, J.-S.; Kim, J.; Jo, J.H.; Myung, S.-T. Role of the Mn substituent in Na3V2(PO4)3 for high-rate sodium storage. J. Mater. Chem. A 2018, 6, 16627–16637. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, X.; Zou, G.; Zhang, L.; Han, S.; Li, Y.; Liu, D.; Fernandez, C.; Li, L.; Ren, L.; et al. Crystal-defect engineering of electrode materials for energy storage and conversion. Mater. Today Nano 2023, 22, 100336. [Google Scholar] [CrossRef]
- Kröger, F.A.; Nachtrieb, N.H. The Chemistry of Imperfect Crystals. Phys. Today 1964, 17, 66–69. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, M.; Zhou, C.; Chen, Y. Concerted Ion-Exchange Mechanism for Sodium Diffusion and Its Promotion in Na3V2(PO4)3 Framework. J. Phys. Chem. C 2018, 122, 16649–16654. [Google Scholar] [CrossRef]
- Shao, Y.; Qian, Y.; Zhang, T.; Zhang, P.; Wang, H.; Qian, T.; Yan, C. Doping modification of sodium superionic conductor Na3V2(PO4)3 cathodes for sodium-ion batteries: A mini-review. Inorg. Chem. Front. 2024, 11, 4552–4567. [Google Scholar] [CrossRef]
- Kuniyil, N.C.M.; Robin, R.; Kumarasamy, R.K.; Nishanthi, S.T.; Sathish, M. Tailoring of High-Valent Sn-Doped Porous Na3V2(PO4)3/C Nanoarchitechtonics: An Ultra High-Rate Cathode for Sodium-Ion Batteries. ACS Appl. Mater. Interfaces 2024, 16, 28599–28612. [Google Scholar] [CrossRef]
- Fang, J.; Wang, S.; Yao, X.; Hu, X.; Wang, Y.; Wang, H. Ration design of porous Mn-doped Na3V2(PO4)3 cathode for high rate and super stable sodium-ion batteries. Electrochim. Acta 2019, 295, 262–269. [Google Scholar] [CrossRef]
- Shen, L.; Li, Y.; Hu, C.; Huang, Z.; Wang, B.; Wang, Y.; Liu, Q.; Ye, F. A high-rate cathode material based on potassium-doped Na3V2(PO4)3 for high/low-temperature sodium-ion batteries. Mater. Today Chem. 2023, 30, 101506. [Google Scholar] [CrossRef]
- Li, H.; Yu, X.; Bai, Y.; Wu, F.; Wu, C.; Liu, L.-Y.; Yang, X.-Q. Effects of Mg doping on the remarkably enhanced electrochemical performance of Na3V2(PO4)3 cathode materials for sodium ion batteries. J. Mater. Chem. A 2015, 3, 9578–9586. [Google Scholar] [CrossRef]
- Dong, H.; Liu, C.; Huang, Q.; Sun, Z.; Liang, T.; Fan, C.; Chen, Y. Sc3+ substituted Na3V2(PO4)3 on N-doped porous carbon skeleton boosting high structural stability and superior electrochemical performance for full sodium ion batteries. J. Colloid Interface Sci. 2024, 667, 371–384. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Li, X.; Liang, Q.; Xu, L.; Ding, C.; Liu, Y.; Gao, Y. Optimization Strategies of Na3V2(PO4)3 Cathode Materials for Sodium-Ion Batteries. Nano-Micro Lett. 2024, 17, 33. [Google Scholar] [CrossRef] [PubMed]
- Tong, S.; Pan, H.; Liu, H.; Zhang, X.; Liu, X.; Jia, M.; Kang, Y.; Yuan, Y.; Du, X.; Yan, X. Titanium Doping Induced the Suppression of Irreversible Phase Transformation at High Voltage for V-based Phosphate Cathodes of Na-Ion Batteries. ChemSusChem 2023, 16, e202300244. [Google Scholar] [CrossRef]
- Wang, D.; Bie, X.; Fu, Q.; Dixon, D.; Bramnik, N.; Hu, Y.-S.; Fauth, F.; Wei, Y.; Ehrenberg, H.; Chen, G.; et al. Sodium vanadium titanium phosphate electrode for symmetric sodium-ion batteries with high power and long lifespan. Nat. Commun. 2017, 8, 15888. [Google Scholar] [CrossRef]
- Ding, H.; He, X.; Tao, Q.; Teng, J.; Li, J. Ti-Doped Na3V2(PO4)3 Activates Additional Ti3+/Ti4+ and V4+/V5+ Redox Pairs for Superior Sodium Ion Storage. Energy Fuels 2023, 37, 4132–4142. [Google Scholar] [CrossRef]
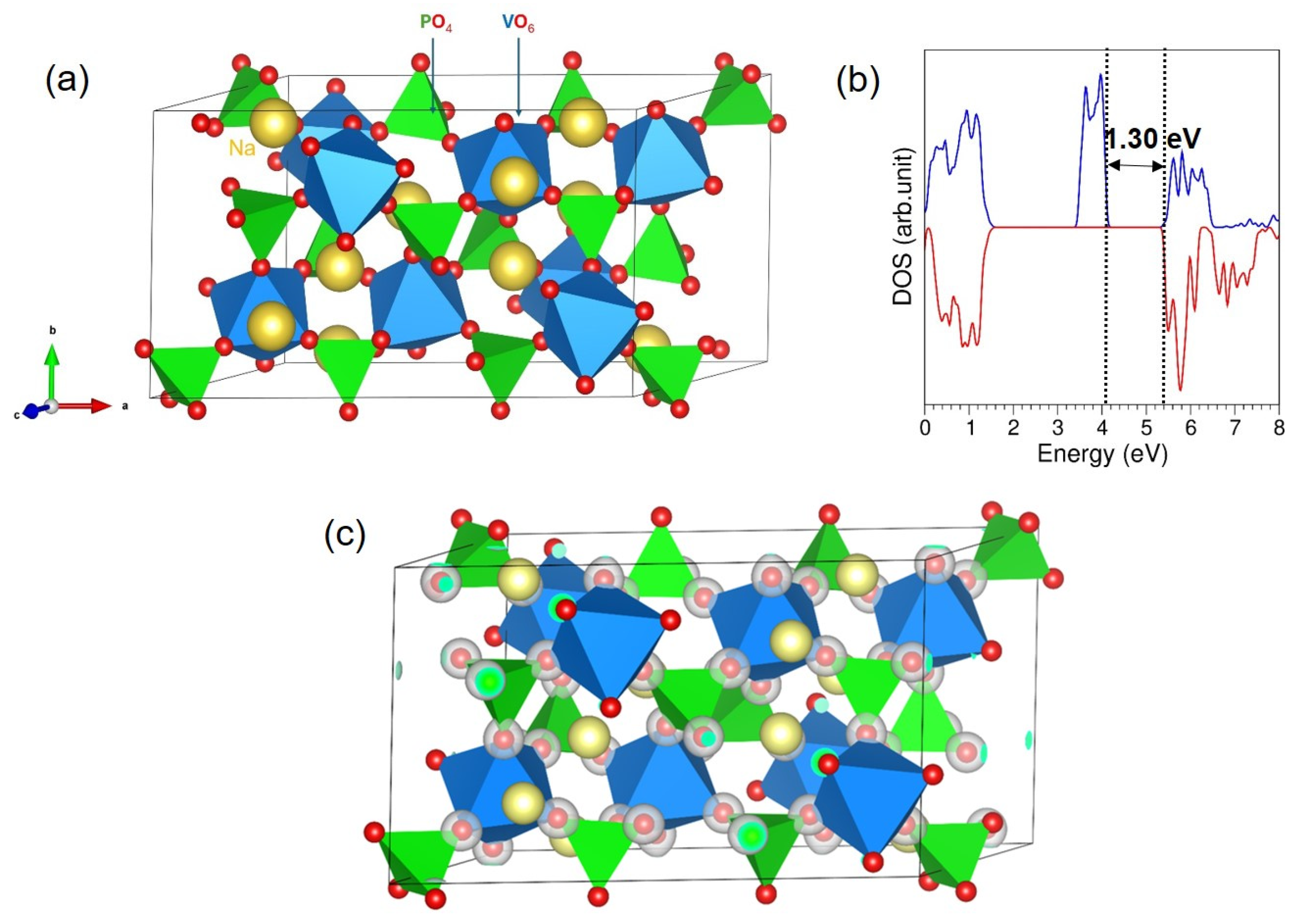

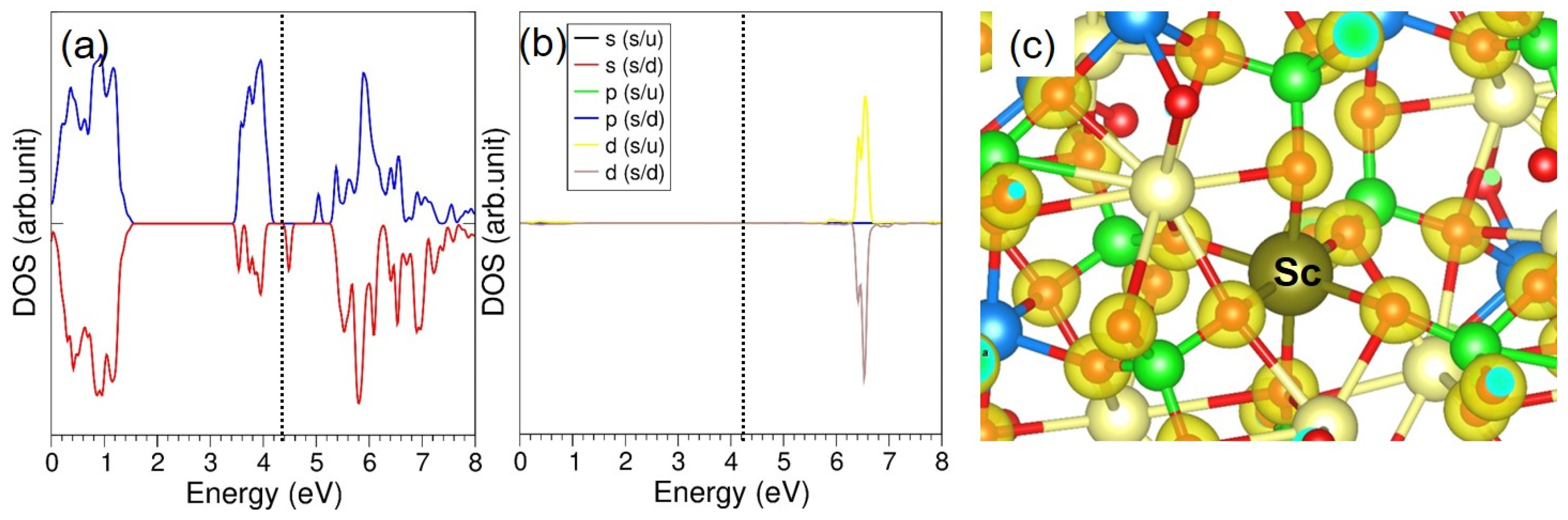
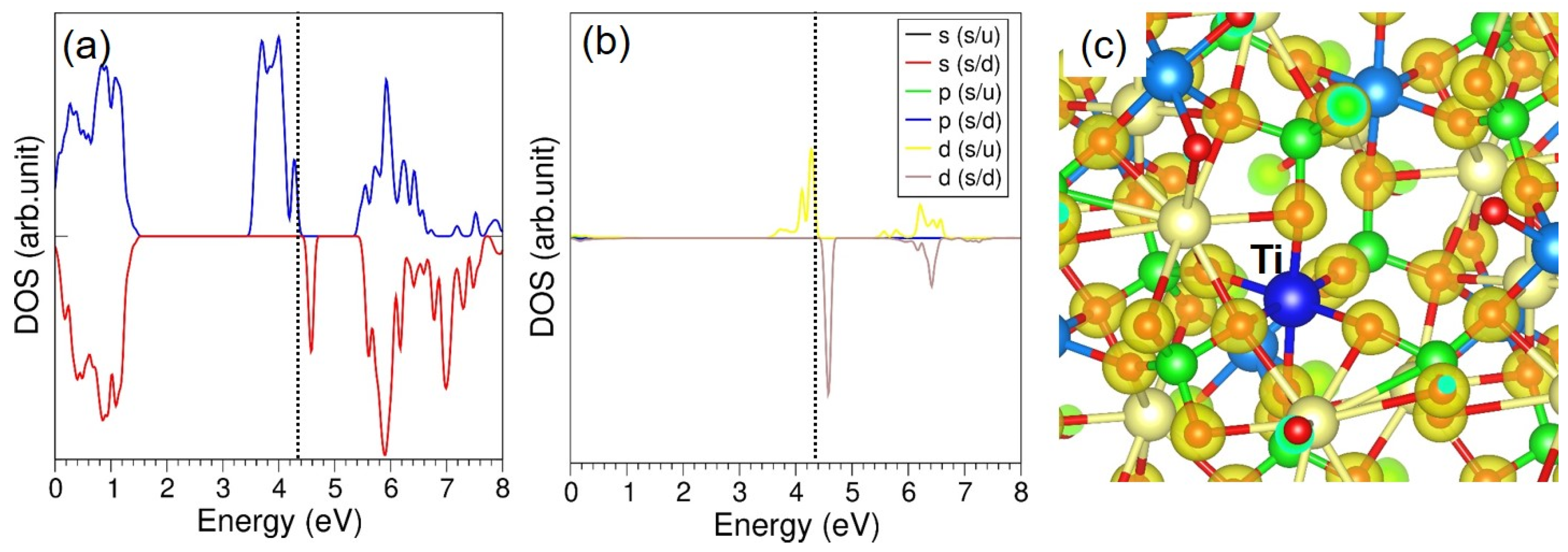
| Interaction | A/eV | ρ/Å | C/eV·Å6 | Y/e | K/eV·Å−2 |
|---|---|---|---|---|---|
| Na+–O2− | 1271.504 | 0.3000 | 0.00 | 1.00 | 99,999 |
| V3+–O2− | 1790.20 | 0.3061 | 0.00 | 3.00 | 36.27 |
| P5+–O2− | 1273.42017 | 0.32272 | 0.00 | 5.00 | 99,999 |
| O2–O2− | 22764.0 | 0.1490 | 27.879 | –2.922 | 81.64857 |
| Lattice Properties | Calculated | Experiment [49] | |∆|(%) | ||
|---|---|---|---|---|---|
| Classical | DFT | Classical | DFT | ||
| a (Å) | 15.23 | 15.25 | 15.34 | 0.67 | 0.59 |
| b (Å) | 8.79 | 8.86 | 8.92 | 1.56 | 0.67 |
| c (Å) | 8.90 | 8.85 | 8.89 | 0.15 | 0.45 |
| α = γ (°) | 90.0 | 90.0 | 90.0 | 0.00 | 0.00 |
| β (°) | 124.9 | 125.8 | 125.2 | 0.23 | 0.47 |
| V (Å3) | 977.76 | 969.1 | 994.79 | 1.71 | 2.58 |
| Atom | Bader Charge (e) |
|---|---|
| Na | +1.00 |
| V | +2.14 |
| P | +5.00 |
| O | −1.86 |
| Defect Process | Equation Number | Defect Energy (eV)/Defect | |
|---|---|---|---|
| Classical | DFT | ||
| Na Frenkel | 1 | 0.46 | 1.41 |
| V Frenkel | 2 | 4.65 | 5.20 |
| O Frenkel | 3 | 4.25 | 4.75 |
| Schottky | 4 | 5.78 | 6.21 |
| Na2O Schottky | 5 | 3.46 | 3.86 |
| V2O3 Schottky | 6 | 4.97 | 5.25 |
| P2O5 Schottky | 7 | 10.40 | 12.46 |
| Na/V Anti-site (isolated) | 8 | 3.04 | 3.96 |
| Na/V Anti-site (cluster) | 9 | 0.95 | 1.73 |
| Na Local Hop | Na-Na Separation (Å) | Activation Energy (eV) |
|---|---|---|
| A | 3.33 | 0.70 |
| B | 3.41 | 0.49 |
| C | 4.64 | 2.56 |
| D | 4.80 | 4.19 |
| E | 4.87 | 4.79 |
| Dopant | Ionic Radius of Dopant Ion (Å) | Bader Charge on Dopant (|e|) | Solution Energy (eV)/Dopant | M-O Distance (Å) | |
|---|---|---|---|---|---|
| Li+ | 0.76 | +1.00 | 1.82 | 2.31, 2.38 | −0.65 |
| K+ | 1.38 | +0.85 | 1.24 | 2.57, 2.68 | +1.51 |
| Rb+ | 1.52 | +0.85 | 1.31 | 2.66, 2.78 | +2.19 |
| Dopant | Ionic Radius of Dopant Ion (Å) | Bader Charge on Dopant (|e|) | Solution Energy (eV)/Dopant | M-O Distance (Å) | |
|---|---|---|---|---|---|
| Fe2+ | 0.61 | +1.65 | 1.42 | 1.96–2.02 | −0.72 |
| Ni2+ | 0.69 | +1.40 | 0.34 | 2.04–2.13 | −0.21 |
| Zn2+ | 0.74 | +1.47 | 0.42 | 2.10–2.24 | +0.11 |
| Mn2+ | 0.83 | +1.76 | −0.15 | 2.09–2.19 | +0.50 |
| Mg2+ | 0.86 | +2.00 | −0.37 | 2.05–2.12 | −0.07 |
| Ca2+ | 1.06 | +1.60 | −0.35 | 2.26–2.35 | +1.68 |
| Sr2+ | 1.18 | +1.63 | −0.15 | 2.41–2.54 | +2.18 |
| Ba2+ | 1.35 | +1.62 | −0.02 | 2.53–2.62 | +2.67 |
| Dopant Ions | Ionic Radius of Dopant Ion (Å) | Bader Charge on Dopant (|e|) | Solution Energy (eV)/Dopant | M-O Distance (Å) | |
|---|---|---|---|---|---|
| Al3+ | 0.54 | +3.00 | −0.32 | 1.84–1.93 | −0.73 |
| Ga3+ | 0.62 | +3.00 | −0.08 | 1.98–2.02 | −0.21 |
| Sc3+ | 0.75 | +2.12 | −0.72 | 1.98–2.13 | +0.97 |
| In3+ | 0.81 | +3.00 | −0.13 | 2.18–2.21 | +1.41 |
| Y3+ | 0.90 | +2.27 | −0.57 | 2.11–2.27 | +2.24 |
| La3+ | 1.03 | +2.20 | −0.31 | 2.36–2.49 | +2.53 |
| Dopant Ions | Ionic Radius of Dopant Ion (Å) | Bader Charge on Dopant (|e|) | Solution Energy (eV)/Dopant | M-O Distance | |
|---|---|---|---|---|---|
| Si4+ | 0.40 | +4.00 | 4.19 | 1.74–1.85 | −1.00 |
| Ge4+ | 0.53 | +4.00 | 3.14 | 1.86–1.97 | +0.02 |
| Ti4+ | 0.61 | +2.54 | 2.39 | 1.91–2.07 | +0.56 |
| Sn4+ | 0.69 | +4.00 | 2.85 | 2.01–2.11 | +1.36 |
| Ce4+ | 0.87 | +2.37 | 2.94 | 2.14–2.33 | +3.30 |
| Dopant | Lattice Parameters | |||||
|---|---|---|---|---|---|---|
| a (Å) | b (Å) | c (Å) | α (°) | β (°) | γ (°) | |
| Li | 15.25 | 8.86 | 8.86 | 89.9 | 125.9 | 90.0 |
| K | 15.23 | 8.23 | 8.96 | 90.1 | 125.2 | 90.0 |
| Rb | 15.21 | 8.82 | 9.01 | 90.1 | 124.9 | 90.1 |
| Fe | 15.21 | 8.83 | 8.83 | 90.0 | 125.8 | 90.0 |
| Ni | 15.24 | 8.84 | 8.84 | 90.0 | 125.8 | 90.0 |
| Zn | 15.26 | 8.85 | 8.85 | 90.0 | 125.8 | 90.0 |
| Mn | 15.28 | 8.87 | 8.86 | 90.1 | 125.8 | 89.9 |
| Mg | 15.24 | 8.85 | 8.85 | 90.1 | 125.8 | 90.0 |
| Ca | 15.35 | 8.90 | 8.89 | 90.2 | 125.7 | 89.8 |
| Sr | 15.43 | 8.89 | 8.88 | 90.2 | 125.6 | 89.7 |
| Ba | 15.43 | 8.82 | 8.85 | 89.8 | 125.1 | 89.8 |
| Al | 15.20 | 8.82 | 8.82 | 89.9 | 125.7 | 90.1 |
| Ga | 15.24 | 8.85 | 8.84 | 90.0 | 125.7 | 90.0 |
| Sc | 15.29 | 8.88 | 8.87 | 90.1 | 125.7 | 89.9 |
| In | 15.33 | 8.89 | 8.88 | 90.1 | 125.7 | 89.9 |
| Y | 15.37 | 8.92 | 8.90 | 90.1 | 125.7 | 89.9 |
| La | 15.45 | 8.91 | 8.88 | 90.1 | 125.6 | 89.7 |
| Si | 15.26 | 8.84 | 8.84 | 90.0 | 125.8 | 90.0 |
| Ge | 15.35 | 8.85 | 8.87 | 90.0 | 125.7 | 90.0 |
| Ti | 15.38 | 8.99 | 8.90 | 90.0 | 126.1 | 90.0 |
| Sn | 15.47 | 8.86 | 8.90 | 90.0 | 125.8 | 90.0 |
| Ce | 15.66 | 8.82 | 8.93 | 90.0 | 126.7 | 90.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seshan, V.; Iyngaran, P.; Abiman, P.; Kuganathan, N. Atomic-Scale Study of NASICON Type Electrode Material: Defects, Dopants and Sodium-Ion Migration in Na3V2(PO4)3. Physchem 2025, 5, 1. https://doi.org/10.3390/physchem5010001
Seshan V, Iyngaran P, Abiman P, Kuganathan N. Atomic-Scale Study of NASICON Type Electrode Material: Defects, Dopants and Sodium-Ion Migration in Na3V2(PO4)3. Physchem. 2025; 5(1):1. https://doi.org/10.3390/physchem5010001
Chicago/Turabian StyleSeshan, Vijayabaskar, Poobalasuntharam Iyngaran, Poobalasingam Abiman, and Navaratnarajah Kuganathan. 2025. "Atomic-Scale Study of NASICON Type Electrode Material: Defects, Dopants and Sodium-Ion Migration in Na3V2(PO4)3" Physchem 5, no. 1: 1. https://doi.org/10.3390/physchem5010001
APA StyleSeshan, V., Iyngaran, P., Abiman, P., & Kuganathan, N. (2025). Atomic-Scale Study of NASICON Type Electrode Material: Defects, Dopants and Sodium-Ion Migration in Na3V2(PO4)3. Physchem, 5(1), 1. https://doi.org/10.3390/physchem5010001







