Pagodane—Solution and Solid-State Vibrational Spectra
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Selection Rules
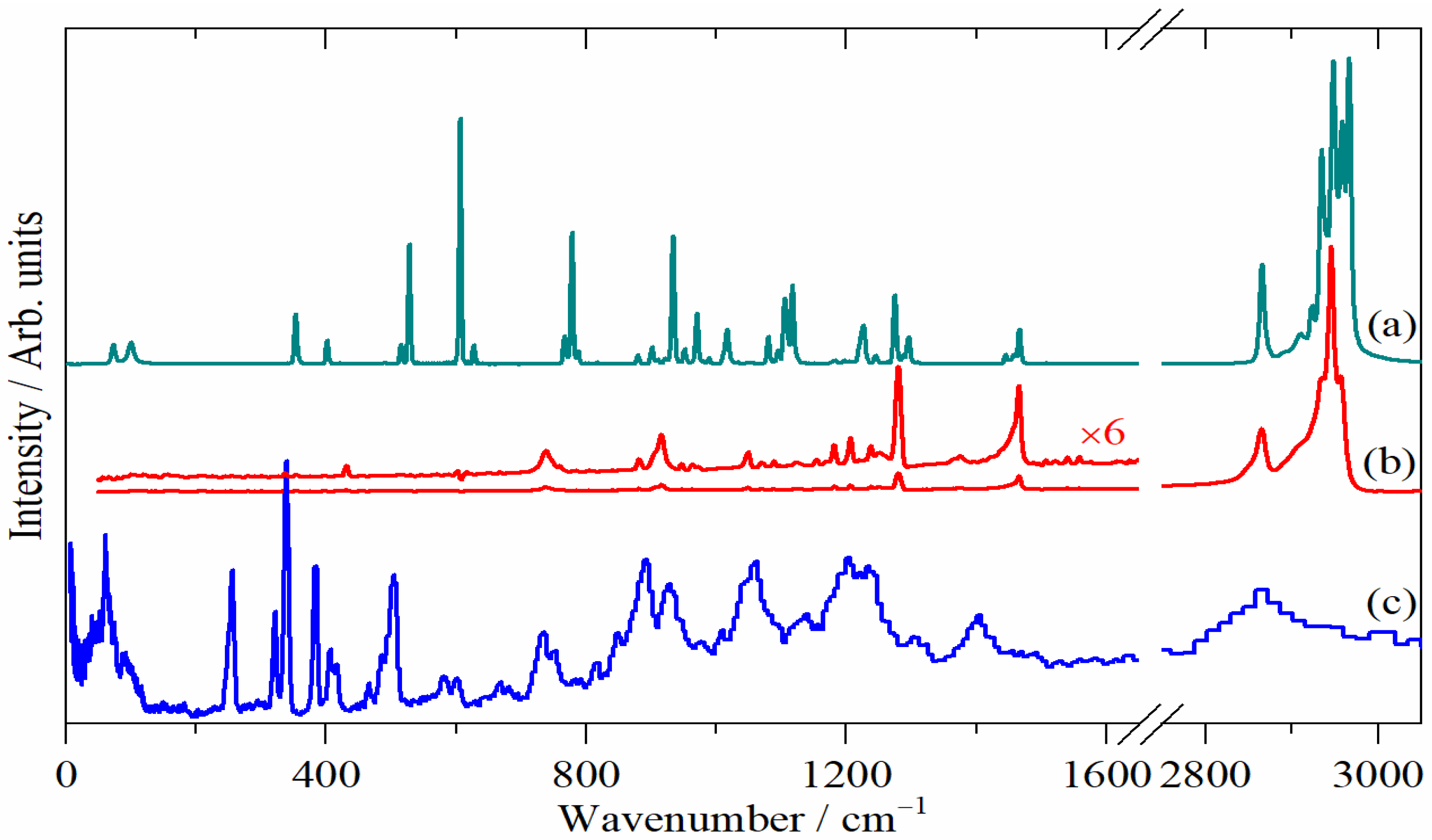
3.2. Pagodane in Solution
3.3. Pagodane in the Solid State
3.4. Computational Studies
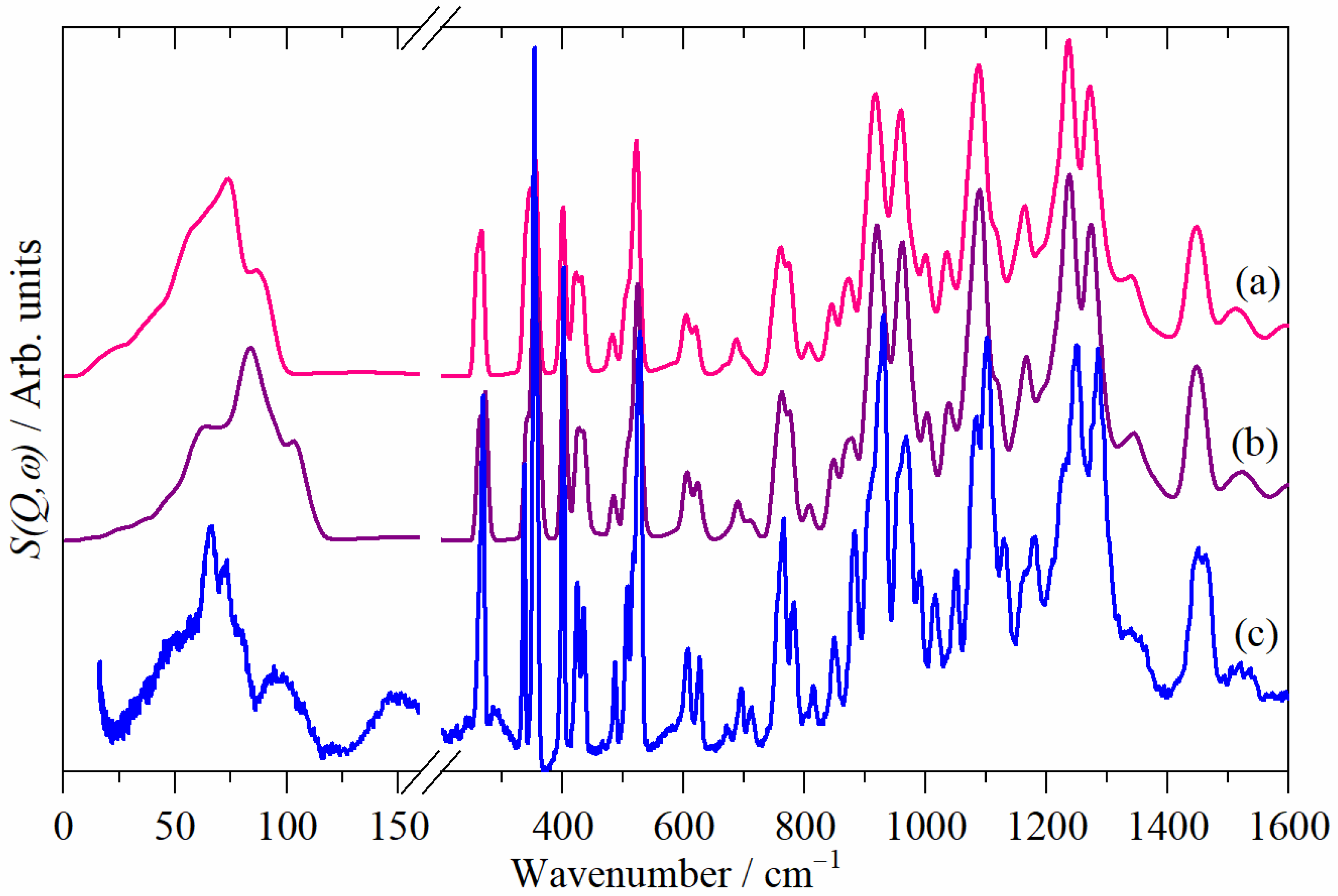
3.4.1. The Lattice Mode Region (<200 cm−1)
3.4.2. The Fingerprint Region (200–1600 cm−1)
3.4.3. The C–H Stretch Region (>2800 cm−1)
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fessner, W.-D.; Prinzbach, H.; Riho, C. Pagodane—An undecacyclic C20H20-polyquinane. Tetrahedron Lett. 1983, 24, 5857–5860. [Google Scholar] [CrossRef]
- Ternansky, R.J.; Balogh, D.W.; Paquette, L.A. Dodecahedrane. J. Am. Chem. Soc. 1982, 104, 4503–4504. [Google Scholar] [CrossRef]
- Prinzbach, H.; Weber, W. From an insecticide to Plato’s universe—The pagodane route to dodecahedranes: New pathways and new perspectives. Angew. Chem. Int. Ed. Engl. 1994, 33, 2239–2257. [Google Scholar] [CrossRef]
- Prakash, G.K.S.; Krishnamurthy, V.V.; Herges, R.; Bau, R.; Yuan, H.; Olah, G.A.; Fessner, W.-D.; Prinzbach, H. [1.1.1.1] and [2.2.1.1] Pagodane dications: Frozen two-electron Woodward-Hoffmann transition state models. J. Amer. Chem. Soc. 1988, 110, 7764–7772. [Google Scholar] [CrossRef]
- Allis, D.G.; Prinzbach, H.; Hudson, B.S. Inelastic neutron scattering spectra of pagodane: Experiment and DFT calculations. Chem. Phys. Lett. 2004, 386, 356–363. [Google Scholar] [CrossRef]
- Mitchell, P.C.H.; Parker, S.F.; Ramirez-Cuesta, A.J.; Tomkinson, J. Vibrational Spectroscopy with Neutrons, with Applications in Chemistry, Biology, Materials Science and Catalysis; World Scientific: Singapore, 2005. [Google Scholar]
- Parker, S.F.; Lennon, D.; Albers, P.W. Vibrational spectroscopy with neutrons—A review of new directions. Appl. Spec. 2011, 65, 1325–1341. [Google Scholar] [CrossRef]
- Parker, S.F.; Fernandez-Alonso, F.; Ramirez-Cuesta, A.J.; Tomkinson, J.; Rudić, S.; Pinna, R.S.; Gorini, G.; Fernández Castañon, J. Recent and future developments on TOSCA at ISIS. J. Phys. Conf. Ser. 2014, 554, 12003. [Google Scholar] [CrossRef]
- Pinna, R.S.; Rudić, S.; Parker, S.F.; Armstrong, J.; Zanetti, M.; Škoro, G.; Waller, S.P.; Zacek, D.; Smith, C.A.; Capstick, M.J.; et al. The neutron guide upgrade of the TOSCA spectrometer. Nucl. Instrum. Methods Phys. Res. Sect. A 2018, 896, 68–74. [Google Scholar] [CrossRef]
- The ISIS Neutron and Muon Source. Available online: https://www.isis.stfc.ac.uk/Pages/About.aspx (accessed on 31 July 2024).
- Griffiths, P.R.; de Haseth, J.A. Fourier Transform Infrared Spectrometry; Wiley-Interscience: New York, NY, USA, 1986. [Google Scholar]
- Rossi Albertini, V.; Colognesi, D.; Tomkinson, J. A study on the calibration of a time-focused inelastic neutron scattering spectrometer. J. Neutron. Res. 2000, 8, 245–259. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Krist. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Matthias Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Tkatchenko, A.; Scheffler, M. Accurate molecular van der Waals interactions from ground-state electron density and free-atom reference data. Phys. Rev. Lett. 2009, 102, 073005. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Pack, J.D.; Monkhorst, H.J. “Special points for Brillouin-zone integrations”—A reply. Phys. Rev. B 1977, 16, 1748–1749. [Google Scholar] [CrossRef]
- Refson, K.; Tulip, P.R.; Clark, S.J. Variational density-functional perturbation theory for dielectrics and lattice dynamics. Phys. Rev. B 2006, 73, 155114. [Google Scholar] [CrossRef]
- Gonze, X.; Lee, C. Dynamical matrices, Born effective charges, dielectric permittivity tensors, and interatomic force constants from density-functional perturbation theory. Phys. Rev. B 1997, 55, 10355–10368. [Google Scholar] [CrossRef]
- Milman, V.; Perlov, A.; Refson, K.; Clark, S.J.; Gavartin, J.; Winkler, B. Structural, electronic and vibrational properties of tetragonal zirconia under pressure: A density functional theory study. J. Phys. Condens. Matter 2009, 21, 485404. [Google Scholar] [CrossRef]
- Biovia Materials Studio. Available online: https://www.3ds.com/products-services/biovia/products/molecular-modeling-simulation/biovia-materials-studio (accessed on 12 July 2024).
- Dymkowski, K.; Parker, S.F.; Fernandez-Alonso, F.; Mukhopadhyay, S. AbINS: The modern software for INS interpretation. Phys. B 2018, 551, 443–448. [Google Scholar] [CrossRef]
- Fair, R.L.; Jackson, A.J.; Voneshen, D.J.; Jochym, D.B.; Le, M.D.; Refson, K.; Perring, T.G. Euphonic: Inelastic neutron scattering simulations from force constants and visualization tools for phonon properties. J. Appl. Cryst. 2022, 55, 1689–1703. [Google Scholar] [CrossRef]
- Fateley, W.G.; Dollish, F.R.; McDevitt, N.T.; Bentley, F.F. Infrared and Raman Selection Rules for Molecular and Lattice Vibrations: The Correlation Method; Wiley-Interscience: New York, NY, USA, 1972. [Google Scholar]
- Lin-Vien, D.; Colthup, N.B.; Fateley, W.G.; Grasselli, J.G. The Handbook of Infrared and Raman Characteristic Frequencies of Organic Molecules; Academic Press: Boston, MA, USA, 1991. [Google Scholar]
- Perrichon, A. On the spectral resolution of the broad-band indirect-geometry time-of-flight neutron spectrometer TOSCA. Nucl. Instrum. Methods Phys. Res. A 2022, 1041, 167401. [Google Scholar] [CrossRef]
- Bellamy, L.J. The Infrared Spectra of Complex Molecules, 3rd ed.; Chapman and Hall: London, UK, 1975; p. 16. [Google Scholar]
- Hudson, B.S.; Allis, D.G.; Parker, S.F.; Ramirez-Cuesta, A.J.; Braden, D.A.; Herman, H.; Prinzbach, H. The infrared, Raman and inelastic neutron scattering spectra of dodecahedrane: An Ih molecule in Th site symmetry. J. Phys. Chem. A 2005, 109, 3418–3424. [Google Scholar] [CrossRef] [PubMed]
- Parker, S.F.; Fortes, A.D.; Nye, D.W.; Day, S.J.; Kuck, D. Centrohexaindane, a unique polyaromatic hydrocarbon bearing the rare Cq(Cq)4 core: Inelastic neutron scattering, infrared and Raman spectroscopy. Chem. Eur. J. 2023, 29, e202302057. [Google Scholar] [CrossRef] [PubMed]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parker, S.F.; Mason, H.E.; Wilson, C.T.; Jackson, A.J. Pagodane—Solution and Solid-State Vibrational Spectra. Physchem 2024, 4, 524-535. https://doi.org/10.3390/physchem4040036
Parker SF, Mason HE, Wilson CT, Jackson AJ. Pagodane—Solution and Solid-State Vibrational Spectra. Physchem. 2024; 4(4):524-535. https://doi.org/10.3390/physchem4040036
Chicago/Turabian StyleParker, Stewart F., Hannah E. Mason, Campbell T. Wilson, and Adam J. Jackson. 2024. "Pagodane—Solution and Solid-State Vibrational Spectra" Physchem 4, no. 4: 524-535. https://doi.org/10.3390/physchem4040036
APA StyleParker, S. F., Mason, H. E., Wilson, C. T., & Jackson, A. J. (2024). Pagodane—Solution and Solid-State Vibrational Spectra. Physchem, 4(4), 524-535. https://doi.org/10.3390/physchem4040036






