Measurement Precision and Thermal and Absorption Properties of Nanostructures in Aqueous Solutions by Transient and Steady-State Thermal-Lens Spectrometry
Abstract
1. Introduction
2. Materials and Methods
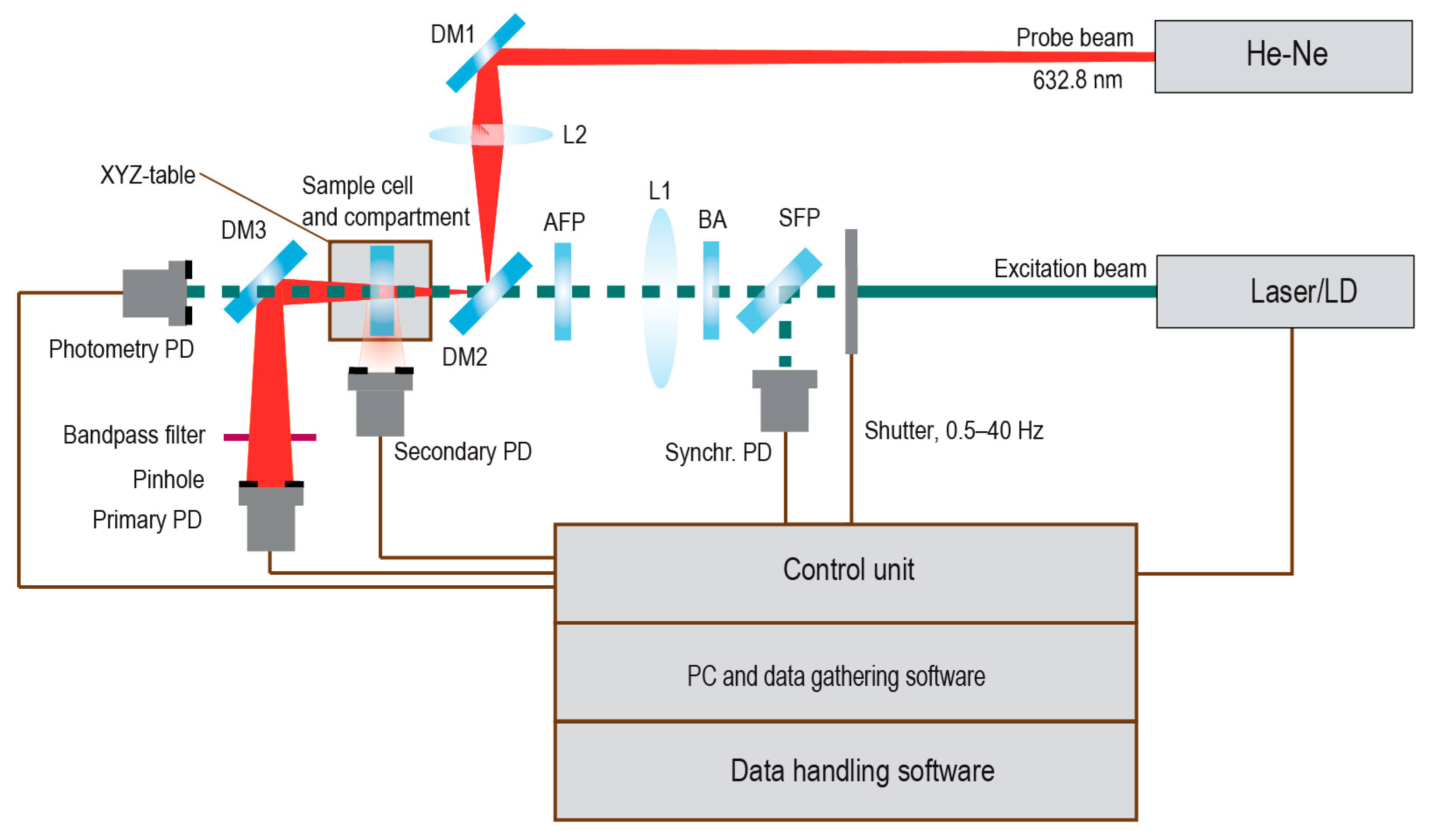
2.1. Thermal-Lens Spectrometer Setups
2.2. Auxiliary Measurements
2.3. Thermal-Lens Data Treatment
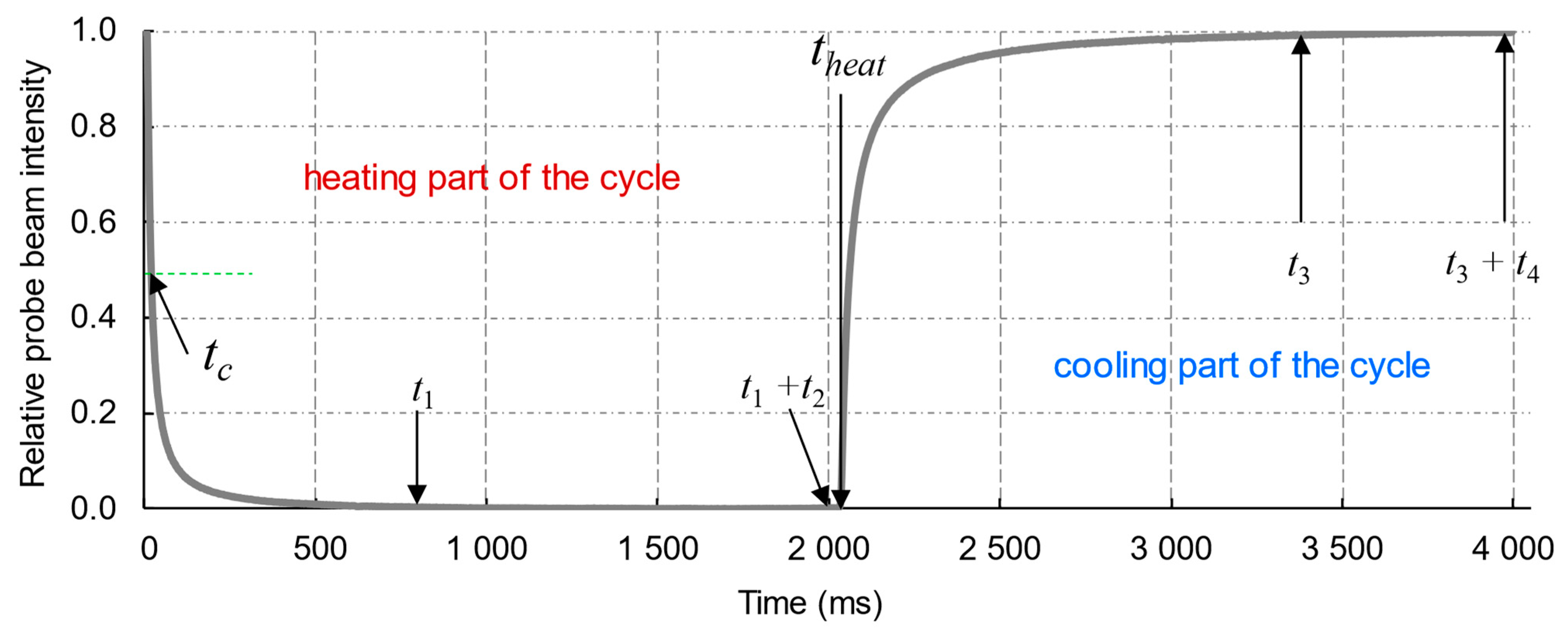
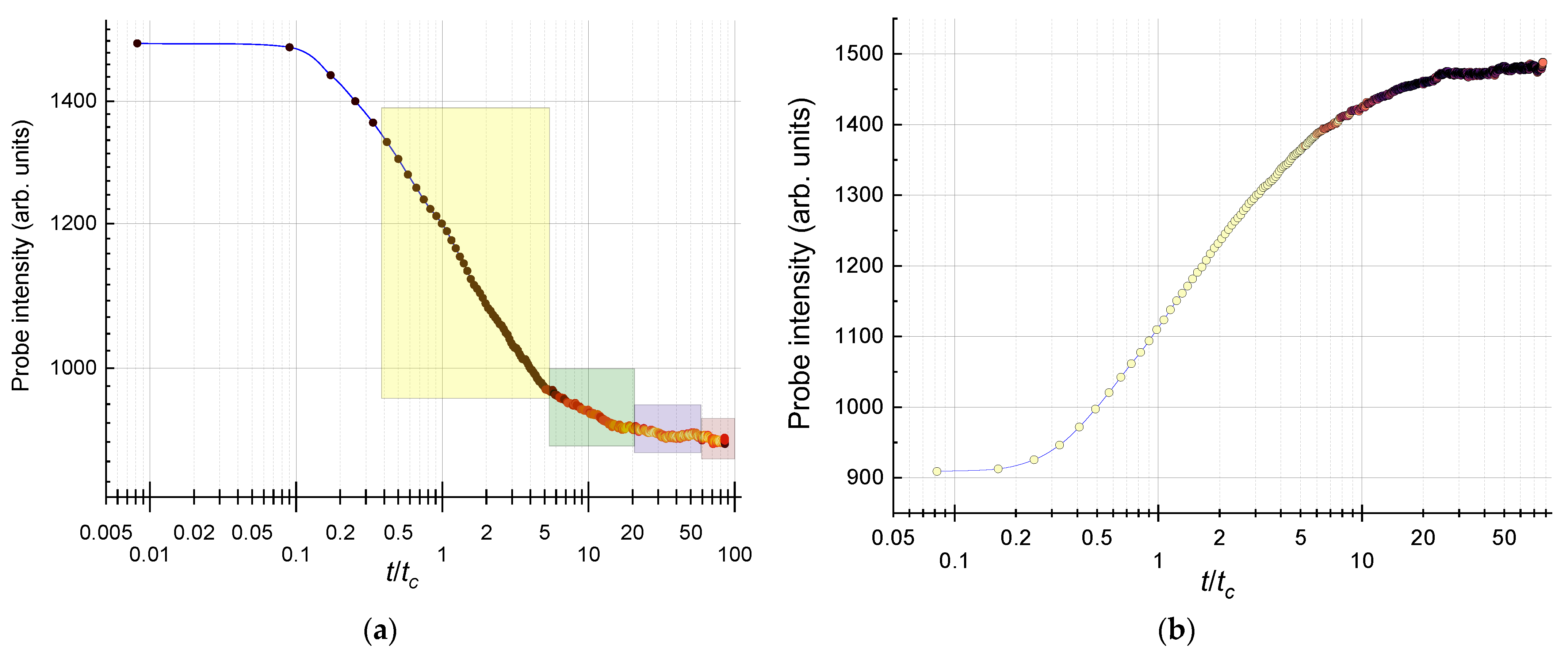
2.3.1. Transient Thermal-Lens Measurements
2.3.2. Steady-State Measurements
2.3.3. Parameters of Thermal-Lens Measurements
2.4. Precision Parameters
2.4.1. Repeatability
2.4.2. Replicability
2.4.3. Reproducibility
2.5. Performance Parameters
2.6. Reagents and Chemicals
2.7. Procedures
3. Results
3.1. Selection of Samples
3.2. Thermal-Lens Setups
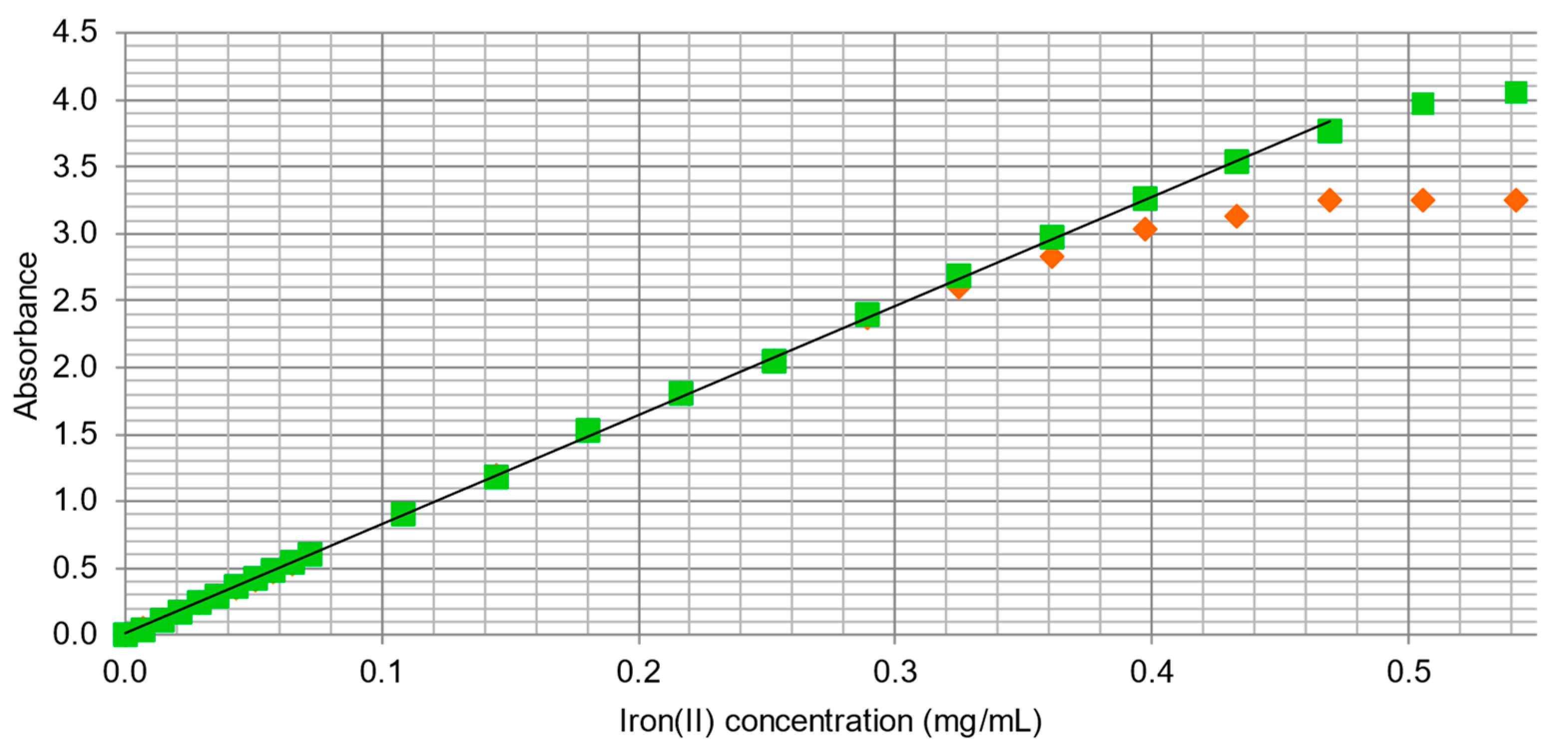
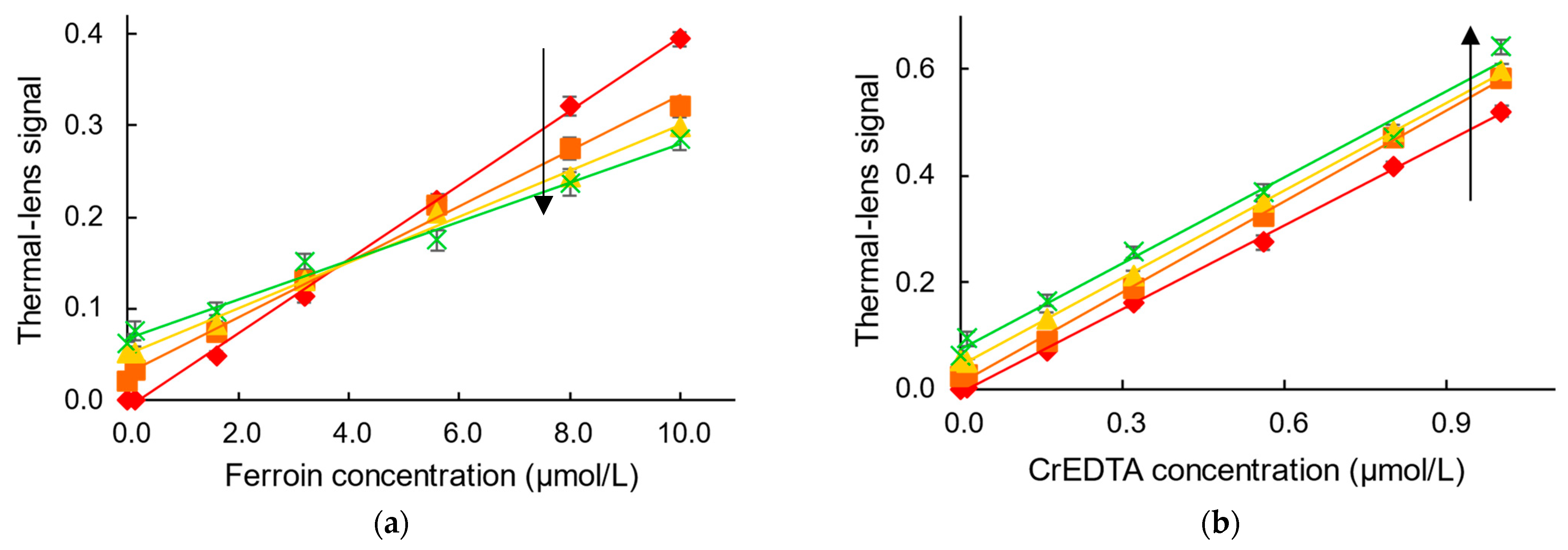
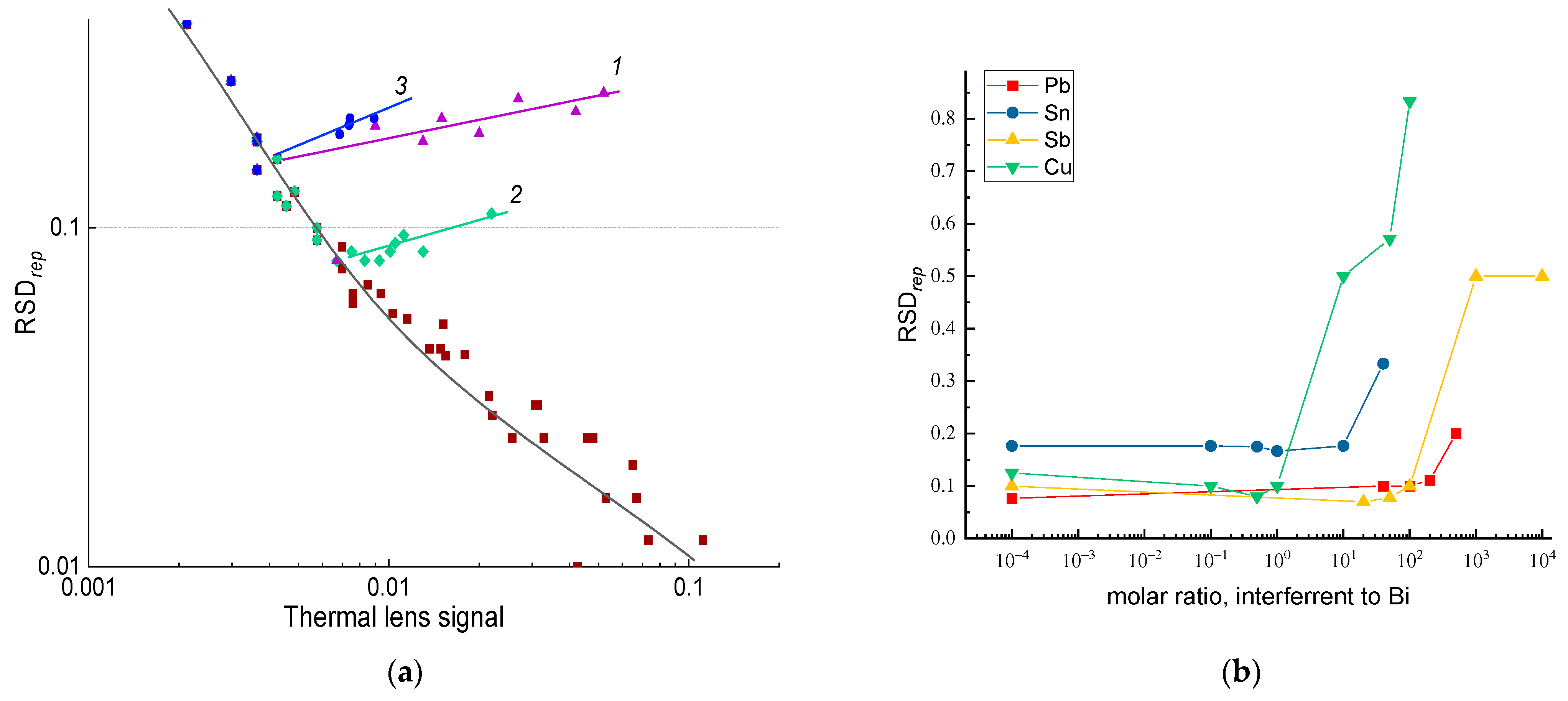
3.3. Accuracy and Precision
3.4. Steady-State Thermal-Lens Measurements
3.4.1. Hemoglobin
3.4.2. Myoglobin
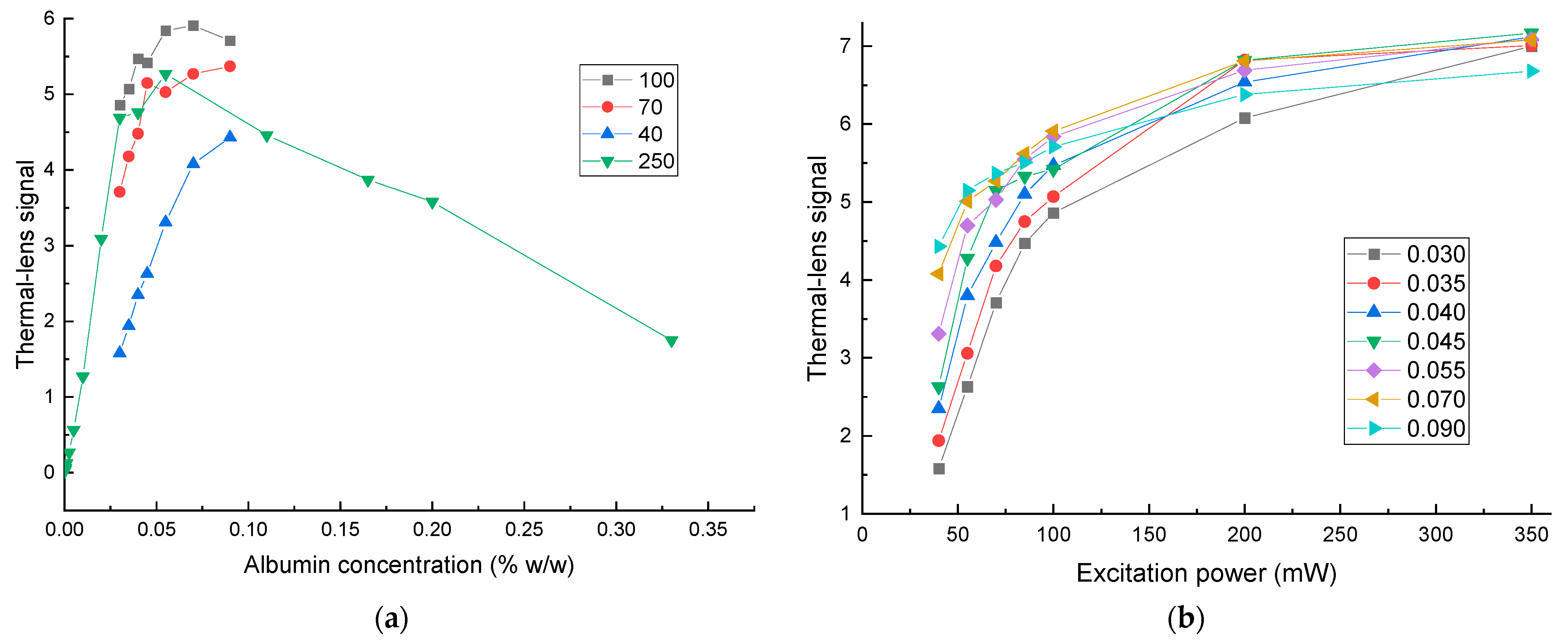
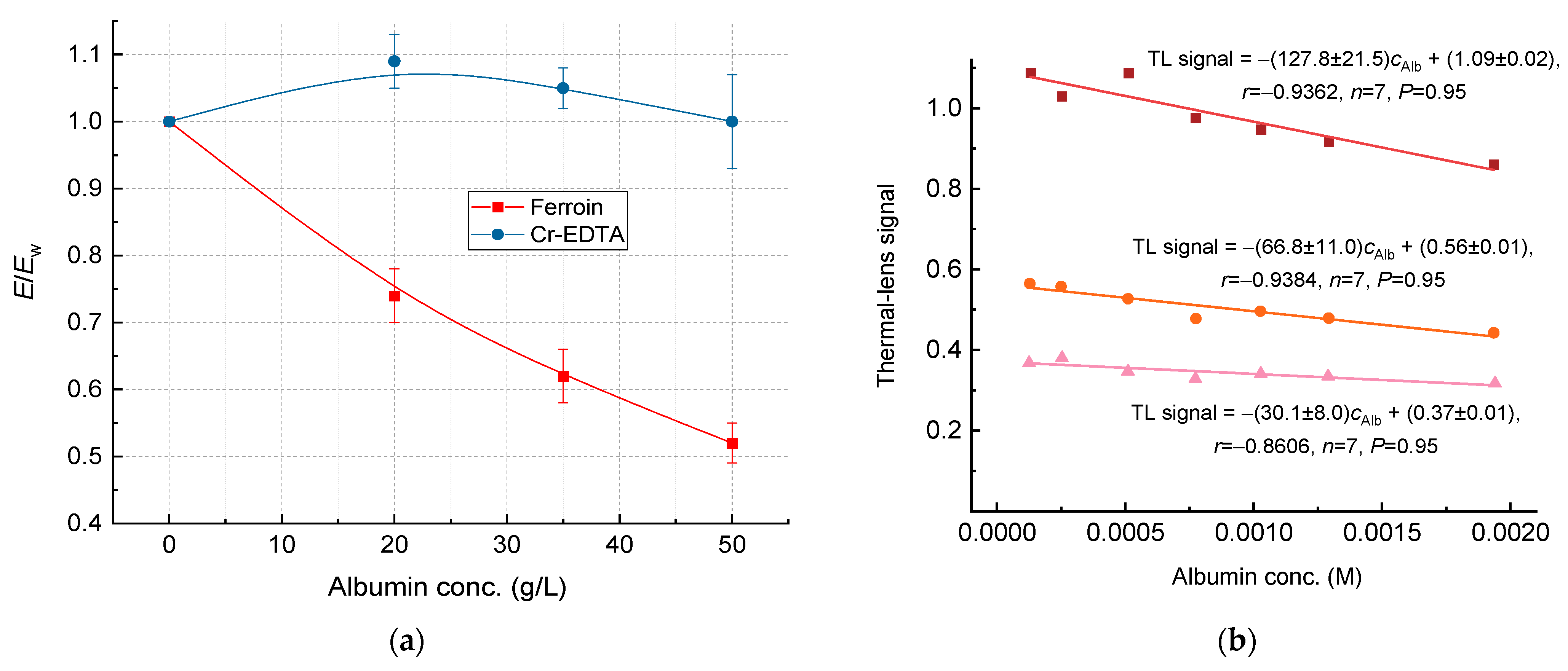
3.4.3. Bovine Serum Albumin
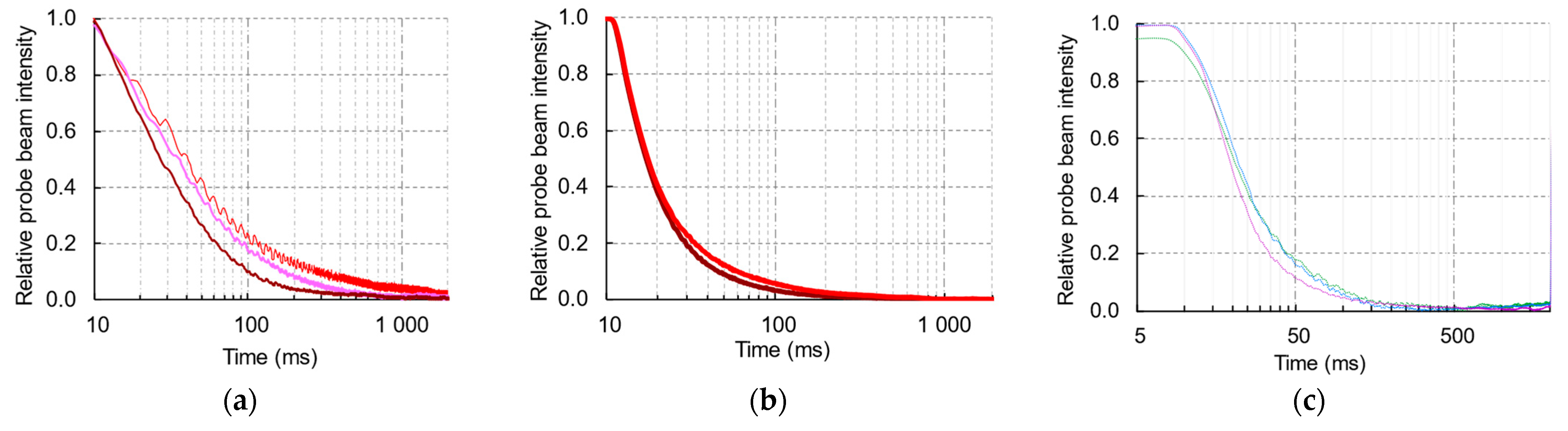
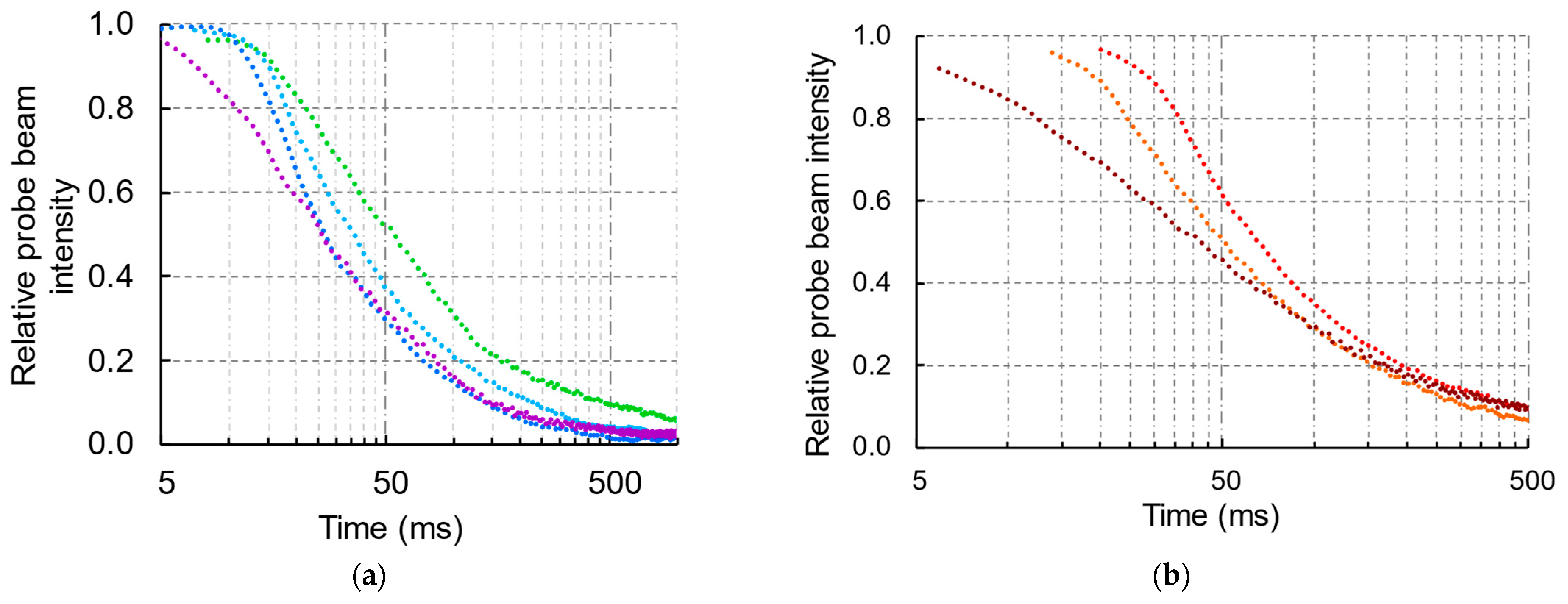
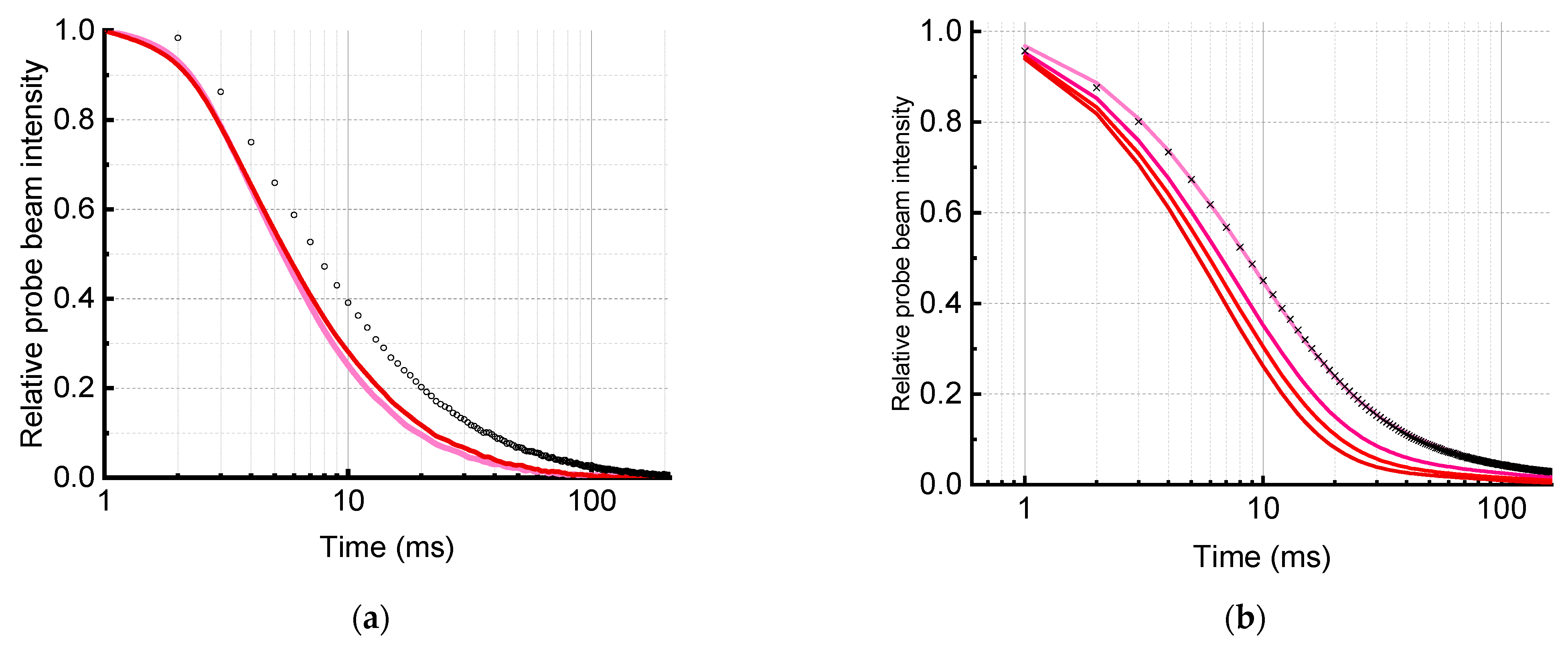
3.5. Transient Thermal-Lens Measurements
4. Discussion
4.1. Back-Synchronized Detection Modality
4.2. Transient and Steady-State Measurements
4.3. Measurement Conditions
4.3.1. Reproducibility and Replicability
4.3.2. Repeatability
4.4. Hemoglobin and Myoglobin
4.5. Bovine Serum Albumin
4.6. Comparison with Engineered Nanoparticles
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Photometry (Transmission) Modality of the Thermal-Lens Setup
| Wavelength, λ, nm | 532.0 | 514.5 | 501.7 | 496.5 | 488 |
| Radiation power p, mW | 150–170 | 250–300 | 70–80 | 150–160 | 450–550 |
| Wavelength, λ, nm | 476.5 | 472.7 | 465.8 | 457.9 | 454.5 |
| Radiation power p, mW | 160–180 | 35–40 | 23–27 | 55–60 | 12–15 |
Appendix B. Modeling of Multipoint Secondary Heating
Appendix C. Preliminary Optical Measurements of True Solutions
References
- Dy, E.; Gu, C.; Shen, J.; Qu, W.; Xie, Z.; Wang, X.; Baesso, M.L.; Astrath, N.G.C. Sensitivity enhancement of thermal lens spectrometry. J. Appl. Phys. 2022, 131, 063102. [Google Scholar] [CrossRef]
- Bialkowski, S.E.; Astrath, N.G.C.; Proskurnin, M.A. Photothermal Spectroscopy Methods; Wiley: Hoboken, NJ, USA, 2019; p. 512. [Google Scholar]
- Mawatari, K.; Ohashi, T.; Ebata, T.; Tokeshi, M.; Kitamori, T. Thermal lens detection device. Lab Chip 2011, 11, 2990–2993. [Google Scholar] [CrossRef] [PubMed]
- Proskurnin, M.A.; Khabibullin, V.R.; Usoltseva, L.O.; Vyrko, E.A.; Mikheev, I.V.; Volkov, D.S. Photothermal and optoacoustic spectroscopy: State of the art and prospects. Phys.-Uspekhi 2022, 65, 270–312. [Google Scholar] [CrossRef]
- Liu, M. Influence of thermal conductivity on photothermal lens spectroscopy. Thermochim. Acta 2019, 672, 126–132. [Google Scholar] [CrossRef]
- Dada, O.O.; Feist, P.E.; Dovichi, N.J. Thermal diffusivity imaging with the thermal lens microscope. Appl. Opt. 2011, 50, 6336–6342. [Google Scholar] [CrossRef] [PubMed]
- Constantino, R.; Lenzi, G.G.; Franco, M.G.; Lenzi, E.K.; Bento, A.C.; Astrath, N.G.C.; Malacarne, L.C.; Baesso, M.L. Thermal Lens Temperature Scanning technique for evaluation of oxidative stability and time of transesterification during biodiesel synthesis. Fuel 2017, 202, 78–84. [Google Scholar] [CrossRef]
- Yamaoka, S.; Kataoka, Y.; Kazama, Y.; Fujii, Y.; Hibara, A. Efficient thermal lens nanoparticle detection in a flow-focusing microfluidic device. Sens. Actuat. B 2016, 228, 581–586. [Google Scholar] [CrossRef]
- Martelanc, M.; Ziberna, L.; Passamonti, S.; Franko, M. Application of high-performance liquid chromatography combined with ultra-sensitive thermal lens spectrometric detection for simultaneous biliverdin and bilirubin assessment at trace levels in human serum. Talanta 2016, 154, 92–98. [Google Scholar] [CrossRef] [PubMed]
- Franko, M.; Liu, M.; Boskin, A.; Delneri, A.; Proskurnin, M.A. Fast Screening Techniques for Neurotoxigenic Substances and Other Toxicants and Pollutants Based on Thermal Lensing and Microfluidic Chips. Anal. Sci. 2016, 32, 23–30. [Google Scholar] [CrossRef]
- Liu, M.; Franko, M. Progress in thermal lens spectrometry and its applications in microscale analytical devices. Crit. Rev. Anal. Chem. 2014, 44, 328–353. [Google Scholar] [CrossRef]
- Cabrera, H.; Goljat, L.; Korte, D.; Marin, E.; Franko, M. A multi-thermal-lens approach to evaluation of multi-pass probe beam configuration in thermal lens spectrometry. Anal. Chim. Acta 2020, 1100, 182–190. [Google Scholar] [CrossRef] [PubMed]
- Fujii, N.; Harata, A. Development of Reflection Objective-Employed Collinear Mode-mismatched Thermal Lens Microscope. Jpn. J. Appl. Phys. 2011, 50, 07HC05. [Google Scholar] [CrossRef]
- Proskurnin, M.A.; Volkov, D.S.; Gor’kova, T.A.; Bendrysheva, S.N.; Smirnova, A.P.; Nedosekin, D.A. Advances in thermal lens spectrometry. J. Anal. Chem. 2015, 70, 249–276. [Google Scholar] [CrossRef]
- Abelha, T.F.; Calvo-Castro, J.; Lima, S.M.; Silva, J.R.; da Cunha Andrade, L.H.; de Mello, J.C.; Dreiss, C.A.; Green, M.; Dailey, L.A. Thermal Lens Spectrometry Reveals Thermo-Optical Property Tuning of Conjugated Polymer Nanoparticles Prepared by Microfluidics. ACS Appl. Polym. Mater. 2022, 4, 6219–6228. [Google Scholar] [CrossRef]
- Liu, M.Q.; Franko, M. Thermal Lens Spectrometry: Still a Technique on the Horizon? Int. J. Thermophys. 2016, 37, 1–16. [Google Scholar] [CrossRef]
- Liu, M.; Korte, D.; Franko, M. Theoretical description of thermal lens spectrometry in micro space. J. Appl. Phys. 2012, 111, 033109. [Google Scholar] [CrossRef]
- Liu, M.; Franko, M. Theoretical Analysis for Sensitivity Enhancement in Broad-band Thermal Lens Microscope. Adv. Mater. Res. 2012, 503, 1480–1483. [Google Scholar] [CrossRef]
- Fischer, M.; Georges, J. Sources of errors in the use of calorimetric references for photothermal spectroscopic methods. Anal. Chim. Acta 1996, 334, 337–344. [Google Scholar] [CrossRef]
- Marcano, A.O.; Delima, F.; Markushin, Y.; Melikechi, N. Determination of linear and nonlinear absorption of metallic colloids using photothermal lens spectrometry. J. Opt. Soc. Am. B 2011, 28, 281–287. [Google Scholar] [CrossRef]
- Nedosekin, D.A.; Galanzha, E.I.; Dervishi, E.; Biris, A.S.; Zharov, V.P. Super-Resolution Nonlinear Photothermal Microscopy. Small 2014, 10, 135–142. [Google Scholar] [CrossRef]
- Nedosekin, D.A.; Foster, S.; Nima, Z.A.; Biris, A.S.; Galanzha, E.I.; Zharov, V.P. Photothermal confocal multicolor microscopy of nanoparticles and nanodrugs in live cells. Drug Metab. Rev. 2015, 47, 346–355. [Google Scholar] [CrossRef]
- Zong, H.; Yurdakul, C.; Bai, Y.; Zhang, M.; Ünlü, M.S.; Cheng, J.-X. Background-Suppressed High-Throughput Mid-Infrared Photothermal Microscopy via Pupil Engineering. ACS Photonics 2021, 8, 3323–3336. [Google Scholar] [CrossRef] [PubMed]
- Adhikari, S.; Spaeth, P.; Kar, A.; Baaske, M.D.; Khatua, S.; Orrit, M. Photothermal Microscopy: Imaging the Optical Absorption of Single Nanoparticles and Single Molecules. ACS Nano 2020, 14, 16414–16445. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Z.-C.; Wang, H.; Johns, P.; Hartland, G.V.; Schultz, Z.D. Photothermal Microscopy of Coupled Nanostructures and the Impact of Nanoscale Heating in Surface-Enhanced Raman Spectroscopy. J. Phys. Chem. C 2017, 121, 11623–11631. [Google Scholar] [CrossRef]
- Georges, J. Advantages and limitations of thermal lens spectrometry over conventional spectrophotometry for absorbance measurements. Talanta 1999, 48, 501–509. [Google Scholar] [CrossRef] [PubMed]
- Marcano, A.; Alvarado, S.; Meng, J.; Caballero, D.; Moares, E.M.; Edziah, R. White Light Photothermal Lens Spectrophotometer for the Determination of Absorption in Scattering Samples. Appl. Spectrosc. 2014, 68, 680–685. [Google Scholar] [CrossRef]
- Georges, J. Matrix effects in thermal lens spectrometry: Influence of salts, surfactants, polymers and solvent mixtures. Spectrochim. Acta. A Mol. Biomol. Spectrosc. 2008, 69, 1063–1072. [Google Scholar] [CrossRef]
- Luna-Sánchez, J.L.; Jiménez-Pérez, J.L.; Carbajal-Valdez, R.; Lopez-Gamboa, G.; Pérez-González, M.; Correa-Pacheco, Z.N. Green synthesis of silver nanoparticles using Jalapeño Chili extract and thermal lens study of acrylic resin nanocomposites. Thermochim. Acta 2019, 678, 178314. [Google Scholar] [CrossRef]
- Deus, W.B.; Ventura, M.; Silva, J.R.; Andrade, L.H.C.; Catunda, T.; Lima, S.M. Monitoring of the ester production by near-near infrared thermal lens spectroscopy. Fuel 2019, 253, 1090–1096. [Google Scholar] [CrossRef]
- Ventura, M.; Deus, W.B.; Silva, J.R.; Andrade, L.H.C.; Catunda, T.; Lima, S.M. Determination of the biodiesel content in diesel/biodiesel blends by using the near-near-infrared thermal lens spectroscopy. Fuel 2018, 212, 309–314. [Google Scholar] [CrossRef]
- Cedeno, E.; Cabrera, H.; Delgadillo-Lopez, A.E.; Delgado-Vasallo, O.; Mansanares, A.M.; Calderon, A.; Marin, E. High sensitivity thermal lens microscopy: Cr-VI trace detection in water. Talanta 2017, 170, 260–265. [Google Scholar] [CrossRef] [PubMed]
- Savi, E.L.; Malacarne, L.C.; Baesso, M.L.; Pintro, P.T.M.; Croge, C.; Shen, J.; Astrath, N.G.C. Investigation into photostability of soybean oils by thermal lens spectroscopy. Spectrochim. Acta. A Mol. Biomol. Spectrosc. 2015, 145, 125–129. [Google Scholar] [CrossRef] [PubMed]
- Han, Q.; Huo, Y.; Yang, N.; Yang, X.; Hao, T. Determination of Cobalt in Water by Thermal Lens Spectrometry with Cloud Point Extraction. Anal. Lett. 2015, 48, 2096–2106. [Google Scholar] [CrossRef]
- Cassano, C.L.; Mawatari, K.; Kitamori, T.; Fan, Z.H. Thermal lens microscopy as a detector in microdevices. Electrophoresis 2014, 35, 2279–2291. [Google Scholar] [CrossRef]
- Ventura, M.; Simionatto, E.; Andrade, L.H.C.; Simionatto, E.L.; Riva, D.; Lima, S.M. The use of thermal lens spectroscopy to assess oil–biodiesel blends. Fuel 2013, 103, 506–511. [Google Scholar] [CrossRef]
- Saavedra, R.; Soto, C.; Gómez, R.; Muñoz, A. Determination of lead(II) by thermal lens spectroscopy (TLS) using 2-(2′-thiazolylazo)-p-cresol (TAC) as chromophore reagent. Microchem. J. 2013, 110, 308–313. [Google Scholar] [CrossRef]
- Ventura, M.; Simionatto, E.; Andrade, L.H.; Lima, S.M. Thermal lens spectroscopy for the differentiation of biodiesel-diesel blends. Rev. Sci. Instrum. 2012, 83, 043902. [Google Scholar] [CrossRef]
- Zharov, V.P.; Galanzha, E.I.; Tuchin, V.V. Integrated photothermal flow cytometry in vivo. J. Biomed. Opt. 2005, 10, 051502. [Google Scholar] [CrossRef]
- Zharov, V.P.; Galanzha, E.I.; Tuchin, V.V. In vivo photothermal flow cytometry: Imaging and detection of individual cells in blood and lymph flow. J. Cell. Biochem. 2006, 97, 916–932. [Google Scholar] [CrossRef]
- Nedosekin, D.A.; Galanzha, E.I.; Ayyadevara, S.; Shmookler Reis, R.J.; Zharov, V.P. Photothermal confocal spectromicroscopy of multiple cellular chromophores and fluorophores. Biophys. J. 2012, 102, 672–681. [Google Scholar] [CrossRef]
- Hibara, A.; Fukuyama, M.; Chung, M.; Priest, C.; Proskurnin, M.A. Interfacial Phenomena and Fluid Control in Micro/Nanofluidics. Anal. Sci. 2016, 32, 11–21. [Google Scholar] [CrossRef]
- Yamamoto, T.; Kazoe, Y.; Mawatari, K.; Kitamori, T. Micro and Nano Chemical Systems. J. Synth. Org. Chem. Jpn. 2011, 69, 526–533. [Google Scholar] [CrossRef]
- Ryasnyanskiy, A.I.; Palpant, B.; Debrus, S.; Pal, U.; Stepanov, A.L. Nonlinear Optical Properties of Gold Nanoparticles Dispersed in Different Optically Transparent Matrices. Phys. Sol. State 2009, 51, 55–60. [Google Scholar] [CrossRef]
- Usoltseva, L.O.; Volkov, D.S.; Nedosekin, D.A.; Korobov, M.V.; Proskurnin, M.A.; Zharov, V.P. Absorption spectra of nanodiamond aqueous dispersions by optical absorption and optoacoustic spectroscopies. Photoacoustics 2018, 12, 55–66. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.; Barrett, K.E.; Barman, S.M.; Brooks, H.L. Ganong’s Review of Medical Physiology, 26th ed.; McGraw-Hill Education: New York, NY, USA, 2019. [Google Scholar]
- Harada, M.; Shibata, M.; Kitamori, T.; Sawada, T. Sub-Attomole Molecule Detection in a Single Biological Cell in-vitro by Thermal Lens Microscopy. Anal. Sci. 1999, 15, 647–650. [Google Scholar] [CrossRef]
- Lenart, V.; Astrath, N.; Turchiello, R.; Goya, G.; Gómez, S. Thermal diffusivity of ferrofluids as a function of particle size determined using the mode-mismatched dual-beam thermal lens technique. J. Appl. Phys. 2018, 123, 085107. [Google Scholar] [CrossRef]
- Nideep, T.K.; Ramya, M.; Nampoori, V.P.N.; Kailasnath, M. The size dependent thermal diffusivity of water soluble CdTe quantum dots using dual beam thermal lens spectroscopy. Phys. E Low-Dimens. Syst. Nanostruct. 2020, 116, 113724. [Google Scholar] [CrossRef]
- Cabrera, H.; Matroodi, F.; Cabrera-Díaz, H.D.; Ramírez-Miquet, E.E. Frequency-resolved photothermal lens: An alternative approach for thermal diffusivity measurements in weak absorbing thin samples. Int. J. Heat Mass Transf. 2020, 158, 120036. [Google Scholar] [CrossRef]
- Lopes, C.; Lenart, V.; Turchiello, R.; Gómez, S. Determination of the thermal diffusivity of plasmonic nanofluids containing PVP-coated Ag nanoparticles using mode-mismatched dual-beam thermal lens technique. Adv. Condens. Matter Phys. 2018, 2018, 3052793. [Google Scholar] [CrossRef]
- Zamiri, R.; Azmi, B.; Husin, M.S.; Zamiri, G.; Ahangar, H.; Rizwan, Z. Thermal diffusivity measurement of copper nanofluid using pulsed laser thermal lens technique. J. Eur. Opt. Soc. 2012, 7, 12022. [Google Scholar] [CrossRef]
- Zamiri, R.; Azmi, B.Z.; Shahriari, E.; Naghavi, K.; Saion, E.; Rizwan, Z.; Husin, M.S. Thermal diffusivity measurement of silver nanofluid by thermal lens technique. J. Laser Appl. 2011, 23, 042002. [Google Scholar] [CrossRef]
- Joseph, S.A.; Hari, M.; Mathew, S.; Sharma, G.; Soumya; Hadiya, V.M.; Radhakrishnan, P.; Nampoori, V.P.N. Thermal diffusivity of rhodamine 6G incorporated in silver nanofluid measured using mode-matched thermal lens technique. Opt. Commun. 2010, 283, 313–317. [Google Scholar] [CrossRef]
- Benitez, M.; Marcano, A.; Melikechi, N. Thermal diffusivity measurement using the mode-mismatched photothermal lens method. Opt. Eng. 2009, 48, 043604. [Google Scholar] [CrossRef]
- Franko, M.; Goljat, L.; Liu, M.; Budasheva, H.; Zorz Furlan, M.; Korte, D. Recent Progress and Applications of Thermal Lens Spectrometry and Photothermal Beam Deflection Techniques in Environmental Sensing. Sensors 2023, 23, 472. [Google Scholar] [CrossRef] [PubMed]
- Jimenez Perez, J.L.; Rangel Vargas, E.; Gutierrez Fuentes, R.; Cruz-Orea, A.; Bautista de Leon, H. Thermal diffusivity study of cheese fats by thermal lens detection. Eur. Phys. J-Spec. Top. 2008, 153, 511–513. [Google Scholar] [CrossRef]
- Jiménez Pérez, J.L.; Gutierrez Fuentes, R.; Sanchez Ramirez, J.F.; Cruz-Orea, A. Study of gold nanoparticles effect on thermal diffusivity of nanofluids based on various solvents by using thermal lens spectroscopy. Eur. Phys. J-Spec. Top. 2008, 153, 159–161. [Google Scholar] [CrossRef]
- Yang, J.; Wang, Y.; Zhang, X.; Li, C.; Jin, X.; Shui, M.; Song, Y. Characterization of the transient thermal-lens effect using top-hat beam Z-scan. J. Phys. B 2009, 42, 225404. [Google Scholar] [CrossRef]
- Bernal-Alvarado, J.; Sosa, M.; Mayén-Mondragón, R.; Yánez-Limón, J.M.; Flores-Farías, R.; Hernández-Cabrera, F.; Palomares, P. Mismatched Mode Thermal Lens for Assessing Thermal Diffusivity of Serum and Plasma from Human Blood. Instrum. Sci. Technol. 2006, 34, 99–105. [Google Scholar] [CrossRef]
- Bernini, U.; Bernini, R.; Maddalena, P.; Massera, E.; Rucco, P. Determination of thermal diffusivity of suspended porous silicon films by thermal lens technique. Appl. Phys. A 2005, 81, 399–404. [Google Scholar] [CrossRef]
- Comeau, D.; Hache, A.; Melikechi, N. Reflective thermal lensing and optical measurement of thermal diffusivity in liquids. Appl. Phys. Lett. 2003, 83, 246–248. [Google Scholar] [CrossRef]
- Bernal-Alvarado, J.; Mansanares, A.M.; da Silva, E.C.; Moreira, S.G.C. Thermal diffusivity measurements in vegetable oils with thermal lens technique. Rev. Sci. Instrum. 2003, 74, 697–699. [Google Scholar] [CrossRef]
- Bernal-Alvarado, J.; Pereira, R.D.; Mansanares, A.M.; da Silva, E.C. Thermal diffusivity measurements for two media systems with thermal lens technique in the two lasers mismatched mode. Anal. Sci. 2001, 17, S178–S180. [Google Scholar]
- Wetzler, D.E.; Aramendia, P.F.; Japas, M.L.; Fernandez-Prini, R. Thermal diffusivity in supercritical fluids measured by thermal lensing. Int. J. Thermophys. 1998, 19, 27–42. [Google Scholar] [CrossRef]
- Bindhu, C.V.; Harilal, S.S.; Nampoori, V.P.N.; Vallabhan, C.P.G. Thermal diffusivity measurements in organic liquids using transient thermal lens calorimetry. Opt. Eng. 1998, 37, 2791–2794. [Google Scholar] [CrossRef]
- Planchon, T.A.; Amir, W.; Childress, C.; Squier, J.A.; Durfee, C.G. Measurement of pump-induced transient lensing in a cryogenically-cooled high average power Ti:sapphire amplifier. Opt. Express 2008, 16, 18557–18564. [Google Scholar] [CrossRef]
- Terazima, M. Transient lens spectroscopy in a fast timescale. Isr. J. Chem. 1998, 38, 143–157. [Google Scholar] [CrossRef]
- Oliveira, G.M.; Zanuto, V.S.; Flizikowski, G.A.S.; Kimura, N.M.; Sampaio, A.R.; Novatski, A.; Baesso, M.L.; Malacarne, L.C.; Astrath, N.G.C. Soret effect in lyotropic liquid crystal in the isotropic phase revealed by time-resolved thermal lens. J. Mol. Liq. 2020, 312, 113381. [Google Scholar] [CrossRef]
- Astrath, N.G.C.; Rohling, J.H.; Medina, A.N.; Bento, A.C.; Baesso, M.L.; Jacinto, C.; Catunda, T.; Lima, S.M.; Gandra, F.G.; Bell, M.J.V.; et al. Time-resolved thermal lens measurements of the thermo-optical properties of glasses at low temperature down to 20 K. Phys. Rev. B 2005, 71. [Google Scholar] [CrossRef]
- Chang, C.-K.; Leu, C.-C.; Wei, T.-H.; Yang, S.; Huang, T.-H.; Song, Y. Study of transient thermal lensing effect in C(60)-toluene solution. Chem. Phys. Lett. 2010, 484, 225–230. [Google Scholar] [CrossRef]
- Ramírez, J.S.; Pérez, J.J.; Valdez, R.C.; Orea, A.C.; Fuentes, R.G.; Herrera-Perez, J.L. Thermal diffusivity measurements in fluids containing metallic nanoparticles using transient thermal lens. Int. J. Thermophys. 2006, 27, 1181–1188. [Google Scholar] [CrossRef]
- Carbajal Valdez, R.; Jimenez Perez, J.L.; Cruz-Orea, A.; San Martin-Martinez, E. Thermal diffusivity measurements in edible oils using transient thermal lens. Int. J. Thermophys. 2006, 27, 1890–1897. [Google Scholar] [CrossRef]
- Bindhu, C.V.; Harilal, S.S.; Nampoori, V.P.N.; Vallabhan, C.P.G. Solvent effect on absolute fluorescence quantum yield of rhodamine 6G determined using transient thermal lens technique. Mod. Phys. Lett. B 1999, 13, 563–576. [Google Scholar] [CrossRef]
- Bindhu, C.V.; Harilal, S.S.; Nampoori, V.P.N.; Vallabhan, C.P.G. Thermal diffusivity measurements in sea water using transient thermal lens calorimetry. Curr. Sci. 1998, 74, 764–769. [Google Scholar]
- Jiménez Pérez, J.L.; Sánchez Ramírez, J.F.; Gutiérrez Fuentes, R.; Cruz-Orea, A.; Herrera Pérez, J.L. Enhanced of the R6G thermal diffusivity on aggregated small gold particles. Braz. J. Phys. 2006, 36, 1025–1028. [Google Scholar] [CrossRef]
- Jimenez-Perez, J.L.; Fuentes, R.G.; Alvarado, E.M.; Ramon-Gallegos, E.; Cruz-Orea, A.; Tanori-Cordova, J.; Mendoza-Alvarez, J.G. Enhancement of the thermal transport in a culture medium with Au nanoparticles. Appl. Surf. Sci. 2008, 255, 701–702. [Google Scholar] [CrossRef]
- Jiménez-Pérez, J.; López-Gamboa, G.; Cruz-Orea, A.; Correa-Pacheco, Z. Thermal parameters study of biodiesel containing Au nanoparticles using photothermal techniques. Rev. Mex. Ing. Química 2015, 14, 481–487. [Google Scholar]
- Kumar, B.R.; Basheer, N.S.; Jacob, S.; Kurian, A.; George, S.D. Thermal-lens probing of the enhanced thermal diffusivity of gold nanofluid-ethylene glycol mixture. J. Therm. Anal. Calorim. 2015, 119, 453–460. [Google Scholar] [CrossRef]
- John, J.; Thomas, L.; Rajesh Kumar, B.; Kurian, A.; George, S.D. Shape dependent heat transport through green synthesized gold nanofluids. J. Phys. D Appl. Phys. 2015, 48, 335301. [Google Scholar] [CrossRef]
- Jimenez-Perez, J.L.; Sanchez-Ramirez, J.F.; Cornejo-Monroy, D.; Gutierrez-Fuentes, R.; Rojas, J.P.; Cruz-Orea, A.; Algatti, M.; Jacinto, C. Photothermal Study of Two Different Nanofluids Containing SiO2 and TiO2 Semiconductor Nanoparticles. Int. J. Thermophys. 2012, 33, 69–79. [Google Scholar] [CrossRef]
- Shahriari, E.; Yunus, W.M.M.; Zamiri, R. The effect of nanoparticle size on thermal diffusivity of gold nano-fluid measured using thermal lens technique. J. Eur. Opt. Soc. Rapid Publ. 2013, 8, 13026. [Google Scholar] [CrossRef]
- Nedosekin, D.A.; Shashkov, E.V.; Galanzha, E.I.; Zharov, V.P. Confocal Linear and Nonlinear Photothermal Microscopy of Intrinsic and Exogenous Probes in Live Cells. Biophys. J. 2011, 100, 316a. [Google Scholar] [CrossRef]
- Proskurnin, M.A.; Zhidkova, T.V.; Volkov, D.S.; Sarimollaoglu, M.; Galanzha, E.I.; Mock, D.; Nedosekin, D.A.; Zharov, V.P. In vivo multispectral photoacoustic and photothermal flow cytometry with multicolor dyes: A potential for real-time assessment of circulation, dye-cell interaction, and blood volume. Cytom. A 2011, 79, 834–847. [Google Scholar] [CrossRef] [PubMed]
- Tuchin, V.V.; Tarnok, A.; Zharov, V.P. In vivo flow cytometry: A horizon of opportunities. Cytom. A 2011, 79, 737–745. [Google Scholar] [CrossRef] [PubMed]
- Zharov, V.P. Ultrasharp nonlinear photothermal and photoacoustic resonances and holes beyond the spectral limit. Nat. Photonics 2011, 5, 110–116. [Google Scholar] [CrossRef] [PubMed]
- Shokoufi, N.; Abbasgholi Nejad Asbaghi, B.; Abbasi-Ahd, A. Microfluidic chip-photothermal lens microscopy for DNA hybridization assay using gold nanoparticles. Anal. Bioanal. Chem. 2019, 411, 6119–6128. [Google Scholar] [CrossRef] [PubMed]
- Radovanović, T.; Liu, M.; Likar, P.; Klemenc, M.; Franko, M. Microfluidic Flow Injection Analysis with Thermal Lens Microscopic Detection for Determination of NGAL. Int. J. Thermophys. 2015, 36, 932–939. [Google Scholar] [CrossRef]
- Liu, M.; Novak, U.; Plazl, I.; Franko, M. Optimization of a Thermal Lens Microscope for Detection in a Microfluidic Chip. Int. J. Thermophys. 2014, 35, 2011–2022. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, Y.; Chuang, C.-J.; Bivolarska, M.; See, C.W.; Somekh, M.G.; Pitter, M.C. Polarization modulation thermal lens microscopy for imaging the orientation of non-spherical nanoparticles. Opt. Express 2011, 19, 2643–2648. [Google Scholar] [CrossRef]
- Shimizu, H.; Mawatari, K.; Kitamori, T. Sensitive Determination of Concentration of Nonfluorescent Species in an Extended-Nano Channel by Differential Interference Contrast Thermal Lens Microscope. Anal. Chem. 2010, 82, 7479–7484. [Google Scholar] [CrossRef]
- Lu, S.; Min, W.; Chong, S.; Holtom, G.R.; Xie, X.S. Label-free imaging of heme proteins with two-photon excited photothermal lens microscopy. Appl. Phys. Lett. 2010, 96, 113701. [Google Scholar] [CrossRef]
- Proskurnin, M.A.; Kononets, M.Y. Modern analytical thermooptical spectroscopy. Uspekhi Khimii 2004, 73, 1235–1268. [Google Scholar] [CrossRef]
- Cabrera, H.; Akbar, J.; Korte, D.; Ramírez-Miquet, E.E.; Marín, E.; Niemela, J.; Ebrahimpour, Z.; Mannatunga, K.; Franko, M. Trace detection and photothermal spectral characterization by a tuneable thermal lens spectrometer with white-light excitation. Talanta 2018, 183, 158–163. [Google Scholar] [CrossRef] [PubMed]
- Nedosekin, D.A.; Proskurnin, M.A.; Kononets, M.Y. Model for continuous-wave laser-induced thermal lens spectrometry of optically transparent surface-absorbing solids. Appl. Opt. 2005, 44, 6296–6306. [Google Scholar] [CrossRef] [PubMed]
- Brusnichkin, A.V.; Nedosekin, D.A.; Proskurnin, M.A.; Zharov, V.P. Photothermal lens detection of gold nanoparticles: Theory and experiments. Appl. Spectrosc. 2007, 61, 1191–1201. [Google Scholar] [CrossRef]
- Proskurnin, M.A.; Ryndina, E.S.; Tsar’kov, D.S.; Shkinev, V.M.; Smirnova, A.; Hibara, A. Comparison of performance parameters of photothermal procedures in homogeneous and heterogeneous systems. Anal. Sci. 2011, 27, 381. [Google Scholar] [CrossRef]
- Smirnova, A.; Proskurnin, M.A.; Bendrysheva, S.N.; Nedosekin, D.A.; Hibara, A.; Kitamori, T. Thermooptical detection in microchips: From macro- to micro-scale with enhanced analytical parameters. Electrophoresis 2008, 29, 2741–2753. [Google Scholar] [CrossRef]
- Galimova, V.R.; Liu, M.; Franko, M.; Volkov, D.S.; Hibara, A.; Proskurnin, M.A. Hemichrome Determination by Thermal Lensing with Polyethylene Glycols for Signal Enhancement in Aqueous Solutions. Anal. Lett. 2018, 51, 1743–1762. [Google Scholar] [CrossRef]
- Ivshukov, D.A.; Mikheev, I.V.; Volkov, D.S.; Korotkov, A.S.; Proskurnin, M.A. Two-Laser Thermal Lens Spectrometry with Signal Back-Synchronization. J. Anal. Chem. 2018, 73, 407–426. [Google Scholar] [CrossRef]
- Tishchenko, K.; Muratova, M.; Volkov, D.; Filichkina, V.; Nedosekin, D.; Zharov, V.; Proskurnin, M. Multi-wavelength thermal-lens spectrometry for high-accuracy measurements of absorptivities and quantum yields of photodegradation of a hemoprotein–lipid complex. Arab. J. Chem 2017, 10, 781–791. [Google Scholar] [CrossRef]
- Usoltseva, L.O.; Korobov, M.V.; Proskurnin, M.A. Photothermal spectroscopy: A promising tool for nanofluids. J. Appl. Phys. 2020, 128, 190901. [Google Scholar] [CrossRef]
- Khabibullin, V.R.; Franko, M.; Proskurnin, M.A. Accuracy of Measurements of Thermophysical Parameters by Dual-Beam Thermal-Lens Spectrometry. Nanomaterials 2023, 13, 430. [Google Scholar] [CrossRef] [PubMed]
- Shen, J.; Lowe, R.D.; Snook, R.D. A model for cw laser induced mode-mismatched dual-beam thermal lens spectrometry. Chem. Phys. 1992, 165, 385–396. [Google Scholar] [CrossRef]
- Baesso, M.L.; Shen, J.; Snook, R.D. Time-resolved thermal lens measurement of thermal diffusivity of soda—Lime glass. Chem. Phys. Lett. 1992, 197, 255–258. [Google Scholar] [CrossRef]
- Proskurnin, M.A.; Usoltseva, L.O.; Volkov, D.S.; Nedosekin, D.A.; Korobov, M.V.; Zharov, V.P. Photothermal and Heat-Transfer Properties of Aqueous Detonation Nanodiamonds by Photothermal Microscopy and Transient Spectroscopy. J. Phys. Chem. C 2021, 125, 7808–7823. [Google Scholar] [CrossRef]
- Mikheev, I.V.; Usoltseva, L.O.; Ivshukov, D.A.; Volkov, D.S.; Korobov, M.V.; Proskurnin, M.A. Approach to the Assessment of Size-Dependent Thermal Properties of Disperse Solutions: Time-Resolved Photothermal Lensing of Aqueous Pristine Fullerenes C60and C70. J. Phys. Chem. C 2016, 120, 28270–28287. [Google Scholar] [CrossRef]
- Brusnichkin, A.V.; Nedosekin, D.A.; Galanzha, E.I.; Vladimirov, Y.A.; Shevtsova, E.F.; Proskurnin, M.A.; Zharov, V.P. Ultrasensitive label-free photothermal imaging, spectral identification, and quantification of cytochrome c in mitochondria, live cells, and solutions. J. Biophoton. 2010, 3, 791–806. [Google Scholar] [CrossRef]
- Doerffel, K. Statistik in der Analytischen Chemie; Deutscher verlag: Leipzig, Germany, 1994. [Google Scholar]
- Czichos, H. Springer Handbook of Metrology and Testing; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Proskurnin, M.A.; Chernysh, V.V.; Filichkina, V.A. Some Metrological Aspects of the Optimization of Thermal-Lens Procedures. J. Anal. Chem. 2004, 59, 818–827. [Google Scholar] [CrossRef]
- Drabkin, D.L.; Austin, J. HSpectrophotometric studies: II. Preparations from washed blood cells; nitric oxide hemoglobin and sulfhemoglobin. J. Biol. Chem. 1935, 112, 51–65. [Google Scholar] [CrossRef]
- Hopp, M.-T.; Schmalohr, B.F.; Kühl, T.; Detzel, M.S.; Wißbrock, A.; Imhof, D. Heme Determination and Quantification Methods and Their Suitability for Practical Applications and Everyday Use. Anal. Chem. 2020, 92, 9429–9440. [Google Scholar] [CrossRef]
- Eidelman, E.D.; Siklitsky, V.I.; Sharonova, L.V.; Yagovkina, M.A.; Vul, A.Y.; Takahashi, M.; Inakuma, M.; Ozawa, M.; Osawa, E. A stable suspension of single ultrananocrystalline diamond particles. Diam. Relat. Mater. 2005, 14, 1765–1769. [Google Scholar] [CrossRef]
- Aleksenskii, A.; Vul, A.Y.; Konyakhin, S.; Reich, K.; Sharonova, L.; Eidel’man, E. Optical properties of detonation nanodiamond hydrosols. Phys. Sol. State 2012, 54, 578–585. [Google Scholar] [CrossRef]
- Osipov, V.Y.; Baidakova, M.; Takai, K.; Enoki, T.; Vul, A. Magnetic Properties of Hydrogen-Terminated Surface Layer of Diamond Nanoparticles. Fuller. Nanotub. Carbon Nanostruct. 2006, 14, 565–572. [Google Scholar] [CrossRef]
- Li, N.; Yan, H.T. Comparison of spectrophotometry and thermal lens spectrometry for absorption measurements under conditions of high scattering backgrounds. Chin. J. Anal. Chem. 2002, 30, 1348–1351. [Google Scholar]
- Kang, H.U.; Kim, S.H.; Oh, J.M. Estimation of Thermal Conductivity of Nanofluid Using Experimental Effective Particle Volume. Exp. Heat Transf. 2006, 19, 181–191. [Google Scholar] [CrossRef]
- Usoltseva, L.O.; Volkov, D.S.; Karpushkin, E.A.; Korobov, M.V.; Proskurnin, M.A. Thermal Conductivity of Detonation Nanodiamond Hydrogels and Hydrosols by Direct Heat Flux Measurements. Gels 2021, 7, 248. [Google Scholar] [CrossRef]
- Hwang, Y.; Lee, J.; Lee, C.; Jung, Y.; Cheong, S.; Lee, C.; Ku, B.; Jang, S. Stability and thermal conductivity characteristics of nanofluids. Thermochim. Acta 2007, 455, 70–74. [Google Scholar] [CrossRef]
- Hwang, Y.; Park, H.; Lee, J.; Jung, W. Thermal conductivity and lubrication characteristics of nanofluids. Curr. Appl. Phys. 2006, 6, e67–e71. [Google Scholar] [CrossRef]
- Zhirkov, A.A.; Nikiforov, A.A.; Tsar’kov, D.S.; Volkov, D.S.; Proskurnin, M.A.; Zuev, B.K. Effect of electrolytes on the sensitivity of the thermal lens determination. J. Anal. Chem. 2012, 67, 290–296. [Google Scholar] [CrossRef]
- Kim, J.-W.; Galanzha, E.I.; Shashkov, E.V.; Moon, H.-M.; Zharov, V.P. Golden carbon nanotubes as multimodal photoacoustic and photothermal high-contrast molecular agents. Nat. Nanotechnol. 2009, 4, 688–694. [Google Scholar] [CrossRef]
- Shrivastava, H.Y.; Nair, B.U. Protein degradation by peroxide catalyzed by chromium (III): Role of coordinated ligand. Biochem Biophys. Res. Commun. 2000, 270, 749–754. [Google Scholar] [CrossRef]
- Mohebbifar, M.R. Study of the effect of temperature on thermophysical properties of ethyl myristate by dual-beam thermal lens technique. Optik 2021, 247, 168000. [Google Scholar] [CrossRef]
- Vijesh, K.R.; Sony, U.; Ramya, M.; Mathew, S.; Nampoori, V.P.N.; Thomas, S. Concentration dependent variation of thermal diffusivity in highly fluorescent carbon dots using dual beam thermal lens technique. Int. J. Therm. Sci. 2018, 126, 137–142. [Google Scholar] [CrossRef]
- Malacarne, L.C.; Astrath, N.G.C.; Pedreira, P.R.B.; Mendes, R.S.; Baesso, M.L.; Joshi, P.R.; Bialkowski, S.E. Analytical solution for mode-mismatched thermal lens spectroscopy with sample-fluid heat coupling. J. Appl. Phys. 2010, 107, 053104. [Google Scholar] [CrossRef]
- Marcano, A.; Cabrera, H.; Guerra, M.; Cruz, R.A.; Jacinto, C.; Catunda, T. Optimizing and calibrating a mode-mismatched thermal lens experiment for low absorption measurement. J. Opt. Soc. Am. B 2006, 23, 1408–1413. [Google Scholar] [CrossRef]
- Marcano, A.; Rodriguez, L.; Alvarado, Y. Mode-mismatched thermal lens experiment in the pulse regime. J. Opt. A-Pure Appl. Opt. 2003, 5, S256. [Google Scholar] [CrossRef]
- Marcano, A.; Loper, C.; Melikechi, N. Pump–probe mode-mismatched thermal-lens Z scan. J. Opt. Soc. Am. B 2002, 19, 119–124. [Google Scholar] [CrossRef]
- Liu, M.; Franko, M. Thermal lens spectrometry under excitation of a divergent pump beam. Appl. Phys. B 2014, 115, 269–277. [Google Scholar] [CrossRef]
- Vincelette, R.L.; Oliver, J.W.; Rockwell, B.A.; Thomas, R.J.; Welch, A.J. Confocal Imaging of Thermal Lensing Induced by Near-IR Laser Radiation in an Artificial Eye. IEEE J. Sel. Top. Quant. Electron. 2010, 16, 740–747. [Google Scholar] [CrossRef]
- Kitagawa, F.; Tsuneka, T.; Akimoto, Y.; Sueyoshi, K.; Uchiyama, K.; Hattori, A.; Otsuka, K. Toward million-fold sensitivity enhancement by sweeping in capillary electrophoresis combined with thermal lens microscopic detection using an interface chip. J. Chromatogr. A 2006, 1106, 36–42. [Google Scholar] [CrossRef]
- Kitamori, T.; Tokeshi, M.; Hibara, A.; Sato, K. Thermal lens microscopy and microchip chemistry. Anal. Chem. 2004, 76, 52A–60A. [Google Scholar] [CrossRef]
- Sato, K.; Egami, A.; Odake, T.; Tokeshi, M.; Aihara, M.; Kitamori, T. Monitoring of intercellular messengers released from neuron networks cultured in a microchip. J. Chromatogr. A 2006, 1111, 228–232. [Google Scholar] [CrossRef] [PubMed]
- Uchiyama, K.; Hibara, A.; Kimura, H.; Sawada, T.; Kitamori, T. Thermal lens microscope. Jpn. J. Appl. Phys. 2000, 39, 5316–5322. [Google Scholar] [CrossRef]
- Zaldivar Escola, F. Photothermal microscopy applied to the study of polymer composites. Polym. Test. 2020, 84, 106378. [Google Scholar] [CrossRef]
- Liu, M. Differential interference contrast-photothermal microscopy in nanospace: Impacts of systematic parameters. J. Microsc. 2018, 269, 221–229. [Google Scholar] [CrossRef] [PubMed]
- Miyazaki, J.; Kobayahsi, T. Photothermal Microscopy for High Sensitivity and High Resolution Absorption Contrast Imaging of Biological Tissues. Photonics 2017, 4, 32. [Google Scholar] [CrossRef]
- Escola, F.Z.; Kunik, D.; Martinez, O.E.; Mingolo, N. Photothermal Microscopy. Procedia Mater. Sci. 2015, 8, 665–673. [Google Scholar] [CrossRef]
- Selmke, M.; Braun, M.; Cichos, F. Gaussian beam photothermal single particle microscopy. J. Opt. Soc. Am. A 2012, 29, 2237–2241. [Google Scholar] [CrossRef]
- Selmke, M.; Braun, M.; Cichos, F. Photothermal single-particle microscopy: Detection of a nanolens. ACS Nano 2012, 6, 2741–2749. [Google Scholar] [CrossRef]
- Proskurnin, M.A.; Slyadnev, M.N.; Tokeshi, M.; Kitamori, T. Optimisation of thermal lens microscopic measurements in a microchip. Anal. Chim. Acta 2003, 480, 79–95. [Google Scholar] [CrossRef]
- Proskurnin, M.A. Photothermal spectroscopy. In Laser Spectroscopy for Sensing; Baudelet, M., Ed.; Woodhead Publishing Series in Electronic and Optical Materials; Woodhead Publ. Ltd.: Cambridge, UK, 2014; pp. 313–361. [Google Scholar]
- Mikheev, I.V.; Volkov, D.S.; Proskurnin, M.A.; Korobov, M.V. Monitoring of Aqueous Fullerene Dispersions by Thermal-Lens Spectrometry. Int. J. Thermophys. 2014, 36, 956–966. [Google Scholar] [CrossRef]
- Nedosekin, D.A.; Sarimollaoglu, M.; Galanzha, E.I.; Sawant, R.; Torchilin, V.P.; Verkhusha, V.V.; Ma, J.; Frank, M.H.; Biris, A.S.; Zharov, V.P. Synergy of photoacoustic and fluorescence flow cytometry of circulating cells with negative and positive contrasts. J. Biophoton. 2013, 6, 425–434. [Google Scholar] [CrossRef] [PubMed]
- Tran, C.D. Simultaneous enhancement of fluorescence and thermal lensing by reversed micelles. Anal. Chem. 2002, 60, 182–185. [Google Scholar] [CrossRef]
- Georges, J.; Ghazarian, S. Study of europium-sensitized fluorescence of tetracycline in a micellar solution of Triton X-100 by fluorescence and thermal lens spectrometry. Anal. Chim. Acta 1993, 276, 401–409. [Google Scholar] [CrossRef]
- Tran, C.D.; Van Fleet, T.A. Micellar induced simultaneous enhancement of fluorescence and thermal lensing. Anal. Chem. 2002, 60, 2478–2482. [Google Scholar] [CrossRef]
- Nedosekin, D.A.; Brusnichkin, A.V.; Luk’yanov, A.Y.; Eremin, S.A.; Proskurnin, M.A. Heterogeneous thermal-lens immunoassay for small organic compounds: Determination of 4-aminophenol. Appl. Spectrosc. 2010, 64, 942–948. [Google Scholar] [CrossRef] [PubMed]
- Alves, S.; Bourdon, A.; Neto, A.M.F. Generalization of the thermal lens model formalism to account for thermodiffusion in a single-beam Z-scan experiment: Determination of the Soret coefficient. J. Opt. Soc. Am. B 2003, 20, 713–718. [Google Scholar] [CrossRef]
- Arnaud, N.; Georges, J. Investigation of the thermal lens effect in water-ethanol mixtures: Composition dependence of the refractive index gradient, the enhancement factor and the Soret effect. Spectrochim. Acta. A Mol. Biomol. Spectrosc. 2001, 57, 1295–1301. [Google Scholar] [CrossRef]
- Cabrera, H.; Cordido, F.; Velasquez, A.; Moreno, P.; Sira, E.; Lopez-Rivera, S.A. Measurement of the Soret coefficients in organic/water mixtures by thermal lens spectrometry. Comptes Rendus Mec. 2013, 341, 372–377. [Google Scholar] [CrossRef]
- Arnaud, N.; Georges, J. Thermal lens spectrometry in aqueous solutions of Brij 35: Investigation of micelle effects on the time-resolved and steady-state signals. Spectrochim. Acta. A Mol. Biomol. Spectrosc. 2001, 57A, 1085–1092. [Google Scholar] [CrossRef]
- Biosca, Y.M.; Alfonso, E.F.S.; Romero, J.S.E.; Baeza, J.J.B.; Ramis-Ramos, G. Optical saturation, diffusion and convection effects in thermal lens spectrometry. Anal. Chim. Acta 1995, 307, 145–154. [Google Scholar] [CrossRef]
- Gruss, C.; Katscher, U.; Bein, B.K.; Pelzl, J. Photothermal beam deflection applied to the study of transient free convection on a vertical plate. Prog. Nat. Sci. 1996, 6, S305–S308. [Google Scholar]
- Karimzadeh, R.; Arshadi, M. Thermal lens measurement of the nonlinear phase shift and convection velocity. Laser Phys. 2013, 23, 115402. [Google Scholar] [CrossRef]
- Singhal, S.; Goswami, D. Thermal Lens Study of NIR Femtosecond Laser-Induced Convection in Alcohols. ACS Omega 2019, 4, 1889–1896. [Google Scholar] [CrossRef] [PubMed]
- Proskurnin, M.A.; Ivleva, V.B.; Ragozina, N.Y.; Ivanova, E.K. The Use of Triton X-100 in Thermal Lensing of Aqueous Solutions. Anal. Sci. 2000, 16, 397–401. [Google Scholar] [CrossRef]
- Topić Božič, J.; Butinar, L.; Ćurko, N.; Kovačević Ganić, K.; Mozetič Vodopivec, B.; Korte, D.; Franko, M. Implementation of high performance liquid chromatography coupled to thermal lens spectrometry (HPLC-TLS) for quantification of pyranoanthocyanins during fermentation of Pinot Noir grapes. SN Appl. Sci. 2020, 2, 1189. [Google Scholar] [CrossRef]
- Kazama, Y.; Hibara, A. Integrated Micro-Optics for Microfluidic Detection. Anal. Sci. 2016, 32, 99–102. [Google Scholar] [CrossRef]
- Shimizu, H.; Mawatari, K.; Kitamori, T. Detection of nonfluorescent molecules using differential interference contrast thermal lens microscope for extended nanochannel chromatography. J. Sep. Sci. 2011, 34, 2920–2924. [Google Scholar] [CrossRef]
- Proskurnin, M.A.; Bendrysheva, S.N.; Kuznetsova, V.V.; Zhirkov, A.A.; Zuev, B.K. Criteria for assessing the effect of the composition of mixed media on analytical sensitivity in thermal lens spectrometry. J. Anal. Chem. 2008, 63, 1168–1175. [Google Scholar] [CrossRef]
- Shen, J.; Soroka, A.J.; Snook, R.D. Model For Cw Laser-Induced Mode-Mismatched Dual-Beam Thermal Lens Spectrometry Based On Probe Beam Profile Image Detection. J. Appl. Phys. 1995, 78, 700–708. [Google Scholar] [CrossRef]
- Shen, J.; Baesso, M.L.; Snook, R.D. Three-dimensional model for cw laser-induced mode-mismatched dual-beam thermal lens spectrometry and time-resolved measurements of thin-film samples. J. Appl. Phys. 1994, 75, 3738–3748. [Google Scholar] [CrossRef]
- Savvin, S.B.; Chernova, R.K.; Shtykov, S.N. Poverkhnostno-Aktivnye Veshchestva; Nauka: Moscow, Russia, 1991. [Google Scholar]
- Chernysh, V.V.; Nesterova, I.V.; Proskurnin, M.A. The studies of the reaction of bismuth(III) with iodide at nanogram level by thermal lensing. Talanta 2001, 53, 1073–1082. [Google Scholar] [CrossRef] [PubMed]
- Sillen, L.G.; Martell, A.E. Stability Constants of Metal-Ion Complexes; Special Publication No. 1.; The Chemical Society: London, UK, 1964; p. 754. [Google Scholar]
- Ryndina, E.S.; Proskurnin, M.A.; Nedosekin, D.A.; Vladimirov, Y.A. Crystallization monitoring by thermal-lens spectrometry. J. Phys. Conf. Ser. 2010, 214, 012126. [Google Scholar] [CrossRef]
- Zharov, V.P.; Galanzha, E.I.; Tuchin, V.V. Photothermal flow cytometry in vitro for detection and imaging of individual moving cells. Cytom. A 2007, 71, 191–206. [Google Scholar] [CrossRef] [PubMed]
- Zharov, V.P.; Galanzha, E.I.; Tuchin, V.V. Photothermal image flow cytometry in vivo. Opt. Lett. 2005, 30, 628–630. [Google Scholar] [CrossRef] [PubMed]
- Escalona, R. Study of a convective field induced by thermal lensing using interferometry. Opt. Commun. 2008, 281, 388–394. [Google Scholar] [CrossRef]
- Sato, K.; Kawanishi, H.; Tokeshi, M.; Kitamori, T.; Sawada, T. Sub-zeptomole detection in a microfabricated glass channel by thermal-lens microscopy. Anal. Sci. 1999, 15, 525–529. [Google Scholar] [CrossRef]
- Lai, Y.-T.; Ohta, S.; Akamatsu, K.; Nakao, S.-i.; Sakai, Y.; Ito, T. Size-dependent interaction of cells and hemoglobin–albumin based oxygen carriers prepared using the SPG membrane emulsification technique. Biotechnol. Prog. 2015, 31, 1676–1684. [Google Scholar] [CrossRef]
- Kumar Rawat, A.; Chakraborty, S.; Kumar Mishra, A.; Goswami, D. Achieving molecular distinction in alcohols with femtosecond thermal lens spectroscopy. Chem. Phys. 2022, 561, 111596. [Google Scholar] [CrossRef]
- Zhu, L.; Zhou, C.; Jia, W. Femtosecond laser-induced thermal lens effect in chromium film. Appl. Opt. 2010, 49, 6512–6521. [Google Scholar] [CrossRef]
- Astrath, N.G.C.; Malacarne, L.C.; Lukasievicz, G.V.B.; Belancon, M.P.; Baesso, M.L.; Joshi, P.R.; Bialkowski, S.E. Pulsed-laser excited thermal lens spectroscopy with sample-fluid heat coupling. J. Appl. Phys. 2010, 107, 083512. [Google Scholar] [CrossRef]
- Li, Y.-C.; Kuo, S.-Z.; Wei, T.-H.; Wang, J.-N.; Yang, S.S.; Tang, J.-L. Control of Thermal Lensing Effect in Transparent Liquids by Femtosecond Laser Pulses. Jpn. J. Appl. Phys. 2009, 48, 09LF06. [Google Scholar] [CrossRef]
- Ghaleb, K.A.; Georges, J. Pulsed-laser crossed-beam thermal lens spectrometry for detection in a microchannel: Influence of the size of the excitation beam waist. Appl. Spectrosc. 2004, 58, 1116–1121. [Google Scholar] [CrossRef] [PubMed]
- Brennetot, R.; Georges, J. Pulsed-laser mode-mismatched dual-beam thermal lens spectrometry: Comparison of the time-dependent and maximum signals with theoretical predictions. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 1998, 54, 111–122. [Google Scholar] [CrossRef]
- Nedosekin, D.A.; Shashkov, E.V.; Galanzha, E.I.; Hennings, L.; Zharov, V.P. Photothermal multispectral image cytometry for quantitative histology of nanoparticles and micrometastasis in intact, stained and selectively burned tissues. Cytom. A 2010, 77, 1049–1058. [Google Scholar] [CrossRef]
- Khodakovskaya, M.V.; de Silva, K.; Nedosekin, D.A.; Dervishi, E.; Biris, A.S.; Shashkov, E.V.; Galanzha, E.I.; Zharov, V.P. Complex genetic, photothermal, and photoacoustic analysis of nanoparticle-plant interactions. Proc. Natl. Acad. Sci. USA 2011, 108, 1028–1033. [Google Scholar] [CrossRef] [PubMed]
- Upstone, S.L. Ultraviolet/Visible Light Absorption Spectrophotometry in Clinical Chemistry. In Encyclopedia of Analytical Chemistry; Meyers, R.A., Ed.; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]





| Group | Parameter | TLS-60 | TLS-150 | TLS-300 |
|---|---|---|---|---|
| Excitation laser | Main wavelengths, λe (nm) | 488.0, 514.5, and 532.0 | 488.0, 514.5, and 532.0 | 445 |
| Confocal distance zce (mm) | 19.5 ± 0.3 | 130 ± 2 | 700 ± 10 | |
| Maximum laser power at cell (mW) | 1500 | 250 | 450 | |
| TEM00 radius at the waist ω0e (µm) | 59.8 ± 0.5 | 150 ± 10 | 300 ± 10 | |
| Focusing lens focal length fe (mm) | 300 | 330 | 330 | |
| Probe laser | Wavelength λp (nm) | 632 | ||
| Focusing lens focal length fp (mm) | 185 | 185 | 100 | |
| Confocal distance zcp (mm) | 3.1 | 3.1 | 4.46 | |
| Laser power at cell (mW) Pp | 3 | 3 | 2–4 | |
| Radius at the waist ω0p (µm) | 25.0 ± 0.2 | 25.0 ± 0.2 | 30.0 ± 0.2 | |
| Other parameters | Cell length l, (mm) | 10 | 10 | 10 |
| Sample-to-detector distance (cm) | 95 | 47 | 47 | |
| m, Equation (3) | 2.1 ± 0.1 | 2.9 ± 0.1 | 2.34 ± 0.08 | |
| V, Equation (3) | 3.1 ± 0.1 | 11.0 ± 0.3 | 13.0 ± 0.3 | |
| Medium | Ionic Strength, M | Substance | LOD, nmol/L | tc, ms | |||
|---|---|---|---|---|---|---|---|
| Calc. | Experiment | Calc. | Experiment | ||||
| Water | 0 | Ferroin | 60 | 8.80 | 8.90 ± 0.05 | 6.2 | 6.2 ± 0.1 |
| MetHbCN | 30 | 5.56 ± 0.09 | 4.8 ± 0.2 | ||||
| 0.2 M KCl + 0.2 M NaCl | 0.4 | Ferroin | 60 | 8.6 | 8.5 ± 0.1 | 6.1 | 6.0 ± 0.2 |
| MetHbCN | 30 | 7.2 ± 0.1 | 4.7 ± 0.2 | ||||
| 0.1 M K2HPO4 + 0.1 M NaH2PO4 | 0.4 | Ferroin | 60 | 9.0 | 9.10 ± 0.07 | 6.2 | 6.2 ± 0.1 |
| MetHbCN | 30 | 8.3 ± 0.1 | 4.8 ± 0.3 | ||||
| 0.1 M PBS | ca. 0.11 | Ferroin | 60 | 10.0 | 9.9 ± 0.1 | 6.2 | 6.2 ± 0.1 |
| MetHbCN | 30 | 6.9 ± 0.2 | 4.7 ± 0.2 | ||||
| 1.0 M PBS | ~1.1 | Ferroin | 60 | 12.3 | 12.3 ± 0.1 | 6.2 | 6.2 ± 0.1 |
| MetHbCN | 20 | 8.8 ± 0.1 | 4.8 ± 0.2 | ||||
| Ferroin:MetHbCN 4:1 | — | 11.6 ± 0.1 | 6.3 | 6.0 ± 0.1 | |||
| Ferroin:MetHbCN 2:1 | — | 11.2 ± 0.1 | 5.7 ± 0.2 | ||||
| Ferroin:MetHbCN 1:1 | — | 10.7 ± 0.1 | 6.3 | 5.3 ± 0.2 | |||
| Ferroin:MetHbCN 1:3 | — | 9.6 ± 0.1 | 4.8 ± 0.2 | ||||
| 2 M NaCl | 2 | Ferroin | 60 | 11.3 | 11.4 ± 0.1 | 6.4 | 6.4 ± 0.2 |
| MetHbCN | 10 | 11.3 ± 0.1 | 6.4 ± 0.2 | ||||
| 0.4 M KCl + 2.8 M NaCl | 3.2 | Ferroin | 60 | 13.2 | 13.0 ± 0.1 | 6.4 | 6.0 ± 0.2 |
| MetHbCN | 20 | 12.7 ± 0.1 | 6.0 ± 0.2 | ||||
| 5 M NaCl | 5 | Ferroin | 60 | 14.0 | 13.8 ± 0.2 | 6.4 | 6.4 ± 0.2 |
| MetHbCN | 20 | 13.9 ± 0.2 | 6.4 ± 0.2 | ||||
| Sample | DT × 107, m2/s | CP × 10−3, J/(kg·K) | ρ, kg/m3 | Cpv, J/(mL·K) | J/(m2·K·s½) | k, W/(m·K) | Increase, % |
|---|---|---|---|---|---|---|---|
| Water (calculation) | 1.43 | 4.18 | 1000 | 4.18 | 1578 | 0.598 | — |
| Water | 1.42 ± 0.03 | 4.2 ± 0.1 | 997 ± 1 | 4.2 ± 0.1 | 1580 ± 100 | 0.59 ± 0.03 | — |
| AM | 1.56 ± 0.05 | 3.7 ± 0.1 | 1103 ± 1 | 4.1 ± 0.1 | 1600 ± 100 | 0.64 ± 0.04 | 7 |
| SM-30 | 1.56 ± 0.06 | 3.7 ± 0.1 | 1105 ± 1 | 4.1 ± 0.1 | 1600 ± 100 | 0.63 ± 0.04 | 7 |
| HS-40 | 1.69 ± 0.07 | 3.4 ± 0.1 | 1150 ± 1 | 3.9 ± 0.1 | 1610 ± 90 | 0.66 ± 0.05 | 11 |
| TMA | 1.60 ± 0.06 | 3.6 ± 0.1 | 1117 ± 1 | 4.0 ± 0.1 | 1610 ± 90 | 0.65 ± 0.06 | 9 |
| CL-X | 1.68 ± 0.05 | 3.3 ± 0.1 | 1192 ± 1 | 4.0 ± 0.1 | 1600 ± 100 | 0.67 ± 0.05 | 13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khabibullin, V.R.; Usoltseva, L.O.; Galkina, P.A.; Galimova, V.R.; Volkov, D.S.; Mikheev, I.V.; Proskurnin, M.A. Measurement Precision and Thermal and Absorption Properties of Nanostructures in Aqueous Solutions by Transient and Steady-State Thermal-Lens Spectrometry. Physchem 2023, 3, 156-197. https://doi.org/10.3390/physchem3010012
Khabibullin VR, Usoltseva LO, Galkina PA, Galimova VR, Volkov DS, Mikheev IV, Proskurnin MA. Measurement Precision and Thermal and Absorption Properties of Nanostructures in Aqueous Solutions by Transient and Steady-State Thermal-Lens Spectrometry. Physchem. 2023; 3(1):156-197. https://doi.org/10.3390/physchem3010012
Chicago/Turabian StyleKhabibullin, Vladislav R., Liliya O. Usoltseva, Polina A. Galkina, Viktoriya R. Galimova, Dmitry S. Volkov, Ivan V. Mikheev, and Mikhail A. Proskurnin. 2023. "Measurement Precision and Thermal and Absorption Properties of Nanostructures in Aqueous Solutions by Transient and Steady-State Thermal-Lens Spectrometry" Physchem 3, no. 1: 156-197. https://doi.org/10.3390/physchem3010012
APA StyleKhabibullin, V. R., Usoltseva, L. O., Galkina, P. A., Galimova, V. R., Volkov, D. S., Mikheev, I. V., & Proskurnin, M. A. (2023). Measurement Precision and Thermal and Absorption Properties of Nanostructures in Aqueous Solutions by Transient and Steady-State Thermal-Lens Spectrometry. Physchem, 3(1), 156-197. https://doi.org/10.3390/physchem3010012






