Performance of Micropiled-Raft Foundations in Sand
Abstract
1. Introduction
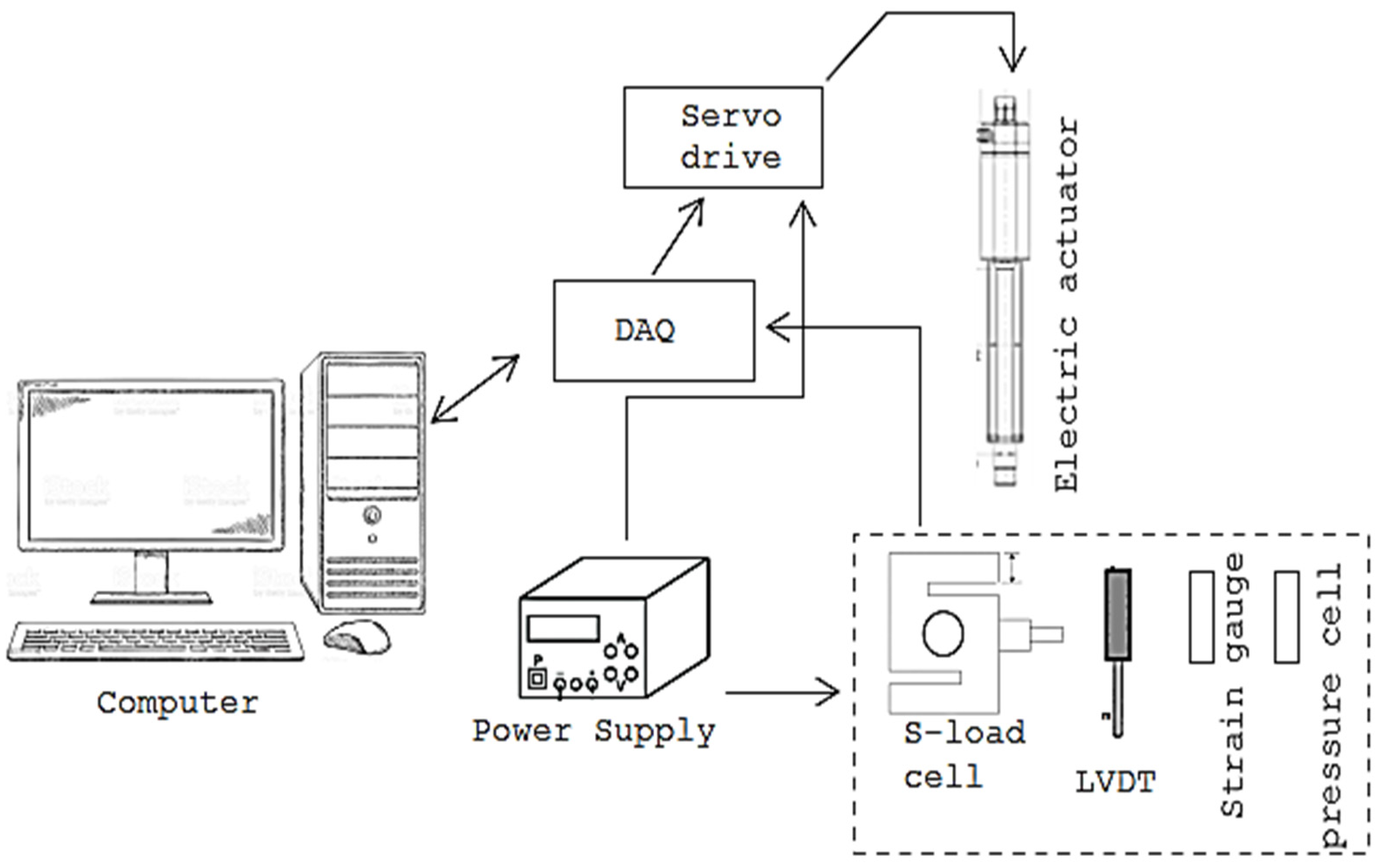
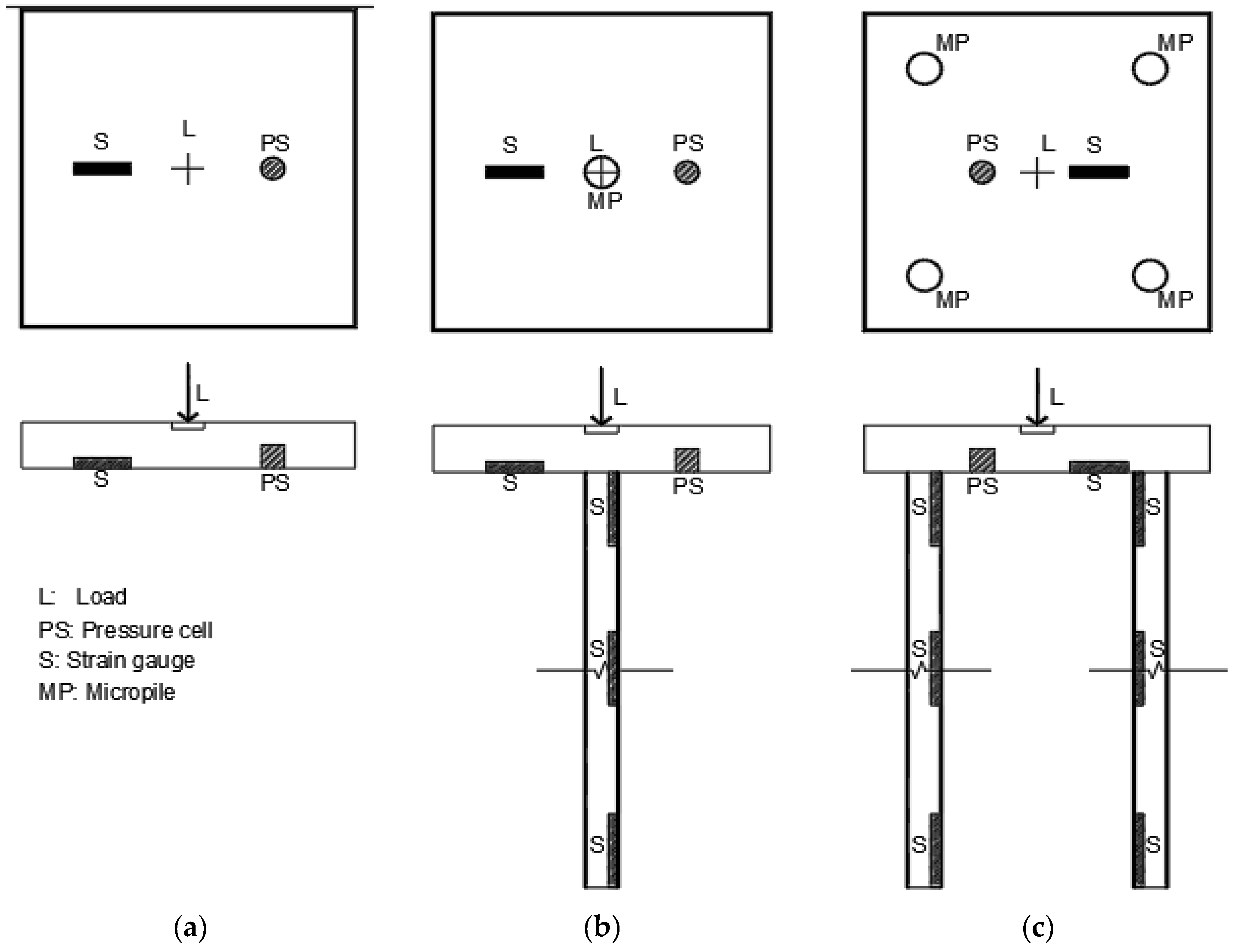
2. Experimental Investigation
3. Test Results and Analysis
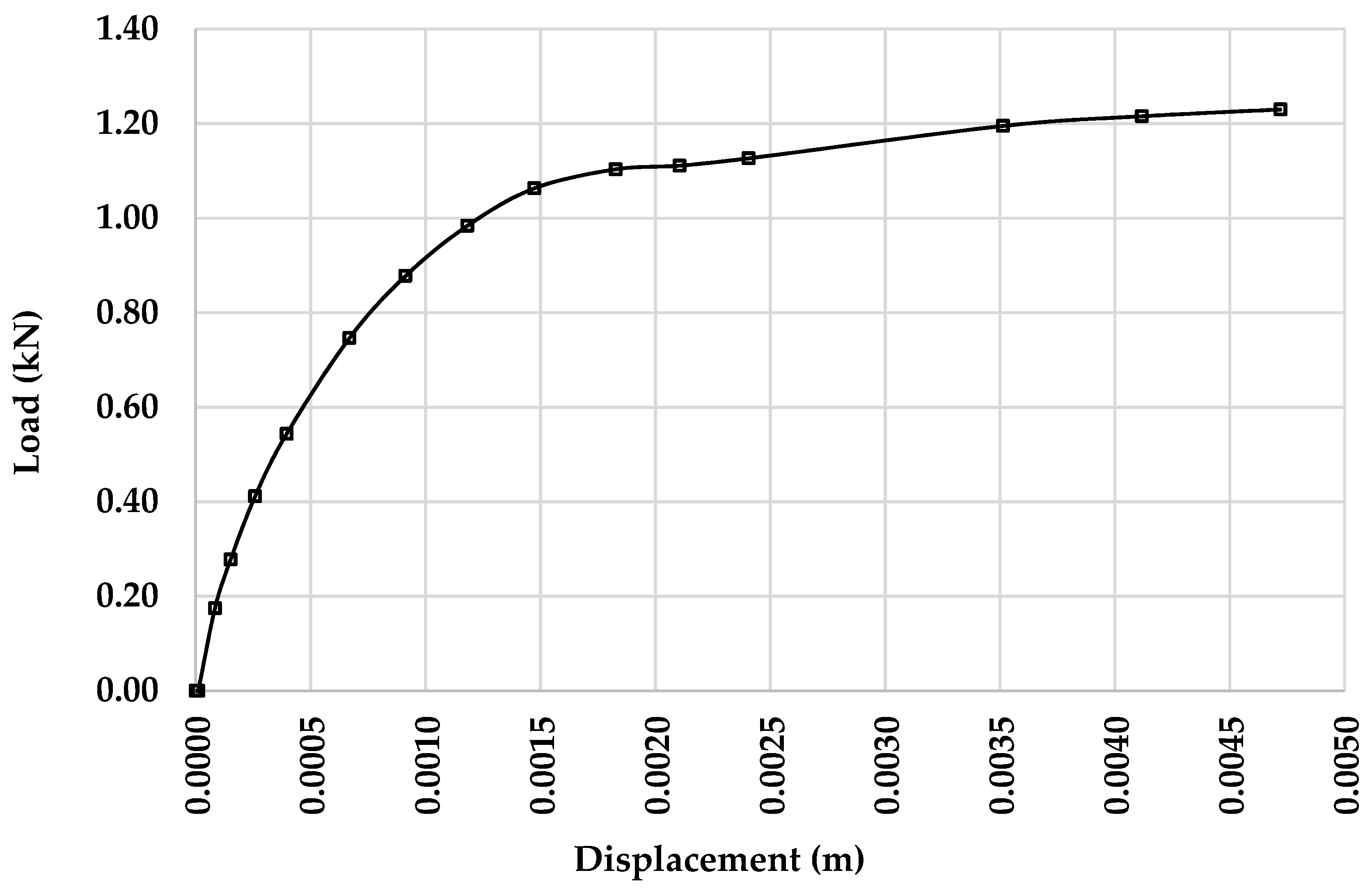
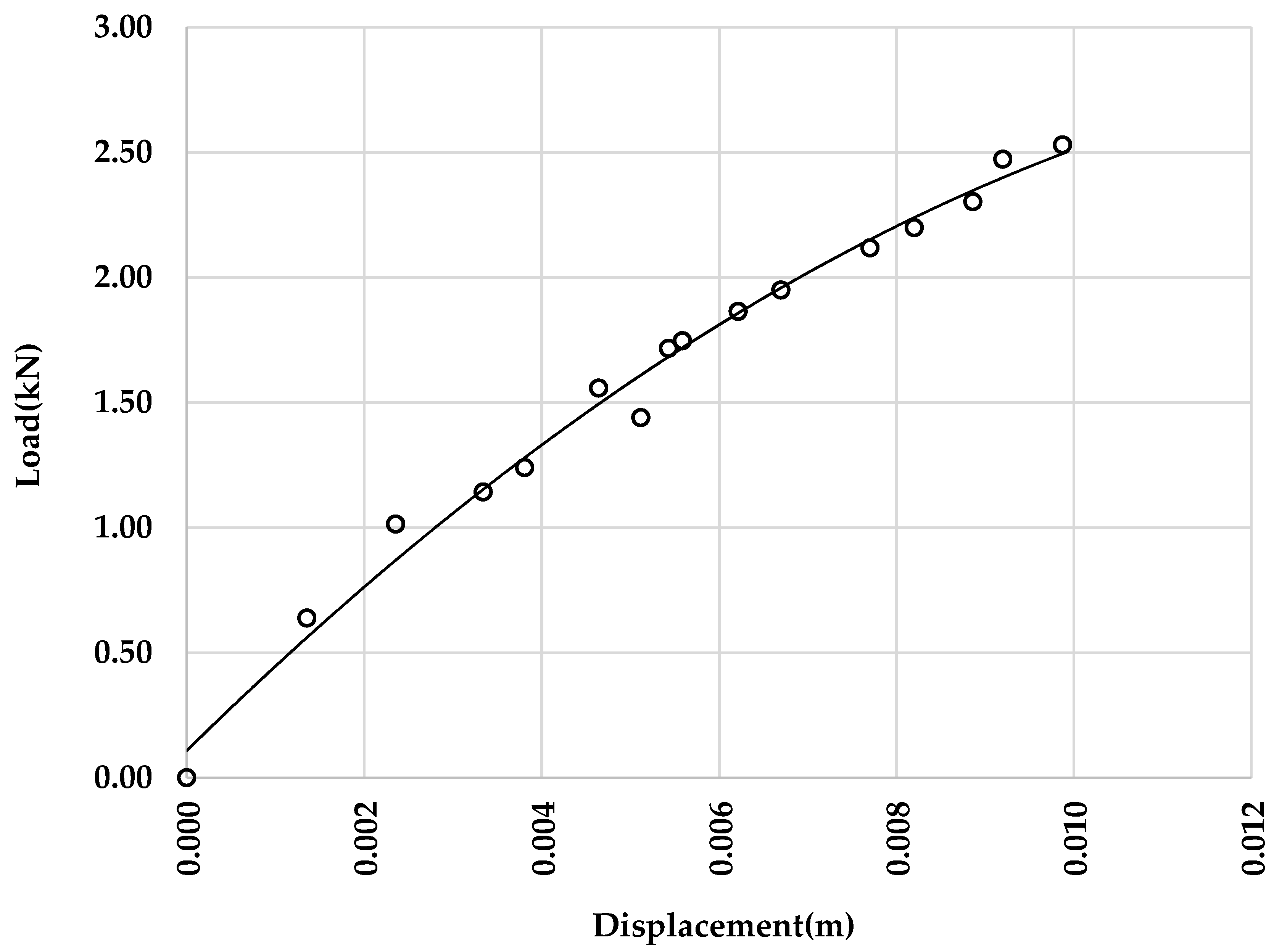
3.1. Validation of the Experimental Tests Results
3.2. Numerical Modeling
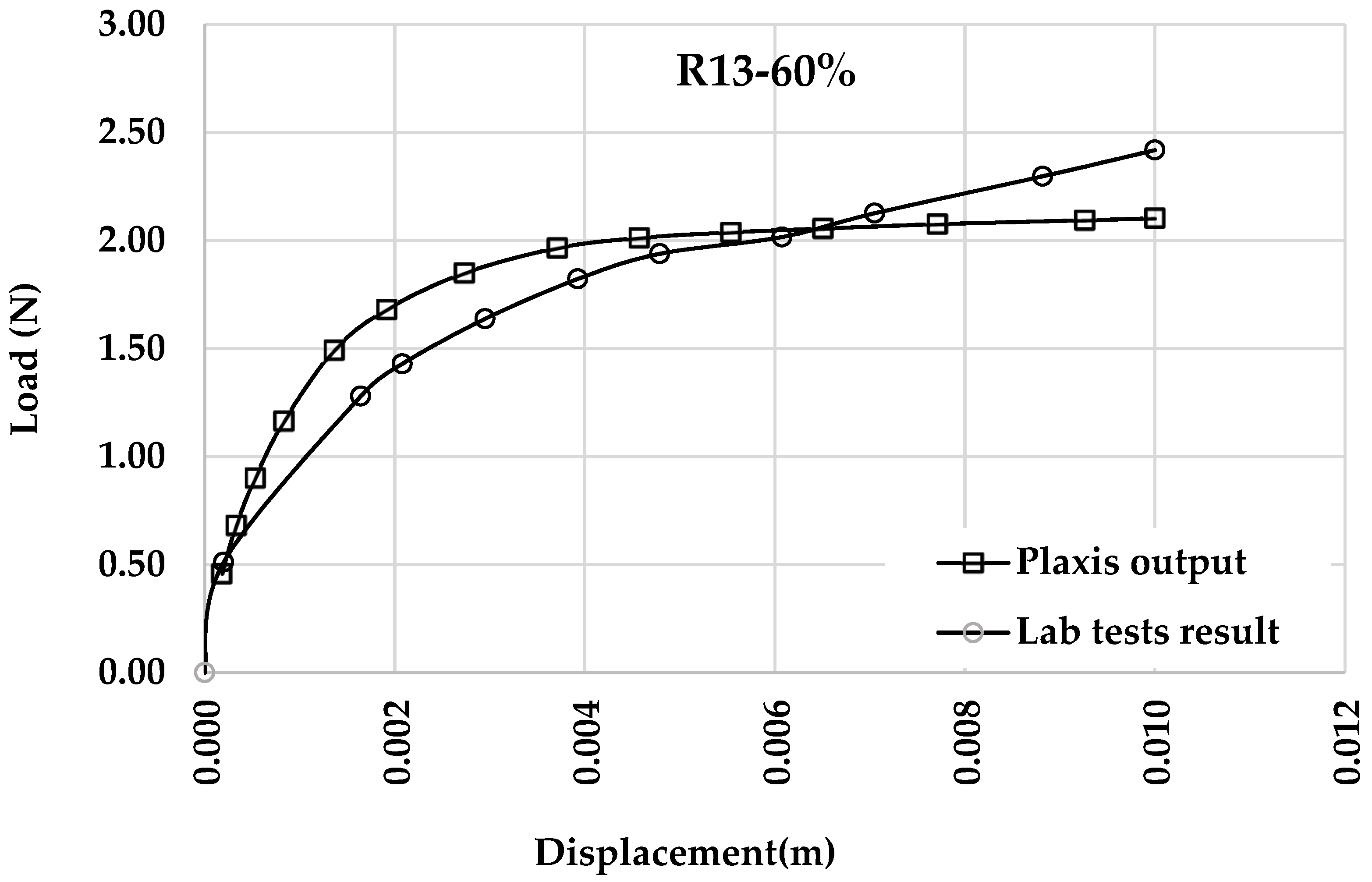
3.3. Validation of the Numerical Model:
3.4. Numerical Test Program
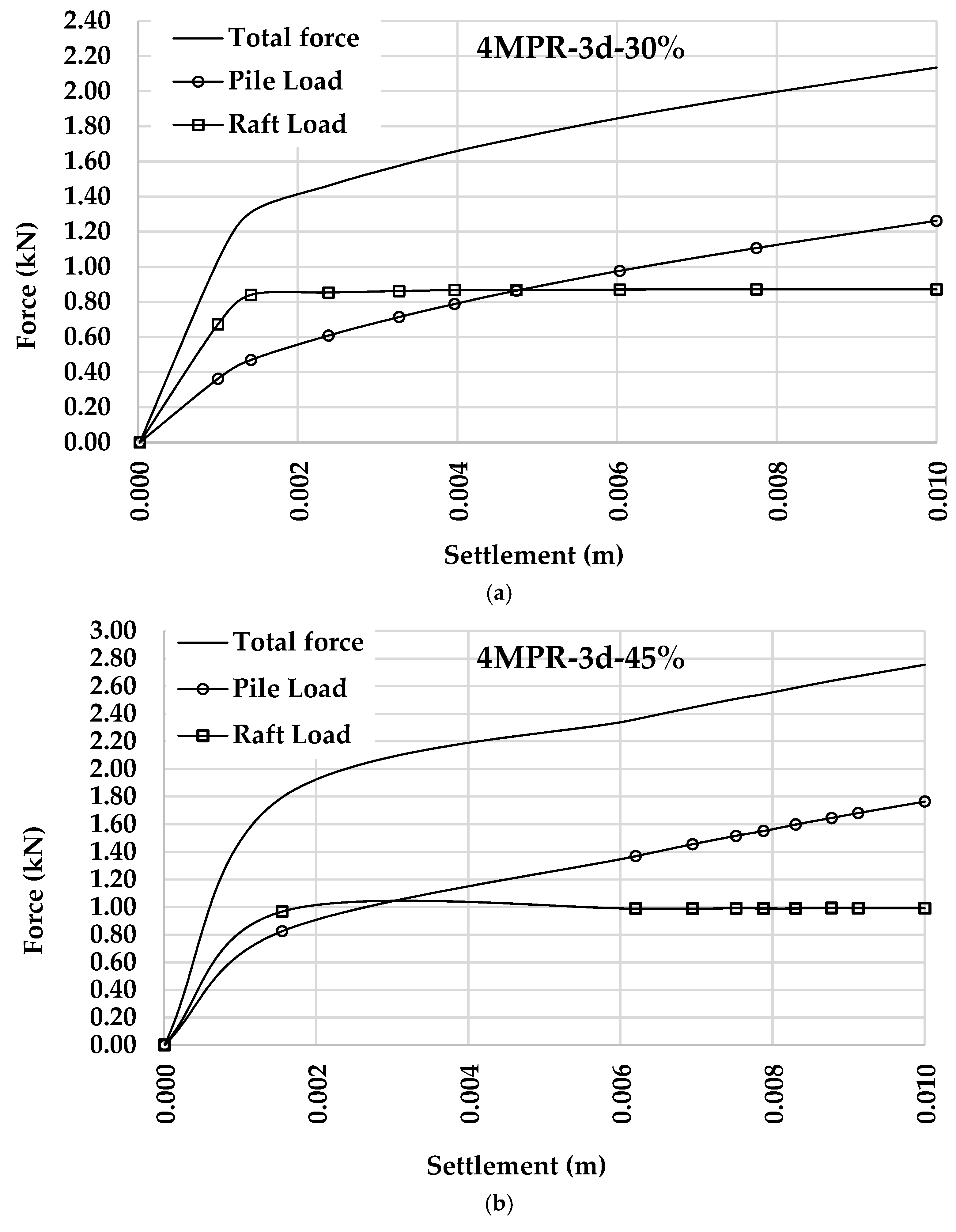
3.5. Test Results and Anaylsis
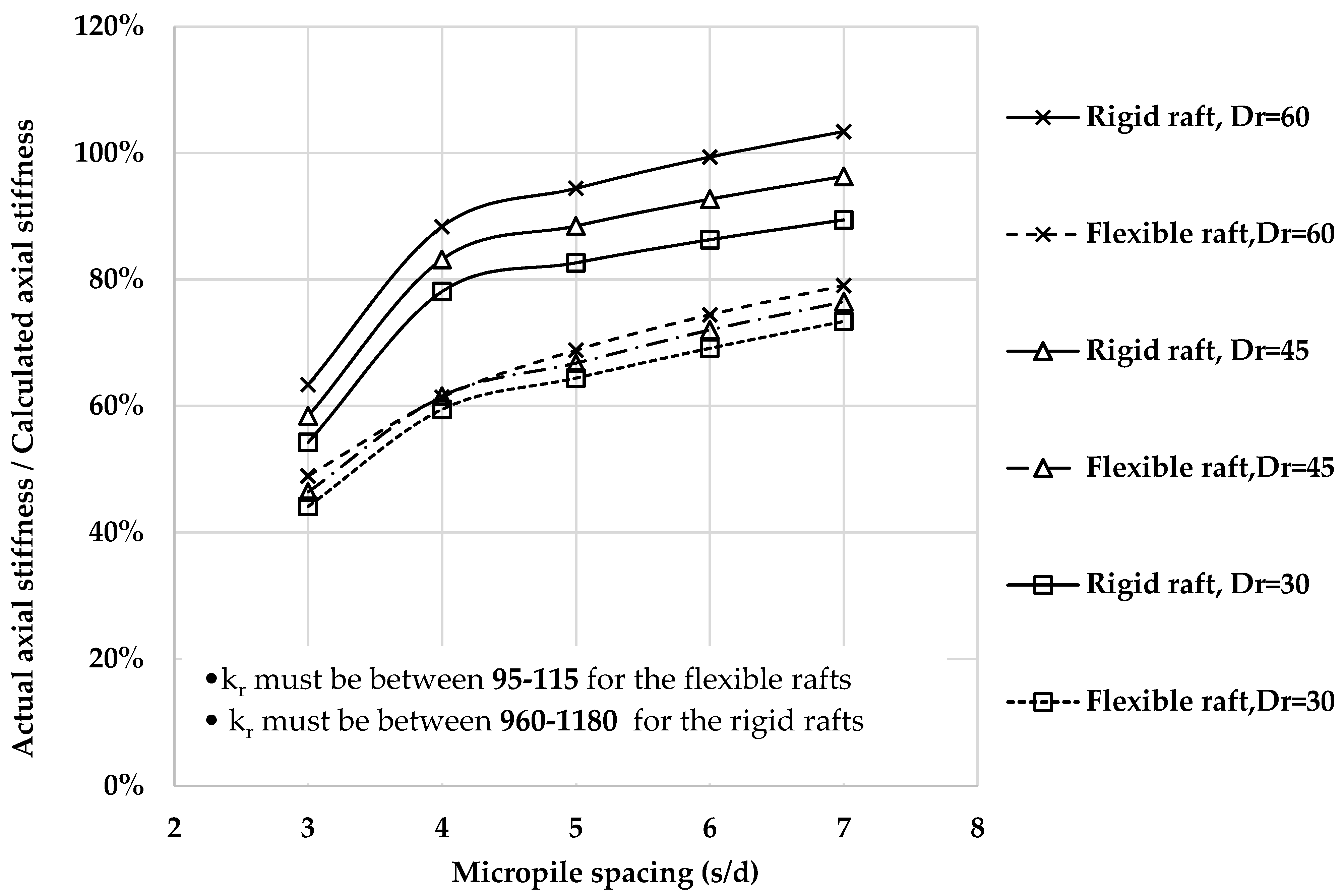
3.6. Design of MPR
| Coefficient\Raft Stiffness | 95 < Kr < 115 | 960 < Kr < 1180 |
| a | −0.07 | −0.41 |
| b | 0.27 | 0.42 |
| c | 0.04 | 0.13 |
4. Conclusions
- MPRs with rigid rafts support more load than those with semi-flexible rafts at any given settlement.
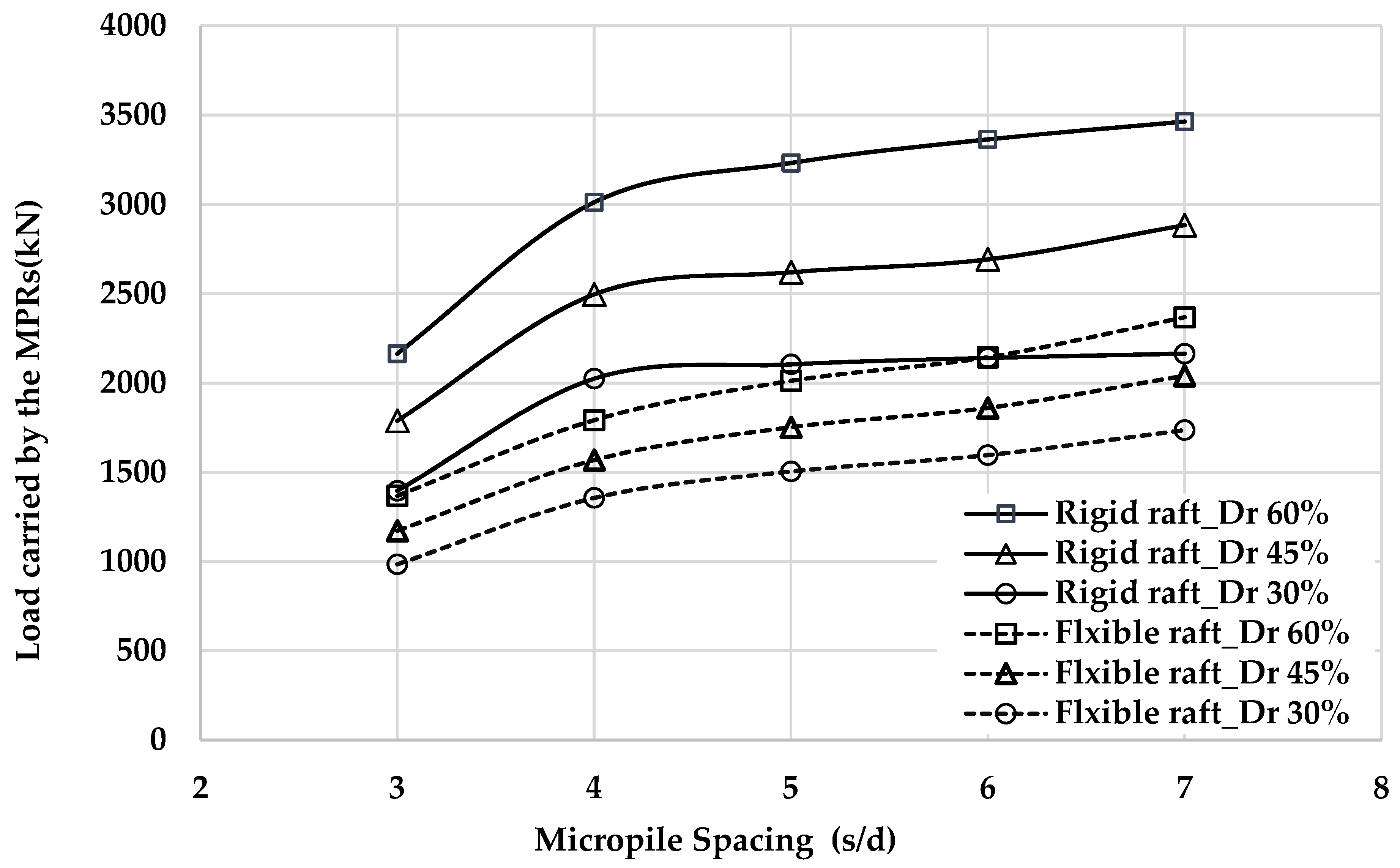
- The capacity of the MPR increases with the increase in the piles spacing for semi-rigid rafts; however, for rigid rafts, the increase is insignificant.
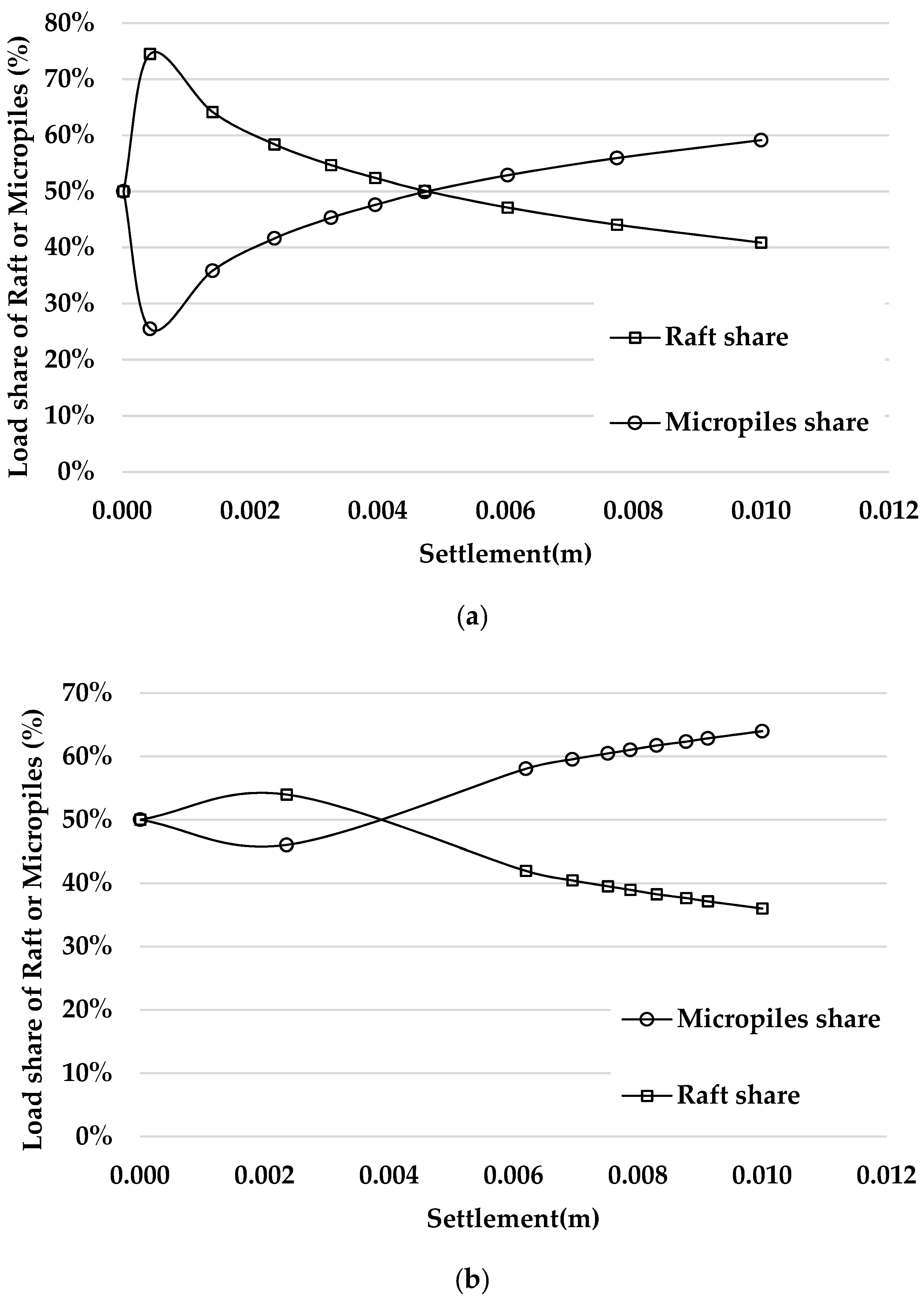
- The load shared by the micropiles decreases with the increase in the pile’s spacing ratio. This is due to the reduced interactions between piles. Furthermore, it increases with the increase in sand relative density.
- The settlement of MPR decreases with the increase in the relative density of the sand.
- The recommended skin friction values by FHWA were in reasonable agreement with the results of the present investigation; however, this agreement was noted only for large settlements.
- The PDR method overestimates the axial stiffness for the MPRs that are subjected to vertical loads, which was higher for MPRs with semi-flexible rafts.
- A correction factor was introduced to adopt the PDR of Poulos, Davis, and Randolph (PDR, 2001) as a method for the design of MPR.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lizzi, F. The Static Restoration of Monuments: Basic Criteria-Case Histories, Strengthening of Buildings Damaged by Earthquakes; Sagep: Genova, Italy, 1982. [Google Scholar]
- Bruce, D.A.; DiMillio, A.F.; Juran, I. Introduction to Micropiles: An International Perspective. In Proceedings of the Conference of the Geotechnical Engineering Division of the ASCE in Conjunction with the ASCE Convention, San Diego, CA, USA, 22–26 October 1995; pp. 1–26. [Google Scholar]
- Horikoshi, K.; Matsumoto, T.; Hashizume, Y.; Watanabe, T.; Fukuyama, H. Performance of piled raft foundations subjected to static horizontal loads. Int. J. Phys. Model. Geotech. 2003, 3, 37–50. [Google Scholar] [CrossRef]
- Tsukada, Y.; Miura, K.; Tsubokawa, Y.; Otani, Y.; You, G.L. Mechanism of Bearing Capacity of Spread Footings Reinforced with Micropiles. Soils Found. 2006, 46, 367–376. [Google Scholar] [CrossRef]
- Alnuaim, A.M.; EI Naggar, M.H.; El Naggar, H. Performance of micropiled raft in sand subjected to vertical concentrated load: Centrifuge modeling. Can. Geotech. J. 2014, 52, 33–45. [Google Scholar] [CrossRef]
- Kyung, D.; Kim, D.; Kim, G.; Lee, J. Vertical load-carrying behavior and design models for micropiles considering foundation configuration conditions. Can. Geotech. J. 2017, 54, 234–247. [Google Scholar] [CrossRef]
- Moghaddam, H.M.; Keramati, M.; Amin, R.; Reza, N. Experimental Evaluation of the Effects of Structural Parameters, Installation Methods, and Soil Density on the Micropile Bearing Capacity. Int. J. Civ. Eng. 2021, 19, 1313–1325. [Google Scholar] [CrossRef]
- FHWA. Micropile Design and Construction; National Highway Institute: Washington, DC, USA, 2005. [Google Scholar]
- Alharthi, Y.; Hanna, A. Shaft Resistance of Driven Piles in Overconsolidated Cohesionless Soils. In Proceedings of the 2nd GeoMEast International Congress and Exhibition on Sustainable Civil Infrastructures, Giza, Egypt, 23–28 November 2018; pp. 232–246. [Google Scholar] [CrossRef]
- Terzaghi, K.; Peck, R.B.; Mesri, G. Soil Mechanics in Engineering Practice, 1st ed.; John Wiley & Sons: New York, NY, USA, 1996. [Google Scholar]
- Akinmusuru, J.O. Interaction of piles and cap in piled footings. J. Geotech. Eng. Div. 1980, 106, 1263–1268. [Google Scholar] [CrossRef]
- Yamashita, K.; Yamada, T.; Hamada, J. Recent case histories on monitoring settlement and load sharing of piled rafts in Japan. In Proceedings of the 5th International Geotechnical Seminar on Deep Foundations on Bored and Auger Piles BAPV, University Main Hall, Ghent, Belgium, 7–11 September 2008. [Google Scholar]
- Plaxis. PLAXIS 3D 2021; Reference Manual; Bentley: Delft, The Netherlands, 2021. [Google Scholar]
- Fraser, R.A.; Wardle, L.J. Discussion: Numerical analysis of rectangular rafts on layered foundations. Géotechnique 1976, 28, 211–212. [Google Scholar] [CrossRef]
- Horikoshi, K.; Randolph, M.F. On the definition of raft—Soil stiffness ratio for rectangular rafts. Géotechnique 1997, 47, 1055–1061. [Google Scholar] [CrossRef]
- El Hammouli, S.; Hanna, A.; Lin, L.; Khalifa, M. Role of Cap Thickness in Pile-Cap Foundation. Int. J. Civ. Infrastruct. 2021, 4, 100–108. [Google Scholar] [CrossRef]
- Hanna, A.M.; Vakili, R. Load Sharing Mechanism of Non-displacement Piled-raft Foundation in Sand. J. Ground Improv. 2021, 174, 105–115. [Google Scholar] [CrossRef]
- Sinha, A.; Hanna, A.M. 3D Numerical Model for Piled-Raft Foundation. ASCE Int. J. Geomech. 2017, 17, 04016055. [Google Scholar] [CrossRef]
- Poulos, H.G. Piled raft foundations: Design and applications. Geotechnique 2011, 51, 95–113. [Google Scholar] [CrossRef]



| Soil Property | Silica 40-10 |
|---|---|
| D10 (mm) | 0.148 |
| D30 (mm) | 0.210 |
| D50 (mm) | 0.256 |
| D60 (mm) | 0.280 |
| Cu | 1.76 |
| CC | 1.00 |
| Soil Classification (USCS) | SP |
| Maximum Dry Unit Weight (KN/m3) | 17.32 |
| Minimum Dry Unit Weight (kN/m3) | 14.05 |
| Minimum Void Ratio | 0.51 |
| Maximum Void Ratio | 0.82 |
| Specific Gravity (Gs) | 2.60 |
| Relative Density (Dr) | Void Ratio | Angle of Shearing Resistance (Degrees) |
|---|---|---|
| 30 | 0.71 | 31.05 |
| 45 | 0.67 | 33.88 |
| 60 | 0.65 | 36.4 |
| Parameter | PVC Models | Prototype Models (Concrete) |
|---|---|---|
| Unit weight (kN/m3) | 14.5 | 24.8 |
| Modulus of elasticity, E (MPa) | 3 × 103 | 30 × 103 |
| Poisson ratio (ν) | 0.3 | 0.2 |
| Settlement (mm) | Model | Measured Axial Load (kN) | ||
|---|---|---|---|---|
| Top | Middle | Tip | ||
| 5 | MPR with s/d = 3; Dr = 30 | 0.138 | 0.067 | 0.045 |
| 7.5 | 0.167 | 0.085 | 0.052 | |
| 10 | 0.191 | 0.099 | 0.057 | |
| 5 | MPR with s/d = 3, Dr = 45 | 0.188 | 0.099 | 0.058 |
| 7.5 | 0.232 | 0.120 | 0.072 | |
| 10 | 0.269 | 0.140 | 0.089 | |
| 5 | MPR with s/d = 3, Dr = 60 | 0.300 | 0.153 | 0.107 |
| 7.5 | 0.371 | 0.197 | 0.124 | |
| 10 | 0.431 | 0.228 | 0.138 | |
| 5 | MPR with s/d = 4, Dr = 30 | 0.150 | 0.077 | 0.036 |
| 7.5 | 0.195 | 0.096 | 0.043 | |
| 10 | 0.226 | 0.113 | 0.056 | |
| 5 | MPR with s/d = 4, Dr = 45 | 0.175 | 0.091 | 0.044 |
| 7.5 | 0.216 | 0.106 | 0.050 | |
| 10 | 0.252 | 0.126 | 0.063 | |
| 5 | MPR with s/d = 4, Dr = 60 | 0.275 | 0.135 | 0.058 |
| 7.5 | 0.341 | 0.171 | 0.085 | |
| 10 | 0.391 | 0.195 | 0.102 | |
| Test Code Name | Relative Density of the Sand | Raft Size (cm) | No of Piles | MP (Length/Dia) | MP Spacing | BC (kN) | Stiffness (MN/m) | PDR (MN/m) | Stiffness (MN/m) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 30 | 13 × 13 × 3.8 | - | - | - | 1.00 | 1.57 | - | - |
| 2 | 45 | 13 × 13 × 3.8 | - | - | - | 1.40 | 2.10 | - | - |
| 3 | 60 | 13 × 13 × 3.8 | - | - | - | 2.00 | 2.94 | - | - |
| 4 | 30 | 9.5 × 9.5 × 3.8 | - | - | - | 0.60 | 0.70 | - | - |
| 5 | 45 | 9.5 × 9.5 × 3.8 | - | - | - | 0.85 | 1.00 | - | - |
| 6 | 60 | 9.5 × 9.5 × 3.8 | - | - | - | 1.15 | 1.20 | - | - |
| 7 | 30 | 12.5 × 12.5 × 3.8 | - | - | - | 0.65 | 0.90 | - | - |
| 8 | 45 | 12.5 × 12.5 × 3.8 | - | - | - | 1.10 | 2.00 | - | - |
| 9 | 60 | 12.5 × 12.5 × 3.8 | - | - | - | 1.40 | 2.40 | - | - |
| 10 | 30 | - | 1 | 80/2.54 | - | 0.52 | 1.95 | - | - |
| 11 | 45 | - | 1 | 80/2.54 | - | 0.71 | 2.32 | - | - |
| 12 | 60 | - | 1 | 80/2.54 | - | 1.06 | 2.68 | - | - |
| 13 | 30 | 13 × 13 × 3.8 | 1 | 80/2.54 | - | 1.75 | 3.00 | - | 0.60 |
| 14 | 45 | 13 × 13 × 3.8 | 1 | 80/2.54 | - | 2.00 | 3.50 | - | 0.75 |
| 15 | 60 | 13 × 13 × 3.8 | 1 | 80/2.54 | - | 2.25 | 4.00 | - | 1.00 |
| 16 | 30 | 9.5 × 9.5 × 3.8 | 4 | 50/1.58 | 3 d | 1.40 | 3.40 | 3.60 | 0.85 |
| 17 | 45 | 9.5 × 9.5 × 3.8 | 4 | 50/1.58 | 3 d | 1.80 | 3.70 | 4.02 | 1.00 |
| 18 | 60 | 9.5 × 9.5 × 3.8 | 4 | 50/1.58 | 3 d | 2.50 | 4.90 | 4.41 | 1.20 |
| 19 | 30 | 12.5 × 12.5 × 3.8 | 4 | 50/1.58 | 4 d | 1.70 | 3.50 | 3.65 | 1.39 |
| 20 | 45 | 12.5 × 12.5 × 3.8 | 4 | 50/1.58 | 4 d | 2.00 | 3.75 | 4.04 | 1.40 |
| 21 | 60 | 12.5 × 12.5 × 3.8 | 4 | 50/1.58 | 4 d | 2.60 | 5.00 | 4.42 | 1.56 |
| Test Code | Relative Density Dr | Raft Size | No of Piles | Micropiles (L/d) | Micropiles Spacing Ratio S/d | Raft Thickness | |
|---|---|---|---|---|---|---|---|
| (m) | (m) | Semi-Flexible | Rigid | ||||
| (m) | (m) | ||||||
| 1 | 30% | 4.2 × 4.2 | 16 | 10/0.15 | 3 | 0.10 | |
| 2 | 45% | 4.2 × 4.2 | 16 | 10/0.15 | 3 | 0.10 | |
| 3 | 60% | 4.2 × 4.2 | 16 | 10/0.15 | 3 | 0.10 | |
| 4 | 30% | 4.2 × 4.2 | unpiled | 0.10 | |||
| 5 | 45% | 4.2 × 4.2 | unpiled | 0.10 | |||
| 6 | 60% | 4.2 × 4.2 | unpiled | 0.10 | |||
| 7 | 30% | 4.2 × 4.2 | 16 | 10/0.15 | 3 | 0.3 | |
| 8 | 45% | 4.2 × 4.2 | 16 | 10/0.15 | 3 | 0.3 | |
| 9 | 60% | 4.2 × 4.2 | 16 | 10/0.15 | 3 | 0.3 | |
| 10 | 30% | 4.2 × 4.2 | unpiled | 0.3 | |||
| 11 | 45% | 4.2 × 4.2 | unpiled | 0.3 | |||
| 12 | 60% | 4.2 × 4.2 | unpiled | 0.3 | |||
| 13 | 30% | 4.2 × 4.2 | 16 | 10/0.15 | 4 | 0.15 | |
| 14 | 45% | 4.2 × 4.2 | 16 | 10/0.15 | 4 | 0.15 | |
| 15 | 60% | 4.2 × 4.2 | 16 | 10/0.15 | 4 | 0.15 | |
| 16 | 30% | 4.2 × 4.2 | unpiled | 0.15 | |||
| 17 | 45% | 4.2 × 4.2 | unpiled | 0.15 | |||
| 18 | 60% | 4.2 × 4.2 | unpiled | 0.15 | |||
| 19 | 30% | 4.2 × 4.2 | 16 | 10/0.15 | 4 | 0.35 | |
| 20 | 45% | 4.2 × 4.2 | 16 | 10/0.15 | 4 | 0.35 | |
| 21 | 60% | 4.2 × 4.2 | 16 | 10/0.15 | 4 | 0.35 | |
| 22 | 30% | 4.2 × 4.2 | unpiled | 0.35 | |||
| 23 | 45% | 4.2 × 4.2 | unpiled | 0.35 | |||
| 24 | 60% | 4.2 × 4.2 | unpiled | 0.35 | |||
| 25 | 30% | 4.2 × 4.2 | 16 | 10/0.15 | 5 | 0.20 | |
| 26 | 45% | 4.2 × 4.2 | 16 | 10/0.15 | 5 | 0.20 | |
| 27 | 60% | 4.2 × 4.2 | 16 | 10/0.15 | 5 | 0.20 | |
| 28 | 30% | 4.2 × 4.2 | unpiled | 0.20 | |||
| 29 | 45% | 4.2 × 4.2 | unpiled | 0.20 | |||
| 30 | 60% | 4.2 × 4.2 | unpiled | 0.20 | |||
| 31 | 30% | 4.2 × 4.2 | 16 | 10/0.15 | 5 | 0.45 | |
| 32 | 45% | 4.2 × 4.2 | 16 | 10/0.15 | 5 | 0.45 | |
| 33 | 60% | 4.2 × 4.2 | 16 | 10/0.15 | 5 | 0.45 | |
| 34 | 30% | 4.2 × 4.2 | unpiled | 0.45 | |||
| 35 | 45% | 4.2 × 4.2 | unpiled | 0.45 | |||
| 36 | 60% | 4.2 × 4.2 | unpiled | 0.45 | |||
| 37 | 30% | 4.2 × 4.2 | 16 | 10/0.15 | 6 | 0.25 | |
| 38 | 45% | 4.2 × 4.2 | 16 | 10/0.15 | 6 | 0.25 | |
| 39 | 60% | 4.2 × 4.2 | 16 | 10/0.15 | 6 | 0.25 | |
| 40 | 30% | 4.2 × 4.2 | unpiled | 0.25 | |||
| 41 | 45% | 4.2 × 4.2 | unpiled | 0.25 | |||
| 42 | 60% | 4.2 × 4.2 | unpiled | 0.25 | |||
| 43 | 30% | 4.2 × 4.2 | 16 | 10/0.15 | 6 | 0.55 | |
| 44 | 45% | 4.2 × 4.2 | 16 | 10/0.15 | 6 | 0.55 | |
| 45 | 60% | 4.2 × 4.2 | 16 | 10/0.15 | 6 | 0.55 | |
| 46 | 30% | 4.2 × 4.2 | unpiled | 0.55 | |||
| 47 | 45% | 4.2 × 4.2 | unpiled | 0.55 | |||
| 48 | 60% | 4.2 × 4.2 | unpiled | 0.55 | |||
| 49 | 30% | 4.2 × 4.2 | 16 | 10/0.15 | 7 | 0.30 | |
| 50 | 45% | 4.2 × 4.2 | 16 | 10/0.15 | 7 | 0.30 | |
| 51 | 60% | 4.2 × 4.2 | 16 | 10/0.15 | 7 | 0.30 | |
| 52 | 30% | 4.2 × 4.2 | unpiled | 0.30 | |||
| 53 | 45% | 4.2 × 4.2 | unpiled | 0.30 | |||
| 54 | 60% | 4.2 × 4.2 | unpiled | 0.30 | |||
| 55 | 30% | 4.2 × 4.2 | 16 | 10/0.15 | 7 | 0.65 | |
| 56 | 45% | 4.2 × 4.2 | 16 | 10/0.15 | 7 | 0.65 | |
| 57 | 60% | 4.2 × 4.2 | 16 | 10/0.15 | 7 | 0.65 | |
| 58 | 30% | 4.2 × 4.2 | unpiled | 0.65 | |||
| 59 | 45% | 4.2 × 4.2 | unpiled | 0.65 | |||
| 60 | 60% | 4.2 × 4.2 | unpiled | 0.65 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hanna, A.; Nabizadeh, F. Performance of Micropiled-Raft Foundations in Sand. Geotechnics 2024, 4, 1065-1080. https://doi.org/10.3390/geotechnics4040054
Hanna A, Nabizadeh F. Performance of Micropiled-Raft Foundations in Sand. Geotechnics. 2024; 4(4):1065-1080. https://doi.org/10.3390/geotechnics4040054
Chicago/Turabian StyleHanna, Adel, and Farhad Nabizadeh. 2024. "Performance of Micropiled-Raft Foundations in Sand" Geotechnics 4, no. 4: 1065-1080. https://doi.org/10.3390/geotechnics4040054
APA StyleHanna, A., & Nabizadeh, F. (2024). Performance of Micropiled-Raft Foundations in Sand. Geotechnics, 4(4), 1065-1080. https://doi.org/10.3390/geotechnics4040054






