Abstract
Artificial ground freezing (AGF) has emerged as a prominent treatment method due to its ability to mechanically strengthen the soil while reducing its permeability. However, its implementation has raised concerns about its impact, particularly with respect to frost heave and subsequent thaw-induced displacements. These soil movements can cause subsidence and pose a significant threat to the integrity of surface structures. Overburden pressure plays a crucial role in AGF and determines the amount of heave generated. This paper presents an analysis of the existing literature about soil freezing and thawing. The aim is to offer an understanding of these processes, specifically with regard to their application in AGF. This paper explains the behavior of soil during freezing, with particular emphasis on the influence of overburden pressure. It also investigates frozen soils’ thawing and freeze–thaw (FT) cycles’ long-term effects on soil properties. AGF offers improved soil strength and reduced water permeability, enhancing construction project stability. However, the interplay between the temperature, soil composition, and initial ground conditions during freezing is complex. This thermo-hydro-chemo-mechanical process strengthens the soil and reduces its permeability, but it can also induce frost heave due to water expansion and ice lens formation. Overburden pressure from the overlying soil limits ice lens growth. FT cycles significantly impact soil properties. In fine-grained soils, FT cycles can lead to over-consolidation, while rapid thawing can generate high pore pressures and compromise stability. Importantly, FT acts as a weathering mechanism, influencing soil properties at both the microscopic and macroscopic scales. These cycles can loosen over-consolidated soil, densify normally consolidated soil, and increase overall hydraulic conductivity due to structural changes. They can also weaken the soil’s structure and deteriorate its mechanical performance.
1. Introduction
Artificial ground freezing (AGF) is a temporary soil treatment method used to create watertight peripheral enclosures during various construction projects. Its field of application concerns a wide range of soft or strongly weathered soils and rocky masses in cases where other temporary consolidation methods would not be suitable, safe enough, or technically feasible. The core principle of AGF revolves around transforming the soil into a frozen state, thereby enhancing its mechanical strength and reducing its hydraulic conductivity compared to its natural state [,,]. The technique has a long history dating back to 1862, when it was first used to construct mine shafts in South Wales [].
A significant challenge associated with AGF lies in accurately predicting the surface deformations arising during the freezing and thawing processes. Frost heave, a phenomenon caused by the volume expansion of water upon freezing, can lead to unexpected upward movements of the soil [,]. Conversely, during the thawing process, soil particles undergo rearrangement, potentially resulting in thaw settlement, particularly if water drainage is unrestricted [,]. Upon the completion of a freeze–thaw (FT) cycle, the soil exhibits profound mechanical and physical characteristic changes. Due to FT cycles, the soils often undergo volume change, crack development, loss of shear strength and stiffness, and a change in hydraulic conductivity [,,].
A persistent difficulty lies in accurately predicting the magnitude of these deformations. Often, these predictions underestimate the actual displacements seen in true-scale projects. For example, during the construction of tunnels beneath railroad tracks in Boston, the maximum predicted heave was 114 mm, but some localized areas experienced heave of up to 178 mm []. Additionally, thaw settlement can be even more significant than frost heave. In 1969, Endo [] reported a case where the thaw settlement was 10% greater than the preceding frost heave during a subway construction project. These discrepancies between the predicted and observed deformations in AGF projects highlight the limitations of our understanding of the complex mechanisms at play during an FT cycle. True knowledge of AGF requires a thorough investigation into how it affects the fundamental characteristics of soil, including the granulometry, porosity, and mechanical strength.
This review was conducted with the ambition of providing a state-of-the-art overview to understand the complex behavior of soil during both the freezing and the thawing phases of an AGF project. In this context, this paper was organized around four main key areas. The first explores the fundamental thermo-hydro-chemo-mechanical processes governing soil freezing. The second analyzes heave deformations and the approaches developed to predict them. The third emphasizes the importance of considering overburden pressure for safe and effective AGF implementation in deep construction projects. The last part goes over frozen soils’ behavior upon thawing. It explores the long-term effects of freeze–thaw cycles on the physical and mechanical properties of soil, which is essential for ensuring long-term project stability.
2. Definition of Ground Freezing
Upon freezing, the soil becomes a complex four-phase material composed of soil particles, ice crystals, air bubbles, and unfrozen water. Figure 1 illustrates the synthesis of the fundamental freezing process on three distinct scales. Figure 1A provides insight into the dynamics of the soil–water system undergoing freezing. Ice formation can be divided into four zones (after [] from []). Figure 1B is a schematic representation of the soil freezing characteristic curve (SFCC), a soil-specific parameter that is used to characterize the variation of the unfrozen water content as a function of increasing suction [,]. Studying the evolution of cryogenic suction during freezing helps in understanding the thermodynamics and behavior of the soil by providing information on the water content and temperature changes in the soil during the freezing process and insights into the microscopic processes that occur. The SFCC describes the freezing process of soil in terms of three distinct zones: the boundary effect zone, the transition zone, and the residual unfrozen state zone. Finally, Figure 1C shows the evolution of the unfrozen water and ice phases in fully saturated soil under freezing conditions at the microscopic level.
The form of the different parts of the curves in Figure 1 and their duration is determined by the mineralogical composition of the soil, the grain size, the specific surface area, the surface tensions at the liquid/grain interface, the presence or absence of impurities in the pore water, and the initial water content [,,].
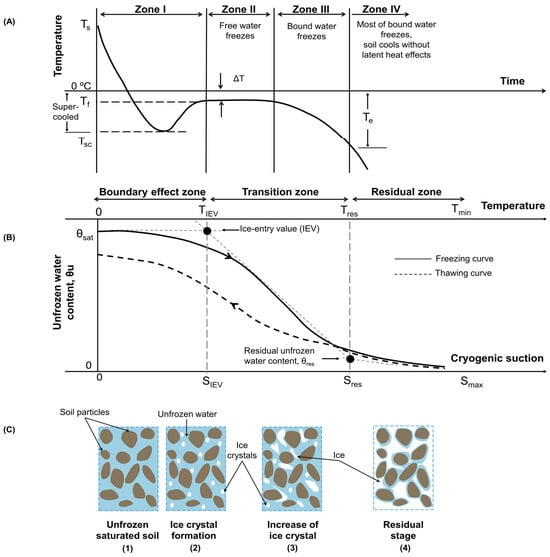
Figure 1.
(A) Schematic representation of the cooling curve for soil water and ice (after []). (B) Schematic representation of a typical soil freezing characteristic curve. (C) Saturated soil freezing: microscopic evolution of unfrozen water and ice phases ([]).
- In Zone I (Figure 1A), the free pore water does not freeze until the temperature drops to a supercooled temperature—Tsc. This is because the supercooled water is in a metastable equilibrium state until nucleation centers cause an abrupt transformation of free water into ice, marking the beginning of Zone II. Nuclei can be aggregates of water molecules or soil particles. Zone I corresponds to the boundary effect zone on the SFCC (Figure 1B) and stage (1) of Figure 1C. Initially, the pores of the saturated soil are filled with liquid water. During the freezing process, the temperature of the pore water decreases, but due to confinement and interaction with soil particles, its freezing point is lower than that of free water. Therefore, even if the soil temperature reaches 0 °C, the pore water will not freeze.
- In Zone II (Figure 1A), ice formation releases latent heat, causing the temperature to rise from Tsc to Tf, the initial freezing temperature. Tf is close to 0 °C for cohesionless soils with low specific surface area, but the temperature decrease (ΔT) can be as much as 5 °C for fine-grained soils []. In Zone II, the supercooled water contained in the large interconnected pores is isothermally converted into ice. Zone II corresponds to the transition zone on the SFCC (Figure 1B) and stage (2) of Figure 1C. The beginning of the transition zone is marked by the onset of ice nucleation as the temperature continues to decrease. Small ice crystals begin to form in large pores, replacing existing water. The cryogenic suction at which ice nucleation begins is referred to as the ice entry value (IEV). As the ice continues to grow, it will gradually enter smaller pores. For the SFCC, the IEV is the intersection of the linear extent of the initial straight segment of the SFCC and its central zone, which is characterized by a significant decrease in the amount of remaining unfrozen water. From this point on, the water bound to the grains is gradually converted into ice, as shown in the third part (Zone III) of the curve in Figure 1A.
- Zone III corresponds to stage (3) in Figure 1C. Unlike free pore water, the solidification of bound water in soil is not a uniform, constant temperature process due to the influence of capillarity and absorption forces []. The resulting latent heat slows down the temperature decrease until a limit temperature Te (about −70 °C) is reached. At this point, all the free water and most of the bound water (unfrozen water film adsorbed on soil particles) is frozen. For fine-grained soils with high specific surface areas, a significant amount of unfrozen water may still be present at higher negative temperatures.
- Zone IV corresponds to the residual zone on the SFCC (Figure 1B) and stage (4) in Figure 1C. As the temperature decreases, once a certain value is reached, most of the pore water has already been converted into ice, and only a small amount of liquid water remains. This water is found as thin films adsorbed on soil particles and can be referred to as the residual unfrozen water content. At this point, the ice phase is continuous while the water phase is not.
The determination of the SFCC often involves solving an inverse problem. This means using a hydro-thermal model and iteratively adjusting its parameters until its response matches data obtained from in situ observations or laboratory tests. However, the present literature also highlights alternative methods for directly measuring the evolution of a porous medium’s freezing state as a function of the temperature. Among the most well-known methods are the following:
- Time Domain Reflectometry (TDR): measures the dielectric permittivity of a soil specimen from the velocity of an electromagnetic wave’s propagation and reflection [,];
- Nuclear Magnetic Resonance (NMR): provides knowledge about the spatial distribution of hydrogen atoms [,];
- Differential Scanning Calorimetry (DSC): measures the variation of the heat fluxes emitted or received by a sample when it is subjected to temperature variations [];
- Acoustic approaches: rely on the difference between the ultrasonic wave propagation speeds in water and ice [].
It is worth noting that these techniques do not provide direct measurements. They all rely on certain assumptions and approximations to calibrate the electronic sensors and correlate the obtained data with the water content.
The Clausius–Clapeyron equation (Equation (1)) is generally assumed to be applicable in relating suction and temperature by considering the ice phase to be under atmospheric pressure. This assumption has been adopted by several authors, including [,,,].
where ψ is the suction in m; L is the latent heat of water fusion (L = 334 kJ/kg); g is the gravitational acceleration; Tm is the freezing temperature of bulk water; and T is the subzero temperature in kelvin.
3. Ground Freezing, a Highly Coupled THMC Process
The transformation of unfrozen (three-phase) soil into frozen (four-phase) soil presents a significant challenge due to its inherent complexity. This multi-physics, multi-scale process involves transient, multi-phase heat transfer and fluid dynamics within a porous medium. Several key properties influence soil freezing and are themselves influenced by it. These include the thermal properties (conductivity, heat capacity, latent heat), chemical properties (salt and mineral concentration), mechanical properties (strength, creep, freeze–thaw deformations), and hydraulic properties (water content, permeability) [,,,,,,,,].
Figure 2 illustrates the coupled thermal (T), hydraulic (H), chemical (C), and mechanical (M) phenomena that occur during ground freezing. Globally, forming a solid hydraulic barrier while freezing will decrease the groundwater flow by reducing the permeability of the porous ground structure. From a mechanical perspective, changes in porosity are likely to impact the bulk thermal conductivity, heat capacity, and groundwater flow, thereby influencing the thermal behavior of the AGF process. Conversely, thermal stresses resulting from phase change and density variation could affect the mechanical response of the ground. Porosity variations are directly linked to the permeability of the ground, which in turn influences the groundwater flow. Furthermore, seepage flow under high pressure will induce significant stress and strain on the frozen wall during the AGF process.
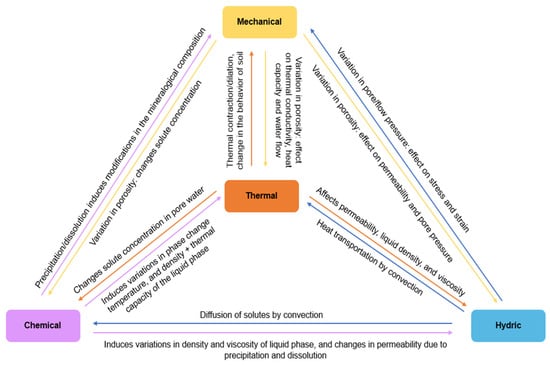
Figure 2.
Coupled thermal, hydraulic, chemical, and mechanical phenomena during the freezing of a porous medium.
In practice, the interactions between the different processes occurring during soil freezing are either simplified into two-way couplings: TH, TM, TC, HM, HC, MC; or they can be studied as three-way couplings: the impact of the TH components on the mechanics of the ground, and vice versa; the impact of the TH aspects on salinity, and vice versa; and the influence of the TM modifications on salinity, and vice versa. The examples of TH, THM, and TC couplings will be further detailed hereafter.
- HT coupling
Water flow is influenced by temperature changes, which can cause changes in the properties of the soil and the pore fluid, such as the dilation or contraction of materials, changes in permeability as water changes phase into ice, and changes in liquid water viscosity. This flow also contributes to heat transfer through convection, further affecting the overall thermal state of the soil. Water flows, on the other hand, can induce convective heat transfer, which significantly impacts the thermal state of the medium. These flows may occur naturally or may be brought about by the ground freezing itself. In the first scenario, if these flows are strong enough, the formation of the frozen barrier can be slowed down or even prevented. The second type of flow is induced by the density difference between ice and liquid water. Due to its density, the freshly produced ice in the pores can expel the liquid pore water to the nearby unfrozen regions, creating a velocity field at the frozen/non-frozen interface. The speed of these flows determines the relative importance of heat transfer by convection compared to conduction [,,].
- HTM coupling
During soil freezing, a complex interplay emerges between mechanical stresses, deformations, and hydraulic properties. Changes in the effective stress and temperature can induce significant soil deformations. Notably, freezing itself alters the soil’s mechanical behavior, creating a coupled system where deformations further modulate the thermal and hydraulic properties. Deformations modify the porosity, which in turn directly influences several parameters like the thermal conductivity, heat capacity, saturation degree, permeability, and groundwater flow [,,]. Furthermore, overburden pressure significantly influences the heave amount. This pressure influences the ice lens formation and thickness, permeability, frozen fringe thickness, and suction potential, contributing to the overall magnitude of heave experienced during soil freezing [,,,,,]. Further elaboration on the effect of overburden pressure on AGF is provided in Section 4.
- TC coupling
The influence of solutes has been explored by examining their impact on the depression of the freezing point, the alteration of hydraulic conductivity, and their broader influence on concentration-driven flows and heat transfer phenomena []. The depression of the freezing point by solutes in the pore fluid is a well-established phenomenon, supported by both laboratory experiments and theoretical models developed for various soil and solute types [,,,]. During freezing, solutes are excluded from the ice crystals, concentrating in the remaining liquid phase []. This concentration effect further depresses the freezing point of the remaining liquid until a solubility limit is reached for the prevailing temperature. At this point, simultaneous solute precipitation and ice crystallization may occur, leading to a decrease in the solute concentration of the remaining liquid. The situation is further complicated by the temperature dependence of the saturation concentration, with lower temperatures promoting faster precipitation, particularly for initially high solute concentrations [].
Generally, AGF is a complex process that involves multi-scale, multi-physics phenomena involving transient heat transfer, fluid dynamics, and phase changes within a porous medium. Numerous soil properties—thermal (conductivity, heat capacity), chemical (salt and mineral concentration), mechanical (strength, creep, freeze–thaw deformations), and hydraulic (water content, permeability)—simultaneously influence and are influenced by the freezing process. The interdependent nature of all these parameters renders AGF a THCM-coupled process with dual effects: enhancing soil strength and reducing permeability, while simultaneously inducing significant ground deformations, particularly heave [,,,,,,]. In practice, these interactions are often simplified into two-way or three-way couplings to facilitate analysis. Key examples include the HT (thermal–hydraulic) coupling, where temperature changes influence water flow through variations in permeability and viscosity, and vice versa. THM coupling further incorporates the impact of mechanical stresses and deformations.
4. Ground Deformations Induced by AGF
Frost heave is driven by two primary mechanisms: the phase change of water into ice and the formation of ice lenses []. When the temperature falls below the freezing point, pore water freezes into ice. The one-dimensional pore water expansion, HPW, of 9% is driven by frost penetration x(t), considering the volumetric porosity n and saturation degree Sr, as given in Equation (2) [].
Ice lenses form when liquid pore water migrates through the soil toward the freezing interface due to suction []. At the microscale, cryogenic suction is explained by pre-melting dynamics, where intermolecular forces cause the migration of pre-melted fluid to feed ice lens growth []. In 1989, Dash [] proposed that the soil and the ice grains reject each other across pre-melted liquid films created by these same intermolecular forces, generating low pressure that attracts surrounding water and causes heave. The extent of the ice lens formation depends on the pore water availability, movement, and freezing duration []. The susceptibility of soil to frost heave is strongly influenced by its nature. Coarse-grained soils, characterized by larger particles, exhibit minimal frost heave, while fine-grained soils, with their smaller particles, are highly prone to frost heave [,]. Figure 3 compares the frost heave caused by freezing in different soil types. Silty clays tend to experience the most heave, especially under lower overburden pressure and higher temperature gradients. This is because these fine-grained soils can hold more unfrozen water at sub-zero temperatures, allowing ice lens formation to contribute to heave alongside water phase change. Clay soils, though generally frost-susceptible, may heave less than coarser-grained silts. Conversely, sandy soils, with their lower water content at freezing temperatures, experience minimal heave as freezing is dominated by simple phase changes.
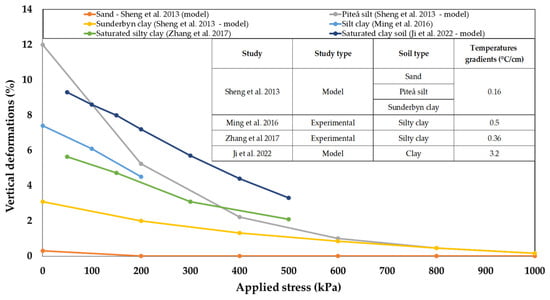
Figure 3.
A summary of the relationship between heave deformations and applied stress based on soil types from four distinct studies (Ming et al. and Sheng et al. [,], Zhang et al. [], Ji et al. []).
Three distinctive zones exist upon freezing the soil under a temperature gradient: the passive frozen zone, the frozen fringe, and the active unfrozen zone [,,,,,].
- Passive frozen zone: This region is ice-bound and experiences ice crystal and lens formation. Temperature changes are driven by thermal diffusion mediated by the presence of ice.
- Frozen fringe: This transition zone marks the interface between the frozen and the unfrozen zone. Here, ice and water coexist in soil pores, and complex processes of ice nucleation, crystallization, and phase transition occur.
- Active unfrozen zone: This zone is dominated by thermal diffusion, water migration, suction, and soil consolidation.
A schematic representation of a typical frozen soil profile is illustrated in Figure 4.
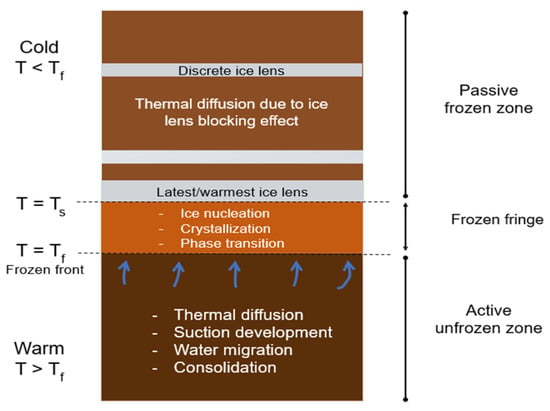
Figure 4.
Schematic representation of a frozen soil profile and the processes that govern freezing—Tf: freezing temperature of water; and Ts: segregation temperature (at the base of the ice lens) [].
For a quantitative theory of frost heave to be robust, it must account for two critical aspects: (1) the migration of water from unfrozen regions of the soil to colder zones where it undergoes a phase change to excess ice, and (2) the tendency of this ice to exert tensile forces within the soil matrix and ultimately accumulate as discrete ice lenses that meet specific criteria for ice lens formation []. Understanding how ice forms as discrete lenses is critical to modeling frost heave in susceptible soils. Researchers in various fields have studied the mechanisms underlying ice lens formation. These criteria can be broadly classified into four groups.
- Total stress criteria: Focuses on pore pressure exceeding a threshold that separates soil particles [,]. O’Neill and Miller [] defined this threshold using neutral stress (overburden pressure minus effective stress).
- Tensile strength criteria: Considers overburden pressure and the soil’s tensile strength [,]. Ice lens formation occurs when the ice pressure overcomes the combined resistance.
- Permeability criteria: Emphasizes the role of frozen fringe permeability linked to segregation temperature []. A new lens forms when reduced permeability restricts water flow to existing lenses.
- Soil freezing characteristic curve criteria: Uses the SFCC to determine ice lens initiation conditions, including the segregation temperature []. This method identifies the IEV within the SFCC for fine-grained soils.
Theories on frost heave fall under two groups: primary frost heave (traditionally known as capillary models) and secondary frost heave (frozen-fringe models). By treating the soil as an open system, Taber [] observed that even when the saturating fluid was changed from water to benzene, which contracts when frozen, frost heave still occurred. This indicated that the volume increase during freezing was not just due to in situ water freezing but also involved water movement from unfrozen areas to the frozen zone. This crucial insight led to the development of the capillary theory, the first fundamental explanation of frost heave. Taber [] also identified key factors governing frost heave: soil particle size, available water content, pore space characteristics, and freezing rate. In 1935, Beskow [] independently offered significant contributions to our understanding of soil freezing. He drew an analogy between soil freezing and drying, emphasizing that both processes involve a change in the water phase (ice formation vs. evaporation) and a reduction in the liquid water content of the soil. This analogy further supported the capillary theory, which is based on two key equations: Clapeyron’s equation, which describes the thermodynamic equilibrium for a system of ice and water at specific pressures and temperatures (Equation (1)), and the Young–Laplace equation, which relates the pressure difference between ice and water to the curvature of the interface between them. The ability of ice to invade a porous medium is governed by the relative sizes of the ice crystals and the effective pore radius. The size and geometry of the pore act as a template, dictating the maximum attainable radius of the ice crystal. When the ice radius (r) exceeds the effective pore radius (rp), the ice becomes too large to pass through the pore throat physically. Capillary theory explains the basic mechanism of frost heave, but limitations became apparent in the 1960s and 1970s. While predictions for idealized soils composed of uniform particle size showed good agreement with experimental data, the predicted heave pressures for soils containing a range of particle sizes were significantly lower than experimental observations. In addition, the model could not account for continuous ice formation, where multiple unconnected ice lenses form at the freezing front instead of a single thick lens. These shortcomings led to the development of a new approach, the frozen-fringe model.
The apparent failure of the capillary theory led some researchers [,] to argue that frost heave can occur even after ice has formed a frozen fringe by expanding into soil pores. This fringe, a partially frozen zone located between the ice lens and the warmest soil with pore ice (the volume of soil where pore water and pore ice coexist), was introduced in []. Water from the unfrozen zone moves slowly but continuously toward the ice lens through this low-permeability frozen fringe Figure 5.
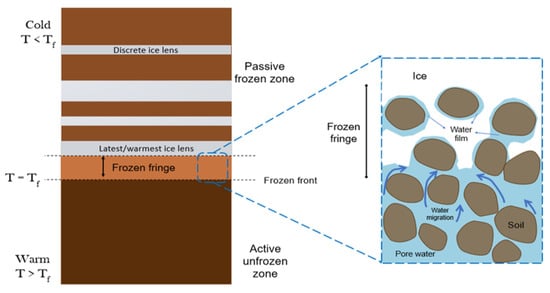
Figure 5.
A schematic diagram (not to scale) of the frozen fringe [].
Building on the limitations identified in the capillary theory, Miller [] proposed the ice-rigid model of frost heave in non-colloidal soils. This model assumes that deformations primarily arise from ice lens formation rather than compression or expansion of the soil matrix. The core concept of the ice-rigid model is a continuous, rigid ice body coexisting with pore water within the frozen fringe. The ice in the frozen fringe remains connected to the growing ice lens above. It moves relative to the surrounding soil particles through a process known as regelation (melting and refreezing). O’Neill and Miller [] further developed the ice-rigid model to predict the ice lens properties and frost heave rate based on environmental factors and ground behavior. Their model focuses on the evolution of ice saturation within the pore space and its impact on permeability. These parameters can be determined through independent laboratory experiments [,].
Many researchers have focused on simplifying the model [,,]. Sheng et al. [] updated the governing equations and interpretations of stress expressions to create an operationally simple model (PC-Heave) that can handle parameters such as the ground frost heave rate, freeze–thaw front velocity, and ice volume content, making it useful for field frost heave monitoring. Bronfenbrener and Bronfenbrener [] presented another generalized model of secondary frost heave in freezing fine-grained soils, recognizing the importance of determining the moisture distribution within the frozen fringe. Shortly after the rigid-ice model, Nixon [] introduced the separate ice lens theory, which assumes distinct pore ice and ignores regelation movement. This theory evolved into the separate-ice frost heave model with improved ice lens formation criteria. However, both the ice-rigid and separate ice models suffer from a practical limitation: the difficulty of accurately measuring some of the crucial physical and mechanical parameters they rely on, which restricts and limits their application [].
A more practical approach is the segregation potential model proposed by Konrad and Morgenstern []. This widely used model estimates a frost heave parameter called the segregation potential (SP), a constant value relating the water intake flux to the temperature gradient. While successful in some cases, the SP model struggles with unstable environments and lacks fundamental soil characteristic parameters. Ji et al. [] built upon the SP model and water activity criteria to propose a new model for ice lens formation under time-varying temperatures. However, this model requires laboratory data for time-varying temperatures, limiting its field application. Beyond these specific models, researchers like Nishimura et al. [] and Casini et al. [] have developed constitutive models that consider the combined effects of thermal, hydraulic, and mechanical processes during frost heave. These models incorporate both frozen and unfrozen soil behaviors, using variables like the ice pressure, water pressure, and total stress. This comprehensive approach allows for a more holistic understanding of the complex interactions that contribute to frost heave in frozen soils.
This section is an overview of the significant contributions that many scientists have made to understand and ultimately modeling frost heave. While it does not cover every model under development, it offers a glimpse of the different approaches being taken to understand frost heave. One critical point that emerges is that most of the existing models of frost heave focus on naturally frozen soils in cold regions. This limitation implies that they do not account for the effects of overburden pressure on the soil during freezing and the resulting heave.
5. AGF in the Presence of Overburden Pressure
The scarcity of surface space in urban environments often drives construction projects underground, where excavations can reach tens of meters below ground level. At these depths, the weight of the overlying soil layers exerts substantial overburden pressure, which plays a critical role in AGF and significantly influences the magnitude of frost heave. Beskow [] was perhaps the first to study the influence of stress on soil freezing nearly a century ago. He noticed that external pressures reduced the heave rates of silty soils upon freezing. Subsequent experimental studies have further identified the connection between the applied pressure and various processes such as water migration, suction development, permeability reduction, and segregation temperature [,,,,]. Therefore, the presence of overburden pressure alters the mechanical, thermal, and hydraulic response of soil to both freezing and thawing.
Researchers, including Konrad and Morgenstern [], Xia et al. [], and Ji et al. [], have shown that overburden pressure influences the thermal response of soil to freezing by impacting the thickness of the frozen fringe and the value of the segregation temperature, the temperature at which ice lenses form. Experiments conducted by Konrad and Morgenstern [] showed that increasing overburden pressure results in a thicker frozen fringe and a reduced hydraulic gradient across the fringe, reducing water migration to the ice lens. Further confirmation came from experiments by Xia et al. [], who used the fluorescent tracer method to track the frozen fringe thickness under various constant vertical stresses. The frozen fringe increased in thickness by up to 5 mm when subjected to 400 kPa axial stress compared to when not subjected to axial stress. The results globally showed a direct correlation between a higher overburden pressure and a thicker frozen fringe (longer flow path for water migration to the ice lens).
The segregation temperature depends on the cooling rate, soil nature, and overburden pressure [,,]. The influence of overburden pressure on the segregation temperature of ice lenses was the subject of three different studies by Konrad [], Azmatch [], and Ji et al. []. Both Konrad [] and Azmatch [] studied the segregation temperature of Devon silt using different approaches (Clausius–Clapeyron equation and SFCC, respectively) but reached similar conclusions. They found that under comparable conditions of cooling rate and applied pressure, the segregation temperature remained relatively constant. Ji et al. [] resorted to numerical simulations to study the impact of overburden pressure on the segregation temperature of clay. Their model accounted for phase transition and multiphase interactions to evaluate the kinetic growth of ice lenses. The model investigates the micro- and meso-physical mechanisms behind ice lens growth by introducing the water activity-controlled growth rate of ice crystals. The results of these three studies are illustrated in Figure 6. These results showed that the increase in the overburden pressure leads to a decrease in the temperature of the warmest ice lens. Overall, these studies consistently show a decrease in the segregation temperature as the overburden pressure increases. Therefore, the overburden pressure increases the thickness of the frozen fringe while reducing the segregation temperature of ice lenses.
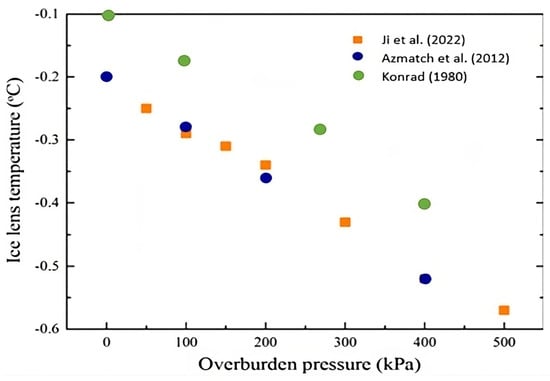
Figure 6.
Ice lens temperature versus overburden pressure of three distinct studies. Numerical simulations of clay (Ji et al. []), SFCC-derived data of Devon silt (Azmatch ([]), and experimental data of Devon silt (Konrad []).
Studies have shown that overburden pressure also impacts the hydraulic responses of soil to freezing by modifying the external water migration and intake. Zhang et al. [] observed reduced water absorption in saturated silty clay samples with increasing pressure. This aligns with the previous research of [,,,] showing less external water intake under higher pressure, potentially mitigating frost heave. Further studies by Lu et al. [] found that both confining and deviator stresses significantly impact water migration and external water buildup and that higher overburden pressure reduces external water absorption, consequently diminishing frost heave.
The analysis of the available literature on the effect of applied stress on soil freezing leads to the diagram shown in Figure 7. It compares two columns of frozen soil with and without overburden pressure. Globally, overburden pressure tends to increase the thickness of the frozen fringe, lower the segregation temperature, reduce the water migration toward the frost front, and reduce the overall amount of frost heave produced.
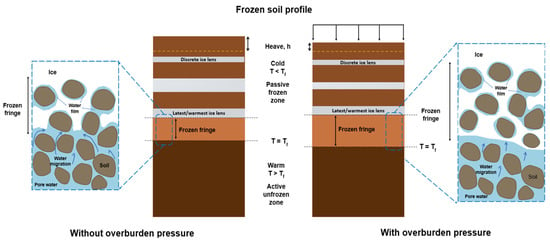
Figure 7.
A schematic diagram of a frozen soil profile with and without overburden pressure [].
6. Properties and Behavior of Soil after FT Cycles
Accurate prediction of frost heave and thaw settlement in models and laboratory tests can be challenging. Often, these predictions underestimate the actual displacements seen in true-scale projects. Key questions regarding the thawing of artificially frozen soils center on the influence of AGF on the post-thaw soil properties (granulometry, porosity, mechanical strength, etc.) and the ability to properly predict surface settlement in AGF projects following thawing.
6.1. Differences behind the Freezing and Thawing Paths
In AGF, the freezing path is different from the thawing path. During freezing and excavation, suction gradients induce moisture migration from unfrozen soil toward the freezing front []. Conversely, thawing can lead to excess pore water pressure and subsequent consolidation if drainage is allowed []. This can lead to thaw settlements that are even greater than the frost heave generated. This can be attributed to several factors. Clays with high plasticity are less prone to frost heave []. Suction-induced freezing forces alter the soil’s fabric [], increasing the permeability [,] and compressibility []. These suction forces cause over-consolidation of the clay, which, when combined with increased permeability, results in undesirable additional settlement during thawing.
A valuable resource for understanding soil behavior during freeze–thaw cycles is the SFCC. Its shape depends on the soil’s nature, initial void ratio, freezing rate, and freeze–thaw history [,]. Figure 8 illustrates the characteristic hysteresis behavior of the SFCC. This hysteresis, where freezing and thawing follow different paths, reflects the distinct processes occurring during each phase. Table 1 presents some of the root causes behind this hysteresis phenomenon.
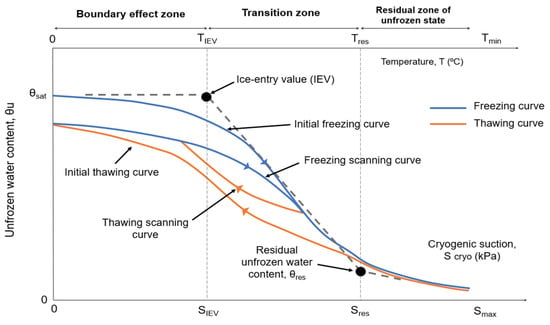
Figure 8.
Schematic representation of a typical soil freezing characteristic curve.

Table 1.
Potential explanations for the hysterical behavior observed in the SFCC.
Therefore, the pathways taken by the freezing and thawing processes are fundamentally different. The core reasons for this discrepancy either entail processes that differ during freezing and thawing or involve processes that occur during one process but not the other. Nevertheless, it is still not fully clear why hysteresis occurs in porous media like soils.
Furthermore, there is a difference between the initial SFCC and subsequent scanning curves. This difference can be attributed to the modification of the soil’s properties during the first freeze–thaw (FT) cycle. As illustrated in Figure 8, the initial thawing curve typically falls below the freezing curve due to hysteresis. The specific reasons behind hysteresis can be found in Table 1. Importantly, subsequent freezing and thawing cycles will occur based on the new soil properties and initial water content established after the first FT cycle. While hysteresis will continue to be observed due to the reasons mentioned earlier, it is crucial to acknowledge that this remains a general scheme of the SFCC upon one or many FT cycles. However, to date, the effect of FT cycling on the SFCC is not well-investigated or -understood in the literature. Current research, like the studies by Kozlowski and Nartowska [] and Ren and Vanapalli [], suggests that the effect of FT cycles on the SFCC can be statistically insignificant in some cases. Kozlowski and Nartowska [] investigated the impact of FT cycles on highly plastic bentonites with varying water contents. They subjected these bentonite specimens to repeated cycles of freezing at −90 °C and thawing at 20 °C within a differential scanning calorimeter (DSC), allowing for free expansion. Their analysis focused on the thawing branches of the SFCC during five FT cycles. While they concluded that the FT cycles had a statistically insignificant effect on the bentonite specimens’ SFCC, they did not delve into the reasons behind this observation. Interestingly, their study did find that subzero temperatures and the specific soil type significantly influenced the SFCC behavior, which aligns with established knowledge about frozen soils. Ren and Vanapalli [] explored the effect of FT cycling on the SFCC of five Canadian soils with low to moderate plasticity. They employed the frequency domain reflectometry (FDR) technique to measure the SFCCs and considered up to three FT cycles. Their findings indicated that these FT cycles had no significant impact on the measured SFCC. They primarily attributed this to the destruction of soil structure during the initial saturation process, suggesting that the subsequent FT cycles had minimal influence on the already disrupted structure (and consequently, the SFCC). Globally, the influence of FT cycles on the SFCC remains far from being fully understood. While some studies have observed statistically insignificant effects on the SFCC in certain scenarios, the overall impact of FT cycles appears to be dependent on several factors. These factors likely include the inherent properties of the soil itself, the methods employed during sample preparation, and the number of freeze–thaw cycles experienced. Further research is necessary to better understand the mechanisms at play and identify the specific soil characteristics that influence the response to FT cycles.
6.2. Stress Path during a Freeze–Thaw Cycle
In 1977, Chamberlain and Blouin [] proposed a framework for understanding the stress paths of soil during a freeze–thaw cycle. They presented a theoretical illustration of the thaw consolidation process in a typical clay soil (Figure 9). It is assumed that the soil is initially saturated and normally consolidated to point “a” on the virgin consolidation curve.
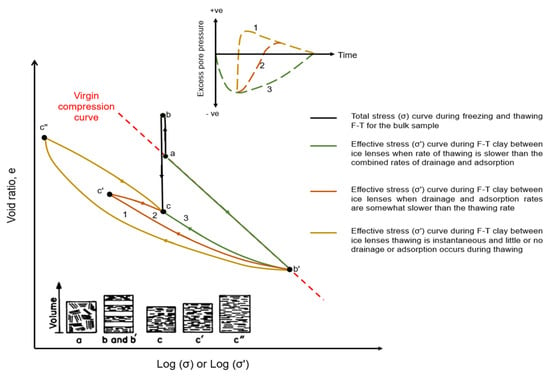
Figure 9.
Schematic illustration of the thaw consolidation process during an FT cycle of a typical clay (after []).
The framework considers the total stress path (abc) representing the soil’s void ratio change during FT. As the soil freezes in an open system (point a), the void ratio increases due to phase change and water migration (point b). Upon thawing, the void ratio decreases as the ice melts (point c).
The effective stress path identifies how the soil strengthens during freezing and weakens during thawing. During freezing, the suction behind the freezing front increases effective stress, leading to over-consolidation (point b′). Three scenarios are considered for the effective stress path during thawing:
- Slow thawing (b′-c): This scenario represents a situation where drainage and adsorption can keep pace with the thawing rate. The effective stress path follows b′-c, reaching equilibrium with no excess pore pressure at point c.
- Moderate thawing rate (b′-c′-c): This intermediate scenario occurs when the drainage and adsorption rates are slightly slower than the thawing rate. The soil swells upon thawing, generating excess pore pressure and a significant increase in the volume change (point c′). As the excess pore pressure dissipates, the soil consolidates further to point c.
- Rapid thawing with minimal drainage/adsorption (b′-c″-c): In this case, thawing is very fast, leading to minimal drainage or adsorption. The excess pore pressure can approach the applied stress, causing the effective stress to drop near zero (b′-c″). Over time, this pressure dissipates and the effective stress returns to the applied stress value (point c).
Despite the variations in the effective stress paths, all the freeze–thaw cycles in fine-grained soils ultimately lead to over-consolidation. During slow thawing, the generated water drains efficiently, resulting in minimal excess pore pressure and settlement as the soil drains the water (point c). However, rapid thawing can lead to significant excess pore pressure (point c′ or c″), compromising the soil stability by reducing the bearing capacity and potentially causing severe differential settlements.
6.3. Modifications in Soil Properties after a Freeze–Thaw Cycle
Throughout a freeze–thaw cycle, the soil undergoes continuous changes. During freezing, ice can develop in different forms, ranging from particle coatings to lenses between soil layers. Upon thawing, the melted water necessitates a new equilibrium void ratio for the soil structure under existing overburden pressure. Freeze–thaw cycles significantly alter the soil properties, including the density, grain size distribution, hydraulic conductivity, strength, compressibility, stiffness, and bearing capacity [,,,,,,,].
Understanding these changes is crucial for AGF projects, as the soil will inevitably experience one complete FT cycle during its lifespan. Research on FT cycles offers comprehension of the associated degradation mechanisms. Notably, the first FT cycle often exerts the most significant impact on the soil [,]. This knowledge is essential for the accurate assessment and control of deformations associated with AGF.
6.3.1. Influence of FT Cycles on the Physical Properties of Soil
- Soil structure and porosity
Over the past few decades, there has been a considerable amount of research conducted on how the soil microstructure changes due to FT cycles. These cycles can alter the size and shape of soil particles, promoting fragmentation of coarse grains (quartz, feldspar, etc.) and aggregation of clay and silt particles. This, in turn, significantly impacts the soil structure and overall properties [,,,,]. Zhai et al. [] investigated the effect of FT cycles on the grain size distribution. Four representative soils from the Qinghai–Tibet Plateau (Adamic earth, Qinghai–Tibet silty red clay, Lanzhou Loess, and Haidong Loess) were subjected to 0, 3, 6, 9, 50, and 100 FT cycles. The results, shown in Figure 10, revealed that FT cycles can significantly alter the initial particle size distribution (PSD), consequently impacting the soil type, structure, and various properties like the water content, porosity, permeability, and density. It is important to acknowledge that the transition in soil type based solely on the PSD (e.g., silt to clay) may not fully capture the changes in the chemical and physical nature of the soil grains themselves.
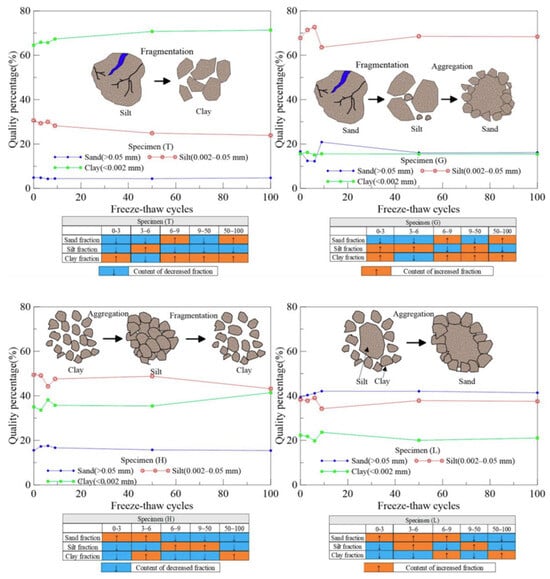
Figure 10.
Variation of the sand, silt, and clay fractions as a function of increasing FT cycles [].
The impact of FT cycles on the soil microstructure extends to its pore structure. Zhang and Cui [] investigated the impact of one FT cycle on the microscopic pore structure of Shanghai grey silty clay using Mercury Intrusion Porosimetry (MIP) tests. Their results revealed a 6.0% increase in the final mercury intrusion volume and a 30.64% increase in the most probable pore size after the FT cycle. These findings suggest that the FT cycle can lead to an enlargement of the microscopic pore structures within the silty clay. An et al. [] employed Nuclear Magnetic Resonance Imaging (NMRI) to assess the microstructural changes induced by AGF upon a single FT cycle in undisturbed granite residual soils (GRSs). The study revealed a decrease in the pore volume of the micropores and an increase in the pore volume of the macro-pores after FT, signifying a significant alteration in the overall PSD of GRSs. Based on the PSD curves, the authors concluded that the FT cycle induced by AGF led to an increase in macropore volume, a slight decrease in micropore volume, and a net increase in overall porosity of approximately 11.1%. Both studies provide compelling evidence that an FT cycle significantly impacts the microscopic pore structure of soils, generally leading to an enlargement of pores and an increase in overall porosity.
- Density and Void Ratio
Freeze–thaw cycles have contrasting effects on soil density (Figure 11). Loose soils tend to densify following FT exposure. This can be due to the formation of ice lenses during freezing, which causes an initial volume increase. Upon thawing, the ice melts, and the soil matrix consolidates, resulting in a denser state characterized by a lower void ratio []. Conversely, dense soils may experience a net loosening effect from FT cycles. While freezing can lead to a temporary volume increase due to ice formation, thawing typically results in some consolidation. However, due to the inherent difficulty of soil particles returning to their exact pre-freezing positions, the void ratio of initially dense soil generally increases after FT cycles. This translates to a net increase in soil volume and a decrease in density, signifying a looser soil structure [].
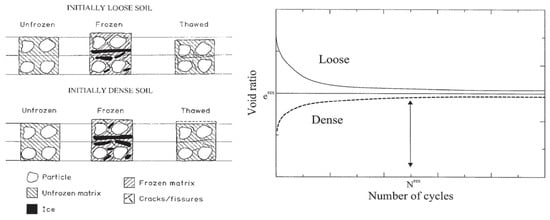
Figure 11.
Microstructural and volume changes of a fine-grained till after several FT cycles [].
Notably, the most significant changes in soil density occur within the first few FT cycles [,]. Beyond a certain number of cycles (Nres), a residual void ratio (eres) is established and further FT exposure has minimal impact on density [,].
- Crack formation
Both freezing and thawing processes can contribute to crack formation. During freezing, three main factors are at play: increased pore volume due to water phase change, formation and growth of ice lenses, and shrinkage caused by negative pore pressure near the freezing front []. The behavior during thawing depends on the soil type (cohesive vs. frictional) and conditions like the water availability and overburden pressure. In clay soils, ice-filled cracks may not fully reseal due to intrinsic strength (cohesion), leading to additional fissures upon thawing. In coarse-grained soils, cracks formed during freezing can be sealed by particle movement during thawing.
Freeze–thaw cycles significantly impact the permeability of fine-grained soils. Studies consistently report significant changes in the permeability of fine-grained soils subjected to FT [,,,,]. Clays experience the most substantial increases in permeability, often exceeding two orders of magnitude. Some studies report even higher increases. Silts generally exhibit smaller permeability changes compared to clays. Dense silty tills (low initial void ratio) show a slight increase in permeability after FT, while loose tills (high initial void ratio) experience a decrease. The changes in the permeability of soils after FT are attributed to two main reasons. The first is related to the emergence of polygonal shrinkage microcracks and the formation of larger pores after the thawing of ice lenses. The second is associated with the movement of fine particles out of the large pores during FT []. The mechanism controlling the process depends on the soil type.
Overburden pressure is a key player in the definition of the permeability of frozen–thawed soils. While shrinkage cracks and ice lenses may develop during freezing and increase hydraulic conductivity, the overburden pressure exerted on the soil can seal the fissures and lower the hydraulic conductivity. Tests on thawed and unfrozen Wisconsin glacial clays by Othman and Benson [] indicated that the degree of the permeability change can be reduced by isotropic loading. The presence of pressure can seal the cracks created by freeze–thaw. Maintaining stress during freeze–thaw had a significant effect, and 70 kPa was sufficient to stop the increase in permeability (Figure 12). However, Viklander [] emphasized that the test procedure (flexible vs. rigid wall permeameter), temperature gradient (1D or 3D freezing), scale effect, hydraulic gradient, and water conditions (closed or open system) affect this influence.
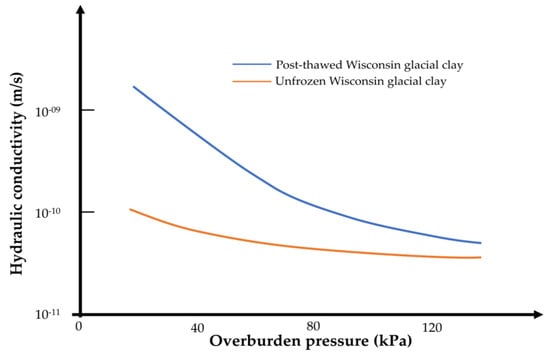
Figure 12.
Hydraulic permeability of Wisconsin glacial clay as a function of the overburden pressure for unfrozen and post-thawed (5 FT cycles) samples [].
6.3.2. Influence of FT Cycles on the Mechanical Properties of Soil
FT cycles significantly impact the mechanical behavior of soils. These cycles alter several key parameters, like the stress–strain relationship and shear strength parameters.
- Stress–strain relationship
Studies show that FT cycles can significantly impact the stress–strain properties of various soil types, including fine-grained sands, clays, residual soils, and saline soils [,,,,,]. These studies generally reveal a common pattern: before FT, the stress–strain curve of soil samples exhibits strain softening, while after FT, it shows a strain hardening tendency. For example, Leroueil et al. [] investigated the mechanical behavior of nine Champlain Sea clays before and after one FT cycle using consolidated isotropic undrained triaxial tests. The results showed a clear change in behavior. The intact clays displayed a peak stress at around 1% strain followed by strain softening. In contrast, the frozen–thawed clays exhibited no peak stress and significantly lower stiffness. Notably, at a strain of 0.5%, the undrained modulus of the frozen–thawed clays was only 20–40% of that of the intact clays. Similar findings were reported by An et al. [] for granite residual soils. They attributed the significant reduction in peak stress after FT to the pressure exerted by ice lens development. This pressure promotes the soil’s friability, leading to lower peak stress when the sample undergoes significant deformation. Liu et al. [] carried out unconsolidated and undrained (UU) triaxial tests on silty sand samples that were subjected to varying numbers of FT cycles at a constant axial strain rate and three different confining pressures (100, 200, and 300 kPa). The results indicated a transition in the stress–strain curve from a weak strain-softening type to a strain-hardening type after FT cycles, particularly under low confining pressures. Both the unfrozen and thawed silty sand samples exhibited strain-hardening behavior at higher confining pressures. Liu et al.’s [] results differ from those reported by Wang et al. [], who found that thawed clay displayed strain-softening behavior under low confining pressure and strain-hardening behavior under higher confining pressure. The discrepancies in these findings are likely attributable to the use of different soil types in the experiments, potentially leading to variations in the critical confining pressures at which the stress–strain behavior transitions from softening to hardening.
- Shear strength parameters
Freeze–thaw cycles have a significant effect on the shear strength of soil. Cohesion generally decreases with more cycles, as soils become less cohesive and more porous. An et al. [] reported a reduction of 15.7% in the cohesion of granite residual soils after one FT cycle, while Han et al. [] observed a similar decrease in saline soil. This cohesion decrease can be associated with the loss of contact between soil particles following the emergence of cracks due to FT.
The impact of FT cycles on the friction angle is less conclusive. Han et al. [] observed a slight increase in the friction angle for saline soil during initial FT cycles, but a decrease after many cycles followed this. They attributed the increase in the angle of friction after the first 10 cycles to the bonding effect of salt crystals.
It is important to acknowledge that various factors beyond temperature and salinity can influence the response of soil to FT cycles. For instance, Yao et al. [] reported an unexpected increase in cohesion for certain fine-grained soils after FT cycles. Their findings highlight the potential influence of the initial soil density on the response to freeze–thaw. They observed that depending on the initial soil density, FT cycles could cause particle connections to become stronger or weaker, increasing or decreasing the apparent cohesion. Interestingly, while FT cycles enhanced the apparent friction angle of the soil regardless of the initial dry unit weight, they decreased the apparent cohesion of the samples prepared at a lower density (16.0 kN/m3) and increased it for those prepared at a higher density (18.3 kN/m3).
Freeze–thaw is a weathering process that has major effects on the mechanical and physical properties of soil at both the microscopic and macroscopic scales. An FT cycle tends to densify loose soil, decreasing its void ratio, and loosen dense soil, increasing its void ratio. Regardless of the void ratio changes, frozen–thawed soil will increase the hydraulic conductivity due to crack development and changes in structure and porosity. FT cycles have also been proven to damage the structure of soils and deteriorate their mechanical performance (peak strength, shear strength, etc.). Damage brought on by freeze–thaw cycles can appear as differential soil heave or settlement that hinders the stability of above-ground or underground structures. These damages originate from thermal and hydraulic deformations induced by the soil’s temperature variations, the freezing of pore water, and the migration of unfrozen water within the pore network.
7. Conclusions
This paper presented the relationship between AGF and its subsequent effects on soil properties. The core findings highlight the highly complex nature of AGF, revealing both its benefits and its potential drawbacks.
- AGF improves soil mechanics and reduces water permeability, creating a more stable environment for construction projects. However, unfrozen water can persist at sub-zero temperatures and migrate in certain soils, forming ice lenses.
- The success of AGF relies on understanding the complex interplay between factors like the temperature, soil composition, and initial ground conditions, which all influence the freezing process. This intricate thermo-hydro-chemo-mechanical process strengthens soil and decreases permeability but can also induce deformations due to water expansion and ice lens formation.
- Frost heave, the upward movement of the ground surface caused by freezing water, has two main contributors: phase change and ice lens formation.
- Overburden pressure, the weight of overlying soil, affects freezing progression and limits ice lens growth by reducing the water flow and lowering the temperature at which ice lenses form.
- Freeze–thaw cycles significantly impact soil properties. In fine-grained soils, FT cycles can lead to over-consolidation, but rapid thawing risks generating high pore pressures and compromising stability.
- The freeze–thaw process by itself acts as a form of weathering that influences the mechanical and physical properties of soil at both the microscopic and macroscopic levels. Notably, FT cycles can loosen dense soil, densify loose soil, and increase the overall hydraulic conductivity due to structural changes within the soil matrix. Additionally, these cycles can weaken the soil structure and deteriorate its mechanical performance.
This review opens up important prospects for furthering our understanding of the complex interactions between the stress, thermal, hydraulic, and mechanical processes underlying frost heave. While significant progress has been made in understanding the influence of overburden pressure on soil freezing, substantial knowledge gaps remain, particularly in the context of large-scale urban AGF applications. A key challenge is the limited experimental data on soil freezing under high stress. Most existing studies rarely explore pressures exceeding 500 kPa, which is not representative of the overburden pressures encountered in urban environments. To address this, future research should focus on developing experimental methods that can simulate the effects of higher overburden pressure on soil freezing behavior while accounting for the presence of a thermal gradient. Moreover, investigating the long-term effects of overburden pressure on soil properties and assessing frost heave mitigation strategies under different ground conditions are crucial areas to be explored in the future.
From a numerical point of view, despite the significant advancements that have been made in the modeling of AGF, it is still far from complete. Capturing the intricate interplay between the soil properties and the multiphysics processes (thermal, hydraulic, mechanical, and chemical) during freezing remains a challenge. Existing models often rely on simplifications or limited couplings and struggle to represent in situ complexities like variations in temperatures, water flows, and external stresses. Furthermore, the validation of the developed model is often faced with limited, high-quality field data. To bridge the gap between complex models and practical applications, future efforts should focus on developing user-friendly, computationally efficient models that can capture the highly coupled and complex nature of AGF projects.
Author Contributions
Writing—original draft preparation, Z.J.; reviewing, F.M., O.C. and A.A., editing, Z.J.; supervision, F.M., O.C. and A.A.; project administration, F.M. and O.C.; funding acquisition, F.M. and O.C. All authors have read and agreed to the published version of the manuscript.
Funding
The study presented in this paper is part of the first author’s Ph.D. thesis, which has been funded by Bouygues Travaux Publics.
Data Availability Statement
No new data were created or analyzed in this study.
Acknowledgments
The authors are grateful for the support of Bouygues Travaux Publics.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Burt, T.P.; Williams, P.J. Hydraulic conductivity in frozen soils. Earth Surf. Process. 1976, 1, 349–360. [Google Scholar] [CrossRef]
- Harris, J.S. Ground Freezing in Practice; Thomas Telford: London, UK; New York, NY, USA, 1995; ISBN 978-0-7277-1995-9. [Google Scholar]
- Andersland, O.B.; Ladanyi, B. Frozen Ground Engineering Second Edition, 2nd ed.; John Wiley & Sons Canada, Ltd.: Toronto, ON, Canada, 1994; ISBN 978-0-471-61549-1. [Google Scholar]
- Taber, S. Frost Heaving. J. Geol. 1929, 37, 428–461. [Google Scholar] [CrossRef]
- Beskow, G. Soil Freezing and Frost Heaving with Special Application to Roads and Railroads. Swed. Geol. Soc. 1935, 26, 145. [Google Scholar] [CrossRef]
- Johansson, T. Artificial Ground Freezing in Clayey Soils Laboratory and Field Studies of Deformations during Thawing at the Bothnia Line. Ph.D. Thesis, Royal Institute of Technology, Stockholm, Sweden, 2009. [Google Scholar]
- Morgenstern, N.R.; Nixon, J.F. One-dimensional Consolidation of Thawing Soils. Can. Geotech. J. 1971, 8, 558–565. [Google Scholar] [CrossRef]
- Zhang, Z.; Pendin, V.V.; Feng, W.; Zhang, Z. The influence of freeze-thaw cycles on the granulometric composition of Moscow morainic clay. Sci. Cold Arid Reg. 2015, 7, 199–205. [Google Scholar] [CrossRef]
- Adeli Ghareh Viran, P.; Binal, A. Effects of repeated freeze–thaw cycles on physico-mechanical properties of cohesive soils. Arab. J. Geosci. 2018, 11, 250. [Google Scholar] [CrossRef]
- Konrad, J.-M. Physical processes during freeze-thaw cycles in clayey silts. Cold Reg. Sci. Technol. 1989, 16, 291–303. [Google Scholar] [CrossRef]
- Chang, D.K.; Lacy, H.S. Artificial Ground Freezing in Geotechnical Engineering. In Proceedings of the Artificial Ground Freezing in Geotechnical Engineering, Arlington, VA, USA, 14 August 2008; p. 12. [Google Scholar]
- Endo, K. Artificial soil freezing method for subway construction. Civ. Eng./Jpn. 1969, 8, 103–117. [Google Scholar]
- Lunardini, V.J. Heat Transfer in Cold Climates, 1st ed.; Van Nostrand Reinhold Co.: New York, NY, USA, 1981. [Google Scholar]
- Koopmans, R.W.R.; Miller, R.D. Soil Freezing and Soil Water Characteristic Curves. Soil Sci. Soc. Am. J. 1966, 30, 680–685. [Google Scholar] [CrossRef]
- Spaans, E.J.A.; Baker, J.M. The Soil Freezing Characteristic: Its Measurement and Similarity to the Soil Moisture Characteristic. Soil Sci. Soc. Am. J. 1996, 60, 13–19. [Google Scholar] [CrossRef]
- Konrad, J.-M.; Morgenstern, N.R. A mechanistic theory of ice lens formation in fine-grained soils. Can. Geotech. J. 1980, 17, 473–486. [Google Scholar] [CrossRef]
- Tounsi, H. Modélisation THMC de la Congélation Artificielle des Terrains: Application à la Mine de Cigar Lake. Ph.D. Thesis, Université Paris Sciences et Lettres, Paris, France, 2019. [Google Scholar]
- Ren, J. Interpretation of the Frozen Soils Behavior Extending the Mechanics of Unsaturated Soils. Ph.D. Thesis, University of Ottawa, Ottawa, ON, Canada, 2019. Available online: http://ruor.uottawa.ca/handle/10393/39555 (accessed on 11 April 2022).
- Spaans, E.J.A.; Baker, J.M. Examining the use of time domain reflectometry for measuring liquid water content in frozen soil. Water Resources Research. 1995, 31, 2917–2926. [Google Scholar] [CrossRef]
- Smith, M.W.; Tice, A.R. Measurement of the Unfrozen Water Content of Soils: Comparison of NMR (Nuclear Magnetic Resonance) and TDR (Time Domain Reflectometry) Methods; US Army Corps of Engineers Cold Regions Research & Engineering Laboratory: Hanover, NH, USA, 1988; Available online: https://apps.dtic.mil/sti/citations/ADA203082 (accessed on 11 April 2022).
- Tice, A.R.; Oliphant, J.L.; Nakano, Y.; Jenkins, T.F. Relationship between the Ice and Unfrozen Water Phases in Frozen Soil as Determined by Pulsed Nuclear Magnetic Resonance and Physical Desorption Data; U.S. Army Corps of Engineers, Cold Regions Research & Engineering Laboratory: Hanover, NH, USA, 1982; Available online: https://apps.dtic.mil/sti/citations/ADA118486 (accessed on 11 April 2022).
- Watanabe, K.; Mizoguchi, M. Amount of unfrozen water in frozen porous media saturated with solution. Cold Reg. Sci. Technol. 2002, 34, 103–110. [Google Scholar] [CrossRef]
- Kozlowski, T. A comprehensive method of determining the soil unfrozen water curves: 2. Stages of the phase change process in frozen soil–water system. Cold Reg. Sci. Technol. 2003, 36, 81–92. [Google Scholar] [CrossRef]
- Fabbri, A.; Fen-Chong, T.; Azouni, A.; Thimus, J.-F. Investigation of Water to Ice Phase Change in Porous Media by Ultrasonic and Dielectric Measurements. J. Cold Reg. Eng. 2009, 23, 69–90. [Google Scholar] [CrossRef]
- Konrad, J.-M. Sixteenth Canadian Geotechnical Colloquium: Frost heave in soils: Concepts and engineering. Can. Geotech. J. 1994, 31, 223–245. [Google Scholar] [CrossRef]
- Azmatch, T.F. Frost Heave: New Ice Lens Initiation Condition and Hydraulic Conductivity Prediction. Ph.D. Thesis, University of Alberta, Edmonton, AB, Canada, 2013. Available online: https://scholar.archive.org/work/n7xgctztgbb7xoaslebmxelbji (accessed on 24 July 2022).
- Sayles, F.H. Creep of Frozen Sands; US Army CRREL: Hanover, NH, USA, 1968; p. 63. [Google Scholar]
- Nixon, J.F. Thaw–Consolidation of Some Layered Systems. Can. Geotech. J. 1973, 10, 15. [Google Scholar] [CrossRef]
- Hampton, C. Strength and Creep Testing of Artificial Ground Freezing. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 1986. [Google Scholar]
- Dysli, M. Le Gel et Son Action Sur Les Sols et Les Fondations; Presses Polytechniques et Universitaires Romandes (PPUR): Lausann, Switzerland, 1991; ISBN 2-88074-229-3. [Google Scholar]
- Rajaei, P.; Baladi, G. Frost Heave: A Semi-Empirical Model Based on Field Data. In Proceedings of the Cold Regions Engineering 2015, Salt Lake City, UT, USA, 19–22 July 2015; American Society of Civil Engineers: Salt Lake City, UT, USA, 2015; pp. 382–393. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, P.; Yang, X.; Qi, J. On the uniaxial compression strength of frozen gravelly soils. Cold Reg. Sci. Technol. 2020, 171, 102965. [Google Scholar] [CrossRef]
- Ji, Y.; Zhou, G.; Vandeginste, V.; Zhou, Y. Thermal-hydraulic-mechanical coupling behavior and frost heave mitigation in freezing soil. Bull. Eng. Geol. Environ. 2021, 80, 2701–2713. [Google Scholar] [CrossRef]
- Sweidan, A.H.; Niggemann, K.; Heider, Y.; Ziegler, M.; Markert, B. Experimental study and numerical modeling of the thermo-hydro-mechanical processes in soil freezing with different frost penetration directions. Acta Geotech. 2022, 17, 231–255. [Google Scholar] [CrossRef]
- Vitel, M. Modélisation Thermo-Hydraulique de la Congélation Artificielle des Terrains. Ph.D. Thesis, Ecole Nationale Supérieure des Mines de Paris, Paris, France, 2015. [Google Scholar]
- Penner, E.; Ueda, T. The dependence of frost heaving on load application—Preliminary results. Proc. Int. Symp. Frost Action Soils 1977, 1, 92–101. [Google Scholar]
- Loch, J.P.G.; Kay, B.D. Water Redistribution in Partially Frozen, Saturated Silt Under Several Temperature Gradients and Overburden Loads. Soil Sci. Soc. Am. J. 1978, 42, 400–406. [Google Scholar] [CrossRef]
- Konrad, J.-M.; Morgenstern, N.R. Effects of applied pressure on freezing soils. Can. Geotech. J. 1982, 19, 494–505. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Springman, S.M. Axial compression stress path tests on artificial frozen soil samples in a triaxial device at temperatures just below 0 °C. Can. Geotech. J. 2014, 51, 1178–1195. [Google Scholar] [CrossRef]
- Banin, A.; Anderson, D.M. Effects of Salt Concentration Changes During Freezing on the Unfrozen Water Content of Porous Materials. Water Resour. Res. 1974, 10, 124–128. [Google Scholar] [CrossRef]
- Pitzer, K.S.; Peiper, J.C.; Busey, R.H. Thermodynamic Properties of Aqueous Sodium Chloride Solutions. J. Phys. Chem. Ref. Data 1984, 13, 1–102. [Google Scholar] [CrossRef]
- Bing, H.; Ma, W. Laboratory investigation of the freezing point of saline soil. Cold Reg. Sci. Technol. 2011, 67, 79–88. [Google Scholar] [CrossRef]
- Wan, X.; Lai, Y.; Wang, C. Experimental Study on the Freezing Temperatures of Saline Silty Soils. Permafr. Periglac. Process. 2015, 26, 175–187. [Google Scholar] [CrossRef]
- Xiao, Z.; Lai, Y.; Zhang, M. Study on the freezing temperature of saline soil. Acta Geotech. 2018, 13, 195–205. [Google Scholar] [CrossRef]
- Zhou, J.; Zhao, W.; Tang, Y. Practical prediction method on frost heave of soft clay in artificial ground freezing with field experiment. Tunn. Undergr. Space Technol. 2021, 107, 103647. [Google Scholar] [CrossRef]
- Dash, J.G. Thermomolecular Pressure in Surface Melting: Motivation for Frost Heave. Science 1989, 246, 1591–1593. [Google Scholar] [CrossRef] [PubMed]
- Tiedje, E. The Experimental Characterization and Numerical Modelling of Frost Heave. Ph.D. Thesis, McMaster University, Hamilton, ON, Canada, 2015. [Google Scholar]
- Taber, S. The Mechanics of Frost Heaving. J. Geol. 1930, 38, 303–317. [Google Scholar] [CrossRef]
- Sheng, D.; Zhang, S.; Yu, Z.; Zhang, J. Assessing frost susceptibility of soils using PCHeave. Cold Reg. Sci. Technol. 2013, 95, 27–38. [Google Scholar] [CrossRef]
- Ming, F.; Zhang, Y.; Li, D. Experimental and theoretical investigations into the formation of ice lenses in deformable porous media. Geosci. J. 2016, 20, 667–679. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, M.; Lu, J.; Pei, W.; Yan, Z. Effect of hydro-thermal behavior on the frost heave of a saturated silty clay under different applied pressures. Appl. Therm. Eng. 2017, 117, 462–467. [Google Scholar] [CrossRef]
- Ji, Y.; Zhou, G.; Hall, M.R.; Vandeginste, V.; Zhao, X. Thermal-Hydraulic-Mechanical Coupling Research on Overburden Pressure Mitigated Ice Lens Growth in the Freezing Soil. KSCE J. Civ. Eng. 2022, 26, 1606–1617. [Google Scholar] [CrossRef]
- Miller, R.D. Freezing and heaving of saturated and unsaturated soils. Highw. Res. Rec. 1972, 393, 1–11. [Google Scholar]
- O’Neill, K.; Miller, R.D. Exploration of a Rigid Ice Model of Frost Heave. Water Resour. Res. 1985, 21, 281–296. [Google Scholar] [CrossRef]
- Akagawa, S. Experimental study of frozen fringe characteristics. Cold Reg. Sci. Technol. 1988, 15, 209–223. [Google Scholar] [CrossRef]
- Xia, D.; Arenson, L.; Biggar, K.; Sego, D. Freezing process in Devon silt-using time-lapse photography. In Proceedings of the 58th Canadian Geotechnical Conference, Saskatoon, SK, Canada, 1 January 2005. [Google Scholar]
- Arenson, L.; Sego, D.; Take, W. Measurement of ice lens growth and soil consolidation during frost penetration using particle image velocimetry (PIV). In Proceedings of the 60th Canadian Geotechnical Conference, Ottawa, ON, Canada, 21 October 2007. [Google Scholar]
- Zhang, L.; Ma, W.; Yang, C.; Wen, Z.; Dong, S. An investigation of pore water pressure and consolidation phenomenon in the unfrozen zone during soil freezing. Cold Reg. Sci. Technol. 2016, 130, 21–32. [Google Scholar] [CrossRef]
- Joudieh, Z. Artificial Ground Freezing: Characterization and Modeling of the Hydromechanical Behavior under Thermal Solicitations. Ph.D. Thesis, Université de Lorraine, Nancy, France, 2024. [Google Scholar]
- Peppin, S.S.L.; Style, R.W. The Physics of Frost Heave and Ice-Lens Growth. Vadose Zone J. 2013, 12, 1–12. [Google Scholar] [CrossRef]
- Henry, K.S. A Review of the Thermodynamics of Frost Heave; Engineer Research and Development Center Hanover NH Cold Regions Research And Engineering Lab: Hanover, Germany, 2000; p. 26. [Google Scholar]
- O’Neill, K.; Miller, R. Numerical Solutions for a Rigid-Ice Model of Secondary Frost Heave; US Army Corps of Engineer: Hanover, NH, USA, 1982; Available online: https://www.semanticscholar.org/paper/Numerical-Solutions-for-a-Rigid-Ice-Model-of-Frost-O%27Neill-Miller/1e8e064cf5f114a8c1eef9ba972894b9794fdd18 (accessed on 5 August 2022).
- Gilpin, R.R. A model for the prediction of ice lensing and frost heave in soils. Water Resour. Res. 1980, 16, 918–930. [Google Scholar] [CrossRef]
- Akagawa, S.; Satoh, M.; Kanie, S.; Mikami, T. Effect of Tensile Strength on Ice Lens Initiation Temperature. In Proceedings of the Cold Regions Engineering 2006, Orono, ME, USA, 23–26 July 2006; pp. 1–12. [Google Scholar] [CrossRef]
- Harlan, R.L. Analysis of coupled heat-fluid transport in partially frozen soil. Water Resour. Res. 1973, 9, 1314–1323. [Google Scholar] [CrossRef]
- Miller, R.D. Frost heaving in non-colloidal soils. In Proceedings of the 3rd International Conference on Permafrost, Edmonton, AB, Canada, 10 July 1978. [Google Scholar]
- Watanabe, K.; Flury, M. Capillary bundle model of hydraulic conductivity for frozen soil. Water Resour. Res. 2008, 44, 9. [Google Scholar] [CrossRef]
- Watanabe, K.; Wake, T. Measurement of unfrozen water content and relative permittivity of frozen unsaturated soil using NMR and TDR. Cold Reg. Sci. Technol. 2009, 59, 34–41. [Google Scholar] [CrossRef]
- Black, P.B. The Rigid Ice Model of Frost Heave and Its Input Functions; Cornell University: Ithaca, NY, USA, 1985. [Google Scholar]
- Ishizaki, T.; Nishio, N. Experimental study of frost heaving of a saturated soil. Tokyo Gas Gijutsu Kenkyusho Hokoku 1988, 88, 65–72. [Google Scholar]
- Sheng, D.; Axelsson, K.; Knutsson, S. Frost Heave due to Ice Lens Formation in Freezing Soils. Hydrol. Res. 1995, 26, 147–168. [Google Scholar] [CrossRef]
- Bronfenbrener, L.; Bronfenbrener, R. Modeling frost heave in freezing soils. Cold Reg. Sci. Technol. 2010, 61, 43–64. [Google Scholar] [CrossRef]
- Nixon, J.F. (Derick) Discrete ice lens theory for frost heave in soils. Can. Geotech. J. 1991, 28, 843–859. [Google Scholar] [CrossRef]
- Ji, Y.; Zhou, G.; Zhou, Y.; Vandeginste, V. Frost heave in freezing soils: A quasi-static model for ice lens growth. Cold Reg. Sci. Technol. 2019, 158, 10–17. [Google Scholar] [CrossRef]
- Nishimura, S.; Gens, A.; Olivella, S.; Jardine, R.J. THM-coupled finite element analysis of frozen soil: Formulation and application. Géotechnique 2009, 59, 159–171. [Google Scholar] [CrossRef]
- Casini, F.; Gens, A.; Olivella, S.; Viggiani, G.M.B. Artificial ground freezing of a volcanic ash: Laboratory tests and modelling. Environ. Geotech. 2016, 3, 141–154. [Google Scholar] [CrossRef]
- Arvidson, W.D.; Morgenstern, N. Water flow induced by soil freezing. Can. Geotech. J. 1977, 14, 237–245. [Google Scholar] [CrossRef]
- Penner, E.; Walton, T. Effects of temperature and pressure on frost heaving. Eng. Geol. 1979, 13, 29–39. [Google Scholar] [CrossRef]
- Konrad, J.-M. Estimation of the segregation potential of fine-grained soils using the frost heave response of two reference soils. Can. Geotech. J. 2005, 42, 38–50. [Google Scholar] [CrossRef]
- Konrad, J.-M. Influence of cooling rate on the temperature of ice lens formation in clayey silts. Cold Reg. Sci. Technol. 1989, 16, 25–36. [Google Scholar] [CrossRef]
- Konrad, J.M. Frost Heave Mechanics. Ph.D. Thesis, University of Alberta, Edmonton, AB, Canada, 1980. [Google Scholar]
- Azmatch, T.F.; Sego, D.C.; Arenson, L.U.; Biggar, K.W. New ice lens initiation condition for frost heave in fine-grained soils. Cold Reg. Sci. Technol. 2012, 82, 8–13. [Google Scholar] [CrossRef]
- Lu, X.; Zhang, F.; Qin, W.; Zheng, H.; Feng, D. Experimental investigation on frost heave characteristics of saturated clay soil under different stress levels and temperature gradients. Cold Reg. Sci. Technol. 2021, 192, 103379. [Google Scholar] [CrossRef]
- Chamberlain, E.J. Overconsolidation effects of ground freezing. Eng. Geol. 1981, 18, 14. [Google Scholar] [CrossRef]
- Chamberlain, E.J.; Gow, A.J. Effect of Freezing and Thawing on the Permeability and Structure of Soils. In Developments in Geotechnical Engineering; Elsevier: Amsterdam, The Netherlands, 1979; Volume 26, pp. 73–92. ISBN 978-0-444-41782-4. [Google Scholar]
- Graham, J.; Au, V.C.S. Effects of freeze–thaw and softening on a natural clay at low stresses. Can. Geotech. J. 1985, 22, 10. [Google Scholar] [CrossRef]
- Bittelli, M.; Flury, M.; Campbell, G.S. A thermodielectric analyzer to measure the freezing and moisture characteristic of porous media. Water Resour. Res. 2003, 39, 10. [Google Scholar] [CrossRef]
- He, H.; Dyck, M. Application of Multiphase Dielectric Mixing Models for Understanding the Effective Dielectric Permittivity of Frozen Soils. Vadose Zone J. 2013, 12, 1–22. [Google Scholar] [CrossRef]
- Tian, H.; Wei, C.; Wei, H.; Zhou, J. Freezing and thawing characteristics of frozen soils: Bound water content and hysteresis phenomenon. Cold Reg. Sci. Technol. 2014, 103, 74–81. [Google Scholar] [CrossRef]
- He, H.; Dyck, M.F.; Si, B.C.; Zhang, T.; Lv, J.; Wang, J. Soil freezing–thawing characteristics and snowmelt infiltration in Cryalfs of Alberta, Canada. Geoderma Reg. 2015, 5, 198–208. [Google Scholar] [CrossRef]
- Homshaw, L.G. Freezing and Melting Temperature Hysteresis of Water in Porous Materials: Application to the Study of Pore Form. J. Soil Sci. 1980, 31, 399–414. [Google Scholar] [CrossRef]
- Anderson, R.; Tohidi, B.; Webber, J.B.W. Gas hydrate growth and dissociation in narrow pore networks: Capillary inhibition and hysteresis phenomena. In Sediment-Hosted Gas Hydrates: New Insights on Natural and Synthetic Systems; Long, D., Lovell, M.A., Rees, J.G., Rochelle, C.A., Eds.; Geological Society of London: London, UK, 2009; Volume 319, pp. 145–159. ISBN 978-1-86239-279-3. [Google Scholar]
- Liu, Z.; Yu, X. Physically Based Equation for Phase Composition Curve of Frozen Soils. Transp. Res. Rec. 2013, 2349, 93–99. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhou, J.; Shi, X.; Zhou, G. Practical models describing hysteresis behavior of unfrozen water in frozen soil based on similarity analysis. Cold Reg. Sci. Technol. 2019, 157, 215–223. [Google Scholar] [CrossRef]
- Kozlowski, T.; Nartowska, E. Unfrozen Water Content in Representative Bentonites of Different Origin Subjected to Cyclic Freezing and Thawing. Vadose Zone J. 2013, 12, 1–11. [Google Scholar] [CrossRef]
- Ren, J.; Vanapalli, S.K. Effect of freeze–thaw cycling on the soil-freezing characteristic curve of five Canadian soils. Vadose Zone J. 2020, 19, e20039. [Google Scholar] [CrossRef]
- Chamberlain, E.J.; Blouin, S.E. Freeze-Thaw Enhancement of the Drainage and Consolidation of Fine-Grained Dredged Material in Confined Disposal Areas: Final Report; Department of Defense, Department of the Army, Corps of Engineers, Waterways Experiment Station, Environmental Effects Laboratory: Vicksburg, MS, USA, 1977. [Google Scholar]
- Othman, M.A.; Benson, C.H. Effect of freeze–thaw on the hydraulic conductivity and morphology of compacted clay. Can. Geotech. J. 1993, 30, 236–246. [Google Scholar] [CrossRef]
- Eigenbrod, K.D.; Knutsson, S.; Sheng, D. Pore-Water Pressures in Freezing and Thawing Fine-Grained Soils. J. Cold Reg. Eng. 1996, 10, 77–92. [Google Scholar] [CrossRef]
- Viklander, P. Compaction and Thaw Deformation of Frozen Soil: Permeability and Structural Effects due to Freezing and Thawing. Ph.D. Thesis, Luleå University of Technology, Luleå, Sweden, 1997. [Google Scholar]
- Han, Y.; Wang, Q.; Wang, N.; Wang, J.; Zhang, X.; Cheng, S.; Kong, Y. Effect of freeze-thaw cycles on shear strength of saline soil. Cold Reg. Sci. Technol. 2018, 154, 42–53. [Google Scholar] [CrossRef]
- Zhai, J.; Zhang, Z.; Melnikov, A.; Zhang, M.; Yang, L.; Jin, D. Experimental Study on the Effect of Freeze—Thaw Cycles on the Mineral Particle Fragmentation and Aggregation with Different Soil Types. Minerals 2021, 11, 913. [Google Scholar] [CrossRef]
- An, R.; Zhang, X.; Kong, L.; Gong, J.; Lei, X. Artificial Ground Freezing Impact on Shear Strength and Microstructure of Granite Residual Soil under an Extremely Low Temperature. Front. Earth Sci. 2021, 9, 772459. [Google Scholar] [CrossRef]
- Viklander, P. Permeability and volume changes in till due to cyclic freeze/thaw. Can. Geotech. J. 1998, 35, 471–477. [Google Scholar] [CrossRef]
- Zhai, J.; Zhang, S.; Zhang, Z.; Melnikov, A.; Li, H. Study on the geometry characteristics of soil primary mineral particles under cryogenic action. Sci. Rep. 2022, 12, 16766. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.-L.; Cui, Z.-D. Effects of freezing-thawing and cyclic loading on pore size distribution of silty clay by mercury intrusion porosimetry. Cold Reg. Sci. Technol. 2018, 145, 185–196. [Google Scholar] [CrossRef]
- Eigenbrod, K.D. Effects of cyclic freezing and thawing on volume changes and permeabilities of soft fine-gained soils. Can. Geotech. J. 1996, 33, 529–537. [Google Scholar] [CrossRef]
- Qi, J.; Ma, W.; Song, C. Influence of freeze–thaw on engineering properties of a silty soil. Cold Reg. Sci. Technol. 2008, 53, 397–404. [Google Scholar] [CrossRef]
- Leroueil, S.; Tardif, J.; Roy, M.; Rochelle, P.L.; Konrad, J.-M. Effects of frost on the mechanical behaviour of Champlain Sea clays. Can. Geotech. J. 1991, 28, 690–697. [Google Scholar] [CrossRef]
- Aubert, J.E.; Gasc-Barbier, M. Hardening of clayey soil blocks during freezing and thawing cycles. Appl. Clay Sci. 2012, 65–66, 1–5. [Google Scholar] [CrossRef]
- Li, G.; Ma, W.; Zhao, S.; Mao, Y.; Mu, Y. Effect of Freeze-Thaw Cycles on Mechanical Behavior of Compacted Fine-Grained Soil. In Sustainable Infrastructure Development in a Changing Cold Environment, Proceedings of Cold Regions Engineering 2012, Quebec City, Canada, 19 August 2012; Morse, B., Doré, G., Eds.; American Society of Civil Engineers: Reston, VA, USA, 2012; pp. 72–81. [Google Scholar] [CrossRef]
- Wang, X.; Li, S.; Sun, Y.; Zhang, C.; Liu, G. Influence of freeze–thaw cycling on the soil mechanical properties of open-pit mine dump under different moisture contents. Environ. Earth Sci. 2021, 80, 279. [Google Scholar] [CrossRef]
- Liu, J.; Chang, D.; Yu, Q. Influence of freeze-thaw cycles on mechanical properties of a silty sand. Eng. Geol. 2016, 210, 23–32. [Google Scholar] [CrossRef]
- Wang, D.; Ma, W.; Niu, Y.; Chang, X.; Wen, Z. Effects of cyclic freezing and thawing on mechanical properties of Qinghai–Tibet clay. Cold Reg. Sci. Technol. 2007, 48, 34–43. [Google Scholar] [CrossRef]
- Yao, X.; Fang, L.; Qi, J.; Yu, F. Study on Mechanism of Freeze-Thaw Cycles Induced Changes in Soil Strength Using Electrical Resistivity and X-Ray Computed Tomography. J. Offshore Mech. Arct. Eng. 2017, 139, 021501. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).