Derivation of Contour Plots for the Characterization of the Behaviour of Sand under Undrained Loading
Abstract
1. Introduction
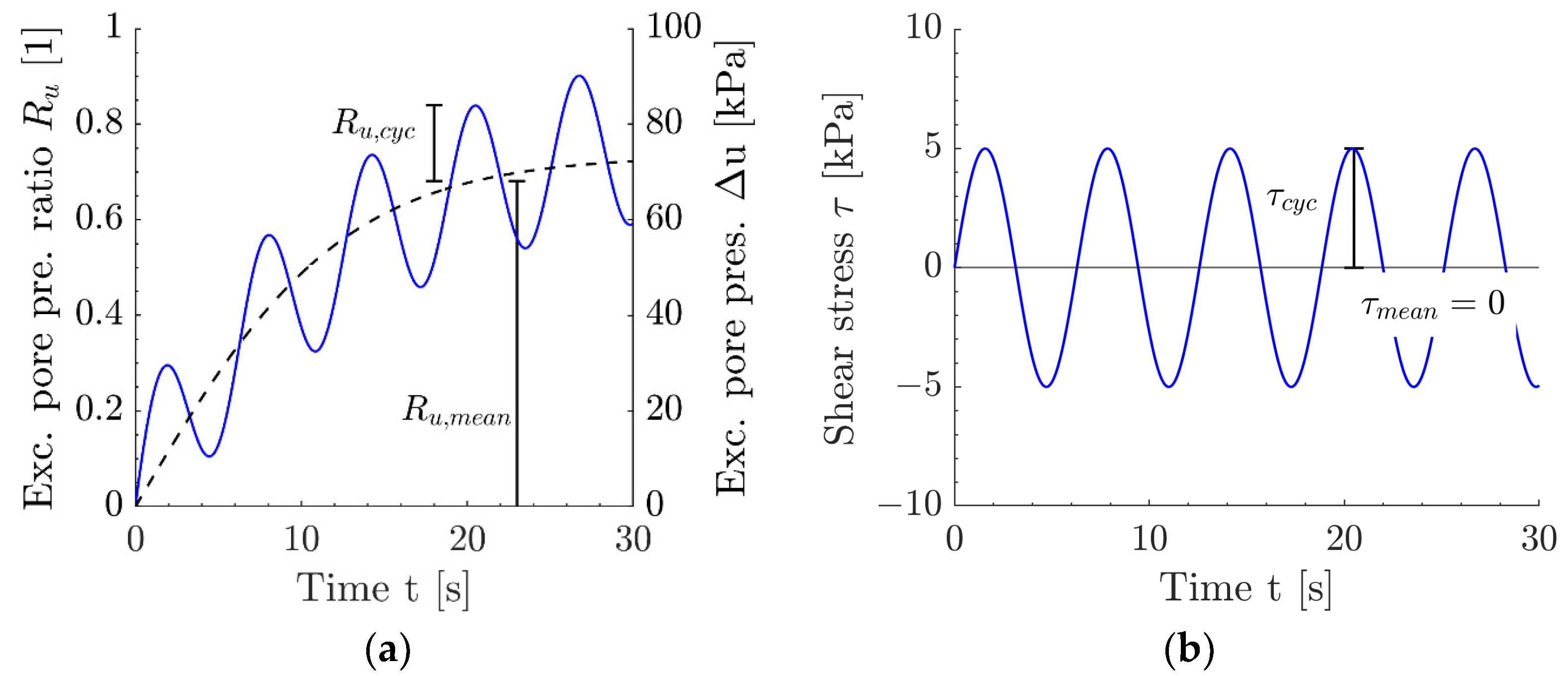
2. State of the Art Regarding Contour Plots for Excess Pore Pressures
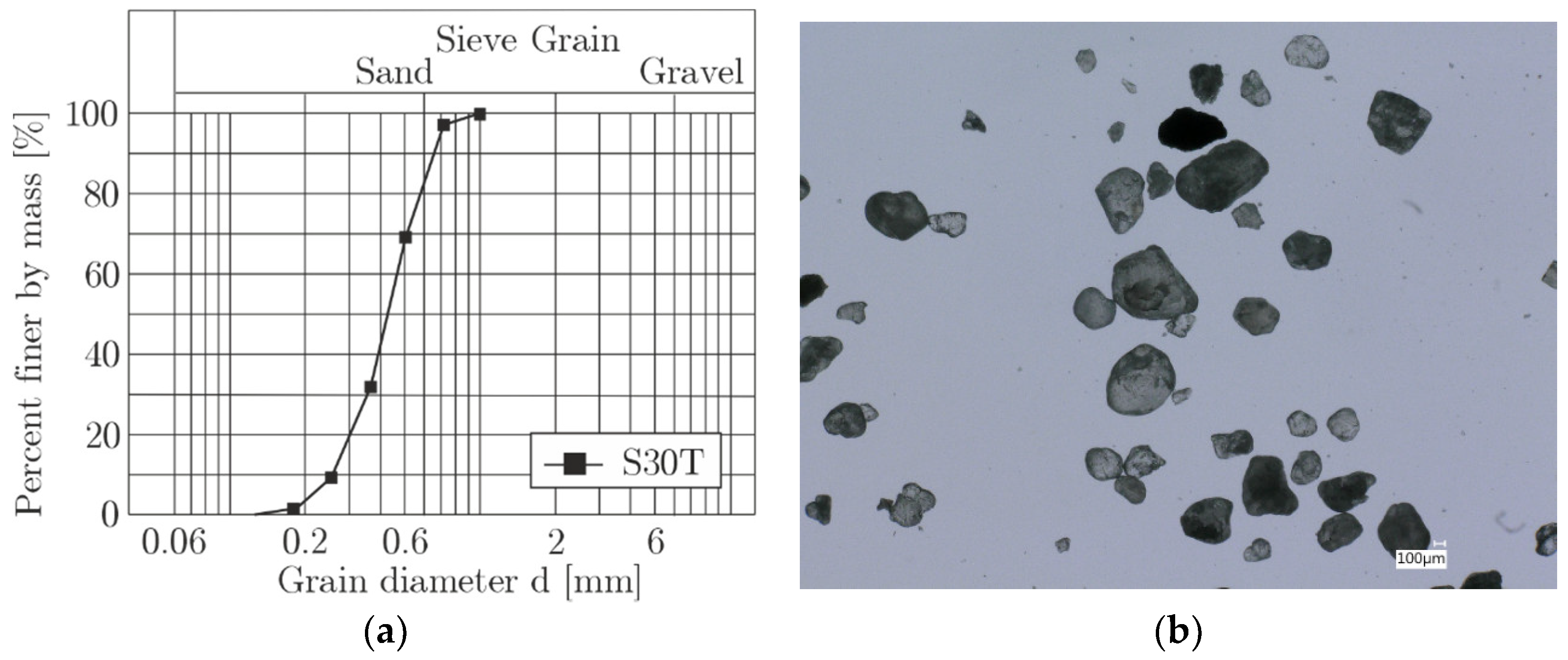
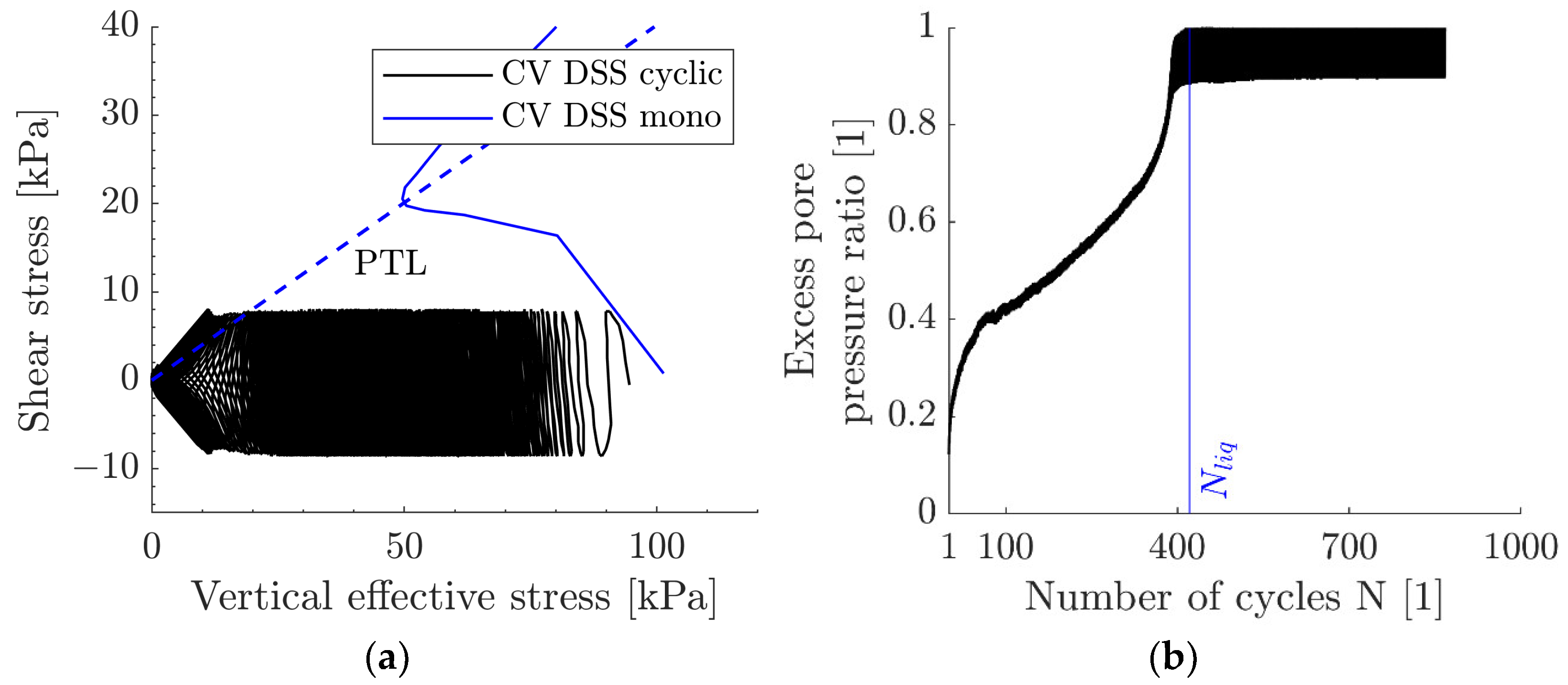
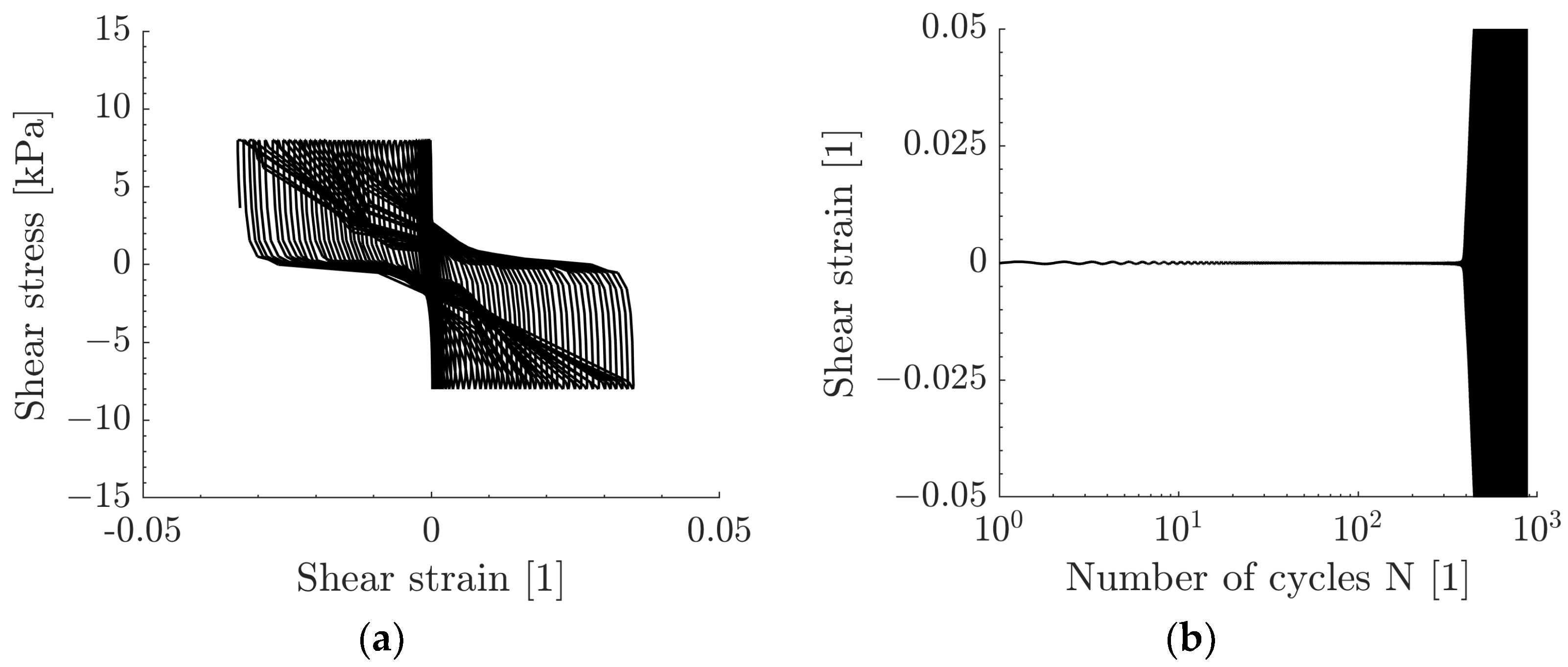
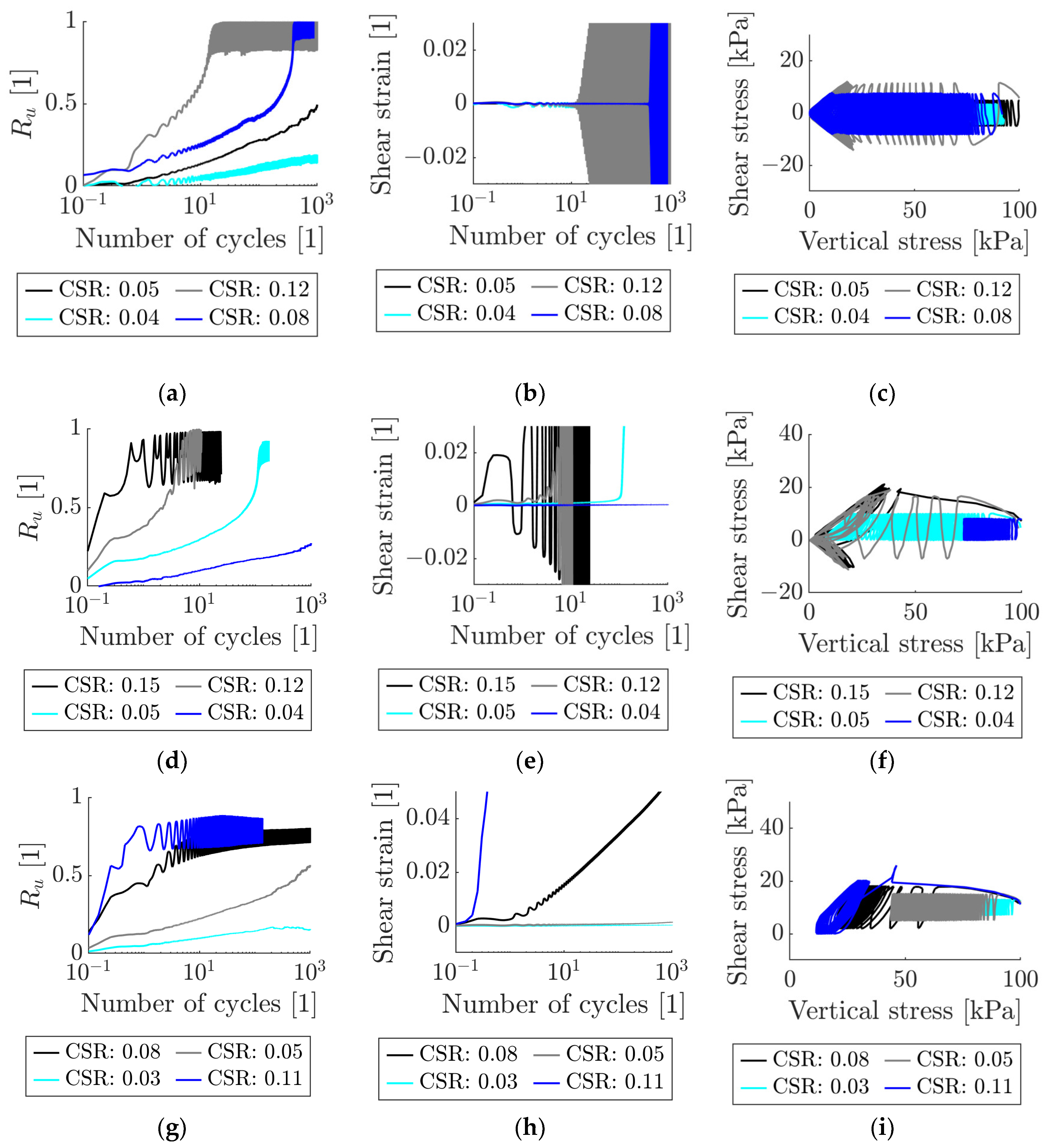
3. Cyclic Laboratory Test Results for a Poorly Graded Medium Sand
4. Contour Plots for Reference Sand
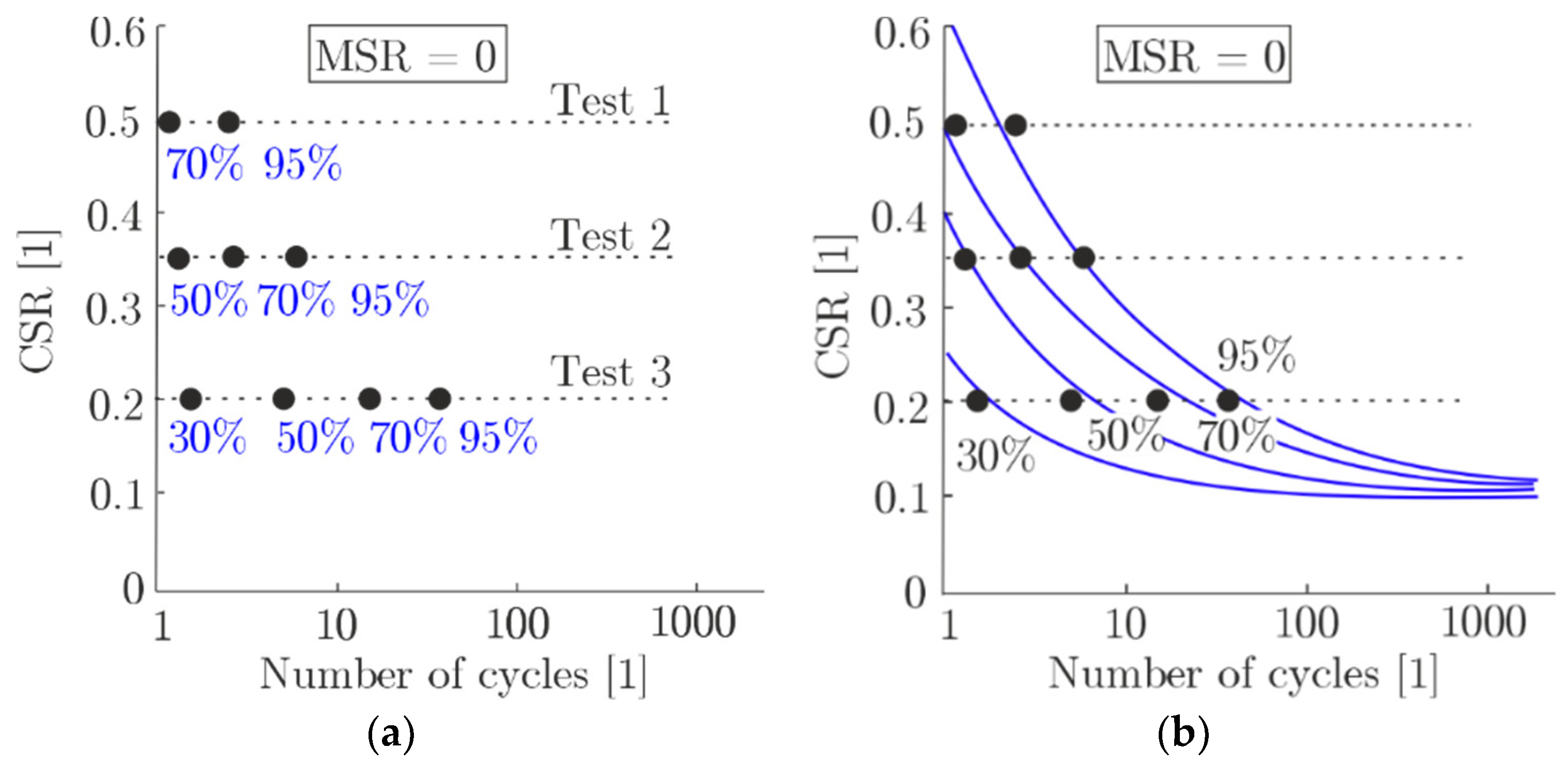
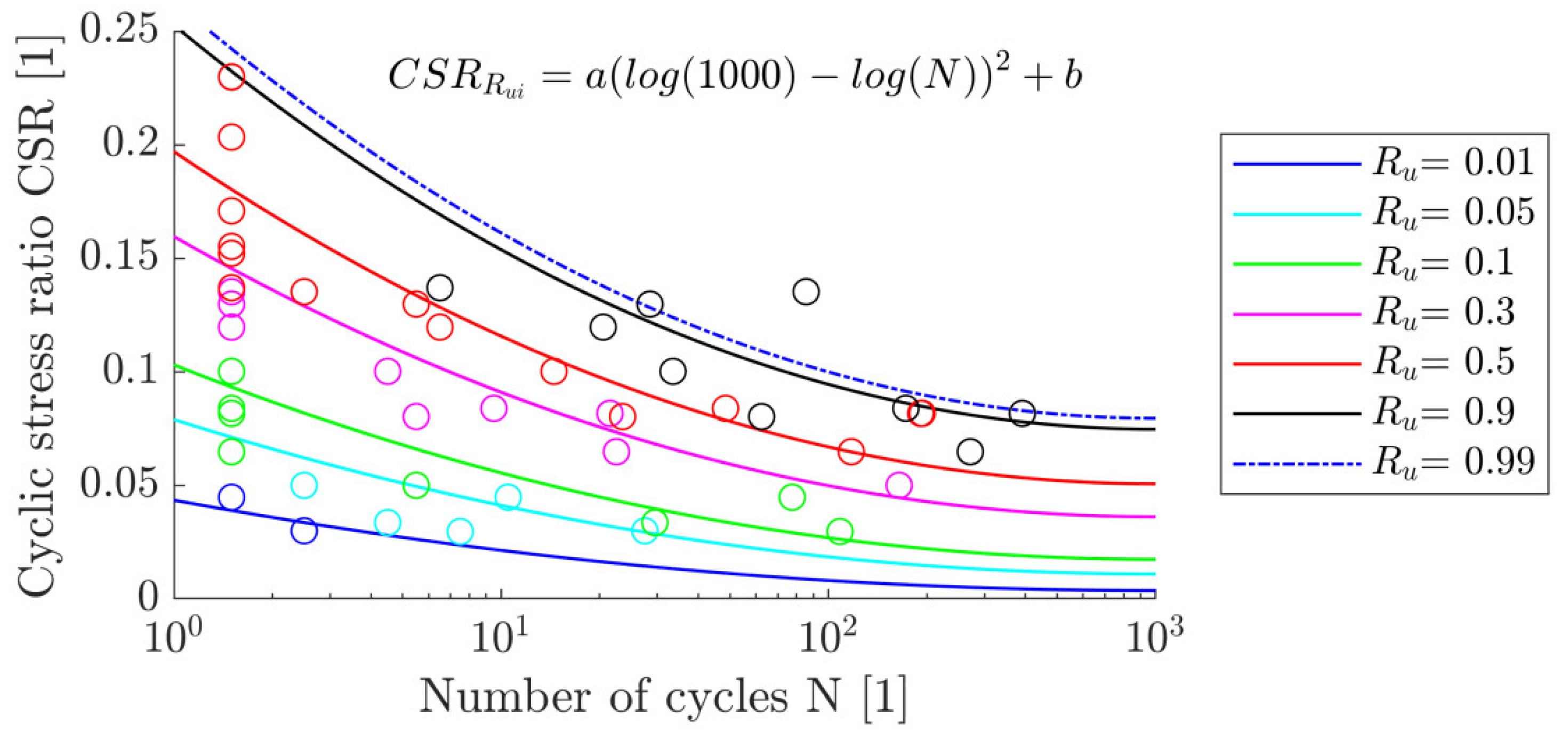
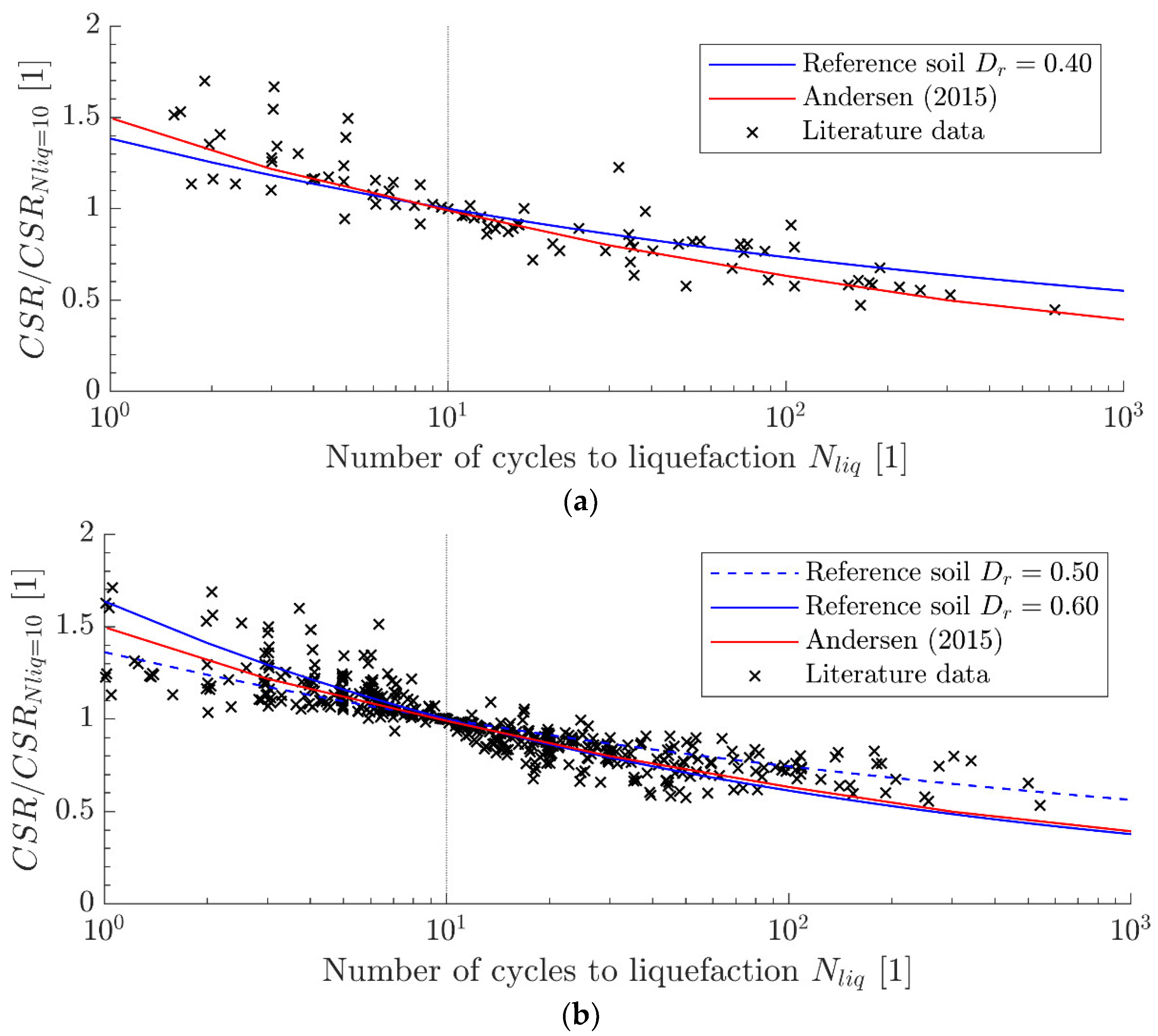
4.1. Existing Approaches
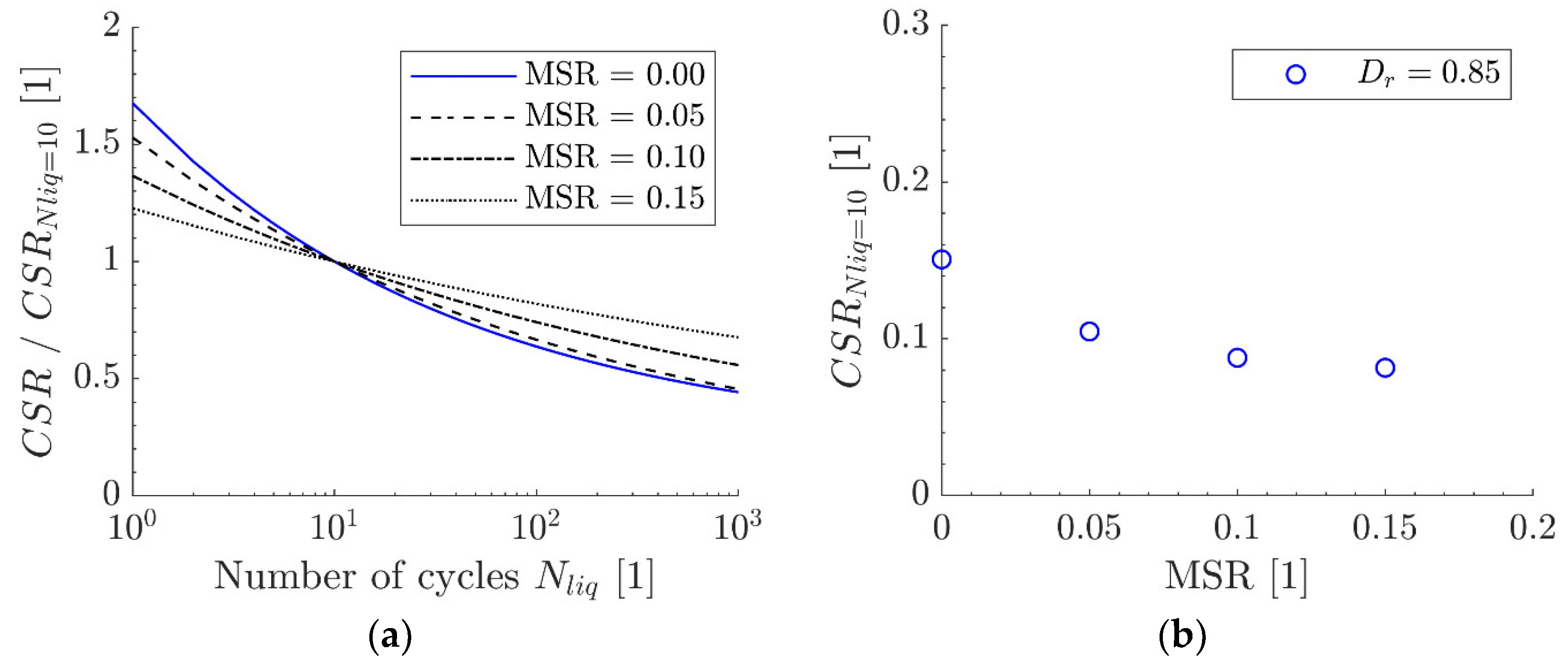
4.2. New Approach
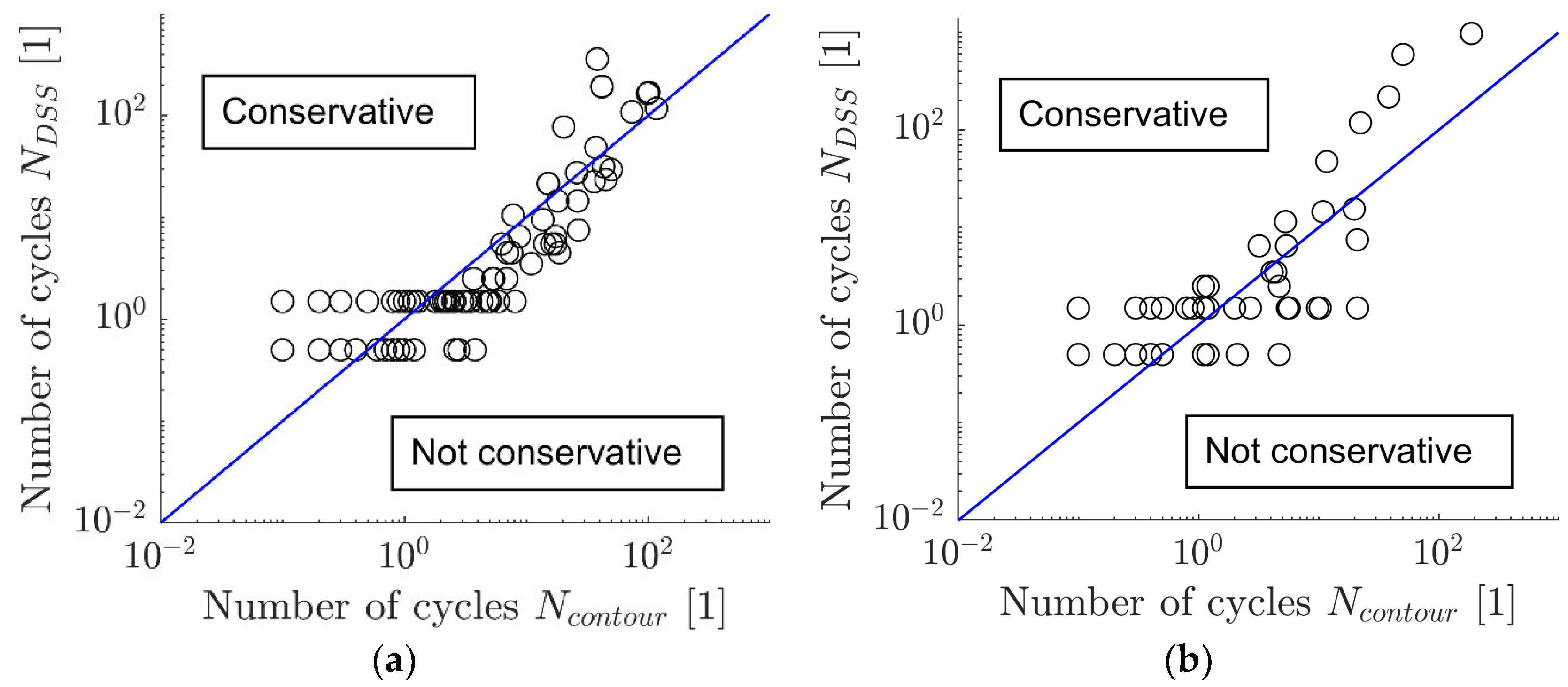
5. Construction of Contour Plots with Minimum Test Results
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. List of References Evaluated with Respect to Normalized CSR-Nliq Curves
| Publication | Stress [kPa] | Relative Density [1] |
|---|---|---|
| Ahn and Park (2013) [29] | 100, 200 | 0.40, 0.53, 0.67, 0.77, 0.80 |
| Carraro et al. (2003) [30] | 100 | 0.40, 0.67, 0.77, 0.82 |
| Chien et al. (2002) [31] | - | 0.40, 0.58, 0.77 |
| De Alba et al. (1976) [32] | 55 | 0.54, 0.68, 0.82 |
| Enomoto (2019) [33] | 25 | 0.44 |
| Evans and Zhou (1995) [34] | 100 | 0.40, 0.60, 0.84 |
| Finn et al. (1976) [35] | - | 0.45 |
| Ghionna and Porcino (2006) [36] | - | 0.35, 0.40 |
| Hosono and Yoshimine (2004) [37] | - | 0.40, 0.62 |
| Hyodo et al. (1991) [38] | 100 | 0.50, 0.70 |
| Hyodo et al. (1994) [39] | 100, 200 | 0.35, 0.66 |
| Hyodo et al. (1996) [40] | 100, 300, 500 | 0.80 |
| Hyodo et al. (2002) [41] | 5000 | 0.80 |
| Ishihara and Li (1972) [42] | - | 0.65 |
| Ishihara and Takatsu (1979) [43] | 20 | 0.55 |
| Ishihara et al. (1980) [44] | 98 | 0.554, 0.68, 0.85 0.94 |
| Ishihara and Yamazaki (1980) [45] | 200 | 0.49 |
| Ishihara et al. (1985) [46] | 200 | 0.50, 0.79, 092 |
| Ishihara (1985) [47] | 98 | 0.55, 0.65, 0.88 |
| Ishihara (1993) [48] | - | 0.50, 0.60 |
| Kokusho (2016) [49] | 98 | 0.55 |
| Konstadinou and Georgiannou (2014) [50] | 120, 320 | 0.25 |
| Nemat-Nasser and Shokooh (1979) [51] | 95, 196, 490, 784 | 0.37, 0.50, 0.68, 0.82 |
| Pan and Yang (2017) [52] | 100 | 0.28 |
| Polito (1999) [7] | 100 | 0.43, 0.58, 0.65, 0.81 |
| Salem et al. (2013) [53] | 50, 100, 200 | 0.40, 0.80 |
| Shahnazari et al. (2016) [54] | 60, 100, 260, 300 | 0.65 |
| Sze and Yang (2014) [55] | 100, 500 | 0.20, 0.35 |
| Tatsuoka et al. (1986) [56] | 100 | 0.50, 0.60, 0.70, 0.80, 0.90 |
| Tatsuoka and Silver (1981) [57] | 100 | 0.50, 0.80 |
| Tokimatsu and Hosaka (1986) [58] | 98 | 0.57 0.83 |
| Vaid and Chern (1983) [59] | 200 | 0.45, 0.55, 0.65 |
| Wijewickreme et al. (2005) [60] | 100, 200 | 0.40 |
| Wu et al. (2004) [61] | 40, 80, 180 | 0.35, 0.45, 0.60, 0.80 |
| Xenaki and Athanasopoulos (2003) [62] | 105, 196 | 0.92 |
| Yang and Sze (2011) [63] | 100, 300 | 0.20, 0.50 |
| Yoshimi et al. (1989) [64] | 78 | 0.54, 0.64, 0.78, 0.84 |
| Yoshimi et al. (1994) [65] | 55, 98 | 0.60, 0.87 |
References
- Andersen, K.H. Behaviour of clay subjected to undrained cyclic loading. In Behaviour of Off-Shore Structures; Norwegian Geotechnical Institute: Oslo, Norway, 1976. [Google Scholar]
- Andersen, K.H.; Lauritzsen, R.; Dyvik, R.; Aas, P.M. Cyclic bearing capacity analysis for gravity platforms. In Proceedings of the International Conference on Behaviour of Offshore Structures, BOSS’88, Trondheim, Norway, 21–25 June 1988. [Google Scholar]
- Andersen, K.H.; Høeg, K. Deformations of Soils and Displacements of Structures subjected to Combined Static and Cyclic Loads; Norgesgeotekniske Institutt: Oslo, Norway, 1992. [Google Scholar]
- Achmus, M.; Saathoff, J.-E.; Thieken, K. Numerical method for evaluation of excess pore pressure build-up at cyclically loaded offshore foundations. In Numerical Methods in Geotechnical Engineering IX; CRC Press: Boca Raton, FL, USA, 2018; pp. 1461–1468. [Google Scholar] [CrossRef]
- Saathoff, J.-E.; Achmus, M. Practical approach for the evaluation of cyclically induced excess pore pressure around offshore foundations in sand. In Proceedings of the 4th International Symposium on Frontiers in Offshore Geotechnics, Austin, TX, USA, 28–31 August 2020. [Google Scholar]
- Saathoff, J.-E.; Achmus, M. Estimation of capacity decrease due to accumulated excess pore pressures around cyclically loaded offshore foundations in sand. Ocean. Eng. 2024, 294, 116743. [Google Scholar] [CrossRef]
- Polito, C.P. The Effects of Non-Plastic and Plastic Fines on the Liquefaction of Sandy Soils; Virginia Polytechnic Institute and State University: Blacksburg, VA, USA, 1999; Available online: http://hdl.handle.net/10919/30243 (accessed on 10 January 2023).
- Vucetic, M.; Dobry, R. Pore Pressure Buildup and Liquefaction at Level Sandy Sites during Earthquakes; Rensselaer Polytechnic Institute: Troy, NY, USA, 1986. [Google Scholar]
- Dobry, R.; Ladd, R.S.; Yokel, F.Y.; Chung, R.M.; Powell, D. Prediction of Pore Water Pressure Buildup and Liquefaction of Sands during Earthquakes by the Cyclic Strain Method; U.S. Department of Commerce, National Bureau of Standards: Gaithersburg, MD, USA, 1982. [Google Scholar] [CrossRef]
- Seed, H.B.; Martin, P.P.; Lysmer, J. The Generation and Dissipation of Pore Water Pressures during Soil Liquefaction; College of Engineering, University of California: Davis, CA, USA, 1975. [Google Scholar]
- Seed, H.B.; Lee, K.L. Liquefaction of saturated sands during cyclic loading. J. Soil Mech. Found. Div. 1966, 92, 105–134. [Google Scholar] [CrossRef]
- Silver, M.L.; Chan, C.K.; Ladd, R.S.; Lee, K.L.; Tiedemann, D.A.; Townsend, F.C.; Valera, J.E.; Wilson, J.H. Cyclic triaxial strength of standard test sand. J. Geotech. Eng. Div. 1976, 102, 511–523. [Google Scholar] [CrossRef]
- Lee, K.L.; Seed, H.B. Cyclic stress conditions causing liquefaction of sand. J. Soil Mech. Found. Div. 1967, 93, 47–70. [Google Scholar] [CrossRef]
- De Alba, P.; Chan, C.K.; Seed, H. Determination of Soil Liquefaction Characteristics by Large-Scale Laboratory Tests; Shannon & Wilson, Inc.: Seattle, WA, USA, 1975. [Google Scholar]
- Airey, D.W.; Wood, D.M. Pore pressures in simple shear. Soils Found. 1986, 26, 91–96. [Google Scholar] [CrossRef]
- Finn, W.D.L.; Vaid, Y.P. Liquefaction potential from drained constant volume cyclic simple shear tests. In Proceedings of the 6th World Conference on Earthquake Engineering, New Delhi, India, 10–14 January 1977. [Google Scholar]
- Feda, J. Constant volume shear tests of saturated sand. Arch. Hydrotech. 1971, 18, 349–367. [Google Scholar]
- ASTM D8296-19; Standard Test Method for Consolidated Undrained Cyclic Direct Simple Shear Test Under Constant Volume with Load Control or Displacement Control. ASTM: West Conshohocken, PA, USA, 2019. Available online: https://www.astm.org/d8296-19.html (accessed on 10 May 2023).
- Andersen, K.H. Cyclic soil parameters for offshore foundation design. In Frontiers in Offshore Geotechnics III, ISFOG’2015; The 3rd McClelland Lecture; Meyer, V., Ed.; Taylor & Francis Group: London, UK, 2015; pp. 5–82. [Google Scholar]
- Andersen, K.H.; Engin, H.K.; D’Ignazio, M.; Yang, S. Determination of cyclic soil parameters for offshore foundation design from an existing data base. Ocean. Eng. 2023, 267, 113180. [Google Scholar] [CrossRef]
- Blaker, O.; Andersen, K.H. Cyclic properties of dense to very dense silica sand. Soils Found. 2019, 59, 982–1000. [Google Scholar] [CrossRef]
- Youd, T.L. Compaction of sands by repeated shear straining. J. Soil Mech. Found. Div. 1972, 98, 709–725. [Google Scholar] [CrossRef]
- Studer, J.A.; Laue, J.; Koller, M. Bodendynamik—Grundlagen, Kennziffern, Probleme und Lösungsansätze; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef]
- Zorzi, G.; Kirsch, F.; Richter, T.; Ostergaard, M.U.; Sorensen, S.P.H. Validation of explicit method to predict accumulation of strain during single and multistage cyclic loading. In Proceedings of the XVII European Conference on Soil Mechanics and Geotechnical Engineering, Reykjavík, Iceland, 1–6 September 2019. [Google Scholar] [CrossRef]
- Boukpeti, N.; Lehane, B.; Carraro, J.A.H. Strain accumulation procedure during staged cyclic loading of carbonate sediments. In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 7–12 June 2014. [Google Scholar] [CrossRef]
- Zografou, D.; Gourvenec, S.; O’Loughlin, C.D. Response of normally consolidated kaolin clay under irregular cyclic loading and comparison with predictions from the accumulation procedure. Géotechnique 2019, 69, 106–121. [Google Scholar] [CrossRef]
- Ronold, K.O. Reliability of Marine Clay Foundations in Cyclic Loading. Ph.D. Thesis, Stanford University, Department of Civil Engineering, Stanford, CA, USA, 1993. [Google Scholar] [CrossRef]
- DNV-RP-C212; Offshore Soil Mechanics and Geotechnical Engineering. Det Norske Veritas: Oslo, Norway, 2019.
- Ahn, J.K.; Park, D. Accumulated Stress Based model for prediction of residual pore pressure. In Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering, Paris, France, 2–6 September 2013; pp. 1567–1570. [Google Scholar]
- Carraro, J.A.H.; Bandini, P.; Salgado, R. Liquefaction resistance of clean and nonplastic silty sands based on cone penetration resistance. J. Geotech. Geoenviron. Eng. 2003, 129, 965–976. [Google Scholar] [CrossRef]
- Chien, L.K.; Oh, Y.N.; Chang, C.H. Effects of fines content on liquefaction strength and dynamic settlement of reclaimed soil. Can. Geotech. J. 2002, 39, 254–265. [Google Scholar] [CrossRef]
- De Alba, P.A.; Chan, C.K.; Seed, H.B. Sand liquefaction in large-scale simple shear tests. J. Geotech. Eng. Div. 1976, 102, 909–927. [Google Scholar] [CrossRef]
- Enomoto, T. Liquefaction and post-liquefaction properties of sand-silt mixtures and undisturbed silty sands. Soils Found. 2019, 59, 2311–2323. [Google Scholar] [CrossRef]
- Evans, M.D.; Zhou, S. Liquefaction behavior of sand-gravel composites. J. Geotech. Eng. 1995, 121, 287–298. [Google Scholar] [CrossRef]
- Finn, W.D.L.; Martin, G.R.; Byrne, P.M. Seismic response and liquefaction of sands. J. Geotech. Eng. Div. 1976, 102, 841–856. [Google Scholar] [CrossRef]
- Ghionna, V.N.; Porcino, D. Liquefaction resistance of undisturbed and reconstituted samples of a natural coarse sand from undrained cyclic triaxial tests. J. Geotech. Geoenviron. Eng. 2006, 132, 194–202. [Google Scholar] [CrossRef]
- Hosono, Y.; Yoshimine, M. Liquefaction of Sand in Simple Shear Condition; Taylor & Francis: London, UK, 2004; pp. 129–136. [Google Scholar]
- Hyodo, M.; Murata, H.; Yasufuku, N.; Fujii, T. Undrained cyclic shear strength and residual shear strain of saturated sand by cyclic triaxial tests. Soils Found. 1991, 31, 60–76. [Google Scholar] [CrossRef]
- Hyodo, M.; Yamamoto, Y.; Sugiyama, M. Undrained cyclic shear behaviour of normally consolidated clay subjected to initial static shear stress. Soils Found. 1994, 34, 1–11. [Google Scholar] [CrossRef]
- Hyodo, M.; Aramaki, N.; Itoh, M.; Hyde, A.F. Cyclic strength and deformation of crushable carbonate sand. Soil Dyn. Earthq. Eng. 1996, 15, 331–336. [Google Scholar] [CrossRef]
- Hyodo, M.; Hyde, A.F.; Aramaki, N.; Nakata, Y. Undrained monotonic and cyclic shear behaviour of sand under low and high confining stresses. Soils Found. 2002, 42, 63–76. [Google Scholar] [CrossRef]
- Ishihara, K.; Li, S. Liquefaction of saturated sand in triaxial torsion shear test. Soils Found. 1972, 12, 19–39. [Google Scholar] [CrossRef]
- Ishihara, K.; Takatsu, H. Effects of overconsolidation and K0, conditions on the liquefaction characteristics of sands. Soils Found. 1979, 19, 59–68. [Google Scholar] [CrossRef]
- Ishihara, K.; Troncoso, J.; Kawase, Y.; Takahashi, Y. Cyclic strength characteristics of tailings materials. Soils Found. 1980, 20, 127–142. [Google Scholar] [CrossRef]
- Ishihara, K.; Yamazaki, F. Cyclic simple shear tests on saturated sand in multi-directional loading. Soils Found. 1980, 20, 45–59. [Google Scholar] [CrossRef]
- Ishihara, K.; Yamazaki, A.; Haga, K. Liquefaction of k0-consolidated sand under cyclic rotation of principal stress direction with lateral constraint. Soils Found. 1985, 25, 63–74. [Google Scholar] [CrossRef]
- Ishihara, K. Stability of natural deposits during earthquakes. In Proceedings of the 11th International Conference on Soil Mechanics and Foundation Engineering, San Francisco, CA, USA, 12–16 August 1985. [Google Scholar]
- Ishihara, K. Liquefaction and flow failure during earthquakes. Géotechnique 1993, 43, 351–451. [Google Scholar] [CrossRef]
- Kokusho, T. Major advances in liquefaction research by laboratory tests compared with in situ behavior. Soil Dyn. Earthq. Eng. 2016, 91, 3–22. [Google Scholar] [CrossRef]
- Konstadinou, M.; Georgiannou, V. Prediction of pore water pressure generation leading to liquefaction under torsional cyclic loading. Soils Found. 2014, 54, 993–1005. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Shokooh, A. A unified approach to densification and liquefaction of cohesionless sand in cyclic shearing. Can. Geotech. J. 1979, 16, 659–678. [Google Scholar] [CrossRef]
- Pan, K.; Yang, Z.X. Effects of initial static shear on cyclic resistance and pore pressure generation of saturated sand. Acta Geotech. 2017, 13, 473–487. [Google Scholar] [CrossRef]
- Salem, M.; Elmamlouk, H.; Agaiby, S. Static and cyclic behavior of north coast calcareous sand in Egypt. Soil Dyn. Earthq. Eng. 2013, 55, 83–91. [Google Scholar] [CrossRef]
- Shahnazari, H.; Jafarian, Y.; Tutunchian, M.A.; Rezvani, R. Probabilistic assessment of liquefaction occurrence in calcareous fill materials of kawaihae harbor, hawaii. Int. J. Geomech. 2016, 16, 05016001. [Google Scholar] [CrossRef]
- Sze, H.Y.; Yang, J. Failure modes of sand in undrained cyclic loading: Impact of sample preparation. J. Geotech. Geoenviron. Eng. 2014, 140, 152–169. [Google Scholar] [CrossRef]
- Tatsuoka, F.; Ochi, K.; Fujii, S.; Okamoto, M. Cyclic undrained triaxial and torsional shear strength of sands for different sample preparation methods. Soils Found. 1986, 26, 23–41. [Google Scholar] [CrossRef]
- Tatsuoka, F.; Silver, M.L. Undrained stress-strain behavior of sand under irregular loading. Soils Found. 1981, 21, 51–66. [Google Scholar] [CrossRef]
- Tokimatsu, K.; Hosaka, Y. Effects of sample disturbance on dynamic properties of sand. Soils Found. 1986, 26, 53–64. [Google Scholar] [CrossRef]
- Vaid, Y.P.; Chern, J.C. Effect of static shear on resistance to liquefaction. Soils Found. 1983, 23, 47–60. [Google Scholar] [CrossRef]
- Wijewickreme, D.; Sanin, M.V.; Greenaway, G.R. Cyclic shear response of fine-grained mine tailings. Can. Geotech. J. 2005, 42, 1408–1421. [Google Scholar] [CrossRef]
- Wu, J.; Kammerer, A.; Riemer, M.F.; Seed, R.B.; Pestana, J.M. Laboratory study of liquefaction triggering criteria. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Xenaki, V.; Athanasopoulos, G. Liquefaction resistance of sand–silt mixtures: An experimental investigation of the effect of fines. Soil Dyn. Earthq. Eng. 2003, 23, 1–12. [Google Scholar] [CrossRef]
- Yang, J.; Sze, H.Y. Cyclic behaviour and resistance of saturated sand under non-symmetrical loading conditions. Géotechnique 2011, 61, 59–73. [Google Scholar] [CrossRef]
- Yoshimi, Y.; Tokimatsu, K.; Hosaka, Y. Evaluation of liquefaction resistance of clean sands based on high-quality undisturbed samples. Soils Found. 1989, 29, 93–104. [Google Scholar] [CrossRef]
- Yoshimi, Y.; Tokimatsu, J.; Ohara, A.N. In situ liquefaction resistance of clean sands over a wide density range. Géotechnique 1994, 44, 479–494. [Google Scholar] [CrossRef]




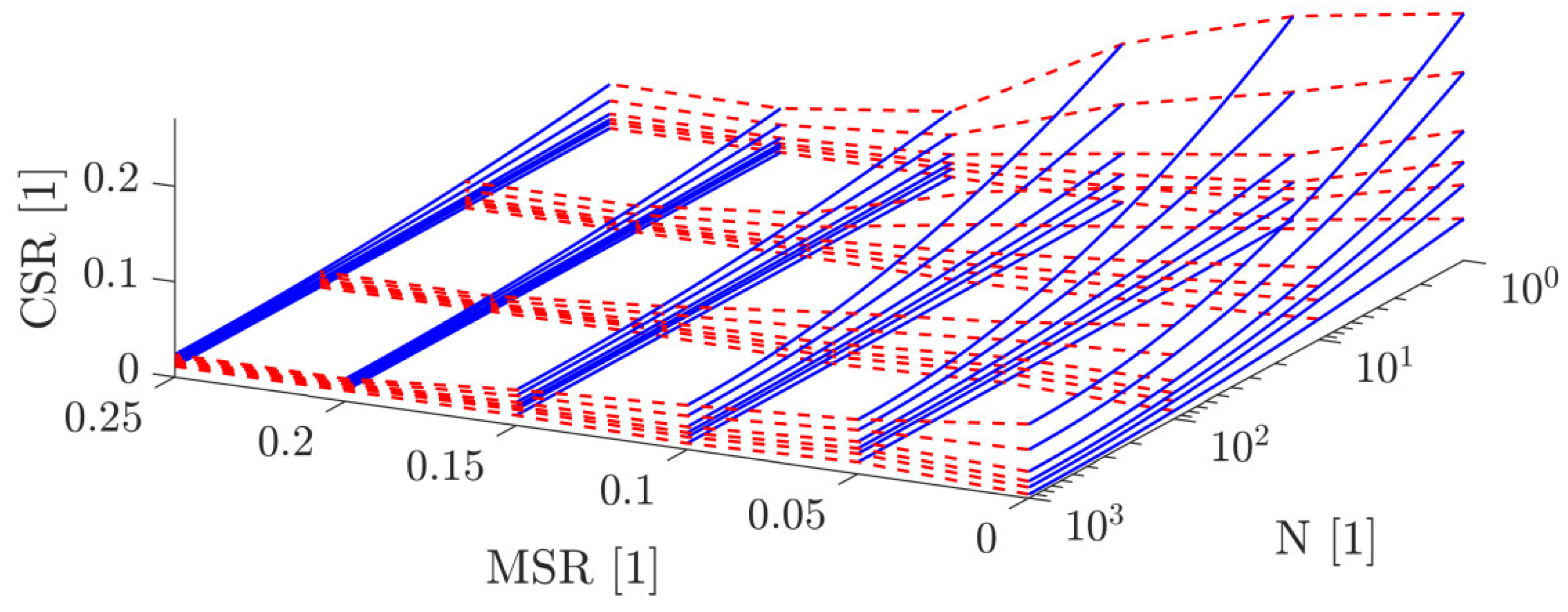


| MSR [1] | [1] | [1] | [1] | [1] |
|---|---|---|---|---|
| 0.00 | 0.0205 | 0.3328 | 0.0804 | 0.6601 |
| 0.05 | 0.0201 | 0.7823 | 0.0580 | 0.3353 |
| 0.10 | 0.0150 | 0.8000 | 0.0476 | 0.4265 |
| 0.15 | 0.0050 | 0.9000 | 0.0378 | 0.2744 |
| >0.25 | 0.0041 | 0.9000 | 0.0237 | 0.1624 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saathoff, J.-E.; Achmus, M. Derivation of Contour Plots for the Characterization of the Behaviour of Sand under Undrained Loading. Geotechnics 2024, 4, 530-548. https://doi.org/10.3390/geotechnics4020029
Saathoff J-E, Achmus M. Derivation of Contour Plots for the Characterization of the Behaviour of Sand under Undrained Loading. Geotechnics. 2024; 4(2):530-548. https://doi.org/10.3390/geotechnics4020029
Chicago/Turabian StyleSaathoff, Jann-Eike, and Martin Achmus. 2024. "Derivation of Contour Plots for the Characterization of the Behaviour of Sand under Undrained Loading" Geotechnics 4, no. 2: 530-548. https://doi.org/10.3390/geotechnics4020029
APA StyleSaathoff, J.-E., & Achmus, M. (2024). Derivation of Contour Plots for the Characterization of the Behaviour of Sand under Undrained Loading. Geotechnics, 4(2), 530-548. https://doi.org/10.3390/geotechnics4020029






