Improved Wave Equation Analysis for Piles in Soil-Based Intermediate Geomaterials with LRFD Recommendations and Economic Impact Assessment
Abstract
1. Introduction
2. Existing Studies on Wave Equation Analysis of Pile Driving
3. Pile Load Test Data
4. Four WEAP Procedures for Bearing Graph Analyses
4.1. WEAP SAD Method
- N ≤ 60: N and γ are used to define the geomaterial.
- N > 60 for coarse-grained soil-based IGM (CG-IGM): ϕ and γ are used to define the geomaterial.
- N > 60 for fine-grained soil-based IGM (FG-IGM): qu and γ are used to define the geomaterial.
4.2. WEAP UWD Method
4.3. WEAP SAR Method
4.4. WEAP UWR Method
5. Back-Calculation Procedure for Dynamic Parameters
5.1. Back-Calculation Results
5.2. Subsurface Condition I (Fine-Grained Soil-Based IGM as Bearing Layer)
5.3. Subsurface Condition II (Coarse-Grained Soil-Based IGM as Bearing Layer)
5.4. Subsurface Condition III (Either Soil or Soil-Based IGM as Bearing Layer)
6. Determination of Pile Resistances from Bearing Graph Analysis
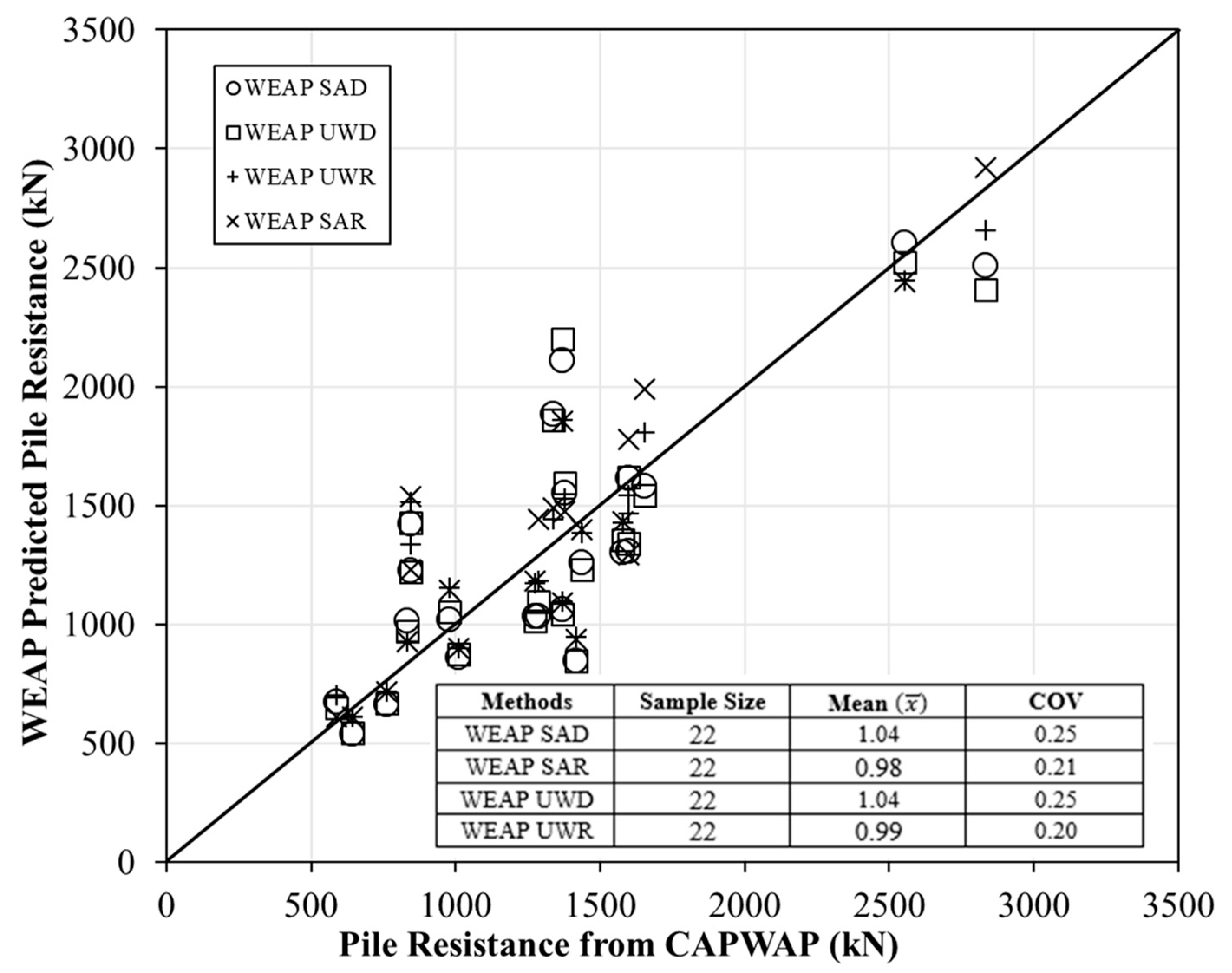
7. Validation of Improved WEAP Methods
8. LRFD Resistance Factors
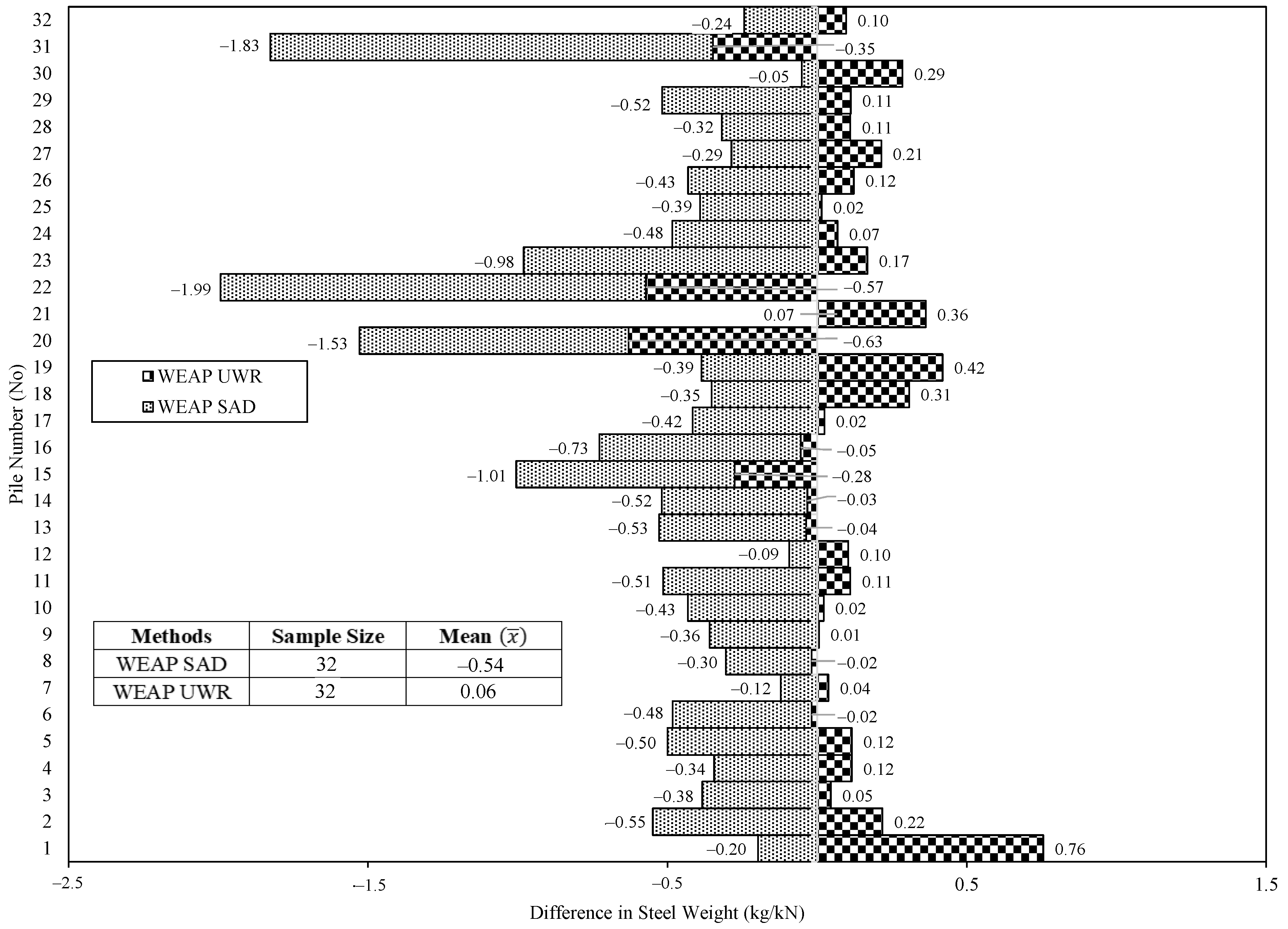
9. Economic Impact Assessment
10. Summary and Conclusions
- Quake values of 2.5 mm and D/120 for Qs and Qt, respectively, are adequate for the S-IGMs. Smith damping factors are found to depend on the pile driving and subsurface conditions. Single values of Smith damping factors are inadequate for different pile and driving conditions. Hence, new Smith damping factors are proposed for three different subsurface conditions.
- Using 34 training pile test data and 22 independent test pile data, it is found that WEAP UWR is the most efficient as it provides a mean resistance bias of 1.02 closer to 1 and the lowest COV of 0.18.
- A φ value of 0.75 for WEAP UWR calibrated based on FOSM at βT = 2.33 for piles driven into S-IGMs is higher than the value of φ of 0.5 recommended in AASHTO [38] for piles in soils. Compared with the default WEAP SAD, the selected proposed WEAP UWR method, on average, reduces the underprediction of pile resistances by 6% and improves the reliability with a 43% reduction in the coefficient of variation (COV) for βT = 2.33.
- The economic impact assessment reveals that the average differences in steel weight per unit load for the WEAP SAD and WEAP UWR are −0.54 kg/kN and 0.06 kg/kN, respectively. Compared with the WEAP SAD method, the WEAP UWR method seems to be more efficient as the average difference in steel weight per unit load is closer to zero, which will reduce construction challenges.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Santi, P.M.; Doyle, B.C. The Locations and Engineering Characteristics of Weak Rock in the US. In Characterization of Weak and Weathered Rock Masses; Santi, P.M., Shakoor, A., Eds.; Association of Engineering Geologists Special Publication 9; Association of Engineering Geologists: Denver, CO, USA, 1997; pp. 1–22. [Google Scholar]
- Clarke, B.G.; Smith, A. Self-boring Pressuremeter Tests in Weak Rocks. In Construction and Building Materials; Elsevier: Amsterdam, The Netherlands, 1992; Volume 6, pp. 91–96. [Google Scholar]
- Marinos, P.G. Hard Soils-Soft Rocks: Geological Features with Special Emphasis to Soft Rocks. In Geotechnical Engineering of Hard Soils-Soft Rocks; A.A. Balkema: Brookfield, The Netherlands, 1997; pp. 1807–1818. [Google Scholar]
- De Freitas, H. Introduction to Session 1.2: Weak Arenaceous Rock. In Proceedings of the 26th Annual Conference of the Engineering Group Geological Society, Leeds, UK, 9–13 September 1993; pp. 115–123. [Google Scholar]
- Martin, D.; Stacey, P. Guidelines for Open Pit Slope Design in Weak Rocks; CSIRO Publishing: Clayton, Australia, 2018. [Google Scholar]
- Mokwa, R.L.; Brooks, H. Axial Capacity of Piles Supportedon Intermediate Geomaterials; Final Report No. FHWA/MT-08-008/8117-32; Western Transportation Institute, Montana State University: Bozeman, MT, USA, 2008. [Google Scholar]
- Masud, N.B.; Ng, K.W.; Wulff, S.S.; Johnson, T. Driven Piles in Fine Grained Soil-based Intermediate GeoMaterials. J. Bridge Eng. 2022, 27, 04022037-1-13. [Google Scholar] [CrossRef]
- Masud, N.B.; Ng, K.W.; Wulff, S.S. New Static Analysis Methods for the Prediction of Driven Pile Resistance in Siltstone. In Proceedings of the Geo-Congress 2022, Geotechnical Special Publication No. 332, ASCE, Charlotte, NC, USA, 20–23 March 2022; pp. 93–103. [Google Scholar]
- Masud, N.B.; Ng, K.W.; Kalauni, H.K.; Wulff, S.S. Reliability-based design improvement and prediction of steel driven pile resistances in rock-based intermediate geomaterials. Acta Geotech. 2023, 19, 1083–1105. [Google Scholar] [CrossRef]
- Islam, M.S.; Ng, K.W.; Wulff, S.S. Improved wave equation analysis of steel H-piles in shales considering LRFD and Economic Impact Studies. J. Bridge Eng. 2022, 27, 04022039-1-13. [Google Scholar] [CrossRef]
- Islam, M.S. Pile Behaviors in Shales through Full-Scale Static Load Testing, Dynamic Testing, and Finite Element Analysis. Master’s Thesis, Department of Civil and Architectural Engineering, University of Wyoming, Laramie, WY, USA, 2021. [Google Scholar]
- Long, H.J. Static Pile Load Tests on Driven Piles in Intermediate Geomaterials; Project No. 0092-12-08; Wisconsin Highway Research Program: Madison, WI, USA, 2016. [Google Scholar]
- Masud, N.B.; Ng, K.W.; Oluwatuyi, O.E.; Islam, M.S.; Kalauni, H.K.; Wulff, S.S. Evaluation of Static Load Test Systems for Driven Piles in Intermediate GeoMaterials. Transp. Res. Rec. 2023, 2677, 741–756. [Google Scholar] [CrossRef]
- Doherty, P.; Igoe, D. A driveability study of precast concrete piles in dense sand. DFI J.-J. Deep Found. Inst. 2013, 7, 3–16. [Google Scholar] [CrossRef]
- Rausche, F.; Nagy, M.; Webster, S.; Liang, L. CAPWAP and refined wave equation analyses for driveability predictions and capacity assessment of offshore pile installations. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Honolulu, HI, USA, 31 May–5 June 2009; Volume 43475, pp. 375–383. [Google Scholar]
- Schneider, J.A.; Ivy, A.H. Analyzing drivability of open ended piles in very dense sands. DFI J.-J. Deep Found. Inst. 2010, 4, 32–44. [Google Scholar] [CrossRef]
- Ramey, G.E.; Hudgins, A.P. Sensitivity and Accuracy of the Pile Wave Equation. Ground Eng. 1977, 10, 45–47. [Google Scholar]
- Coyle, H.M.; Bartoskewitz, R.E.; Berger, W.J. Bearing Capacity by Wave Equation Analysis—State of Art; Texas Transportation Institute, Texas A&M University: College Station, TX, USA, 1973. [Google Scholar]
- Raines, R.D.; Ugaz, O.G.; O’Neill, M.W. Driving characteristics of open-toe piles in dense sand. J. Geotech. Eng. 1992, 118, 72–88. [Google Scholar] [CrossRef]
- Bartoskewitz, R.E.; Coyle, H.M. Wave Equation Prediction of Pile Bearing Capacity Compared with Field Test Results; Research Report 125-5; Texas Transportation Institute, Texas A&M University: College Station, TX, USA, 1970. [Google Scholar]
- Rausche, F.; Thendean, G.; Abou-Matar, H.; Likins, G.E.; Goble, G.G. Determination of Pile Driveability and Capacity from Penetration Tests, Volume I (No. FHWA-RD-96-179); Department of Transportation, Federal Highway Administration: Washington, DC, USA, 1997.
- Iskander, M.G.; Stachula, A. Wave equation analyses of fiber-reinforced polymer composite piling. J. Compos. Constr. 2002, 6, 88–96. [Google Scholar] [CrossRef]
- Ta, A.N.; Hammann, M. Application of adjusted wave equation analysis for optimized pile acceptance criteria. In Proceedings of the 5th International Young Geotechnical Engineers’ Conference, Paris, France, 31 August–1 September 2013; pp. 230–233. [Google Scholar]
- Masud, N.B.; Ng, K.W.; Wulff, S.S. Resistance responses and design recommendations for driven piles in coarse-grained soil-based intermediate geomaterials. Soils Found. 2023, 63, 101381. [Google Scholar] [CrossRef]
- Pile Dynamics, Inc. GRLWEAP Manual for Windows; Pile Dynamics, Inc.: Cleveland, OH, USA, 2010. [Google Scholar]
- Smith, T.; Banas, A.; Gummer, M.; Jin, J. Recalibration of the GRLWEAP LRFD Resistance Factor for Oregon DOT; No. FHWA-OR-RD-11-08; Research Unit, Oregon Department of Transportation: Salem, OR, USA, 2011.
- Smith, E.A.L. Pile-Driving Analysis by the Wave Equation. Trans. Am. Soc. Civ. Eng. 1962, 127, 1145–1171. [Google Scholar] [CrossRef]
- Goble, G.G.; Rausche, F. Wave Equation Analysis of Pile Driving—WEAP Program Manual; Report No. FHWA IP-76-14.1 through IP-76-14.4; U.S. Department of Transportation: Washington, DC, USA, 1976; Volume 1–4.
- Lawton, E.C.; Fragaszy, R.J.; Higgins, J.D.; Kilian, A.P.; Peters, A.J. Review of Methods for Estimating Pile Capacity; No. 1105: Structure Foundations; Transportation Research Board: Washington, DC, USA, 1986; pp. 32–40. [Google Scholar]
- Forehand, P.W.; Reese, J.L. Prediction of capacity by the wave equation. J. Soil Mech. Found. Div. ASCE 1964, 90, 1–26. [Google Scholar] [CrossRef]
- Liang, R.Y.; Sheng, Y. Wave Equation Parameters from Driven-Rod Test. J. Geotech. Eng. 1993, 119, 1037–1057. [Google Scholar] [CrossRef]
- McVay, M.C.; Kuo, C.L. Estimate Damping and Quake by Using Traditional Soil Testing; Department of Civil Engineering, University of Florida: Gainesville, FL, USA, 1999. [Google Scholar]
- Coyle, H.M.; Gibson, G.C. Closure to Empirical Damping Constants for Sands and Clays. J. Soil Mech. Found. Div. 1970, 97, 1487–1488. [Google Scholar] [CrossRef]
- Hannigan, P.J.; Goble, G.G.; Thendean, G.; Likins, G.E.; Rausche, F. Design and Construction of Driven Pile Foundations—Volume II; FHWA-HI-97-013; National Highway Institute, Federal Highway Administration, U.S. Department of Transportation: Washington, DC, USA, 1998.
- Adhikari, P. Load and Resistance Factor Design and Construction Control of Driven Piles in Intermediate Geomaterials. Ph.D. Dissertation, Department of Civil and Architectural Engineering, University of Wyoming, Laramie, WY, USA, 2019. [Google Scholar]
- Smith, E.A.L. Pile driving analysis by the wave equation. American Society of Civil Engineers. ASCE J. Soil Mech. Found. Eng. 1960, 86, 35–61. [Google Scholar] [CrossRef]
- Long, J.; Anderson, A. Improved Design for Driven Piles on a Pile Load Test Program in Illinois; Resarch Report FHWA-ICT-12-011; Center for Transportation: Urabana, IL, USA, 2012. [Google Scholar]
- AASHTO. AASHTO LRFD Bridge Design Specifications, 9th ed.; U.S. Customary Units. American Association of State Highway and Transportation Officials (AASHTO): Washington, DC, USA, 2020. [Google Scholar]
- Bougataya, Y.; Stuedlein, A.W. Region-specific calibration of resistance factors for use with static and wave equation analyses of driven piles. DFI J.-J. Deep Found. Inst. 2016, 10, 143–152. [Google Scholar] [CrossRef]
- Paikowsky, S.G.; Birgisson, B.; McVay, M.; Nguyen, T.; Kuo, C.; Baecher, G.; Ayyab, B.; Stenersen, K.; O’Malley, K.; Chernauskas, L.; et al. Load and Resistance Factor Design (LRFD) for Deep Foundations; NCHRP Report No. 507; Transportation Research Board of the National Academics: Washington, DC, USA, 2004. [Google Scholar]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Anderson, T.W.; Darling, D.A. Asymptotic Theory of Certain Goodness-of-fit Criteria based on Stochastic Processes. Ann. Math. Stat. 1952, 23, 193–212. [Google Scholar] [CrossRef]





| References | Dynamic Parameter | |||
|---|---|---|---|---|
| Qs | Qt | Js | Jt | |
| Smith [27] | 2.5 mm | 2.5 mm | 0.16 s/m | 0.49 s/m |
| Coyle and Gibson [33] | NA | NA | NA | |
| Coyle et al. [18] | 2.5 mm | 2.5 mm | 0.66 s/m (clay) 0.16 s/m (sand) 0.33 s/m (silt) | 0.03 s/m (clay) 0.49 s/m (sand and silt) |
| Hannigan et.al. [34] | 2.5 mm | D/120 (very dense and hard soil) D/60 (soft soils) | 0.66 s/m (cohesive soil) 0.16 s/m (non-cohesive soil) | 0.49 s/m for all soils |
| Liang and Sheng [31] | 1/3 of toe damping | |||
| McVay and Kuo [32] | ||||
| Soil Type | Unit Shaft Resistance, qs (kPa) | Unit End Bearing, qb (kPa) |
|---|---|---|
| Sand and Gravel | 250 | 12,000 |
| Clay | 75 | 3240 |
| Silts | 75 (non-cohesive); 250 (cohesive) | 6000 |
| Dynamic Parameter | Geomaterial Type | Pile Type | WEAP Recommended Value |
|---|---|---|---|
| Js | Non-cohesive Soils | All Pile Types | 0.16 s/m |
| Cohesive soils | 0.66 s/m | ||
| Jt | All soil types | 0.5 s/m | |
| Qs | All soil types | All Types | 2.5 mm |
| Qt | All soil types, soft rock | Non- Displacement piles | 2.5 mm |
| Very dense or hard soils | Displacement piles | D/120 | |
| Soils that are not very dense or hard | Displacement piles | D/60 | |
| Hard rock | All Types | 1 mm |
| State | Project | Location | ID | Pile Type | L (m) | Bearing IGM Layer | EOD Information | |||
|---|---|---|---|---|---|---|---|---|---|---|
| S (m) | B | Qm (kN) | Hammer Types | |||||||
| MT | M FK Po. CK | P-4 at B-1 * | 1 * | OEP 406 mm | 14.4 | FG-IGM | 2.44 | 23 | 1416 | ICE I-30 |
| Cottonwood Cr | P-3 at B-1 * | 2 * | OEP 508 mm | 41.6 | FG-IGM | 2.90 | 313 | 2888 | ICE I-36 | |
| Capitol Interchange | P-47 at B-4 # | 3 | CEP 406 mm | 9.8 | CG-IGM | 2.68 | 37 | 2895 | ICE I-36 | |
| P-8 at B-5 # | 4 | CEP 406 mm | 14.8 | CG-IGM | 2.68 | 32 | 2253 | ICE I-36 | ||
| P-8 at B-1 # | 5 | CEP 406 mm | 8.8 | CG-IGM | 2.65 | 48 | 2148 | ICE I-30 | ||
| P-2 at B-1 # | 6 | CEP 406 mm | 8.5 | CG-IGM | 3.05 | 60 | 2973 | ICE I-30 | ||
| P-11 at B-5 # | 7 | CEP 406 mm | 14.7 | CG-IGM | 2.90 | 74 | 2442 | ICE I-30 | ||
| P-1 at B-1 # | 8 | CEP 406 mm | 9.0 | CG-IGM | 2.87 | 30 | 2323 | ICE I-36 | ||
| P-38 at B-4 # | 9 | CEP 406 mm | 8.4 | CG-IGM | 2.68 | 44 | 2538 | ICE I-30 | ||
| ID | US-95 WR B | P-10 at Pi-1 * | 10 * | HP 360×174 | 12.7 | FG-IGM | 2.87 | 590 | 4217 | ICE I-30 |
| SH-55 SR Bridge | P-3 at Pi-1 * | 11 * | HP 360×174 | 17.1 | FG-IGM | 2.50 | 1158 | 4168 | Del D 36-32 | |
| P-1 at Pi-4 * | 12 * | HP 360×174 | 6.1 | FG-IGM | 2.44 | 333 | 4191 | Del D 36-32 | ||
| P-1 at Pi-5 * | 13 * | HP 360×174 | 10.4 | FG-IGM | 2.32 | 144 | 3522 | Del D 36-32 | ||
| P-10 at A-2 * | 14 * | HP 360×174 | 10.1 | FG-IGM | 2.35 | 105 | 4178 | Del D 36-32 | ||
| P-4 at A-1 * | 15 | HP 360×174 | 17.2 | FG-IGM | 1.95 | 420 | 4455 | Del D 36-32 | ||
| P-1 at Pi-2 ^ | 16 | HP 360×174 | 14.6 | FG-IGM | 2.41 | 71 | 3403 | Del D 36-32 | ||
| P-2 at Pi-3 ^ | 17 | HP 360×174 | 10.7 | CG-IGM | 2.35 | 72 | 3190 | Del D 36-32 | ||
| SH-51 SR Bridge | P-1 at A-1 ^ | 18 | HP 360×174 | 21.0 | FG-IGM | 2.56 | 73 | 2825 | ICE I-30 V2 | |
| P at A-2 ^ | 19 | HP 360×174 | 21.0 | FG-IGM | 2.74 | 52 | 2578 | ICE I-30 V2 | ||
| SH-28 LR B | P-2 at A-1 ^ | 20 | HP 360×132 | 12.5 | CG-IGM | 2.29 | 16 | 1721 | Pileco 30-32 | |
| SH-52 UPPR B | P-4 at A-1 ^ | 21 | HP 360×174 | 13.1 | CG-IGM | 2.59 | 31 | 2234 | ICE I-30 V2 | |
| ND | Memorial Bridge | P-1 at Pi-10(N) ^ | 22 | HP 360×152 | 27.4 | CG-IGM | 2.59 | 40 | 3044 | Del D-36 |
| P-1 at Pi-10(S) ^ | 23 | HP 360×152 | 29.6 | CG-IGM | 2.59 | 49 | 3015 | Del D-36 | ||
| WY | PB-Muddy Creek | P-1 at A-2 * | 24 * | HP 310×79 | 16.3 | FG-IGM | 2.26 | 109 | 1695 | Del D16-32 |
| P-1 at B-2 * | 25 * | HP 310×79 | 10.8 | FG-IGM | 2.41 | 108 | 2006 | Del D16-32 | ||
| PB-Beech Street | P-1 at A-2 * | 26 * | HP 310×79 | 13.6 | FG-IGM | 2.07 | 62 | 1272 | Del D16-32 | |
| P-3 at A-2 * | 27 * | HP 310×79 | 14.1 | FG-IGM | 2.32 | 82 | 1357 | Del D16-32 | ||
| PBME (BS) | BS P-2 at A-2 * | 28 * | HP 310×79 | 12.5 | FG-IGM | 1.77 | 35 | 1477 | APE D 30-32 | |
| Hunter Creek | P-3 at A-1 # | 29 | HP 310×79 | 5.9 | CG-IGM | 1.68 | 850 | 1090 | MKT DE 40 | |
| P-2 at A-1 ^ | 30 | HP 310×79 | 11.0 | CG-IGM | 1.92 | 63 | 1010 | MKT DE 40 | ||
| Elk Fork Creek | P-5 at A-2 ^ | 31 | HP 360×108 | 12.2 | CG-IGM | 2.50 | 49 | 1802 | ICE 42S | |
| Clark’s Fork | P-1 at A-2 # | 32 | HP 360×108 | 13.7 | CG-IGM | 2.13 | 119 | 1957 | Del. D 19-42 | |
| PBME (Parson Street) | PS P-4 at A-1 * | 33 * | HP 310×79 | 22.3 | FG-IGM | 1.92 | 32 | 1481 | APE D 30-32 | |
| PS P-3 at A-2 * | 34 * | HP 310×79 | 21.3 | FG-IGM | 2.04 | 35 | 1446 | APE D 30-32 | ||
| Method | Geomaterial Input for qs and qb | Quake | Damping |
|---|---|---|---|
| WEAP-SAD (Default) | SPT N-based (SA) Procedure | = 2.5 mm; = D/60 or D/120 | = 0.16 s/m (Coarse); = 0.66 s/m (Fine); = 0.50 s/m |
| WEAP-UWD | Proposed Static Analysis Methods | = 2.5 mm; = D/120 | = 0.16 s/m (Coarse); = 0.66 s/m (Fine); = 0.50 s/m |
| WEAP-UWR | Proposed Static Analysis Methods | = 2.5 mm; = D/120 | Recommended & from Back-calculation |
| WEAP-SAR | SPT N-based (SA) Procedure | = 2.5 mm; = D/120 | Recommended & from Back-calculation |
| New Prediction Equations for S-IGMs | |
|---|---|
| S-IGM | Unit Shaft Resistance |
| ML-IGM (H-pile & Pipe pile) | |
| CL-IGM (H-pile & Pipe pile) | |
| CH-IGM (H-pile & Pipe pile) | |
| CG-IGM (H-Pile) | |
| CG-IGM (Pipe-Pile) | |
| S-IGM | Unit End Bearing |
| FG-IGM (H-pile & Pipe pile) | |
| CG-IGM (H-pile & Pipe pile) | |
| Subsurface Condition | Geomaterial | Qs (mm) | Qt (mm) | Js (s/m) | Jt (s/m) |
|---|---|---|---|---|---|
| I | Soil | 2.5 | D/120 (very dense/hard soil); D/60 (soft soil) | 0.66 (Fine-grained); 0.16 (coarse-grained); 0.33 (silts) | 0.5 |
| FG-IGM | D/120 | ||||
| II | Soil | D/120 (very dense/hard soil); D/60 (soft soil) | 0.66 (Fine-grained); 0.16 (coarse-grained); 0.33(silts) | 0.5 | |
| CG-IGM | D/120 | ||||
| III | Soil | D/120 (very dense/hard soil); D/60 (soft soil) | 0.66 (Fine-grained); 0.16 (coarse-grained); 0.33(silts) | 0.5 | |
| CG-IGM | D/120 | 0.59 | |||
| FG-IGM | 0.33 | ||||
| Site | Location | Pile Type | L (m) | Bearing Geo-Material | EOD Information | |||
|---|---|---|---|---|---|---|---|---|
| S (m) | B | Rm | Hammer | |||||
| Jules | SW wing, Pile 1 | HP 310×79 | 7.8 | FG-IGM | 2.5 | 48 | 589.6 | Delmag D 8-32 |
| I-78 Over S. | HP | HP 360×132 | 19.5 | CG-IGM | 1.8 | 30 | 1337.7 | Delmag D 36-32 |
| Greenville | Pile 3 | CEP 356 mm | 8.5 | CG-IGM | 1.9 | 42 | 843.7 | Delmag D 25-32 |
| Pile 12 | CEP 356 mm | 6.7 | CG-IGM | 2.2 | 17 | 845.9 | Delmag D 36-32 | |
| Pile 13 | CEP 356 mm | 15.2 | FG-IGM | 2.2 | 33 | 1438.7 | Delmag D 25-32 | |
| Mahomet | North Abt. | HP 360×108 | 20.7 | CG-IGM | 2.1 | 126 | 2553.9 | Delmag D 30-32 |
| South Abt. | HP 360×108 | 12.6 | CG-IGM | 2.2 | 42 | 1276.3 | Pileco D 19-42 | |
| Pier 2 | HP 360×108 | 15.2 | CG-IGM | 2.5 | 81 | 2833.3 | Delmag D 30-32 | |
| Godfrey | West Abt. | CEP 356 mm | 12.5 | FG-IGM | 2.6 | 52 | 1012.4 | Delmag D 12-32 |
| Bloomington | K-pile | HP 310×93 | 30.8 | CG-IGM | 2.4 | 115 | 1367.9 | APE D 19-42 |
| Panther creek | South Abt. | HP 250×85 | 12.0 | CG-IGM | 2.7 | 144 | 1599.8 | ICE 42-S |
| Oquawka | East Abt. | CEP 356 mm | 17.7 | CG-IGM | 2.1 | 37 | 763.6 | MKT DE 42 |
| Pier | CEP 356 mm | 16.0 | CG-IGM | 2.5 | 49 | 1416.9 | MKT DE 42 | |
| West Abt. | CEP 356 mm | 20.1 | FG-IGM | 2.3 | 22 | 645.3 | MKT DE 42 | |
| Stronghurst | North Abt. | CEP 356 mm | 16.6 | FG-IGM | 2.7 | 40 | 1367.9 | Delmag D 19-42 |
| Pier 1 | CEP 356 mm | 21.0 | FG-IGM | 2.9 | 34 | 833.0 | Delmag D 19-42 | |
| Pier 2 | CEP 356 mm | 17.2 | CG-IGM | 2.7 | 38 | 1288.7 | Delmag D 19-42 | |
| Jacksonville | Pier 1 | HP 310×93 | 11.9 | FG-IGM | 2.4 | 120 | 1651.8 | Delmag D 19-32 |
| Pier 2 | HP 310×93 | 19.0 | FG-IGM | 2.1 | 200 | 1376.8 | Delmag D 19-32 | |
| RCS Godfrey | North Abt. | CEP 356 mm | 11.9 | CG-IGM | 2.2 | 90 | 1596.7 | Delmag D 19-32 |
| North pier | CEP 356 mm | 9.0 | CG-IGM | 1.8 | 72 | 977.7 | Delmag D 19-32 | |
| South pier | CEP 356 mm | 5.9 | CG-IGM | 2.1 | 81 | 1579.8 | Delmag D 19-32 | |
| Method | Sample Size | COV | Normal | Log-Normal | Log-Likelihood | ||||
|---|---|---|---|---|---|---|---|---|---|
| SW | AD | SW | AD | ||||||
| p-Value | Normal | Log-Normal | |||||||
| WEAP SAD | 56 | 1.10 | 0.24 | 0.08 | 0.22 | 0.90 | 0.62 | −4.99 | −2.86 |
| WEAP UWD | 56 | 1.11 | 0.23 | 0.10 | 0.13 | 0.46 | 0.24 | −2.21 | −1.05 |
| WEAP UWR | 56 | 1.02 | 0.18 | 0.007 | 0.003 | 0.001 | 0.000 | NA | NA |
| WEAP SAR | 56 | 1.01 | 0.19 | 0.005 | 0.03 | 0.03 | 0.02 | NA | NA |
| WEAP SAD * | 54 | 1.08 | 0.21 | 0.76 | 0.70 | 0.32 | 0.33 | 3.28 | 4.23 |
| WEAP UWD * | 54 | 1.08 | 0.21 | 0.08 | 0.25 | 0.19 | 0.11 | 2.58 | 2.90 |
| WEAP UWR * | 50 | 1.02 | 0.12 | 0.08 | 0.13 | 0.26 | 0.15 | 33.49 | 34.04 |
| WEAP SAR * | 51 | 1.00 | 0.14 | 0.23 | 0.28 | 0.65 | 0.52 | 29.07 | 29.80 |
| Method | FOSM | FORM | MCS | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| βT = 2.33 | βT = 3.00 | βT = 2.33 | βT = 3.00 | βT = 2.33 | βT = 3.00 | |||||||
| WEAP SAD | 0.70 | 0.64 | 0.57 | 0.52 | 0.82 | 0.75 | 0.70 | 0.64 | 0.82 | 0.75 | 0.69 | 0.63 |
| WEAP UWD | 0.70 | 0.64 | 0.57 | 0.52 | 0.82 | 0.75 | 0.70 | 0.64 | 0.82 | 0.75 | 0.69 | 0.63 |
| WEAP UWR * | 0.75 | 0.74 | 0.64 | 0.63 | 0.94 | 0.92 | 0.84 | 0.82 | 0.93 | 0.91 | 0.83 | 0.81 |
| WEAP SAR | 0.72 | 0.72 | 0.61 | 0.61 | 0.88 | 0.88 | 0.79 | 0.79 | 0.88 | 0.88 | 0.77 | 0.77 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalauni, H.K.; Masud, N.B.; Ng, K.; Wulff, S.S. Improved Wave Equation Analysis for Piles in Soil-Based Intermediate Geomaterials with LRFD Recommendations and Economic Impact Assessment. Geotechnics 2024, 4, 362-381. https://doi.org/10.3390/geotechnics4020020
Kalauni HK, Masud NB, Ng K, Wulff SS. Improved Wave Equation Analysis for Piles in Soil-Based Intermediate Geomaterials with LRFD Recommendations and Economic Impact Assessment. Geotechnics. 2024; 4(2):362-381. https://doi.org/10.3390/geotechnics4020020
Chicago/Turabian StyleKalauni, Harish K., Nafis Bin Masud, Kam Ng, and Shaun S. Wulff. 2024. "Improved Wave Equation Analysis for Piles in Soil-Based Intermediate Geomaterials with LRFD Recommendations and Economic Impact Assessment" Geotechnics 4, no. 2: 362-381. https://doi.org/10.3390/geotechnics4020020
APA StyleKalauni, H. K., Masud, N. B., Ng, K., & Wulff, S. S. (2024). Improved Wave Equation Analysis for Piles in Soil-Based Intermediate Geomaterials with LRFD Recommendations and Economic Impact Assessment. Geotechnics, 4(2), 362-381. https://doi.org/10.3390/geotechnics4020020






