Equilibrium Stage of Soil Cracking and Subsidence after Several Wetting and Drying Cycles
Abstract
1. Introduction
2. Material and Image Processing Method
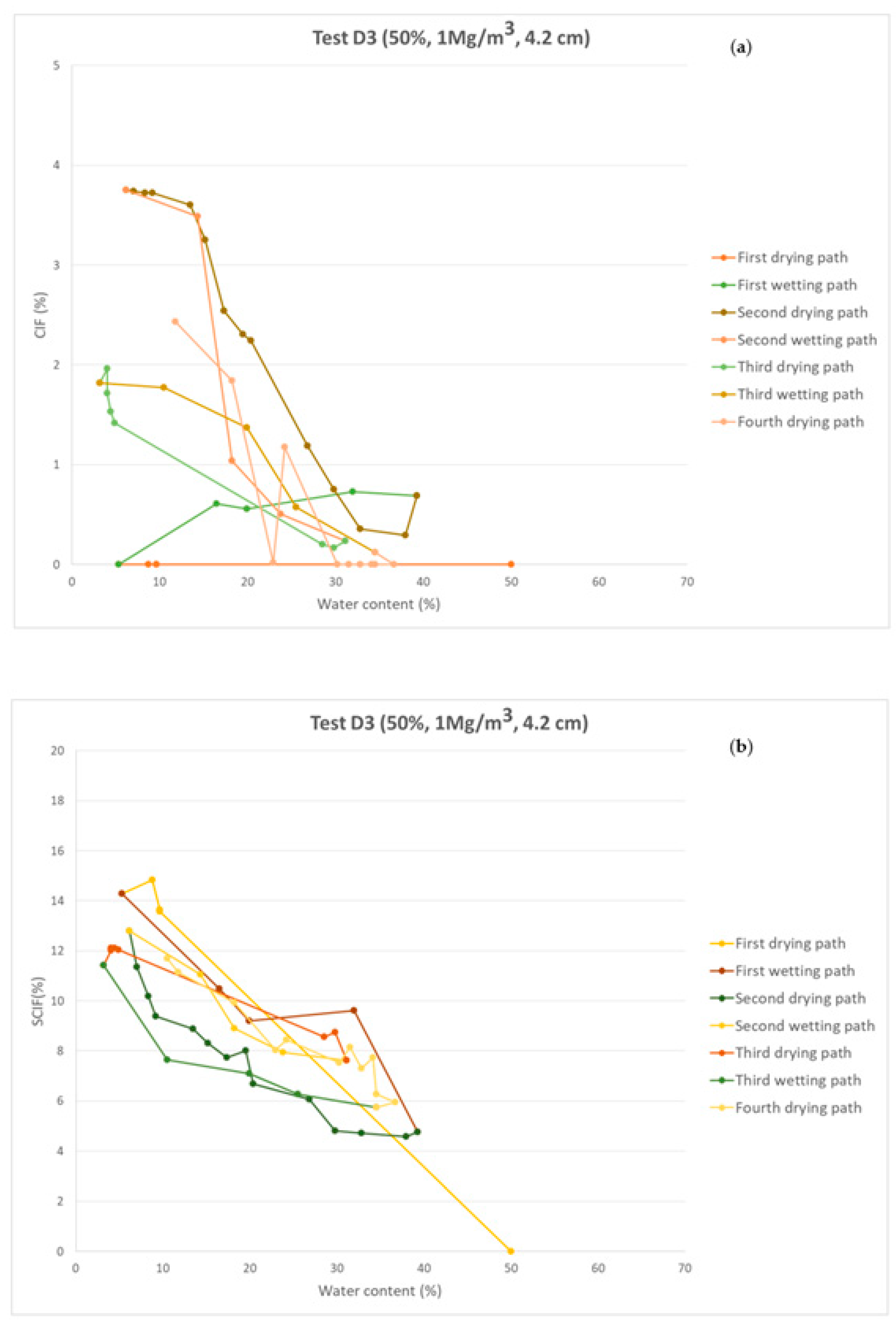
3. Cracking Equilibrium Stage after Successive Wetting and Drying Cycles
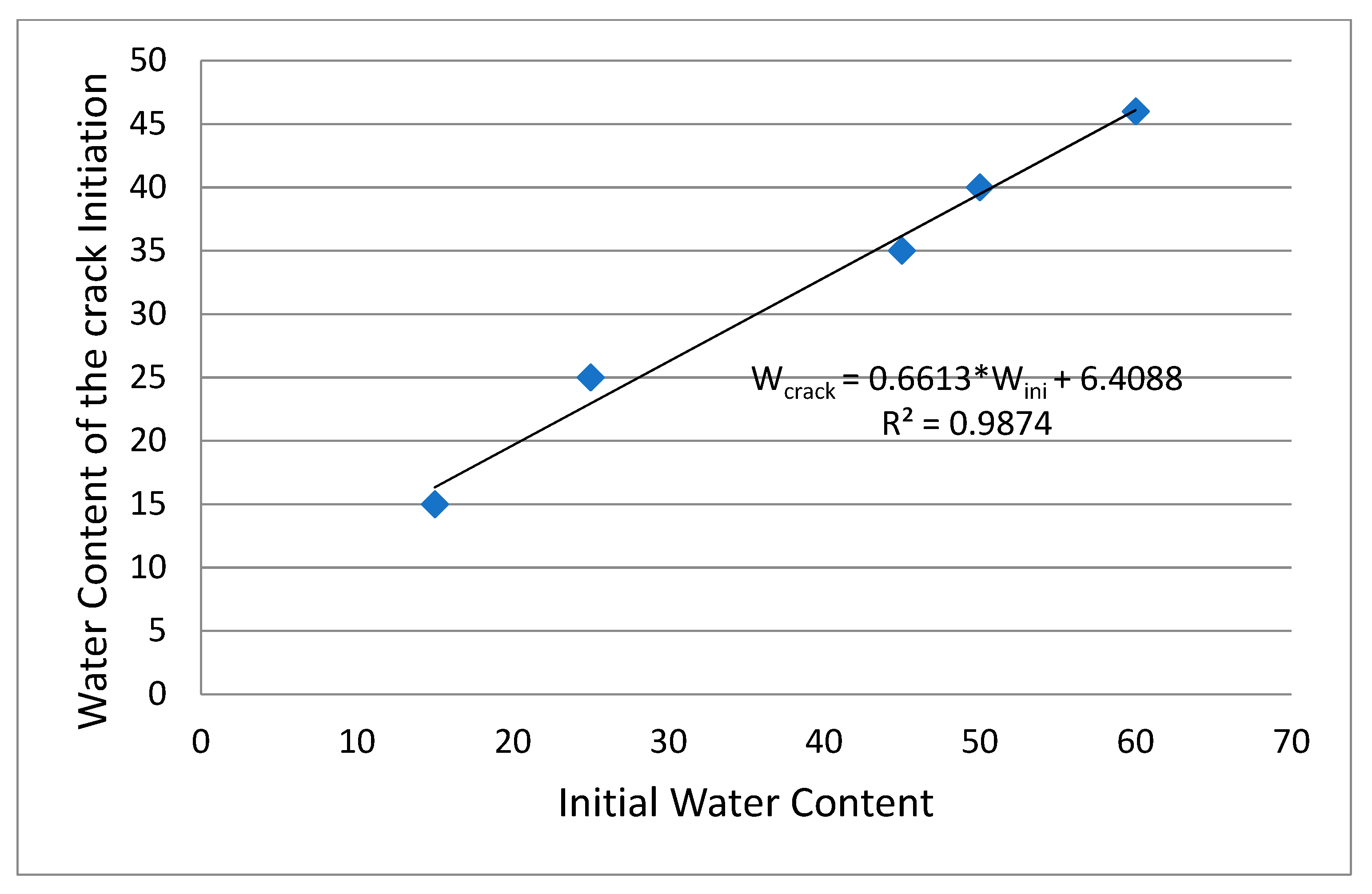
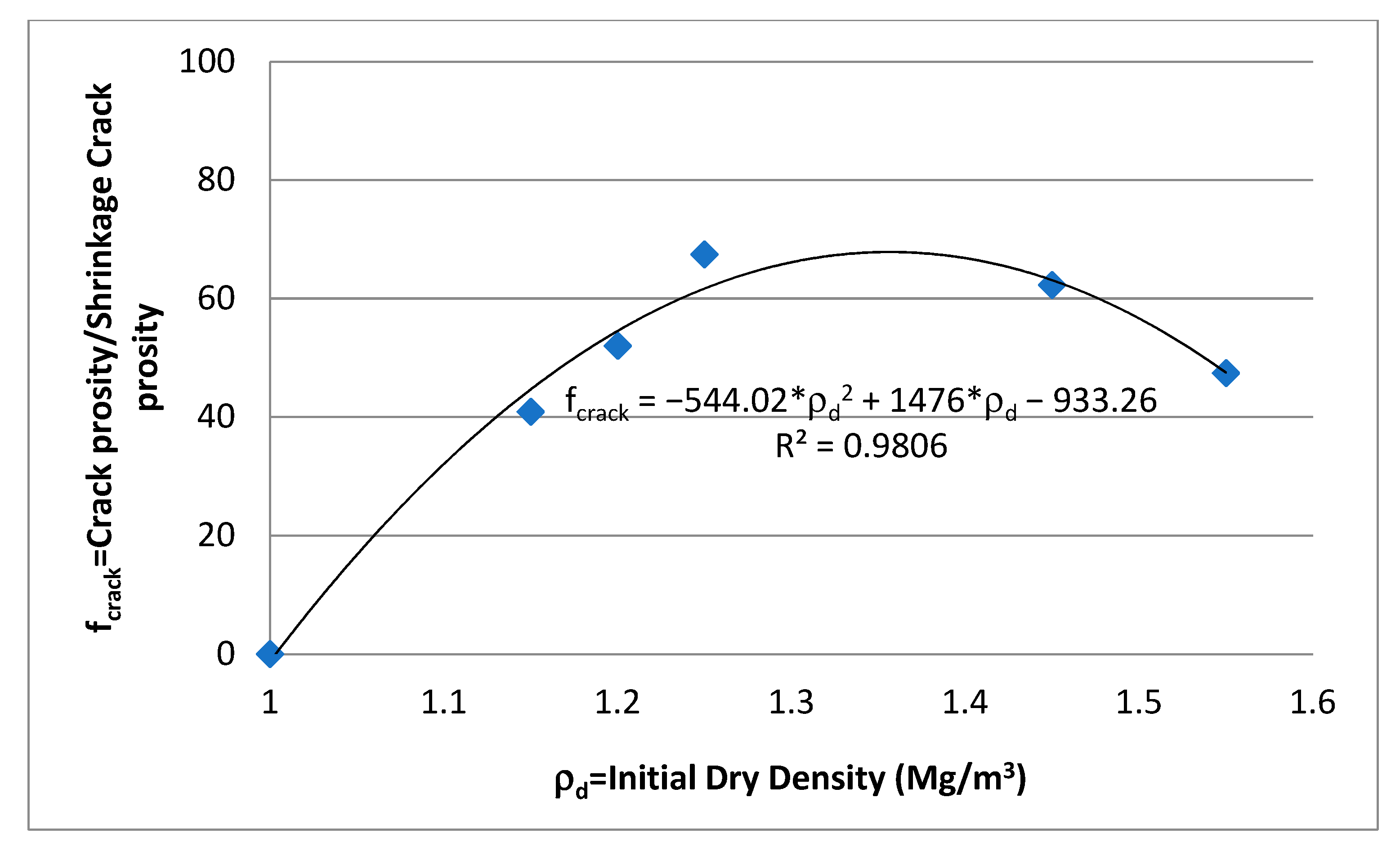
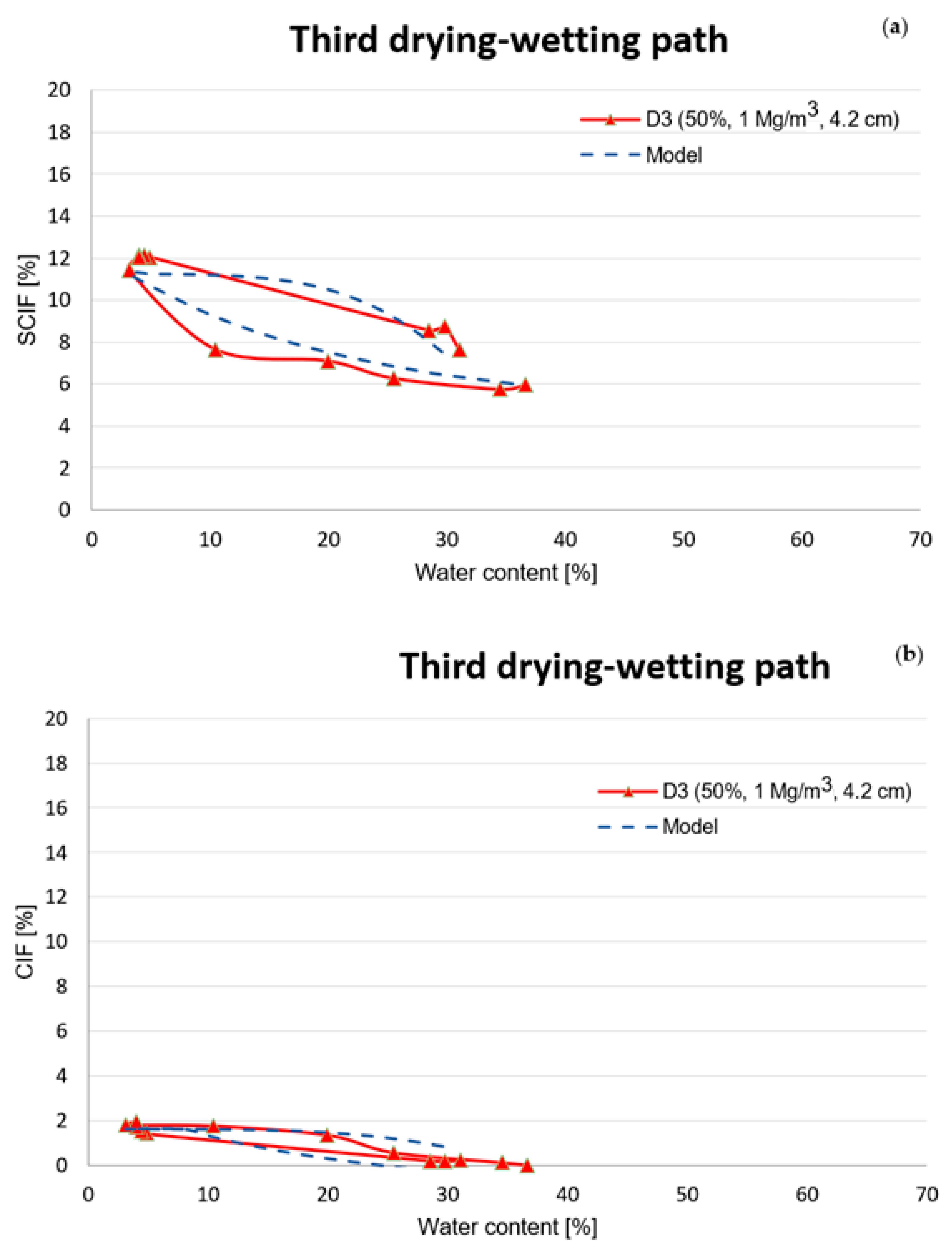
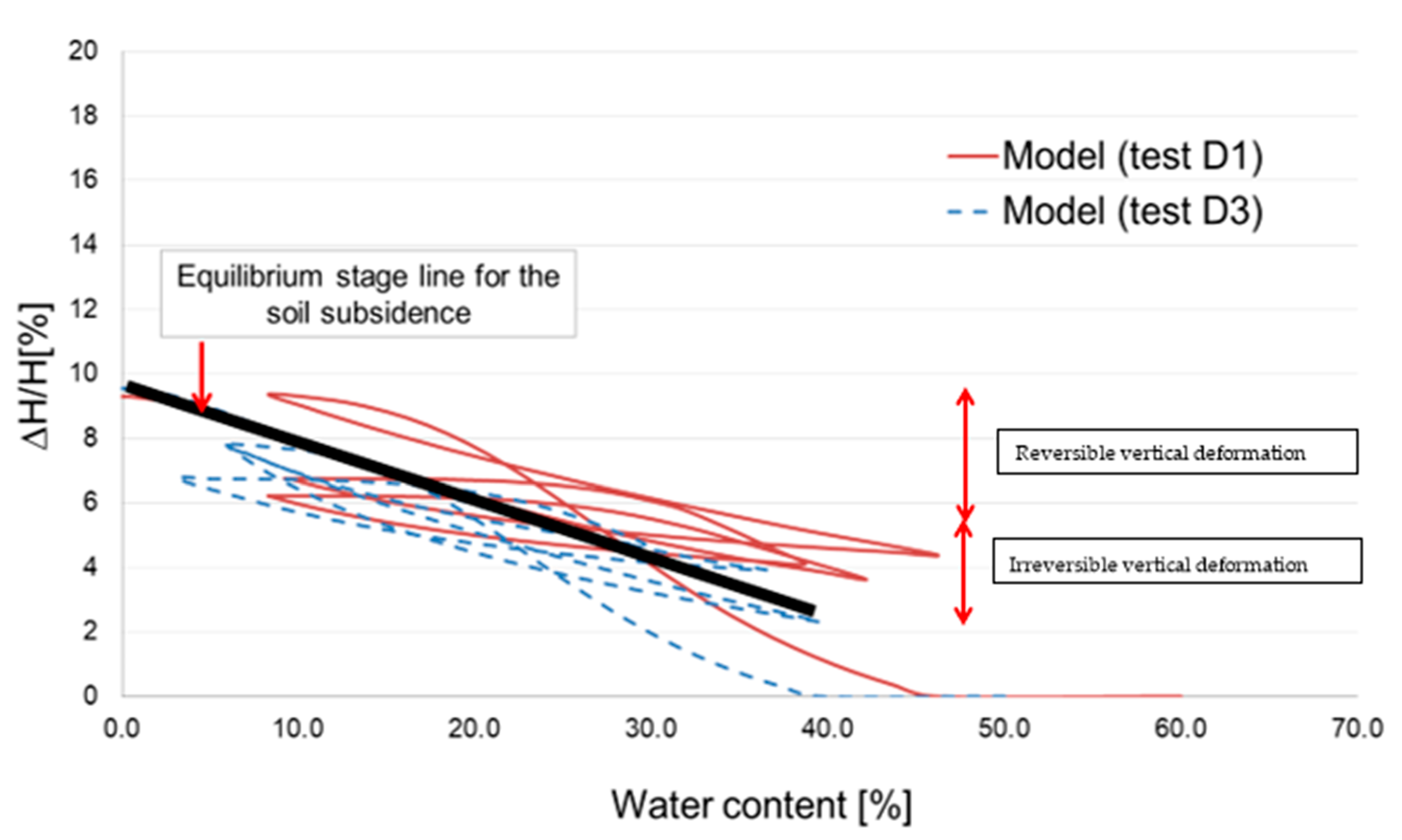
4. Prediction of the Cracking Equilibrium Stage and the Soil Subsidence after Several Wetting and Drying Cycles
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nowamooz, H.; Masrouri, F. Density-dependent hydromechanical behaviour of a compacted expansive soil. Eng. Geol. 2009, 106, 105–115. [Google Scholar] [CrossRef]
- Koliji, A.; Laloui, L.; Cusinier, O.; Vulliet, L. Suction induced effects on the fabric of a structured soil. Transp. Porous Media 2006, 64, 261–278. [Google Scholar] [CrossRef]
- Nowamooz, H. Effective stress concept on the multi-structural swelling soils. Appl. Clay Sci. 2014, 101, 205–214. [Google Scholar] [CrossRef]
- Nowamooz, H.; Jahagir, E.; Masrouri, F.; Tisot, J.P. Effective stress in multiscale soils. Eng. Geol. 2016, 210, 33–44. [Google Scholar] [CrossRef]
- Messing, I.; Jarvis, N.J. Seasonal variation in field-saturated hydraulic conductivity in two swelling clay soils in Sweden. J. Soil Sci. 1990, 41, 229–237. [Google Scholar] [CrossRef]
- Chertkov, V.Y. The horizontal hydraulic conductivity of vertical interaggregate capillary cracks in clay soils. In Physical Methods in Agriculture; Blahovec, J., Kutílek, M., Eds.; Springer: New York, NY, USA, 2002; pp. 39–50. [Google Scholar]
- Chertkov, V.Y.; Ravina, I. Shrinking–swelling phenomenon of clay soils attributed to capillary-crack network. Theor. Appl. Fract. Mech. 2000, 34, 61–71. [Google Scholar] [CrossRef]
- Das Gupta, S.; Mohanty, B.P.; Köhne, J.M. Soil hydraulic conductivities and their spatial and temporal variations in a Vertisol. Soil Sci. Soc. Am. J. 2006, 70, 1872–1881. [Google Scholar] [CrossRef]
- Al-homoud, A.S.; Basma, A.A.; Malkawi, A.I.H.; Al-bashabsheh, M.A. Cyclic swelling behavior of clays. J. Geotech. Eng. 1995, 121, 562–565. [Google Scholar] [CrossRef]
- Alonso, E.E.; Romero, E.; Hoffemann, C.; García-Escudero, E. Expansive bentonite/sand mixtures in cyclic controlled suction drying and wetting. Eng. Geol. 2005, 81, 213–226. [Google Scholar] [CrossRef]
- Chu, T.Y.; Mou, C.H. Volume Change Characteristics of Expansive Soils Determined by Controlled Suction Tests. In Proceedings of the 3rd International Conference on Expansive Soils, Haïfa, Israel, 30 July–1 August 1973; Volume 2, pp. 177–185. [Google Scholar]
- Dif, A.E.; Bluemel, W.F. Expansive soils under cyclic drying and wetting. Geotech. Test. J. 1991, 14, 96–102. [Google Scholar]
- Nowamooz, H.; Masrouri, F. Hydromechanical behaviour of an expansive bentonite/silt mixture in cyclic suction-controlled drying and wetting tests. Eng. Geol. 2008, 101, 154–164. [Google Scholar] [CrossRef]
- Nowamooz, H.; Masrouri, F. Shrinkage-swelling of compacted clayey dense and loose soils. Comptes Rendus Mécanique 2009, 337, 781–790. [Google Scholar] [CrossRef]
- Nowamooz, H.; Masrouri, F. Mechanical behaviour of expansive soils after several drying and wetting cycles. Int. J. Geomech. Geoengin. 2010, 5, 213–221. [Google Scholar] [CrossRef]
- Tripathy, S.; Rao, K.S.S.; Fredlund, D.G. Water content–void ratio swell–shrink paths of compacted expansive soils. Can. Geotech. J. 2002, 39, 938–959. [Google Scholar] [CrossRef]
- Qi, W.; Wang, C.; Zhang, Z.; Huang, M.; Xu, J. Experimental Investigation on the Impact of Drying–Wetting Cycles on the Shrink–Swell Behavior of Clay Loam in Farmland. Agriculture 2022, 12, 245. [Google Scholar] [CrossRef]
- Najm, M.R.A.; Jabro, J.D.; Iversen, W.M.; Mohtar, R.H.; Evans, R.G. New method for the characterization of three-dimensional preferential flow paths in the field. Water Resour. Res. 2010, 46, W02503. [Google Scholar] [CrossRef]
- Chertkov, V.Y.; Ravina, I. Effect of interaggregate capillary cracks on the hydraulic conductivity of swelling clay soils. Water Resour. Res. 2001, 37, 1245–1256. [Google Scholar] [CrossRef]
- Kutílek, M. Water relations and water management of Vertisols. Dev. Soil Sci. 1996, 24, 201–230. [Google Scholar] [CrossRef]
- Cabidoche, Y.-M.; Ruy, S. Field shrinkage curves of a swelling clay soil: Analysis of multiple structural swelling and shrinkage phases in the prisms of a Vertisol. Soil Res. 2001, 39, 143–160. [Google Scholar] [CrossRef]
- Konrad, J.M.; Ayad, R. An idealized framework for the analysis of cohesive soils undergoing desiccation. Can. Geotech. J. 1997, 34, 477–488. [Google Scholar] [CrossRef]
- Greco, R. Preferential flow in macroporous swelling soil with internal catchment: Model development and applications. J. Hydrol. 2002, 269, 150–168. [Google Scholar] [CrossRef]
- Bouma, J.; Jongerius, A.; Boersma, O.; Jager, A.; Schoonderbeek, D. The function of different types of macropores during saturated flow through four swelling soil horizons. Soil Sci. Soc. Am. J. 1997, 41, 945–950. [Google Scholar] [CrossRef]
- Cabidoche, Y.-M.; Guillaume, P. A casting method for the three-dimensional analysis of the intraprism structural pores in Vertisols. Eur. J. Soil Sci. 1998, 49, 187–196. [Google Scholar] [CrossRef]
- Favre, F.; Boivin, P.; Wopereis, M. Water movement and soil swelling in a dry, cracked Vertisol. Geoderma 1997, 78, 113–123. [Google Scholar] [CrossRef]
- Costa, S.; Kodikara, J.; Shannon, B. Salient factors controlling desiccation cracking of clay in laboratory experiments. Géotechnique 2013, 63, 18–29. [Google Scholar] [CrossRef]
- Hallaire, V. Evolution of Crack Networks during Shrinkage of a Clay Soil under Grass and Winter Wheat Crops. In Proceedings of the ISSS Symposium on Water and Solute Movement in Heavy Clay Soils, Wageningen, The Netherlands, 27–31 August 1984; Bouma, J., Raats, P.A.C., Eds.; ILRI Publication 37. International Institute for Land Reclamation and Improvement: Wageningen, The Netherlands, 1984. [Google Scholar]
- Liu, C.; Tang, C.H.; Shi, B.; Suo, W.B. Automatic quantification of crack patterns by image processings. Comput. Geosci. 2013, 57, 77–80. [Google Scholar] [CrossRef]
- Peron, H.; Hueckel, T.; Laloui, L.; Hu, L. Fundamentals of desiccation cracking of finegrained soils: Experimental characterisation and mechanisms identification. Can. Geotech. J. 2009, 46, 1177–1201. [Google Scholar] [CrossRef]
- Shin, H.; Santamarina, J.C. Desiccation cracks in saturated fine-grained soils: Particle-level phenomena and effective-stress analysis. Géotechnique 2011, 61, 961–972. [Google Scholar] [CrossRef]
- Shit, P.K.; Bhunia, G.S.; Maiti, R. Soil crack morphology analysis using image processing techniques. Earth Syst. Environ. 2015, 1, 35. [Google Scholar] [CrossRef]
- Tang, C.S.; Shi, B.; Liu, C.; Zhao, L.; Wang, B. Influencing factors of geometrical structure of surface shrinkage cracks in clayey soils. Eng. Geol. 2008, 101, 204–217. [Google Scholar] [CrossRef]
- Tang, C.S.; Cui, Y.J.; Tang, A.M.; Shi, B. Experiment evidence on the temperature dependence of desiccation cracking behavior of clayey soils. Eng. Geol. 2010, 141, 261–266. [Google Scholar] [CrossRef]
- Cordero, J.A.; Prat, P.C.; Ledesma, A. Experimental analysis of desiccation cracks on a clayey silt from a large-scale test in natural conditions. Eng. Geol. 2021, 292, 106256. [Google Scholar] [CrossRef]
- Chaduvula, U.; Viswanadham, B.V.S.; Kodikara, J. Centrifuge model studies on desiccation cracking behaviour of fiber-reinforced expansive clay. Geotext. Geomembr. 2022, 50, 480–497. [Google Scholar] [CrossRef]
- DeCarlo, K.F.; Shokri, N. Salinity effects on cracking morphology and dynamics in 3-D desiccating clays. Water Resour. Res. 2014, 50, 3052–3072. [Google Scholar] [CrossRef]
- Diamond, R.; Varghese, R.M. Desiccation Cracking Behavior and Strength Characteristics of Areca Fiber-Reinforced Fine Grained Soils. In Ground Improvement and Reinforced Soil Structures, Satyanarayana Reddy, C.N.V., Saride, S., Krishna, A.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2022; pp. 105–118. [Google Scholar]
- Návar, J.; Mendez, J.; Bryan, R.B.; Kuhn, N.J. The contribution of shrinkage cracks to bypass flow during simulated and natural rainfall experiments in northeastern Mexico. Can. J. Soil Sci. 2002, 82, 65–74. [Google Scholar] [CrossRef]
- Stewart, R.D.; Abou Najm, M.R.; Rupp, D.E.; Selker, J.S. Measurement tool for dynamics of soil cracks. Vadose Zone J. 2012, 11, vzj2011.0048. [Google Scholar] [CrossRef]
- Stewart, R.D.; Najm, M.R.A.; Rupp, D.E.; Selker, J.S. Nondestructive quantification of macropore volume using shear-thinning fluid. Soil Sci. Soc. Am. J. 2014, 78, 445–453. [Google Scholar] [CrossRef]
- Arnold, J.G.; Potter, K.N.; King, K.W.; Allen, P.M. Estimation of soil cracking and the effect on surface runoff in a Texas Blackland Prairie watershed. Hydrol. Process. 2005, 19, 589–603. [Google Scholar] [CrossRef]
- Brake, B.T.; van der Ploeg, M.J.; de Rooij, G.H. Water storage change estimation from in situ shrinkage measurements of clay soils. Hydrol. Earth Syst. Sci. 2013, 17, 1933–1949. [Google Scholar] [CrossRef]
- Coppola, A.; Comegna, A.; Dragonetti, G.; Gerke, H.H.; Basile, A. Simulated preferential water flow and solute transport in shrinking soils. Vadose Zone J. 2015, 14, vzj2015.02.0021. [Google Scholar] [CrossRef]
- Salager, S.; El Youssoufi, M.S.; Saix, C. Definition and experimental determination of a soil-water retention surface. Can. Geotech. J. 2010, 47, 609–622. [Google Scholar] [CrossRef]
- Lee, F.H.; Lo, K.W.; Lee, S.L. Tension crack development in soils. J. Geotech. Eng. 1988, 114, 915–929. [Google Scholar] [CrossRef]
- Bronswijk, J.J.B. Modeling of water balance, cracking and subsidence of clay soils. J. Hydrol. 1988, 97, 199–212. [Google Scholar] [CrossRef]
- Morris, P.H.; Graham, J.; Williams, D.J. Cracking in drying soils. Can. Geotech. J. 1992, 29, 263–277. [Google Scholar] [CrossRef]
- Hallett, P.D.; Newson, T.A. Describing soil crack formation using elastic–plastic fracture mechanics. Eur. J. Soil Sci. 2005, 56, 31–38. [Google Scholar] [CrossRef]
- Amarasiri, A.L.; Kodikara, J.K.; Costa, S. Numerical modelling of desiccation cracking. Int. J. Numer. Anal. Methods Geomech. 2011, 35, 82–96. [Google Scholar] [CrossRef]
- Amarasiri, A.L.; Costa, S.; Kodikara, J.K. Determination of cohesive properties for mode I fracture from compacted clay beams. Can. Geotech. J. 2011, 48, 1163–1173. [Google Scholar] [CrossRef]
- Stewart, R.D.; Rupp, D.E.; Najm, M.R.A.; Selker, J.S. A unified model for soil shrinkage, subsidence, and cracking. Vadose Zone J. 2016, 15, vzj2015.11.0146. [Google Scholar] [CrossRef]
- Auvray, R.; Rosin-Paumier, S.; Abdallah, A.; Masrouri, F. Quantification of soft soil cracking during suction cycles by image processing. Eur. J. Environ. Civ. Eng. 2014, 18, 11–32. [Google Scholar] [CrossRef]
- Louatia, F.; Trabelsia, H.; Jameia, M.; Taibi, S. Impact of wetting-drying cycles and cracks on the permeability of compacted clayey soil. Eur. J. Environ. Civ. Eng. 2018, 25, 696–721. [Google Scholar] [CrossRef]
- Haines, W.B. The volume-changes associated with variations of water content in soil. J. Agriculture. Sci. 1923, 13, 296–311. [Google Scholar] [CrossRef]
- McGarry, D.; Daniells, I.G. Shrinkage curves indices to quantify cultivation effects on soil structure of a Vertisol. Soil Sci. Soc. Am. J. 1987, 51, 1575–1580. [Google Scholar] [CrossRef]
- Peng, X.; Horn, R. Identifying six types of soil shrinkage curves from a large set of experimental data. Soil Sci. Soc. Am. J. 2013, 77, 372–381. [Google Scholar] [CrossRef]
- SPOSITO, G. Volumes changes in swelling soils. Soil Sci. 1973, 115, 315–320. [Google Scholar] [CrossRef]
- Chertkov, V.Y.; Ravina, I.; Zadoenko, V. An approach for estimating the shrinkage geometry factor at a moisture content. Soil Sci. Soc. Am. J. 2004, 68, 1807–1817. [Google Scholar] [CrossRef]
- Fityus, S.; Buzzi, O. The place of expansive clays in the framework of unsaturated soil mechanics. Appl. Clay Sci. 2009, 43, 150–155. [Google Scholar] [CrossRef]
- Bronswijk, J. Shrinkage geometry of a heavy clay soil at various stresses. Soil Sci. Soc. Am. J. 1990, 54, 1500–1502. [Google Scholar] [CrossRef]




| Soil Property | Value |
|---|---|
| Specific gravity | 2.65 |
| Liquid limit | 30.9% |
| Plastic limit | 17.7% |
| Plasticity index | 13.2% |
| USUC Classification | ML-CL |
| Grain size analysis | |
| Sand (pores between 50 and 80 µm) | 20% |
| Silt (pores between 2 and 50 µm) | 45% |
| Clay (pores less than 2 µm) | 35% |
| Test | Water Content (%) | Dry Density (Mg/m3) | Sample Height (cm) |
|---|---|---|---|
| D1 | 60 | 1 | 4 |
| D2 | 60 | 1.15 | 3.6 |
| D3 | 50 | 1 | 4.2 |
| D4 | 45 | 1.25 | 1.05 |
| D5 | 45 | 1.2 | 1.3 |
| D6 | 30 | 1.4 | 2 |
| D7 | 25 | 1.55 | 4.5 |
| Initial Water Content (%) | Cycle | First Drying | First Wetting | Second Drying | Second Wetting | Third Drying | Third Wetting | Fourth Drying |
|---|---|---|---|---|---|---|---|---|
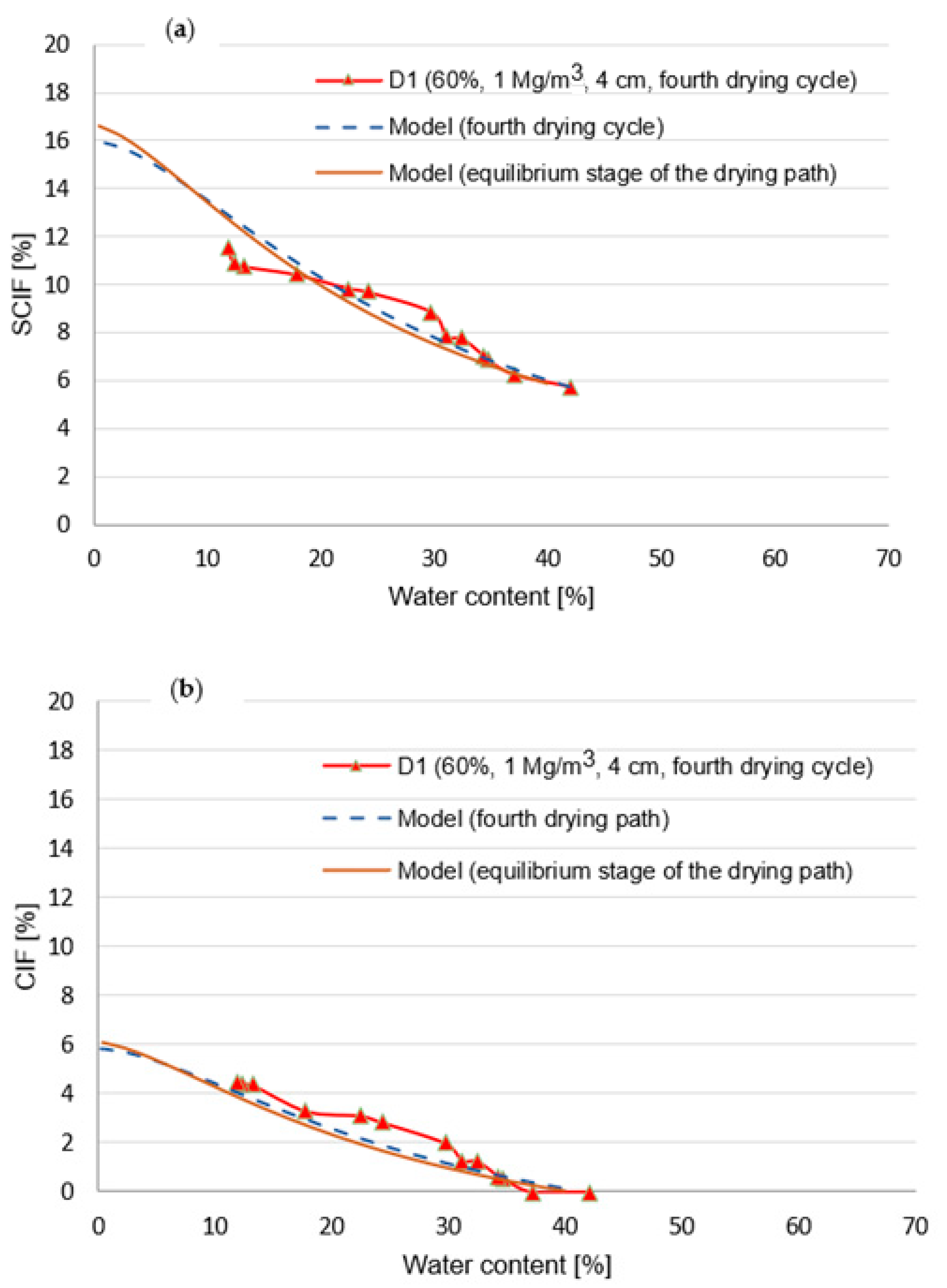
| 60 | Final water content (%) | 7.7 | 46.7 | 10.0 | 38.0 | 7.75 | 42.1 | 11.9 |
| SCIF (%) | 16.03 | 7.5 | 10.57 | 6.91 | 11.04 | 5.74 | 11.51 | |
| CIF (%) | 0.00 | 0.00 | 4.27 | 0.11 | 3.50 | 0.00 | 4.48 | |
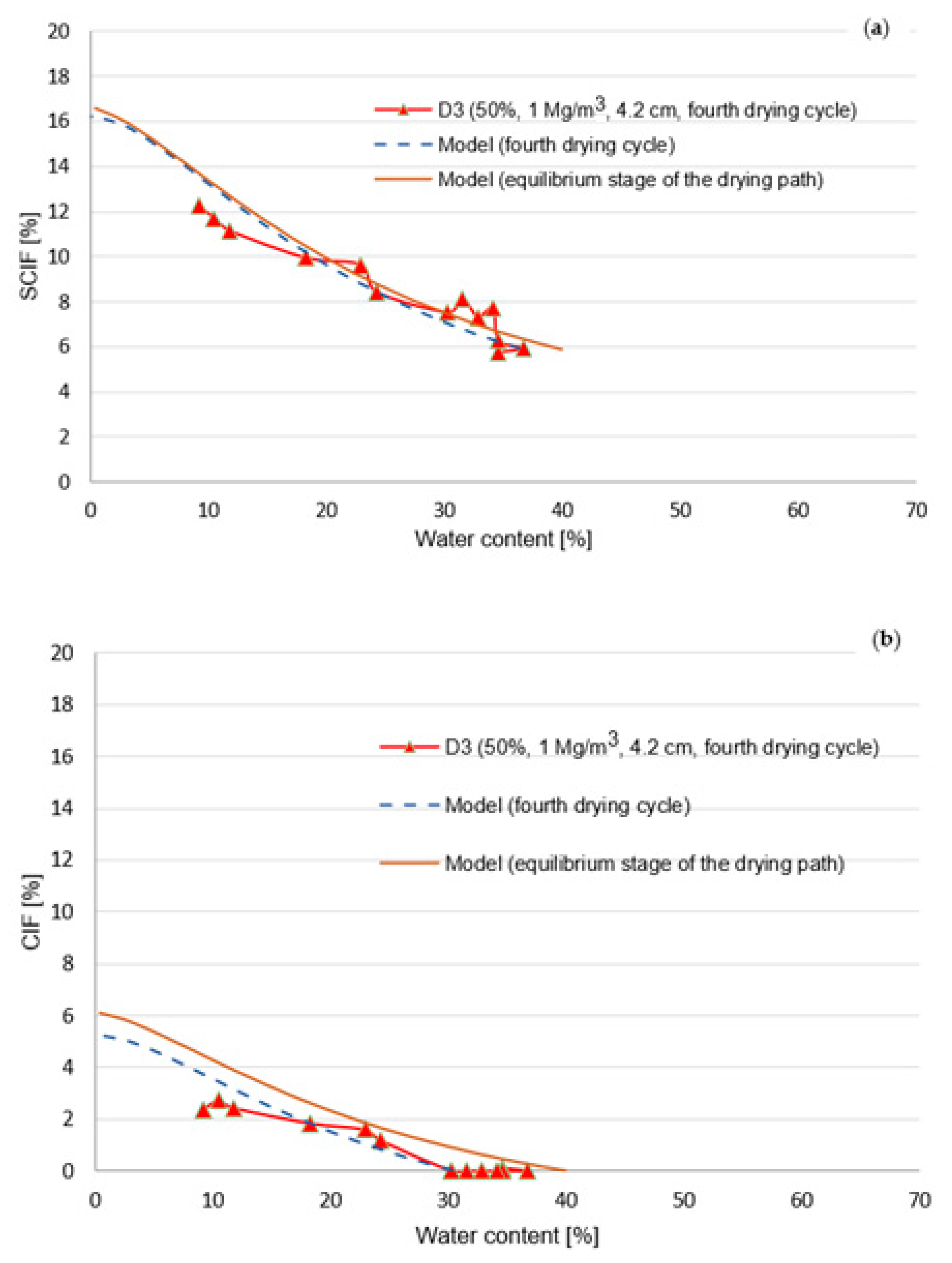
| 50 | Final water content (%) | 5.3 | 39.3 | 6.2 | 31.1 | 4.0 | 36.7 | 9.2 |
| SCIF (%) | 14.29 | 4.76 | 12.81 | 7.61 | 12.03 | 5.95 | 12.25 | |
| CIF (%) | 0 | 0.69 | 3.75 | 0.24 | 1.97 | 0.00 | 2.4 |
| Cycle | First Drying | First Wetting | Second Drying | Second Wetting | Third Drying | Third Wetting | Fourth Drying | Equilibrium Stage | |
|---|---|---|---|---|---|---|---|---|---|
| Parameter | |||||||||
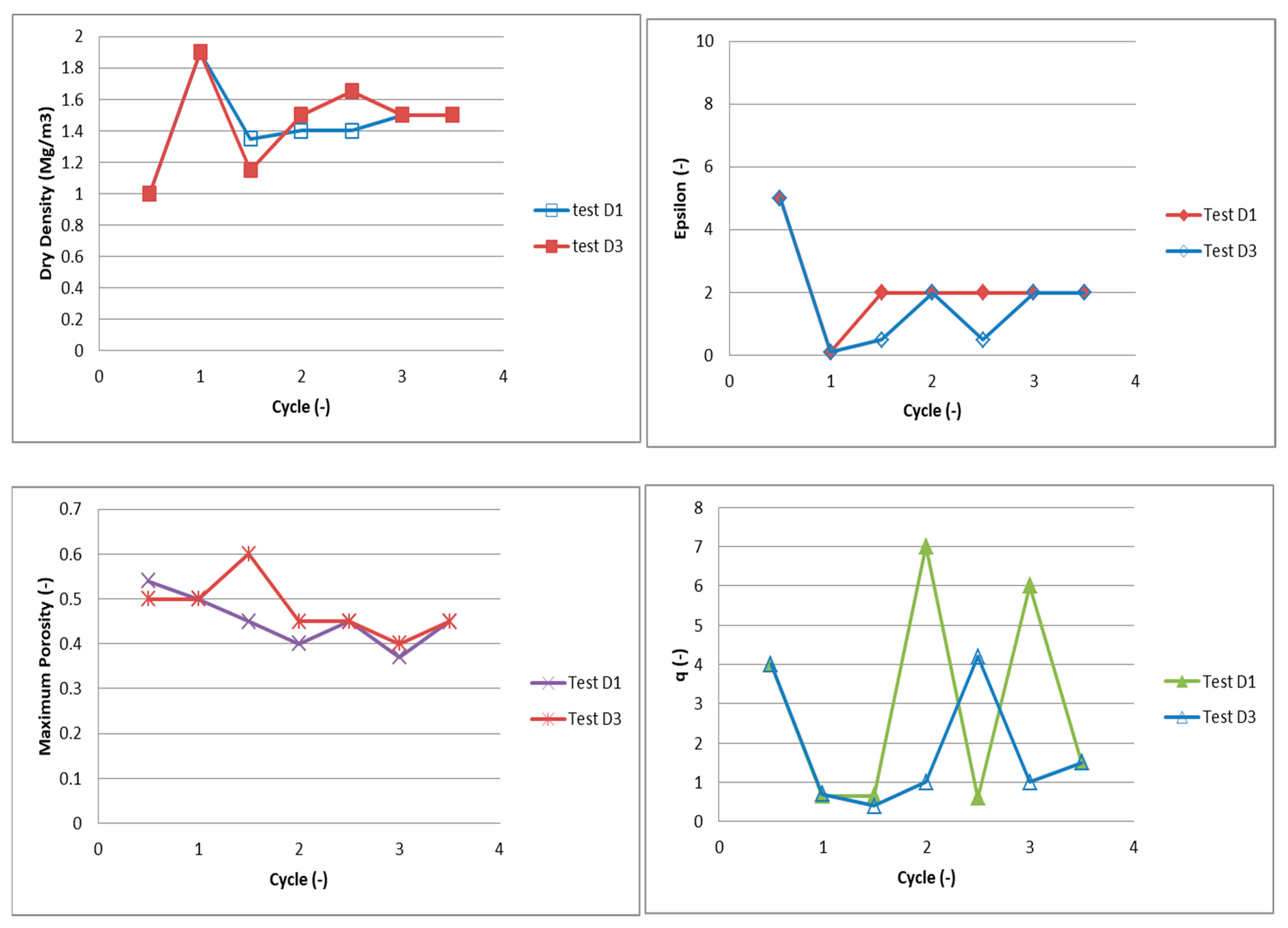
| Initial dry density | 1 | 1.9 | 1.35 | 1.4 | 1.4 | 1.5 | 1.5 | 1.5 | |
| 5 | 0.1 | 2 | 2 | 2 | 2 | 2 | 2 | ||
| 4 | 0.65 | 0.65 | 7 | 0.6 | 6 | 1.5 | 1.5 | ||
| 0.54 | 0.5 | 0.45 | 0.4 | 0.45 | 0.37 | 0.45 | 0.45 | ||
| 0.283 | 0.283 | 0.283 | 0.283 | 0.283 | 0.283 | 0.283 | 0.283 | ||
| Parameter | First Drying | First Wetting | Second Drying | Second Wetting | Third Drying | Third Wetting | Fourth Drying | Equilibrium Stage | |
|---|---|---|---|---|---|---|---|---|---|
| Cycle | |||||||||
| Initial dry density | 1 | 1.9 | 1.15 | 1.5 | 1.65 | 1.5 | 1.5 | 1.5 | |
| 5 | 0.1 | 0.5 | 2 | 0.5 | 2 | 2 | 2 | ||
| 4 | 0.7 | 0.4 | 1 | 4.2 | 1 | 1.5 | 1.5 | ||
| 0.5 | 0.5 | 0.6 | 0.45 | 0.45 | 0.4 | 0.45 | 0.45 | ||
| 0.283 | 0.283 | 0.283 | 0.283 | 0.283 | 0.283 | 0.283 | 0.283 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nowamooz, H. Equilibrium Stage of Soil Cracking and Subsidence after Several Wetting and Drying Cycles. Geotechnics 2023, 3, 193-211. https://doi.org/10.3390/geotechnics3020012
Nowamooz H. Equilibrium Stage of Soil Cracking and Subsidence after Several Wetting and Drying Cycles. Geotechnics. 2023; 3(2):193-211. https://doi.org/10.3390/geotechnics3020012
Chicago/Turabian StyleNowamooz, Hossein. 2023. "Equilibrium Stage of Soil Cracking and Subsidence after Several Wetting and Drying Cycles" Geotechnics 3, no. 2: 193-211. https://doi.org/10.3390/geotechnics3020012
APA StyleNowamooz, H. (2023). Equilibrium Stage of Soil Cracking and Subsidence after Several Wetting and Drying Cycles. Geotechnics, 3(2), 193-211. https://doi.org/10.3390/geotechnics3020012





