Explanation and Application of the Evolving Contact Traction Fields in Shallow Foundation Systems
Abstract
1. Introduction
- (i)
- By treating the problem in the context of continuum elastoplasticity, researchers have described this phenomena through the presence of plastic yielding [5,12,13]. Localized plasticity is initialized at various loading stages due to the arbitrarily large edge pressures present in the case of a purely elastic rigid punch [14,15].
- (ii)
- Using a simpler two-dimensional model containing only springs, Kerr [9] was able to replicate this behavior by extending the classic Winkler model [16] by adding a second layer of normal springs separated by a shear layer; in this way the phenomena is mechanically linked with the concept of shear resistance. In this model, evolution of the peak location in the normal traction is related to the size of the footing and not necessary the magnitude of the load, although both of these quantities obviously contribute to the magnitudes of pressure applied to the underlying soil.
- (iii)
- Smoltczyk [8] developed an analytical expression for the normal contact traction based on an assumed probability distribution that force be transferred to the ground between the edge and center of the footing. This represents the statistical likelihood of force propagation along granular contact chains.
2. Results
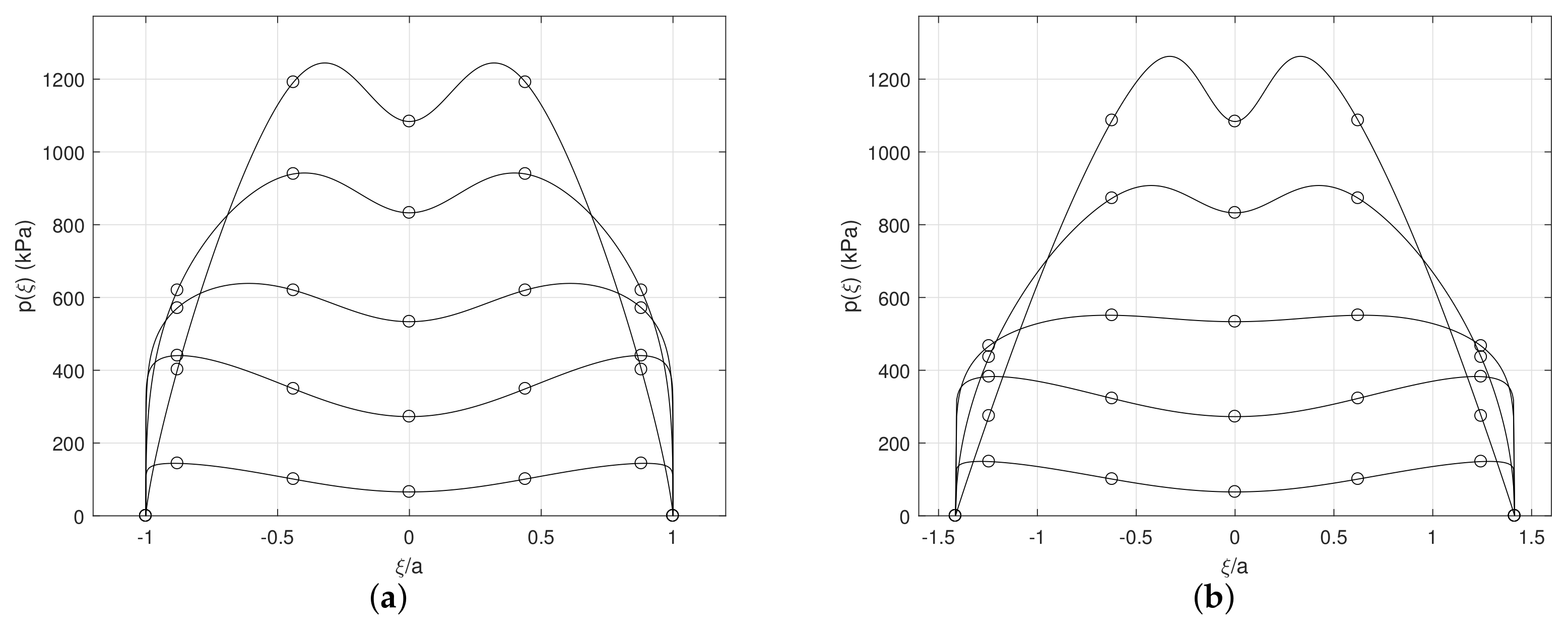
2.1. Contact Traction, Mobilized Shear Resistance, and the Static Sandpile
2.1.1. The Foundation-Sandpile Analogy
- The free-standing sandpile distributes the weight of its own body forces alone, while the resultant traction on the footing is the response to externally applied forces.
- The boundary of the sandpile is stress-free and at a state of incipient failure, while the boundary of the foundation wedge is supported and confined by the surrounding soil bed.

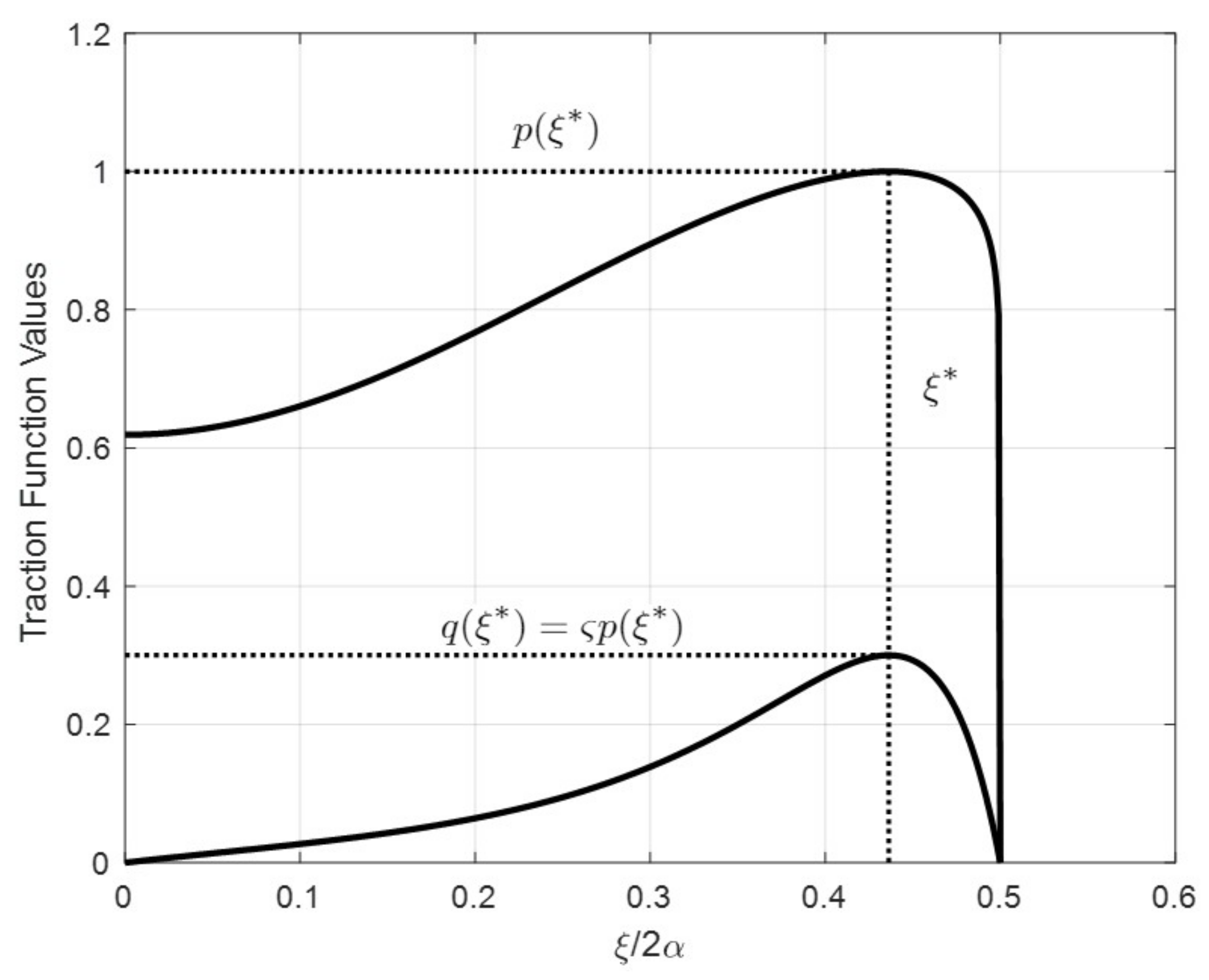
2.1.2. Semi-Empirical Traction Functions
2.2. Parametric Study for Boundary Conditions in an Analytic Elastic Foundation Model
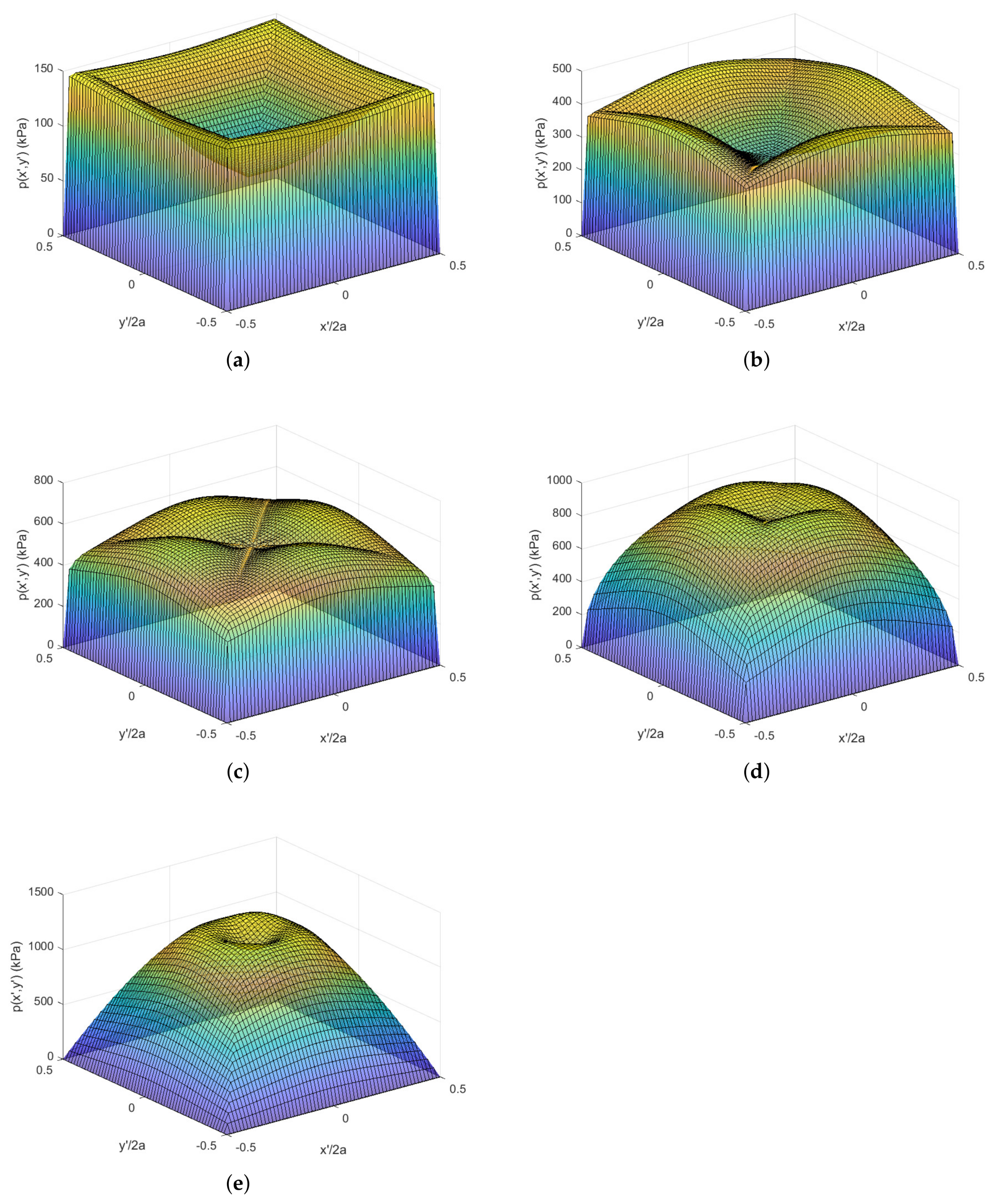
2.2.1. Behavior Due to Evolving Normal Load
2.2.2. Effects of Tangential Traction Fields
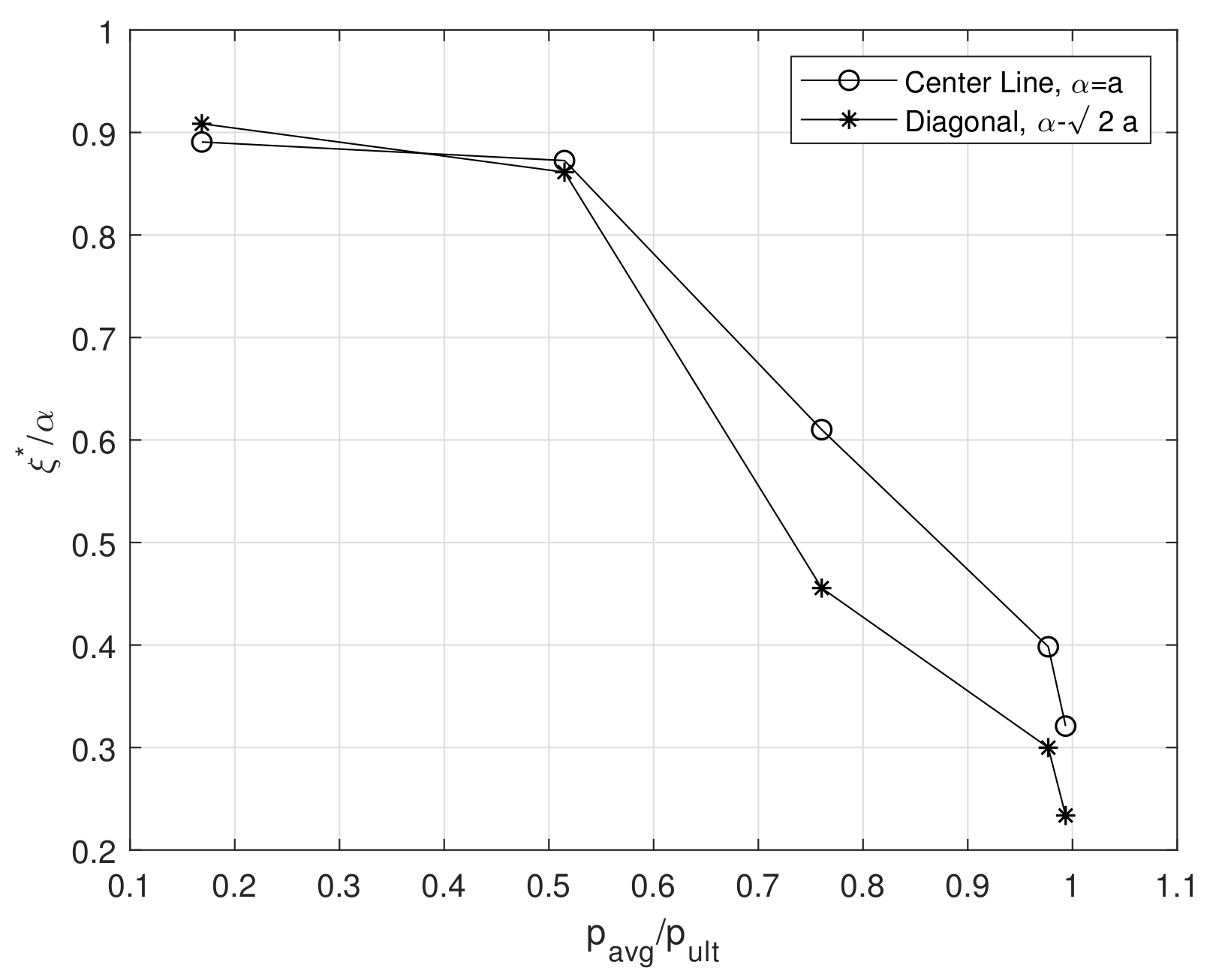
| Case | ||||||
|---|---|---|---|---|---|---|
| 1 | 166.056 | 41.413 | 0.2356 | 0.3041 | 0.8907 | 1.2848 |
| 2 | 850.628 | 474.082 | 0.2551 | 0.3774 | 0.8726 | 1.2180 |
| 3 | 8091.466 | 4031.808 | 0.5741 | 1.2330 | 0.6101 | 0.6443 |
| 4 | 12,180.771 | 4437.509 | 0.5954 | 0.6060 | 0.3983 | 0.4241 |
| 5 | 13,072.097 | 4512.017 | 0.4545 | 0.5076 | 0.3209 | 0.3305 |
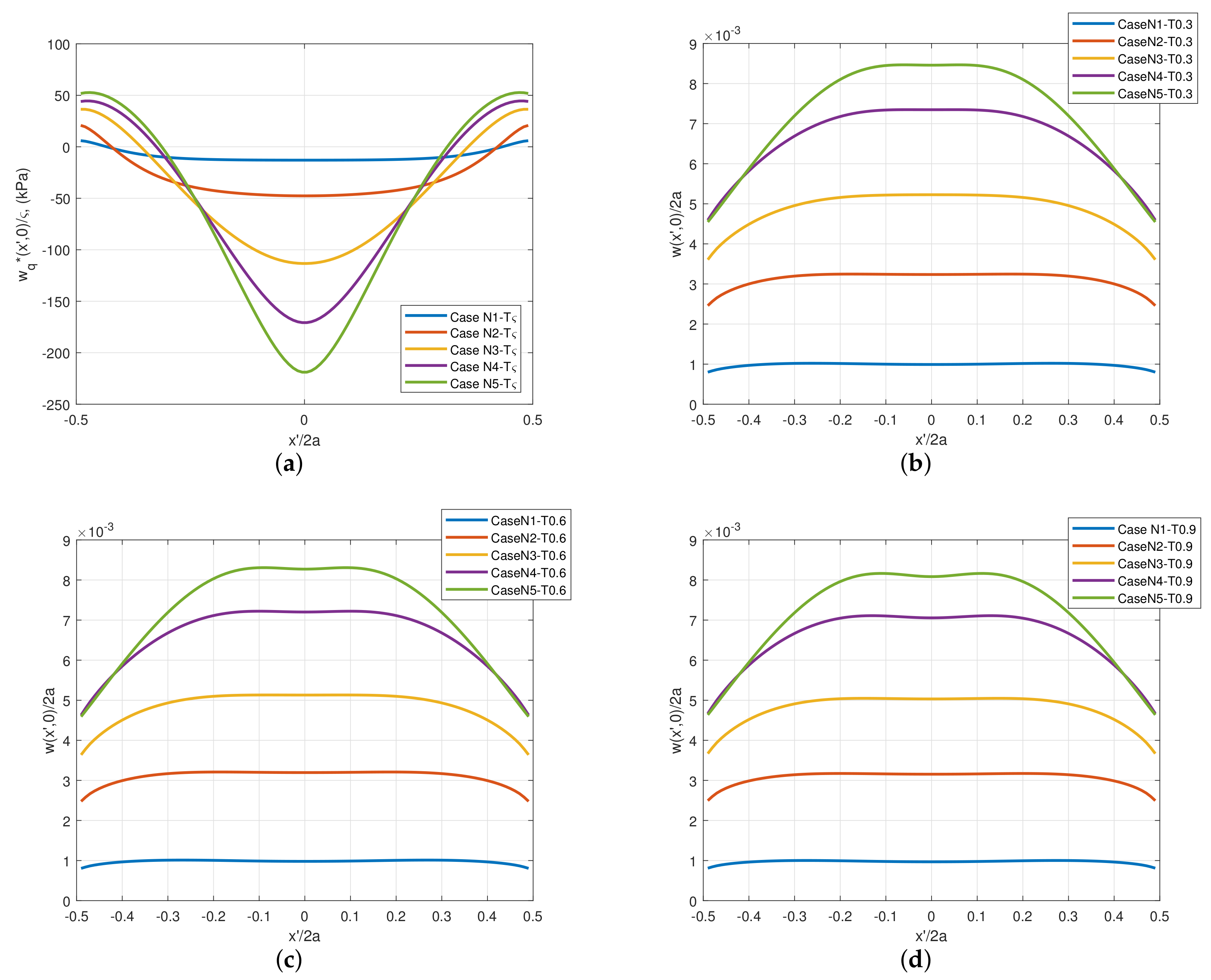
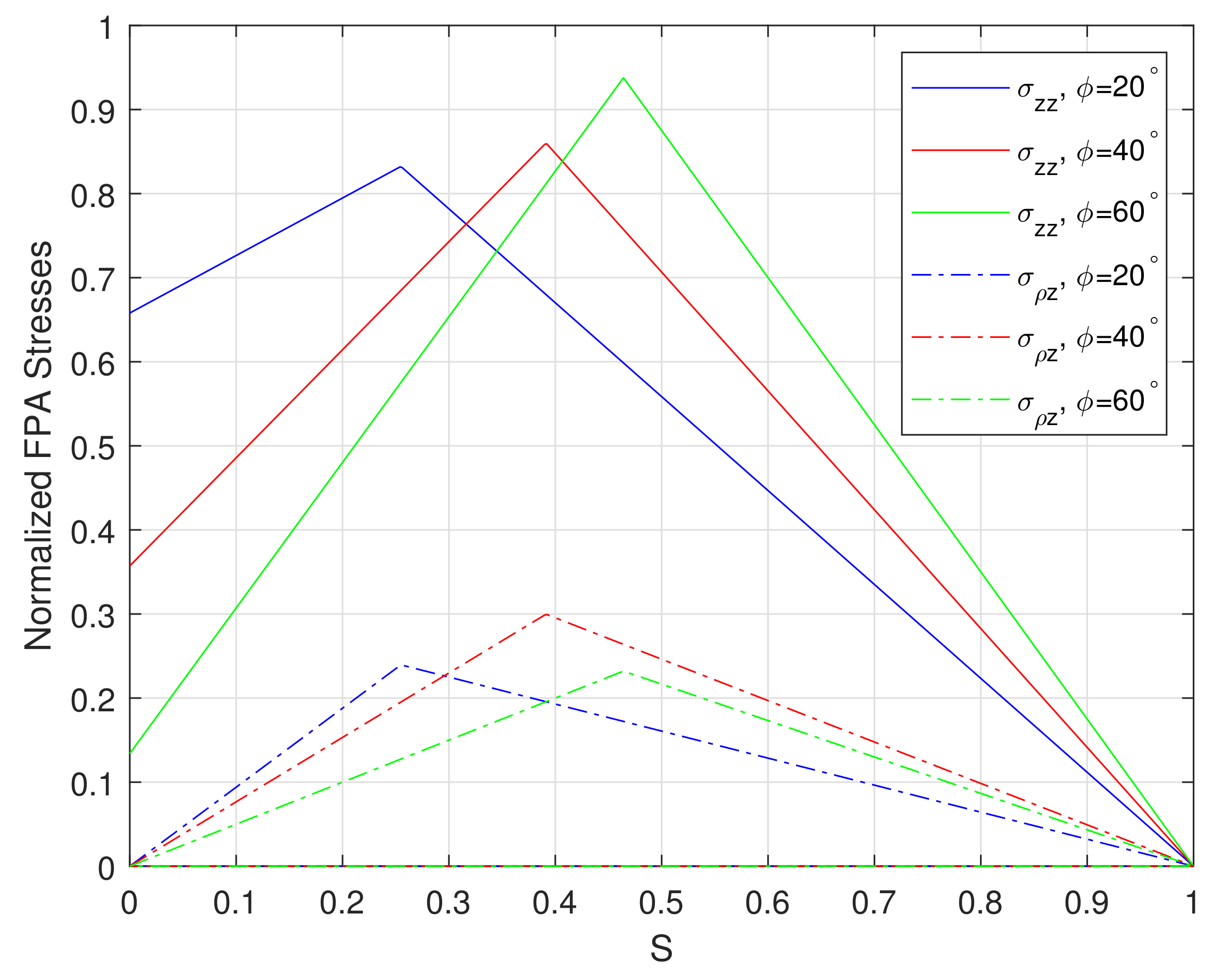
2.2.3. Effects of Remaining Stress Components
3. Discussion
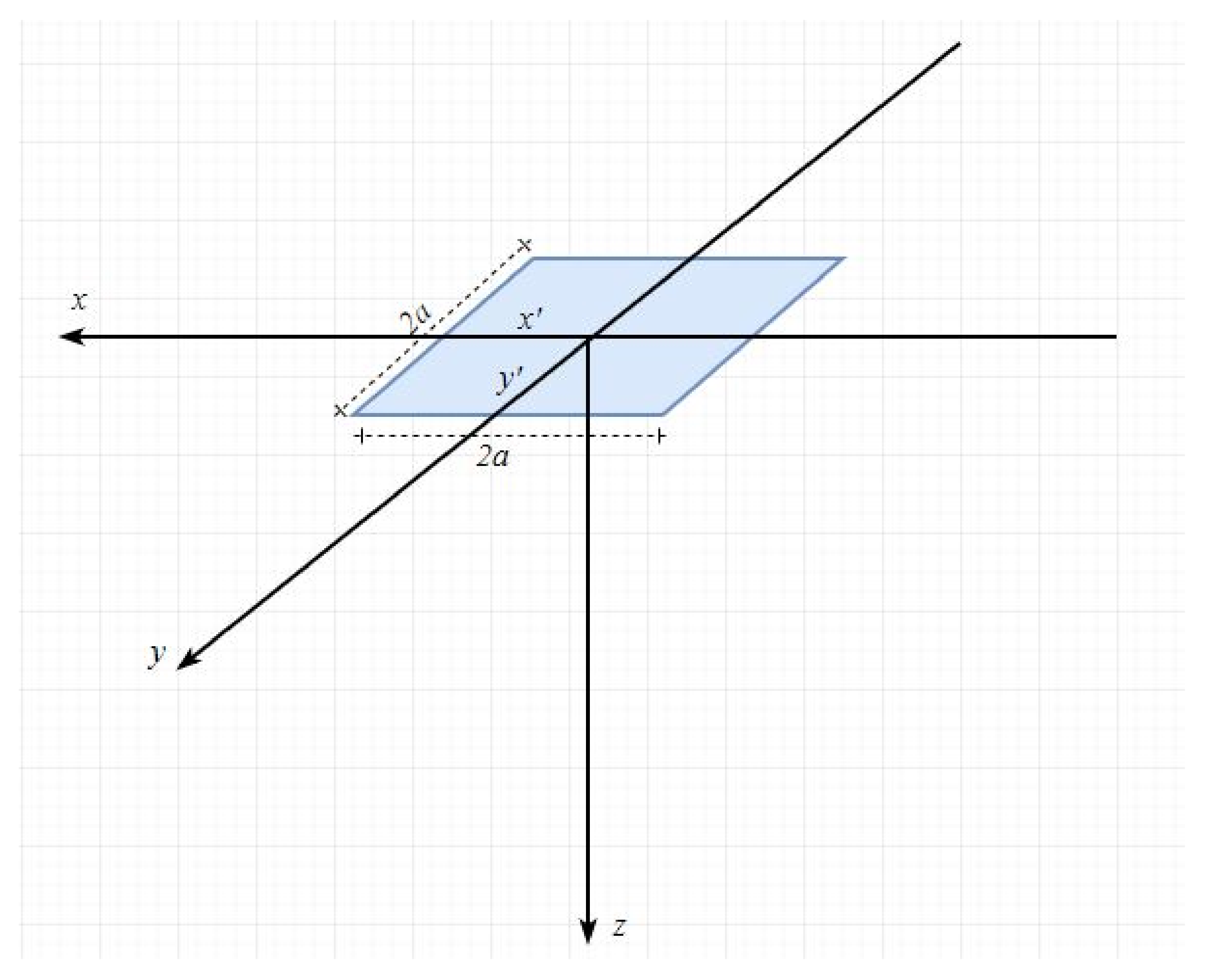
4. Materials and Methods
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FEM | Finite Element Method |
| DEM | Discrete Element Method |
| FPA | Fixed Principal Axis |
References
- Lazebnik, G.E.; Smirnov, A.A. Measurement of stresses under a rigid foundation block in the field. Soil Mech. Found. Eng. 1964, 1, 71–78. [Google Scholar] [CrossRef]
- Muhs, H.; Bub, H. On the measurement of friction in the base of flat footings founded in sand and first test results gained by a new gauge developed for the combined measurement of normal and tangential stresses. In Proceedings of the 6th International Conference of Soil Mechanics and Foundation Engineering, Montreal, QC, Canada, 8–15 September 1965; University of Toronto Press: Toronto, Canada, 1965. [Google Scholar]
- Murzenko, Y. Experimental results on the distribution of normal contact pressure on the base of a rigid foundation resting on sand. Soil Mech. Found. Eng. 1965, 2, 69–73. [Google Scholar] [CrossRef]
- Ho, M.; Lopes, R. Contact pressure of a rigid circular foundation. J. Soil Mech. Found. Div. Proc. Am. Soc. Civ. Eng. 1969, 93, 791–802. [Google Scholar] [CrossRef]
- Schultze, E. Distribution of stress beneath a rigid foundation. In Proceedings of the 5th International Conference on Soil Mechanics and Foundation Engineering, Paris, France, 17–22 July 1961; pp. 807–813. [Google Scholar]
- Sedykh, E. On the diagram or reaction pressures under the base of a rigid foundation. Soil Mech. Found. Eng. 1964, 3, 153–157. [Google Scholar] [CrossRef]
- Gorbunov-Possadov, M. Calculations for the stability of a sand bed by a solution combining the theories of elasticity and plasticity. In Proceedings of the Sixth International Conference on Soil Mechanics and Foundation Engineering, Montreal, QC, USA, 8–15 September 1965; Volume 2, pp. 51–55. [Google Scholar]
- Smoltczyk, H. Stress computation in soil media. J. Soil Mech. Found. Div. 1967, 93, 101–124. [Google Scholar] [CrossRef]
- Kerr, A. Tests and analyses of footings on a sand base. Soils Found. 1989, 29, 83–94. [Google Scholar] [CrossRef][Green Version]
- Nwabuokei, S. Measurements of Normal and Shear Stresses at the Base of a Rigid Footing Founded on Quartz Sand. Master’s Thesis, University of Ottawa, Ottawa, ON, Canada, 1976. [Google Scholar]
- Bauer, G.; Shields, D.; Scott, J.; Nwabuokei, S. Normal and shear stress measurements on a strip footing. Can. Geotech. J. 1979, 16, 177–189. [Google Scholar] [CrossRef]
- Balakrishna, C.; Murthy, B.; Nagaraj, T. Stress distribution beneath rigid circular foundations on sands. Int. J. Numer. Anal. Methods Geomech. 1992, 16, 65–72. [Google Scholar] [CrossRef]
- Abdullah, W. New elastoplastic method for calculating the contact pressure distribution under rigid foundations. Jordan J. Civ. Eng. 2008, 2, 71–89. [Google Scholar]
- Harding, J.; Sneddon, I. The elastic stresses produced by the indentation of the plane surface of a semi-infinite elastic solid by a rigid punch. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1945; Volume 41, pp. 16–26. [Google Scholar]
- Sneddon, I. Boussinesq’s problem of a flat-ended cylinder. Math. Proc. Camb. Philos. Soc. 1946, 42, 29–39. [Google Scholar] [CrossRef]
- Winkler, E. Die Lehre von der Elastizitat und Festigkeit; Dominicus: Prague, Czech Republic, 1867. [Google Scholar]
- Johnson, K. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Hartikainen, J. The distribution and direction of contact pressure under a rigid foundation. Acta Polytech. Scand. Civ. Eng. Build. Constr. 1972, 74, 9. [Google Scholar]
- Schweickert, K. Über den Einfluss von Reibungskräften in der Sohlfuge eines starren Streifenfundamentes auf die Sohldruckverteilung; Herr Klaus Boettcher: Karlsruhe, Germany, 1964. [Google Scholar]
- Taylor, A.G.; Chung, J.H. Application of low-order potential solutions to higher order vertical traction boundary problems in an elastic half-space. R. Soc. Open Sci. 2018, 5, 180203. [Google Scholar] [CrossRef] [PubMed]
- Taylor, A.G.; Chung, J.H. Analysis of tangential contact boundary value problems using potential functions. R. Soc. Open Sci. 2019, 6, 182106. [Google Scholar] [CrossRef]
- Smid, J.; Novosad, J. Pressure distribution under heaped bulk solids. In Proceedings of the 1981 PowTech Conference, Institution of Chemical Engineers, Birmingham, UK, 10–13 March 1981; Volume 63. pp. D3V 1–12. [Google Scholar]
- Brockbank, R.; Huntley, J.; Ball, R. Contact force distribution beneath a three-dimensional granular pile. J. Phys II 1997, 7, 1521–1532. [Google Scholar] [CrossRef]
- Vanel, L.; Howell, D.; Clark, D.; Behringer, R.P.; Clement, E. Memories in sand: Experimental tests of construction history on stress distributions under sandpiles. Phys. Rev. E 1999, 60, R5040–R5043. [Google Scholar] [CrossRef] [PubMed]
- Ai, J.; Ooi, J.; Chen, J.; Rotter, J.; Zhong, Z. The role of deposition process on pressure dip formation underneath a granular pile. Mech. Mater. 2013, 66, 160–171. [Google Scholar] [CrossRef]
- Zuriguel, I.; Mullin, T. The role of particle shape on the stress distribution in a sandpile. Proc. R. Soc. A Math. Phys. Eng. Sci. 2008, 464, 99–116. [Google Scholar] [CrossRef]
- Edwards, S.; Mounfield, C. A theoretical model for the stress distribution in granular matter. III. Forces in sandpiles. Phys. A Stat. Mech. Its Appl. 1996, 226, 25–33. [Google Scholar] [CrossRef]
- Wittmer, J.; Claudin, P.; Cates, M.; Bouchard, J. An explanation for the central stress minimum in sand piles. Nature 1996, 382, 336–338. [Google Scholar] [CrossRef]
- Wittmer, J.; Cates, M.; Claudin, P. Stress propagation and arching in static sandpiles. J. Phys. I 1997, 7, 39–80. [Google Scholar] [CrossRef][Green Version]
- Terzaghi, K. Theoretical Soil Mechanics; John Wiley and Sons, Inc.: New York, NY, USA, 1943. [Google Scholar]
- Biarez, J.; Burel, M.; Wack, B. Contribution a l’etude de la force portante des fondations. In Proceedings of the 5th International Conference on Soil Mechanics and Foundation Engineering, Paris, France, 17–22 July 1961; Volume 1, p. 603. [Google Scholar]
- Abd El Samee, W.N. Effect of Shape and Depth of Shallow Foundations on Failure Mechanism and Wedge Angle of Sandy Soil. In Advanced Research on Shallow Foundations; Shehata, H., Das, B., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 197–216. [Google Scholar]
- Li, N.; Cheng, M. Discrete Element Modeling on Bearing Capacity Problems. Int. J. Geol. Environ. Eng. 2016, 10, 618–625. [Google Scholar]
- Li, L.; Jiang, M.; Li, T.; Chen, S. DEM Analyses of the Whole Failure Process of Shallow Foundation in Plate Load Test on Dense Sand. 2018. Available online: https://www.researchgate.net/publication/327208070_DEM_analyses_of_the_whole_failure_process_of_shallow_foundation_in_plate_load_test_on_dense_sand (accessed on 8 November 2021).
- da Rocha, J.; de Faria, M.; Albuquerque, B.; Neto, J. Shallow foundation analysis using the discrete element method. Mater. Sci. Eng. Int. J. 2019, 3, 136–139. [Google Scholar]
- Watson, A. Searching for the sand-pile pressure dip. Science 1996, 273, 579–580. [Google Scholar] [CrossRef]
- Boussinesq, J. Application des Potentials a L’etude de L’equilibre et du Mouvement des Solides Elastiques; Gauthier-Villars: Paris, France, 1885. [Google Scholar]
- Love, A.E.H. The stress produced in a semi-infinite solid by pressure on part of the boundary. Philos. Trans. R. Soc. London. Ser. A Contain. Pap. A Math. Phys. Character 1929, 228, 377–420. [Google Scholar]
- Newmark, N.M. Simplified computation of vertical pressures in elastic foundations. In Report, Engineering Experiment Station; University of Illinois at Urbana-Champaign: Champaign, IL, USA, 1935. [Google Scholar]
- Davis, R.O.; Selvadurai, A.P.S. Elasticity and Geomechanics; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- von Mises, R. On Saint Venant’s principle. Bull. AMS 1945, 51, 555–562. [Google Scholar] [CrossRef]
- Lambe, T.; Whitman, R. Soil Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Forsbach, F. Stress Tensor and Gradient of Hydrostatic Pressure in the Half-Space Beneath Axisymmetric Bodies in Normal and Tangential Contact. Front. Mech. Eng. 2020, 6, 39. [Google Scholar] [CrossRef]
- Goldenberg, C.; Goldhirsch, I. Friction enhances elasticity in granular solids. Nature 2005, 435, 188–191. [Google Scholar] [CrossRef]
- Güllü, H.; Fedakar, H.I. On the prediction of unconfined compressive strength of silty soil stabilized with bottom ash, jute and steel fibers via artificial intelligence. Geomech. Eng. 2017, 12, 441–464. [Google Scholar] [CrossRef]
- Çanakçi, H.; Güllü, H.; Dwle, M.I.K. Effect of Glass Powder Added Grout for Deep Mixing of Marginal Sand with Clay. Arab. J. Sci. Eng. 2018, 43, 1583–1595. [Google Scholar] [CrossRef]

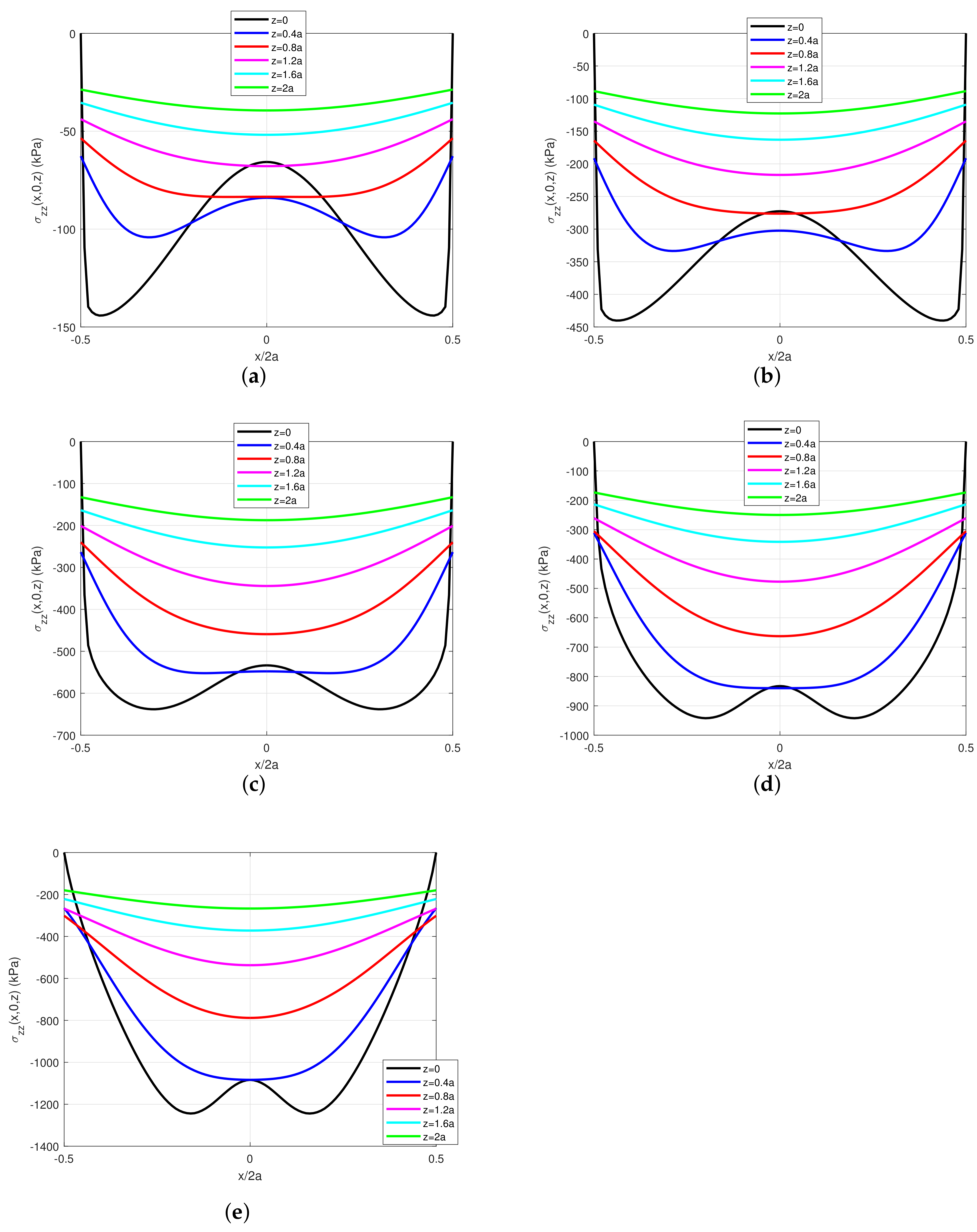
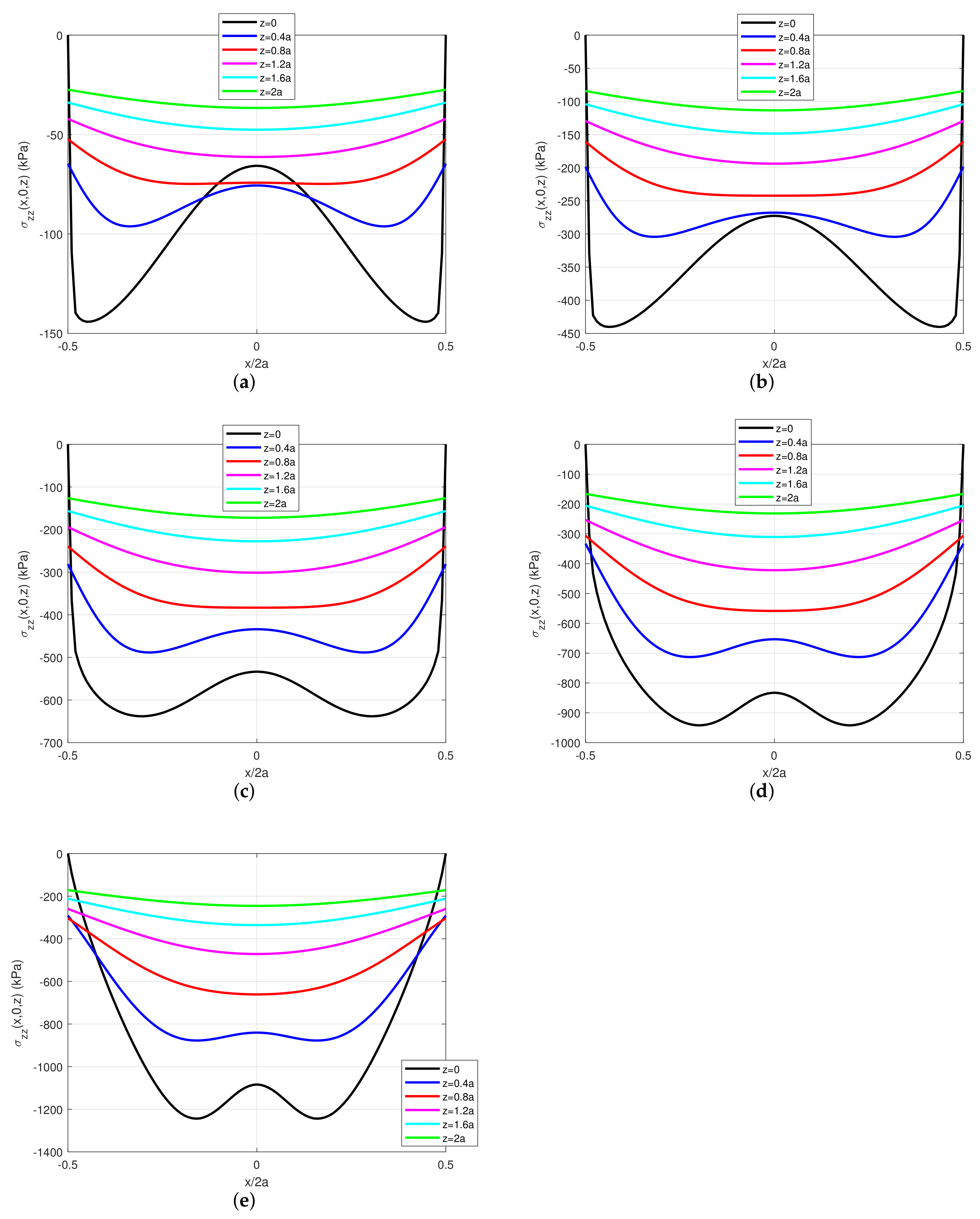
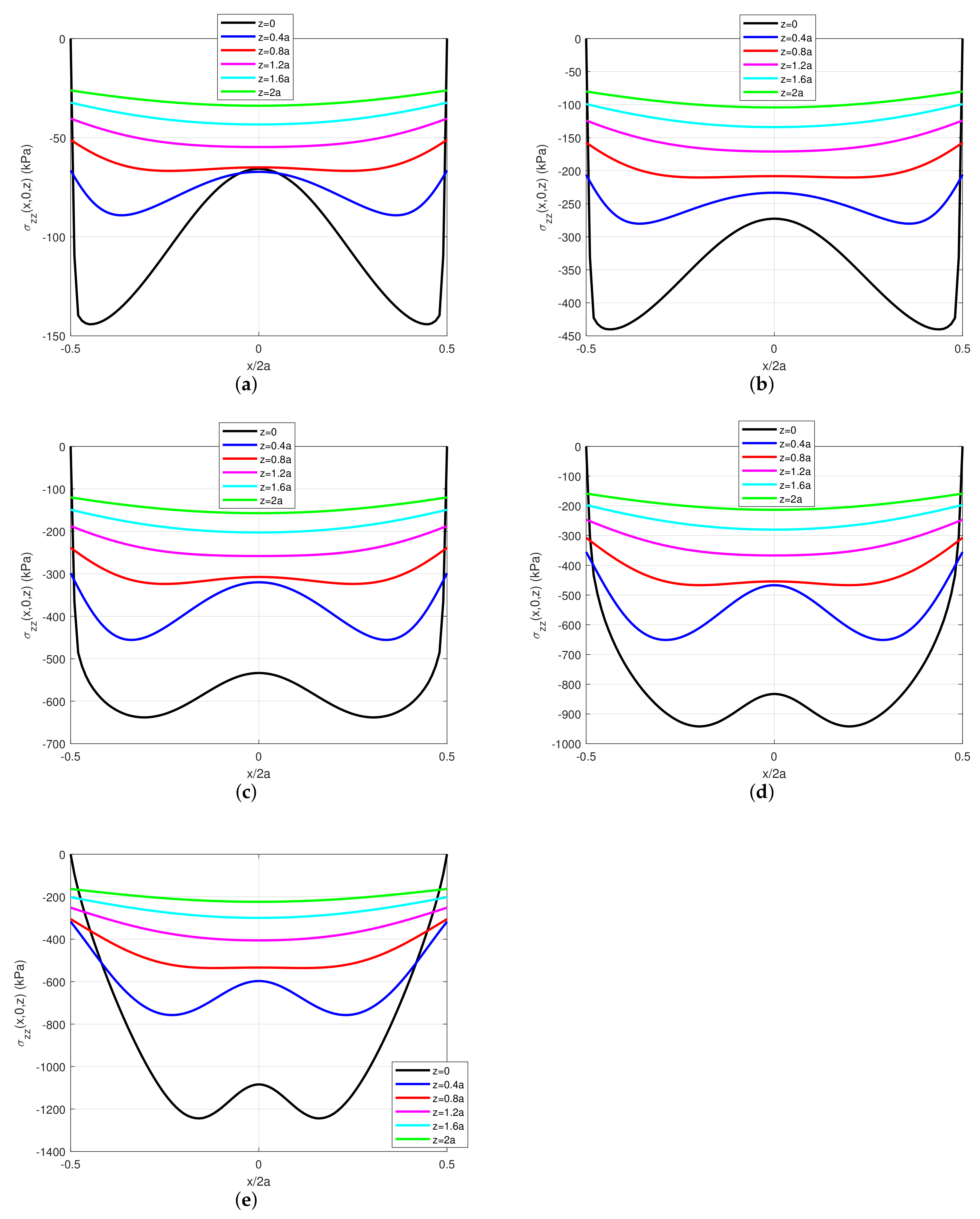

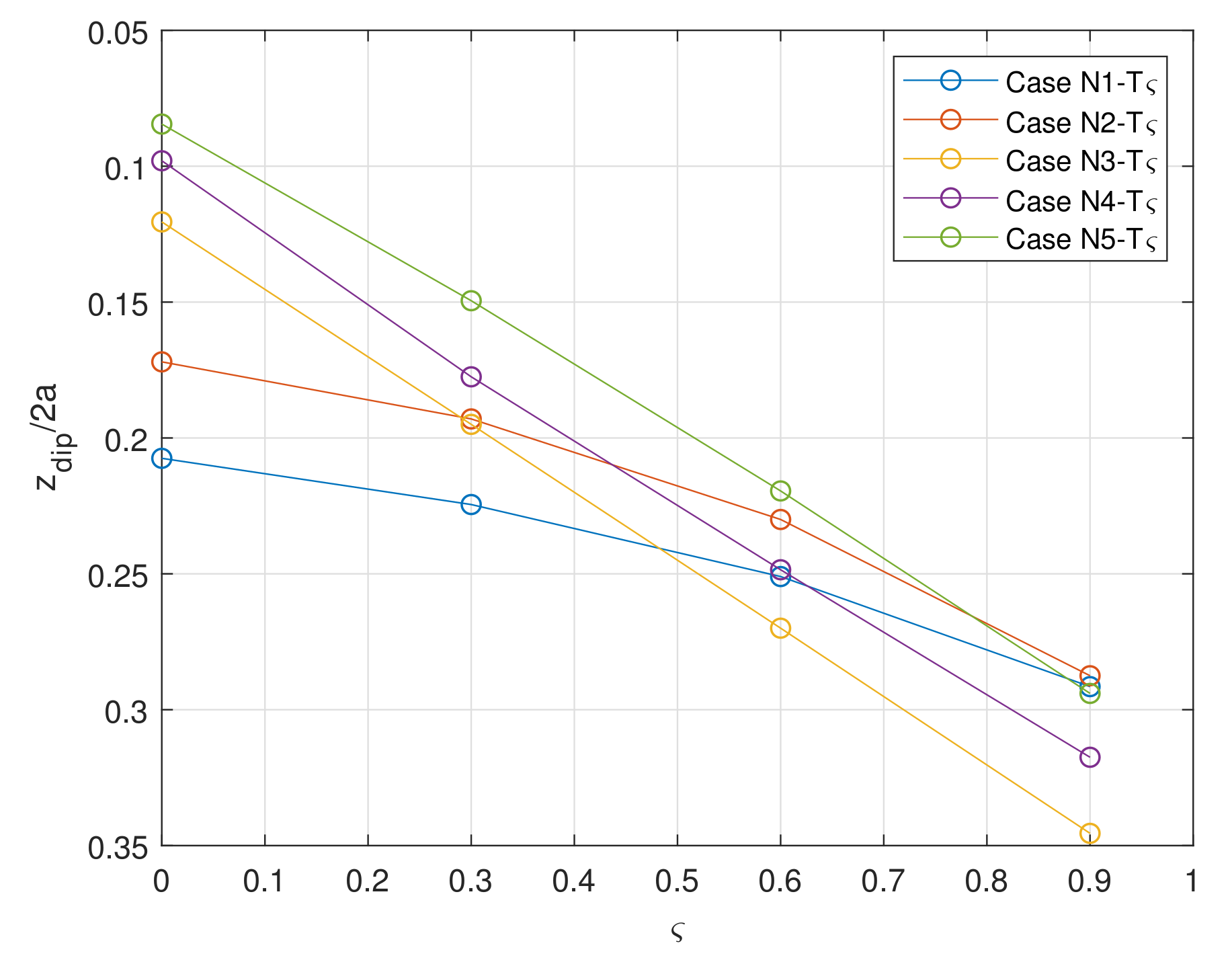
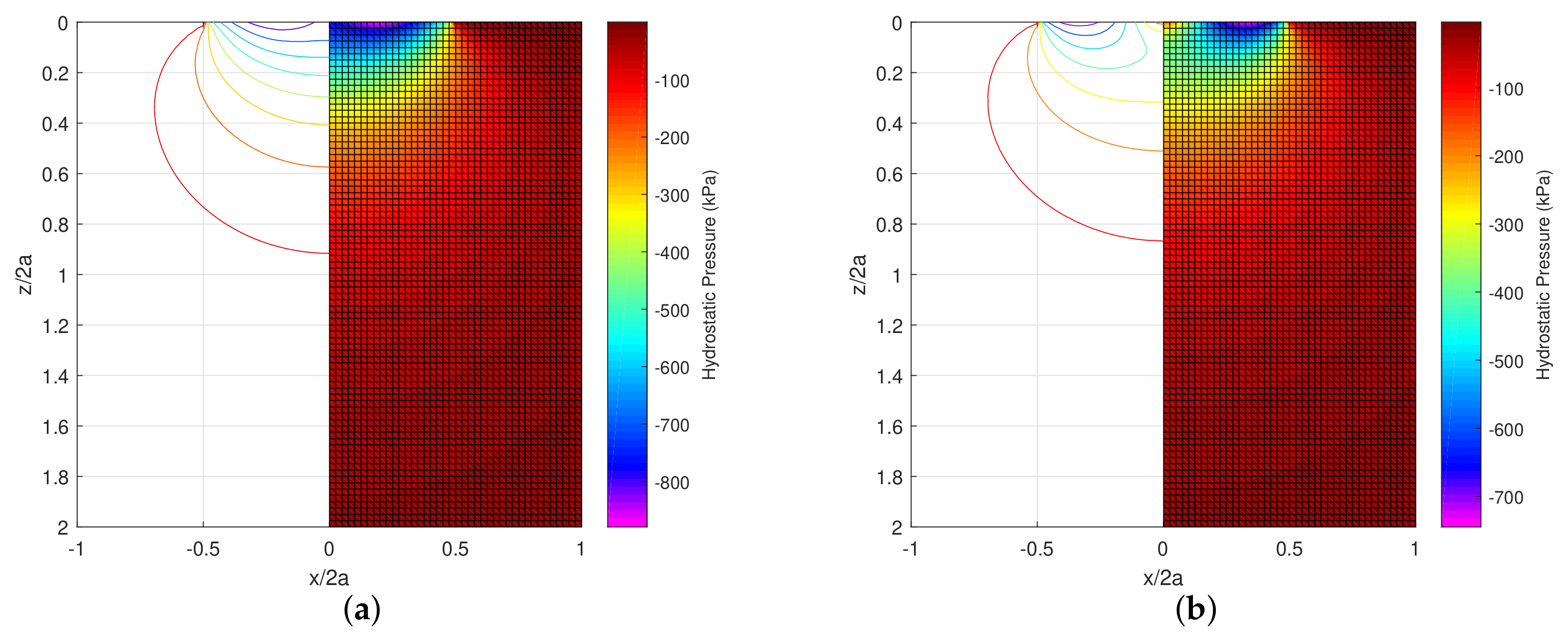
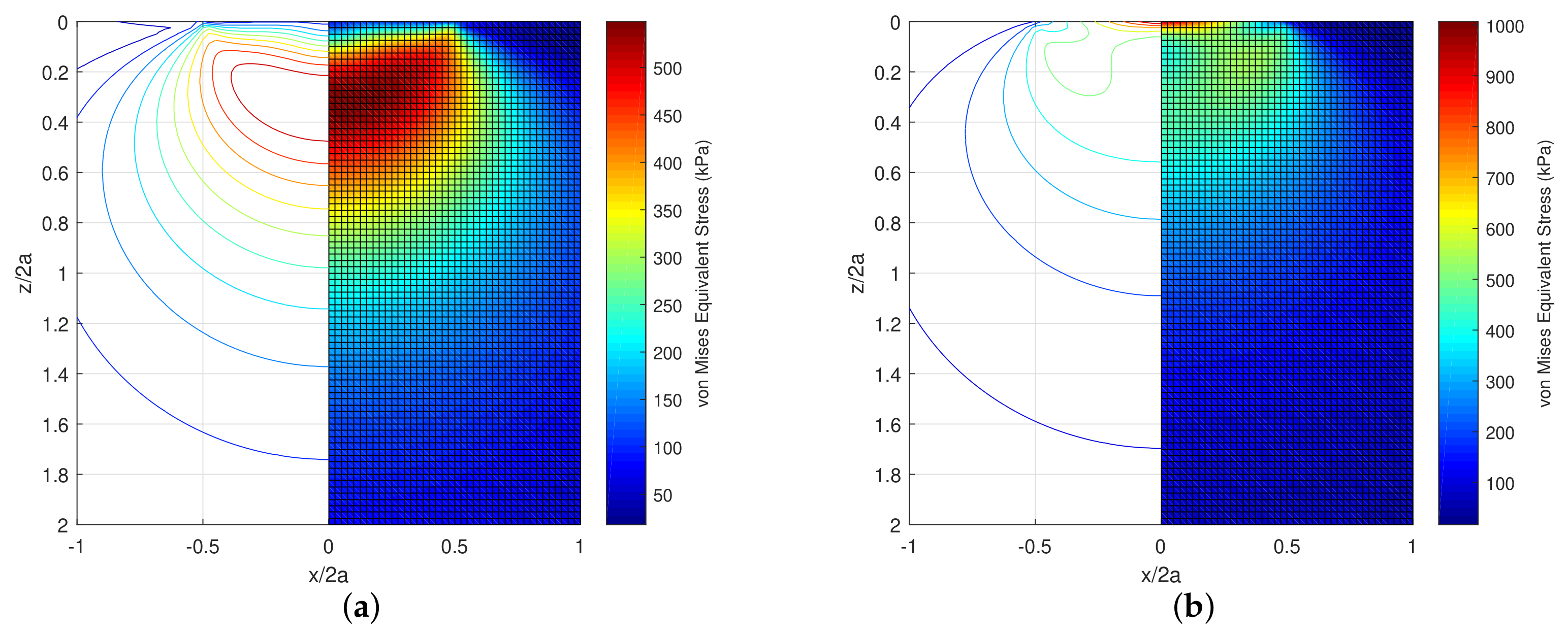
| Case N1 | 1935.557 | 2069.007 | 127.751 | 141.196 | 0.0605 | 0.0539 | 0.7367 | 0.7838 |
| Case N2 | 5819.266 | 5047.482 | 309.301 | 232.123 | 0.0619 | 0.0605 | 0.7719 | 0.8213 |
| Case N3 | 7391.370 | 6138.864 | 205.655 | 80.404 | 0.1454 | 0.1585 | 0.4888 | 0.5074 |
| Case N4 | 10,532.047 | 10,006.803 | 220.551 | 168.095 | 0.3166 | 0.4956 | 0.3123 | 0.2446 |
| Case N5 | 15,063.014 | 14,008.211 | 422.666 | 317.186 | 0.7887 | 0.9731 | 0.2785 | 0.1694 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taylor, A.G.; Chung, J.H. Explanation and Application of the Evolving Contact Traction Fields in Shallow Foundation Systems. Geotechnics 2022, 2, 91-113. https://doi.org/10.3390/geotechnics2010004
Taylor AG, Chung JH. Explanation and Application of the Evolving Contact Traction Fields in Shallow Foundation Systems. Geotechnics. 2022; 2(1):91-113. https://doi.org/10.3390/geotechnics2010004
Chicago/Turabian StyleTaylor, Adam G., and Jae H. Chung. 2022. "Explanation and Application of the Evolving Contact Traction Fields in Shallow Foundation Systems" Geotechnics 2, no. 1: 91-113. https://doi.org/10.3390/geotechnics2010004
APA StyleTaylor, A. G., & Chung, J. H. (2022). Explanation and Application of the Evolving Contact Traction Fields in Shallow Foundation Systems. Geotechnics, 2(1), 91-113. https://doi.org/10.3390/geotechnics2010004






