On the Dilatancy of Fine-Grained Soils

Abstract

A new evaluation method for the dilatancy of fine-grained soils based on monotonic and cyclic undrained triaxial tests has been established using two elasticity approaches: isotropic and transverse isotropic hypoelasticity. The evaluation of two clays, Kaolin and Lower Rhine Clay, with the new method also shows that the dilatancy of fine-grained soils is dependent on the stress ratio, the void ratio, and the straining direction along with the intrinsic material parameters. Similar to sand, we can observe a Phase Transformation Line beyond which further shearing induces a volume increase. A generalization of the Taylor dilatancy rule from direct shear to multiaxial space is established, and an extension accounting for the behaviour of soft soils is proposed. We formulate a simple hypoplastic constitutive relation with a modified flow rule that reproduces the observed dilatant as well as contractant behaviour. Some simulations of monotonic as well as cyclic tests prove the accurate performance of the proposed dilatancy relation.

1. Notation and Symbols

The notation of this article is as follows.

Scalar quantities are denoted with italic fonts (e.g., e, m), vectors with bold non-italic fonts (e.g., $\mathbf{m},\mathbf{f}$), second rank tensors with bold fonts (e.g., $\mathit{\sigma }$, $\mathit{\epsilon }$), and fourth rank tensors with Sans Serif type (e.g., $𝗘$, $𝗜$). Tensors represented with the indicial notation are denoted with italic symbols and their respective lower indices (e.g., ${\mathit{\sigma }}_{ij}$, $g_i$). The tensorial operations follow the Einstein’s summation convention.

Multiplication with two dummy indices, also known as double contraction, is marked with a colon “:” (e.g., $\mathit{\sigma }:\mathit{\epsilon }={\sigma }_{ij}{\epsilon }_{ij}$). When the symbol is omitted, it is understood as a dyadic product (e.g., $\mathit{\sigma }\mathit{\epsilon }={\sigma }_{ij}{\epsilon }_{kl}$). The trace of a tensor is denoted by $\mathrm{tr}\bigsqcup ={\bigsqcup }_{ii}$, where ⊔ represents, in general, a second rank tensor. The unit tensor $\mathbf{1}$ corresponds to the Kronecker delta ${\delta }_{ij}$:

$$\begin{array}{c}\hfill \mathbf{1}={\delta }_{ij}=\left\{\begin{array}{cc}1,\hfill & i=j\hfill \\ 0,\hfill & i\ne j\hfill \end{array}\right.\end{array}$$

(1)

The unit symmetric four rank tensor 𝗜 is defined as ${𝗜}_{ijkl}=1/2\left({\delta }_{ik}{\delta }_{jl}+{\delta }_{il}{\delta }_{jk}\right)$. The brackets $\parallel \bigsqcup \parallel$ extract the Euclidean norm (e.g., $\parallel \mathit{\sigma }\parallel =\sqrt{{\sigma }_{ij}{\sigma }_{ij}}$). Normalised tensors are denoted by $\overrightarrow{\bigsqcup }=\bigsqcup /\parallel \bigsqcup \parallel$ or, in general, as ${\bigsqcup }^{\to }$. The deviatoric part of a tensor is denoted with a superscript ${\bigsqcup }^{*}$ (e.g., ${\mathit{\sigma }}^{*}=-1/3\mathrm{tr}\left(\mathit{\sigma }\right)\mathbf{1}$).

The components of the effective stress tensor (hereafter referred to simply as the stress tensor) $\mathit{\sigma }$, displacement vector $\mathit{u}$, or strain tensor (${\epsilon }_{ij}={\displaystyle \frac{1}{2}}\left(u_{i,j}+u_{j,i}\right)$) $\mathit{\epsilon }$ follow the geotechnical convention; thus, compression is defined as negative. The Roscoe invariants are defined as $p=-\mathrm{tr}\mathit{\sigma }/3$, $q=\sqrt{3/2}\parallel {\mathit{\sigma }}^{*}\parallel$, ${\epsilon }_v=-\mathrm{tr}\mathit{\epsilon }$ and ${\epsilon }_q=\sqrt{2/3}\parallel {\mathit{\epsilon }}^{*}\parallel$. The stress ratio $\eta$ is defined as $\eta =q/p$. The deviator stress tensor is defined as ${\mathit{\sigma }}^{*}=\mathit{\sigma }+p\mathbf{1}$ and the stress ratio tensor is ${\widehat{\mathit{\sigma }}}^{*}={\mathit{\sigma }}^{*}/p=\sqrt{2/3}\eta \overrightarrow{{\mathit{\sigma }}^{*}}$.

2. Introduction

The design of different geotechnical installations, ranging from simple foundations over combined pile and raft foundation systems to complex soil improvements with e.g., stone columns, requires the accurate description of the entire material behaviour of the underground. The mechanical response of the underground consisting of fine-grained soils is governed by dilatancy and contractancy, here referred to collectively as dilatancy. Under undrained conditions in triaxial tests, the prevented dilatancy leads to an increase in the mean effective pressure $p^{\prime }$ and the prevented contractancy can lead to considerable decay of the same pressure. The consequences are then a reduction in mean effective pressure $p^{\prime }$, a decay of the barotropic stiffness, as well as a considerable reduction in the undrained shear strength $q_{max}$. Accurate and reliable predictions of post-seismic irreversible displacements in retaining structures supporting fine-grained and low-permeable soils can therefore be obtained only if the adopted constitutive model is capable of capturing correctly the soil dilatancy as a function of the current stress and loading history [1]. Furthermore, the dilatancy is shown to depend also on other state variables, such as the void ratio e [2,3,4,5,6,7].

Although the particular forms proposed by Taylor [2] and by Rowe [3] for sand were different, both of them recommended a unique function dependent on the stress ratio $\eta =q/p^{\prime }$ for the dilatancy, as depicted by Been and Jefferies [8] or later by Li and Dafalias [5] $d=d(\eta ,C)$ whereby C is a set of inherent material properties. However, experimental evidence [4,9,10,11,12] shows a density dependence of the dilatancy as well—for example, dense sand dilates after minor initial contractancy and loose sand contracts during shearing. For this purpose, researchers have proposed various expressions of state-dependent dilatancy for sands [5,8,13,14].

On the other hand, too little attention has been paid to the dilatant behaviour of fine-grained soils. Li and Dafalias [5] indicate that $d=d(\eta ,M)$, with the slope of the critical state line denoted as M, works quite well for clays. This may hold for normally consolidated clays under monotonic loading (comparable to the behaviour of loose sands). However, experimental evidence has shown that initially overconsolidated clays (the overconsolidation ratios ${\mathrm{OCR}}_0$ and $\mathrm{OCR}$ will precisely be defined in Section 3.2) ${\mathrm{OCR}}_0>2$ dilate [11,15,16,17,18], exhibiting a similar response to medium dense and dense sands.

Therefore, the behaviour of clays is governed to a large extent by the initial state of the soil. A soft, initially normally consolidated clay subjected to undrained cyclic loading passes through different overconsolidation ratios $\mathrm{OCR}\ge 1$. However, if the undrained cyclic behaviour of a normally consolidated clay with a moderate number of cycles is successfully described, the behaviour of an overconsolidated clay is captured simultaneously. Different peculiarities of the mechanical behaviour of fine-grained soils become increasingly important at different stages during, for example, undrained cyclic triaxial loading:

(i)

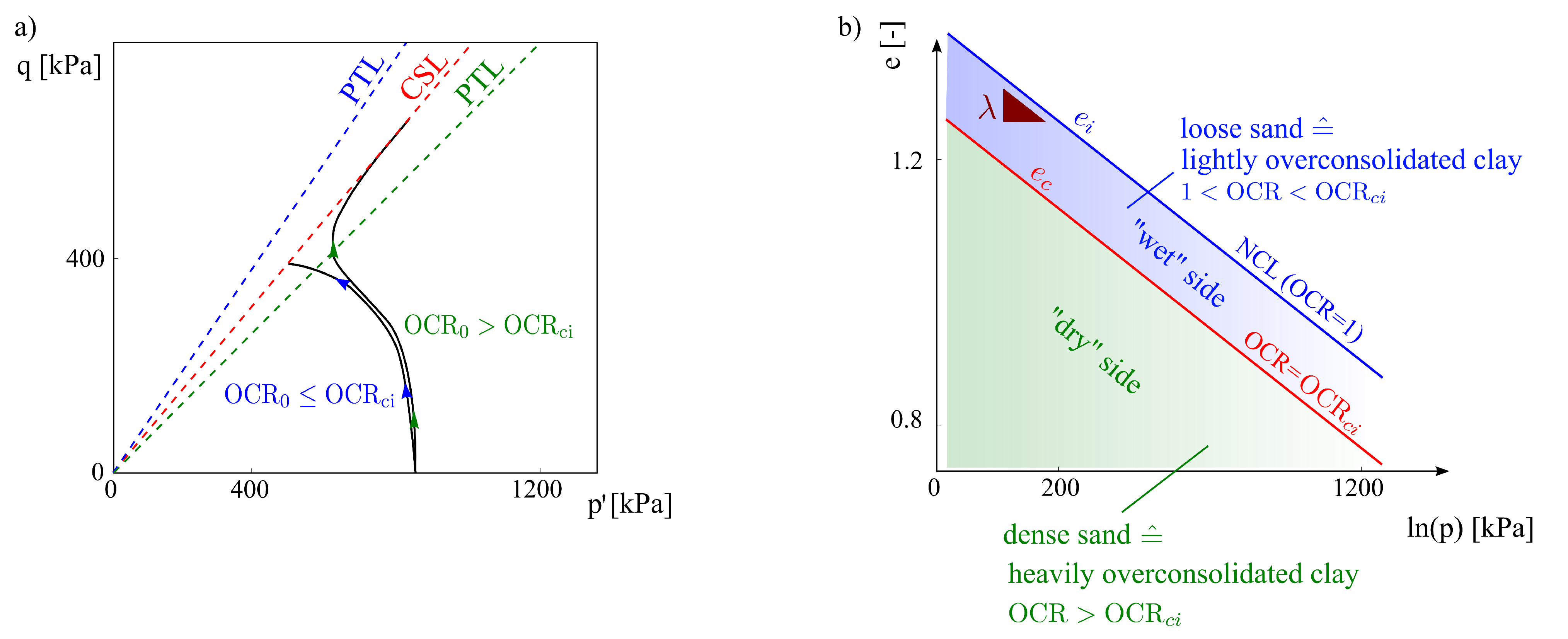
at the beginning, ${\mathrm{OCR}}_0=1$, and the rate-dependent behaviour of a plastic clay achieves its maximum.

(ii)

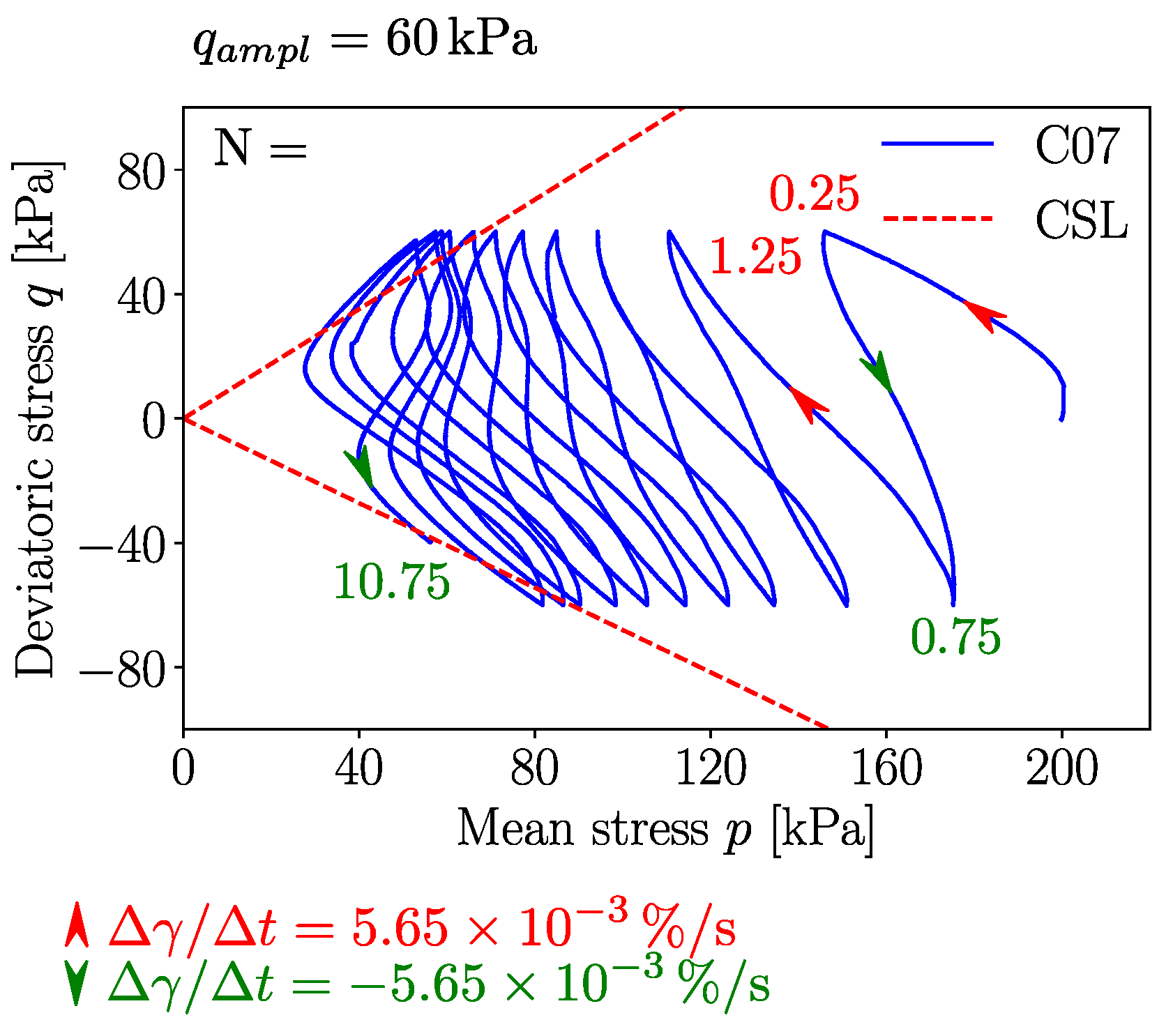
After some cycles of constant stress amplitude, the mean effective pressure decreases while the void ratio and the preconsolidation pressure remain constant, i.e., the current OCR increases.

(iii)

For $1<\mathrm{OCR}\le 2$, the rate dependency of the clay decays sparsely and, depending on the subjected loading magnitude, the response of the material is contractant. This leads to a reduction in the effective mean stress p, resulting in a decay of the shear strength and of the barotropic stiffness.

(iv)

Towards higher $\mathrm{OCR}>2$, a significant reduction in the viscous effects is evident. We will show that, in this case, the phase transformation line (PTL) lies below the critical state line. Thus, besides contractancy, dilatant behaviour can also be observed when overpassing the PTL (similar to the behaviour of sands, widely reported in the literature [11,14,19,20]).

However, constitutive modellers dealing with fine-grained soils in the literature indicate that the introduction of the overcritical dilatant behaviour (PTL lies above or at the critical state line) is sufficient [5,21,22,23,24]. The present work is devoted to highlighting the fact that dilatancy and contractancy are highly relevant for geotechnical issues on silts and clays dealing with volumetric change due to shearing and depend on the initial state of the soil. Inferring from this, it is not enough only to describe the overcritical dilatancy correctly.

In Section 3, a new approach to the evaluation of experimental data on normally and overconsolidated fine-grained soils regarding their dilatancy is provided. Then, in Section 4, based on this approach, a state-dependent dilatancy rule for fine-grained soils is formulated. Finally, in Section 4.2, the proposed dilatancy relation is incorporated into a simple hypoplastic model for soft soils [18]. The model performance is evaluated through simulations of laboratory tests on two cohesive soils, Kaolin (low-plasticity silt) and Lower Rhine Clay (high-plasticity clay), in Section 4.4. The experiments include also variation of the initial OCR${}_0$. Note that, in the same context, the proposed dilatancy rule can be introduced into elastoplastic models as well. At the end, some conclusions and a short outlook are provided.

3. Dilatancy of Fine-Grained Soils Evaluated from Monotonic and Cyclic Triaxial Tests

Many publications have claimed that the dilatancy of fine-grained soils is only dependent on the stress ratio [21,23,25,26,27]. However, experimental evidence gained, for example, in [11] shows that with increasing initial ${\mathrm{OCR}}_0$, the mechanical response of the soil sample is rendered more dilative and higher undrained shear strengths are reached. For normally consolidated samples, the PTL may not be reached during undrained shearing $M_d\ge M$ ($M_d$ denotes the stress ratio at the PTL) and, therefore, the material response becomes contractant. However, the PTL is observed to lie below the CSL for overconsolidated samples $M_d<M$. Figure 1a includes these relationships qualitatively for undrained shearing of samples with different initial overconsolidation ratios in the effective stress space. Similar dependencies of the dilatancy on the overconsolidation ratio can be concluded from the experiments reported in [15,28,29,30,31,32,33,34,35,36,37,38]. Nevertheless, the dilatancy and its dependence on the void ratio (i.e., OCR) was mostly ignored in the constitutive modelling of soft soils.

3.1. Basic Postulates and Assumptions

As noted before, stress–dilatancy relations have been proposed mainly for sands and mostly based on constant pressure triaxial tests. In this case, the volumetric change, and hence the volumetric strain rate ${\dot{\epsilon }}_v$, corresponds to the dilatant one ${\dot{\epsilon }}_v^d$ (since $p^{\prime }=const.$, all volumetric changes are induced by shearing, which, by definition, is dilatancy). Since drained tests for cohesive soils are highly time-consuming and therefore very difficult to find in the literature, we will use undrained triaxial tests (monotonic and cyclic) of Kaolin [17] and of Lower Rhine Clay [12]. For the evaluation of the dilatancy behaviour, some assumptions and relations need to be established.

We divide the total strain rate $\dot{\mathit{\epsilon }}$ into an elastic ${\dot{\mathit{\epsilon }}}^{el}$ and a plastic ${\dot{\mathit{\epsilon }}}^p$ portion:

$$\begin{array}{c}\hfill \dot{\mathit{\epsilon }}={\dot{\mathit{\epsilon }}}^{el}+{\dot{\mathit{\epsilon }}}^p.\end{array}$$

(2)

Note that a fundamental assumption is made: even though the tests are performed with a constant strain rate, the viscosity of the soil is neglected in this evaluation.

An elastoplastic constitutive equation has the form:

$$\begin{array}{c}\hfill \dot{\mathit{\sigma }}=𝗘:\left({\dot{\mathit{\epsilon }}}^{el}+{\dot{\mathit{\epsilon }}}^p\right)\mathrm{with}{\dot{\mathit{\epsilon }}}^p=\dot{\xi }\mathbf{m}.\end{array}$$

(3)

The tangential stiffness tensor is adopted from [18,39,40,41]:

$$\begin{array}{c}\hfill {𝗘}_{iso}=3K\overrightarrow{\mathbf{1}}\overrightarrow{\mathbf{1}}+2G{𝗜}^{dev}\end{array}$$

(4)

The barotropic bulk and shear modulus follow the relations presented in [18,39,40,41]:

$$\begin{array}{c}\hfill K={\displaystyle \frac{p^{\prime }(1+e)}{\kappa }},G={\displaystyle \frac{3(1-2\nu )}{2(1+\nu )}}K,\end{array}$$

(5)

whereby the framework for a theoretically acceptable adjustment of the pressure-dependent shear modulus proposed by Houlsby [42] has been used. To account for the transversal isotropic elasticity of some fine-grained soils [43], the isotropic one is transformed (scaled and rotated) as suggested in [44] and analyzed in [45]:

$$\begin{array}{ccc}& {\displaystyle {𝗘}_{abcd}={𝗤}_{abij}:{𝗘}_{iso,ijkl}:{𝗤}_{klcd}}& \hfill \end{array}$$

(6)

$$\begin{array}{ccc}& {𝗤}_{abcd}={\mu }_{ac}{\mu }_{bd}& \hfill \end{array}$$

(7)

$$\begin{array}{ccc}& \mathbf{\mu }=\sqrt{\alpha }\mathbf{1}+(1-\sqrt{\alpha }){\mathbf{m}}_s\otimes {\mathbf{m}}_s,& \hfill \end{array}$$

(8)

where the vector ${\mathbf{m}}_s$ is aligned with the sedimentation axis and the anisotropic coefficient $\alpha$ is a material parameter [18] similar to the Poisson’s ratio $\nu$; see also Appendix B.

For axialsymmetric conditions (e.g., triaxial test), we can rewrite Equation (3) in $P-Q$ ($P^{\prime }$ and Q are isometric invariants $P^{\prime }=\overrightarrow{\mathbf{1}}:{\mathit{\sigma }}^{\prime }\stackrel{triax.}{=}({{\sigma }_1}^{\prime }+2{{\sigma }_3}^{\prime })/\sqrt{3}$ and $Q=-\overrightarrow{{\mathbf{1}}^{*}}:{\mathit{\sigma }}^{\prime }\stackrel{triax.}{=}2({\sigma }_1-{\sigma }_3)/\sqrt{6}$. Its counterpart strain variables are calculated through: ${\epsilon }_P=\overrightarrow{\mathbf{1}}:\mathit{\epsilon }\stackrel{triax.}{=}({\epsilon }_1+2{\epsilon }_3)/\sqrt{3}$, ${\epsilon }_Q=-\overrightarrow{{\mathbf{1}}^{*}}:\mathit{\epsilon }\stackrel{triax.}{=}2({\epsilon }_1-{\epsilon }_3)/\sqrt{6}$) components:

$$\begin{array}{c}\hfill \left[\begin{array}{c}{\dot{P}}^{\prime }\\ \dot{Q}\end{array}\right]=\left[\begin{array}{cc}{E}_{PP}& E_{PQ}\\ E_{QP}& E_{QQ}\end{array}\right]·\left[\begin{array}{c}{\dot{\epsilon }}_P\left(isom\right)-\dot{\xi }{m}_P\\ {\dot{\epsilon }}_Q\left(isom\right)-\dot{\xi }{m}_Q\end{array}\right].\end{array}$$

(9)

In addition, the ratio between volumetric and deviatoric plastic strain rate is defined as dilatancy:

$$\begin{array}{c}\hfill d=-{\displaystyle \frac{d{\epsilon }_v^p}{d{\epsilon }_q^p}}=-C{\displaystyle \frac{d{\epsilon }_P^p}{d{\epsilon }_Q^p}}=C{\displaystyle \frac{m_P}{m_Q}}\end{array}$$

(10)

where C is a scaling constant. Solving (9) and (10) for a constant pressure triaxial test $(\dot{P}=0)$ and isotropic elasticity of the material $(E_{PQ}=E_{QP}=0)$, the following expression is obtained:

$$\begin{array}{c}\hfill {\displaystyle \frac{m_P}{m_Q}}={\displaystyle \frac{{\dot{\epsilon }}_P}{{\dot{\epsilon }}_Q-\dot{Q}/E_{QQ}}}\end{array}$$

(11)

corresponding to the relations obtained for sand by Pradhan et al. [4].

In the case of a triaxial undrained test (i.e., assuming constant volume ${\dot{\epsilon }}_P=0$) and the isotropic elasticity of the material, the dilatancy relation is rearranged to:

$$\begin{array}{c}\hfill {\displaystyle \frac{m_P}{m_Q}}={\displaystyle \frac{\dot{P}{E}_{QQ}}{\dot{Q}{E}_{PP}-{\dot{\epsilon }}_Q{E}_{PP}{E}_{QQ}}}.\end{array}$$

(12)

In the case of a trixial undrained test and anisotropic elasticity of the material $(E_{PQ},E_{QP}\ne 0)$, as is the case with Kaolin [17,18,40] and various other fine-grained soils [17,43], we find an expression for dilatancy as follows:

$$\begin{array}{c}\hfill {\displaystyle \frac{m_P}{m_Q}}={\displaystyle \frac{\dot{Q}{E}_{PQ}-\dot{P}{E}_{QQ}}{-\dot{Q}{E}_{PP}+\dot{P}{E}_{QP}-{\dot{\epsilon }}_Q{E}_{PQ}{E}_{QP}+{\dot{\epsilon }}_Q{E}_{PP}{E}_{QQ}}}.\end{array}$$

(13)

Equations (11)–(13) above represent the basis for the evaluation of the experimental data. Furthermore, for the reduction of experimental data scatter the approximation of the mean stress is provided in Appendix A.

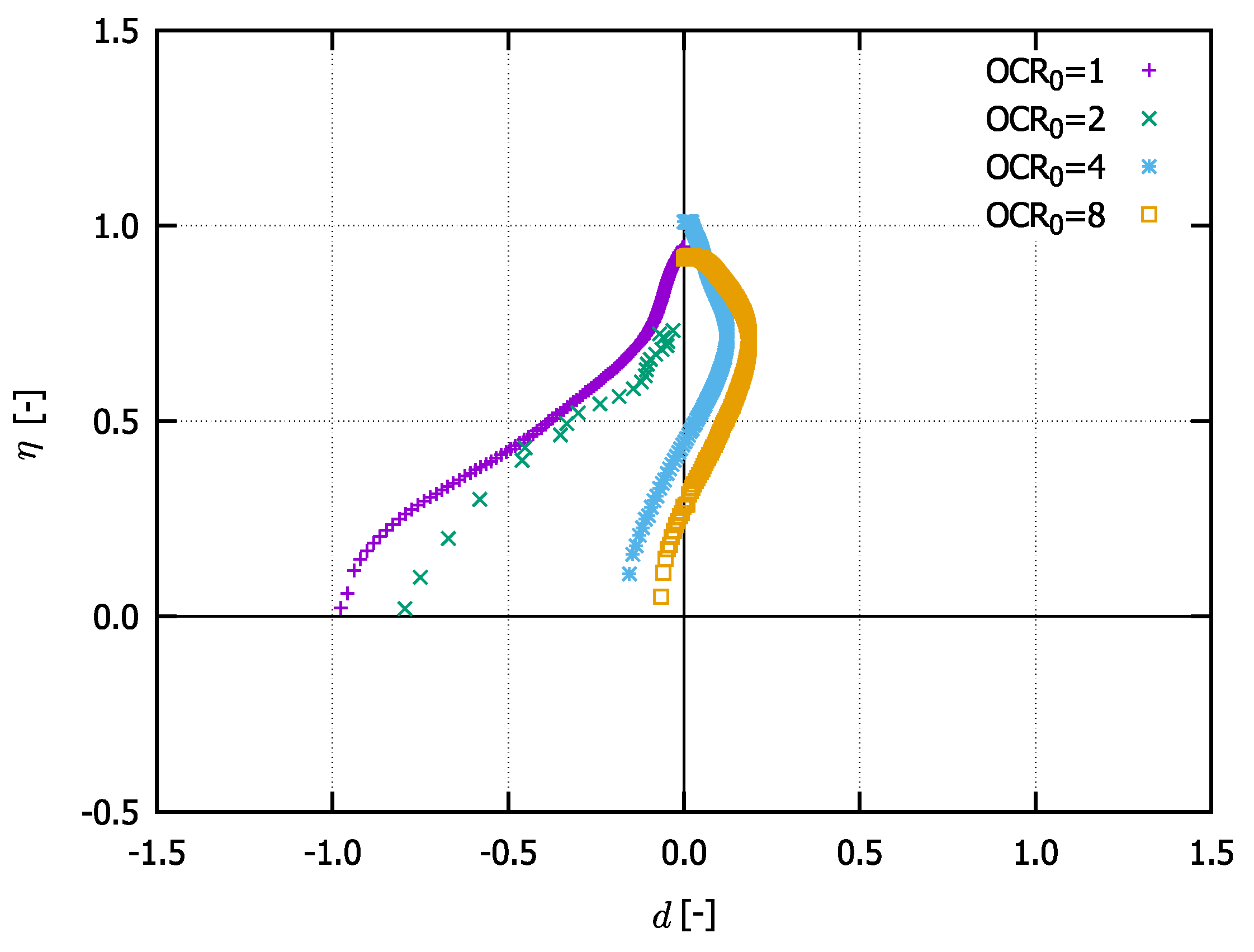
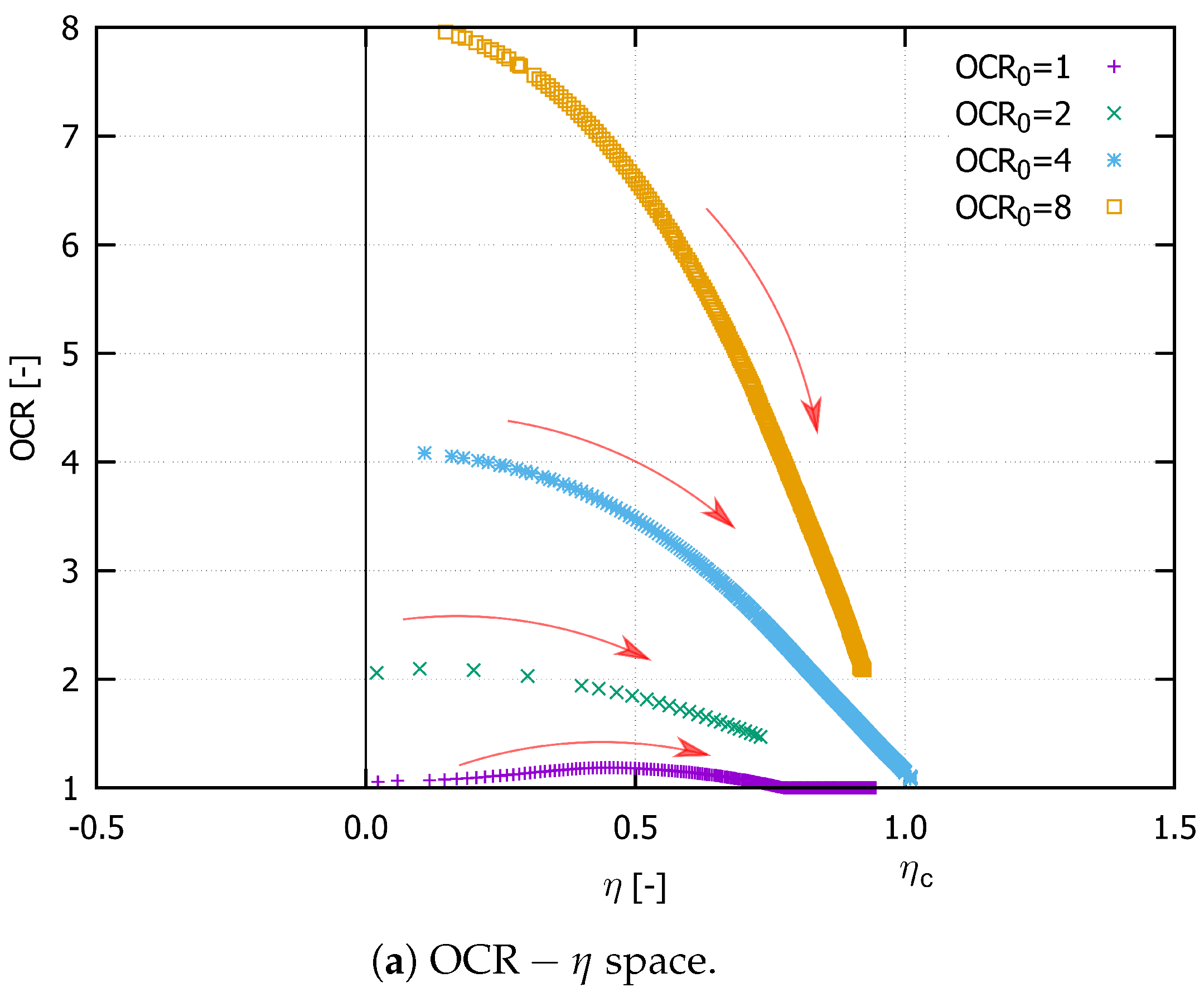
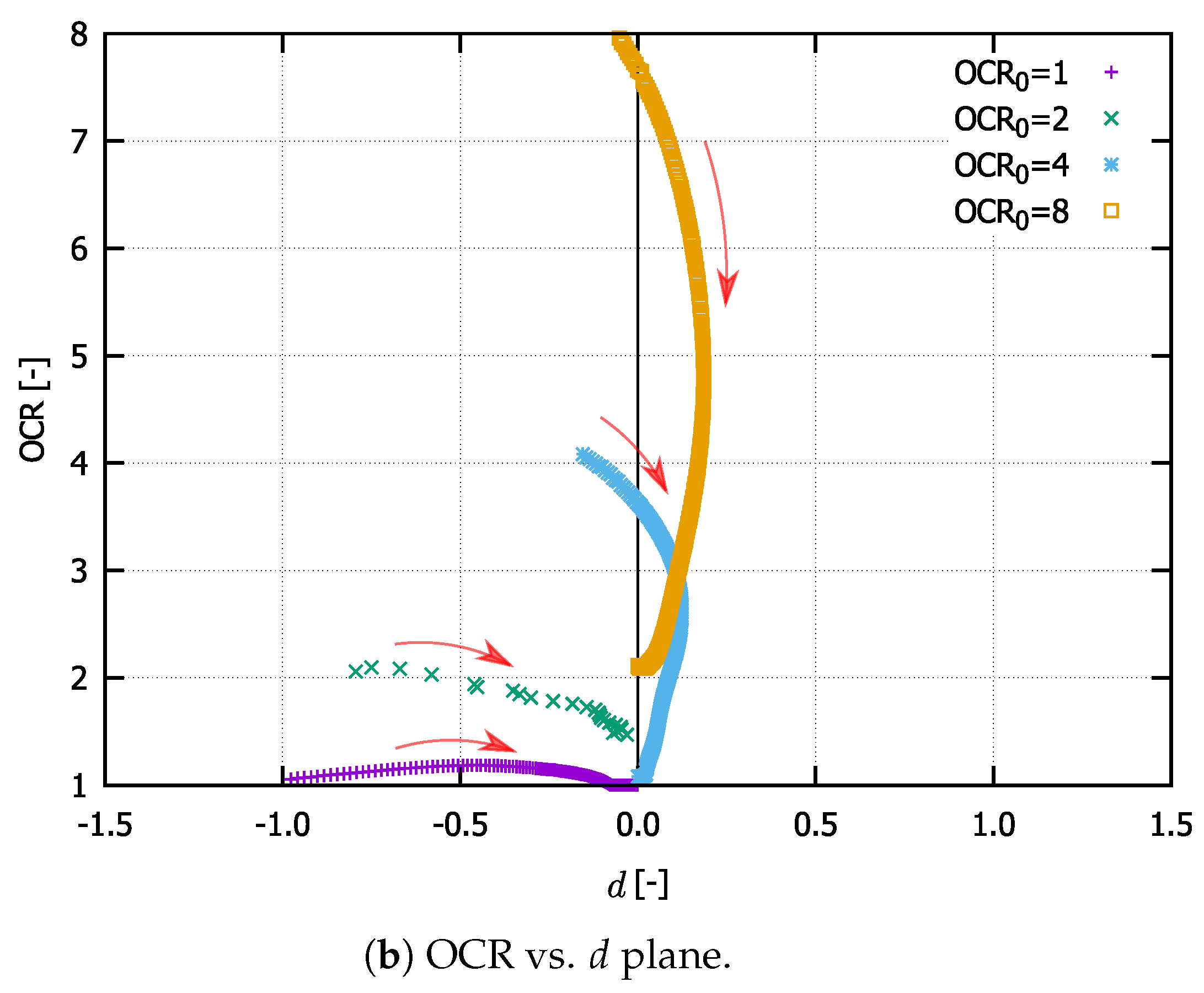
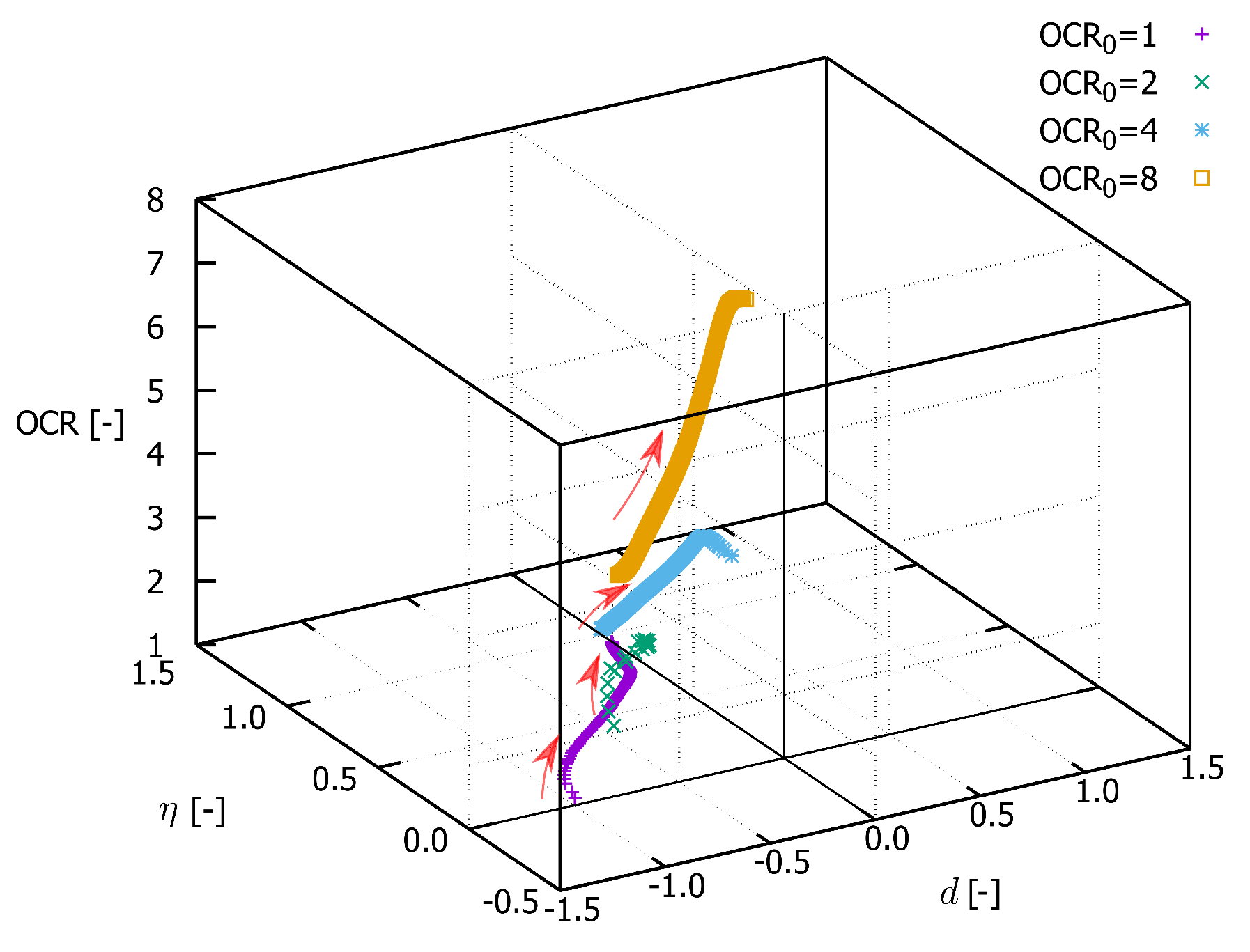
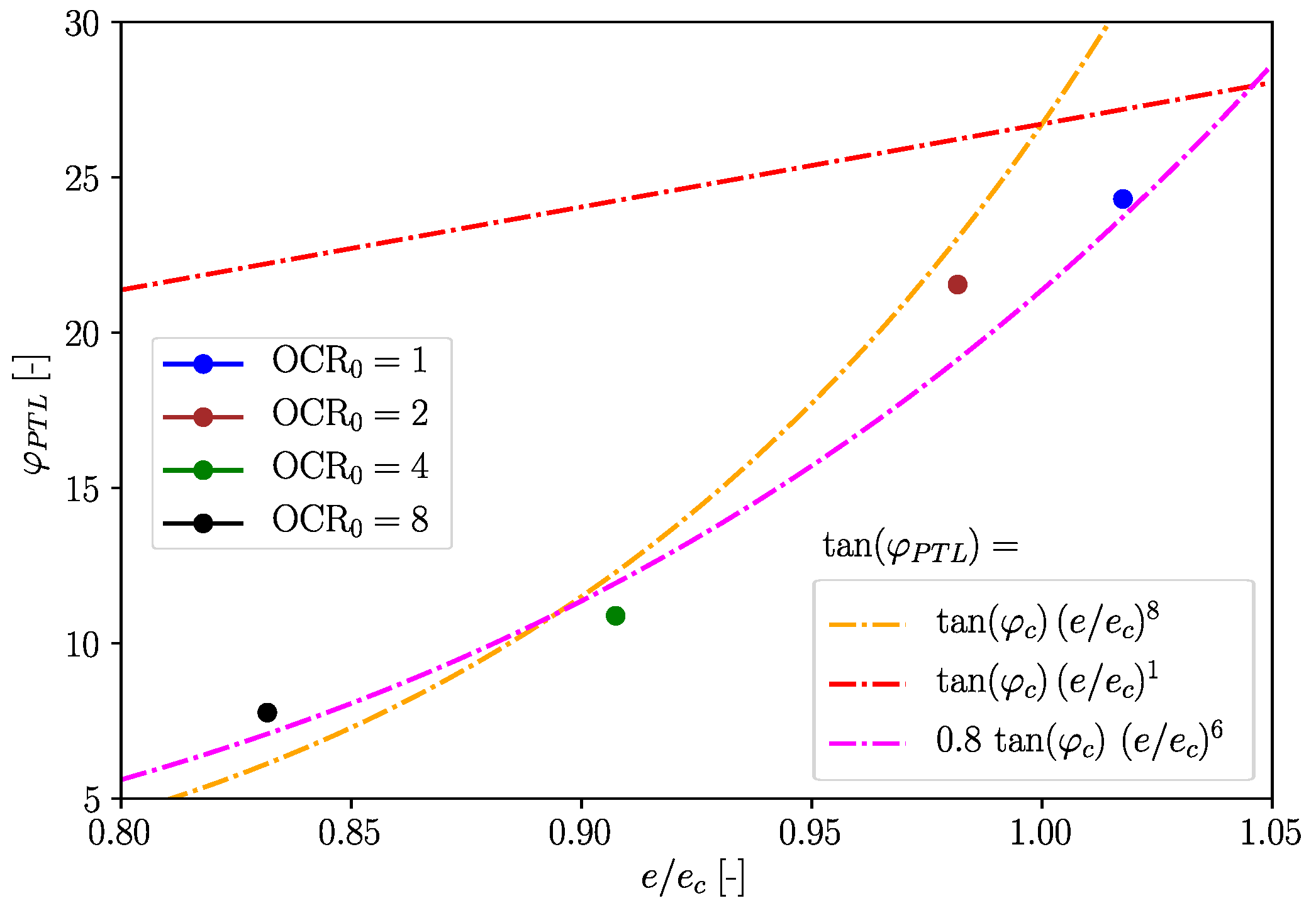
3.2. Overconsolidation Ratio

We continue with the definition of the terms normally consolidated, slightly overconsolidated and heavily overconsolidated. The state of the material is defined by a combination between the void ratio e and the mean effective pressure $p^{\prime }$. The normally consolidated state (OCR = 1) is given by the maximum void ratio $e_i$, as depicted in Figure 1.

$$\begin{array}{c}\hfill e_i=e_{i0}-\lambda ln(p^{\prime }/{p_{ref}}^{\prime }).\end{array}$$

(14)

Hence, the slope of the normally consolidated line (NCL) in e vs. $ln\left(p\right)$ diagram is determined through the compression index $\lambda$ and its position is defined through the material constant $e_{i0}$ specified at a reference mean effective pressure ${p_{ref}}^{\prime }$. Equation (14) can be solved for the void ratio equivalent normally consolidated pressure imposing the condition $e=e_i$. Then, ${p_{ei}}^{\prime }=p^{\prime }$ proposed first by Hvorslev [46] is obtained:

$$\begin{array}{c}\hfill {p_{ei}}^{\prime }=exp\left({\displaystyle \frac{e_{i0}-e}{\lambda }}\right).\end{array}$$

(15)

${p_{ei}}^{\prime }$ can be termed also the preconsolidation pressure (similar to ${p_c}^{\prime }$ in Cam Clay).

Sands are denoted as dense or loose in terms of their relative density. The classification depending on the void ratio itself is not the most appropriate for clays, because there are no tests to determine the reference void ratios $e_{max}$ or $e_{min}$ for fine-grained soils. Instead, in the laboratory, the overconsolidation ratio is used:

$$\begin{array}{c}\hfill \mathrm{OCR}={\displaystyle \frac{{p_{ei}}^{\prime }}{p^{\prime }}}\end{array}$$

(16)

with the Hvorslev stress ${p_{ei}}^{\prime }$ defined in Equation (15). Note that the generalisation of the overconsolidation ratio to account for the shear stress can be found in the dissertation of the first author [47].

Similar to the NCL, the critical void ratio line in the e vs. p diagram can be defined through:

$$\begin{array}{c}\hfill e_c=e_{i0}-\lambda ln\left({\mathrm{OCR}}_{ci}\right)-\lambda ln(p^{\prime }/{p_{ref}}^{\prime }).\end{array}$$

(17)

In analogy to sands and gravels, which are defined as loose or dense depending on the position of the state $(e,p^{\prime })$ with respect to the critical void ratio line, clays can also be defined as slightly overconsolidated or heavily oversoncolidated. We define a material state lying between the NCL $(\mathrm{OCR}=1)$ and the critical void ratio line $(\mathrm{OCR}={\mathrm{OCR}}_{ci}>1)$ (blue area in Figure 1) as slightly overconsolidated $(1<\mathrm{OCR}<{\mathrm{OCR}}_{ci})$, similar to the definitions in [48]. The subscript $ci$ stays for the critical isotropic line. The aforementioned states of soils are likely to be considered on the “wet” side of the critical, not to be confused with the saturation of the soil. For a heavily overconsolidated clay $\mathrm{OCR}>{\mathrm{OCR}}_{ci}$ (green area in Figure 1), the void ratio is lower than the critical one. Therefore, the soil is considered on the “dry” side, i.e., drier than at the critical line.

Thus, we suggest that there is an overconsolidation ratio ${\mathrm{OCR}}_{ci}$ and, upon shearing for a given void ratio $e=e_c$, there is a stress ratio at which the behaviour of clays changes from contractant to dilatant. In the next sections, this assumption will be justified with experimental evidence.

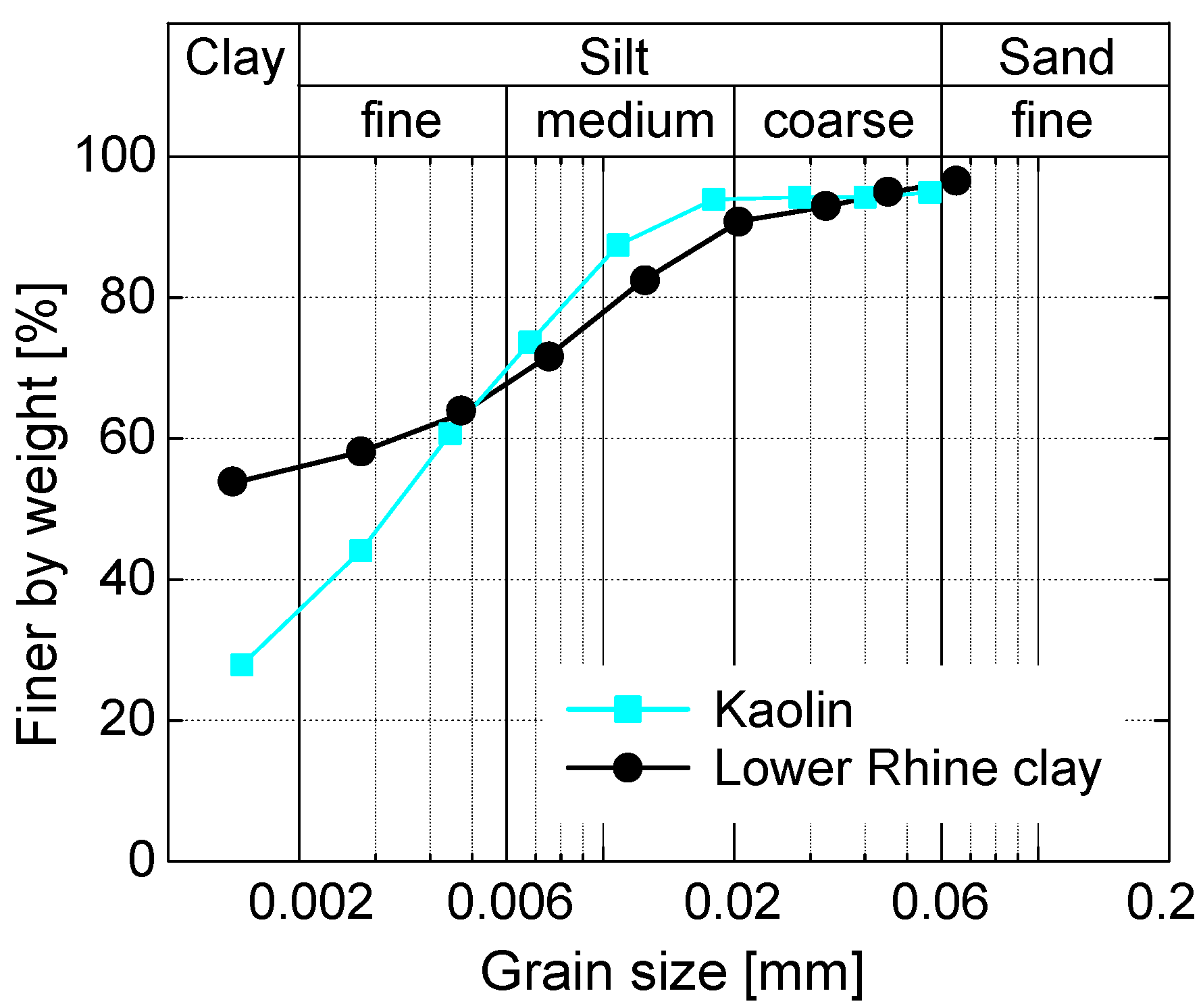
3.3. Results for Kaolin

Kaolin is a low-plasticity, soft soil ($I_P=12.2\%$) lying below the A-line in Casagrandes’ plasticity diagram (thus, it should be classified as silt). The grain size distribution curve of the treated Kaolin is presented in Figure 2. In the following, monotonic as well as cyclic undrained triaxial tests on Kaolin [17] are evaluated using the definitions from Section 3.1. The adopted parameters are listed in

Table 1. Parameters used for evaluation purposes.

Material	$\mathit{\nu }$	$\mathit{\alpha }$	$\mathit{\lambda }$	$\mathit{\kappa }$	${\mathit{e}}_{\mathit{i}0}$
	[-]	[-]	[-]	[-]	[-]
Kaolin	$0.3$	1 *,1.8 *	$0.13$	$0.05$	$1.76$
Lower Rhine Clay	$0.2$	$1.0$	$0.26$	$0.04$	$2.47$

* $\alpha =1$ for isotropic hypoelasticity, $\alpha =1.8$ for transversal isotropic hypoelasticity.

.

3.3.1. Triaxial Tests under Monotonic Loading

In Figure 3, Figure 4 and Figure 5, the evaluation results of four undrained triaxial tests with different initial overconsolidation ratios of ${\mathrm{OCR}}_0=\{1,2,4,8\}$ are presented. The test data are borrowed from [17]. Thereby, the samples were consolidated out of a slurry having a water content of $w/w_L=2.5$. After being built into the triaxial device, the samples were subjected to a drained isotropic preloading towards $p_{max}^{\prime }=\{100,200,400\mathrm{or}800\}$ kPa, followed by a drained unloading to $p_0^{\prime }=100$ kPa, reaching the respective overconsolidation ratios. For the evaluation procedure, we account for transversal isotropic hypoelasticity; see Equation (13). The stiffness components $E_{PP},E_{PQ},E_{QP}$ and $E_{QQ}$ are solved using Equations (4)–(9) and the calibrated parameters are listed in Table 1. For the calibration process, the attentive reader is referred to [18,39,50,51].

Figure 3 shows the relationship between the stress ratio and the dilatancy for the different initial overconsolidation ratios. Obviously, the normally consolidated sample ${\mathrm{OCR}}_0=1$ as well as the slightly overconsolidated sample ${\mathrm{OCR}}_0=2$ show a prevented contractant behaviour $d<0$ upon undrained triaxial compression $d{\epsilon }_q>0$, whereas the heavily overconsolidated samples with ${\mathrm{OCR}}_0=4$ and ${\mathrm{OCR}}_0=8$ show a prevented dilatant behaviour $d>0$ for $d{\epsilon }_q>0$ after an initial prevented contractancy. The initial prevented contractancy decays with increasing initial overconsolidation ratio. Hence, the subsequent dilation increases and the phase transformation stress ratio $\eta ={\eta }_{PTL}$ at $d=0$ is reduced. These observations form the basis for the classification of clays’ dilatancy behaviour being very similar to that of sands. The question arises as to which value can be assigned to ${\mathrm{OCR}}_{ci}$ (see Equation (17)). The modified Cam Clay theory renders the value ${\mathrm{OCR}}_{ci}=exp\left(1\right)=2.71$ as a constant value for each clay. It is more reasonable to account for a varying ${\mathrm{OCR}}_{ci}$ representing a material parameter to be freely calibrated for each soil. Thus, preliminarily, we will allow this value as a material parameter to be calibrated until we evaluate some cyclic undrained triaxial tests in the next section.

The dilatancy relationships for Kaolin are once more, for this approach, illustrated in Figure 4a,b. Hereby, the critical state is reached when $\mathrm{OCR}=1$ is obtained. Note that this limit state is reached only when $\eta ={\eta }_c$ (note that here ${\eta }_c\approx 1$). Figure 4a,b indicate that for the samples with ${\mathrm{OCR}}_0=2$ and 8, the critical state was not reached, which is often reported for heavily overconsolidated fine-grained soils, e.g., [17,48]. In [48], Atkinson explained: “The critical state will normally be reached after strains greater than $10\%$.”… At this stage “the movements of grains are essentially turbulent, involving relative movements and rotations of both clay and sand grains. At larger displacements, however, the strains become localised into distinct zones of intense shearing and the shear stresses applied to the clay soil decrease.” Thus, it is likely that, for these samples, the critical state was not reached, but a sort of “laminar flow” of flat clay grains, which became parallelly oriented to a very thin shearing zone, occurred. Furthermore, it is very likely that the limits of the application of continuum theory have been reached at this stage.

Figure 5 presents the above-discussed relations in the three-dimensional space $d-\eta -\mathrm{OCR}$. Note that these observations, along with Equations (14)–(17) and ${p_{ei}}^{\prime }={p_0}^{\prime }$ (for initially isotropically consolidated samples), can be used for the determination of the critical state, avoiding the experimental void ratio scatter. Thus, the OCR value calculated through Equation (16) is a very good indicator of whether the ultimate state has been reached or not.

In general, we can conclude that, following the experimental evidence gained on Kaolin in [17], considering only monotonic loading, and the present evaluation, dilatancy is a function of the stress ratio $\eta$ and the void ratio e along with the intrinsic material parameters summarised under C, hence $d=f(\eta ,e,C)$.

3.3.2. Triaxial Tests under Cyclic Loading

We will now examine the dilatancy relation using the cyclic undrained triaxial test named C07 from [17] on the same Kaolin as in the previous monotonic tests. The test was performed with a constant rate of axial strain ${\dot{\epsilon }}_1=0.12$/h and a deviatoric amplitude of $q_{ampl}=70$ kPa. Until the test termination criterion of $|{\epsilon }_1|=10\%$, the sample could withstand nearly 7 cycles. For the purposes of the dilatancy evaluation, the cycles are separated according to the direction of the shear strain increment $\Delta \gamma /\Delta t$ (separation points correspond to the loading direction reversals; see Figure 6) in N = 0.5 cycles, beginning with N = 0.25 cycle, as depicted in Figure 6. An essential requirement (for all time-dependent materials) is that the shear rate was held constant during the test to $|\Delta \gamma /\Delta t|=5.65\times {10}^{-3}\%/\mathrm{s}=const$.

Two different approaches are used for the estimation of the elastic properties. First, the isotropic hypoelasticity—see Equation (11)—is adopted. The compression index $\lambda$ and the swelling index $\kappa$ are calibrated to fit the oedometric tests provided in [17]: $\lambda$ as the slope of the virgin compression line and $\kappa$ the average slope of the unloading–reloading hystheresis in the $e-ln\left(p\right)$ space. The initial void ratio in the evaluation was adjusted to account for the initial overconsolidation ratio $e_0=e_{i0}-\lambda ln({p_0}^{\prime }·{\mathrm{OCR}}_0)$. Wichtmann and Triantafyllidis [17] reported a normally consolidated sample for C07; thus, ${\mathrm{OCR}}_0=1$ was initialised in the evaluation. The maximum void ratio $e_{i0}$ was calibrated at a reference pressure of ${p_{ref}}^{\prime }=1$ kPa for the $\mathrm{OCR}=1$ isotache, as described in [18,39,50]. Secondly, the transverse isotropic hypoelasticity as introduced by the authors in [18,40] is utilised; see Equation (13). Therefore, the calibration of the anisotropic coefficient $\alpha$ is required. A calibration scheme of $\alpha$ in conjunction with the Poisson ratio $\nu$ is also given in [18,40]. Table 1 lists the parameters’ values used for the evaluation of the elasticity in C07.

Note that, throughout all evaluations, $d=-d{\epsilon }_v^d/d{\gamma }^{tot}$ has been used. In the absence of $p^{\prime }=const.$ tests with intermediate small loops of unloading and reloading, ${\gamma }^{tot}$ presents a good approximation for ${\gamma }^p$. Further research on this point is, however, required.

Finally, Figure 7 shows the resulting dilatancy relations. The figures on the left-hand side (Figure 7a,c,e) account for isotropic hypoelasticity, while the figures on the right-hand side (Figure 7b,d,f) account for the transverse isotropic hypoelasticity. Note that, at loading reversals, the responses of the individual approaches are completely different. Hence, the correct description of the elasticity is essential. By comparing Figure 7a–f, the following points may be noticed:

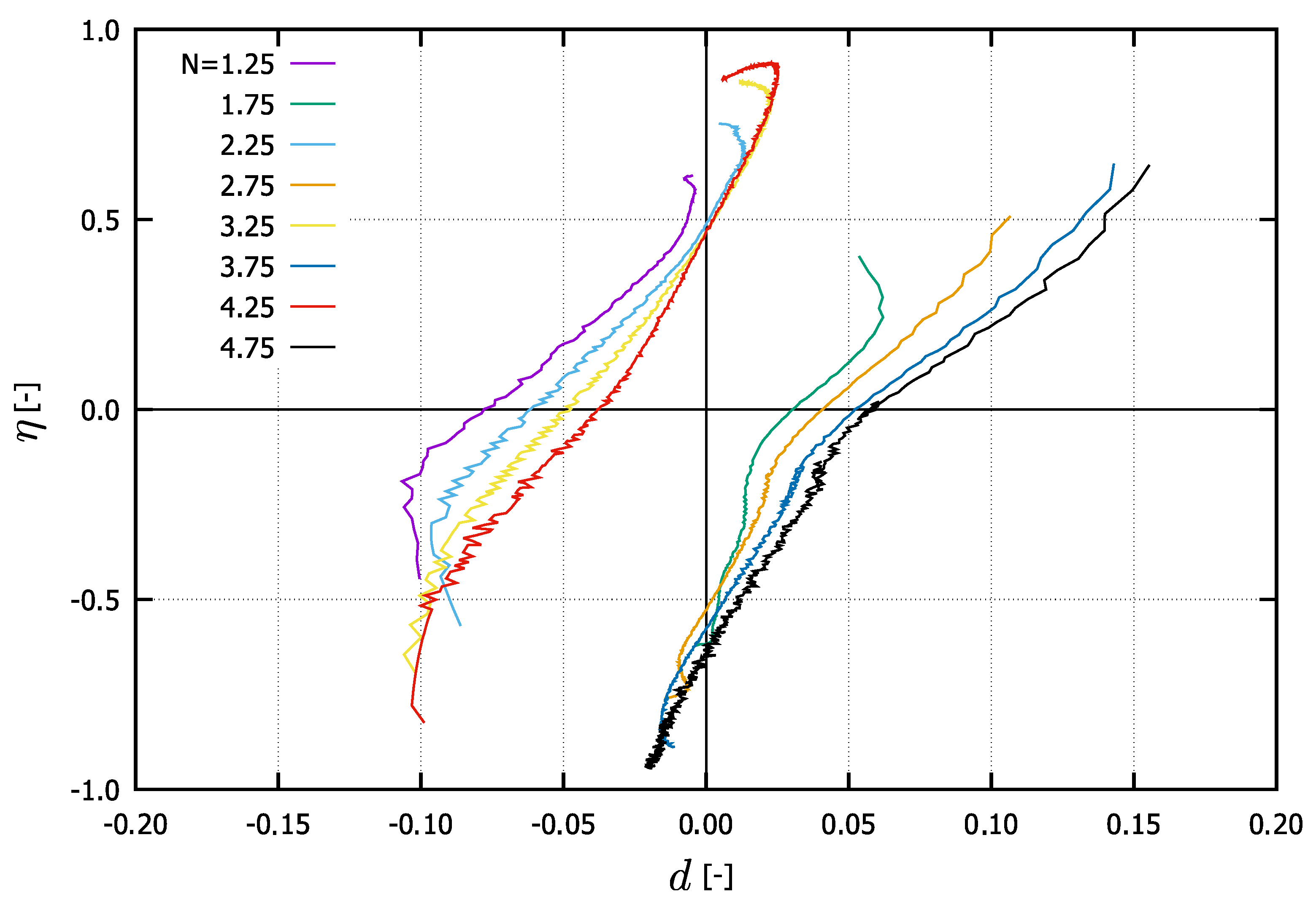
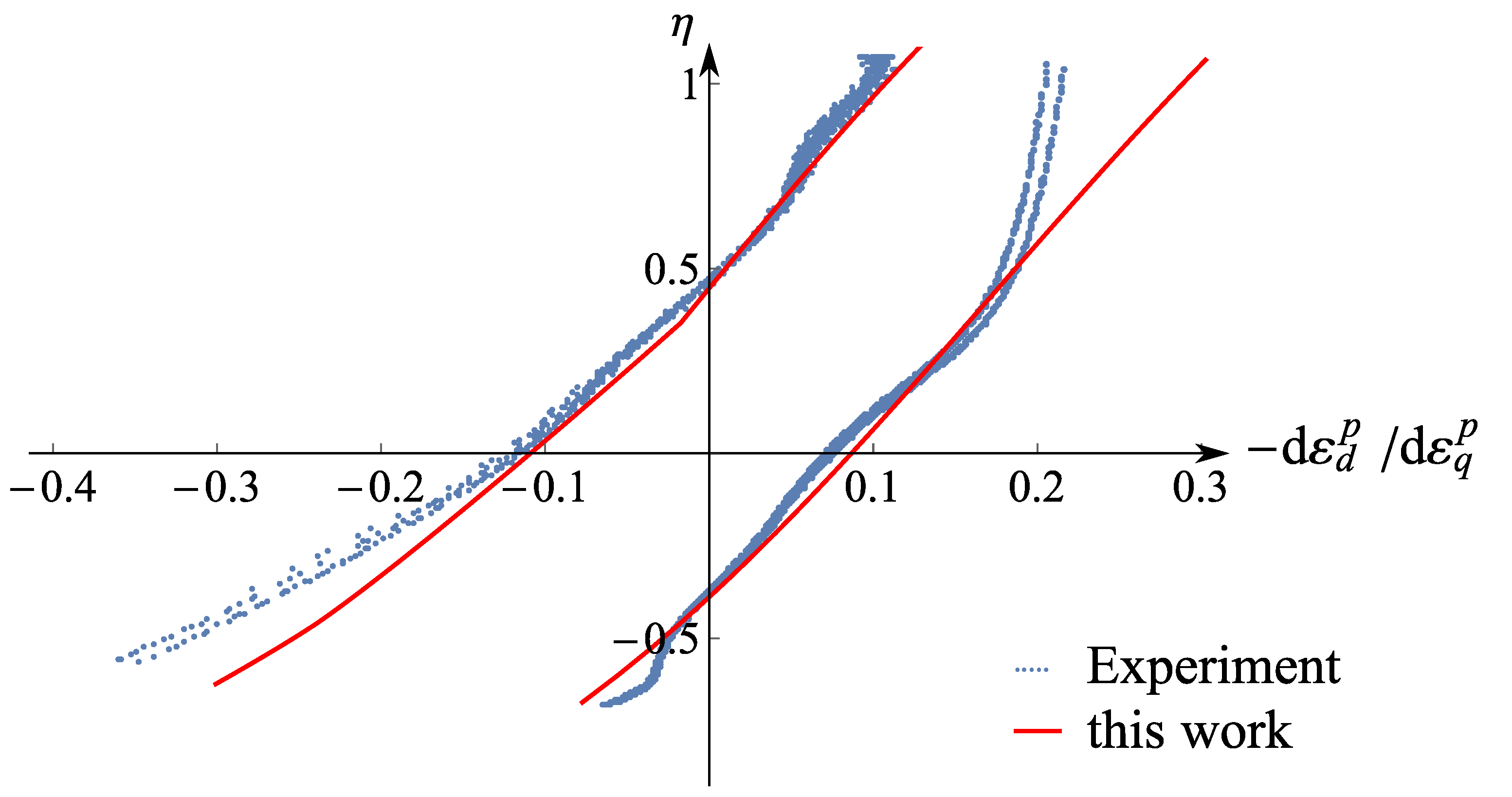
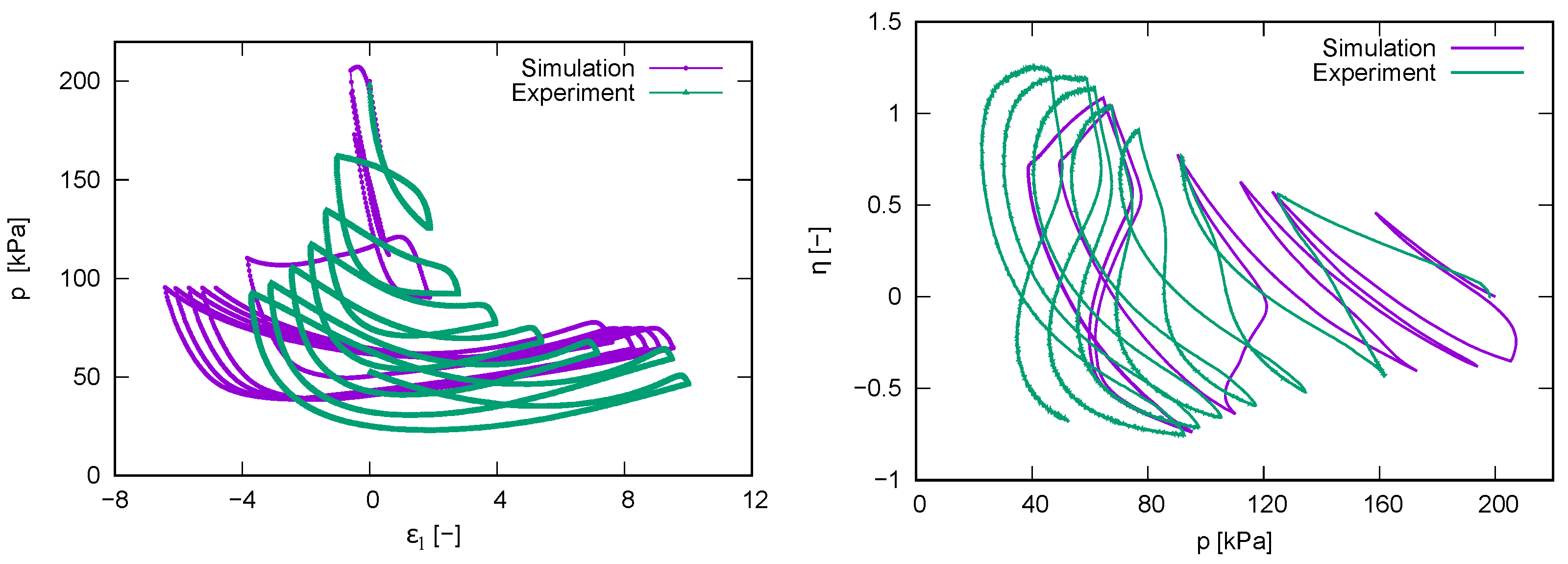
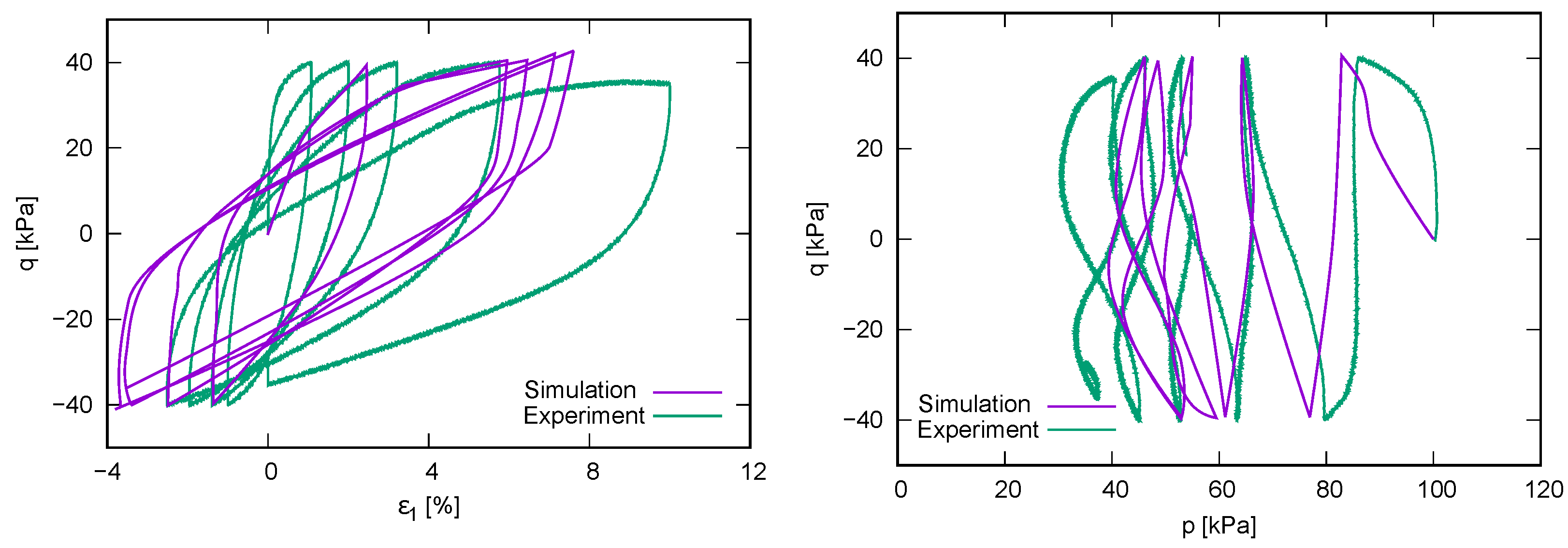
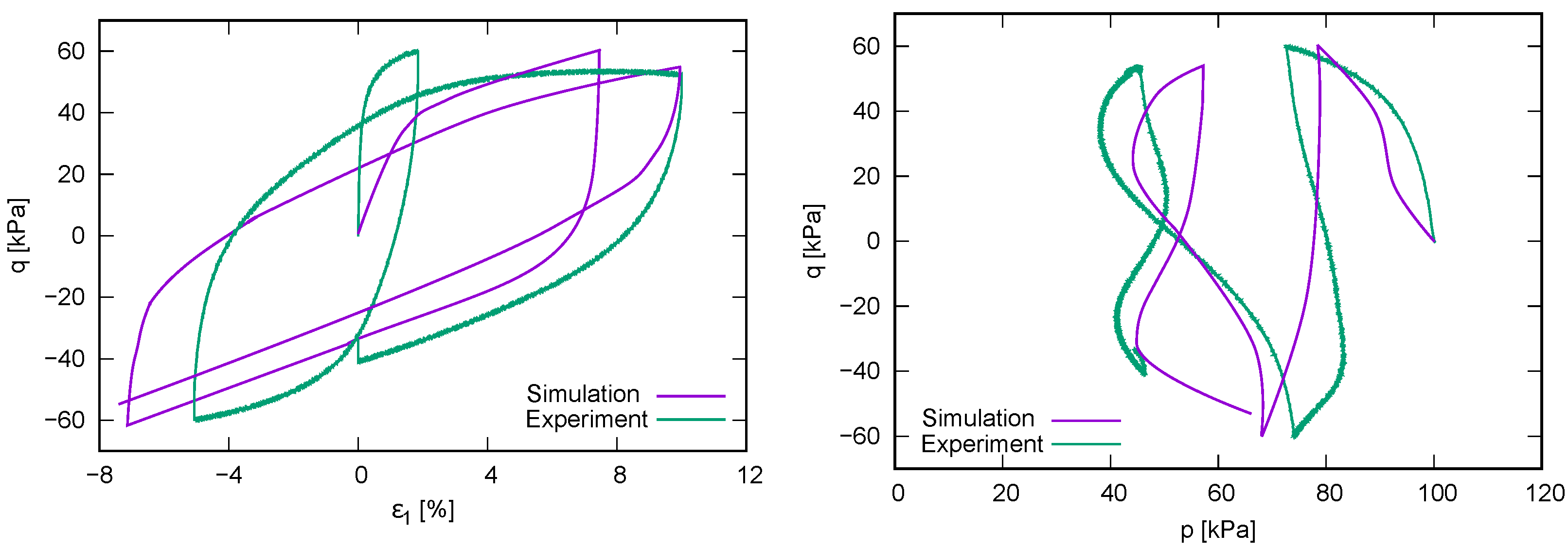
• In Figure 7a–d, all cycles are considered. A comparison between the figures on the left and those on the right (hence between the approaches proposed in Section 3.1) shows that the main difference is noticed at loading reversals in triaxial extension. These discrepancies are particularly noticeable when comparing Figure 7a with Figure 7d or Figure 7c with Figure 7d. Thereby, the evaluation accounting for isotropic hypoelasticity leads to dilatancy at the stress reversal points (from loading in triaxial compression to loading in triaxial extension). On the other hand, the use of transversal isotropic hypoelasticity leads to increased contractancy at stress reversals from loading in triaxial compression to loading in triaxial extension. The latter observations are in accordance with studies conducted on sand, e.g., [4], even though some data scatter can be observed in these figures. At this point, one should be aware that no data points have been omitted during these evaluations.
• On the other hand, only regular (not initial) cycles have been considered in Figure 7e,f. Hereby, the data scatter is almost absent and the aforementioned trends are even more pronounced. Hence, a correct description of the elasticity is essential for the evaluation of the dilatancy curves. Of course, as soon as a hyperelastic potential is evaluated experimentally and described mathematically for Kaolin, it makes sense to validate these evaluations again. At the moment, it may be concluded that the transversal isotropic hypoelasticity corresponds better than the isotropic hypoelasticity to the behaviour of Kaolin.
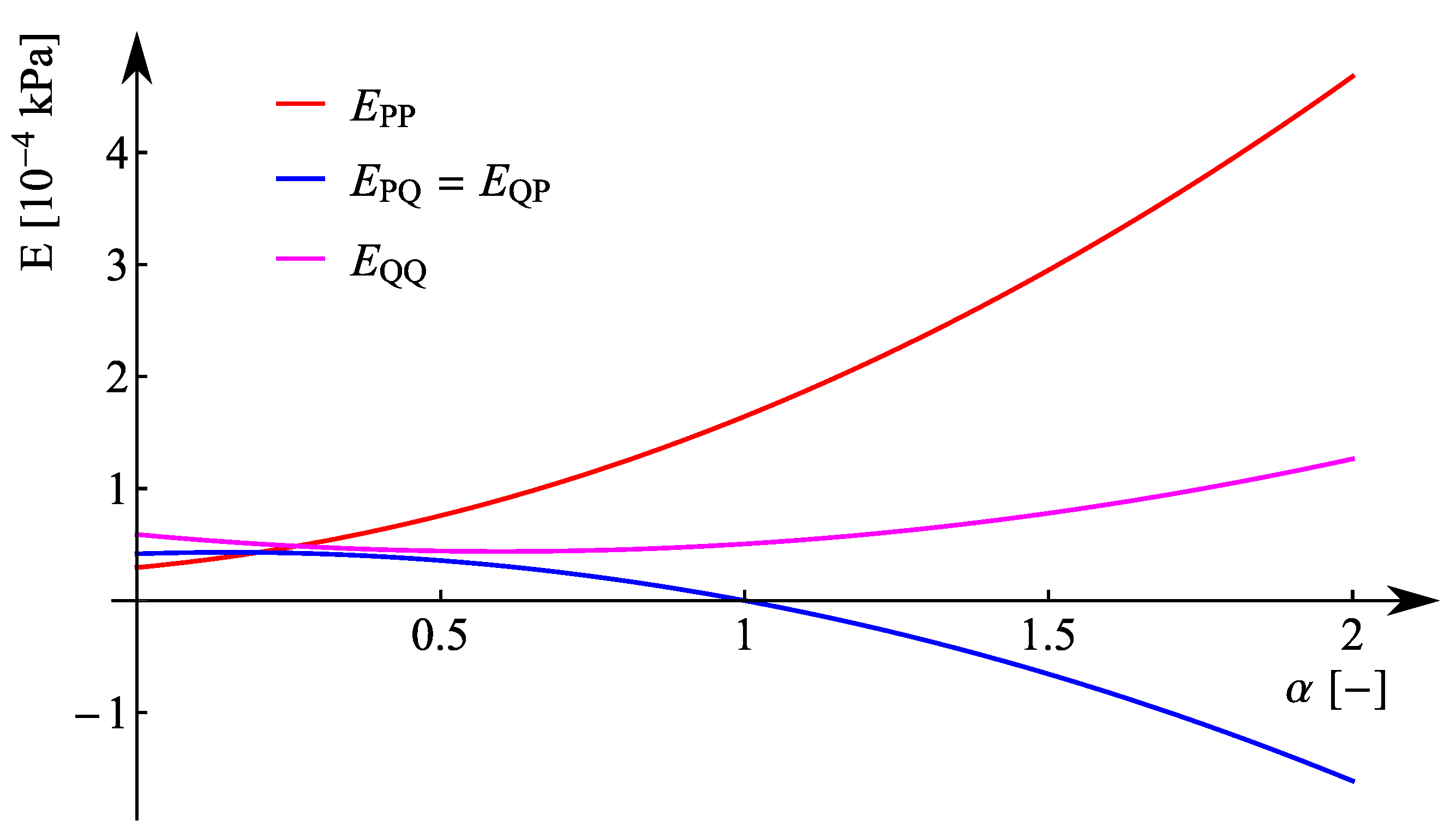
• This evaluation scheme can furthermore be verified by conducting tests with $p^{\prime }=const.$ (e.g., in hollow cylinder apparatus). Thereby, intermediate small loops of unloading–reloading elastic cycles are also necessary to evaluate the portion of $d{\gamma }^{el}$ and should be the target of further research. Note that, in this work, $d{\gamma }^{tot}$ instead of $d{\gamma }^p$ was used. As claimed in some works [4,9,52], the use of $d{\gamma }^p$ would reduce the scattering in the dilatancy vs. stress ratio relations for sand.
• As stated also in [40], the “elastic dilatancy” after reversals is evident, for example, in Figure 7c. Using the transversal isotropic hypoelasticity, it is eliminated, as depicted in Figure 7d. This elasticity provokes an increase in the effective mean stress, resulting in a slope to the upper left of the effective stress path [17,18,40]. It is well known that clays possess a greater elastic locus compared to sands. If the elasticity was isotropic, then the described $p-q$ path would be vertical with respect to the $p-$axis. Thus, we can consider the inherent anisotropy to be responsible for an even lower reduction in effective pressure after loading reversal. For sands, in contrast, after a loading reversal, the largest contractancy has been observed. Hence, the greater elastic regime of fine-grained soils cannot be overcome through the contractancy and it results in a non-vanishing mean effective pressure at cyclic mobility $p^{\prime }\ne 0$.
  This effect may be explained by the inherent anisotropy caused by specific sedimentation along a given axis. Thus, the question arises as to whether a cutting direction of the sample may be found at which the soft soil would also liquify (weak axis). This requires further research. Some authors [25,28,36] explain the non-liquefaction behaviour of clays in terms of the viscosity and its cohesive effect. Supposing this to be true, then the intensity of creep would not vanish with a higher overconsolidation ratio, as has been experimentally documented in [21,53]. On the other hand, this implies the existence of a special strain rate (loading velocity) with which the cyclic undrained shearing of a clay sample would result in liquefaction. Following our theory, this would be the case for the greatest velocity ${\dot{\epsilon }}_1\to \infty$; hence, the viscous effects would not have time to develop. The experiments presented in [17] and the discussions made in [40] hint at this phenomenon. However, further research work is required in order to shed more light and explain this phenomenon.

Figure 7. d-$\eta$ relationship evaluated for C07 (experiment borrowed from [17]).

Figure 7. d-$\eta$ relationship evaluated for C07 (experiment borrowed from [17]).

3.4. Results for Lower Rhine Clay

In order to cover a wide plasticity range of fine-grained soils, another material, the highly plastic Lower Rhine Clay (LRC) ($I_P=34.1\%$), is evaluated in the sequel. The grain size distribution curve of the treated LRC is presented in Figure 2. It has been tested on the same triaxial device as Kaolin reported in [17]. Herein, we will show the evaluation of an undrained triaxial test with $q_{ampl}=40$ kPa and approximately 4.5 cycles until the failure criterion of $|{\epsilon }_1|=10\%$ [12]. To avoid locally drained conditions, the displacement rate was chosen to be lower than that for the low-plasticity Kaolin ($\dot{s}=0.02$ mm/min $={\dot{s}}_{Kaolin}/5$) and was held constant during the test. The parameters adopted for the stiffness tensor are listed in Table 1.

Figure 8 presents the evaluation results, whereby only the regular cycles separated into 0.5 units of cycles and starting at separation from N = 0.25 are shown. Irregular cycles are defined as the ones with a different shape to the other cycles. A first difference between these curves and those presented in Figure 7 is that, for the LRC, only the first cycles, i.e., N = 0.25 and 0.5 cycles, are irregular. For Kaolin, the regular cycles were detected foremost at N = 4.25. Despite this, all comments on Kaolin also apply to LRC.

In general, we can conclude that, following the experimental evidence gained on Kaolin and on Lower Rhine Clay, the dilatancy of fine-grained soils is a function of the stress ratio $\eta$, the void ratio e, and the straining direction $\overrightarrow{\dot{\mathit{\epsilon }}}$ along with the intrinsic material parameters summarised under C, hence $d=f(\eta ,e,\overrightarrow{\mathit{\epsilon }},C)$.

If the widespread assumption $d=f(\eta ,C)$ for fine-grained soils would hold, then the direction of plastic flow influencing the direction of the undrained stress path would be able to render a dilatant direction only for $\eta =M\Rightarrow M_d=M$, independent of the overconsolidation ratio. Thus, the same behaviour would be rendered for different OCR. This contradicts the findings gained in this article; see also Figure 4, Figure 5, Figure 7 and Figure 8.

4. Constitutive Description of the State-Dependent Dilatancy for Cohesive Soils

4.1. Generalisation to Multiaxial Space

In general, the material state is described through the stress tensor $\mathit{\sigma }$, replacing the normal stress $\sigma$ and the shear stress $\tau$, and through the strain rate (increment tensor) $\dot{\mathit{\epsilon }}\left(d\mathit{\epsilon }\right)$. The dilatancy is then defined as the negative ratio between the plastic volumetric strain increment $d{\epsilon }_v^p$ and the plastic deviatoric strain increment $d{\epsilon }_q^p$:

$$\begin{array}{c}\hfill d=-d{\epsilon }_v^p/\left|d{\epsilon }_q^p\right|.\end{array}$$

(18)

In analogy to the friction angle ${\phi }_c$ used for the critical state, the dilatancy angle $\psi$ has been introduced by most authors, e.g., [5,8,9,14,40]. Pradhan and Tatsuoka [9] suggested the following two relations between d and $\psi$ for isobaric triaxial conditions:

$$\begin{array}{c}\hfill d=\left\{\begin{array}{cc}{\displaystyle \frac{6sin\psi }{3-sin\psi }}\hfill & \mathrm{for}\mathrm{triaxial}\mathrm{compression}\left(d{\epsilon }_q>0\right)\hfill \\ -{\displaystyle \frac{6sin\psi }{3+sin\psi }}\hfill & \mathrm{for}\mathrm{triaxial}\mathrm{extension}\left(d{\epsilon }_q<0\right)\hfill \end{array}\right.\end{array}$$

(19)

Note that the factor $3/2$ on the RHS is introduced in [9] because Pradhan and Tatsuoka [9] used $d{\gamma }^p$ instead of the invariant $d_q^p=2/3d{\gamma }^p$ appearing in Equation (18). According to, for example, the Matsuoka–Nakai failure criterion [54] or the Mohr–Coulomb criterion, the slope of the critical state line in triaxial compression and triaxial extension with respect to the critical friction angle ${\phi }_c$ reads:

$$\begin{array}{c}\hfill M=\left\{\begin{array}{cc}{\displaystyle \frac{6sin{\phi }_c}{3-sin{\phi }_c}}\hfill & \mathrm{for}\mathrm{compression}\left(q>0\right)\hfill \\ -{\displaystyle \frac{6sin{\phi }_c}{3+sin{\phi }_c}}\hfill & \mathrm{for}\mathrm{extension}\left(q<0\right)\hfill \end{array}\right.\end{array}$$

(20)

The analogy between d given in Equation (19) and M presented in Equation (20) is obvious. However, it is essential to realise the difference in the definition of compression and extension whether using the stress or the strain. The definition for the critical state (CS) is realised in the stress space with $q>0$ for compression and $q<0$ for extension. Thus, the generalisation of M to multiaxial space is executed by means of the Lode angle of the stress ${\theta }_{\sigma }$ (with the Lode angle definition: $cos\left(3{\theta }_{\bigsqcup }\right)=-\sqrt{6}\left[\left(\overrightarrow{{\bigsqcup }^{*}}·\overrightarrow{{\bigsqcup }^{*}}\right):\overrightarrow{{\bigsqcup }^{*}}\right]=-\sqrt{6}{\overrightarrow{{\bigsqcup }^{*}}}_{ik}{\overrightarrow{{\bigsqcup }^{*}}}_{kl}{\overrightarrow{{\bigsqcup }^{*}}}_{ki}.$):

$$\begin{array}{c}\hfill M={\displaystyle \frac{6sin{\phi }_c}{3-sin{\phi }_{c}cos\left(3{\theta }_{\sigma }\right)}}\end{array}$$

(21)

A similar relation leading to the same results was proposed by Argyris et al. [55] and was used for some constitutive models, e.g., [50,56,57]. The link between the stress and the strain in CS is established through the critical void ratio given in Equation (17).

In the same context, but considering that Equation (19) is defined in the strain space, the generalisation of d can be achieved taking into account the direction of the strain rate through its Lode angle ${\theta }_{\dot{\mathit{\epsilon }}}={\theta }_{{\dot{\mathit{\epsilon }}}^{*}}$:

$$\begin{array}{c}\hfill d={\displaystyle \frac{6sin\psi }{3-sin\psi cos\left(3{\theta }_{\dot{\mathit{\epsilon }}}\right)}},\end{array}$$

(22)

which is also in accordance with the experimental behaviour of sand reported, for example, in [4,9,14,52].

Thus, the stress ratio at the phase transformation line ${\eta }_{PTL}$, which we will denote in general with $M_d$ (in analogy to the stress ratio at CSL ${\eta }_c=M$), reads:

$$\begin{array}{c}\hfill {\eta }_{PTL}={\displaystyle \frac{6sin{\phi }_{PTL}}{3-sin{\phi }_{PTL}cos\left(3{\theta }_{\dot{\mathit{\epsilon }}}\right)}}\stackrel{!}{=}{M}_d.\end{array}$$

(23)

Note that Equation (23) establishes the interrelation between the strain space and the stress space for the dilatancy.

4.2. Dilatancy Rule

In order to provide a relation $d=f(\mathit{\sigma },e,\dot{\mathit{\epsilon }},C)$, supported by the experiments evaluated in Section 3, we start with the generalisation of Taylor’s interlocking concept [2]. We assume that the division of the peak strength into a portion due to internal friction and another due to interlocking (dilatancy) holds also for states different to the peak ${\tau }_m\ne {\tau }_{peak}$. Then, the mobilised friction angle ${\phi }_m$ (with $sin\left({\phi }_m\right)={\displaystyle \frac{3\eta }{6+\eta cos\left(3{\theta }_{\mathit{\sigma }}\right)}}$) is composed of the critical friction angle ${\phi }_c$ and the dilatancy angle $\psi$:

$$\begin{array}{ccc}\hfill tan{\phi }_m& =& tan{\phi }_c+tan\psi .\hfill \end{array}$$

(24)

Note that this relation is deduced considering $\mathit{\sigma }=const.$ and it provides a constraint on the plastic strain rate (i.e., on the flow rule) during shearing. During, for example, undrained shearing, a constitutive model is necessary in order to distinguish which part of the volume change is due to the change in mean effective pressure $p^{\prime }$ and which is simply due to dilatancy.

Equation (24) assumes that the phase transformation line is independent of the void ratio—hence, $tan{\phi }_{PTL}=tan{\phi }_c$—which would not capture the effects highlighted in Section 3. These experiments showed that, similar to the behaviour of sands [19], dilatancy equals zero at two states: at the critical state CS and at the phase transformation line PTL. Therefore, we replace the CS friction angle ${\phi }_c$ with the PTL angle ${\phi }_{PTL}$, proposing a void ratio dependence of the phase transformation line angle expressed through:

$$\begin{array}{c}\hfill tan{\phi }_{PTL}=tan{\phi }_c{\left({\displaystyle \frac{e}{e_c}}\right)}^n.\end{array}$$

(25)

Hence, for lightly overconsolidated states $1<\mathrm{OCR}<2$ (i.e., $e>e_c$), the PTL lies above the critical state line CSL ${\phi }_{PTL}>{\phi }_c$ and may not be reached upon, for example, undrained shearing. At the critical state $e=e_c$, the CSL coincides with the PTL, resulting in $tan\psi =0$. For overconsolidated states $\mathrm{OCR}>2$ (i.e., $e<e_c$), the PTL lies below the CSL ${\phi }_{PTL}<{\phi }_c$ and can be reached upon, for example, undrained shearing resulting in $tan\psi =0$. The parameter n introduced in Equation (25) is calibrated through dilatancy curves, as shown in Figure 9. Thereby, the PTL points of the monotonic undrained triaxial tests evaluated in Figure 3 are plotted in the ${\phi }_{PTL}$ vs. $e/e_c$ space. The simulations using Equation (25) and a CS angle of ${\phi }_c=25.4^{\circ }$ varying the parameter n are compared, whereby an optimum was reached for $n=8$.

As shown in Section 3, the dilatancy of fine-grained soils is i.a. a function of the direction of shearing $d=f(\mathit{\sigma },e,\overrightarrow{{\dot{\mathit{\epsilon }}}^{*}},C)$. This dependency has been also stated for granular soils by Grandas et al. [14]. In order to reproduce this observation, the factor $\overrightarrow{{\mathit{\sigma }}^{*}}:\overrightarrow{{\dot{\mathit{\epsilon }}}^{*}}$ has been introduced in [14]. Using the replacement of ${\phi }_c$ through ${\phi }_{PTL}$ and the influence of the straining direction, we propose the following dilatancy rule for soft soils:

$$\begin{array}{c}\hfill tan\psi =\beta \left(\overrightarrow{{\mathit{\sigma }}^{*}}:\overrightarrow{{\dot{\mathit{\epsilon }}}^{*}}tan{\phi }_m-tan{\phi }_{PTL}\right).\end{array}$$

(26)

Comparing this relation to the one provided in [14] for sands, it turns out that the same relation holds for both types of soils, but with different material parameters. For clays, an additional parameter $\beta$, to be calibrated in the next section, is necessary. Notice that, for a given stress state, Equation (26) provides two different dilatancy angles $\psi$ depending on the straining direction, which confirms the experimental evidence in Section 3.

4.3. Incorporation of Dilatancy into a General Hypoplastic Model

The approach described in this section is first presented in [40] and is summarised here once again for the sake of completeness. The coupling between the dilatancy d and its angle $\psi$ is provided through Equation (22). Thus, we can now concentrate on the dilatancy relation given in Equation (18) (note the difference between this definition of d and the one determined by Pradhan et al. in [4,9], $d=-d{\epsilon }_v^p/\left|d{\gamma }^p\right|$ with $d\gamma =3/2d{\epsilon }_q$), which can be rewritten as:

$$\begin{array}{c}\hfill d=-{\displaystyle \frac{\mathrm{tr}\left({\dot{\mathit{\epsilon }}}^p\right)}{\sqrt{2/3}\left|\right|{\dot{\mathit{\epsilon }}}^{*p}\left|\right|}}\Rightarrow -\mathbf{1}:{\dot{\mathit{\epsilon }}}^p=d\sqrt{2/3}\left|\right|{\dot{\mathit{\epsilon }}}^{*p}\left|\right|\end{array}$$

(27)

whereby ${\dot{\mathit{\epsilon }}}^{*p}$ is the deviator of the plastic strain rate. For the evaluations presented in Figure 4, Figure 5, Figure 7 and Figure 8, we used the total deviatoric strain rate instead of the plastic one; thus, in Equation (27), we can substitute $\left|\right|{\dot{\mathit{\epsilon }}}^{*p}\left|\right|\approx \left|\right|{\dot{\mathit{\epsilon }}}^{*}\left|\right|$ to obtain:

$$\begin{array}{c}\hfill -\mathbf{1}:{\dot{\mathit{\epsilon }}}^p=d\sqrt{2/3}\left|\right|{\dot{\mathit{\epsilon }}}^{*}\left|\right|.\end{array}$$

(28)

Let us now express ${\dot{\mathit{\epsilon }}}^p$ by its isotropic and deviatoric components with unknown magnitudes a and b, respectively:

$$\begin{array}{c}\hfill {\dot{\mathit{\epsilon }}}^p=a\mathbf{1}+b\overrightarrow{{\dot{\mathit{\epsilon }}}^{*p}}\end{array}$$

(29)

By multiplying both sides from the left of Equation (29) with $\mathbf{1}$ and inserting Equation (28), we obtain, for the isotropic magnitude a:

$$\begin{array}{c}\hfill a=-{\displaystyle \frac{1}{3}}\sqrt{{\displaystyle \frac{2}{3}}}d\left|\right|{\dot{\mathit{\epsilon }}}^{*}\left|\right|.\end{array}$$

(30)

Then, Equation (29) is as follows (for the derivation of Equation (31), the assumption $\overrightarrow{{\dot{\mathit{\epsilon }}}^{*p}}\approx \overrightarrow{{\dot{\mathit{\epsilon }}}^{*}}$ was involved as well, which even justifies the introduction of this assumption for the derivation of the dilatancy relations in Section 3):

$$\begin{array}{c}\hfill {\displaystyle \frac{{\dot{\mathit{\epsilon }}}^p}{\left|\right|{\dot{\mathit{\epsilon }}}^{*}\left|\right|}}=-{\displaystyle \frac{1}{3}}\sqrt{{\displaystyle \frac{2}{3}}}d\mathbf{1}+\overrightarrow{{\dot{\mathit{\epsilon }}}^{*}}.\end{array}$$

(31)

Finally, we consider the well-known hypoplastic constitutive equation ( note that, in the same context, the dilatancy rule proposed in this article can be included in elastoplastic models. For the sake of brevity, we will show herein its introduction into hypoplasticity):

$$\begin{array}{c}\hfill \dot{\mathit{\sigma }}=𝗘:(\dot{\mathit{\epsilon }}-{\dot{\mathit{\epsilon }}}^{hp})=𝗘(\dot{\mathit{\epsilon }}-Y\mathsf{m}|\left|\dot{\mathit{\epsilon }}\right|\left|\right).\end{array}$$

(32)

For simplicity reasons, and to avoid a loss of generality, hereby, the viscous strain rate is neglected. Using Equation (31), the flow rule $\mathsf{m}$ and the degree of nonlinearity Y are reduced to:

$$\begin{array}{c}\hfill \mathsf{m}={\left(-{\displaystyle \frac{1}{3}}\sqrt{{\displaystyle \frac{2}{3}}}d\mathbf{1}+\overrightarrow{{\dot{\mathit{\epsilon }}}^{*}}\right)}^{\to }.\end{array}$$

(33)

An interpolation function between $Y_0$ for isotropic and radial loading directions and $Y_D$ for shearing is adopted for the general Y:

$$\begin{array}{c}\hfill Y=\left[Y_0+(1-Y_0)Y_D\right]{\mathrm{OCR}}^{-n_{\mathrm{OCR}}}\end{array}$$

(34)

whereby $n_{\mathrm{OCR}}$ is a material parameter.

For radial compression, the $Y_0$ relations proposed in [18,41,50] or in [13] can be used for clays or sands, respectively:

$$\begin{array}{c}\hfill Y_0={\displaystyle \frac{\lambda -\kappa }{\lambda +\kappa }}{\left({\displaystyle \frac{{p_{ei}}^{\prime }}{p^{\prime }}}\right)}^2\end{array}$$

(35)

and the degree of nonlinearity for shearing (not be combined or used for the isotropic or radial compression):

$$\begin{array}{c}\hfill Y_D={\left[{\displaystyle \frac{\left|\right|{\dot{\mathit{\epsilon }}}^{*}\left|\right|}{\left|\right|\dot{\mathit{\epsilon }}\left|\right|}}\left|\left|-{\displaystyle \frac{1}{3}}\sqrt{{\displaystyle \frac{2}{3}}}d\mathbf{1}+\overrightarrow{{\dot{\mathit{\epsilon }}}^{*}}\right|\right|\right]}^{n_{YD}}.\end{array}$$

(36)

whereby $n_{YD}$ is a material parameter.

Nonetheless, the flow rule presented in Equation (33) is not the most suitable for hypoplastic models, because the deviatoric direction is equal to the deviatoric strain rate. This would result in overshooting at loading reversals from stress states lying at the critical state and thus loss of controllability of FE simulations. For this purpose, a modified flow rule for hypoplastic models should be used:

$$\begin{array}{c}\hfill \mathsf{m}={\left(-{\displaystyle \frac{1}{3}}\sqrt{{\displaystyle \frac{2}{3}}}d\mathbf{1}+{\left({\displaystyle \frac{{\mathit{\sigma }}^{*}}{p^{\prime }}}\right)}^{\to }\right)}^{\to }\end{array}$$

(37)

The tangential stiffness tensor $𝗘$ is defined in Equation (6).

Note that the explicit involvement of the dilatancy d in the constitutive equation greatly simplifies the formulation and calibration. In fact, one only needs to derive the $d-\eta$ relationship of the material through monotonic or, even better, cyclic triaxial tests and calibrate the elasticity of the material through, for example, an oedometric test with loading–unloading–reloading.    

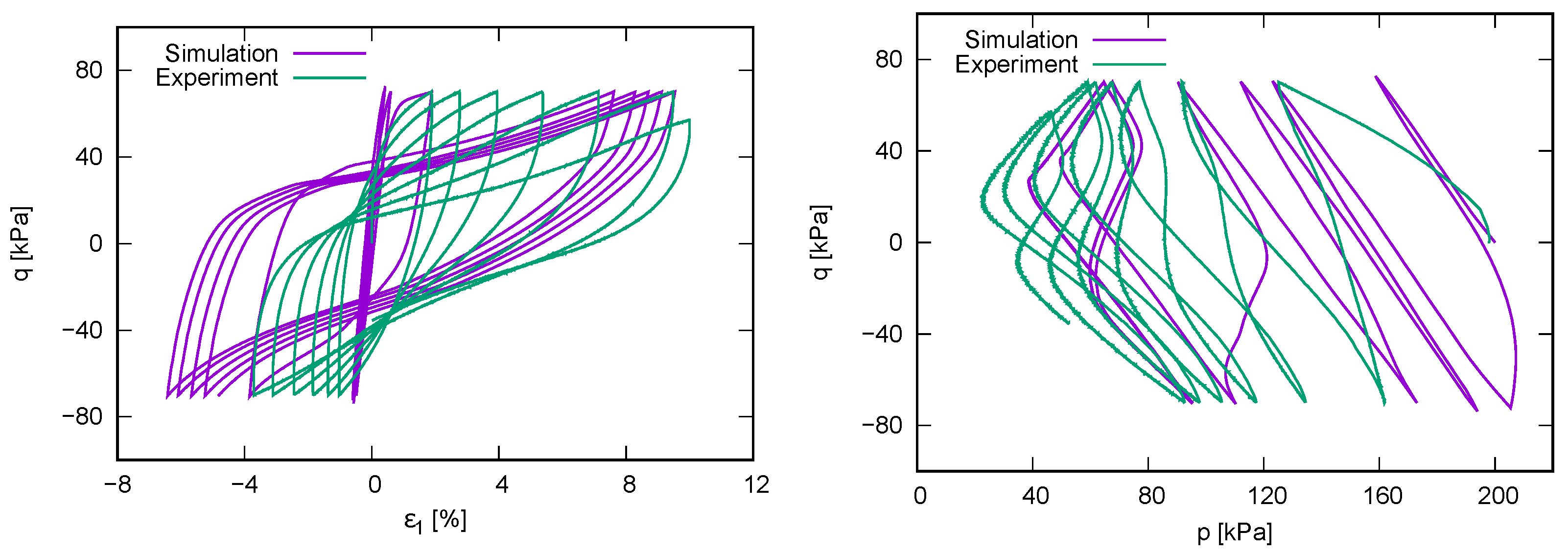
4.4. Simulations with Experiments

The above-described and discussed experimental results (see Section 3.3 and Section 3.4) will be compared with simulations in this section. All tests are simulated with the same set of material parameters (for each material); see

Table 2. Material parameters.

Material	$\mathit{\nu }$	$\mathit{\alpha }$	$\mathit{\lambda }$	$\mathit{\kappa }$	${\mathit{e}}_{\mathit{i}0}$	${\mathit{M}}_{\mathit{c}}$	$\mathit{\beta }$	${\mathit{n}}_{\mathit{PTL}}$	${\mathit{n}}_{\mathbf{OCR}}$	${\mathit{n}}_{\mathit{YD}0}$
Kaolin	0.3	1.8	0.13	0.05	1.76	1.0	0.3	6	2	0.8
LRC	0.2	1.0	0.26	0.04	2.47	0.95	0.5	6	2	0.5

. The reference pressure at which the parameter $e_{i0}$ is calibrated amounts to ${p_{ref}}^{\prime }=1$ kPa.

First, the accuracy of the dilatancy rule proposed in Equation (26) is shown. Therefore, the experimental data evaluated on Kaolin in Section 3.3, Figure 7f, are used. A comparison between simulation and experiment is given in Figure 10, proving the good performance of Equation (26).

Figure 11 and Figure 12 present an undrained triaxial cyclic test of a normally consolidated Kaolin sample ${\mathrm{OCR}}_0=1$ with a deviatoric amplitude of $q_{ampl}=70$ kPa. The termination criterion for the experiment was defined as an axial strain of 10%. This becomes also a limit criterion for the simulation. The simulation and experiment results are compared in different spaces. In the right-hand part of Figure 11, the $q-{\epsilon }_1$ relation shows good agreement between the experiment and simulation, also capturing the hysteresis when reaching cyclic mobility (despite some discrepancies on the enclosed area in extension). The same conclusions can be drawn for the effective stress path, whereby approximately seven cycles have been surpassed by both the simulation and experiment. The 8-shaped cyclic mobility of the $p-q$ path is in good agreement with the experiment, evidencing the accuracy of the dilatancy relation. The ${\epsilon }_1-p$ and $p-\eta$ relations, which are very useful to understand the main features of a model and also of the soil behaviour, are plotted in Figure 12. Among all effects, such as anisotropic elasticity, dilatancy, the degree of nonlinearity, and accumulated strain, only the peak behaviour appears to require further improvement.

Figure 13 and Figure 14 show simulations compared with experiments of normally consolidated LRC samples with different deviatoric amplitudes $q_{ampl}=40$ and 60 kPa. The good agreement between the simulations and experiments is evident in both the effective stress plane and the stress–strain space. The slope of the phase transformation line is captured well in both loading directions: axial compression and extension. At present, monotonic undrained triaxial tests with heavily overconsolidated LRC samples (which are very time-consuming due to the low permeability of LRC) are performed in order to evaluate and possibly further modify the model.

5. Conclusions

A new evaluation method of the dilatancy relations from monotonic and cyclic undrained triaxial tests has been proposed in this work and it has been realised for the experiments performed on Kaolin [17] and on Lower Rhine Clay [12]. In general, we can conclude that the dilatancy is a function of the stress ratio $\eta$, the void ratio e, and the shearing direction $\overrightarrow{{\dot{\mathit{\epsilon }}}^{*}}$ along with the intrinsic material parameters C: $d=f(\mathit{\sigma },e,\overrightarrow{{\dot{\mathit{\epsilon }}}^{*}},C)$ (as observed for sands). The form of the curves differs, however, from those of sands; hence, the dilatancy rule of Taylor had to be modified for soft soils. It was found that the derived dilatancy rule of fine-grained soils is qualitatively similar to that of sands, proposed by Grandas et al. [14], but needs an additional material parameter. These findings provide a new perspective in the field of constitutive modelling, because the same model with different material parameters could be used for both types of soils.

Furthermore, a constitutive relation has been established, which showed accurate agreement with the experimental data of montonic and cyclic triaxial tests of both examined materials: Kaolin (low plasticity) and Lower Rhine Clay (high plasticity). Moreover, a new method has been suggested, whereby, based on the deduced $d-\eta$ relation, a hypoplastic model can simply be calibrated by changing the dilatancy relation in the flow rule and degree of nonlinearity. The elasticity needs, of course, to be calibrated as well. For these purposes, either monotonic triaxial tests of normally and overconsolidated samples or cyclic triaxial tests of normally consolidated samples, as well as an oedometer test with loading–unloading–reloading, are necessary. Note that, in the same context, the proposed dilatancy rule can be introduced into elastoplastic models as well.

To further validate these results for plastic fine-grained soils, other highly plastic soft soils should be evaluated using the approach proposed in this article. In addition, laboratory tests with constant mean effective pressure are required for final validation and, if necessary, an improvement of the dilatancy rule of fine-grained soils should be developed.