Regional Impacts of Public Transport Development in the Agglomeration of Budapest in Hungary

Abstract

Budapest and its metropolitan area serve as a key railway hub both within Hungary and across Europe, intersected by multiple European rail corridors and characterized by substantial suburban traffic driven by daily commuters from surrounding areas. The Budapest agglomeration is served by 11 rail lines to Budapest managed by the MÁV Group Company (MÁV: Magyar Államvasutak Co., Budapest, Hungary) is a railway company owned by the Hungarian state). The majority of these are high-capacity, mostly double-track electrified main lines, which play a major role in long-distance and international transport. The main goal of the MÁV Group Company is the continuous development of the quality of passenger transport in Hungary and Europe, quality improvement in passenger comfort, sales, and passenger information systems, and the introduction of up-to-date, environmentally friendly means and solutions. Infrastructure plays a decisive role in the development and transformation of the country and its regions, municipalities, and settlement systems. The development of transport infrastructure not only dynamically transforms and shapes spatial structures but also initiates processes of internal differentiation. In our study, statistical analysis of municipalities and rail-based public transport confirmed a positive correlation between the modernization of transport infrastructure and selected demographic indicators.

1. Introduction

Public transport development plays a pivotal role in shaping the socio-economic landscape of urban regions worldwide [1]. The agglomeration of Budapest, one of Central Europe’s prominent urban areas, has witnessed significant transformations in its public transportation infrastructure over the years [2]. The evolution of public transport in Budapest’s agglomeration can be traced back to the late 19th century, when horse-drawn trams were introduced, gradually transitioning to electric trams and buses in the early 20th century [3]. In Hungary, the spatial separation of residential and working areas, along with the rise in commuting, began as early as the beginning of the 20th century [4,5]. The possibility of regular (daily, weekly) suburban commuting first appeared in the Budapest area with the development of public transport (tram, suburban railway) and the explosive development of the manufacturing industry [6]. However, it was in the post-World War II era that the city underwent substantial expansion and modernization, underscoring its emerging role as a key regional hub.

In urban planning practice, there has been a growing trend toward the displacement of individual motorized transportation, thereby reducing traffic congestion and air pollution, creating the foundations of a healthier, more livable urban environment [7].

The agglomeration of Budapest boasts a diverse public transport network, comprising metro lines, trams, buses, and suburban railways. The Budapest Metro, inaugurated in 1896, was the first underground railway system in continental Europe and has since expanded to four lines, serving both the city and its outskirts. Trams and buses complement the metro, providing extensive coverage within the agglomeration and connecting suburban areas to the city center. Additionally, suburban railways facilitate commuter travel, linking satellite towns and villages to Budapest [8].

The expansion of public transportation in the Budapest agglomeration has significantly enhanced regional connectivity and accessibility. Efficient transport links have shortened travel times between peripheral areas and the city center, fostering mobility and providing better access to employment, education, and recreational opportunities. Enhanced connectivity has also stimulated economic growth in suburban areas, attracting businesses and investments while helping to reduce congestion in the city center. The choice of location for firms in the Budapest agglomeration is generally strongly influenced by hard factors (e.g., price and the infrastructure of offices, transport, and public transport) [9]. The agglomeration sector of Budapest is well endowed, with intermodal service providers and a central location within trans-European transport corridors, serving freight trips to the west, northeast, and southeast [10].

The socio-economic impacts of public transport development extend beyond mere transportation benefits. Enhanced mobility options have promoted social inclusion by ensuring access to essential services for all residents, including those with limited mobility or financial means. Moreover, the development of transit-oriented developments (TODs) around transport hubs has fostered mixed-use urban spaces, promoting densification and sustainable urban growth [1,11,12].

Agglomeration infrastructure is becoming increasingly significant from geographical, political, and conceptual perspectives in the context of accelerating global urbanization. As cities expand and urban regions merge into larger metropolitan clusters, the development and integration of infrastructure systems—such as transportation networks, utilities, and digital connectivity—play a critical role in shaping spatial organization, enabling economic integration and influencing governance models. This growing importance reflects not only the physical demands of urban concentration but also the strategic role of infrastructure in fostering regional competitiveness, social cohesion, and sustainable development across increasingly interconnected urban landscapes [13]. Railways have played a key role in urbanization processes in many parts of the world since the mid-19th century. However, since the mid-20th century, the role of rail networks has declined significantly worldwide. In Europe, the railways and other modes of public transport continue to play a significant role in everyday mobility [14].

One of the key advantages of urban agglomerations is the efficient sharing of infrastructure. Larger cities, with their higher population densities and increased passenger volumes, are able to optimize the use of transportation networks. The substantial initial investment required for developing transport infrastructure creates a strong incentive for shared usage, allowing multiple sectors and communities to benefit from the same systems. This shared approach not only maximizes the return on infrastructure investment but also reduces overall operational costs, making public transport systems more sustainable and efficient in the long term [15]. As companies locate in closer proximity to one another, the associated infrastructure costs can be significantly reduced due to shared resources, shorter transportation routes, and more efficient logistics. Simultaneously, spatial concentration fosters the benefits of agglomeration, including knowledge spillovers, increased specialization, access to a skilled labor pool, and enhanced collaboration opportunities between firms. This dual effect—lower operational expenditures combined with amplified innovation and productivity gains—highlights the strategic importance of industrial clustering in regional economic development [16]. However, some studies have concluded that transport investments can weaken agglomerations by diverting growth away from denser urban areas [17]. Within cities, some locations are easier to access due to factors such as better road accessibility, which can affect the benefits of living in large agglomerations [18].

Budapest, together with its suburban agglomeration, serves as the primary economic, social, cultural, and administrative hub of Hungary. This metropolitan region is home to approximately one-third of the nation’s population, underscoring its central role in shaping national development, governance, and societal dynamics. The concentration of human capital, infrastructure, and institutional resources in and around the capital significantly influences the spatial organization and economic performance of the country. The development of the suburban and major railway network from Budapest has played a decisive role in the agglomeration around the capital. The rail and HÉV (HÉV means suburban railway) lines located in the agglomeration continue to play an important role in serving travel needs. The mass out-migration of the population to settlements around Budapest started in the early 1990s and peaked at the beginning of the new millennium [19]. The target settlements of the growing suburbanization were mainly the rural settlements in the western and northern parts of the agglomeration, where the hilly and mountainous areas offered an attractive natural environment for the out-migrants [4].

Between 1990 and 2011, the most dynamic growth was in commuting from Budapest to the surrounding cities (177%) [20]. Nowadays, around 1.2 million people cross the borders of Budapest in both directions every day. Of these, 202,000 passengers travel on the main railway lines, 47,000 on the HÉV lines, 198,000 on intercity buses, and 755,000 by car. Today’s transport demand is on a scale that cannot be met by a network of lines that is in a dilapidated state and designed to meet the needs of the last century. The need for infrastructure development on a scale that can meet these needs justifies an analysis of the impact of rail transport on the Budapest conurbation.

This paper investigates the economic and social impacts of public transport development within the Budapest metropolitan area, contextualized by international experiences and best practices. The primary objective of this study is to assess whether the reconstruction of railway lines post-2008 can be forecasted using data from the Budapest agglomeration. By drawing comparisons with global trends, this research aims to provide insights into the effectiveness of public transport infrastructure development in fostering regional growth and improving the socio-economic landscape of urban and suburban areas. Furthermore, it seeks to determine the extent to which the reconstruction efforts align with or diverge from established patterns observed in similar international contexts.

The research questions are the following:

• Is there a demonstrable link between the development of linear infrastructure (railways) and economic and social processes in the area under study?
• Will the renovation and modernization of the MÁV and HÉV railway lines serving the Budapest agglomeration have a positive impact on the residents concerned?

The rest of the study is structured as follows. Section 2 provides a brief review of the major national and international literature using the PRISMA method. Section 3 covers the data sources as well as factor analysis and logistic regression. Section 4 presents the statistical analysis and results, while Section 5 discusses the opportunities in the international context. Finally, Section 6 concludes the paper.

This study contributes novel insights by employing a data-driven approach to assess whether railway infrastructure upgrades initiated after 2008 have had measurable socio-economic impacts within the Budapest agglomeration. Unlike earlier research, which often focused either on network efficiency [9] or modal split shifts [10], this paper integrates recent demographic, mobility, and economic indicators through logistic regression and factor analysis to evaluate the structural effects of linear transport development. The study is unique in that it applies updated statistical modeling and recent empirical datasets (2015–2023) to explicitly test the relationship between rail infrastructure modernization and commuter behavior. Furthermore, it provides an original regional comparison with successful European S-Bahn and tram–train systems, thus contextualizing Budapest’s situation within broader continental trends [21,22]. In doing so, the study fills a gap in the existing literature by connecting infrastructure renewal with regional equity and sustainable urbanization in post-socialist urban contexts.

This paper explores the regional impacts of public transport development in the Budapest agglomeration within the context of international experiences and practices. The aim of this study is to analyze whether the reconstruction of the railway lines after 2008 can be predicted from the data in the agglomeration of Budapest.

2. Literature Review

The Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) method is a systematic, comprehensive processing of the literature in a given field. PRISMA aims to help authors improve the reporting of systematic reviews and meta-analyses [23]. The method has since become more and more popular in other disciplines. The 10 rules were used in our review of the literature on public transport in urban rail transport [24].

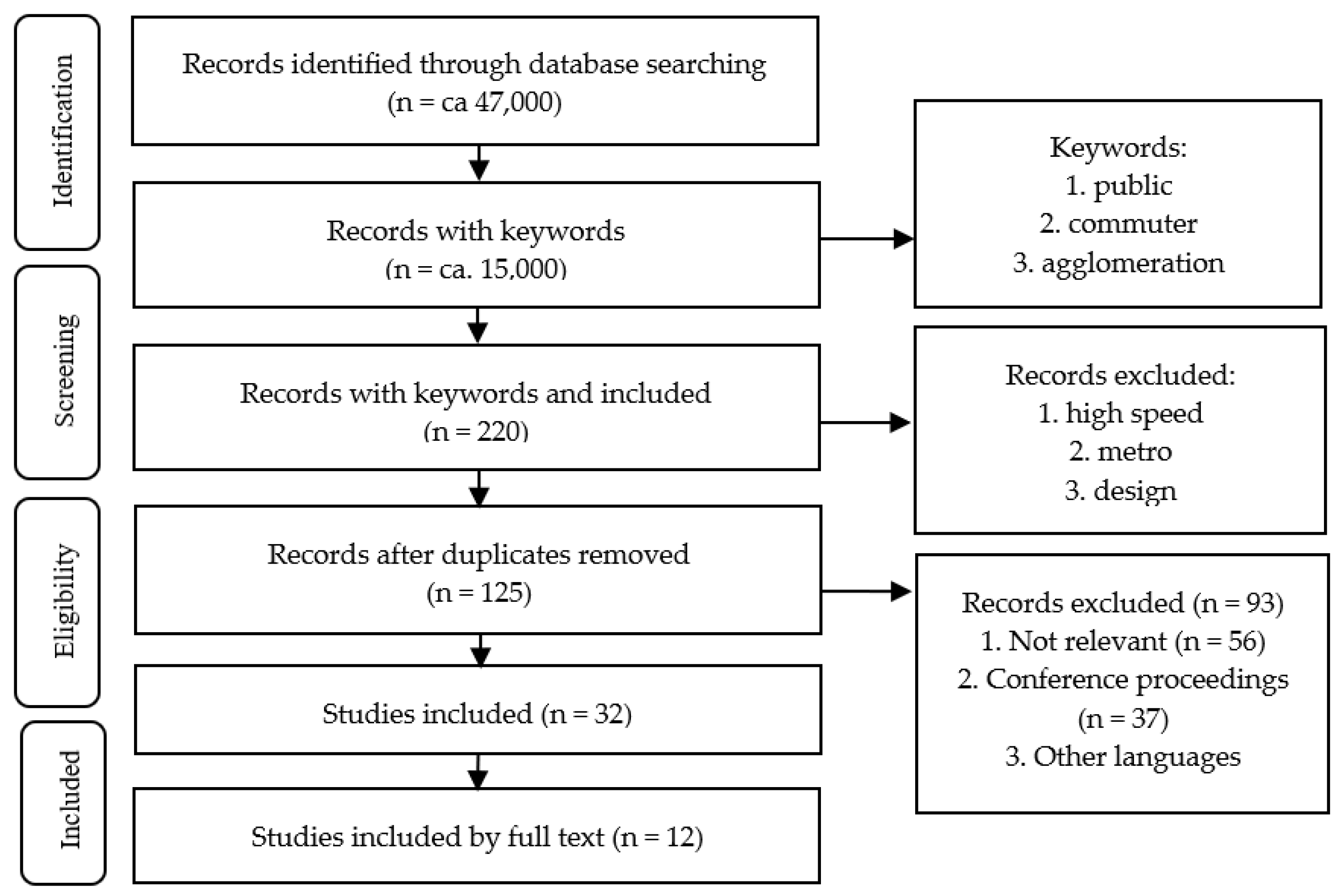
The studies included in the analysis were published between 2000 and 2020 in the Hungarian or English languages. To search for literature in the Hungarian language, the Google Scholar database was used, and for English-language literature, the Web of Science and Google Scholar databases were used.

Table 1. Terms used in the literature (Hungarian and English) for suburban public transport (2021).

Hungarian	English	Hungarian	English
közösségi közlekedés	public transport	agglomeráció	agglomeration, urban area, urban agglomeration
kötöttpályás közlekedés	fixed-track transport	előváros, peremváros	suburb, city and surroundings
vasút, vonat	rail, railway	periféria	periphery
vasútvonal	railroad, rail line, railroad line, railway line	külterület	outskirts
elővárosi vasút	suburban railway	külváros	suburb
helyiérdekű vasút	commuter railway	agglomerációs övezet	agglomeration zone

shows the terms used in the literature for suburban public transport.

Through the process of searching, the numbers of records steadily decreased (see Figure 1). The number of studies included in the quantitative synthesis was 12.

The Hungarian-language publications focus on the development of infrastructure and rail transport in Budapest and its agglomeration as well as in some rural agglomerations (Pécs, Győr). International publications also include papers on rail transport development in agglomerations in major cities of the world (Montreal, Madrid, Bratislava, Paris, Zurich, Sydney).

Ďurček and Hornak [25] analyzed the deficiencies and potential for the improvement of the transport infrastructure in Bratislava, which is not able to meet the demands of increasing mobility, including transport needs within the city and from the agglomeration. According to the authors, upgrading the conventional rail network within the city is one of the most important options for significantly improving the public transport capacity available for urban and regional (suburban) passenger transport. The traditional (sectoral) cost–benefit assessment of public transport projects shows that it is particularly difficult to assess whether project ideas are economically justified [26].

According to the study of De Ona [27], in the southern metropolitan area of Madrid, significant commuter cities began to emerge during the 1960s. While several of these newly developed urban areas were integrated into the pre-existing suburban rail network, others were located at considerable distances from it. To address this transportation gap, the Madrid region has actively supported the development of a number of ‘light-rail’ lines, aiming to improve connectivity and alleviate transit challenges for these expanding communities. These initiatives are part of broader efforts to enhance urban mobility and ensure seamless integration between the city center and its peripheral districts. The light-rail systems combine the characteristics of both trams and the subway. The authors identified three key characteristics that demonstrate the success of a light-rail system: an interconnected transportation network serving a variety of important destinations in the metropolitan area (such as hospitals, shopping centers, etc.), a high-speed regional rail service served by a local bus system, and easy transfers on light-rail, bus, and rail systems. Another study examines the impact of Switzerland’s agglomeration policies (in Bern–Mittelland, Geneva, Lausanne–Morges, and Zurich–Glatt) on the coordination of transport and urbanization [28].

According to Hardi and Nárai [29], suburbanization is the constantly evolving demand for transportation. While suburbanization can change transport demand characteristics within a few years, transportation infrastructure is inflexible and requires many years, coordination among numerous stakeholders, and changes in legal frameworks to adapt to new needs.

According to Jekli and Péli [30], the existence of linear infrastructure and the ability to connect to the urban core significantly influence a region’s competitiveness. Proximity to established infrastructure, such as highway junctions and train or suburban railway (HÉV) stations, always promotes regional development and improves accessibility.

3. Materials and Methods

In our study, fixed-track transport is when a vehicle is traveling on a fixed route (such as rail, HÉV) and the vehicle cannot leave the fixed route [31]. Budapest’s suburban rail transport network consists of five suburban railway lines and 11 railway lines.

Statistical data on municipalities in Hungary are available (e.g., from censuses, regional statistics) and can be used to investigate the links with economic and social factors. The selection of statistical data was based on methodology accepted in the social sciences [32,33].

Based on the literature, factor analysis is a particularly suitable method for researching problems because it can be used to ‘map’ even large datasets. Factor analysis is a multivariate statistical method that is used to compress data, reduce the number of variables, and explore the data structure. In factor analysis, variables that are characteristic of a municipality can be arranged into groups (factors) in such a way that variables in a group are highly correlated with each other but not highly correlated with variables outside that group. Factor analysis is a statistical technique used to identify underlying relationships between variables. There are two main types of factor analysis, along with some subtypes and related methods. Exploratory factor analysis (EFA) is used when the researcher does not have a predefined hypothesis about the structure of the data. It helps in identifying the number of factors and their loadings. Confirmatory factor analysis (CFA) is used when the researcher has a specific hypothesis or theory about the factor structure and seeks to confirm it [34].

In our case, the EFA method was chosen, as we did not have any prior theoretical model or specific hypotheses.

Factor analysis (FA) is a statistical technique used to model the underlying structure of a set of observed variables. It identifies a smaller number of latent variables (factors) that explain the correlations between the observed variables.

The used program, IBM SPSS (Statistical Package for the Social Sciences) for Windows, Version 27 (IBM, New York, NY, USA), provides a straightforward interface for performing factor analysis, but understanding the underlying mathematical process enhances transparency and reproducibility. Here is a step-by-step explanation, along with the corresponding mathematical formulation [35].

• Step 1: Data Input and Correlation Matrix

First, IBM SPSS for Windows, Version 27 computes the correlation matrix R of the observed variables. The data matrix X consists of n observations and p variables.

The correlation matrix R is a symmetric p x p matrix that represents the pairwise correlations between the variables.

• Step 2: Factor Extraction

IBM SPSS for Windows, Version 27 offers several methods for extracting factors. The most common methods are principal component analysis (PCA) and maximum likelihood (ML) estimation. The goal is to extract a smaller number of factors, which are linear combinations of the observed variables.

Let L be the matrix of factor loadings, with each element l_ij representing the loading of the i-th variable on the j-th factor.

The factor extraction model is as follows:

$$\mathrm{X}=\mathrm{L}\mathrm{F}+\mathrm{E}$$

where

• L is the p × m matrix of the factor loadings;
• F is the m × n matrix of the factor scores;
• E is the p × n matrix of the residuals or unique errors.

The goal is to minimize the error terms E while explaining as much variance as possible with a smaller number of factors.

• Step 3: Factor Rotation

Since the factor solution is not uniquely determined, rotation is often performed to make the factors more interpretable. IBM SPSS for Windows, Version 27 offers both orthogonal (varimax) and oblique (promax) rotation methods. Varimax rotation keeps the factors uncorrelated (orthogonal), while promax rotation allows the factors to be correlated (oblique). The rotation process modifies the factor loading matrix L through a rotation matrix Q:

$${\mathrm{L}}_{\mathrm{r}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d}}=\mathrm{L}\mathrm{Q}$$

where

• L_rotated is the new rotated factor loading matrix;
• Q is the rotation matrix.

• Step 4: Estimating Factor Scores

Factor scores represent the latent variables for each observation. In IBM SPSS for Windows, Version 27, factor scores can be computed using the regression method or the Bartlett method. The regression method computes the factor scores as follows:

$$\mathrm{F}={\mathrm{L}}^{\mathrm{T}}(\mathrm{L}{\mathrm{L}}^{\mathrm{T}}{)}^{-1}\mathrm{X}$$

where

• F is the m × n matrix of factor scores;
• L is the factor loading matrix.

These scores indicate how each observation scores on the latent factors, which can be used for further analysis or interpretation.

• Step 5: Evaluating Model Fit

IBM SPSS for Windows, Version 27 provides several goodness-of-fit statistics to assess the adequacy of the factor solution. Common measures include the following:

• The Kaiser–Meyer–Olkin (KMO) test: Assesses sampling adequacy for factor analysis. Values closer to 1 indicate good suitability for factor analysis.
• Bartlett’s Test of Sphericity: Tests the null hypothesis that the variables are uncorrelated. A significant result indicates that factor analysis is appropriate.

Additionally, the total variance explained by the extracted factors is reported. This can be visualized with a scree plot, which shows the eigenvalues for each factor, helping determine the optimal number of factors.

Component validity testing is an important step in factor analysis. Several methods are available, such as the calculation and evaluation of Cronbach’s alpha. However, in the case of explanatory factor analysis (EFA), the use of this indicator does not always give reliable results. Instead, according to Fabrigar et al. [36], other measures, such as factor loadings or eigenvalues, are more commonly reported.

Logistic regression is a multivariate method for categorizing cases according to the categories of the dependent variable. In this case, the authors check whether, and to what extent, membership of the group can be estimated. Regression can be bivariate or multivariate [37].

In their book Statistical and Econometric Methods for Transportation Data Analysis, Washington et al. [38] provide a comprehensive guide to applying logistic regression in transportation research. Logistic regression is particularly useful when the dependent variable is binary, such as modeling whether a person walks to work or whether a driver is involved in a crash. In our case, the dependent binary variable is the renovation of the track. The factors from the factor analysis were used as independent variables in the logistic regression.

The data are from the National Spatial Development and Planning Information System (TeIR, Hungary), including the Spatial Development Monitoring and Evaluation System (T-MER, Hungary), the Municipal Data Collection System, the System of Spatial Statistical Data (T-STAR, Hungary), and passenger data from MÁV-START Zrt. (Budapest, Hungary) and MÁV-HÉV Zrt. (Budapest, Hungary). The data were statistically analyzed using IBM SPSS Statistics for Windows, Version 27 (IBM, New York, NY, USA).

Before analysis, we examined our indicators and the indicators derived from the baseline data for the applicability of factor analysis. The MSA (measure of sampling adequacy) refers to individual variables.

4. Results

Detailed studies were carried out on the statistical analysis of the municipalities and public transport by rail in the Budapest agglomeration. The study sample included the municipalities of the Budapest agglomeration ring where rail transport is available. The aim of the study was to identify the main differences between the group of municipalities where track renewal has taken place and the group of municipalities where no track renewal has taken place since 2008 in terms of indicators at the municipal level.

In their study, the authors analyzed the relationship between the settlement-level characteristics in 2008 and the likelihood of track renewal occurring after that year. Specifically, they aimed to determine whether any statistically significant correlation exists between the conditions of the settlements and the occurrence of track renewal. The year 2008 was selected for this analysis for several reasons. Firstly, tracks that were 12 to 15 years old at that time were still considered relatively new in terms of railway infrastructure, establishing 2008 as a reference point or ‘frontier’ for the study. Additionally, it marks the first year in which significant track renewal activity took place in the region. This dual significance made 2008 an ideal benchmark for examining the factors influencing the initiation of track renewal.

Based on the MSA values for the municipality-specific variables, we excluded from the analysis several original indicators that we had constructed from the baseline data.

In our publication, we have drawn on the methodological elements and results of the PhD dissertation of our co-author Attila Erdei [39].

The remaining indicators have MSA values between 0.485 and 0.866. Their average, the KMO measure (for all variables simultaneously), is medium, with a value of 0.667, which confirmed the suitability of the data for performing factor analysis. The Bartlett chi-square test is a function of whether the correlations between variables are significantly different from zero overall. The significant result of the Bartlett’s test (khí² = 426.786, df = 66, sig. < 0.001) confirmed the adequacy of the correlation structure.

The remaining indicators are provided in

Table 2. Definition of the statistical indicators used. Source [40].

Statistical Indicator	Unit	Definition
Resident population	number	The total number of persons with a place of residence in the respective area with no place of residence elsewhere, as well as of persons with a place of residence in the same area.
Migration balance	‰	The sum of temporary and permanent internal migration balances in a given territorial unit.
Inequality of incomes (S80/S20 ratio)	%	Ratio of the total income received by the 20% of the country’s population with the highest income (top quintile) to that received by the 20% of the country’s population with the lowest income (lowest quintile).
Number of deaths per thousand inhabitants	number	Ratio of all deaths in Hungary and those abroad where the person has an address in Hungary to the resident population.
Number of live births per thousand inhabitants	number	All live births in Hungary and those abroad where the mother has an address in Hungary if the event is registered in Hungary as well.
Aging index (%)	%	The 65-year-old and older population as a percentage of the 14-year-old and younger child population.
Percentage of the permanent population aged 18–59	%	Rate of the permanent population aged 18–59 on 31 December of the reference year.
Number of libraries per 100 inhabitants	number
Number of registered businesses per thousand inhabitants	number	Number of registered corporations and unincorporated enterprises per 1000 inhabitants.
Number of registered non-profit and other non-profit organizations per thousand inhabitants	number	Number of registered non-profit and other non-profit organizations per thousand inhabitants.
Net income per capita	HUF	Net income per capita
Number of cultural events per thousand inhabitants	number	Number of cultural programs in the reference year per thousand inhabitants.

.

These factors were considered due to their significant potential to impact the social and economic dynamics of settlements. Initially, the factor analysis encompassed a broader range of settlement-level variables derived from the databases outlined in the Materials and Methods Section. However, after careful evaluation, only those factors with the greatest relevance and influence on the local socio-economic conditions were retained for further analysis. This approach ensures a more focused and meaningful exploration of the key determinants shaping settlement development. The variables and the indicators derived from them were designed to include as many characteristics of the municipalities as possible that could be used for the situation analysis. Variables with a low weight (explanatory power), as defined by the statistical analysis software (IBM SPSS Statistics for Windows, Version 27, IBM, New York, NY, USA) or factor analysis, were dropped.

After factor analysis, correlation analysis was performed using binary logistic regression, with the dependent variable being the binary variable (renew_2008) recording the fact of track renewal after 2008, with a value of 1 if renewal occurred and 0 if no renewal occurred after 2008. The logistic regression method was chosen because non-metric explanatory variables (e.g., sector code, type of vehicle) were also tested in the analysis before the final model was constructed, in addition to the factors. These variables could not be tested using discriminant analysis.

As described above, the independent variables are the characteristics of the municipalities; so, due to the large number of these factors, a dimensionality reduction was necessary, which was performed by factor analysis. The factors (groups of settlement characteristics) obtained as a result of factor analysis can also be used as explanatory variables in binary logistic regression. In logistic regression models, the dependent variable is categorical and the probability of each category occurring is a nonlinear (logistic) function of the dependent variables and their parameters [41].

Factor analysis to reduce the dimensionality of the settlement characteristics was performed using a principal component method based on a correlation matrix. Factor values were calculated by regression, and factor rotation was performed by varimax rotation. The basic objective of varimax rotation is to generate as many principal component weights close to zero as possible. In doing so, the number of variables for which many factors are included with high weights will be small. Varimax rotation maximizes the sum of variances for each factor. Kaiser proposed this approach and later modified it slightly. In the modification, he normalized the factor weights before maximizing the variance of their squares, as this gives a better result. Varimax rotation can therefore be performed with or without Kaiser’s normalization. Several other right-angle rotation procedures have been developed, but, in general, the use of varimax rotation is recommended for a problem approach [42].

In this analysis, four factors were created. The number of factors was determined using the Kaiser criterion, which recommends retaining all factors with an eigenvalue of at least 1. The same number of factors was obtained using the variance-ratio method, which suggests that the number of factors should be as many as can retain at least 60% of the total variance.

Table 3. Variance results for the four factors in the study (2008). Source [39].

Total Variance Explained
Component	Initial Eigenvalues			Extraction Sums of Squared Loadings			Rotation Sums of Squared Loadings
	Total	% of Variance	Cumulative %	Total	% of Variance	Cumulative %	Total	% of Variance	Cumulative %
1	3.065	25.543	25.543	3.065	25.543	25.543	2.790	23.247	23.247
2	2.622	21.854	47.397	2.622	21.854	47.397	2.289	19.076	42.324
3	1.297	10.807	58.204	1.297	10.807	58.204	1.762	14.684	57.008
4	1.077	8.972	67.177	1.077	8.972	67.177	1.220	10.169	67.177
5	0.938	7.819	74.995
6	0.797	6.642	81.638
7	0.595	4.954	86.592
8	0.509	4.243	90.835
9	0.448	3.730	94.565
10	0.377	3.142	97.707
11	0.245	2.041	99.749
12	0.030	0.251	100.000

Extraction method: Principal component analysis.

shows the four factors in the study that can retain 67.177% of the total variance.

The four factors created are shown in

Table 4. Factor structure of the characteristics of settlements (2008). Source [39].

	Factor (FAC)
	1	2	3	4
Proportion of high- and low-income earners (persons)	0.930
Net income per capita (HUF)	0.915
Number of registered enterprises per thousand inhabitants (number)	0.805
Aging index (%)		0.809
Deaths per thousand inhabitants (persons)		0.640
Live births per thousand inhabitants (persons)		−0.601
Migration balance (%)		−0.470
Registered non-profit and other non-profit institutions per thousand inhabitants (number)			0.725
Number of cultural events per thousand inhabitants (number)			0.714
Permanent population (persons)			−0.632
Number of libraries per 100 inhabitants (number)				0.735
Percentage of permanent population aged 18–59 (%)				0.686

.

Dimensionality reduction does not require an interpretation of the factors, but a possible interpretation is given below. After performing factor analysis, an attempt was made to identify the resulting factors based on the variables sorted into a factor. Thus, the following groups of characteristics were formed:

• FAC1₂₀₀₈: economic situation
• FAC2₂₀₀₈: social erosion
• FAC3₂₀₀₈: community cohesion (small town character)
• FAC4₂₀₀₈: municipality’s cultural activity

The factor scores indicate the degree to which a given factor is ‘strong’ or ‘characteristic’ in a given municipality. For example, the factor scores for the 11 municipalities in the eastern sector of the Budapest agglomeration are shown in

Table 5. Factor scores of municipalities (2008). Source [39].

Municipality	FAC12008	FAC22008	FAC32008	FAC42008
Csömör	0.15493	−0.33479	0.357983	0.37472
Erdőkertes	−1.12755	−0.50014	0.039236	−0.04929
Gödöllő	1.352184	1.112017	−0.80549	−0.06706
Isaszeg	−1.04208	0.513946	−0.87077	0.531585
Kerepes	−0.23003	−0.12934	−0.7946	0.184872
Kistarcsa	−0.32062	−0.25966	−0.21194	−0.48078
Mogyoród	0.275617	−0.83656	−0.07277	0.494479
Nagytarcsa	−0.16174	−1.31105	−0.02958	1.541943
Pécel	−0.62027	0.445825	−0.89084	−0.40351
Szada	0.014332	−0.36358	0.141691	−0.67484
Veresegyház	0.730353	−0.78721	−0.20537	−0.4197

.

Factor scores may assume either positive or negative values. These scores indicate the relative positioning of municipalities along the dimensions represented by each extracted factor. For example, these are based on the factor scores of Gödöllő, and their meanings are as follows:

• FAC1₂₀₀₈ = 1.35 (the economic situation of the municipality is relatively strong)
• FAC2₂₀₀₈ = 1.11 (the municipality is weakly affected by aging and erosion)
• FAC3₂₀₀₈ = −0.81 (the small settlement character is low)
• FAC4₂₀₀₈ = −0.067 (the municipality’s cultural activity is average)

The factor score for each municipality (FAC1₂₀₀₈-FAC4₂₀₀₈) is calculated as the sum of the original variable values multiplied by the factor weights as coefficients in the factor coefficient matrix (

Table 6. Factor coefficient matrix (2008). Source [39].

	Component
	1	2	3	4
Permanent population (persons)	0.173	0.355	-0.513	0.166
Migration balance (%)	−0.012	−0.255	0.157	−0.124
Proportion of high- and low-income earners (persons)	0.328	−0.049	−0.010	0.013
Deaths per thousand inhabitants (persons)	−0.088	0.246	0.076	−0.137
Live births per thousand inhabitants (persons)	−0.018	−0.278	0.044	−0.053
Aging index (%)	0.029	0.392	−0.082	−0.173
Percentage of permanent population aged 18–59 (%)	−0.107	−0.174	−0.006	0.563
Number of libraries per 100 inhabitants (number)	0.073	0.091	0.141	0.615
Number of registered enterprises per thousand inhabitants (number)	0.290	0.053	0.063	−0.059
Registered non-profit and other non-profit institutions per thousand inhabitants (number)	0.124	0.006	0.404	0.038
Net income per capita (HUF)	0.327	−0.042	−0.060	0.048
Number of cultural events per thousand inhabitants (number)	−0.012	−0.028	0.429	0.184

).

Some descriptive statistical characteristics of the factor scores are shown in

Table 7. Descriptive statistical characteristics of factor scores (2008). Source [39].

	Minimum	Maximum	Average	Standard Deviation
FAC12008	−2.1024	3.0953	0	1
FAC22008	−2.3156	3.6208	0	1
FAC32008	−3.4172	4.7825	0	1
FAC42008	−2.6002	4.1261	0	1

.

In the next step, a binary logistic regression model was constructed using the factors FAC1₂₀₀₈-FAC4₂₀₀₈ as independent variables and renovation (renew_2008) as a dependent variable. The binary logistic regression model was constructed in order to estimate the effect of the settlement characteristic factors FAC1₂₀₀₈-FAC4₂₀₀₈ on the probability of renovation. The model was constructed using a forward (Wald) variable selection method.

The Wald statistic is the square of the quotient of the beta (B) and the standard error (S.E.). If the Wald statistic is significant, the variable is contributing to the process. Exp(B) is also an important indicator, as it shows how much each value improves the estimate. The results are shown in

Table 8. Results of the (forward Wald) binary logistic regression (2008). Source [39].

	B	S.E.	Wald	df	Sig.	Exp(B)	95% C.I. Exp(B)
							Lower	Upper
FAC32008	−1.426	0.536	7.077	1	0.008	0.240	0.084	0.687
Constant	−1.655	0.355	21.721	1	0.000	0.191

Comments: S.E. = standard error; C.I. = confidence interval.

.

The resulting regression model can be written as the following equation:

logit = −1.655 − 1.426∙FAC32008

(1)

Thus, among the explanatory variables, only FAC3₂₀₀₈ (Wald = 7.077, df = 1, sig. = 0.008) and the constant (Wald = 21.721, df = 1, sig. < 0.001) were found to be significant.

An increase in the FAC3₂₀₀₈ factor score (i.e., the community cohesion factor score) was associated with a decrease in the odds of renewal (a one-unit increase in exp(−1.426) = 0.240 odds of renewal). Two of the three FAC3₂₀₀₈ factors had a positive value, and one had a negative value. Their impact is in line with their value; i.e., for those with a positive value (registered non-profit and other non-profit organizations per thousand inhabitants, number of cultural events per thousand inhabitants), an increase in the factor does indeed imply a lower probability of renewal. However, for the factor with a negative value (permanent population), an increase in the absolute value implies an increase in the chance of renewal. To put it more simply, we can say that three of the FAC3₂₀₀₈ factor indicators have two different effects. A change in the two factors with positive values has the opposite effect to a change in the indicator for the probability of renewal; i.e., an increase in the two factors leads to a decrease in the indicator for the probability of renewal. In the case of the factor with the negative value, ‘constant population’, an increase in the factor implies an increase in the renewal indicator.

The logistic regression model is statistically significant according to the likelihood ratio chi-square test: χ2 (1) = 11.664, sig. < 0.001. Two indicators are also used to explore how much of the variance of the dependent variable is explained by the combination of independent variables: one is the Cox and Snell R² indicator, and the other is the Nagelkerke R² indicator. Among the pseudo R2 indicators, a Cox and Snell R² of 0.136 and a Nagelkerke R² of 0.210 indicate a not very strong effect size.

According to Hosmer et al. [43], goodness-of-fit measures are crucial for evaluating how well a logistic regression model explains the observed outcomes, especially since logistic regression deals with binary or categorical outcomes rather than continuous variables. Below (

Table 9. Overview of the key goodness-of-fit measures used in logistic regression.

Measure	Type	Interpretation	Use Case
Deviance	Fit statistic	Lower is better	Overall model fit
Hosmer–Lemeshow Test	Fit test	Non-significant p-value = good fit	Model calibration
Cox and Snell R2/Nagelkerke R2	Pseudo R2	Closer to 1 = better fit	Model explanation
Confusion Matrix	Classification	Depends on TP, FP, etc.	Predictive performance
Brier Score	Probabilistic error	Lower = better probability estimate	Calibration/performance
Akaike Information Criterion (AIC)/Bayesian Information Criterion (BIC)	Model selection	Lower = better	Comparing models

) is a detailed overview of the key goodness-of-fit measures used in logistic regression, along with their interpretation, use cases, and references.

A logistic regression model with a pseudo R² of 0.210—such as Nagelkerke’s R²—indicates that approximately 21% of the variation in the dependent variable is explained by the model. While this value is not necessarily poor in behavioral or transportation studies, it does carry several important implications for model interpretation and practical application. A pseudo R² value of 0.210 suggests that the model does not account for a large portion of the variability in the outcome variable. This may reduce the model’s effectiveness for prediction or decision-making. In their work, Washington et al. [38] emphasize that model robustness is influenced by the quality and completeness of the explanatory variables. They argue that missing key variables can lead to misleading inferences about variable significance and impact. Including additional, theory-driven variables and exploring model extensions can improve predictive power and robustness.

The classification table summarizes the correct and incorrect classifications in a 2 × 2 table. The model correctly classified 77.5% of the cases. It is more accurate in identifying non-renovations (95.2%) than renovations (11.8%) (

Table 10. Classification (confusion) table (2008). Source [39].

Observed		Estimated
		Renew_2008		Correct Rating (%)
		No (0)	Yes (1)
Renew_2008	No (0)	60	3	95.2
	Yes (1)	15	2	11.8
Total				77.5

With C = 0.500 cut-off value.

). Changing the value of the cut-off also changes the classification into classes, as either a higher value or a lower value is drawn so that items near the original cut-off may be reclassified into the other group. In the test, the cut-off value is 0.500.

The fitting of the logistic regression was also performed using training–testing sets to determine the validated accuracy of the model. The method consists of splitting the dataset into two parts: a training set and a test set. The teaching set is used to build the model, and the test set is used to measure the performance of the constructed model. The sample is randomly split into 65% of the municipalities in the teaching set and 35% in the test set.

After performing the fitting on the teaching set, the following model was obtained:

logit = 1.806 – 2.019 FAC3₂₀₀₈

(2)

We then looked at the success rate with which the function obtained from the teaching sample classifies the municipalities in the testing set. The validated accuracy of the model (when tested on the testing subsample) is 70.8%. The model identifies non-renovations more accurately (82.4%) than renovations (20.0%). Thus, a similar accuracy to the previous fit was obtained (

Table 11. Classification table on teaching and testing sets (2008). Source [39].

		Estimated
Observed		Teaching			Tester
		Renew_2008		Correct Rating (%)	Renew_2008		Correct Rating (%)
		No (0)	Yes (1)		No (0)	Yes (1)
Renew_2008	No (0)	42	2	95.5	16	3	82.4
	Yes (1)	11	1	8.3	4	1	20.0
Total				76.8			70.8

With C = 0.500 cut-off value.

).

The aim of our analysis was to explore which factors are good predictors of development. From the above analysis, we can therefore conclude the following:

• The number of registered non-profit and other not-for-profit organizations per thousand inhabitants;
• The number of cultural events;
• The permanent population.

The municipality characteristic factor FAC3₂₀₀₈, constructed from the number of permanent residents, had a significant effect on the likelihood of renovation. Increases in the number of registered non-profit and other not-for-profit organizations and the number of cultural events were associated with a decrease in the probability of renovation, while an increase in the permanent population was associated with a higher probability of renovation.

As Kákai [44] points out, the various NGOs can play a key role in the design, implementation, and monitoring of regional and county-level socio-economic programs that reduce the differences between types of settlement, social groups, sectors, and forms of enterprise. According to the study, it can be observed that the strengthening of NGOs is particularly marked in municipalities with a strong rural character. The increase in the number of cultural events was mainly observed in developing but smaller municipalities. It is important to note that while the model is excellent in identifying ‘no renovation’ (correct validated classification of 82.4%), it is weak in identifying renovations (correct validated classification of 20.0%). This is probably due to the fact that the number of renovations carried out is significantly lower compared to the total data.

Thus, our analysis suggests that there is a demonstrable positive correlation between the renovation of public transport infrastructure and the permanent population indicator, while a small population is more of a factor working against renovation.

5. Discussion

The experiences of cities around the world provide valuable insights for understanding the regional impacts of public transport development. However, it is crucial to focus the discussion on the results of our study conducted in Budapest. A direct comparison with selected cities such as Vienna, Prague, Zurich, and Kraków will allow for a thorough examination of both the commonalities and differences in the effects of public transport initiatives, providing a more nuanced perspective on the regional context and underlying factors. This comparative analysis not only contextualizes our findings but also contributes to a broader understanding of the dynamics shaping urban mobility in diverse European settings [45,46].

In contrast to Vienna, where the S-Bahn and U-Bahn systems are highly integrated and play a pivotal role in regional connectivity and urban development, Budapest’s suburban rail services (HÉV) have experienced more limited integration with urban transport. While Vienna benefits from seamless multimodal connectivity and unified ticketing systems, Budapest still faces challenges in achieving similar levels of interoperability across modes. Despite these differences, both cities share a strong emphasis on affordability and accessibility in public transport policy, contributing to high public transport usage rates [21,47,48].

Interestingly, our analysis revealed a negative correlation between the development of cultural infrastructure and railway accessibility in Budapest—a surprising divergence from trends observed in cities like Prague or Kraków. In Prague, for example, investment in cultural heritage sites often coincides with improvements in tram and metro accessibility, suggesting a synergistic urban development strategy. In Budapest, however, cultural institutions tend to be concentrated in historic central areas, while railway development has prioritized peripheral connectivity. This may reflect legacy urban planning decisions or a lack of coordinated development strategies between cultural and transport authorities. Further research is needed to understand whether this reflects a broader trend in post-socialist urban environments or is specific to Budapest’s development trajectory.

Zurich’s integrated transport system, marked by punctuality and sustainability, offers another point of comparison. Unlike Budapest, which continues to modernize its rolling stock and ticketing systems, Zurich has already achieved high standards in environmental performance through the widespread adoption of electric and low-emission vehicles [49]. Kraków and Budapest, on the other hand, both illustrate the growing importance of urban rail systems in mid-sized Central European cities, though Kraków’s SKA network is still in a developmental phase compared to Budapest’s longer-established suburban lines.

In the V4 countries, capital cities play extremely dominant roles in terms of the economy [50]. Public transportation in Prague serves as the lifeblood of the city’s mobility, offering residents and visitors an efficient and accessible means of travel. With a rich history dating back over a century, Prague’s public transport system has evolved into a sophisticated network comprising trams, buses, metro lines, and ferries [51]. Prague’s public transportation network is characterized by its extensive coverage and integration across various modes. The Prague Metro, inaugurated in 1974, consists of three lines (A, B, and C) intersecting at key transport hubs, facilitating rapid transit within the city and connecting it to suburban areas. Complementing the metro are the iconic trams, which traverse the city’s historic streets, providing a flexible and frequent service to passengers. Additionally, buses operate on a vast network of routes, serving areas not accessible by metro or tram. The integration of these modes, along with the inclusion of ferries on the Vltava River, ensures comprehensive coverage and seamless connectivity across Prague. In recent years, Prague has placed increasing emphasis on sustainability and innovation within its public transportation system. Efforts to reduce carbon emissions and improve air quality have led to the introduction of eco-friendly initiatives, such as the expansion of electric tram lines and the adoption of low-emission buses [52]. Despite its successes, Prague’s public transportation system faces challenges that require careful attention and strategic planning. Urban congestion, especially in the city center, poses a significant obstacle to the smooth operation of tram and bus services. Addressing this issue necessitates measures to prioritize public transport, such as dedicated bus lanes and pedestrian zones. Additionally, aging infrastructure and capacity constraints on certain metro lines require ongoing investment and modernization efforts to ensure reliability and efficiency [53].

Kraków boasts a well-developed public transportation system comprising buses and trams operated by the Municipal Transport Company (MPK Kraków) [54] and a developing train network, including four ‘Kraków Fast Urban Railway’ lines (SKA—Szybką Kolej Aglomeracyjną 1–4). With an extensive network covering the city center, suburbs, and surrounding areas, public transport serves as the backbone of urban mobility in Kraków. The integration of various modes of transportation facilitates seamless travel across different parts of the city, enhancing accessibility and convenience for passengers. MPK Kraków operates a fleet of modern vehicles equipped with amenities such as air conditioning, Wi-Fi, and accessibility features for passengers with disabilities. The tram network, consisting of over 20 lines, forms the backbone of Kraków’s public transportation system, providing efficient and environmentally friendly travel options. Additionally, an extensive bus network complements tram services, offering connectivity to areas not covered by the tram lines. The urban railway system in Kraków, commonly referred to as the Kraków Fast Urban Railway (SKA), plays a crucial role in the city’s transportation network. It consists of several lines connecting various parts of the city, suburbs, and neighboring towns. One of its significant strengths lies in its integration with other modes of transportation, such as trams and buses, providing commuters with seamless transfers and efficient multimodal travel options. This integration enhances accessibility and facilitates smooth commuting experiences for residents and visitors alike, contributing to the overall efficiency and sustainability of Kraków’s transportation infrastructure. The introduction of electronic ticketing systems and real-time passenger information further enhances the user’s experience, making it easier for passengers to plan their journeys and navigate the city. Looking ahead, Kraków’s public transportation system is poised for further development and innovation [55]. Plans for expanding the tram and train network, upgrading the infrastructure, and introducing low-emission vehicles demonstrate the city’s commitment to sustainable urban mobility. Moreover, initiatives aimed at enhancing intermodal connectivity and integrating public transport with emerging technologies hold promise for improving the efficiency and effectiveness of the transportation system. Kraków can continue to enhance its public transportation system, fostering sustainable urban development and improving the quality of life for its inhabitants [56].

These comparisons underline the distinctive characteristics of Budapest’s transport development while also situating it within a broader regional context. The observed discrepancies—in particular, the unexpected disconnection between cultural activity and rail development—highlight the need for more integrated urban strategies that align the transport infrastructure with social and cultural investments.

6. Conclusions

The local and suburban rail infrastructure in Hungary is currently facing several significant challenges. One of the primary issues is the lack of consistent interoperability between different modes of transportation, specifically between the MÁV (Hungarian State Railways) and HÉV (suburban railway) lines. While interconnection points exist, the design and functionality of passenger transfer hubs remain inadequate, hindering seamless transitions between services. Despite the relatively robust structure and density of Hungary’s rail network—an asset that compares favorably with European standards—the national and suburban rail systems serving Budapest are increasingly struggling to adapt to the evolving economic and demographic demands of recent years. Specifically, suburban rail traffic in Budapest frequently experiences severe undercapacity and congestion, particularly during peak hours, exacerbating the challenges faced by commuters. This growing mismatch between the infrastructure’s capacity and the demand highlights the pressing need for targeted interventions and modernization efforts in the system. A major step toward solving these problems was the connection of the Budapest–Hatvan line and H8 HÉV at Gödöllő station, which will be a new common terminus. The renovation and revitalization of the railway and HÉV lines and their regular service with modern vehicles are vital to meet the growing demand for mobility. New rolling stock should not only improve reliability and regularity but also reduce operating costs and environmental impacts. Unfortunately, Hungary does not yet have a technically and organizationally complex integrated system—such as the German and Austrian S-Bahn and tram–train systems—that would make the various national, regional, conurbation, and local transport systems a coherent and interoperable whole.

Demographic indicators in the study area have exhibited a notable upward trend in recent years. A substantial increase in population size has been observed within the agglomeration, reflecting a significant demographic expansion. This growth is indicative of broader social and economic dynamics within the region, which may have implications for urban planning, resource management, and infrastructure development. Further investigation into the underlying factors driving this population increase could provide valuable insights into future demographic shifts and their potential impact on the area. Statistical data show that the proportion of the population of the agglomeration compared to the population of Budapest was only 43% in 1970. This proportion has now increased to 68%. Today, around 270,000 cars enter Budapest from the agglomeration every day. Looking at the queues of cars on the roads, it is clear that this phenomenon cannot be remedied by road improvements alone. It is forecast that further population growth in the near future will generate additional mobility needs that will make it much more difficult to get from the agglomeration to the center by private transport (car).

The expected future growth of the agglomeration will generate additional high mobility needs that cannot be met without competitive rail and HÉV connections. Unfortunately, the quantitative increase in linear infrastructure has not been achieved in the last 40 years, but the recent (2018–2021) development of rail lines could have an important impact on the agglomeration area under study. The recent railway renewal projects (Budapest–Esztergom, Budapest–Székesfehérvár, Budapest–Pusztaszabolcs) can serve as a positive example and starting point for such a railway development. Other development directions could be the development of suburban-type transport in large cities with agglomeration catchment areas, such as the tram–train system between Szeged and Hódmezővásárhely, and the development of further suburban (Miskolc, Debrecen) or even interregional lines.

The deterioration of the rail network in Hungary over several decades has put it at a significant competitive disadvantage vis-à-vis private and even long-distance bus transport. In order to reduce this competitive disadvantage, it is absolutely necessary and indispensable to develop public rail transport (rail, HÉV) in order to ‘switch’ as much commuter traffic as possible to these modes. By extending these improvements at a regional and national level, the objective of improving public transport services in all municipalities and shifting urban and conurbation traffic to environmentally friendly public transport can be achieved. The long-term goal is to develop a uniform timetable, a uniform ticketing and tariff system, uniform passenger information, and a uniform image and to improve feeder networks and connections.

Demographic indicators in the study area have exhibited a notable upward trend in recent years. This growth is indicative of broader social and economic dynamics within the region, which may have implications for urban planning, resource management, and infrastructure development.

The population of the Budapest agglomeration has grown substantially; in 1970, it comprised only 43% of Budapest’s population, whereas, today, it stands at 68%. Every day, approximately 270,000 cars enter the capital from the surrounding region. The resulting traffic congestion clearly cannot be solved through road expansion alone. Forecasts indicate that ongoing population growth will continue to generate increasing mobility demands, rendering private car travel from the suburbs to the city center increasingly inefficient.

The projected expansion of the agglomeration will place further pressure on the transport system—demands that cannot be met without competitive and well-integrated rail and HÉV services. Notably, the linear infrastructure of Hungary’s railway system has seen minimal expansion in the past four decades. However, recent developments between 2018 and 2021, including the renovation of the Budapest–Esztergom, Budapest–Székesfehérvár, and Budapest–Pusztaszabolcs lines, represent significant progress and can serve as models for future development.

Furthermore, suburban-type rail solutions like the Szeged–Hódmezővásárhely tram–train project demonstrate the potential of hybrid systems in enhancing urban–rural connectivity. Expanding this approach to other regional hubs, such as Miskolc, Debrecen, or even interregional corridors, could alleviate the pressure on road networks and support sustainable mobility goals.