Quantitative Structure–Activity Relationship Models for the Angiotensin-Converting Enzyme Inhibitory Activities of Short-Chain Peptides of Goat Milk Using Quasi-SMILES

Abstract

The inhibitory activity of peptides on angiotensin-converting enzyme (ACE) is a measure of their antihypertensive potential. Quantitative structure–activity relationship (QSAR) models obtained based on the analysis of sequences of amino acids are suggested. The average determination coefficient for the active training sets is 0.36 ± 0.07. The average determination coefficient for validation sets is 0.79 ± 0.02. The paradoxical situation is caused by applying the vector of ideality of correlation, which improves the statistical quality of a model for the calibration and validation sets but is detrimental to the statistical quality of models for the training sets.

1. Introduction

Currently, computer methodologies are often used to evaluate the physicochemical and biochemical behavior of various substances [1,2,3,4,5,6,7,8,9,10]. The possibility of creating and distributing databases and software largely determines the semantic framework of modern scientific research activities. In other words, one of the main drivers of the research is the development of mathematical models, which can facilitate the theoretical framework in a field and explore new scenarios. An unexpected obstacle on this path is the contradiction between the mathematical aiming of accuracy or ideality, on the one hand, and the aiming of instability and dispersion of many natural phenomena, including the values of endpoints used for the characterization and evaluation of substances for various purposes. Monte Carlo methods [11,12,13,14,15,16,17,18,19,20], in principle, can be a compromise in resolving the aforementioned contradiction between nature and mathematics. However, the cost of this compromise is uncertain; consequently, one can discuss some intervals as a more useful indicator compared with pseudo-reliable and pseudo-accurate theoretical values for physicochemical and biochemical endpoints.

To think that one can construct an ideal, reliable model is quite a naive conception. Again, there is a poisonous contradiction between the desire to build a “super-excellent” model in a certain area of space called the applicability domain and the inevitability of obtaining a group of outliers even for a very carefully planned applicability domain. Any software designed to estimate the experimental value of any endpoint is only a simulacrum (surrogate) of a real experiment to determine this endpoint.

The classic idea of endpoint modeling is to base the model on the molecular structure of the substance under study. For these purposes, the molecular structure is represented by a mathematical graph in which the vertices represent atoms and the edges represent covalent bonds [21,22].

It is possible to radically change the physical meaning of the graph if its vertices represent not atoms but molecular orbitals (1s², 2s², 3p⁶, etc.). The edges in such a graph will be a fragmented representation of the classical covalent bond between atoms split into orbitals. Such graphs are called graphs of atomic orbitals (GAOs). GAOs were used to develop quantitative structure-property/activity relationships (QSPRs/QSARs) [23,24,25].

In the case of studying peptides and proteins, representing these substances for modeling in the form of graphs becomes inconvenient for the following reasons: Firstly, the corresponding graphs are doomed to be of enormous size, that is, to have a very large number of atoms (vertices of the graph). If the graph is represented through an adjacency matrix, then for the case of n atoms, a square n × n matrix is required. Even the rapid growth of memory and computer speed cannot provide the ability to process databases with such representations of peptide and protein molecules in an acceptable time if we are talking about hundreds or even thousands of such molecules/molecular graphs. Secondly, the repetition of molecular fragments that are slightly different and carry similar physicochemical and biomedical functions is inevitable. This makes it a very tempting alternative to consider the structures containing data about these similar fragments in a more compact form. In other words, it is tempting to build models of proteins and peptides using amino acid identities as a basis [26,27].

In this way, three levels of representation of substances for QSPR/QSAR can be considered and/or compared. The most detailed level is the GAO. The intermediate level is the “classical” molecular graph (hydrogen-filled graph or hydrogen-suppressed graph). Moreover, an option that is somewhat out of the logical chain is the presentation of the structure of the peptide as a sequence of amino acids. It should be noted that the representation of peptide structure via a sequence of amino acids is quite similar to the representation of the molecular structure of organic compounds via SMILES [28].

The famous saying “knowledge is power” makes one think about the following: It is quite natural to accept that knowledge is information. If one solves a certain problem, one needs information (knowledge). If there is not enough information, solving the problem will require a lot of “extra” effort. If there is exactly as much information as needed, solving the problem will require a minimum of effort. The key point is as follows: if there is more information than is needed to solve a problem, then solving the problem will require additional effort to filter out and ignore unnecessary information. Thus, excess information is nothing more than a variant of disinformation. From this point of view, it is very likely that for constructing models of the biochemical behavior of peptides, the traditional graph and GAO are rather misinformation, despite the fact that simulation of the biochemical behavior of peptides using graphs has been described in the literature [4].

In addition to SMILES, so-called quasi-SMILES can be used for QSPR/QSAR research. Quasi-SMILES have been used to construct models of the physicochemical and biochemical behavior of nanomaterials under various experimental conditions [29,30]. It should be noted that the sequence of amino acids that make up the peptide could be considered as quasi-SMILES [31,32,33]. By the way, quasi-SMILES are able to serve as a tool to establish QSPR/QSAR for “usual” organic molecules if the experimental conditions are taken into account [34,35]. However likely, the main application of the quasi-SMILES is the development of models for the physicochemical and biochemical behavior of diverse nanomaterials [36,37,38,39,40].

Pesticides are one of the major sources of contamination of dairy products due to the presence of their residues in animal feedstuffs. Other contributory factors in this regard may include the application of pesticides to farm animals, environmental contamination, and accidental spills. Milk contamination may be avoided by hindering the entry of pesticide residues into dairy animals through contaminated feedstuffs/food chains [41].

This work attempts to use the Monte Carlo method to construct a model of the inhibitory activity of short-chain peptides in goat milk.

Angiotensin-converting enzyme (ACE) inhibitory peptides are a significant component of food technology. The peptide activities are expressed by IC50 values, which represent the peptide concentration (in μM) required to block ACE activity by 50%. The above-mentioned activity is valuable information; therefore, the quantitative structure–activity relationships (QSARs) for the above endpoint are developed here.

The study aims to build up QSAR models for the pIC50 and estimate the stability of the predictive potential of the model observed for different distributions in the training and validation sets. However, unlike previous works devoted to developing models using the Monte Carlo technique, here we consider fragments of local symmetry in the amino acid sequences that make up the peptides [7]. Local symmetry is the coincidence of one-character abbreviations of amino acids in a three-character fragment included in the peptide. This can be considered a composition of three symbols, i.e., xyx, where x and y are arbitrary, but x is not equal to y.

2. Materials and Methods

2.1. Data

Here, models of the inhibitory activity of peptides in goat milk are developed and evaluated. The peptides are represented by sequences of amino acids. Experimental data on inhibitory activity are taken from [42]. The work [42] presents data on 268 peptides, but our software identified two duplicates, which were eliminated from further consideration. In this way, 266 peptides are considered. These sequences are applied as the quasi-SMILES [43].

2.2. Splitting Available Data into Training and Validation Sets

The CORAL-2023 (http://www.insilico.eu/coral, accessed on 20 May 2024) software provides the user with several options for constructing models. One can build a model by dividing the available data into a training set and a validation set. However, in this case, a number of doubts remain unexamined. First, the division may be too successful. Then, the model can inspire the user with false hopes, which will be dispelled when trying to apply the model to new data that was not available at the time of its construction. Secondly, the splitting of training and validation sets may be too unfortunate. Then, the model again misinforms the user about the real state of affairs, making him think that the model for the endpoint and set of connections being measured is impossible (although this may not be the case).

These doubts led to the development of the concept of simulation, based on the following principles: 1. The statistical quality of the model depends on the chosen division of data into a training and validation set. 2. In the process of building a model based on correlation weighting, there must be feedback between the currently observed statistical quality of the model for the objects under consideration in the training set and the statistical quality of the model for similar objects that are not visible to the simulation. 3. Overtraining (when the model becomes excellent for objects involved in building the model and useless for external objects not involved in building the model) should be blocked.

To practically follow the above principles, the peptides considered were distributed into the following four subsets: (i) the active training set; (ii) the passive training set; (iii) the calibration set; and (iv) the validation set. Thus, instead of a traditional monolithic training set, a structured training set is used, which includes active and passive learning together with a calibration set. The active training set is a list of those objects (peptides) that are involved in the development of the model (their structure, expressed by the sequence of amino acids, for which correlation weights are optimized using the Monte Carlo method). A passive training set is a list of peptides whose data are not used for the specified optimization; however, the quality of the model for them is taken into account. Finally, the calibration set is a list of peptides that are used to recognize the moment when optimization begins to produce the statistical quality of the active learning model significantly better than the one observed on the calibration set.

2.3. Optimal Descriptor

By the Monte Carlo method, using active and passive training sets together with a calibration set, the so-called correlation weights of amino acids were calculated, which give the maximum value of the objective function, defined as follows:

$$TF=r_{AT}+r_{PT}-\left|r_{AT}-r_{PT}\right|\times \alpha +(IIC+CII)\times \beta$$

(1)

where r_AT and r_PT are determination coefficients for active and passive training sets; IIC is the index of ideality of correlation [24]; CII is the correlation intensity index [24]; and α = 0.1 and β = 0.3. Alpha and beta coefficients are selected empirically. The indicated values for other QSPR/QSAR tasks may vary depending on the results of the corresponding computational experiments.

Calculations of IIC and CII are described in the literature [44]. The main idea of the IIC is an attempt to combine the statistical quality of the model, transmitted through the values of the coefficients of determination, and the statistical quality of the model, transmitted through the values of the average absolute error. Instead of the latter, one can use the root mean square error, but the use of the absolute error turned out to be more effective in terms of the results of the stochastic process of the optimization by the Monte Carlo method. The basic idea of CII is to evaluate how individual peptides influence the overall correlation in the set. In the case of CII, the overall total contribution of all opponents of the correlation is examined, that is, those peptides whose removal from consideration leads to an improvement in the correlation.

The optimal descriptor calculated with quasi-SMILES is calculated as follows:

$$DCW\left(T,N\right)=\sum CW\left(A\right)+\sum CW\left(A_x{A}_y\right)+\sum CW\left(FLS\right)$$

(2)

where A is one symbol abbreviation of an amino acid and A_xA_y is a pair of neighboring amino acids. FLS is a fragment of local symmetry suggested in [45]. Here T = 3 and N = 15 are used.

3. Results

Models for five random splits of available data into the active training, passive training, calibration, and validation sets are as follows:

pIC50 = 1.491 (±0.045) + 0.5435 (±0.0082) × DCW(3, 15)

(3)

pIC50 = 2.395 (±0.035) + 0.3710 (±0.0063) × DCW(3, 15)

(4)

pIC50 = 2.646 (±0.040) + 0.2532 (±0.0062) × DCW(3, 15)

(5)

pIC50 = 2.366 (±0.049) + 0.3063 (±0.0070) × DCW(3, 15)

(6)

pIC50 = 1.314 (±0.051) + 0.4341 (±0.0075) × DCW(3, 15)

(7)

Table 1. The statistical characteristics of models of inhibitory activity observed for five random splits into the training and validation sub-systems.

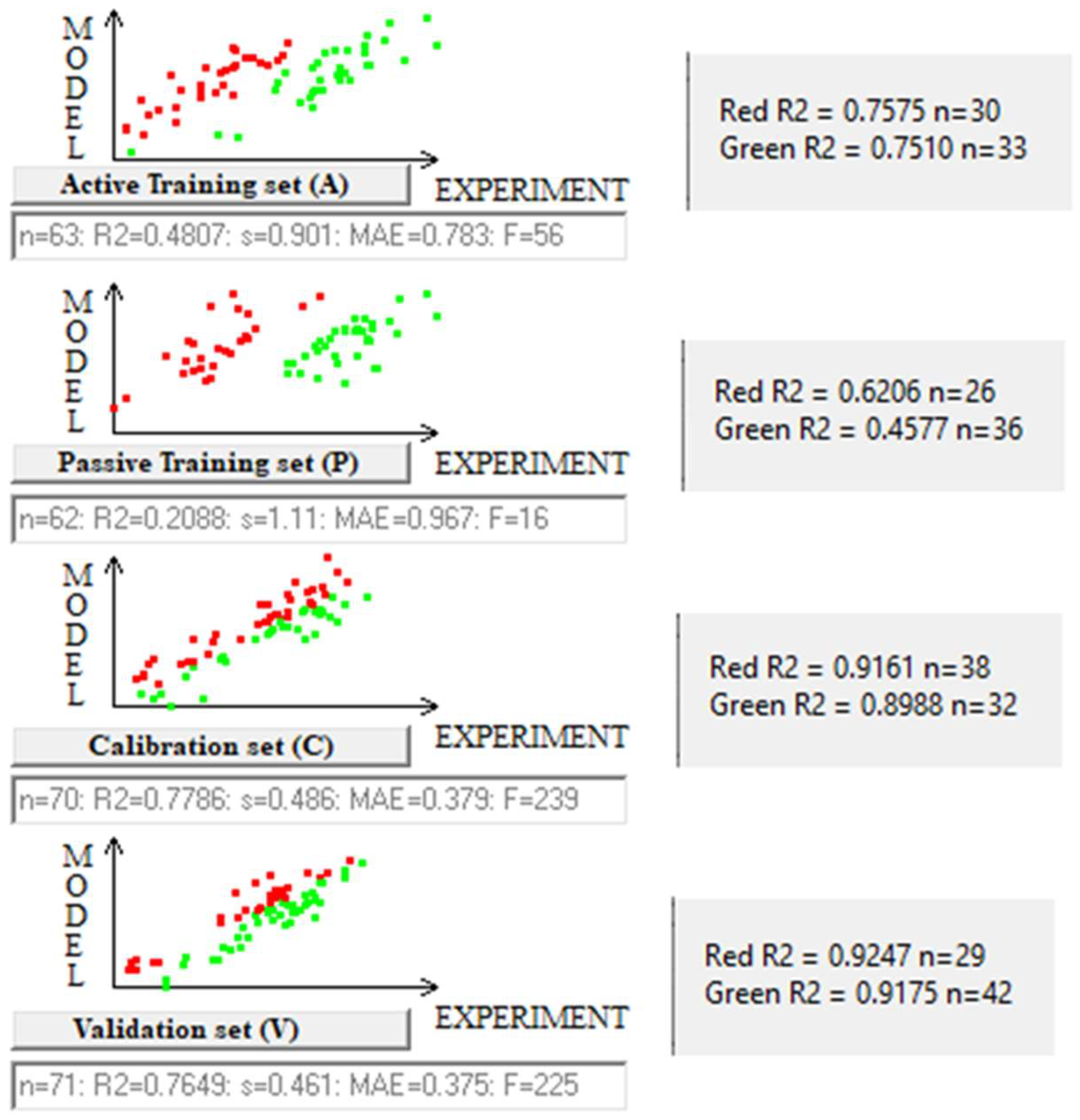
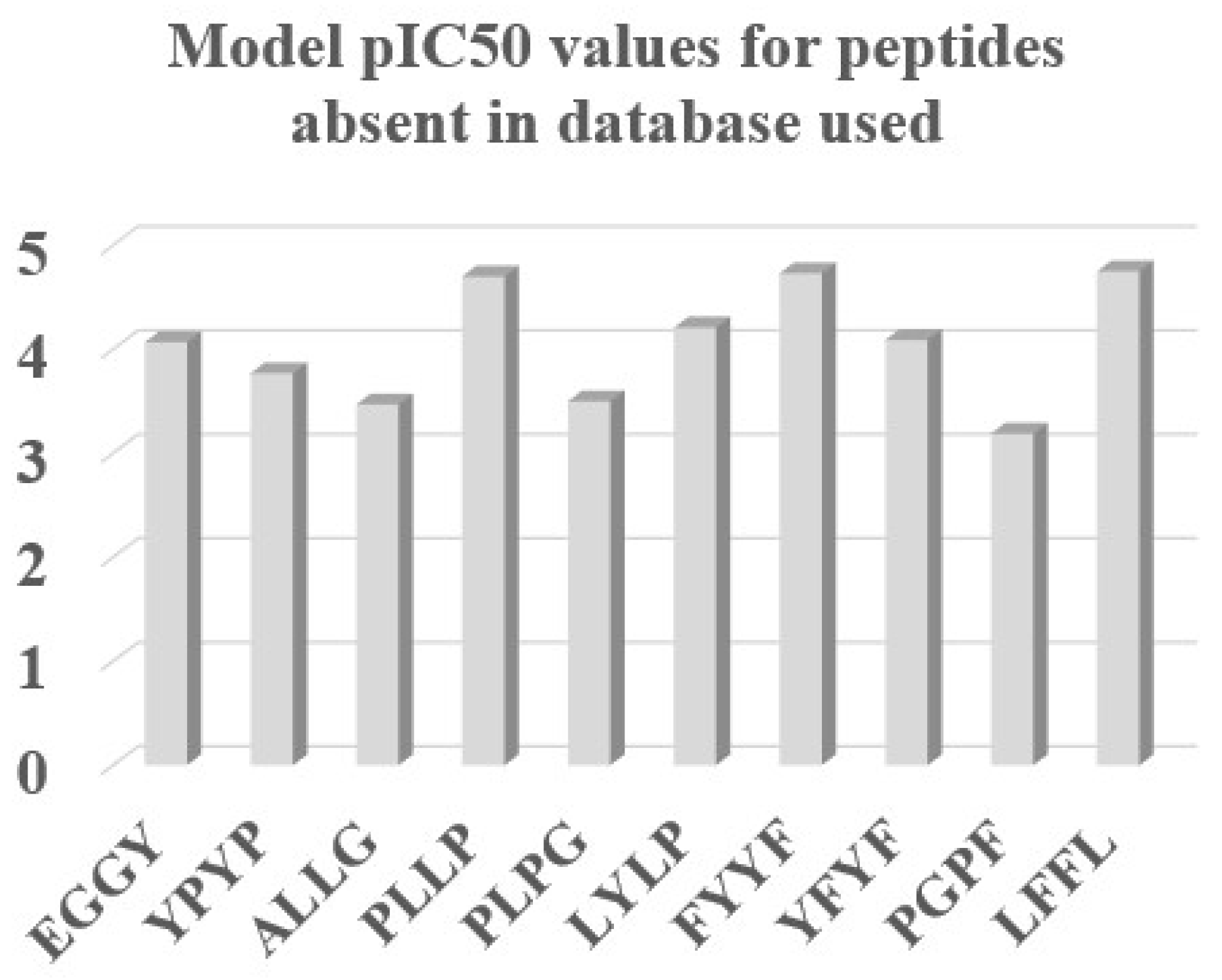
Split/Eq.		n *	R2	IIC	CII	Q2	Q2F1	Q2F2	Q2F3	<Rm2>	MAE	F	Nact
1/3	A	63	0.4807	0.6303	0.7322	0.4501					0.783	56
	P	62	0.2088	0.4045	0.7011	0.1430					0.967	16
	C	70	0.7786	0.8822	0.8910	0.7638	0.7844	0.7583	0.8475	0.6895	0.379	239
	V	71	0.7649	-	-	-	-	-	-	-	0.38	-	28
2/4	A	69	0.3732	0.5600	0.7187	0.3399					0.892	40
	P	66	0.3837	0.6073	0.7125	0.3486					0.840	40
	C	65	0.7876	0.8869	0.8767	0.7745	0.8024	0.7875	0.8681	0.6886	0.375	234
	V	66	0.7867	-	-	-	-	-	-	-	0.33	-	25
3/5	A	71	0.2836	0.5178	0.6979	0.2391					0.939	27
	P	64	0.2507	0.3968	0.7318	0.2000					0.945	21
	C	65	0.7654	0.8748	0.8793	0.7493	0.7869	0.7580	0.8763	0.5959	0.342	206
	V	66	0.8339	-	-	-	-	-	-	-	0.30	-	25
4/6	A	71	0.2832	0.4622	0.6927	0.2418					0.938	27
	P	69	0.4217	0.5024	0.7158	0.3913					0.904	49
	C	62	0.8326	0.9120	0.8942	0.8219	0.8106	0.8051	0.8913	0.5924	0.341	299
	V	64	0.8083	-	-	-	-	-	-	-	0.32	-	22
5/7	A	65	0.3926	0.6076	0.7115	0.3582					0.859	41
	P	67	0.5001	0.6846	0.7267	0.4753					0.908	65
	C	66	0.7889	0.8880	0.8561	0.7760	0.7930	0.7827	0.9122	0.7011	0.299	239
	V	68	0.7748	-	-	-	-	-	-	-	0.34	-	26

⁽*⁾ A = active training set; P = passive training set; C = calibration set; V = validation set; R² = determination coefficient; IIC = index of ideality of correlation; CII = correlation intensity index; Q²–Q²_F3 are statistical criteria suggested in the literature [4]; <R_m²> is a metric suggested in [5]; MAE = mean absolute error; F = Fischer F-ratio; N_act is the number of parameters under optimization.

contains the statistical characteristics of models for pIC50 related to considered peptides calculated with Equations (3)–(7).

One can see that for all five splits into training and validation sets, the predictive potential (statistics on the validation set) is quite good. At the same time, the determination coefficient for active and passive training samples is very poor. As noted above, this is due to the use of the idealization vector in the corresponding Monte Carlo calculations. Indeed, at the stage of the active and passive training sets, the model is not yet complete, but it is complete with the results shown for the calibration set, which is still part of the modeling phase. The results of the calibration set represent those of the model when finished. The results of the validation set are obtained using peptides never used by the software. Thus, it is appropriate to compare the results of the validation set with those of the calibration set. Graphically, the situation under discussion can be illustrated by the splitting of correlation clusters (Figure 1). In fact, instead of the traditional single correlations for training samples, they are divided into pairs of correlations. These clusters are defined by the magnitude of the differences between the observed and model values. If this value is positive (including zero), then the corresponding point is indicated in green; if this value is negative, the corresponding point is indicated in red. Figure 1 shows that such clustering occurs for all four sets considered (active and passive training sets, calibration sets, and validation sets). However, these clusters for the training samples are located quite far from each other, while for the control and validation samples, these clusters are much closer.

Table 2. The technical details of the model observed in the case of split 1 for the validation set.

Quasi-SMILES	DCW(3, 15)	pIC50(Expr)	pIC50(Calc)	Defect of Quasi-SMILES	Applicability Domain *
ADDA	4.9121	3.8300	4.1611	5.0143	YES
AEEL	5.5666	4.2400	4.5168	5.0078	YES
AFFL	4.6788	4.2000	4.0344	3.0151	YES
AGAG	0.5240	2.6000	1.7763	3.0179	YES
AKKK	7.6277	5.4900	5.6370	2.0211	YES
AYAY	4.2358	4.0600	3.7936	3.0133	YES
DGDG	1.5879	2.1500	2.3545	2.0099	YES
FAAL	5.1709	4.5800	4.3018	2.0226	YES
FFFP	4.5058	4.9200	3.9403	3.0170	YES
FGGK	3.8671	3.8000	3.5932	2.0221	YES
GSGS	2.0150	2.4200	2.5866	5.0099	YES
GYGY	2.6355	3.6300	2.9238	3.0110	YES
IAAE	5.5930	4.4600	4.5312	3.0191	YES
IAAQ	5.5433	4.4600	4.5042	3.0191	YES
IGIG	2.2514	2.9200	2.7151	3.0142	YES
IKKP	7.4584	5.6800	5.5450	3.0184	YES
IPIP	3.3166	3.8900	3.2940	3.0171	YES
IRRA	5.2918	5.0100	4.3675	2.0370	YES
ITTF	5.9388	4.3100	4.7191	4.0076	YES
LWLW	5.6253	4.4500	4.5488	3.0262	YES
LYLY	4.5575	4.4100	3.9684	3.0093	YES
MYMY	5.8750	3.7100	4.6845	5.0054	YES
PLPL	4.4238	3.4700	3.8957	0.0292	YES
RARA	2.1150	3.3400	2.6409	0.0413	YES
RFRF	2.8395	3.7900	3.0347	3.0406	YES
RGGP	4.2545	4.2700	3.8037	1.0406	YES
YEEY	6.6675	5.4000	5.1152	3.0074	YES
YGGY	5.2962	4.8300	4.3699	2.0189	YES
YLYL	4.5575	3.9900	3.9684	3.0093	YES
YNYN	4.9150	4.2900	4.1627	5.0054	YES
YPPR	5.7054	4.7800	4.5923	2.0278	YES
YPYY	4.8573	4.0500	4.1314	2.0182	YES
FPFP	2.7609	3.5000	2.9920	3.0201	YES
FPPF	4.9269	4.6800	4.1692	2.0245	YES
FQQP	5.4828	4.9200	4.4713	4.0098	YES
FVAP	6.6277	5.0000	5.0935	1.0501	YES
FYFY	4.7808	4.6300	4.0898	3.0126	YES
GDGD	1.5879	2.0400	2.3545	2.0099	YES
GEEG	4.4691	3.7200	3.9204	5.0120	YES
GLGL	1.0321	2.6000	2.0524	0.0631	YES
GNGN	1.7778	2.8900	2.4577	2.0099	YES
GQGQ	2.1003	2.1500	2.6330	5.0099	YES
GRRP	4.8240	4.7000	4.1133	3.0380	YES
KAKA	2.1131	3.4200	2.6399	0.0224	YES
KGKG	1.9467	2.4900	2.5495	3.0201	YES
KPPF	5.2113	4.4900	4.3238	2.0214	YES
LDDP	5.5989	4.3700	4.5344	4.0081	YES
LEEE	6.4487	4.0000	4.9963	6.0039	No
LEEL	6.9531	4.8100	5.2704	5.0103	YES
LFLF	4.1444	3.4600	3.7439	3.0155	YES
LGGI	4.1162	4.5400	3.7286	1.0338	YES
LGGL	4.0173	4.4800	3.6748	0.0546	YES
LIYP	6.4530	5.0000	4.9986	3.0108	YES
LKKA	6.3239	5.0700	4.9284	2.0180	YES
LLLF	5.0405	4.1000	4.2309	1.0239	YES
LLLP	5.2143	4.8000	4.3254	0.0287	YES
LNNP	5.7607	4.2400	4.6223	5.0081	YES
LQQW	7.0176	5.4200	5.3054	4.0128	YES
RPPP	5.3047	4.2200	4.3745	1.0338	YES
RPRP	3.3487	3.7400	3.3115	3.0419	YES
RRRR	6.8579	4.2300	5.2187	3.0600	YES
RWRW	5.2161	4.8000	4.3264	0.0513	YES
SGSG	2.0150	2.0700	2.5866	5.0099	YES
SYSY	4.9354	4.1800	4.1738	5.0054	YES
VAAA	5.8424	4.8900	4.6668	0.0573	YES
VAAF	5.2781	4.4500	4.3601	1.0498	YES
VGGP	4.7551	4.5800	4.0758	1.0298	YES
VIIY	6.9351	5.1200	5.2606	3.0104	YES
VLLY	6.1322	4.5100	4.8242	2.0164	YES
VVVF	5.9261	4.4500	4.7122	1.0386	YES
VYVY	5.5250	4.9200	4.4943	3.0128	YES

⁽*⁾ Applicability domain is defined by the statistical defect [40].

contains an example of the technical details of the model obtained with split 1 for the validation set (Equation (3)).

Peptides are quite a popular object of research, both in medical aspects [46,47] and in food chemistry [48]. The study discussed here is useful in both of these areas. The presented approach can also be applied to modeling arbitrary biological phenomena based on the behavior of peptides. Thus, the considered approach can be used for practical applications [33].

Table 3. Comparison of the statistical quality models for the ACE inhibitory activities of short-chain peptides.

Method	Determination Coefficient for Training or Calibration Set	Determination Coefficient for the Validation Set	Reference
Partial least-squares	0.61 for training set	0.40	[42]
Support vector machine	0.93 for training set	0.65	[42]
Monte Carlo method
Split #1	0.78 * for calibration set	0.76	This work
Split #2	0.79 for calibration set	0.79	-
Split #3	0.76 for calibration set	0.83	-
Split #4	0.83 for calibration set	0.81	-
Split #5	0.79 for calibration set	0.77	-

⁽*⁾ Average value over training and calibration sets (in the case of models obtained with the Monte Carlo method).

contains a comparison of the statistical quality of the suggested models with the statistical quality of analogic models from the literature. It has been shown that the predictive potential of the models obtained by the described approach is better than the statistical quality of the models described in the literature [42].

Carrying out several runs of the described optimization procedure makes it possible to determine the probabilistic mechanistic interpretation of the considered models.

Table 4. The lists of promoters for increase and decrease in ACE inhibitory activities of short-chain peptides.

A or FLS	CWs Probe 1	CWs Probe 2	CWs Probe 3	CWs Probe 4	CWs Probe 5	NA	NP	NC	Statistical Defect
Increase
[xyyx0].....	0.5362	0.7174	0.0494	0.1663	0.2945	59	58	63	0.0004
[xyx0]......	2.0153	1.9219	2.4935	2.1093	1.3410	44	49	48	0.0015
P...........	0.2332	0.2868	0.5592	0.3310	0.2543	23	27	20	0.0043
L...........	0.5570	0.3970	0.7452	0.3197	0.6662	15	18	20	0.0020
Y...........	0.8356	0.7732	1.0343	0.9938	0.7029	15	14	16	0.0005
V...........	0.7098	1.0258	1.2453	0.6531	0.2719	13	9	15	0.0037
I...........	0.8481	0.5378	0.9922	0.6733	0.5455	11	9	10	0.0021
F...........	0.1322	0.2310	0.2963	0.2405	0.1434	10	14	13	0.0036
K...........	0.3180	0.7672	1.0451	0.8752	0.1288	6	5	4	0.0051
G...G.......	0.6542	1.2557	0.7237	0.7341	0.6380	5	5	3	0.0058
W...........	0.9591	1.4843	1.7561	1.5675	1.1600	5	10	5	0.0090
A...A.......	1.1490	0.7535	0.6467	0.9423	0.8890	4	4	2	0.0072
P...A.......	1.0247	1.4088	1.6942	1.8574	1.1433	4	4	2	0.0072
R...........	0.6049	0.5535	0.6594	0.5883	0.2712	4	13	4	0.0145
Decrease
G...........	−0.6792	−0.7316	−0.4849	−0.6757	−0.3397	20	16	24	0.0028
[xyx2]......	−0.3288	−0.5771	−0.4390	−0.9101	−0.5755	19	13	22	0.0039
P...G.......	−0.0676	−0.4900	−0.1707	−0.1083	−0.3139	5	8	4	0.0085
L...G.......	−0.1497	−0.3795	−0.1461	−0.6752	−0.4425	4	1	1	0.0164
Y...Y.......	−0.7225	−0.4130	−0.6068	−0.6308	−0.6269	4	1	3	0.0118

presents the results of five runs of the Monte Carlo optimization procedure. It can be seen that the absence of fragments of local symmetry is favorable for increasing the studied endpoint. At the same time, the presence of [xyx2] is favorable for reducing the endpoint value. Some examples of the individual effects of amino acids and their combinations are also presented in Table 4. It is obvious, however, that for a constructive comparison of the features of the peptides under consideration, it is necessary to take into account the frequencies of their presence in the active and passive training sets, as well as in the calibration set. From this point of view, case Proline (P) is the most reliable, while case Arginine (R) is the least reliable.

Based on consideration of these data and assuming that they are true, one can attempt to design the activity of peptides that are not in the peptide inhibitory activity database used here. The following peptides (combinations of amino acids) are not in the database used: EGGY, YPYP, ALLG, PLLP, PLPG, LYLP, FYYF, YFYF, PGPF, and LFFL. Figure 2 shows the relative values of the inhibitory activity of these peptides.

Supplementary Materials (Tables S1–S5) contain the technical details of the described models for all splits considered.

4. Discussion

This study was planned as a means of testing the ability of local symmetry fragments to improve the predictive potential of models obtained based on optimal descriptors, which are the sum of the correlation weights of the codes forming quasi-SMILES. These quasi-SMILES are unusual in that they are built on the use of amino acids as independent, indivisible parts of the peptide structure. The fragments of local symmetry proposed here are very ambiguous since, on the one hand, they certainly exist as a special concrete phenomenon in the structure of peptides, and on the other hand, they are “almost” not related to traditional mathematical symmetry. The only more or less mathematical term that can be associated with fragments of local symmetry is equivalent positions. For example, for ‘xyx’, both ‘x’ are in equivalent positions, but only for a selected fragment of the peptide (the sequence of amino acids).

At the same time, three amino acids may turn out to be an information codon in DNA or RHA, e.g., AAA, AGA, and GGG are codons [49]. Therefore, considering triplets of amino acids as carriers of some topological symmetry may be a useful marker in the study of peptides, at least in the QSPR/QSAR aspects [49].

Regarding the mechanistic interpretation of the model, it should be noted that there are some logical inconsistencies between the data presented in Table 4 and the results of the virtual analysis presented in Figure 2. Firstly, according to Table 4, FLS of the type ‘xyyx0’ (but not ‘xyyx1’) should contribute to an increase in inhibitory activity. However, from Figure 2, it is clear that the highest values of the endpoint are observed for the case ‘xyyx1’ (PLLP, FYYF, and LFFL). Secondly, ‘xyx2’, according to Table 4, should help reduce inhibitory activity. However, according to Figure 2, this feature accompanies medium activity levels but not low ones. These inconsistencies can be resolved by using a larger database. In particular, it is quite promising to carry out similar computational experiments with peptides represented by chains of amino acids of various lengths.

However, the main goal is to assess the predictive potential of models based on Monte Carlo calculations. The main advantage of the Monte Carlo method is the use of randomness to solve problems that, in principle, may be more or less deterministic. Nowadays, computers easily supply randomness to the interested user through random variable generators [50,51,52,53,54,55,56,57,58,59,60]. The models considered are certainly largely random. The splitting of available peptides into training sets and validation sets is random. Modifications of correlation weights are random. The sequence of calls to correlation weights to modify them in the stochastic Monte Carlo process is random. However, an important result of this and other works is that there is reproducibility of the results, which consists of the obvious similarity of the determination coefficients for the calibration set and the validation set for all five random partitions considered. Last but not least, quasi-SMILES is a user-friendly language for formulating problems solved by a computer [61].

The approach used here obeys the OECD principles (defined endpoint; unambiguous algorithm; defined applicability domain; measure of predictive potential; mechanistic interpretation). Possible ways to improve the represented approach are as follows: 1. Extending the work set of peptides by taking into account the ones of different lengths. 2. Considering more diversity of fragments of local symmetry (‘xxyxx’, ‘xyyyx’, etc.). 3. Improving the algorithm of Monte Carlo optimization via the use of new statistical criteria [62]. In addition, quasi-SMILES can be a suitable representation for polymers [37] and nanomaterials [63].

5. Conclusions

The optimal descriptor calculated using quasi-SMILES (sequence of amino acids) by the Monte Carlo method using the Internet-available software “CORAL-2023” (http://www.insilico.eu/coral, accessed on 20 May 2024) can be a completely satisfactory basis for predicting the inhibitory activity of angiotensin-converting enzyme (ACE) peptides, expressed through pIC50 values. Recently proposed local symmetry fragments can be used to improve the predictive potential of the model by correlation weighting them through optimization, also carried out by the Monte Carlo method. The index of ideality of correlation and correlation intensity index one more had confirmed their suitability as a tool to improve the predictive potential of the model. The quasi-SMILES concept may have applications not only for structure-property/activity studies of peptides but also for other substances (such as copolymers and nanomaterials).