Next Article in Journal
The Expanding Threat of Crimean-Congo Haemorrhagic Fever Virus: Role of Migratory Birds and Climate Change as Drivers of Hyalomma spp. Dispersal in Europe
Previous Article in Journal
Bridging Continents: The Expansion and Establishment of the House Bunting (Emberiza sahari) from North Africa to Europe
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Birds
Volume 6
Issue 2
10.3390/birds6020030
birds-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Dynamics of Sex and Age Correlation of Eurasian Woodcock (Scolopax rusticola L.) During Spring Migration in Hungary

by
Attila Bende
1,*,
Sándor Faragó
1,
Richárd László
1,
Viktória Csanády
2,
István Fekete
3,
Tibor Pecsics
1 and
László Bozó
4
1
Institute of Wildlife Biology and Management, University of Sopron, Bajcsy-Zsilinszky út 4., 9400 Sopron, Hungary
2
Institute of Informatics and Mathematics, University of Sopron, Bajcsy-Zsilinszky út 4., 9400 Sopron, Hungary
3
Amity Institute of Psychology & Allied Sciences, Amity University Kolkata, Major Arterial Road, Action Area II, Rajarhat, New Town, Kolkata 700156, West Bengal, India
4
Department of Systematic Zoology and Ecology, ELTE Eötvös Loránd University, Pázmány Péter stny. 1/C., 1117 Budapest, Hungary
*
Author to whom correspondence should be addressed.
Birds 2025, 6(2), 30; https://doi.org/10.3390/birds6020030
Submission received: 30 April 2025 / Revised: 13 June 2025 / Accepted: 13 June 2025 / Published: 16 June 2025
Browse Figures
Versions Notes

Simple Summary

Our research provides detailed insights into the migratory patterns of the Eurasian Woodcock. By focusing on the dynamics of sex- and age-dependent migration of the species, our study adds valuable knowledge to understanding the ecological needs and conservation priorities for this species during critical periods of their annual life cycle. We used data of 24,167 individuals collected during spring migration in Central Europe, Hungary. This manuscript details statistical analyses and methodologies employed to discern variations in migration patterns, contributing to a broader understanding of avian ecology under the influence of climatic and geographical variables.

Abstract

Based on samples collected in the framework of the Eurasian Woodcock Bagging Program in Hungary between 2010 and 2019, we investigated the spring migration of Eurasian Woodcock by age class and sex. The dynamical properties of each year’s trajectory are represented using Gaussian smoothing. The models were used to determine the peak of the migration by sex and age in each year. In the comparative analysis by sex, an ARIMA regression model was used as a time-series analysis, which showed that there was a strong positive correlation between the migration of females and males in each year, which indicates that there is no statistically verifiable time difference in the migration pattern of each sex. We found a positive correlation in the same ARIMA model for each year of migration, which indicates that there is no statistically verifiable difference in the spring migration of males and females of the same age groups in Hungary. This study also demonstrates that there is a sharp ratio shift in the spring migration in favour of males. This significant imbalance can be explained by the selective hunting during spring roding, which is of particular importance for the sustainable utilisation of the species.

1. Introduction

With the exception of a few countries (e.g., Slovenia, the Netherlands, and the Czech Republic [1]) and geographical regions (Flanders (Belgium) and the Canary Islands (Spain) [2]) the Eurasian Woodcock is a huntable species throughout Europe [3,4], with a European population estimated at 13.8–17.4 million adults and considered stable [5,6]. In Hungary, only occasional breeding records of Eurasian Woodcock are known, so the size of the nesting population does not exceed a few tens of specimens per year [7,8,9]. In the Carpathian Basin, the species is found in larger numbers only during its spring and autumn migration. It has a wide frontal migration [10]; its main migration route is north of the Carpathian Basin [11]. The majority of birds arriving in Hungary winter in France, with a smaller proportion wintering in Italy [9,10,12], from where they move on to nesting areas in western Siberia [13,14,15,16,17], as confirmed by ringed specimens found in Hungary [10,18] and by data from birds equipped with transmitters [19]. It is possible that birds migrating through Hungary may also breed further east, as shown by the data from birds fitted with transmitters in Spain [20].
There is no precise data on the extent of utilisation at the European level. Based on known data, the bag of the species in the 2000s was around 2–4 million individuals [2]. According to recent data, including 50–60,000 specimens caught annually in European areas of Russia [21], the annual utilisation is estimated at 2.3–3.4 million specimens [22]. The majority of them come from a few Western European countries. The highest hunting utilisation is in France (1.2 million specimens per year) [23] and Greece (1 million specimens), which accounts for about 70% of the total European bag. In addition to these two countries, Italy and Portugal limit the annual quantity that can be bagged [2], as does Hungary, where a maximum of 5500 Eurasian Woodcocks can be bagged under quota [9].
Nowadays, Eurasian Woodcock hunting during spring roding has been almost completely side-lined, and the species is typically hunted during the autumn–winter season by dog tracking [3,22,23,24]. Traditional spring hunting is now only permitted in Russia [21] and Hungary [9]. As a consequence, little information is available on the age and sex ratios during spring migration [4,25,26,27,28]. It is known, however, that the winter survival of first-year birds is significantly lower than that of adults [29,30,31].
In many bird species, both sex-specific and age-specific migration are known [32,33,34,35]. In spring, protandric migration is usually the dominant pattern, i.e., males precede females [36,37,38,39,40,41,42]. Protandric migration is driven by the need to occupy territories of the highest quality [43] and to maximise mating success [44]. In the autumn, on the other hand, females very often leave earlier (protoginia), including wader species, such as the Ruff (Philomachus pugnax) [45]. One of the main reasons for this might be that males mark and occupy territories for the following year [33]. Age-dependent migration is also a feature of many species, but in this case the situation is not so obvious. There may be significant interspecific differences in the timing of migration of adults and juveniles in both spring and autumn [46,47]. Studies in NE Poland showed that the second-year individuals of Wood Sandpipers (Tringa glareola) migrated significantly later than adult birds [40]. Different migration strategies between specimens should also be considered, as has been shown in recent studies of the Black-tailed Godwit (Limosa limosa) [48] and the Whimbrels (Numenius phaeopus) [49].
The latest knowledge on the spring migration of Eurasian Woodcock in Hungary was summarised by [50]. Their work was based on the bagging data collected within the Hungarian Woodcock Bag Monitoring programme (1990–1999). The results on the age and sex ratios of the Eurasian Woodcock bags from 2000 to 2008 and 2010 to 2014 were published by [51,52,53,54,55,56,57,58]. These studies, however, focused only on the annual evolution of age and sex ratios, leaving the dynamics of sex- and age-specific migration unexplored. This is important, as if the departure of wintering areas occurs at different times, then there must be a temporal shift in the arrival of the sexes during the migration to the nesting area [9]. On the other hand, this is important in the case of the utilisation of the species, since the different arrivals of the sexes (possibly by sex and age) can also have an impact on the distribution of the bags; therefore, the timing of the migration also affects judgement of the spring hunting utilisation.
The sample collection module of the Woodcock Bag Monitoring programme started in 2010, which was initiated by the implementation of Article 4 (2) of the European Union Birds Directive (79/409 EEC) [59], as after this international convention was implemented in the Hungarian hunting regulations, no hunting season was established for Eurasian Woodcock in Hungary from 2009. However, the hunting of Eurasian Woodcock during the spring roding is an integral part of the Hungarian hunting culture [60], so Hungary has taken the opportunity to derogate from the Directive. As a result, a nationwide survey of the bags of this species was launched, coordinated by the Hungarian Hunters’ National Association. This large-sample, time-series study, in addition to revealing migratory patterns, will also contribute greatly to a better understanding of the extent to which and how hunting habits in different countries affect Eurasian Woodcock populations. Although estimates suggest that European populations of the species are stable [5], hunting is the most significant threat to the species, in addition to weather extremes [61], and the knowledge gained from examining the bagging data collected during the autumn/winter and spring hunting seasons can greatly contribute to meeting the requirements of international conventions on hunting sustainability in the utilisation of the species.
In the present study, we used the ARIMA model, which is suitable for analysing and evaluating age- and sex-specific features of migration dynamics. The following hypotheses were formulated: (I) Our aim was to investigate whether there is any difference regarding age group and sex on the spring migration route in order to reveal the possible timing differences between age groups of each sex during spring migration. (II) We examined the sex distribution of the bags in order to assess the impact of the utilisation during spring migration on the Eurasian Woodcock population. Whether there is any difference an important question; it can be a result of the different migration timings of the different age groups (adult and juvenile) by sex or due to the fact that females and males are bagged with different probabilities during spring spot hunts. Therefore, it emerges from the selectivity by sex of the hunting method.

2. Materials and Methods

2.1. Hungarian Woodcock Bag Monitoring Programme

Our work was based on data from the spring monitoring of Eurasian Woodcocks (n = 24,167 specimens) collected between 2010 and 2019 (Table 1). During the monitoring, hunting permit holders participated in the data collection each year, with more than 800 sampling points. Countrywide, up to 5500 Eurasian Woodcocks per year (mean = 2417 SD = 546.8) could be bagged by the data providers under a quota system. During the sampling, the place where the birds were bagged (municipality, gamekeeper), the exact time of sampling (month, day) and the sex of the birds were recorded. For age determination purposes, all data providers were required to send in at least 25%, and from 2011 onwards 40%, of one of the wings of the Eurasian Woodcocks they had killed, stretched at 130 degrees and prepared. Age determination was carried out at the Institute of Wildlife Biology and Management of the University of Sopron. Age determination was performed according to the conventional ornithological methods, i.e., age determination was based on the state and degree of moulting and the characteristic marks of each feather group, moulted or unmoulted [13,14,50,62,63,64]. During the monitoring we determined the age of 16,907 individuals in total. Sex determination was performed using a destructive method. Data providers recorded sex (n = 23,882 individuals) based on the gonads of birds bagged after capture. Since the Eurasian Woodcocks are already preparing for the mating period in March, the sexes can be distinguished based on the hyperplasia of the testes and the small-sized ovaries that include developing follicles [65].

2.2. Statistical Analysis

For the statistical analysis, we processed annual bagging data recorded in the sampling periods between 1 March and 10 April (41 days) between 2010 and 2019. The sample size required for statistical representativeness was determined using the Cochran formula [66] for an annual migratory bird population of at least 1.5 million individuals. The approximate minimum of 1.5 million individuals for the annual migratory bird population under study helps determine the total population size (N). In this regard, our calculations reinforce that the sampling strategy achieves representative results despite the generalisation derived from sampling error. A confidence interval (CI) of 99% and margin of error (E) of 3% were selected in order to achieve precision and accuracy in estimating population metrics. A stringent CI of 99% was chosen to minimise the chances of committing a Type I error, especially in an ecological and conservational context. A margin of error of 3% was deemed reasonable in measuring significant population change while still maintaining a realistic sample size. Utilising these conditions within Cochran’s formula provides a reliable minimum sample size while ensuring logistical practicality. A Z-score of 2.576 was used with the 99% CI for this study, which represents a very strict criterion meant to reduce Type I error risk in population estimation. The estimated proportion (p) was set to 0.5, which is standard practice. This approach maximises the product of p and q (where q = 1 − p), thereby providing the largest possible sample size. Adopting this approach guarantees that the resulting sample size will be more than adequate for providing reliable, robust, and generalizable estimates, even in high-variability conditions. This approach resulted in a sample size estimated at approximately 1844 specimens per year, which is considered to be a sufficient number of samples for statistical representativeness. Hence, statistical representativeness was met in each of the years of the ten-year period we examined.
Edited Gaussian smoothing was performed to represent the spring migration process by plotting a set of coordinates for each sampling day, matched to the characteristics of the point set of the catch numbers per sex and age. The criteria for the smoothing used were as follows: boundedness, the existence of one or more extreme values, and differentiability. These requirements were met by a linear combination of two Gaussian functions:
y = b 6 e b 5 x − b 4 2 + b 3 e b 2 x − b 1 2 + b 0
The model is characterised by seven parameters—different stretching and offsets—which ensure sufficient flexibility of the function, so that a model with appropriate fitting accuracy to the asymmetry of the data series is created.
The initial values of model (a) are determined from the values of the data series as follows:
  • b6 = var2 first max. − var2min. or b6 = var2first min. − var2max.
  • b3 = var2 sec. max. − var2min. or b3 = var2 sec. min. − var2 max.
  • b4 = var1 first max. or var1 first min.
  • b1 = var1 sec. max. or var1 sec. min.
  • b0 = var2min.
  • b5 = b2~0.05
The initial values of the model can be determined from the values of the test data set as indicated above, based on the interval boundaries of the independent (var1) and dependent (var2) variables, and the maximum and minimum values of the dependent variable within the point set and their locations [67,68]. The coordinates of the extreme values were determined using WinPlot 10.7 [69]. Gaussian smoothing was created in Statistica 13.0 [70]. Spearman’s rank correlation was used to test whether there was a significant temporal shift in the spring migration by age within each sex. Further statistical analyses were conducted in R-Studio [71].
To verify our first hypothesis (I.), the count of individuals, i.e., the dependent variable, was first log-transformed because of skewness occurring between the sexes. Then, the variables “Year”, “Month”, and “Day” were merged to create a single time-series variable. We also observed significant imbalance in the two independent variables, “Proportion of sex” (hen and cock) and “Proportion of age” (adult and juvenile). Handling imbalances was performed by replacing missing values in the variables mentioned above with the median values. The ARIMA (1, 0, 1) default model was fitted with “Sex”, “Age”, and their interaction as exogenous variables. The key results can be seen in Table 3 below in Section 3.
Subsequently, we performed an Augmented Dickey–Fuller (ADF) test on the log-transformed dependent variable with the following critical values: 1% level: −3.45, 5% level: −2.87, 10% level: −2.57. Mean Absolute Error (MAE) and the Root Mean Squared Error (RMSE) were also computed. MAE, which is less sensitive to outliers, is the average of the absolute differences between the predicted and actual values, providing a measure of the average magnitude of the errors without considering their direction. Similarly to MAE, RMSE is the square root of the average of the squared differences between the predicted and actual values. RMSE penalises larger errors more heavily, making it more sensitive to outliers and particularly useful in case of large errors.
We ran an ARIMA time-series model, with the constant representing the baseline level of the log-transformed dependent variable of “Count_of_Individuals”, when all other variables are zero. Two more terms were in the model. (i) The autoregressive coefficient reflects the impact of the previous period’s value of the dependent variable on the given period. (ii) The moving average coefficient term reflects the impact of the lagged forecast errors on the current value. Sigma2 represents the variance of the residuals or the model’s error term. Consequently, a higher value indicates more variability in the model’s predictions.
We employed the Ljung–Box Test to assess autocorrelation in the residuals. To check the normality of residuals, we used a Q-Q plot to visually assess the normality of the residuals. Additionally, the Jarque–Bera Test was used to evaluate if the residuals followed a normal distribution. In the case of homoscedasticity, if plots of residuals vs. fitted values show no clear pattern, this indicates homoscedasticity (constant variance). The Breusch–Pagan Test was used to test heteroscedasticity in the residuals. The AIC (Akaike Information Criterion) and BIC (Bayesian Information Criterion) were employed to assess model fit.
Regarding forecasting accuracy, the model’s fit was assessed using in-sample residuals. MAE, RMSE, and Mean Absolute Percentage Error (MAPE) were assessed. These values indicate that the model’s errors are small or large. A holdout sample was used to validate the model’s forecasting ability. The RMSE for out-of-sample data was calculated.
The CUSUM and CUSUM of Squares tests were applied to check for structural stability of the model coefficients over time. A Variance Inflation Factor (VIF) analysis was performed for the independent variables with a very strict threshold of 5 for VIF. Overall, the ARIMA (1, 0, 1) model is suitable for time-series forecasting of the log-transformed count of individuals.
As earlier mentioned, there is a conspicuously strong imbalance between females and males in the variable “Sex”. Hence, to show the imbalance between females and males for every year, we performed binomial tests. Since there are multiple years and, consequently, multiple comparisons, we employed the binomial tests with the Benjamini–Hochberg correction for multiple comparisons to control the false discovery rate (FDR). This test will compare the observed proportions of females and males to an expected proportion of 50%, which represents a balanced population. If the p-value is significant, it indicates a significant imbalance in the given year.

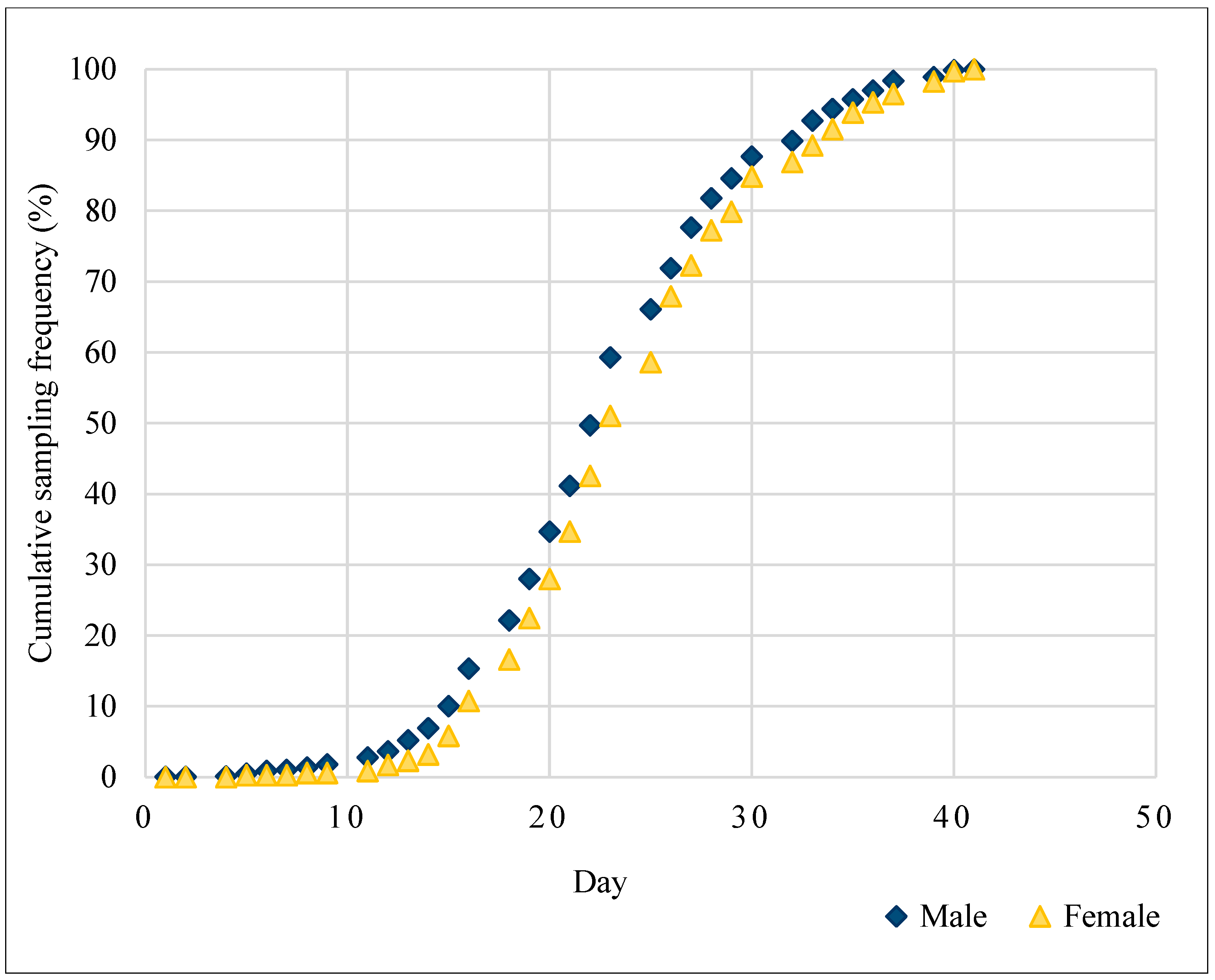
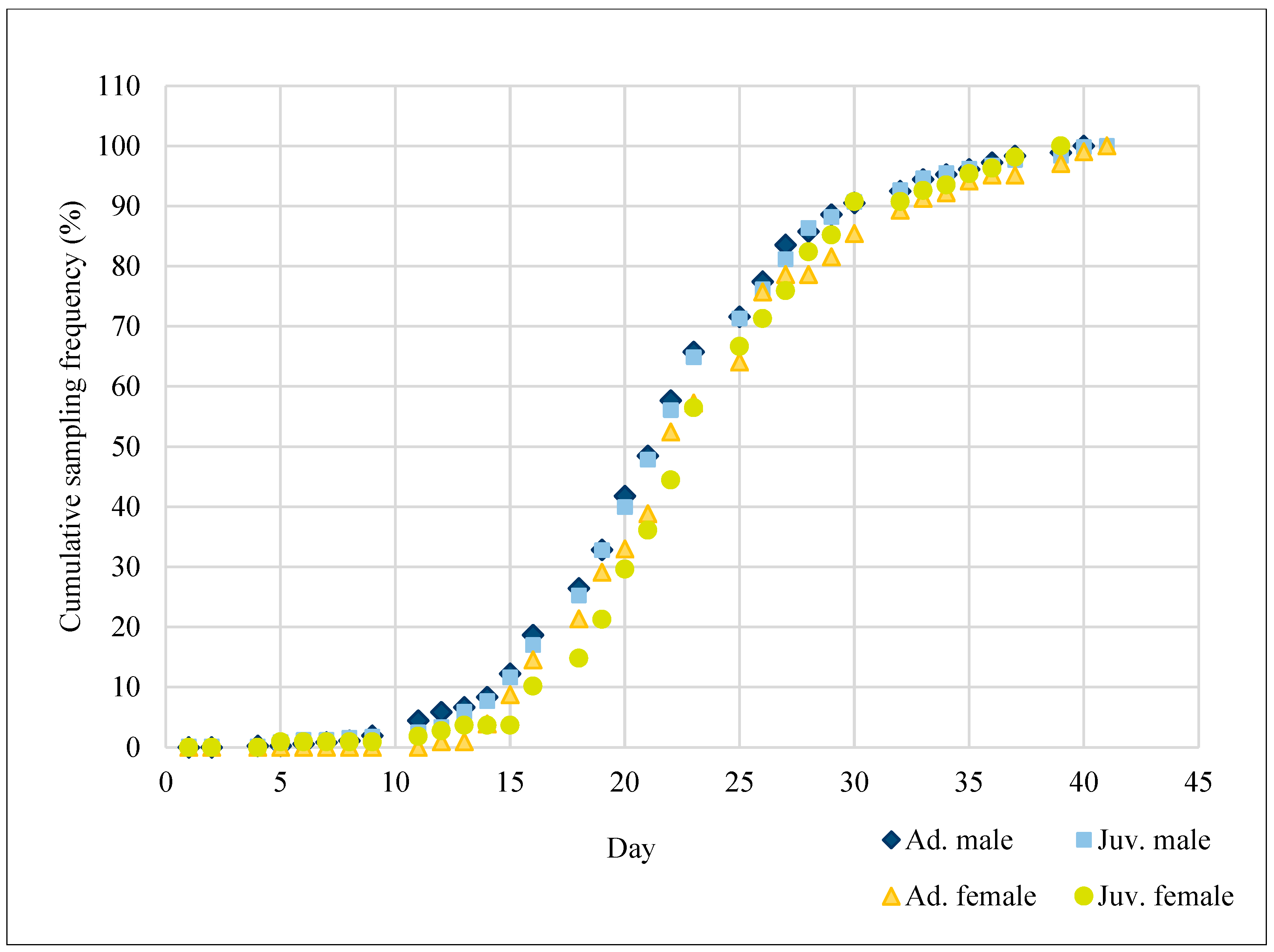
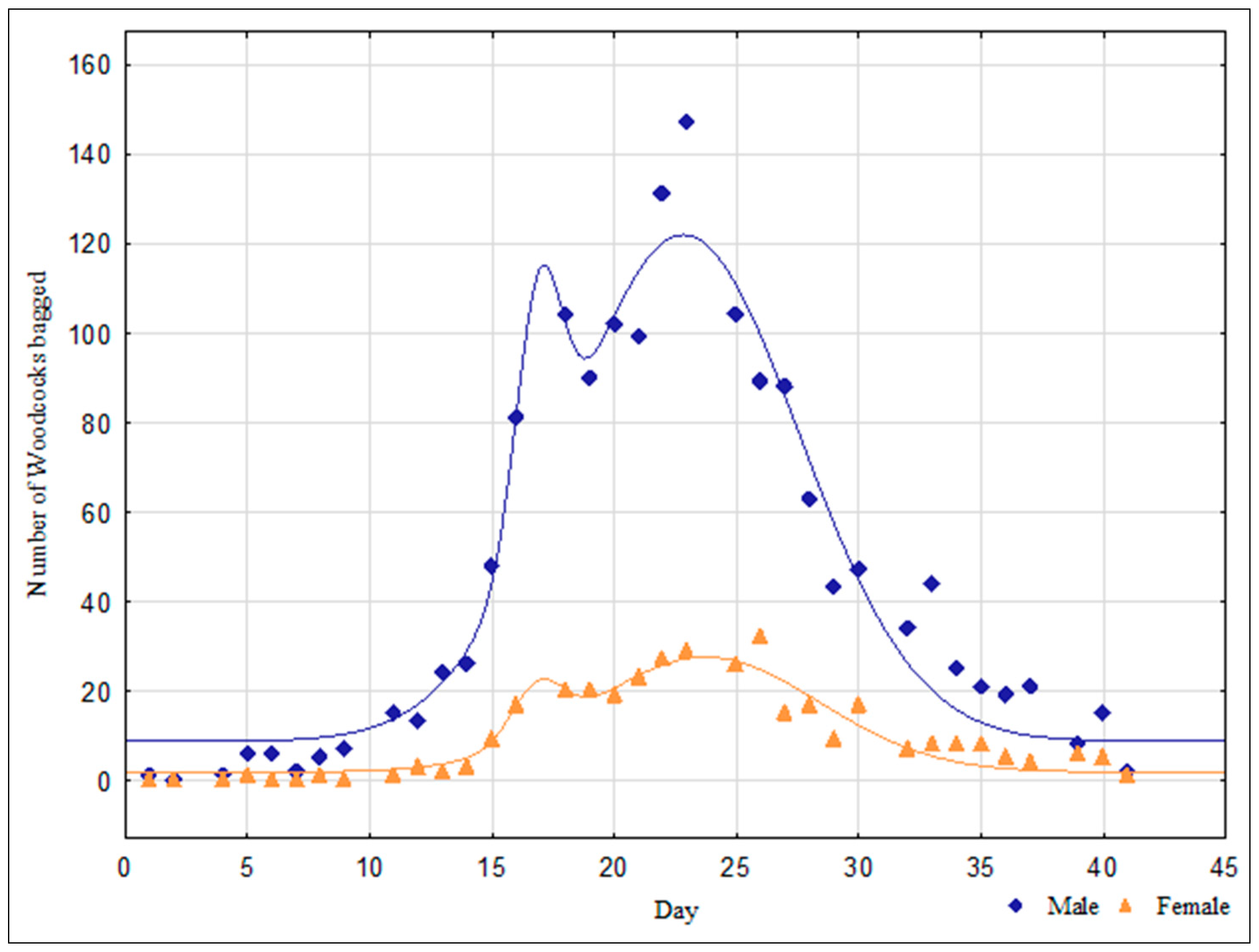
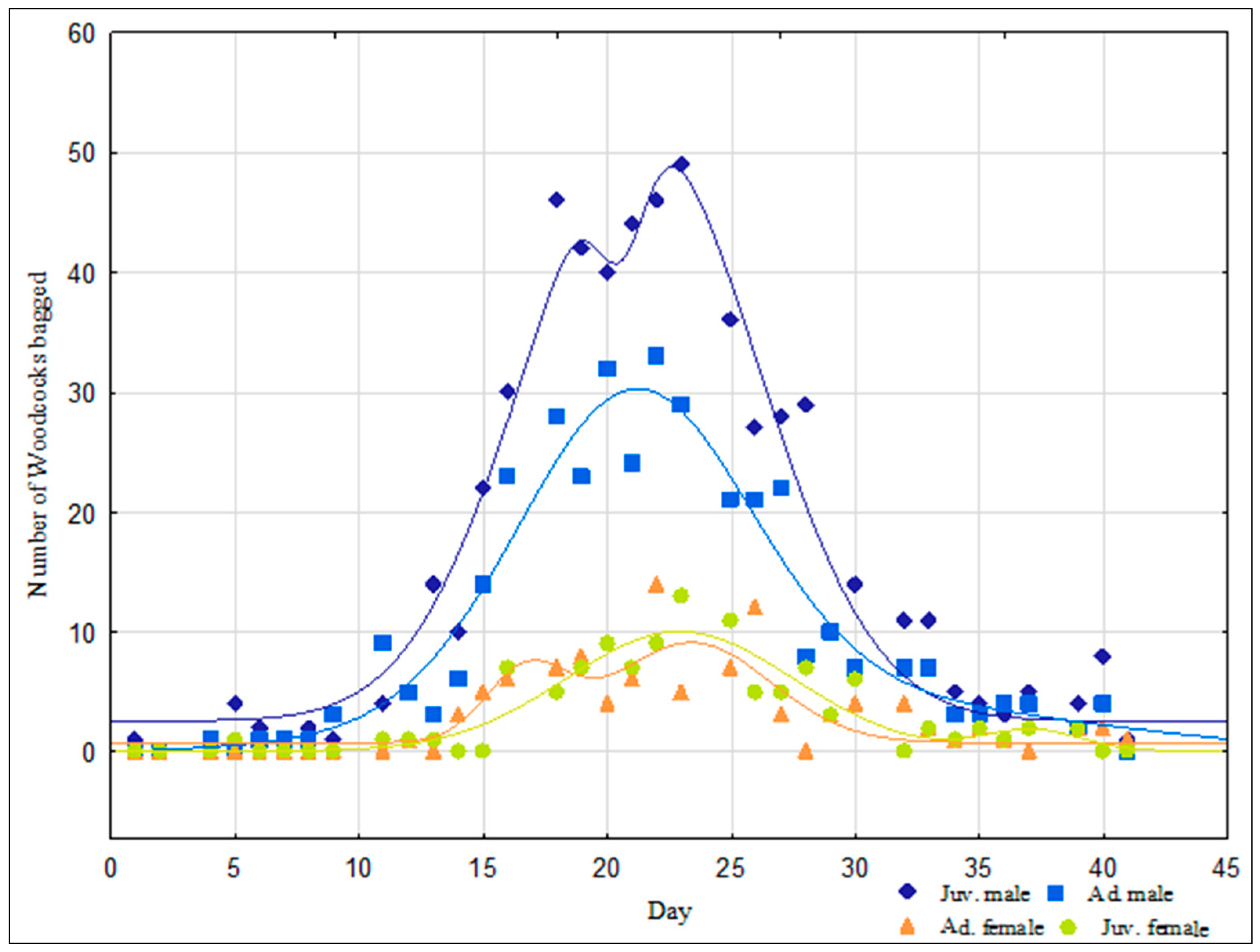
3. Results

In the sample collected during 10 years of sampling in Hungary, there is no statistically verifiable temporal shift in the spring migration. We present the modelled migration characteristics of spring migration by sex using data from 2012 (n = 1925 specimens). The point sets of cumulative sampling frequencies of males and females follow each other closely (Figure 1), and it was assumed that there is no difference in the course of the temporal pattern between different sexes.
No temporal shifts were observed in the spring migration dynamics of males and females in Hungary, illustrated by the example of the year 2012. The time of sampling and the closely co-moving point set of cumulative sampling frequencies plotted using sex and age data also show no temporal variation (Figure 2).
In the case of the Gaussian function, which provides a double representation of the temporal variation in the number of Eurasian Woodcocks during spring migration, it can be seen that despite the significant shift in the proportions between the sexes, there is no difference in the temporal course of the process (Figure 3). The model peak dates of the migration data series by sex fell on sampling days 18 and 23 for males and on days 17 and 24 for females. For both sexes, the model follows the same pattern, with a small decline after the first local maximum, followed by an increase until the absolute peak of migration, followed by a declining phase indicating the end of migration. In terms of proportions, the sampling dynamics for females closely reflect the trends of the overall migratory flock.
We also modelled the spring migration pattern by age and sex, also using Gaussian functions (Table 2). There was a difference of only two days between the absolute maximum of the functions modelling the migration of males with a higher number of samples in both ages (ad. ♂: 370 individuals; juv. ♂: 573 individuals) (ad. ♂: sampling day 21, juv. ♂: sampling day 19). According to the models of spring migration of females, the absolute maximum for both adult (105 individuals) and juvenile (112 individuals) ages was on sampling day 23, so there was no difference in the peak of migration between the female ages (Figure 4).
To test the first hypothesis, where we investigated whether the process of migration is influenced by the age and sex of the birds, we performed ARIMA time-series analysis on the log-transformed dependent variable. The results of the corresponding ADF test were as follows: ADF statistic: −6.51, p < 0.001. The ADF statistic (−6.51) is lower (more negative) than all the critical values at the level of 1%, indicating that the model’s assumptions about stationarity are satisfied. This indicates that the log-transformed series is stationary, making it suitable for time-series modelling without the need for additional differencing.
The analysis revealed that the variables proportion of female and male and proportion of adult and juvenile do not have statistically significant effects on the log of count of individuals, nor does the interaction term. MAE yielded a value of 1.05, with the RMSE being 1.17. The small difference between MAE and RMSE values indicates that the model does not contain large outliers or extremely high errors.
We now report on the results of the ARIMA model (see Table 3).
The variables “Proportion of sex” and “Proportion of age” and their interaction do not significantly affect the dependent variable. With a Z-value of 9.91 (p < 0.001) for the constant, this coefficient is statistically significant, indicating that the constant is significantly different from zero. The coefficient belonging to the variable “Proportion_hen_cock” (0.0229) indicates that for each one-unit increase in the Proportion_hen_cock, the log-transformed dependent variable is expected to increase by 0.0229 units, holding all other variables constant. The Z-value (0.11) and p-value (0.9119) show that proportion of sex is not statistically significant, indicating no impact on the dependent variable. Proportion_adult and juvenile yielded a value of 0.1087, showing that for each one-unit increase in proportion of age, the log-transformed dependent variable is expected to increase by 0.1087 units, holding all else constant. The Z-value (1.68) and p-value (0.0925) suggest that adult and juvenile proportion is not significant.
Importantly, an AR(1) coefficient of 0.8849 indicates a strong positive relationship between the previous values of Log_Count_of_Individuals and the current values. The Z-value (23.52) and p-value (p < 0.001) indicate that this term is significant, suggesting that the dependent variable is highly influenced by its own past values. Also, crucially, the Ma.L1 term is −0.4025, indicating that the moving average term reflects the impact of the lagged forecast errors on the current values.
A negative coefficient suggests that past forecast errors negatively influence the current period. With a Z-value of −6.43 (MA1) and a p-value less than 0.001, this term is also highly significant, demonstrating that the forecast errors are an important part of explaining the fluctuations in the dependent variable. Not surprisingly, the sigma2 yielded a value of 0.8846, as the dependent variable fluctuates significantly in magnitude and the independent variables are not significant. Hence, a residual variance of 0.8846 might be reasonable. Consistent with this result, the Z-value (10.57) and p-value (p < 0.001) suggest that the residual variance is significantly different from zero.
The autoregressive term (Ar.L1) is the strongest predictor, indicating that past values of the dependent variable are highly influential. Both the moving average term (Ma.L1) and the constant are significant, showing that past forecast errors and the baseline values are important in predicting the dependent variable. In sum, the time-series components (i.e., past values and forecast errors) play a major role in explaining variations in the count of individuals, while the proportion variables do not have one.
The Ljung–Box Test assessed autocorrelation in the residuals and indicated no significant autocorrelation in residuals (p > 0.05). A Q-Q plot was generated to visually assess the normality of the residuals. Additionally, the Jarque–Bera Test confirmed that the residuals follow a normal distribution (p > 0.05). Plots of residuals vs. fitted values show no clear pattern, indicating homoscedasticity (constant variance). The Breusch–Pagan Test confirmed no significant heteroscedasticity in the residuals (p > 0.05). The AIC was 1051.87, while the BIC yielded a value of 1063.01, supporting the adequacy of the model specification.
MAE was 1.07, while RMSE yielded a value of 1.19. MAPE yielded 6.89%. These values indicate that the model’s errors are small, reflecting a good model fit. A holdout sample was used to validate the model’s forecasting ability. The RMSE for out-of-sample data was 1.23, which is only slightly higher than the in-sample RMSE, indicating good forecasting performance.
The CUSUM and CUSUM of Squares tests were applied to check for structural stability of the model coefficients over time (p > 0.05). Both tests showed that the model parameters remained stable throughout the analysis period (p > 0.05), indicating no significant structural breaks. The VIF values for proportion of female and male (1.03), “Proportion_adult and juvenile” (1.06), and their interaction (1.02) indicated no multicollinearity (Table 3).
The strongest predictor of the dependent variable is its own past value (AR(1)), and the forecast errors (MA(1)) play a significant role in explaining the fluctuations. The AR(1) and MA(1) terms remain the most influential predictors, while the variables “Proportion_hen_cock” and proportion of adult and juvenile, both individually and in interaction, have no effects on the log-transformed count of individuals.
The assumptions of the model have been tested for residual autocorrelation, normality, and stability. The model’s in-sample and out-of-sample performance is strong, with low forecast error values. The model diagnostics confirm that all assumptions of the ARIMA model are met, and the forecasting accuracy remains consistent. Therefore, the interaction term does not offer any added value in this specific time-series model, i.e., hypothesis (I.), that neither sex nor age affect the temporal variation in the number of migrating birds, is confirmed.
Our second hypothesis, that spring hunting is selective intensively for the male, has already been shown clearly in the Gaussian models. The results from the binomial tests with the Benjamini–Hochberg corrected p-values are highly significant for each year (both before and after correction), confirming that the proportion of males is significantly higher than the expected 50% across all investigated years. The average proportion of males over the sampling period from 2010 to 2019 was 82.7% (Figure 5).

4. Discussion

Our study confirms the hypothesis that there are no statistically verifiable differences in the spring migration of Eurasian Woodcock between females and males, or between age groups of females and males.
Protandrous spring migration is typical of many bird species, including several shorebirds [72,73]. However, some species do not exhibit differential migration, as reflected not only in the timing of migration but also in the different migration distances of males and females, and some species may exhibit spring protandry or even protogynia [74,75,76,77]. Among the close relatives of the Eurasian Woodcock, research has also confirmed the presence of spring protandry in the common snipe (Gallinago gallinago) [78] and Wilson’s snipe (G. delicata) [79].
According to [80], the first-year Eurasian Woodcocks have a close one-to-one breeding ratio, and significant sex ratio deviations from this value are rare in natural conditions. The significant shift in breeding in favour of males in Hungarian spring bags can be explained by the selectivity of hunting during roding [9,50,53,54,55,56,57,58,81,82,83,84,85,86,87,88,89,90,91,92,93], but so far, we have no data on whether there is a statistically verifiable difference in the migration patterns of females and males during spring migration. Studies in Spain revealed that the effect of hunting was the main reason for winter death, and it affected the first-year birds more than adults [31]. Our results indicate that there is no statistically verifiable difference in the timing of spring migration of each sex. Based on the above, the time and method of hunting result in a significant shift in ratio regarding the different moving patterns between the sexes, which means the short 20–30 min interval of the dawn and dusk movements during hunting. [94].
The temporal development of the age and sex characterising the spring migration of the Eurasian Woodcock is also a poorly researched topic, and only a few studies discuss the characteristics of the autumn migration. In Denmark, there is a confirmed temporal difference in the autumn migration of Eurasian Woodcock by sex and age, with young females starting the migration in October–November, followed by young males and finally old birds [4]. This result also confirms the results of Danish [27] and French studies [95,96] carried out between 1969 and 1971, which showed that females arrive earlier at their wintering grounds. It is assumed that males try to stay as close as possible to breeding territories in autumn and winter, so that their early arrival and territory occupation helps their reproductive success [4,27,28]. This latter pattern of behaviour was demonstrated in the American Eurasian Woodcock (Scolopax minor) [25]. According to [97,98], males typically only engage in reproduction from the second year of life. In this case, it would be logical for adult males to leave for their breeding grounds earlier in the spring, so that they would predominate in the breeding territories at the start of migration. However, our results do not support an earlier start of the spring migration of adult males, as in this case there would be a time-series verifiable phase lag between the migration patterns of different age classes of males. According to [99], however, males are already involved in reproduction in their first year. This assumption is supported by our results. Although several authors [14,100,101] report aggressive reactions to vocalisations observed during roding, territorial behaviour has not been confirmed in case of the Eurasian Woodcock [99,102,103]. Otherwise, there would be an advantage for adult males to reach the nesting area earlier, but the timing of the two sexes and the spring migration of the males’ ages did not differ.
When evaluating migration, it is also important to consider the fact that hunting and sample collecting can also cause age and sex differences. Ref. [104] also drew attention to the fact that in Denmark there is a difference of about 10% in the share of young birds in favour of hunting with dogs (61%) compared to other hunting methods (52%). Hunting during spring roding is known to be sex-selective [9,59,81,82,83,84]. However, in addition to the shift in proportions caused by sampling, the models describing sampling dynamics should also indicate a temporal shift if migration was different between sexes and ages. Examining the sex distribution of Eurasian Woodcocks from France [105,106,107,108,109,110,111,112,113,114,115,116,117,118,119] bagged between 2001 and 2015, the average ratio of males to females was found to be 1:1.56. In the most closely related species, the American Woodcock (Scolopax minor), females also predominate in the bags (58.8–53.8%) [26,120,121,122]. According to the hypothesis of [95], the hunting mortality of females is higher in autumn because they arrive earlier from the breeding grounds and thus are under greater hunting pressure in the wintering grounds, but the significant increase in the number of females between seasons is due to the different selectivity of the hunting methods. The selectivity of drive and dog-hunting for females is a known fact, as is the marked shift in spring bags towards males [9,60]. In addition to climatic extremes, hunting utilisation has a significant impact on the species’ populations. In two hunting areas in Spain, where the number of days of hunting per week was 50% longer, the chances of bird survival decreased by 10% [123]. Autumn–winter hunting, with its higher female numbers, remains popular among European hunters [2,3]; it is not unimportant to integrate the impact of hunting on population sizes into national species management plans by taking into account the size of the hunting bags [124], in order to better meet the standards defined by the African-Eurasian Waterbird Agreement (AEWA) and the European Union Birds Directive, and the sustainability criteria for hunting utilisation.
In relation to the limits of our research, it is important to note that we were only able to research a narrow period (1 March–10 April) each year, in order to comply with the EU Convention on the Conservation of Birds [59]. Accordingly, it was not possible to collect samples directly from the beginning to the end of migration. However, the findings from this data provide a valuable contribution to a better understanding of the spring migration, which can be used as a basis for species management plans in connection with hunting opportunities for this species in Europe. A more detailed (direct) method than our bagging analyses, i.e., the examination of birds fitted with transmitters, could provide further opportunities.

Author Contributions

Conceptualization, A.B., I.F., L.B. and R.L.; methodology, I.F. and V.C.; software and validation, A.B., I.F. and L.B.; formal analysis I.F. and V.C.; investigation, funding, and data curation, A.B., R.L. and T.P.; writing—original draft preparation, A.B., L.B., I.F., R.L. and T.P.; writing—review and editing, A.B., L.B., I.F., R.L. and T.P.; visualisation, I.F. and A.B.; supervision S.F.; project administration A.B.; funding acquisition, A.B. and S.F. All authors have read and agreed to the published version of the manuscript.

Funding

Project no. RH-75-1-39/2024 has been implemented with the support provided by the Ministry of Culture and Innovation of Hungary from the National Research, Development and Innovation Fund, financed under the EKÖP-24-4-II-SOE-25 funding scheme.

Institutional Review Board Statement

Ethical review and approval were waived for this study, because the monitoring permit was not issued to the research centre (Institute of Wildlife Biology and Management), but to the hunting permit holders who voluntarily agreed to participate in the national monitoring programme and to provide the data required by the monitoring contracts. Each data provider was contracted separately by the Hungarian Hunters’ National Association. Our institute was responsible for the formulation of the data collection methodology, data processing, age estimation, and publication of the results. The monitoring programme was coordinated by the Ministry of Agriculture and the Hungarian Hunters’ National Association. During the period between 2010 and 2019, the hunting of woodcock was only allowed for participants who fulfilled the obligation to sample each bird according to strict regulations (fixed sampling location and adherence to the quota system). The primary objective of the sampling was to assess the sex and age structure of the population, evaluate trends, describe migration characteristics, and evaluate biometric features. The status of the woodcock in Hungary did not change in 2009 and after the enforcement of 79/409/EEC also has not changed, and the species has been and still is considered as a game bird.

Data Availability Statement

All data are available directly by request from the corresponding author.

Acknowledgments

The evaluation of the migration dynamics of the Eurasian Woodcock was made possible by a monitoring programme coordinated by the Hungarian Hunters’ National Association. Special thanks are due to the hunters who, in addition to collecting the shooting data, also helped the Hungarian Woodcock Bag Monitoring by sending in the wing samples necessary for age determination.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Dvořák, J.; Plhal, R.; Kamler, J.; Drimaj, J. Game Management; Department of Forest Protection and Wildlife Management, Faculty of Forestry and Wood Technology, Mendel University: Brno, Czech Republic, 2014. [Google Scholar]
  2. Ferrand, Y.; Gossmann, F. Elements for a woodcock (Scolopax rusticola) management plan. Game Wildl. Sci. 2001, 18, 115–139. [Google Scholar]
  3. Hirschfeld, A.; Heyd, A. Mortality of migratory birds caused by hunting in Europe: Bag statistics and proposals for the conservation of birds and animal welfare. Berichte Vogelschutz 2005, 42, 47–74. [Google Scholar]
  4. Christensen, T.K.; Fox, A.D.; Sunde, P.; Hounisen, P.J.; Andersen, L.W. Seasonal variation in the sex and age composition of the Woodcock bag in Denmark. Eur. J. Wildl. Res. 2017, 63, 52–61. [Google Scholar] [CrossRef]
  5. Keller, V.; Herrando, S.; Voríšek, P.; Franch, M.; Kipson, M.; Milanesi, P.; Martí, D.; Anton, M.; Klvanová, A.; Kalyakin, M.V.; et al. European Breeding Bird Atlas 2. Distribution, Abundance and Change; European Bird Census Council & Lynx Edicions: Barcelona, Spain, 2020. [Google Scholar]
  6. BirdLife International. Species factsheet: Eurasian Woodcock Scolopax rusticola. Available online: https://datazone.birdlife.org/species/factsheet/eurasian-woodcock-scolopax-rusticola (accessed on 6 June 2025).
  7. Hadarics, T.; Zalai, T. Magyarország Madarainak Névjegyzéke—Nomenclator Avium Hungariae—An Annotated List of the Birds of Hungary; MME, BirdLife International: Budapest, Hungary, 2008; p. 118. [Google Scholar]
  8. Bende, A.; László, R. Woodcock (Scolopax rusticola L.) nesting in Hungary from the second half of the 19th century to the present day. Ornis Hung. 2020, 28, 92–103. [Google Scholar] [CrossRef]
  9. Bende, A. Spring migration dynamics, age and sex ratio, and breeding biology of the Woodcock (Scolopax rusticola L.) in Hungary. Ph.D. Thesis, University of Sopron, Sopron, Hungary, 2021. [Google Scholar]
  10. Faragó, S. Erdei szalonka. In Magyar Madárvonulási Atlasz; Csörgő, T., Karcza, Z., Halmos, G., Magyar, G., Gyurácz, J., Szép, T., Bankovics, A., Schmidt, A., Schmidt, E., Eds.; Kossuth Kiadó Zrt.: Budapest, Hungary, 2009; pp. 304–305. [Google Scholar]
  11. Le Rest, K.; Hoodless, A.; Heward, C.; Cazenave, J.L.; Ferrand, Y. Effect of weather conditions on the spring migration of Eurasian Woodcock and consequences for breeding. Ibis 2019, 161, 559–572. [Google Scholar] [CrossRef]
  12. Faragó, S. A vadászható vízivadfajok magyarországi vonulása jelölt madarak megkerülése alapján. Hung. Waterfowl Publ. 2000, 6, 337–375. [Google Scholar]
  13. Cramp, S.; Simmons, K.E.L. Handbook of the Birds of Europe, the Middle East and North Africa; Oxford University Press: Oxford, UK, 1983; Volume 3, pp. 444–457. [Google Scholar]
  14. Glutz von Blotzheim, U.N. Handbuch der Vögel Mitteleuropas; Band 7. Charadriiformes; AULA: Wiesbaden, Germany, 1986; pp. 121–174. [Google Scholar]
  15. Hagemejer, W.; Blair, M. The EBCC Atlas of European Breeding Birds: Their Distribution and Abundance; Poyser: London, UK, 1997. [Google Scholar]
  16. Van Gils, J.; Wiersma, P.; Kirwan, G.M. Eurasian Woodcock (Scolopax rusticola), version 1.0. In Birds of the World; del Hoyo, J., Elliott, A., Sargatal, J., Christie, D.A., de Juana, E., Eds.; Cornell Lab of Ornithology: Ithaka, NY, USA, 2020. [Google Scholar]
  17. Spina, F.; Baillie, S.R.; Bairlein, F.; Fiedler, W.; Thorup, K.; The Eurasian African Bird Migration Atlas. EURING/CMS. Available online: https://migrationatlas.org (accessed on 3 April 2025).
  18. Schally, G. Woodcock ringing in Hungary between 1913 and 2014. WI-WSSG Newsl. 2015, 41, 33–36. [Google Scholar]
  19. Schally, G.; Csányi, S.; Palatitz, P. Spring migration phenology of Eurasian Woodcocks tagged with GPS-Argos transmitters in Central Europe. Ornis Fenn. 2022, 99, 104–116. [Google Scholar] [CrossRef]
  20. Arizaga, J.; Crespo, A.; Telletxea, I.; Ibáñez, R.; Díez, F.; Tobar, J.; Minondo, M.; Ibarrola, Z.; Fuente, J.; Pérez, J. Solar/Argos PTTs contradict ring-recovery analyses: Woodcocks wintering in Spain are found to breed further east than previously stated. J. Ornithol. 2014, 156, 515–523. [Google Scholar] [CrossRef]
  21. Blokhin, Y.; Solokha, A.; Gorokhowsky, K.; Mezhnev, A.; Fokin, S. Hunting bags of Woodcock, snipes and other waders in Russia. WI-WSSG Newsl. 2015, 41, 13–18. [Google Scholar]
  22. Lutz, M.; Jensen, F.P. Draft European Union management Plan for Woodcock Scolopax rusticola 2006–2009; European Commission (DG ENV B2): Brussels, Belgium, 2005. [Google Scholar]
  23. Ferrand, Y.; Gossmann, F.; Bastat, C.; Guénézan, M. Monitoring of the wintering and breeding woodcock population in France. Rev. Catalana d’Ornitologia 2008, 24, 44–52. [Google Scholar]
  24. Ferrand, Y.; Gossmann, F. La bécasse des Bois; Effet de lisiére: Saint-Lucien, France, 2009. [Google Scholar]
  25. Sheldon, W.G. The Book of the American Woodcock; The University of Massachusetts Press: Amherst, MA, USA, 1967. [Google Scholar]
  26. Glasgow, L.L. Contributions to the Knowledge of the Ecology of the American Woodcock, Philohela Minor, on the Wintering Range in Louisiana. Ph.D. Thesis, Texas A&M, College Station, TX, USA, 1958. [Google Scholar]
  27. Clausager, I. Migration of Scandinavian Woodcock (Scolopax rusticola) with special reference to Denmark. Dan. Rev. Game Biol. 1974, 8, 38. [Google Scholar]
  28. Fokin, S.; Blokhin, Y. Roding activity, spring hunting and hunting bags of Woodcock (Scolopax rusticola) in Russia. In Fifth European Woodcock and Snipe Workshop—Proceedings of an International Symposium of the Wetlands International/IUCN Woodcock & Snipe Specialist Group; Kalchreuter, H., Ed.; Wetlands International Global Series No. 4; International Wader Studies 11: Wageningen, The Netherlands, 2000; pp. 19–24. [Google Scholar]
  29. Tavecchia, G.; Pradel, R.; Gossmann, F.; Bastat, C.; Ferrand, Y.; Lebreton, J.D. Temporal variation in annual survival probability of the Eurasian woodcock Scolopax rusticola wintering in France. Wildl. Biol. 2002, 8, 21–30. [Google Scholar] [CrossRef]
  30. Péron, G.; Ferrand, Y.; Gossmann, F.O.; Bastat, C.; Guénézan, M.; Gimenez, O. Escape migration decisions in Eurasian Woodcocks: Insights from survival analyses using large-scale recovery data. Behav. Ecol. Sociobiol. 2001, 65, 1949–1955. [Google Scholar] [CrossRef]
  31. Guzmán, J.L.; Caro, J.; Arroyo, B. Factors influencing mobility and survival of Eurasian Woodcock wintering in Spain. ACE 2017, 12, 21. [Google Scholar] [CrossRef]
  32. Stewart, R.L.M.; Francis, C.M.; Massey, C. Age-related differential timing of spring migration within sexes in passerines. Wilson Bull. 2002, 114, 264–271. [Google Scholar] [CrossRef]
  33. Lehikoinen, A.; Santaharju, J.; Anders, M. Sex-specific timing of autumn migration in birds: The role of sexual size dimorphism, migration distance and differences in breeding investment. Ornis Fenn. 2017, 94, 53–65. [Google Scholar] [CrossRef]
  34. Pedersen, L.; Jakobsen, N.M.; Strandberg, R.; Thorup, K.; Tøttrup, A.P. Sex-specific difference in migration schedule as a precursor of protandry in a long-distance migratory bird. Sci. Nat. 2019, 106, 1–10. [Google Scholar] [CrossRef]
  35. Wobker, J.; Heim, W.; Schmaljohann, H. Sex, age, moulting strategy, and migration distance explain the phenology of songbirds at a stopover along the East Asian flyway. Behav. Ecol. Sociobiol. 2021, 75, 1–14. [Google Scholar] [CrossRef]
  36. Logan, C.A.; Hyatt, L.E. Mate attraction by autumnal song in the Northern Mockingbird (Mimus polyglottos). Auk 1991, 108, 429–432. [Google Scholar]
  37. Forstmeier, W. Benefits of early arrival at breeding grounds vary between males. J. Anim. Ecol. 2002, 71, 1–9. [Google Scholar] [CrossRef]
  38. Mills, A.M. Protogyny in autumn migration: Do male birds ”Play Chicken”? Auk 2005, 122, 71–81. [Google Scholar] [CrossRef]
  39. Coppack, T.; Both, C. Predicting life-cycle adaptation of migratory birds to global climate change. Ardea 2002, 55, 369–378. [Google Scholar] [CrossRef]
  40. Remisiewicz, M.; Wennerberg, L. Differential migration strategies of the Wood Sandpiper (Tringa glareola)–genetic analyses reveal sex differences in morphology and spring migration phenology. Ornis Fenn. 2006, 83, 1–10. [Google Scholar]
  41. Bozó, L.; Heim, W. Sex-specific migration of Phylloscopus warblers at a stopover site in Far Eastern Russia. Ring. Migr. 2016, 31, 41–46. [Google Scholar] [CrossRef]
  42. Briedis, M.; Bauer, S.; Adamík, P.; Alves, J.A.; Costa, J.S.; Emmenegger, T.; Hahn, S. A full annual perspective on sex-biased migration timing in long-distance migratory birds. Proc. R. Soc. B Biol. Sci. 2019, 286, 20182821. [Google Scholar] [CrossRef]
  43. Kokko, H.; Gunnarsson, T.G.; Morrell, L.J.; Gill, J.A. Why do female migratory birds arrive later than males? J. Anim. Ecol. 2006, 75, 1293–1303. [Google Scholar] [CrossRef]
  44. Morbey, Y.E.; Ydenberg, R.C. Protandrous arrival timing to breeding areas: A review. Ecol. Lett. 2001, 4, 663–673. [Google Scholar] [CrossRef]
  45. Jaatinen, K.; Lehikoinen, A.; Lank, D.B. Female-biased sex ratios and the proportion of cryptic male morphs of migrant juvenile ruffs (Philomachus pugnax) in Finland. Ornis Fenn. 2010, 87, 125–134. [Google Scholar] [CrossRef]
  46. Kokko, H. Competition for early arrival in migratory birds. J. Anim. Ecol. 1999, 68, 940–950. [Google Scholar] [CrossRef]
  47. McKinnon, E.A.; Fraser, K.C.; Stanley, C.Q.; Stutchbury, B.J. Tracking from the tropics reveals behaviour of juvenile songbirds on their first spring migration. PLoS ONE 2014, 9, e105605. [Google Scholar] [CrossRef] [PubMed]
  48. Brlík, V.; Pakanen, V.M.; Jaakkonen, T.; Arppe, H.; Jokinen, J.; Lakka, J.; Blomqvist, D.; Hahn, S.; Valkama, J.; Koivula, K. Survival fluctuation is linked to precipitation variation during staging in a migratory shorebird. Sci. Rep. 2022, 12, 19830. [Google Scholar] [CrossRef]
  49. Carneiro, C.; Gunnarsson, T.G.; Alves, J.A. Why are whimbrels not advancing their arrival dates into Iceland? Exploring seasonal and sex-specific variation in consistency of individual timing during the annual cycle. Front. Ecol. Evol. 2018, 7, 248. [Google Scholar] [CrossRef]
  50. Faragó, S.; László, R.; Sándor, G. Body size, age and sex ratio of the woodcock (Scolopax rusticola) in Hungary between 1990–1999. Hung. Waterfowl Publ. 2000, 6, 409–461. [Google Scholar]
  51. Faragó, S. Trend of Woodcock hunting bag in Hungary and its effect on the population. WI-WSSG Newsl. 2003, 29, 6–8. [Google Scholar]
  52. Faragó, S.; László, R. Long-term monitoring of the Hungarian Woodcock bag during 1995–2008. In Seventh European Woodcock and Snipe Workshop—Proceedings of an International Symposium of the IUCN/WI Woodcock & Snipe Specialist Group, Office National de la Chasse et de la Faune Sauvage; Ferrand, Y., Ed.; Office National de la Chasse et de la Faune Sauvage: Paris, France, 2013; pp. 41–44. [Google Scholar]
  53. Faragó, S.; László, R.; Bende, A. Az erdei szalonka (Scolopax rusticola) teríték monitoring eredményei 2010-ben Magyarországon. Hung. Waterfowl Publ. 2012, 22, 285–296. [Google Scholar]
  54. Faragó, S.; László, R.; Bende, A. Az erdei szalonka (Scolopax rusticola) teríték monitoring eredményei 2011-ben Magyarországon. Hung. Waterfowl Publ. 2012, 22, 297–310. [Google Scholar]
  55. Faragó, S.; László, R.; Bende, A. Az erdei szalonka (Scolopax rusticola) teríték monitoring eredményei 2012-ben. Hung. Waterfowl Publ. 2014, 24, 283–295. [Google Scholar]
  56. Faragó, S.; László, R.; Bende, A. Az erdei szalonka (Scolopax rusticola) teríték monitoring eredményei 2013-ban Magyarországon. Hung. Waterfowl Publ. 2015, 25, 289–302. [Google Scholar] [CrossRef]
  57. Faragó, S.; László, R.; Bende, A. Development of the woodcock (Scolopax rusticola) sex ratio in Hungary between 2010–2014. In V. Faculty Scientific Conference, Conference Publication; Bidló, A., Facskó, F., Eds.; University of Sopron Publishing: Sopron, Hungary, 2015; pp. 105–107. [Google Scholar]
  58. Faragó, S.; László, R.; Bende, A. Az erdei szalonka (Scolopax rusticola) teríték monitoring eredményei 2014-ben Magyarországon. Hung. Waterfowl Publ. 2016, 27, 284–296. [Google Scholar]
  59. Directive 79/409/EEC of 2 April 1979 on the Conservation of Wild Birds. OJ L 103, 25.4.1979, pp. 1–18. Available online: https://eur-lex.europa.eu/legal-content/EN/ALL/?uri=celex:31979L0409 (accessed on 12 June 2025).
  60. Faragó, S. History of the development of spring woodcock hunting in Hungary and the reasons for its maintenance. Hung. Waterfowl Publ. 2013, 23, 311–332. [Google Scholar]
  61. Blokhin, Y.Y.; Artemenkov, D.V. Impact of the Hunting Ban on the Population and Hunting Bag of the Eurasian Woodcock Scolopax rusticola (Scolopacidae, Aves) in European Russia. Povolzhskii Ekol. Zhurnal 2022, 4, 375–387. [Google Scholar] [CrossRef]
  62. Jackson, A.C. The moults and sequence of plumages of the British waders. Brit. Birds 1919, 12, 172–179. [Google Scholar]
  63. Dementiev, G.P.; Gladkov, N.A. Ptitsy Sovietskogo Soyuza; State Publishing House Soviet Science: Moscow, Russia, 1951; Volume III, pp. 320–326. [Google Scholar]
  64. Bende, A. Az erdei szalonka (Scolopax rusticola L.) tollváltása, a tollazat alapján történő kormeghatározás lehetőségei. Magy. Vízivad Közlemények 2023, 37, 45–58. [Google Scholar] [CrossRef]
  65. Bende, A.; Palinkas-Bodzsar, N.; Boa, L.; László, R. Sex determination of eurasian woodcock (Scolopax rusticola L.) by genetic and imaging diagnostic methods. Biodivers. Environ. 2023, 15, 29–35. [Google Scholar]
  66. Cochran, W.G. Sampling Techniques, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1977. [Google Scholar]
  67. Csanády, V. Nonlinear regressions applied to practical examples. Dimens. Math. Publ. 2013, 1, 19–26. [Google Scholar]
  68. Csanády, V. Double Gaussian function application. Dimens. Math. Publ. 2019, 7, 37–47. [Google Scholar]
  69. Parris, R. Winplot for Windows 95/98/ME/2K/XP/Vista/7 (846K). In Peanut Software; Phillips Exeter Academy: Exeter, NH, USA, 2012. [Google Scholar]
  70. Dell Inc. Dell Statistica, (Version 13.0) [Computer Software]; Dell Inc.: Round Rock, TX, USA, 2016. [Google Scholar]
  71. RStudio Team. RStudio: Integrated Development for R. RStudio, PBC. Available online: https://posit.co/download/rstudio/ (accessed on 4 March 2025).
  72. Cristol, D.A.; Baker, M.B.; Carbone, C. Differential migration revisited: Latitudinal segregation by age and sex class. Curr. Ornithol. 1999, 15, 33–88. [Google Scholar]
  73. Nebel, S. Differential migration of shorebirds in the east Asian–Australasian flyway. Emu 2007, 107, 14–18. [Google Scholar] [CrossRef]
  74. Barter, M. Sex-related differences in adult Curlew Sandpipers Caldiris ferruginea caught in Victoria. Stilt 1986, 8, 2–8. [Google Scholar]
  75. Barter, M. Are Curlew Sandpipers sexist—And if so, why? Stilt 1987, 11, 14–17. [Google Scholar]
  76. Barter, M. Bar-tailed Godwit Limosa lapponica in Australia. Part 1: Races, breeding areas and migration routes. Stilt 1989, 14, 43–48. [Google Scholar]
  77. Gosbell, K.; Minton, C. The biometrics and moult of Sanderling Calidris alba in Australia. Stilt 2001, 40, 7–22. [Google Scholar]
  78. McCloskey, J.T.; Thompson, J.E. Sex-related differences in migration chronology and winter habitat use of Common Snipe. Wilson Bull. 2000, 112, 143–148. [Google Scholar] [CrossRef]
  79. Cline, B.B.; Haig, S.M. Seasonal movement, residency, and migration patterns of Wilson’s Snipe (Gallinago delicata). Auk 2008, 128, 543–555. [Google Scholar] [CrossRef]
  80. Clutton-Brock, T.H. Sex ratio variation in birds. Ibis 1986, 128, 317–329. [Google Scholar] [CrossRef]
  81. Merán, P. Some observations on Woodcock Migration in Austria and Western Hungary 1995. IWRB-WSRG Newsl. 1996, 22, 5–6. [Google Scholar]
  82. Merán, P. Some observations on Woodcock Migration in Austria and Western Hungary 1996. IWRB-WSRG Newsl. 1997, 23, 4–5. [Google Scholar]
  83. Merán, P. Some observations on Woodcock Migration in Austria and Western Hungary 1997. IWRB-WSRG Newsl. 1998, 24, 5–6. [Google Scholar]
  84. Merán, P. Some observations on Woodcock Migration in Austria and Western Hungary 1998. IWRB-WSRG Newsl. 1999, 25, 4–5. [Google Scholar]
  85. Faragó, S.; László, R. Az erdei szalonka (Scolopax rusticola) teríték monitoring eredményei 2000-ben Magyarországon. Hung. Waterfowl Publ. 2002, 9, 323–340. [Google Scholar]
  86. Faragó, S.; László, R. Az erdei szalonka (Scolopax rusticola) teríték monitoring eredményei 2001-ben Magyarországon. Hung. Waterfowl Publ. 2003, 11, 343–359. [Google Scholar]
  87. Faragó, S.; László, R. Az erdei szalonka (Scolopax rusticola) teríték monitoring eredményei 2002-ben Magyarországon. Hung. Waterfowl Publ. 2005, 12, 247–261. [Google Scholar]
  88. Faragó, S.; László, R. Az erdei szalonka (Scolopax rusticola) teríték monitoring eredményei 2003-ban Magyarországon. Hung. Waterfowl Publ. 2006, 13, 235–249. [Google Scholar]
  89. Faragó, S.; László, R. Az erdei szalonka (Scolopax rusticola) teríték monitoring eredményei 2004-ben Magyarországon. Hung. Waterfowl Publ. 2007, 14, 211–225. [Google Scholar]
  90. Faragó, S.; László, R. Az erdei szalonka (Scolopax rusticola) teríték monitoring eredményei 2005-ben Magyarországon. Hung. Waterfowl Publ. 2007, 15, 221–235. [Google Scholar]
  91. Faragó, S.; László, R. Az erdei szalonka (Scolopax rusticola) teríték monitoring eredményei 2006-ban Magyarországon. Hung. Waterfowl Publ. 2008, 17, 215–229. [Google Scholar]
  92. Faragó, S.; László, R. Az erdei szalonka (Scolopax rusticola) teríték monitoring eredményei 2007-ben Magyarországon. Hung. Waterfowl Publ. 2010, 18–19, 205–220. [Google Scholar]
  93. Faragó, S.; László, R. Az erdei szalonka (Scolopax rusticola) teríték monitoring eredményei 2008-ban Magyarországon. Hung. Waterfowl Publ. 2010, 18–19, 421–435. [Google Scholar]
  94. Sterbetz, I. Magyarországi adatok az erdei szalonka (Scolopax rusticola L., 1758) nászrepülésének fényviszonyairól. Állattani Közlemények 1982, 69, 123–126. [Google Scholar]
  95. Fadat, C. Modalités Zoogéographiques de la Migration et de L’hivernage en France de la Bécasse des Bois (Scolopax rusticola L.) et Gestion Cynégétique de ses Populations. 3 Tomes. Ph.D. Thesis, Université Montpellier, Montpellier, France, 1989. [Google Scholar]
  96. Boidot, J.-P.; Cau, J.-F.; Audrousseau, G. Evaluation of the 2014/15. WI-WSSG Newsl. 2015, 41, 49–50. [Google Scholar]
  97. Asbóth, R.; Hopp, F.; Molnár, L.; Novics, G.; Sasvári, Z.; Szabó, Z.; Szigethy, G. More data on woodcock. Nimród 1980, 104, 450. [Google Scholar]
  98. Faragó, S. Hunting Zoology; Agricultural Publishing House: Budapest, Hungary, 2007; pp. 206–214. [Google Scholar]
  99. Marcström, V. Removal of roding Woodcock. IWRB-WSRG Newsl. 1980, 6, 63–70. [Google Scholar]
  100. Ostermeyer, R.; Ferrand, Y. Approche du Comportement de la Bécasse des Bois Scolopax rusticola en Période de Reproduction en Forêt Domaniale de Compiègne (OiseFrance). Essai de Mise en Place D’une Méthode D’étude par Télémétrie; Office National de la Chasse Section Bécasse: Clermont l’Hérault, France, 1979. [Google Scholar]
  101. Pertunnen, E. The roding male count by hunting in Finland. IWRB—Woodcock Snipe Res. Group. Newsl. 1980, 6, 17–27. [Google Scholar]
  102. Shorten, M. The European Woodcock (Scolopax rusticola). A Search of the Literature since 1940. Rep. Game Conserv. Trust 1974, 21, 95. [Google Scholar]
  103. Hirons, G. The Significance of Roding by Woodcock Scolopax rusticola: An Alternative Explanation Based on Observations of Marked Birds. Ibis 1980, 122, 350–354. [Google Scholar] [CrossRef]
  104. Christensen, T.K.; Asferg, T. Woodcock hunting in Denmark–Status and recent changes. In Seventh European Woodcock and Snipe Workshop—Proceedings of an International Symposium of the IUCN/Wetlands International Woodcock & Snipe Specialist Group; Ferrand, Y., Ed.; ONCFS Publication: Paris, France, 2013; pp. 36–40. [Google Scholar]
  105. Cau, J.-F. Synthèse Nationale des lectures d’alies et études pondérales. Diagnose des echantillons sex-ratio age ratio repartition spatio-temporelle des oiseaux variations ponderales muses suspendues. Mordorée 2002, 224, 321–331. [Google Scholar]
  106. Cau, J.-F. Bilans concernant certains paramenters biomeriques releves cheé la becasse des bois sur le territorie Francais au niveau national, regional et departemental. Mordorée 2003, 228, 286–303. [Google Scholar]
  107. Cau, J.-F. Bilans concernant certains parameters biometriques et biologiques releves chez la becasse des bois sur le territoire Francais. Mordorée 2004, 232, 268–284. [Google Scholar]
  108. Cau, J.-F. Répartition des échantillons recus par département. Mordorée 2005, 236, 311–327. [Google Scholar]
  109. Cau, J.-F. La saison bécassiérre 2007/2008 par le C.N.B. Mordorée 2008, 247, 225–251. [Google Scholar]
  110. Boidot, J.-P. Répartition des échantillons recus par département saison 05/06. Mordorée 2006, 240, 319–331. [Google Scholar]
  111. Boidot, J.-P. Bilans CNB 2006/2007. La Mordorée 2007, 244, 337–347. [Google Scholar]
  112. Boidot, J.-P. La saison bécassiérre 2008/2009 par le C.N.B. Mordorée 2009, 252, 333–343. [Google Scholar]
  113. Boidot, J.-P. Bilans concernant certains paramèters biometriques et biologiques relevés chez la bécasse des bois lors de la saison 2009/2010 en France. Mordorée 2010, 256, 370–382. [Google Scholar]
  114. Boidot, J.-P. Bilans concernant certains paramèters biometriques et biologiques relevés chez la bécasse des bois lors de la saison 2010/2011 en France. Mordorée 2011, 259, 181–195. [Google Scholar]
  115. Boidot, J.-P. Bilans concernant certains paramèters biometriques et biologiques relevés chez la bécasse des bois lors de la saison 2011/2012 en France. Mordorée 2012, 263, 42–55. [Google Scholar]
  116. Aurousseau, G. Compte-rendu saison 2012/2013. Bilans concernant certains paramèters biometriques et biologiques relevés chez la bécasse des bois lors de la saison 2012/2013 en France. Mordorée 2013, 268, 3–13. [Google Scholar]
  117. Aurousseau, G. Saison Bécassière saison 2016–2017. Chass. Pays d’Azur 2017, 64, 12–14. [Google Scholar]
  118. Lepetit, J.-P. Bilans concernant certains paramèters biometriques et biologiques relevés chez la bécasse des bois lors de la saison 2013/2014 en France. Mordorée 2014, 271, 53–67. [Google Scholar]
  119. Bagnol, G. Tableau de Bord Saison 2017/2018. Fédération Départementale des Chasseurs du Gard 182 Route de Sauve—BP 57012—30910 NIMES Cedex 2. 2018; pp. 62–63.
  120. Mendall, H.L.; Aldous, C.M. The Ecology and Management of the American Woodcocok; USGS Maine Cooperative Fish and Wildlife Research Unit, University of Maine: Orono, ME, USA, 1943. [Google Scholar]
  121. Greeley, F. Sex and age studies in fall-shot woodcock (Philohela minor) from southern Wisconsin. J. Wildl. Manag. 1953, 17, 29–32. [Google Scholar] [CrossRef]
  122. Blankenship, L.H. Investigations of the American Woodcock in Michigan. Mich. Dep. Consum. Rep. 1957, 2123, 217. [Google Scholar]
  123. Prieto, N.; Tavecchia, G.; Telletxea, I.; Ibañez, R.; Ansorregi, F.; Galdos, A.; Urruzola, A.; Iriarte, I.; Arizaga, J. Survival probabilities of wintering Eurasian Woodcocks Scolopax rusticola in northern Spain reveal a direct link with hunting regimes. J. Ornithol. 2019, 160, 329–336. [Google Scholar] [CrossRef]
  124. Bende, A.; Faragó, S. Woodcock (Scolopax rusticola L.) management plan in Hungary. Hung. Waterfowl Publ. 2023, 37, 71–105. [Google Scholar]
Birds 06 00030 g001
Figure 1. Cumulative spring sampling frequency of Eurasian Woodcock by sex in 2012. Days were counted from the first day of the sampling period (1 March).
Figure 1. Cumulative spring sampling frequency of Eurasian Woodcock by sex in 2012. Days were counted from the first day of the sampling period (1 March).
Birds 06 00030 g001
Birds 06 00030 g002
Figure 2. Cumulative spring sampling frequency of Eurasian Woodcock by sex and age in 2012. Days were counted from the first day of the sampling period (1 March).
Figure 2. Cumulative spring sampling frequency of Eurasian Woodcock by sex and age in 2012. Days were counted from the first day of the sampling period (1 March).
Birds 06 00030 g002
Birds 06 00030 g003
Figure 3. Spring migration dynamics models of the Eurasian Woodcock by sex in 2012. Days were counted from the first day of the sampling period (1 March).
Figure 3. Spring migration dynamics models of the Eurasian Woodcock by sex in 2012. Days were counted from the first day of the sampling period (1 March).
Birds 06 00030 g003
Birds 06 00030 g004
Figure 4. Spring migration dynamics models of the Eurasian Woodcock by sex and age in 2012. Days were counted from the first day of the sampling period (1 March).
Figure 4. Spring migration dynamics models of the Eurasian Woodcock by sex and age in 2012. Days were counted from the first day of the sampling period (1 March).
Birds 06 00030 g004
Birds 06 00030 g005
Figure 5. Proportion of males by age during the spring migration in Hungary between 2010 and 2019.
Figure 5. Proportion of males by age during the spring migration in Hungary between 2010 and 2019.
Birds 06 00030 g005
Table 1. Eurasian Woodcock samples of specified sex (males (♂) and females (♀)) and age collected in Hungary between 2010 and 2019.
Table 1. Eurasian Woodcock samples of specified sex (males (♂) and females (♀)) and age collected in Hungary between 2010 and 2019.
YearBagged Specimens Known Sex
(Specimens)		Known Age
(Specimens)		SexAgeSex and Age
♂♀Ad.Juv.Ad.
♂		Juv.
♂		Ad.
♀		Juv.
♀
2010238923852386198839715118751278709230166
20113402339219132844548997916844767150147
20121941192511621671354476686370573105112
20132913290117382411490939799777666156132
20142727270516392250455766873646727120143
2015278727511661236738475590661879512894
20162215219212571784408605652469539127104
20171683166113251255406661664482517174138
2018234922672132187639111171015891811182174
20191761170316941397306793901619722146151
Sum.24,16723,88216,90719,8434139862082876994682615181361
Table 2. Double Gaussian extreme value data, regression coefficient, and monotonicity coefficient of variation values for migration by sex and age in 2012.
Table 2. Double Gaussian extreme value data, regression coefficient, and monotonicity coefficient of variation values for migration by sex and age in 2012.
SexExtreme Value CoordinatesRegression
Coefficient (R)
T Max.N Max.
♂181150.9768
23121
♀17230.9539
2428
Sex × Age
Ad. ♂21300.9629
Ad. ♀1780.8228
239
Juv. ♂19430.9772
2349
Juv. ♀23100.9177
Independent variable: T: number of sampling days in the study; dependent variable: N: sample number (specimen). Period (1 March–10 April).
Table 3. Results of the ARIMA model.
Table 3. Results of the ARIMA model.
PredictorEstimate95% CI (Estimates)Z-Valuep-Value
Constant0.8829[0.6974, 1.068]9.91p < 0.001
Proportion ♀, ♂0.0154[−0.3716, 0.4024]0.12p = 0.9045
Proportion ad., juv.0.1007[−0.0215, 0.223]1.63p = 0.1033
Proportion ♀, ♂ × ♀ Proportion ad., juv.0.0041[−0.0912, 0.0994]0.08p = 0.9332
AR(1) (ar.L1)0.8854[0.8231, 0.9477]23.6p < 0.001
MA(1) (ma.L1)−0.4031[−0.5240, −0.2823]−6.44p < 0.001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Bende, A.; Faragó, S.; László, R.; Csanády, V.; Fekete, I.; Pecsics, T.; Bozó, L. Dynamics of Sex and Age Correlation of Eurasian Woodcock (Scolopax rusticola L.) During Spring Migration in Hungary. Birds 2025, 6, 30. https://doi.org/10.3390/birds6020030

AMA Style

Bende A, Faragó S, László R, Csanády V, Fekete I, Pecsics T, Bozó L. Dynamics of Sex and Age Correlation of Eurasian Woodcock (Scolopax rusticola L.) During Spring Migration in Hungary. Birds. 2025; 6(2):30. https://doi.org/10.3390/birds6020030

Chicago/Turabian Style

Bende, Attila, Sándor Faragó, Richárd László, Viktória Csanády, István Fekete, Tibor Pecsics, and László Bozó. 2025. "Dynamics of Sex and Age Correlation of Eurasian Woodcock (Scolopax rusticola L.) During Spring Migration in Hungary" Birds 6, no. 2: 30. https://doi.org/10.3390/birds6020030

APA Style

Bende, A., Faragó, S., László, R., Csanády, V., Fekete, I., Pecsics, T., & Bozó, L. (2025). Dynamics of Sex and Age Correlation of Eurasian Woodcock (Scolopax rusticola L.) During Spring Migration in Hungary. Birds, 6(2), 30. https://doi.org/10.3390/birds6020030

Article Metrics

Back to TopTop