Assessing the Potential of a Long-Term Climate Forecast for Cuba Using the WRF Model †
Abstract
1. Introduction
2. Materials and Methods
2.1. Design of Experiments
2.2. Real Data and Evaluation Methodology
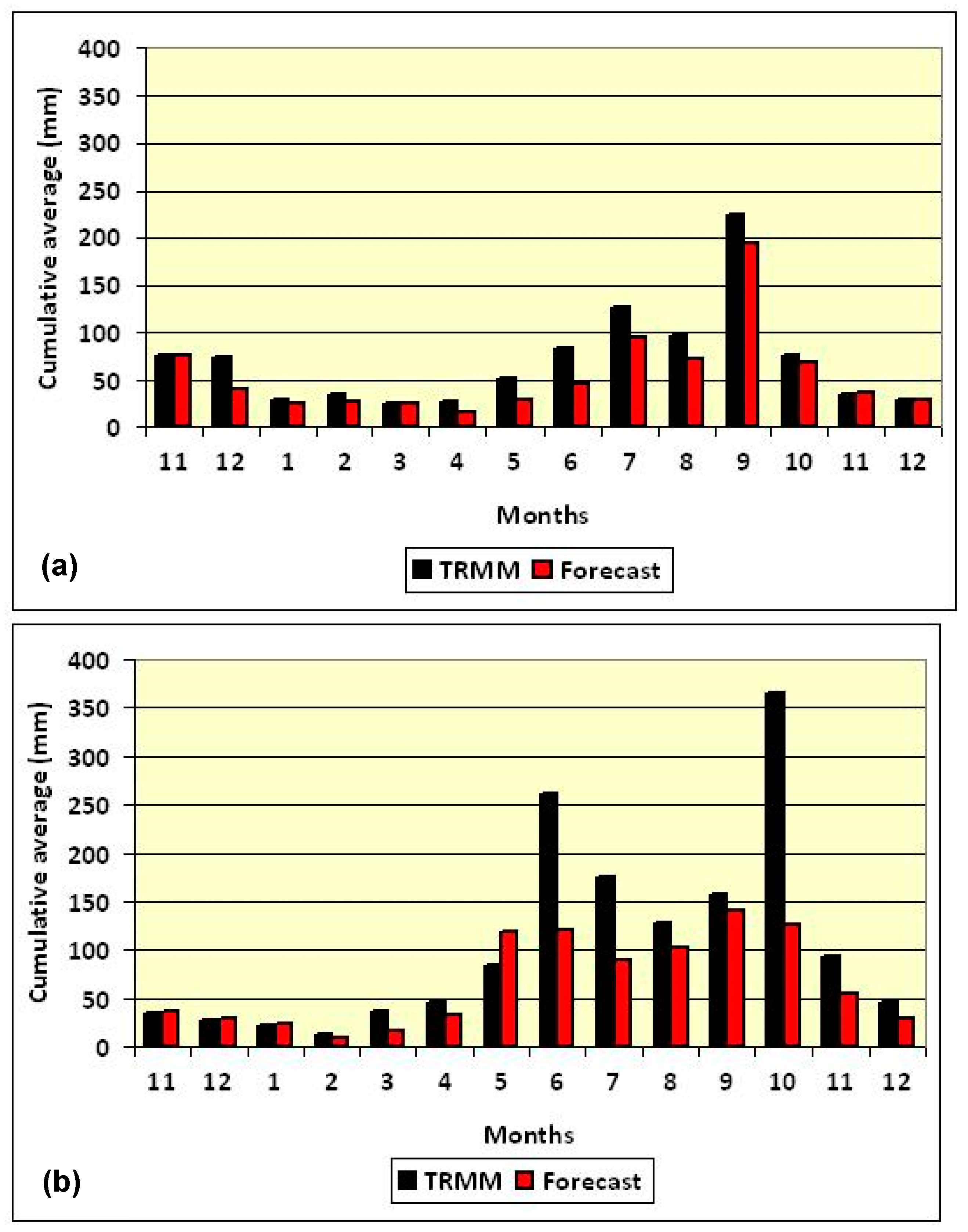
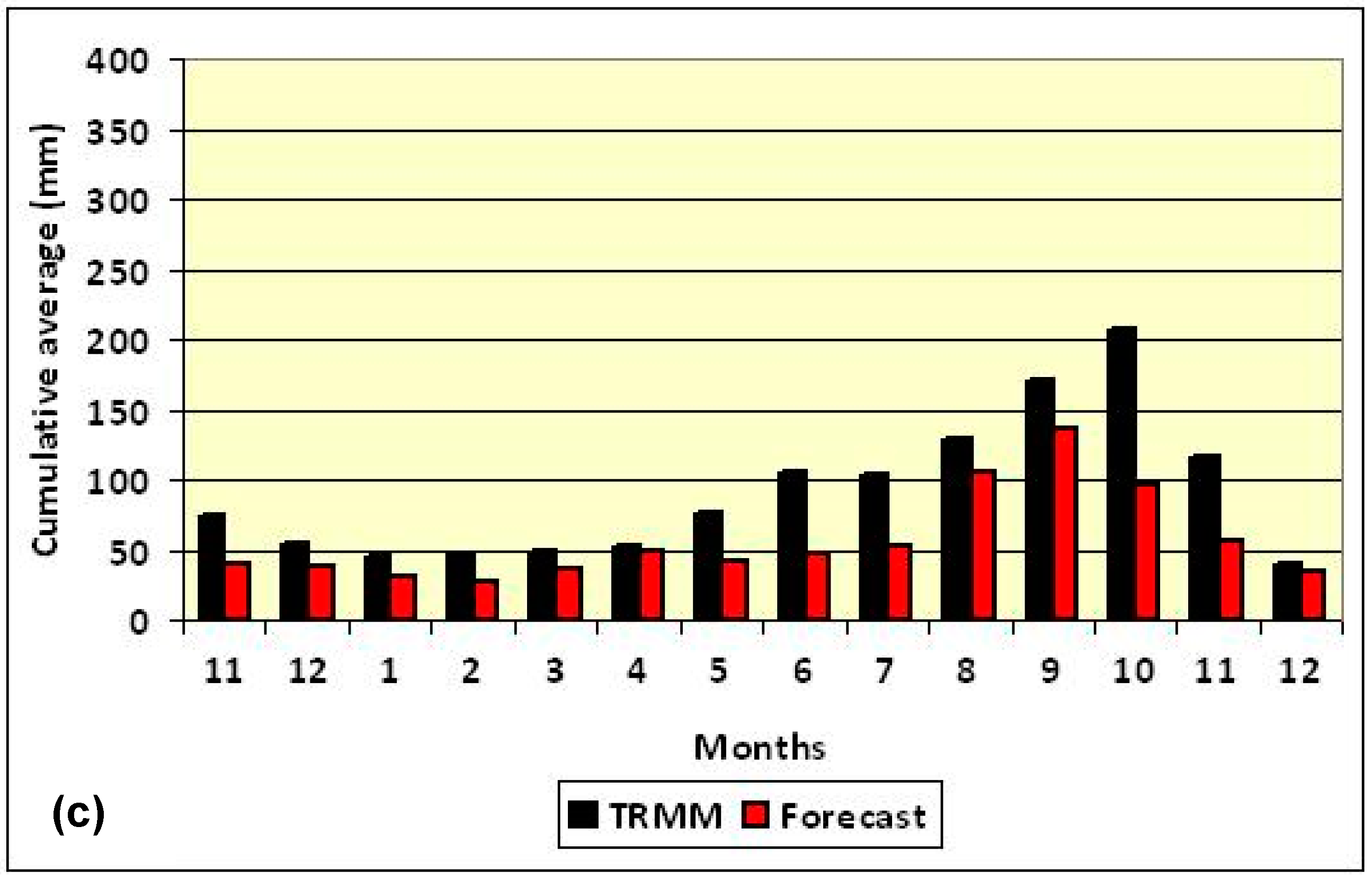
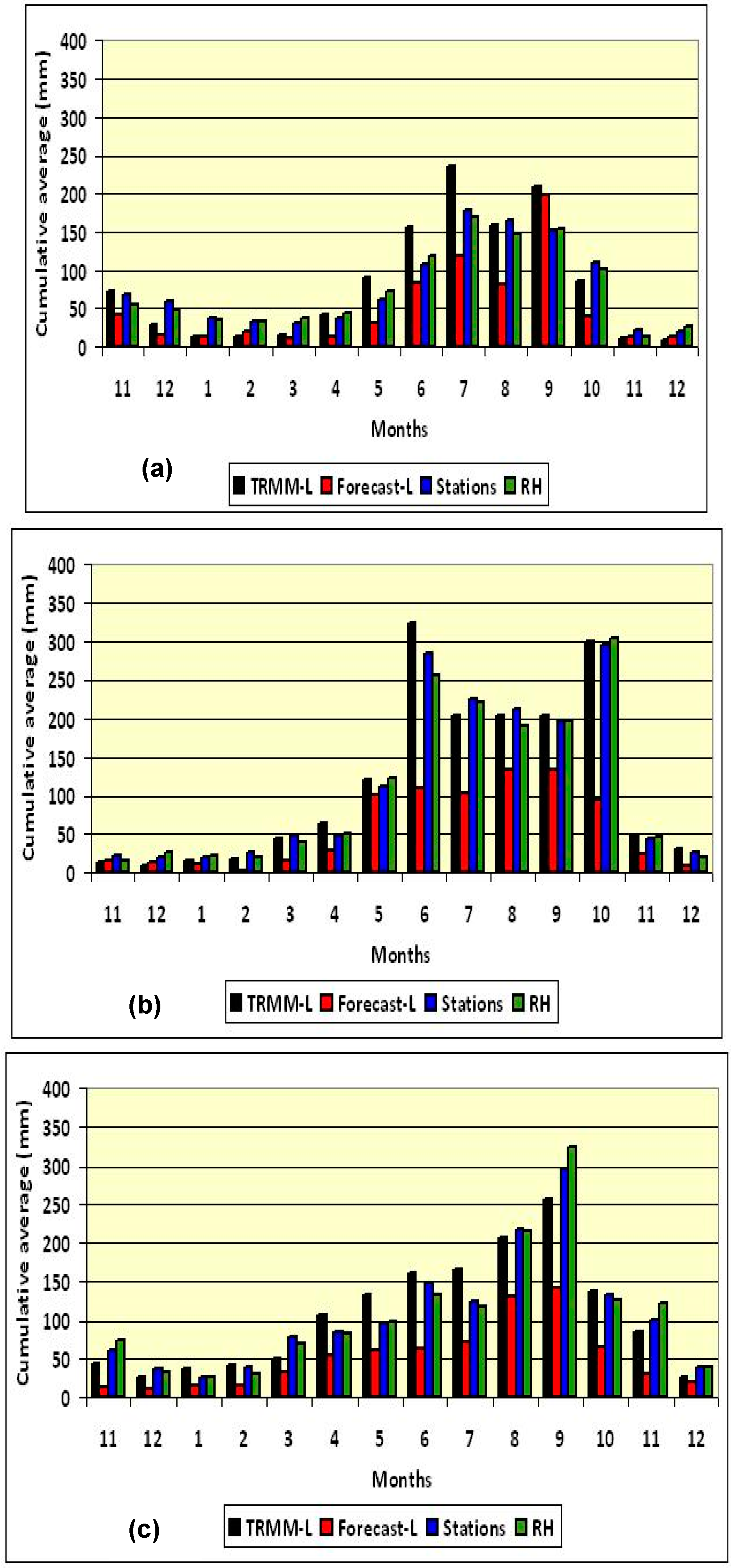
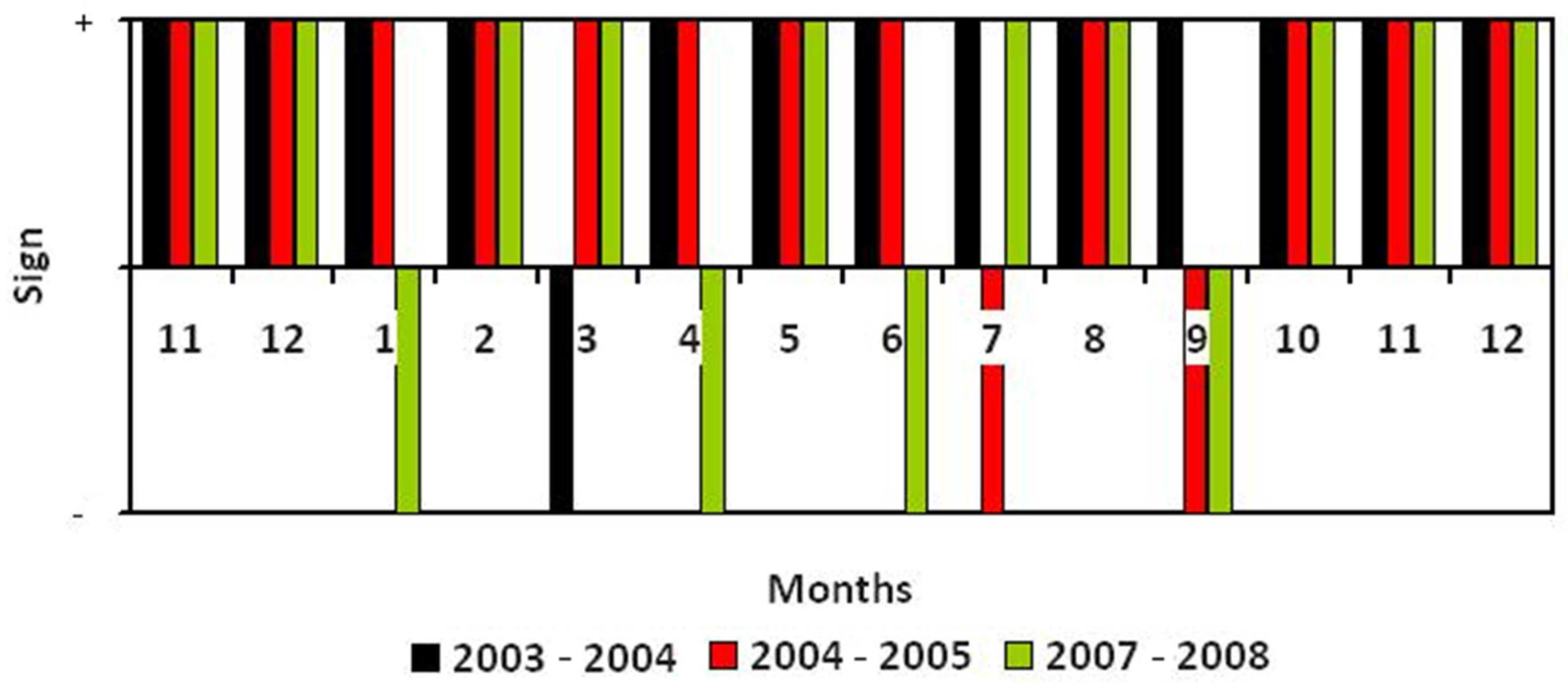
3. Results and Discussion
4. Conclusions and Recommendations
Data availability Statement
Conflicts of Interest
References
- WWRP/THORPEX-WCRP. Sub-seasonal to Seasonal Prediction Research Implementation Plan. 2012. Available online: https://www.wmo.int/pages/prog/arep/wwrp/new/documents/capabilities_in_sub_seasonal_prediction_final.pdf (accessed on 12 September 2013).
- Fu, X.; Wang, B.; Lee, J.Y.; Wang, W.; Gao, L. Sensitivity of dynamical intraseasonal prediction skills to different initial conditions. Mon. Weather Rev. 2011, 139, 2572–2592. [Google Scholar] [CrossRef]
- Stockdale, T.N.; Anderson, D.L.T.; Balmaseda, M.A.; Doblas-Reyes, F.; Ferranti, L.; Mogensen, K.; Palmer, T.; Molteni, F.; Vitart, F. ECMWF seasonal forecast system 3 and its prediction of sea surface temperature. Clim. Dyn. 2011, 37, 455–471. [Google Scholar] [CrossRef]
- Arribas, A.; Glover, M.; Maidens, A.; Peterson, K.; Gordon, M.; MacLachlan, C.; Graham, R.; Fereday, D.; Camp, J.; Scaife, A.A.; et al. The GloSea4 Ensemble Prediction System for Seasonal Forecasting. Mon. Weather Rev. 2011, 139, 1891–1910. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.-T.; Chuang, H.-Y.; Iredell, M.; et al. The NCEP Climate Forecast System Version 2. J. Clim. 2014, 27, 2185–2208. [Google Scholar] [CrossRef]
- Landman, W.A.; Kgatuke, M.-J.; Mbedzi, M.; Beraki, A.; Bartman, A.; Du Piesanie, A. Performance comparison of some dynamical and empirical downscaling methods for South Africa from a seasonal climate modelling perspective. Int. J. Clim. 2009, 29, 1535–1549. [Google Scholar] [CrossRef]
- Cavalcanti, I.F.A.; Marengo, J.A.; Satyamurty, P.; Nobre, C.A.; Trosnikov, I.; Bonatti, J.P.; Manzi, A.O.; Tarasova, T.; Pezzi, L.P.; D’Almeida, C.; et al. Global Climatological Features in a Simulation Using the CPTEC–COLA AGCM. J. Clim. 2002, 15, 2965–2988. [Google Scholar] [CrossRef]
- Coelho, C.A.S.; Stephenson, D.B.; Balmaseda, M.; Doblas-Reyes, F.J.; Van Oldenborgh, G.J. Toward an integrated seasonal forecasting system for South America. J. Clim. 2006, 19, 3704–3721. [Google Scholar] [CrossRef]
- Palmer, T.N.; Anderson, D.L.T. The prospects for seasonal forecasting—A review paper. Q. J. R. Meteorol. Soc. 1994, 120, 755–793. [Google Scholar]
- Jin, E.K.; Kinter, J.L.; Wang, B.; Park, C.K.; Kang, I.S.; Kirtman, B.P.; Kug, J.S.; Kumar, A.; Luo, J.J.; Schemm, J. Current status of ENSO prediction skill in coupled ocean-atmosphere model. Clim. Dyn. 2008, 31, 647–664. [Google Scholar] [CrossRef]
- Cárdenas, P.A. Pronóstico de totales mensuales de lluvia en Cuba. Un modelo con varios meses de adelanto. Rev. Cuba. De Meteorol. 1999, 6, 47–51. [Google Scholar]
- Martinez-Castro, D.; Rocha RP da Bezanilla-Morlot, A.; Álvarez-Escudero, L.; Reyes-Fernández, J.P.; Silva-Vidal, Y.; Arritt, R.W. Sensitivity studies of the RegCM3 simulation of summer precipitation, temperature and local wind field in the Caribbean Region. Theor. Appl. Climatol. 2006, 86, 5–22. [Google Scholar] [CrossRef]
- Rummukainen, M. State-of-the-art with regional climate models. WIREs Clim. Chang. 2010, 1, 82–96. [Google Scholar] [CrossRef]
- Grotch, S.L.; MacCracken, M.C. The use of general circulation models to predict regional climatic change. J Clim. 1991, 4, 286–303. [Google Scholar] [CrossRef]
- Jones, R.G.; Murphy, J.M.; Noguer, M.M. Simulation of climate change over Europe using a nested regional climate model. I: Assessment of control climate, including sensitivity to location of lateral boundaries. Q. J. R. Meteorol. Soc. 1995, 121, 1413–1449. [Google Scholar]
- Feser, F. Enhanced detectability of added value in limited-area model results separated into different spatial scales. Mon. Weather Rev. 2006, 134, 2180–2190. [Google Scholar] [CrossRef]
- Winterfeldt, J.; Weisse, R. Assessment of value added for surface marine wind speed obtained from two Regional Climate Models (RCM). Mon. Weather Rev. 2009, 137, 2955–2965. [Google Scholar] [CrossRef]
- Deque, M.; Jones, R.G.; Wild, M.; Giorgi, G.; Christensen, J.H.; Hassell, D.C.; Vidale, P.L.; Rockel, B.; Jacob, D.; Kjellstrom, E.; et al. Global high resolution versus Limited Area Model climate change projections over Europe: Quantifying confidence level from PRUDENCE results. Clim. Dyn. 2005, 25, 653–670. [Google Scholar] [CrossRef]
- Rummukainen, M.; Bergstrom, S.; Persson, G.; Rodhe, J.; Tjernstrom, M. The Swedish regional climate modelling programme, SWECLIM: A review. AMBIO J. Hum. Environ. 2004, 33, 176–182. [Google Scholar] [CrossRef]
- Giorgi, F.; Diffenbaugh, N.S.; Gao, X.J.; Coppola, E.; Dash, S.K.; Frumento, O.; Rauscher, S.A.; Remedio, A.; Sanda, I.S.; Steiner, A.; et al. The regional climate change hyper-matrix framework. Eos Trans. Am. Geophys. Union 2008, 89, 445–446. [Google Scholar] [CrossRef]
- Giorgi, F.; Jones, C.; Asrar, G. Addressing climate information needs at the regional level: The CORDEX framework. WMO Bull. 2009, 58, 175–183. [Google Scholar]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.; Huang, X.-Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3, NCAR Technical Note. 2008. Available online: http://www2.mmm.ucar.edu/wrf/users/docs/arw_v3.pdf (accessed on 15 September 2013).
- Courtier, P.; Thépaut, J.N.; Hollingsworth, A. A Strategy for Operational Implementation of 4D-Var, Using an Incremental Approach. Q. J. R. Meteorol. Soc. 1994, 120, 1367–1387. [Google Scholar] [CrossRef]
- Veerse, F.; Thepaut, J.N. Multiple-Truncation Incremental Approach for Four-Dimensional Variational Data Assimilation. Q. J. R. Meteorol. Soc. 1998, 124, 1889–1908. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U. The ERA-Interim Reanalysis: Configuration and Performance of the Data Assimilation System. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Janjic, Z.I. The step-mountain eta coordinate model: Further developments of the convection, viscous sublayer and turbulence closure schemes. Mon. Weather Rev. 1994, 122, 927–945. [Google Scholar] [CrossRef]
- Weisman, M.L.; Wang, W.; Dudhia, J.; Manning, K.W. Systematic boundary-layer biases in the WRF-ARW real-time convective forecasts. In Proceedings of the 7th WRF Users’ Workshop, Boulder, CO, USA, 19 June 2006; Available online: http://nldr.library.ucar.edu/repository/collections/OSGC-000-000-005-764 (accessed on 18 September 2013).
- Grell, G.A.; Freitas, S.R. A scale and aerosol aware stochastic convective parameterization for weather and air quality modeling. Atmos. Chem. Phys. 2014, 14, 5233–5250. [Google Scholar] [CrossRef]
- Mayor, Y.G.; Mesquita, M.D.S. Numerical Simulations of the 1 May 2012 Deep Convection Event over Cuba: Sensitivity to Cumulus and Microphysical Schemes in a High-Resolution Model. Adv. Meteorol. 2015, 2015, 973151. [Google Scholar] [CrossRef]
- Lin, Y.L.; Farley, R.D.; Orville, H.D. Bulk parameterization of the snow field in a cloud model. J. Appl. Meteorol. Climatol. 1983, 22, 1065–1092. [Google Scholar] [CrossRef]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. 2008, 113, D13103. [Google Scholar] [CrossRef]
- Vichot-Llano, A.; Martínez-Castro, D.; Centella-Artola, A.; Bezanilla-Morlot, A. Sensibilidad al cambio de dominio y resolución de tres configuraciones del modelo climático regional RegCM 4.3 para la región de América Central y el Caribe. Rev. Climatol. 2014, 14, 45–62. [Google Scholar]
- Giorgi, F.; Coppola, E.; Solmon, F.; Mariotti, L.; Sylla, M.B.; Bi, X.; Elguindi, N.; Diro, G.T.; Nair, V.; Giuliani, G.; et al. RegCM4: Model description and preliminary tests over multiple CORDEX domains. Clim. Res. 2012, 52, 7–29. [Google Scholar] [CrossRef]
- Tiedtke, M. A Comprehensive Mass Flux Scheme for Cumulus Parameterization in large-scale models. Mon. Weather Rev. 1989, 117, 1779–1800. [Google Scholar] [CrossRef]



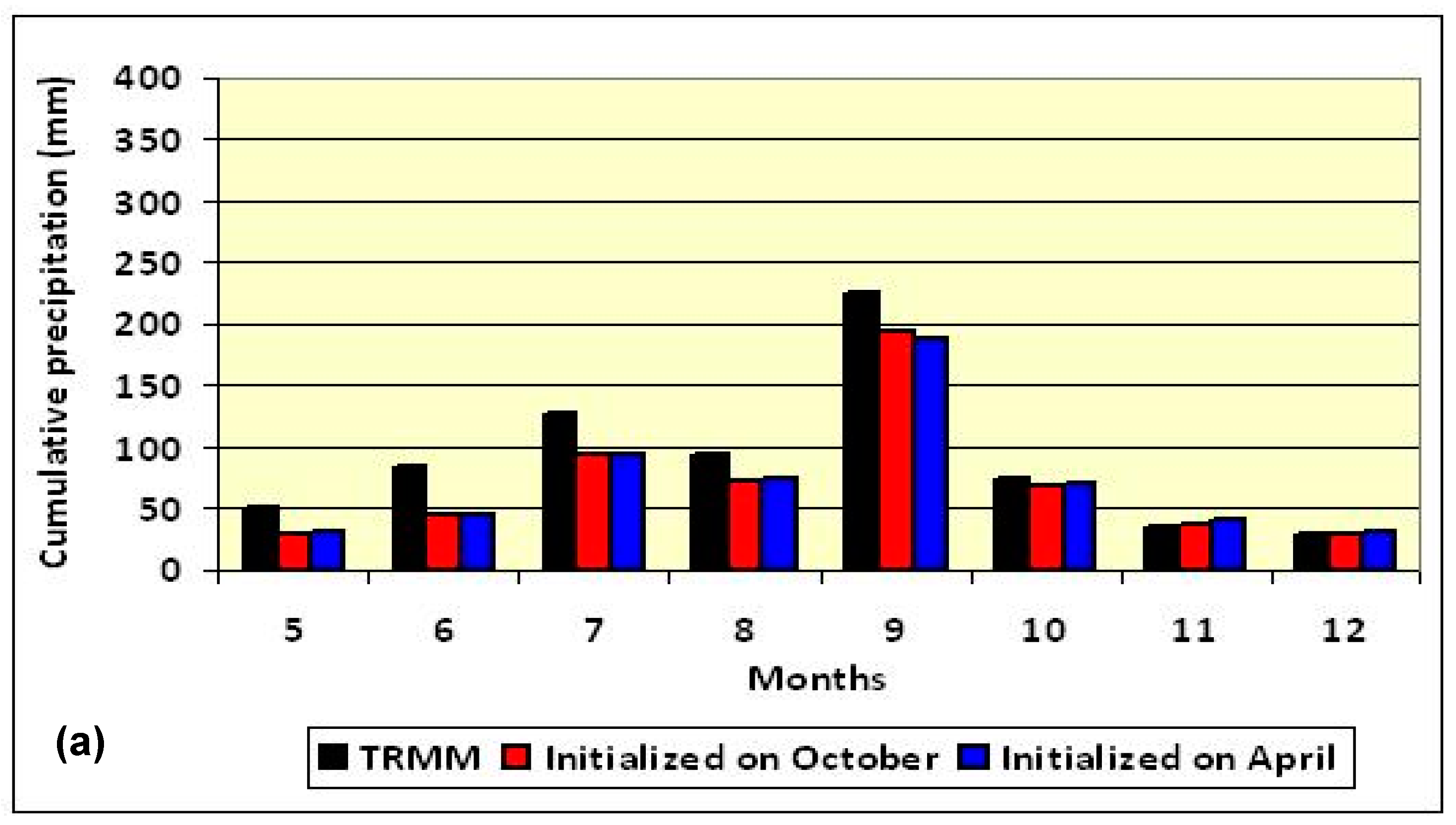
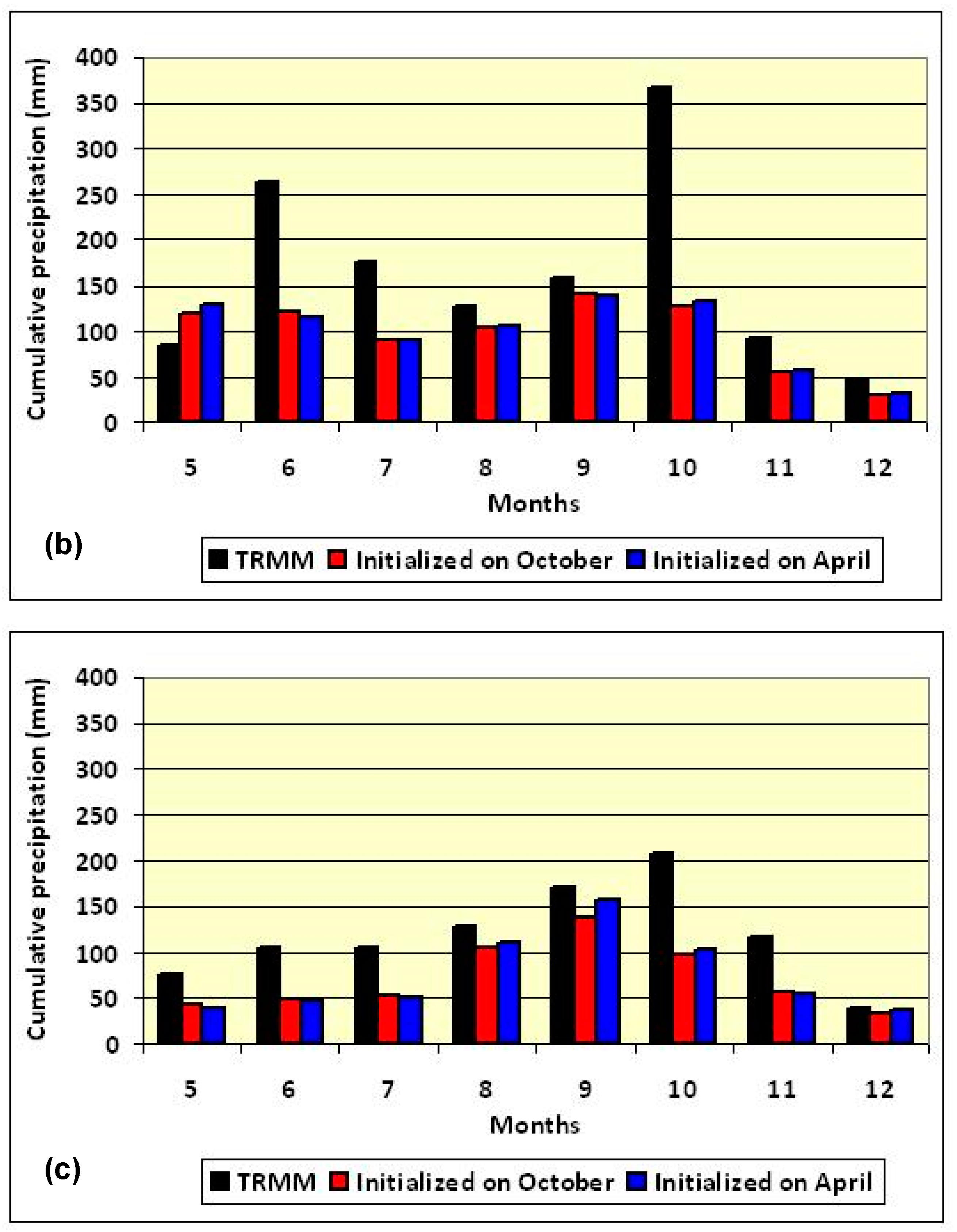
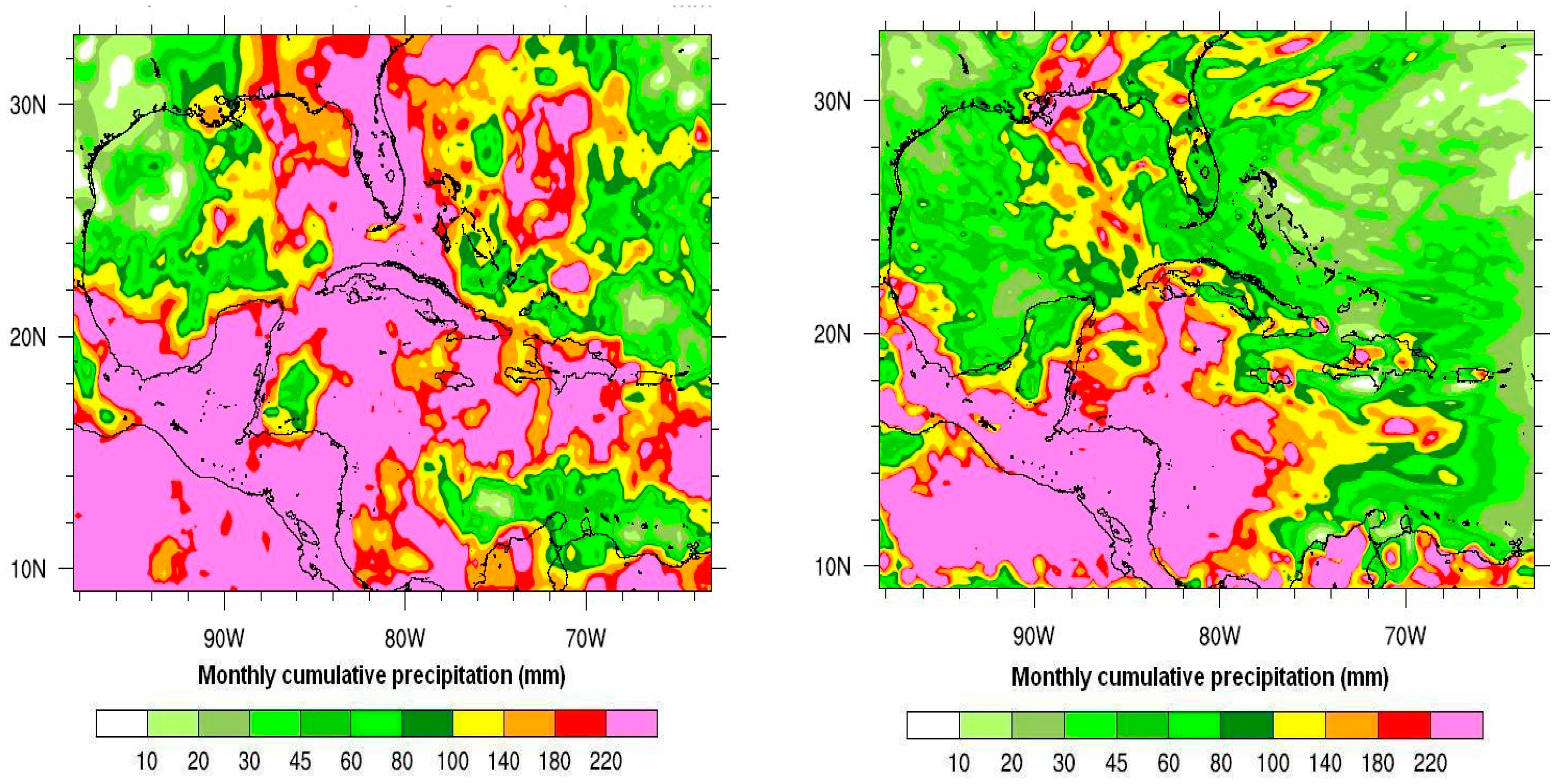
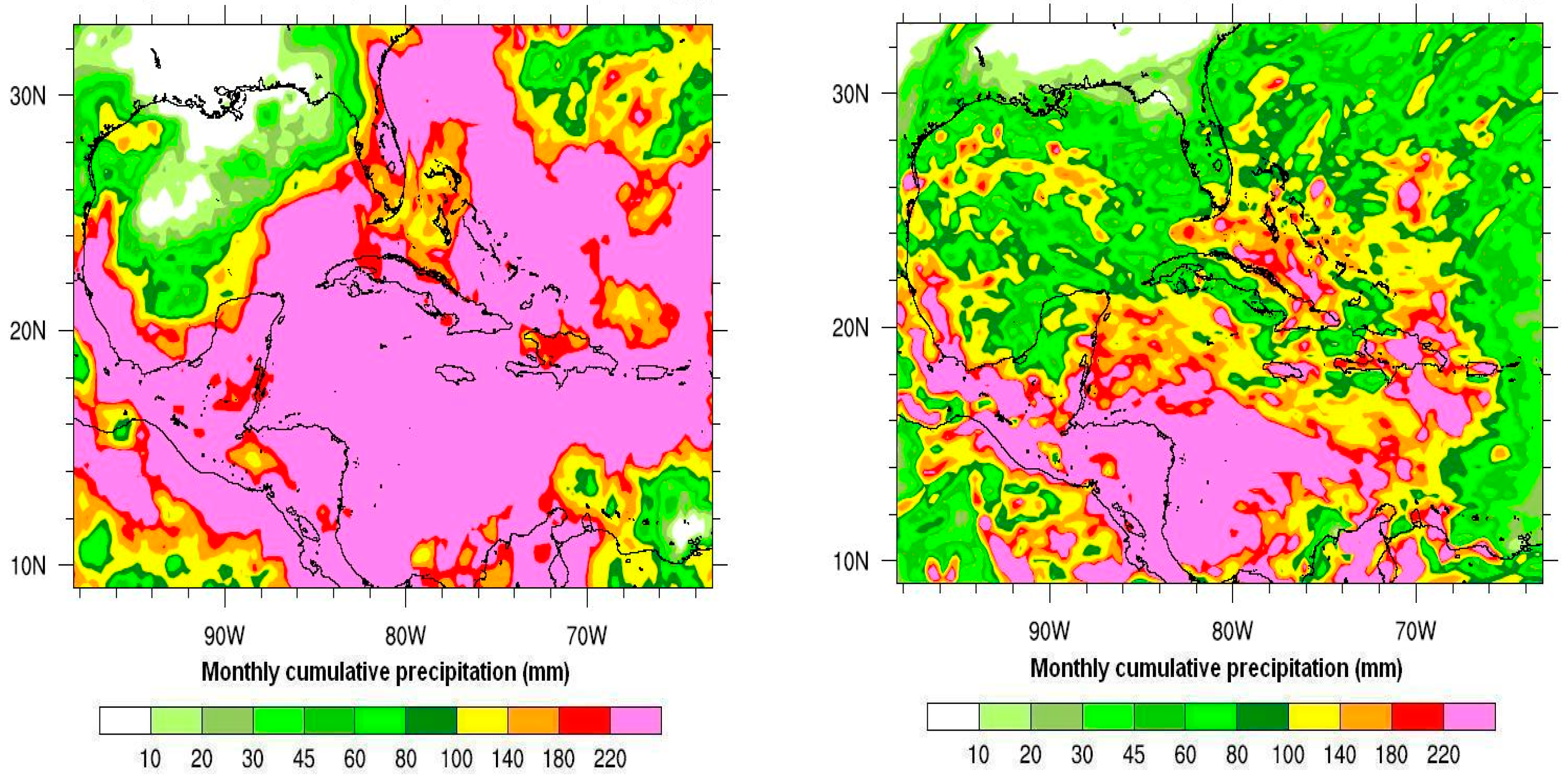

| Parameters | Option | Comments/References |
|---|---|---|
| Experiments | 6 | In the table they are referred to as Exp. 1 to 6. |
| Start Dates | Exp. 1: 1/10/2003 Exp. 2: 1/04/2004 Exp. 3: 1/10/2004 Exp. 4: 1/04/2005 Exp. 5: 1/10/2007 Exp. 6: 1/04/2008 | The periods studied were chosen taking into account the availability of data, ensuring that different meteorological conditions would be met (dry and rainy periods, presence of tropical storms and hurricanes, etc.). Start dates and periods were chosen in a manner such that experiments would overlap. |
| Simulation Times | 15 months | The first month was considered as the period of model self-tunning (spin up). |
| Ocean–Atmosphere Interaction | sst_update = 1 | Sea surface temperature was updated every 6 h. Data from Era-Interim. |
| Boundary Layer Parameterization | Mellor-Yamada-Janjic | Janjic, (1994) [26]. This parameterization obtained satisfactory results in convective forecasts [27] |
| Parameterization of Cumuli | Grell-Freitas | Grell and Freitas, (2013) [28]. This scheme was chosen as it was used at the Institute of Meteorology of Cuba with favorable results [29]. |
| Microphysics Parameterization | Lin et al. | Lin et al. (1983) [30]. This was a parameterization of a relatively low computational cost, which included ice and graupel formation processes adequate for simulations with real data. |
| Short- and Long-Wave Parameterization | Rapid Radiative Transfer Model (RRTMG) | Iacono et al. (2008) [31]. These schemes represent the variability of the clouds field, which was not attached to the domain resolution. |
| Season | Category | T-F | TL-FL | FL-S |
|---|---|---|---|---|
| 2003–2004 | NL | 93 | 79 | 79 |
| NH | 100 | 79 | 71 | |
| 2004–2005 | NL | 93 | 79 | 79 |
| NH | 79 | 86 | 86 | |
| 2007–2008 | NL | 86 | 86 | 86 |
| NH | 86 | 71 | 79 | |
| Average NL | 90.6 | 81.3 | 81.3 | |
| Average NH | 88.3 | 78.6 | 78.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Álvarez-Escudero, L.; Mayor, Y.G.; Borrajero-Montejo, I.; Bezanilla-Morlot, A. Assessing the Potential of a Long-Term Climate Forecast for Cuba Using the WRF Model. Environ. Sci. Proc. 2021, 8, 44. https://doi.org/10.3390/ecas2021-10338
Álvarez-Escudero L, Mayor YG, Borrajero-Montejo I, Bezanilla-Morlot A. Assessing the Potential of a Long-Term Climate Forecast for Cuba Using the WRF Model. Environmental Sciences Proceedings. 2021; 8(1):44. https://doi.org/10.3390/ecas2021-10338
Chicago/Turabian StyleÁlvarez-Escudero, Lourdes, Yandy G. Mayor, Israel Borrajero-Montejo, and Arnoldo Bezanilla-Morlot. 2021. "Assessing the Potential of a Long-Term Climate Forecast for Cuba Using the WRF Model" Environmental Sciences Proceedings 8, no. 1: 44. https://doi.org/10.3390/ecas2021-10338
APA StyleÁlvarez-Escudero, L., Mayor, Y. G., Borrajero-Montejo, I., & Bezanilla-Morlot, A. (2021). Assessing the Potential of a Long-Term Climate Forecast for Cuba Using the WRF Model. Environmental Sciences Proceedings, 8(1), 44. https://doi.org/10.3390/ecas2021-10338






