Simulation of Indirect 13C–13C J-Coupling Tensors in Diamond Clusters Hosting the NV Center †
Abstract
:1. Introduction
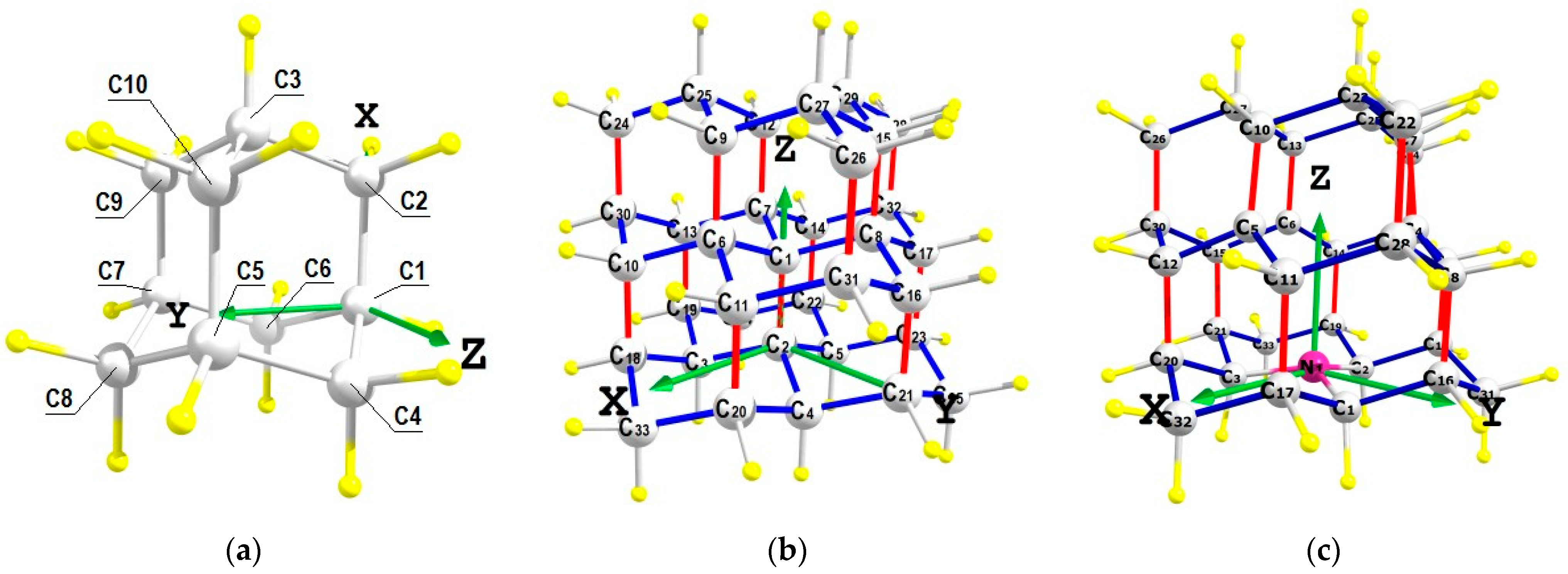
2. Methods and Materials
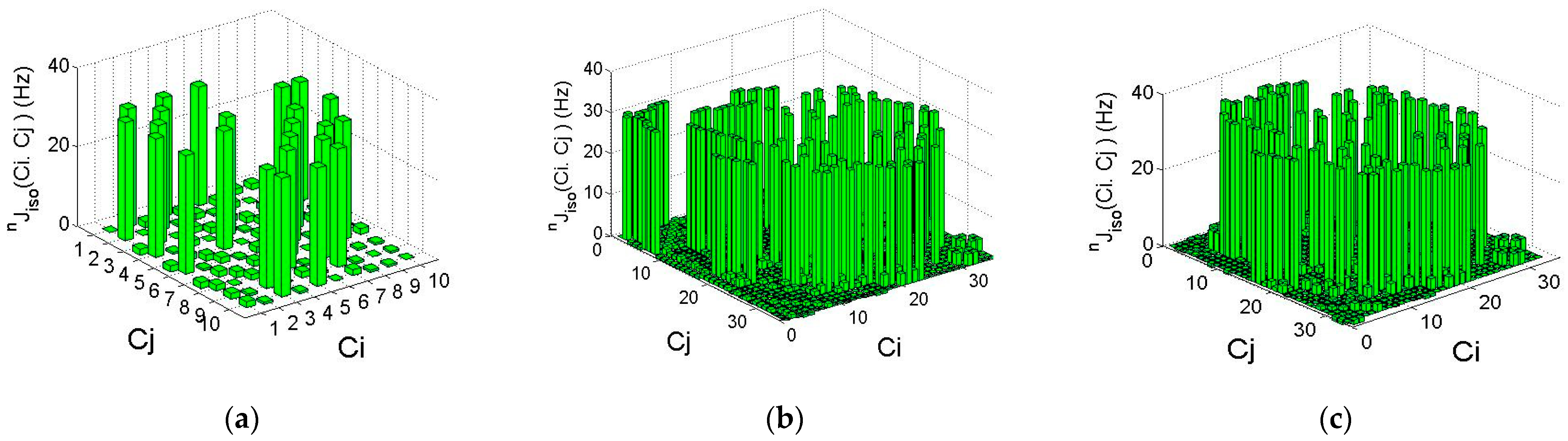
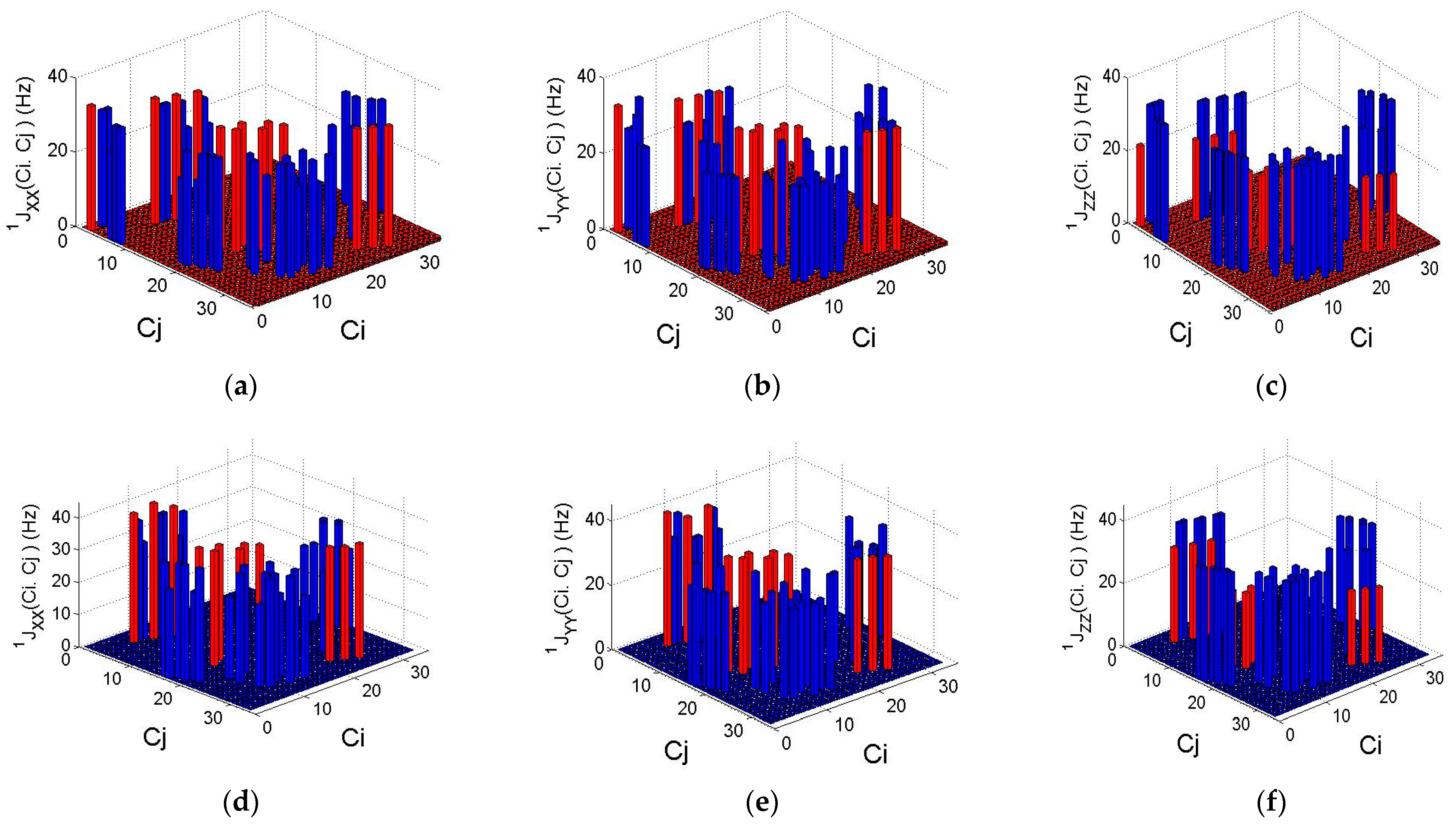
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schwartz, I.; Rosskopf, J.; Schmitt, S.; Tratzmiller, B.; Chen, Q.; McGuinness, L.P.; Jelezko, F.; Plenio, M.B. Blueprint for nanoscale NMR. Sci. Rep. 2019, 9, 6938. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barry, J.F.; Schloss, J.M.; Bauch, E.; Turner, M.J.; Hart, C.A.; Pham, L.M.; Walsworth, R.L. Sensitivity optimization for NV-diamond magnetometry. Rev. Mod. Phys. 2020, 92, 015004. [Google Scholar] [CrossRef]
- Chen, Q.; Schwarz, I.; Plenio, M.B. Steady-state preparation of long-lived nuclear spin singlet pairs at room temperature. Phys. Rev. B 2017, 95, 224105. [Google Scholar] [CrossRef] [Green Version]
- Glenn, D.R.; Bucher, D.B.; Lee, J.; Lukin, M.D.; Park, H.; Walsworth, R.L. High-resolution magnetic resonance spectroscopy using a solid-state spin sensor. Nature 2018, 95, 55535. [Google Scholar] [CrossRef] [Green Version]
- Harris, K.J.; Bryce, D.L.; Wasylishen, R.E. NMR line shapes from AB spin systems in solids—The role of antisymmetric spin-spin coupling. Can. J. Chem. 2009, 87, 1338–1351. [Google Scholar] [CrossRef]
- Frydman, L. Spin-1/2 and beyond: A perspective in solid state NMR spectroscopy. Annu. Rev. Phys. Chem. 2001, 52, 463–498. [Google Scholar] [CrossRef] [Green Version]
- Reif, B.; Ashbrook, S.E.; Emsley, L.; Hong, M. Solid-state NMR spectroscopy. Nat. Rev. Methods Primers 2021, 1, 2. [Google Scholar] [CrossRef]
- Vaara, J.; Jokisaari, J.; Wasylishen, R.E.; Bryce, D.L. Spin-spin coupling tensors as determined by experiment and computational chemistry. Prog. Nucl. Magn. Reson. Spectrosc. 2002, 41, 233–304. [Google Scholar] [CrossRef]
- Christensen, B.; Price, J.C. NMR lineshape of 29Si in single-crystal silicon. Phys. Rev. B 2017, 95, 134417. [Google Scholar] [CrossRef] [Green Version]
- Lefmann, K.; Buras, B.; Pedersen, E.J.; Shabanova, E.S.; Thorsen, P.A.; Rasmussen, F.B.; Sellschop, J.P.F. NMR spectra of pure 13C diamond. Phys. Rev B 1994, 50, 15623–15627. [Google Scholar] [CrossRef]
- Ramsey, F. Electron Coupled Interactions between Nuclear Spins in Molecules. Phys. Rev. 1953, 91, 303–307. [Google Scholar] [CrossRef]
- Wray, V. Carbon-carbon coupling constants: A compilation of data and a practical quide. Prog. NMR Spectrosc. 1979, 13, 177–256. [Google Scholar] [CrossRef]
- Helgaker, T.; Jaszunski, M.; Ruud, K. Ab Initio Methods for the Calculation of NMR Shielding and Indirect Spin−Spin Coupling Constants. Chem. Rev. 1999, 99, 293–352. [Google Scholar] [CrossRef]
- Helgaker, T.; Jaszuński, M.; Pecul, M. The quantum-chemical calculation of NMR indirect spin–spin coupling constants. Prog. Nucl. Magn. Reson. Spectrosc. 2008, 53, 249–268. [Google Scholar] [CrossRef]
- Antušek, A.; Kędziera, D.; Jackowski, K.; Jaszuński, M.; Makulski, W. Indirect spin–spin coupling constants in CH4, SiH4 and GeH4–Gas-phase NMR experiment and ab initio calculations. Chem. Phys. 2008, 352, 320–326. [Google Scholar] [CrossRef]
- Krivdin, L.B.; Contreras, R.H. Recent Advances in Theoretical Calculations of Indirect Spin–Spin Coupling Constants. Annu. Rep. Nucl. Magn. Reson. Spectrosc. 2007, 61, 133–245. [Google Scholar]
- Kamienska-Trela, K. One-bond 13C-13C Spin-Spin Coupling Constants. Annu. Rep. NMR Spectrosc. 1995, 30, 131–222. [Google Scholar]
- Jaszunsi, M.; Ruud, R.; Helgaker, T. Density-functional theory calculation of the nuclear magnetic resonance indirect nuclear spin—spin coupling constants in C60. Mol. Phys. 2003, 101, 1997–2002. [Google Scholar] [CrossRef]
- Peralta, J.E.; Barone, V.; Scuseria, G.E.; Contrera, R.H. Density Functional Theory Calculation of Indirect Nuclear Magnetic Resonance Spin-Spin Coupling Constants in C70. J. Am. Chem. Soc. 2004, 126, 7428–7429. [Google Scholar] [CrossRef]
- Gay, I.D.; Jones, C.H.W.; Sharma, R.D. INADEQUATE in the Solid State. Homonuclear Couplings in [(CH3)2SnE]3. J. Magn. Reson. 1991, 91, 186–189. [Google Scholar]
- NMR Spectra. Available online: https://www.orcasoftware.de/tutorials_orca/spec/NMR.html (accessed on 22 April 2022).
- ORCA Manual Version 5.0.2P.320. Available online: https://orcaforum.kofo.mpg.de/app.php/dlext/?cat=18 (accessed on 22 April 2022).
- Nizovtsev, A.P.; Kilin, S.Y.; Pushkarchuk, A.L.; Pushkarchuk, V.A.; Kuten, S.A.; Zhikol, O.A.; Schmitt, S.; Unden, T.; Jelezko, F. Non-flipping 13C spins near an NV center in diamond: Hyperfine and spatial characteristics by density functional theory simulation of the C510[NV]H252 cluster. New J. Phys. 2018, 20, 023022. [Google Scholar] [CrossRef]
- Theis, T.; Blanchard, J.W.; Butler, M.C.; Ledbetter, M.P.; Budker, D.; Pines, A. Chemical analysis using J-coupling multiplets in zero-field NMR. Chem. Phys. Lett. 2013, 580, 160–165. [Google Scholar] [CrossRef]
- Blanchard, J.W.; Budker, D. Zero- to Ultralow-field NMR. eMagRes 2016, 5, 1395–1410. [Google Scholar]
- Jiang, M.; Wu, T.; Blanchard, J.W.; Feng, G.; Peng, X.; Budker, D. Experimental benchmarking of quantum control in zero-field nuclear magnetic resonance. Sci. Adv. 2018, 4, eaar6327. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- DeVience, S.J.; Greer, M.; Mandal, S.; Rosen, M.S. Homonuclear J-Coupling Spectroscopy at Low Magnetic Fields using Spin-Lock Induced Crossing. ChemPhysChem 2021, 22, 2128–2137. [Google Scholar] [CrossRef] [PubMed]
| Diamagnetic contribution: | Paramagnetic contribution: | Fermi-Contact contribution: | ||||||
| [−0.80 | 0 | 0.00 | [0.21 | 0 | 0.00 | [28.91 | 0 | 0 |
| 0 | −0.85 | 0.08 | 0 | −0.08 | −0.03 | 0 | 28.91 | 0 |
| 0.00 | −0.06 | 2.53]; | 0.00 | 0.04 | −1.81]; | 0 | 0 | 28.91]; |
| Spin-Dipolar contribution: | SD/FC cross-term contribution: | Total coupling tensor: | ||||||
| [0.54 | 0 | 0.00 | [5.01 | 0 | −0.00 | [33.87 | 0 | −0.00 |
| 0 | 0.59 | −0.07 | 0 | 4.98 | −0.06 | 0 | 33.55 | −0.08 |
| 0.00 | 0.08 | 2.34]; | −0.00 | −0.06 | −9.99]; | −0.00 | 0.01 | 21.97] |
| Cluster C35H36 | Cluster C33[NV−]H36 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Pair Ci,Cj | 1Jxx | 1Jyy | 1Jzz | 1Jiso | Pair Ci,Cj | 1Jxx | 1Jyy | 1Jzz | 1Jiso |
| C2,C1 | 33.45 | 33.45 | 22.41 | 29.77 | C4,C7 | 39.93 | 41.41 | 30.08 | 37.14 |
| C6,C9 | 33.66 | 33.44 | 22.52 | 29.87 | C5,C10 | 42.06 | 39.12 | 30.01 | 37.06 |
| C7,C12 | 33.49 | 33.60 | 22.51 | 29.87 | C6,C13 | 39.93 | 41.41 | 30.08 | 37.14 |
| C8,C15 | 33.49 | 33.60 | 22.51 | 29.87 | C8,C16 | 35.88 | 35.50 | 23.99 | 31.79 |
| C18,C10 | 32.71 | 32.79 | 21.56 | 29.02 | C11,C17 | 35.68 | 35.71 | 24.02 | 31.80 |
| C20,C11 | 32.71 | 32.79 | 21.57 | 29.02 | C9,C18 | 35.53 | 35.89 | 24.00 | 31.81 |
| C19,C13 | 32.86 | 32.67 | 21.58 | 29.04 | C14,C19 | 35.53 | 35.89 | 24.00 | 31.81 |
| C22,C14 | 32.71 | 32.82 | 21.58 | 29.04 | C12,C20 | 35.68 | 35.71 | 24.02 | 31.80 |
| C21,C16 | 32.85 | 32.66 | 21.57 | 29.03 | C15,C21 | 35.88 | 35.50 | 23.99 | 31.79 |
| C23,C17 | 32.71 | 32.82 | 21.58 | 29.03 | C22,C28 | 35.41 | 35.18 | 23.79 | 31.46 |
| C30,C24 | 32.44 | 32.32 | 20.90 | 28.55 | C24,C29 | 35.07 | 35.53 | 23.80 | 31.47 |
| C31,C26 | 32.44 | 32.31 | 20.90 | 28.55 | C26,C30 | 35.40 | 35.18 | 23.79 | 31.46 |
| C32,C28 | 32.25 | 32.51 | 20.91 | 28.56 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nizovtsev, A.; Pushkarchuk, A.; Kuten, S.; Michels, D.; Lyakhov, D.; Kargin, N.; Kilin, S. Simulation of Indirect 13C–13C J-Coupling Tensors in Diamond Clusters Hosting the NV Center. Mater. Proc. 2022, 9, 4. https://doi.org/10.3390/materproc2022009004
Nizovtsev A, Pushkarchuk A, Kuten S, Michels D, Lyakhov D, Kargin N, Kilin S. Simulation of Indirect 13C–13C J-Coupling Tensors in Diamond Clusters Hosting the NV Center. Materials Proceedings. 2022; 9(1):4. https://doi.org/10.3390/materproc2022009004
Chicago/Turabian StyleNizovtsev, Alexander, Aliaksandr Pushkarchuk, Semen Kuten, Dominik Michels, Dmitry Lyakhov, Nikolai Kargin, and Sergei Kilin. 2022. "Simulation of Indirect 13C–13C J-Coupling Tensors in Diamond Clusters Hosting the NV Center" Materials Proceedings 9, no. 1: 4. https://doi.org/10.3390/materproc2022009004
APA StyleNizovtsev, A., Pushkarchuk, A., Kuten, S., Michels, D., Lyakhov, D., Kargin, N., & Kilin, S. (2022). Simulation of Indirect 13C–13C J-Coupling Tensors in Diamond Clusters Hosting the NV Center. Materials Proceedings, 9(1), 4. https://doi.org/10.3390/materproc2022009004







