Resonance Fluorescence of a Quantum Dot near a Metallic Nanoparticle: Quantum Interference Effects †
Abstract
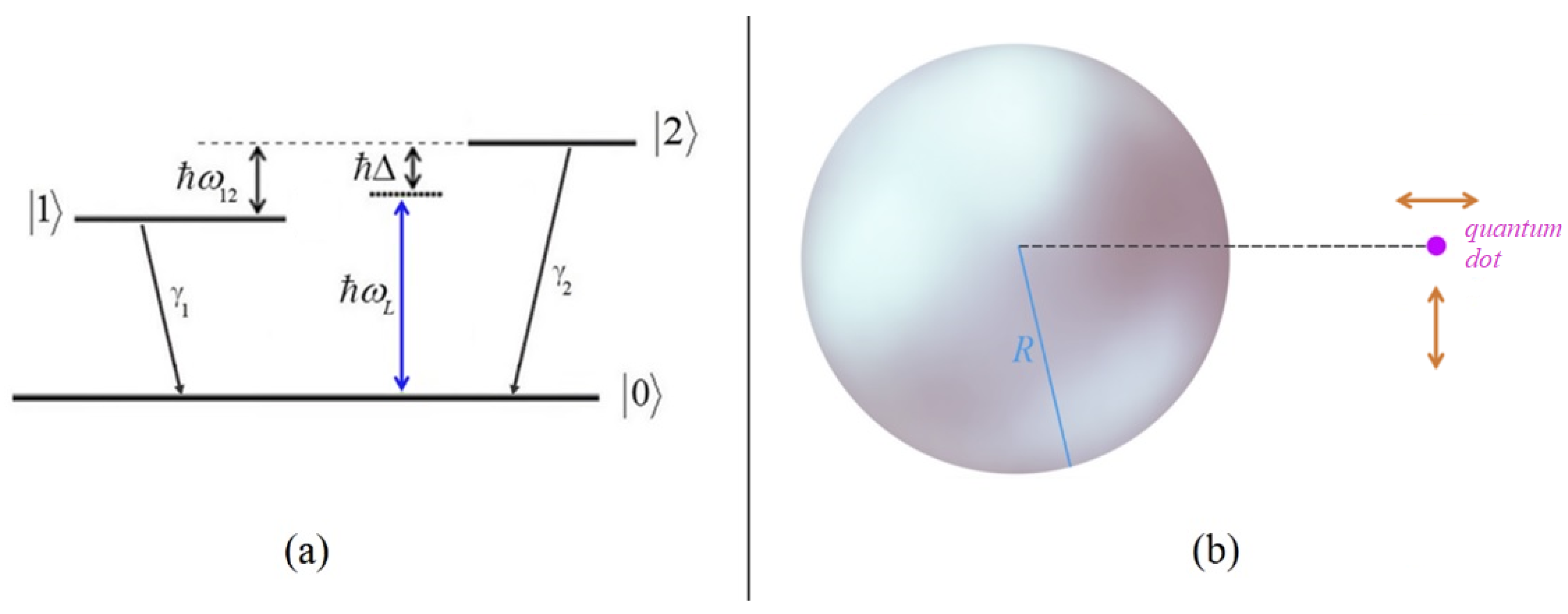
:1. Introduction
2. Methods
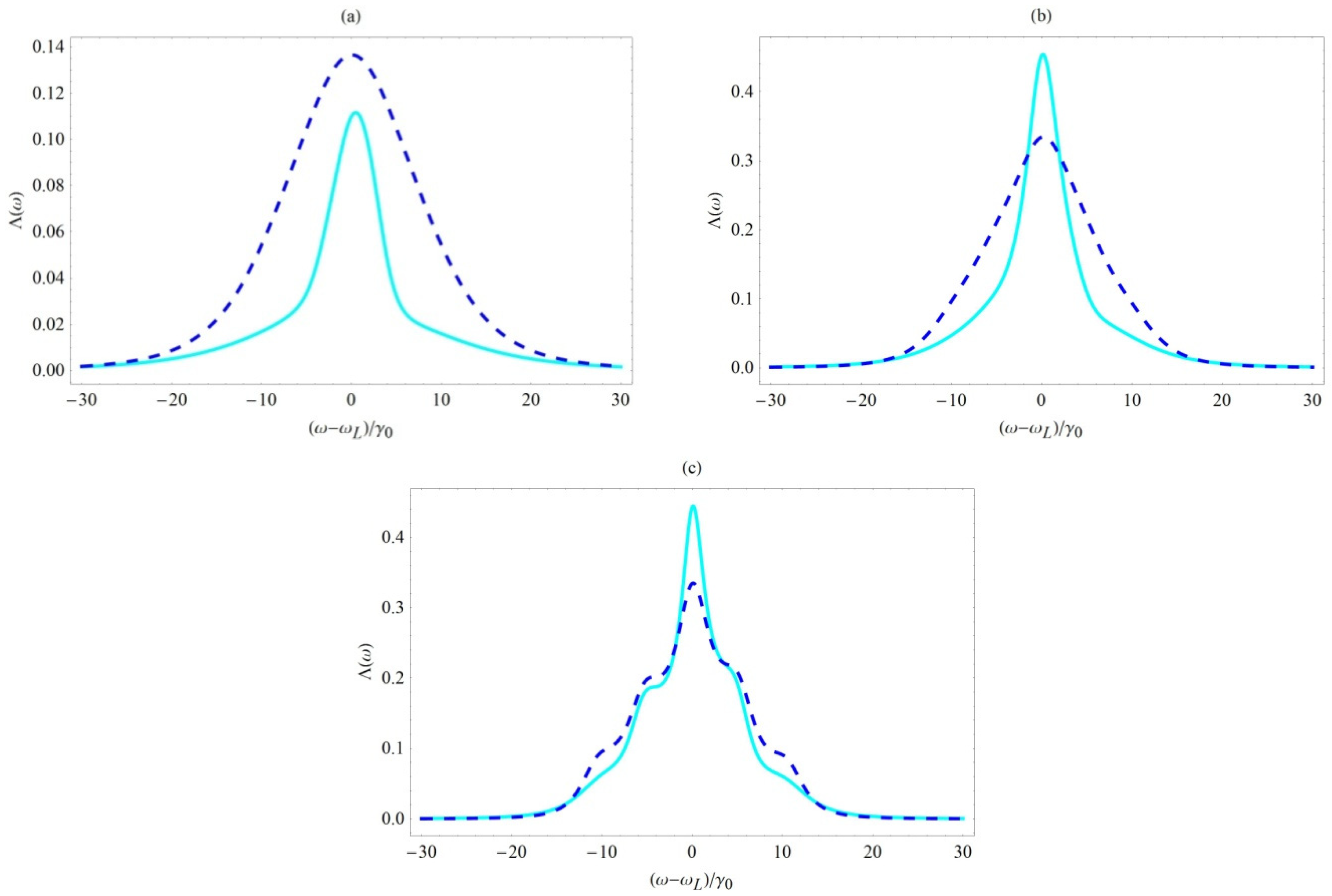
3. Parameters and Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vladimirova, Y.; Zadkov, V. Quantum optics in nanostructures. Nanomaterials 2021, 11, 1919. [Google Scholar] [CrossRef] [PubMed]
- Ridolfo, A.; Di Stefano, O.; Fina, N.; Saija, R.; Savasta, S. Quantum plasmonics with quantum dot-metal nanoparticle molecules: Influence of the Fano effect on photon statistics. Phys. Rev. Lett. 2010, 105, 263601. [Google Scholar] [CrossRef] [PubMed]
- Carreño, F.; Antón, M.A.; Yannopapas, V.; Paspalakis, E. Resonance fluorescence spectrum of a Λ-type quantum emitter close to a metallic nanoparticle. Phys. Rev. A 2016, 94, 013834. [Google Scholar] [CrossRef] [Green Version]
- Carreño, F.; Antón, M.A.; Yannopapas, V.; Paspalakis, E. Control of resonance fluorescence of a four-level quantum emitter near a plasmonic nanostructure. Phys. Rev. A 2017, 95, 043825. [Google Scholar] [CrossRef]
- Gu, Y.; Wang, L.; Ren, P.; Zhang, J.; Zhang, T.; Martin, O.J.F.; Gong, Q. Surface-plasmon-induced modification on the spontaneous emission spectrum via subwavelength-confined anisotropic Purcell factor. Nano Lett. 2012, 12, 2488–2493. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, P.; Swain, S. Ultranarrow spectral lines via quantum interference. Phys. Rev. Lett. 1996, 77, 3995–3998. [Google Scholar] [CrossRef] [PubMed]
- Yannopapas, V.; Paspalakis, E.; Vitanov, N.V. Plasmon-induced enhancement of quantum interference near metallic nanostructures. Phys. Rev. Lett. 2009, 103, 063602. [Google Scholar] [CrossRef] [PubMed]
- Lax, M. Quantum noise. XI. Multitime correspondence between quantum and classical stochastic processes. Phys. Rev. 1968, 172, 350–361. [Google Scholar] [CrossRef]
- Yannopapas, V.; Vitanov, N.V. Electromagnetic Green’s tensor and local density of states calculations for collections of spherical scatterers. Phys. Rev. B 2007, 75, 115124. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kosionis, S.G.; Yannopapas, V.; Thanopulos, I.; Paspalakis, E. Resonance Fluorescence of a Quantum Dot near a Metallic Nanoparticle: Quantum Interference Effects. Mater. Proc. 2022, 9, 19. https://doi.org/10.3390/materproc2022009019
Kosionis SG, Yannopapas V, Thanopulos I, Paspalakis E. Resonance Fluorescence of a Quantum Dot near a Metallic Nanoparticle: Quantum Interference Effects. Materials Proceedings. 2022; 9(1):19. https://doi.org/10.3390/materproc2022009019
Chicago/Turabian StyleKosionis, Spyridon G., Vassilios Yannopapas, Ioannis Thanopulos, and Emmanuel Paspalakis. 2022. "Resonance Fluorescence of a Quantum Dot near a Metallic Nanoparticle: Quantum Interference Effects" Materials Proceedings 9, no. 1: 19. https://doi.org/10.3390/materproc2022009019
APA StyleKosionis, S. G., Yannopapas, V., Thanopulos, I., & Paspalakis, E. (2022). Resonance Fluorescence of a Quantum Dot near a Metallic Nanoparticle: Quantum Interference Effects. Materials Proceedings, 9(1), 19. https://doi.org/10.3390/materproc2022009019








