Steady-State and Transient Electrical Properties of Liquid Crystal Cells †
Abstract
:1. Introduction
2. Model
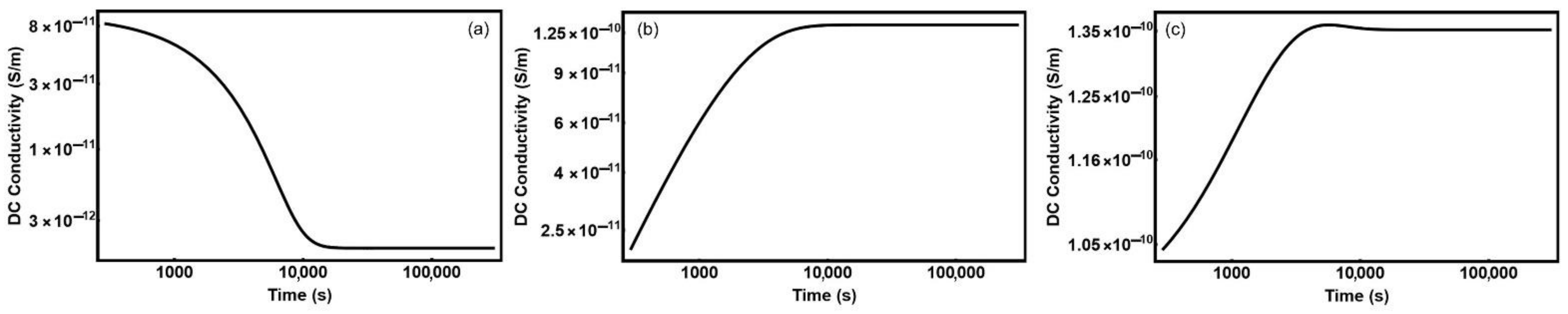
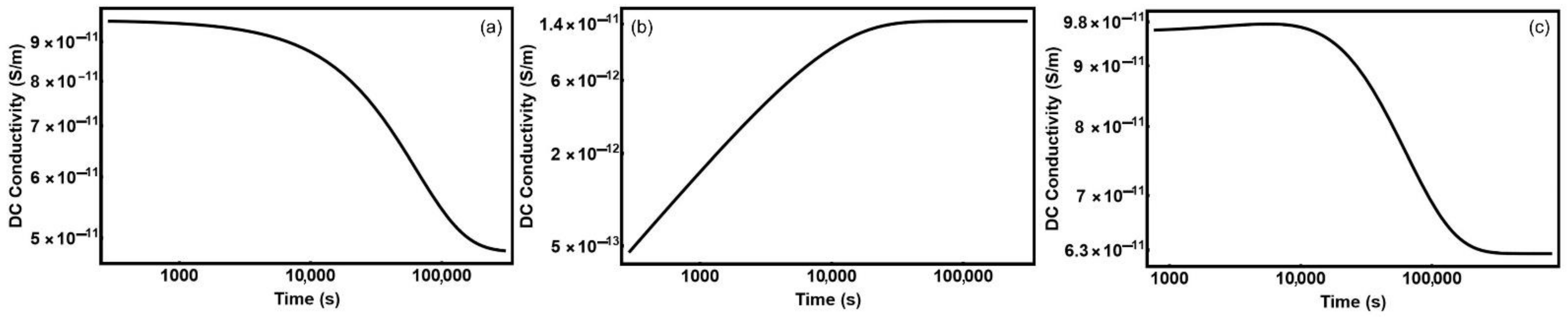
3. Results: DC Electrical Conductivity of Liquid Crystal Cells
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Koide, N. (Ed.) 50 years of liquid crystal R&D that lead the way to the future. In The Liquid Crystal Display Story; Springer: Tokyo, Japan, 2014. [Google Scholar] [CrossRef]
- Jones, C. The fiftieth anniversary of the liquid crystal display. Liq. Cryst. Today 2018, 27, 44–70. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Liao, E.; Chen, R.; Wu, S.-T. Liquid-Crystal-on-Silicon for Augmented Reality Displays. Appl. Sci. 2018, 8, 2366. [Google Scholar] [CrossRef] [Green Version]
- Xiong, J.; Hsiang, E.-L.; He, Z.; Zhan, T.; Wu, S.-T. Augmented reality and virtual reality displays: Emerging technologies and future perspectives. Light Sci. Appl. 2021, 10, 216. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.-J.; Lin, Y.-H. Liquid crystal technology for vergence-accommodation conflicts in augmented reality and virtual reality systems: A review. Liq. Cryst. Rev. 2021, 9, 35–64. [Google Scholar] [CrossRef]
- Abdulhalim, I. Non-display bio-optic applications of liquid crystals. Liq. Cryst. Today 2011, 20, 44–60. [Google Scholar] [CrossRef] [Green Version]
- Chigrinov, V.G. Liquid Crystal Photonics; Nova Science Pub Inc.: New York, NY, USA, 2014; 204p. [Google Scholar]
- Lin, Y.; Wang, Y.; Reshetnyak, V. Liquid crystal lenses with tunable focal length. Liq. Cryst. Rev. 2017, 5, 111–143. [Google Scholar] [CrossRef]
- Schenning, A.P.H.J.; Crawford, G.P.; Broer, D.J. (Eds.) Liquid Crystal Sensors; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2018; 164p. [Google Scholar]
- De Sio, L.; Roberts, D.E.; Liao, Z.; Hwang, J.; Tabiryan, N.; Steeves, D.M.; Kimball, B.R. Beam shaping diffractive wave plates. Appl. Opt. 2018, 57, A118–A121. [Google Scholar] [CrossRef] [PubMed]
- Otón, J.M.; Otón, E.; Quintana, X.; Geday, M.A. Liquid-crystal phase-only devices. J. Mol. Liq. 2018, 267, 469–483. [Google Scholar] [CrossRef]
- Morris, R.; Jones, C.; Nagaraj, M. Liquid Crystal Devices for Beam Steering Applications. Micromachines 2021, 12, 247. [Google Scholar] [CrossRef]
- Chen, W.T.; Zhu, A.Y.; Capasso, F. Flat optics with dispersion-engineered metasurfaces. Nat. Rev. Mater. 2020, 5, 604–620. [Google Scholar] [CrossRef]
- Jeng, S.C. Applications of Tamm plasmon-liquid crystal devices. Liq. Cryst. 2020, 47, 1223–1231. [Google Scholar] [CrossRef]
- Lininger, A.; Zhu, A.Y.; Park, J.S.; Palermo, G.; Chatterjee, S.; Boyd, J.; Capasso, F.; Strangi, G. Optical properties of metasurfaces infiltrated with liquid crystals. Proc. Natl. Acad. Sci. USA 2020, 117, 20390–20396. [Google Scholar] [CrossRef]
- Camley, R.; Celinski, Z.; Garbovskiy, Y.; Glushchenko, A. Liquid crystals for signal processing applications in the microwave and millimeter wave frequency ranges. Liq. Cryst. Rev. 2018, 6, 17–52. [Google Scholar] [CrossRef]
- Jakoby, R.; Gaebler, A.; Weickhmann, C. Microwave Liquid Crystal Enabling Technology for Electronically Steerable Antennas in SATCOM and 5G Millimeter-Wave Systems. Crystals 2020, 10, 514. [Google Scholar] [CrossRef]
- Dabrowski, R.; Dziaduszek, J.; Bozetka, J.; Piecek, W.; Mazur, R.; Chrunik, M.; Perkowski, P.; Mrukiewicz, M.; Żurowska, M.; Weglowska, D. Fluorinated smectics—New liquid crystalline medium for smart windows and memory displays. J. Mol. Liq. 2017, 267, 415–427. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, X.; Zhan, Y.; Zhang, Y.; He, J.; Lv, P.; Yuan, D.; Hu, X.; Liu, D.; Broer, D.J.; et al. Electroconvection in zwitterion-doped nematic liquid crystals and application as smart windows. Adv. Opt. Mater. 2020, 27, 2001465. [Google Scholar] [CrossRef]
- Geis, M.W.; Bos, P.J.; Liberman, V.; Rothschild, M. Broadband optical switch based on liquid crystal dynamic scattering. Opt. Express 2016, 24, 13812–13823. [Google Scholar] [CrossRef]
- Konshina, E.A.; Shcherbinin, D.P. Study of dynamic light scattering in nematic liquid crystal and its optical, electrical and switching characteristics. Liq. Cryst. 2018, 45, 292–302. [Google Scholar] [CrossRef]
- Shaban, H.; Wu, P.-C.; Lee, J.-H.; Lee, W. Dielectric and electro-optical responses of a dielectrically negative nematic liquid crystal doped with cationic surfactant. Opt. Mater. Express 2021, 11, 3208–3222. [Google Scholar] [CrossRef]
- Castellón, E.; Levy, D. (Eds.) Smart Windows Based on Liquid Crystal Dispersions. In Transparent Conductive Materials; Chapter 5.4; Wiley-VCH: Weinheim, Germany, 2018; pp. 337–365. [Google Scholar] [CrossRef]
- Blinov, L.M. Structure and Properties of Liquid Crystals; Springer: New York, NY, USA, 2010. [Google Scholar]
- Neyts, K.; Beunis, F. Ion Transport in Liquid Crystals. In Handbook of Liquid Crystals: Physical Properties and Phase Behavior of Liquid Crystals; Chapter 11; Wiley-VCH: Weinheim, Germany, 2014; Volume 2, pp. 357–382. [Google Scholar]
- Éber, N.; Salamon, P.; Buka, Á. Electrically induced patterns in nematics and how to avoid them. Liq. Cryst. Rev 2016, 4, 101–134. [Google Scholar] [CrossRef]
- Colpaert, C.; Maximus, B.; Meyere, D. Adequate measuring techniques for ions in liquid crystal layers. Liq. Cryst. 1996, 21, 133–142. [Google Scholar] [CrossRef]
- Barbero, G.; Evangelista, L.R. Adsorption Phenomena and Anchoring Energy in Nematic Liquid Crystals; Taylor & Francis: Boca Raton, FL, USA, 2006. [Google Scholar]
- Garbovskiy, Y. Conventional and unconventional ionic phenomena in tunable soft materials made of liquid crystals and nanoparticles. Nano Express 2021, 2, 012004. [Google Scholar] [CrossRef]
- Khazimullin, M.V.; Lebedev, Y.A. Influence of dielectric layers on estimates of diffusion coefficients and concentrations of ions from impedance spectroscopy. Phys. Rev. E 2019, 100, 062601. [Google Scholar] [CrossRef] [Green Version]
- Karaawi, A.R.; Gavrilyak, M.V.; Boronin, V.A.; Gavrilyak, A.M.; Kazachonok, J.V.; Podgornov, F.V. Direct current electric conductivity of ferroelectric liquid crystals–gold nanoparticles dispersion measured with capacitive current technique. Liq. Cryst. 2020, 47, 1507–1515. [Google Scholar] [CrossRef]
- Garbovskiy, Y. Evaluating the Concentration of Ions in Liquid Crystal Cells: Hidden Factors and Useful Techniques. Proceedings 2020, 62, 10. [Google Scholar] [CrossRef]
- Webb, D.; Garbovskiy, Y. Overlooked Ionic Phenomena Affecting the Electrical Conductivity of Liquid Crystals. Eng. Proc. 2021, 11, 1. [Google Scholar] [CrossRef]
- Dhara, S.; Madhusudana, N.V. Ionic contribution to the dielectric properties of a nematic liquid crystal in thin cells. J. Appl. Phys. 2001, 90, 3483–3488. [Google Scholar] [CrossRef]
- Kovalchuk, O.V. Adsorption of ions and thickness dependence of conductivity in liquid crystal. Semicond. Phys. Quantum Electron. Optoelectron. 2011, 14, 452–455. [Google Scholar] [CrossRef]
- Kumar, A.; Varshney, D.; Prakash, J. Role of ionic contribution in dielectric behaviour of a nematic liquid crystal with variable cell thickness. J. Mol. Liq. 2020, 303, 112520. [Google Scholar] [CrossRef]
- Murakami, S.; Naito, H. Electrode and Interface Polarizations in Nematic Liquid Crystal Cells. Jpn. J. Appl. Phys. 1997, 36, 2222–2225. [Google Scholar] [CrossRef]
- Naito, H.; Yasuda, Y.; Sugimura, A. Desorption processes of adsorbed impurity ions on alignment layers in nematic liquid crystal cells. Mol. Cryst. Liq. Cryst. Sci. Technol. Sect. A Mol. Cryst. Liq. Cryst. 1997, 301, 85–90. [Google Scholar] [CrossRef]
- Mizusaki, M.; Enomoto, S.; Hara, Y. Generation mechanism of residual direct current voltage for liquid crystal cells with polymer layers produced from monomers. Liq. Cryst. 2016, 44, 609–617. [Google Scholar] [CrossRef]
- Kravchuk, R.; Koval’chuk, O.; Yaroshchuk, O. Filling initiated processes in liquid crystal cell. Mol. Cryst. Liq. Cryst. 2002, 384, 111–119. [Google Scholar] [CrossRef]
- Garbovskiy, Y. Time-dependent electrical properties of liquid crystal cells: Unravelling the origin of ion generation. Liq. Cryst. 2018, 45, 1540–1548. [Google Scholar] [CrossRef]
- Garbovskiy, Y. Ion capturing/ion releasing films and nanoparticles in liquid crystal devices. Appl. Phys. Lett. 2017, 110, 041103. [Google Scholar] [CrossRef]
- Garbovskiy, Y. Ions and size effects in nanoparticle/liquid crystal colloids sandwiched between two substrates. The case of two types of fully ionized species. Chem. Phys. Lett. 2017, 679, 77–85. [Google Scholar] [CrossRef]


| Physical Parameter | Value |
|---|---|
| 10−21 m3 (Figure 1a,c, Figure 2a,c, Figure 3a,c and Figure 4a,c) | |
| 10−26 m3/s (Figure 1a,c, Figure 2a,c, Figure 3a,c and Figure 4a,c) | |
| 10−5 s−1 (Figure 1a,c, Figure 2a,c, Figure 3a,c and Figure 4a,c) | |
| 10−22 m3 (Figure 1b,c, Figure 2b,c, Figure 3b,c and Figure 4b,c) | |
| 10−26 m3/s (Figure 1b,c, Figure 2b,c, Figure 3b,c and Figure 4b,c) | |
| 10−4 s−1 (Figure 1b,c, Figure 2b,c, Figure 3b,c and Figure 4b,c) | |
| 5 × 1016 m−2 (Figure 1, Figure 2, Figure 3 and Figure 4) | |
| 10−10 m2/Vs (Figure 1, Figure 2, Figure 3 and Figure 4) | |
| 0 (Figure 1a,c, Figure 2a,c, Figure 3a,c and Figure 4a,c) | |
| 10−3 (Figure 1b,c, Figure 2b,c, Figure 3b,c and Figure 4b,c) | |
| 6 × 1018 m−3 (Figure 1a,c, Figure 2a,c, Figure 3a,c and Figure 4a,c) | |
| 0 (Figure 1b,c, Figure 2b,c, Figure 3b,c and Figure 4b,c) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Webb, D.; Garbovskiy, Y. Steady-State and Transient Electrical Properties of Liquid Crystal Cells. Chem. Proc. 2022, 9, 15. https://doi.org/10.3390/IOCC_2022-12147
Webb D, Garbovskiy Y. Steady-State and Transient Electrical Properties of Liquid Crystal Cells. Chemistry Proceedings. 2022; 9(1):15. https://doi.org/10.3390/IOCC_2022-12147
Chicago/Turabian StyleWebb, David, and Yuriy Garbovskiy. 2022. "Steady-State and Transient Electrical Properties of Liquid Crystal Cells" Chemistry Proceedings 9, no. 1: 15. https://doi.org/10.3390/IOCC_2022-12147
APA StyleWebb, D., & Garbovskiy, Y. (2022). Steady-State and Transient Electrical Properties of Liquid Crystal Cells. Chemistry Proceedings, 9(1), 15. https://doi.org/10.3390/IOCC_2022-12147







