A Study of the Minimum Thermal Power of a Nuclear Reactor
Abstract
:1. Introduction
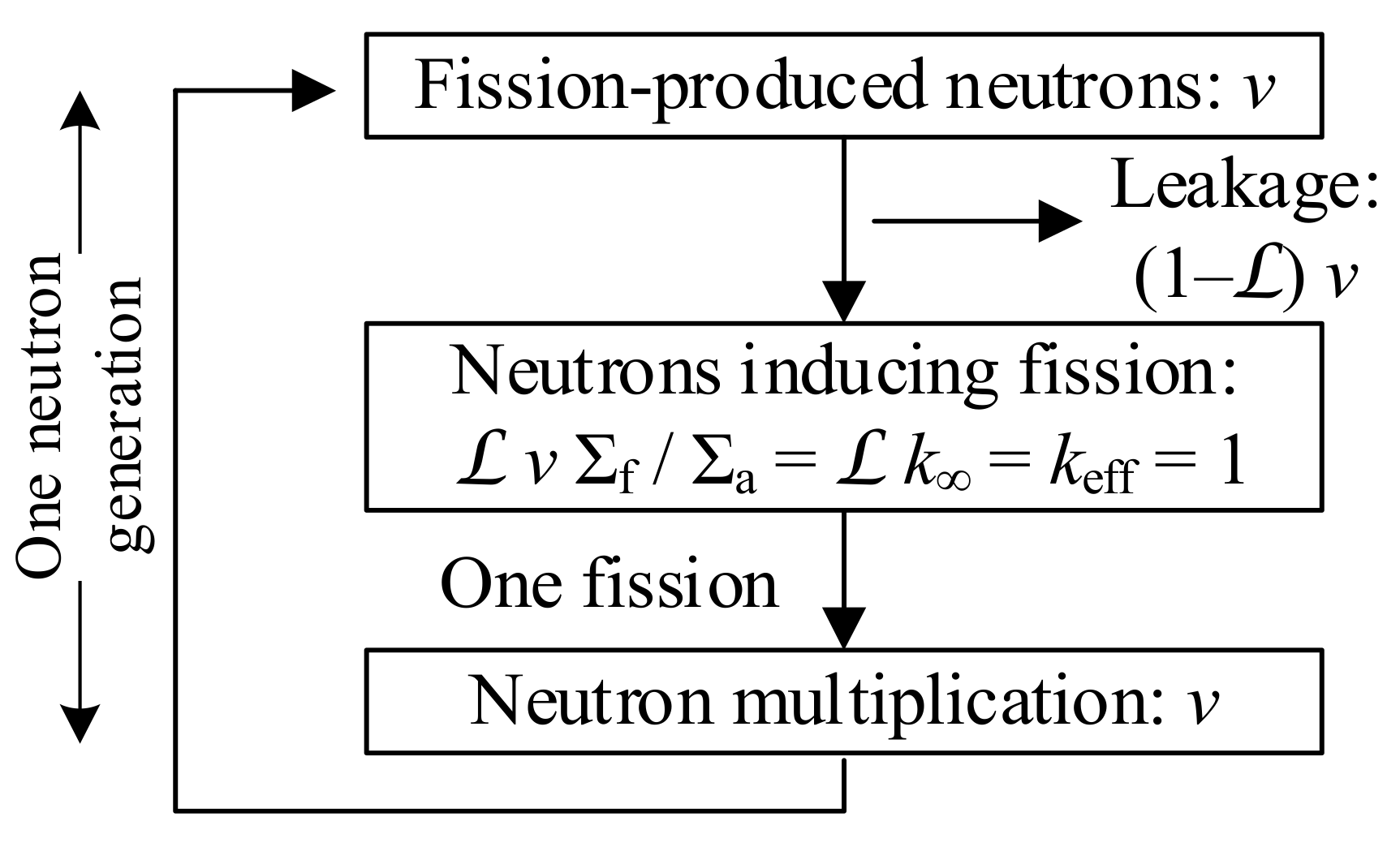
2. Minimum Power of an Ideal Critical Reactor
2.1. Analytical Formula
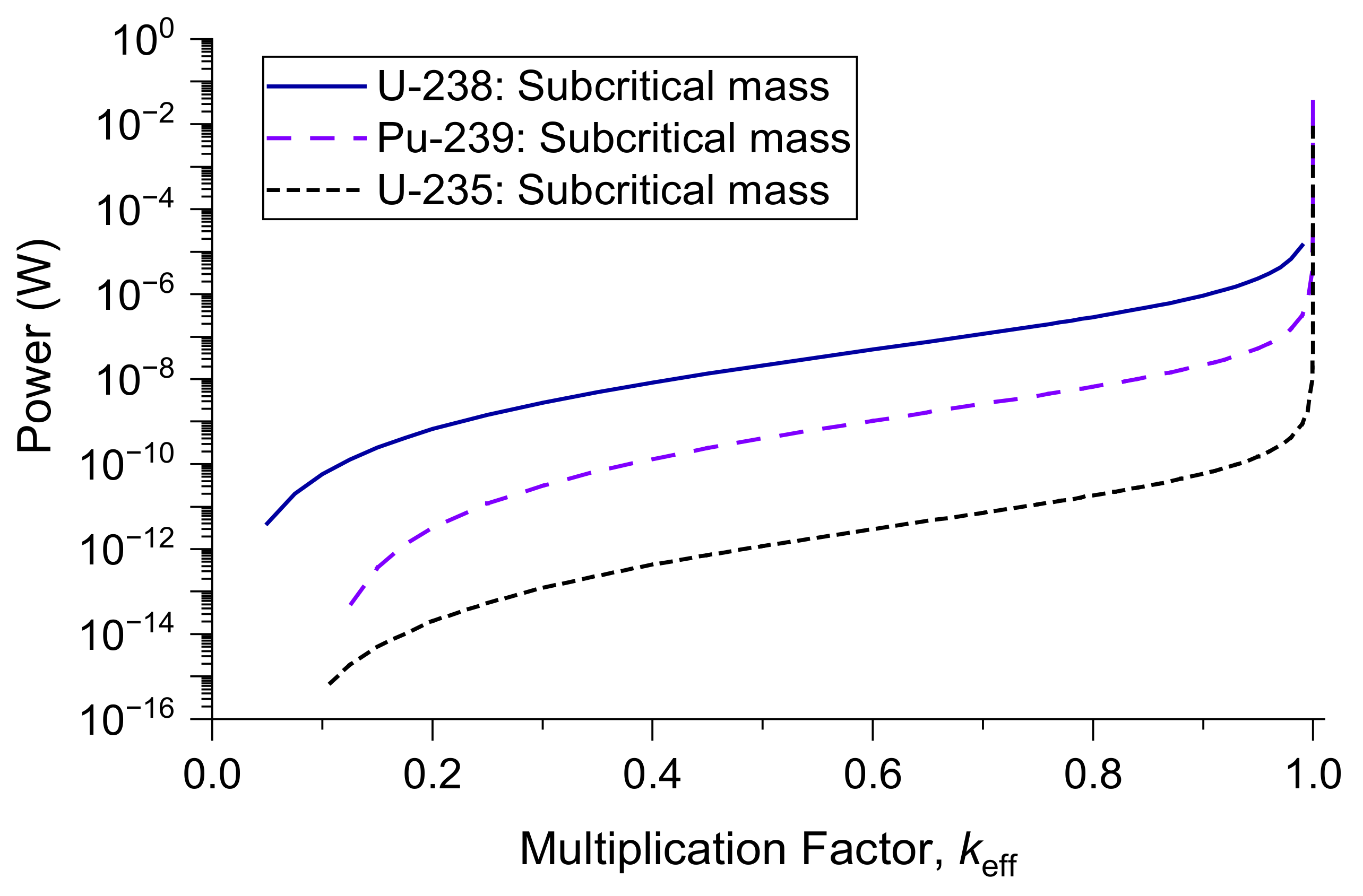
2.2. Numerical Results
3. Minimum Power of Subcritical Reactor with Intrinsic Source(s)
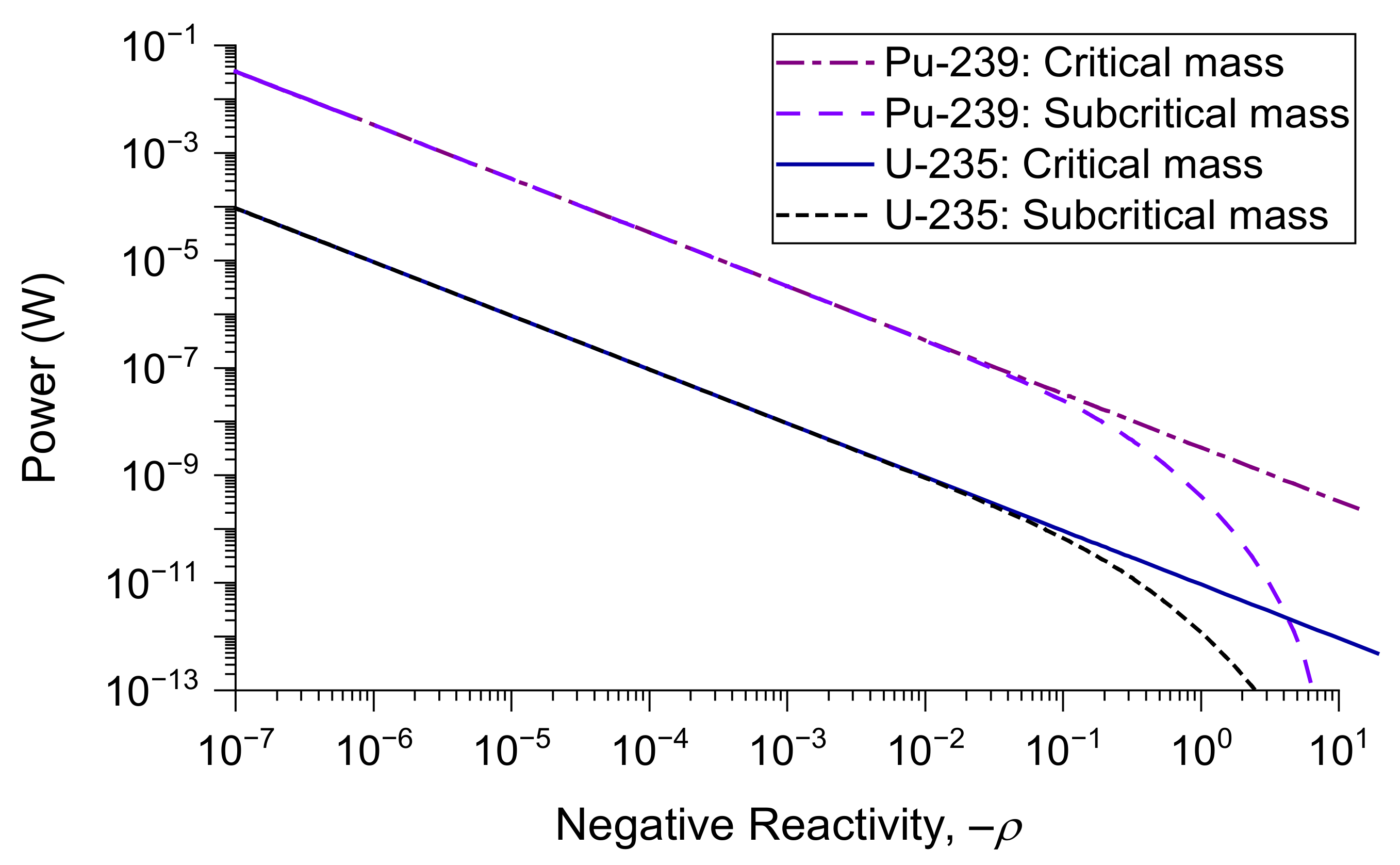
3.1. Analytical Formula
3.2. Spontaneous Fission Neutron Yields
3.3. Numerical Results
4. Radioisotopic Heat Production
5. Summary
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Fermi, E. Experimental Production of a Divergent Chain Reaction. Am. J. Phys. 1952, 20, 536–558. [Google Scholar] [CrossRef] [Green Version]
- Liverhant, S.E. Elementary Introduction to Nuclear Reactor Physics; Wiley: New York, NY, USA, 1960; p. 291. [Google Scholar]
- Yadigaroglu, G. Nuclear Reactors: Physics and Materials. Chimia 2005, 59, 877–886. [Google Scholar] [CrossRef]
- Lewis, E.E. Fundamentals of Nuclear Reactor Physics; Academic Press: London, UK, 2008; pp. 126, 221. [Google Scholar]
- Geppert, C.; Eberhardt, K.; Karpuk, S. Status and scientific use of the TRIGA research reactor at the University of Mainz. In Proceedings of the European Research Reactor Conference, European Nuclear Society, Berlin, Germany, 13–17 March 2016; pp. 208–214. [Google Scholar]
- Riemer, J.; Eberhardt, K.; Geppert, C.; Gorges, C.; Karpuk, S. Status and scientific use of the TRIGA research reactor at the University of Mainz. Int. J. Nucl. Power 2019, 64, 463–468. [Google Scholar]
- Dumonteil, E.; Bahran, R.; Cutler, T.; Dechenaux, B.; Grove, T.; Hutchinson, J.; McKenzie, G.; McSpaden, A.; Monange, W.; Nelson, M.; et al. Patchy nuclear chain reactions. Commun. Phys. 2021, 4, 1–10. [Google Scholar] [CrossRef]
- Goertzel, G. Minimum critical mass and flat flux. J. Nucl. Energy (1954) 1956, 2, 193–201. [Google Scholar] [CrossRef]
- Wilkins, J.E., Jr.; Srivastava, K.N. Minimum critical mass nuclear reactors. Part I. Nucl. Sci. Eng. 1982, 82, 307–315. [Google Scholar] [CrossRef]
- Seifritz, W.; Wydler, P. Criticality of Neptunium-237 and Its Possible Utilization in Nuclear Reactors. Nucl. Sci. Eng. 1979, 72, 272–276. [Google Scholar] [CrossRef]
- Sanchez, R.; Loaiza, D.; Kimpland, R.; Hayes, D.; Cappiello, C.; Chadwick, M. Criticality of a 237Np sphere. Nucl. Sci. Eng. 2008, 158, 1–14. [Google Scholar] [CrossRef]
- Ronen, Y.; Fridman, E.; Shwageraus, E. The Smallest Thermal Nuclear Reactor. Nucl. Sci. Eng. 2006, 153, 90–92. [Google Scholar] [CrossRef]
- Weaver, L.E. Reactor Dynamics and Control; Elsevier: New York, NY, USA, 1968; p. 39. [Google Scholar]
- Lewins, J. Nuclear Reactor Kinetics and Control; Pergamon: Oxford, UK, 1978; p. 57. [Google Scholar]
- Lamarsh, J.R.; Baratta, A.J. Introduction to Nuclear Engineering, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2001; pp. 330–333. [Google Scholar]
- Ott, K.O.; Neuhold, R.J. Introductory Nuclear Reactor Dynamics; American Nuclear Society: La Grange Park, IL, USA, 1985; pp. 23–26. [Google Scholar]
- Lamarsh, J.R. Introduction to Nuclear Reactor Theory; Addison-Wesley: Reading, MA, USA, 1966; pp. 435–436. [Google Scholar]
- Paxton, H.C. Critical assemblies at Los Alamos. Nucleonics 1955, 13, 48–50. [Google Scholar]
- Argonne National Laboratory. Reactor Physics Constants, 2nd ed.; ANL-5800; U.S. Atomic Energy Commission: Washington, DC, USA, 1963; pp. 581–585, 617–619.
- Brown, D.G.; Busch, R.D. Hand Calculation Methods for Criticality Safety—A Primer; LA-14244-M; Los Alamos National Laboratory: Los Alamos, NM, USA, 2006; pp. 31–36.
- Watt, B.E. Energy Spectrum of Neutrons from Thermal Fission of U235. Phys. Rev. 1952, 87, 1037–1041. [Google Scholar] [CrossRef]
- Kodeli, I.; Trkov, A.; Capote, R.; Nagaya, Y.; Maslov, V. Evaluation and use of the prompt fission neutron spectrum and spectra covariance matrices in criticality and shielding. Nucl. Instrum. Methods Phys. Res. Sect. A 2009, 610, 540–552. [Google Scholar] [CrossRef]
- Sher, R. Fission energy release for 16 fissioning nuclides. In Proceedings of the Conference on Nuclear Data Evaluation Methods and Procedures, Brookhaven National Laboratory, BNL-NCS-51363, Upton, NY, USA, 22–25 September 1980; Volume 2, pp. 835–860. [Google Scholar]
- Peterson, R.E.; Newby, G.A. An Unreflected U-235 Critical Assembly. Nucl. Sci. Eng. 1956, 1, 112–125. [Google Scholar] [CrossRef]
- Jarvis, G.A.; Linenberger, G.A.; Orndoff, J.D.; Paxton, H.C. Two Plutonium-Metal Critical Assemblies. Nucl. Sci. Eng. 1960, 8, 525–531. [Google Scholar] [CrossRef]
- Shibata, K.; Iwamoto, O.; Nakagawa, T.; Iwamoto, N.; Ichihara, A.; Kunieda, S.; Chiba, S.; Furutaka, K.; Otuka, N.; Ohsawa, T.; et al. JENDL-4.0: A new library for nuclear science and engineering. J. Nucl. Sci. Technol. 2011, 48, 1–30. Available online: https://wwwndc.jaea.go.jp/jendl/j40/j40.html (accessed on 13 August 2021).
- Preskitt, C.A.; Nephew, E.A.; Brown, J.R.; Van Howe, K.R. Interpretation of Pulsed-Source Experiments in the Peach Bottom HTGR. Nucl. Sci. Eng. 1967, 29, 283–295. [Google Scholar] [CrossRef]
- Harrer, J.M.; Beckerley, J.G. Nuclear Power Reactor Instrumentation Systems Handbook, Volume 1; U.S. Atomic Energy Commission: Springfield, VA, USA, 1973; pp. 24–25.
- Ruby, L. A problem in the teaching of reactor kinetics. Nucl. Sci. Eng. 1991, 107, 394–396. [Google Scholar] [CrossRef]
- Kerlin, T.W.; Upadhyaya, B.R. Dynamics and Control of Nuclear Reactors; Academic Press: London, UK, 2019; pp. 23–24, 53. [Google Scholar]
- Escalona, J. Evaluation de la Puissance d’un Reacteur en Regime Sous-Critique (Power Assessment of a Reactor in Subcritical Regime). C.E.A. Report No. 305. 1960, pp. 13, 24. Available online: https://inis.iaea.org/search/search.aspx?orig_q=RN:46012581 (accessed on 3 March 2020).
- Murray, R.L. Nuclear Reactor Physics; Prentice-Hall: Englewood Cliffs, NJ, USA, 1957; pp. 164–167. [Google Scholar]
- Holden, N.E.; Hoffman, D.C. Spontaneous fission half-lives for ground-state nuclides. Pure Appl. Chem. 2000, 72, 1525–1562. [Google Scholar] [CrossRef]
- Holden, N.E.; Hoffman, D.C. Errata: Spontaneous fission half-lives for ground-state nuclides. Pure Appl. Chem. 2001, 73, 1225–1227. [Google Scholar] [CrossRef]
- Holden, N.E. Table of the isotopes. In CRC Handbook of Chemistry and Physics, 102nd ed.; Rumble, J.R., Ed.; CRC Press/Taylor & Francis: Boca Raton, FL, USA, 2021. [Google Scholar]
- Perry, R.T.; Wilson, W.B. Neutron Production from (α,n) Reactions and Spontaneous Fission in ThO2, UO2, and (U,Pu)O2 Fuels; LA-8869-MS; Los Alamos National Laboratory: Los Alamos, NM, USA, 1981.
- Manero, F.; Konshin, V.A. Status of the energy-dependent ν-values for the heavy isotopes (Z > 90) from thermal to 15 MeV and of ν-values for spontaneous fission. At. Energy Rev. 1972, 10, 637–756. Available online: https://www-nds.iaea.org/publications/indc/indc-nds-0034/ (accessed on 14 August 2021).
- Ensslin, N. The origin of neutron radiation. In Passive Nondestructive Assay of Nuclear Materials; Reilly, D., Ensslin, N., Smith, H., Jr., Eds.; NUREG/CR-5550, LA-UR-90-732; Los Alamos National Laboratory: Los Alamos, NM, USA, 1991; pp. 337–356. [Google Scholar]
- Ensslin, N.; Harker, W.C.; Krick, M.S.; Langner, D.G.; Pickrell, M.M.; Stewart, J.E. Application Guide to Neutron Multiplicity Counting; LA-13422-M; Los Alamos National Laboratory: Los Alamos, NM, USA, 1998; p. 43.
- Shores, E.F. Data updates for the SOURCES-4A computer code. Nucl. Instrum. Methods Phys. Res. B 2001, 179, 78–82. [Google Scholar] [CrossRef]
- Verbeke, J.; Hagmann, C.; Wright, D. Simulation of Neutron and Gamma Ray Emission from Fission and Photofission; UCRL-AR-228518; Lawrence Livermore National Laboratory: Livermore, CA, USA, 2014.
- Wilson, W.; Perry, R.; Charlton, W.; Parish, T. Sources: A code for calculating (alpha, n), spontaneous fission, and delayed neutron sources and spectra. Prog. Nucl. Energy 2009, 51, 608–613. [Google Scholar] [CrossRef]
- Santi, P.; Miller, M. Reevaluation of Prompt Neutron Emission Multiplicity Distributions for Spontaneous Fission. Nucl. Sci. Eng. 2008, 160, 190–199. [Google Scholar] [CrossRef]
- White, R.H. Topsy, A Remotely Controlled Critical Assembly Machine. Nucl. Sci. Eng. 1956, 1, 53–61. [Google Scholar] [CrossRef]
- Koch, L.J.; Paxton, H.C. Fast reactors. Annu. Rev. Nucl. Sci. 1959, 9, 437–472. [Google Scholar] [CrossRef]
- National Nuclear Data Center. NuDat 2.8 Database. Brookhaven National Laboratory. Available online: www.nndc.bnl.gov/nudat2/ (accessed on 12 August 2021).
- Wang, M.; Audi, G.; Wapstra, A.H.; Kondev, F.G.; MacCormick, M.; Xu, X.; Pfeiffer, B. The AME2012 atomic mass evaluation (II): Tables, graphs and references. Chin. Phys. C 2012, 36, 1603–2014. [Google Scholar] [CrossRef]
- Stout, J.W.; Jones, W.M. A Calorimetric Determination of the Energy Produced by Plutonium (239). Phys. Rev. 1947, 71, 582–585. [Google Scholar] [CrossRef]
| Nuclide | Pmin (mW) from Circa 1960s Neutron Physics Data 1 | Pmin (mW) from JENDL 4.0 Neutron Physics Data |
|---|---|---|
| U-233 | n/a | 14 |
| U-235 | 11 | 9 |
| Np-237 | n/a | 11 |
| Pu-239 (α) | 17 | 16 |
| Pu-239 (δ) | 14 | 13 |
| Am-242m | n/a | 11 |
| Moderator | Diffusion Time (s) 1 | Minimum Power (nW) |
|---|---|---|
| Light water | 0.00021 | 150 |
| Heavy water | 0.043 | 0.75 |
| Beryllium | 0.0039 | 8.2 |
| Graphite | 0.017 | 1.9 |
| Nuclide | Total Half-Life (y) | Branching Factor (%) | Neutrons Released per Fission, νsp | Neutron Yield (n/(g·s)) |
|---|---|---|---|---|
| U-233 | 1.59 × 105 | <6 × 10−11 | 1.76 | 3.76 × 10−4 |
| U-235 | 7.04 × 108 | 7 × 10−9 | 1.86 | 1.04 × 10−5 |
| U-238 | 4.46 × 109 | 5 × 10−5 | 2.01 | 1.25 × 10−2 |
| Np-237 | 2.14 × 106 | 2.1 × 10−10 | 2.05 | 1.12 × 10−4 |
| Pu-239 | 2.411 × 104 | 3 × 10−10 | 2.16 | 1.49 × 10−2 |
| Am-242m | 141 | <4.7 × 10−9 | 2.34 | 4.26 × 101 |
| Cf-252 | 2.65 | 3.1 | 3.765 | 2.32 × 1012 |
| Nuclide | Pmin (µW/g) 1 | SP (µW/g) |
|---|---|---|
| U-233 | 0.724 | 280 |
| U-235 | 0.17 | 0.0599 |
| Np-237 | 0.337 | 20.7 |
| Pu-239 (α) | 0.648 | 1930 |
| Pu-239 (δ) | 1.26 | 1930 |
| Am-242m | 0.51 | 4600 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Holbert, K.E. A Study of the Minimum Thermal Power of a Nuclear Reactor. J. Nucl. Eng. 2021, 2, 412-421. https://doi.org/10.3390/jne2040031
Holbert KE. A Study of the Minimum Thermal Power of a Nuclear Reactor. Journal of Nuclear Engineering. 2021; 2(4):412-421. https://doi.org/10.3390/jne2040031
Chicago/Turabian StyleHolbert, Keith E. 2021. "A Study of the Minimum Thermal Power of a Nuclear Reactor" Journal of Nuclear Engineering 2, no. 4: 412-421. https://doi.org/10.3390/jne2040031
APA StyleHolbert, K. E. (2021). A Study of the Minimum Thermal Power of a Nuclear Reactor. Journal of Nuclear Engineering, 2(4), 412-421. https://doi.org/10.3390/jne2040031






